第四章答案(完整资料).doc

第4章练习题参考答案第4章练习题参考答案第四章练习题参考答案【4-1】已知某轴心受拉杆的截面尺寸300400b h mm mm=?，配有820φ钢筋，混凝土和钢筋的材料指标为：22.0/tf N mm =，42.110cE =?2/N mm ，2270/yfN mm =，522.110/s E N mm =?。

试问此构件开裂时和破坏时的轴向拉力分别为多少？【解】配820φ钢筋，查混凝土结构设计规范（GB50010-2010）附录A ，表A.0.1得22513sA mm =。

25132.09%3.0%300400s A bh ρ===300400120000A bh mm ==?=，542.110102.110s E c E E α?===?（1）由式（4-5），开裂荷载为 0(1)(1)tcrcEt tEN E A f A αρεαρ=+=+2.0120000(1100.0209)=??+?290160N= 209.16kN =（2）由式（4-7），构件的抗拉极限承载力为2702513678510678.51tuysN f A N kN ==?==【4-2】已知某钢筋混凝土轴心受拉构件，截面尺寸为200300b h mm mm ?=?，构件的长度2000l mm =，混凝土抗拉强度22.95/tfN mm =，弹性模量422.5510/cEN mm =?，纵向钢筋的截面积2615sAmm =，屈服强度2270/yfN mm =，弹性模量522.110/sEN mm =?，求（1）若构件伸长0.2mm ，外荷载是多少？混凝土和钢筋各承担多少外力？（2）若构件伸长0.5mm ，外荷载是多少？混凝土和钢筋各承担多少外力？（3）构件开裂荷载是多少？即将开裂时构件的变形是多少？（4）构件的极限承载力是多少？【解】615 1.025% 3.0%200300s A bh ρ===220030060000A bh mm ==?=542.1108.2352.5510s E c E E α?===?，442.95 1.157102.5510t t c f E ε-===??（1）○1由0.2l mm ?=可知，构件的应变为 440.2 1.010 1.157102000t l l εε--?===?<=? 构件未开裂，处于弹性工作状态，csεεε==，构件所受的拉力为44(1) 2.551060000(18.235 1.025%) 1.010t c E N E A αρε-=+=+3165.9110N=?165.91kN=○2此时混凝土承担的外力 4432.5510 1.010********.010153.0ts c N E A N kNε-===?=○3钢筋承担的外力165.91153.012.91ts t tc N N N kN=-=-=（2）○1由0.5l mm ?=可知，构件的应变为4400.52.510 1.157102000t l l εε--?===?>=?，且35270 1.286102.110y y sf E εε-<===??构件开裂，钢筋未屈服，sεε=，构件所受的拉力为542.110 2.51061532287.532.29t s s N E A N kNε-====○2此时，混凝土开裂，在开裂处混凝土应力0c σ= ○3钢筋的应力5422.110 2.51052.5/s s E N mm σε-=== （3）○1开裂荷载为 0(1)tcrcEt N E A αρε=+442.551060000(18.235 1.025%) 1.15710-=+191.96kN=○2即将开裂时构件的变形 41.1571020000.23t l l mm ε-?=?=??=（4）构件的极限承载力为 270615166050166.05tuysN f A N kN ==?==【4-3】某钢筋混凝土轴心受拉构件的截面尺寸为300300b h mm mm ?=?，配有822的纵向受力钢筋，已知22.3/t f N mm =，422.410/c E N mm =?，2345/y f N mm =，521.9610/s E N mm =?。

微观经济学第四章习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第四章生产论1. 下面(表4—1)是一张一种可变生产要素的短期生产函数的产量表：可变要素的数量可变要素的总产量可变要素的平均产量可变要素的边际产量122103244125606677080963(2)该生产函数是否表现出边际报酬递减如果是，是从第几单位的可变要素投入量开始的解答：(1)利用短期生产的总产量(TP)、平均产量(AP)和边际产量(MP)之间的关系，可以完成对该表的填空，其结果如表4—2所示：可变要素的数量可变要素的总产量可变要素的平均产量可变要素的边际产量1222212610324812448122456012126661167701048708\f(34)09637－7高点以后开始逐步下降的这样一种普遍的生产现象。

本题的生产函数表现出边际报酬递减的现象，具体地说，由表4—2可见，当可变要素的投入量从第4单位增加到第5单位时，该要素的边际产量由原来的24下降为12。

2. 用图说明短期生产函数Q＝f(L，eq \o(K,\s\up6(－)))的TPL曲线、APL 曲线和MPL曲线的特征及其相互之间的关系。

解答：短期生产函数的TPL曲线、APL曲线和MPL曲线的综合图如图4—1所示。

图4—1由图4—1可见，在短期生产的边际报酬递减规律的作用下，MPL曲线呈现出先上升达到最高点A以后又下降的趋势。

从边际报酬递减规律决定的MPL曲线出发，可以方便地推导出TPL 曲线和APL曲线，并掌握它们各自的特征及相互之间的关系。

关于TPL 曲线。

由于MPL＝eq \f(d TP L,d L)，所以，当MP L＞0时，TP L曲线是上升的；当MPL ＜0时，TPL曲线是下降的；而当MPL＝0时，TPL曲线达最高点。

换言之，在L＝L3时，MPL曲线达到零值的B点与TPL曲线达到最大值的B′点是相互对应的。

习 题 答 案4.1 已知钢筋混凝土矩形梁，安全等级为二级，处于一类环境，其截面尺寸b ×h =250mm×500mm ，承受弯矩设计值M =150kN ⋅m ，采用C30混凝土和HRB335级钢筋。

试配置截面钢筋。

【解】（1）确定基本参数查附表1-2和附表1-7及表4.3~4.4可知，C30混凝土f c =14.3N/mm 2，f t =1.43N/mm 2；HRB335级钢筋f y =300N/mm 2；α1=1.0，ξb =0.550。

查附表1-14，一类环境，c =25mm ，假定钢筋单排布置，取a s =35mm ，h 0=h –35=565mm 查附表1-18，%2.0%215.030043.145.045.0y t min >=⨯==f f ρ。

（2）计算钢筋截面面积由式（4-11）可得⎪⎪⎭⎫ ⎝⎛--=20c 10211bh f M h x α 3.1014652509.110.11015021146526=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯⨯--⨯=mm 8.25546555.00b =⨯=<h ξmm 由式（4-6-1）可得2y c 1s mm 12073003.1012503.140.1=⨯⨯⨯==f bx f A α2min m m 215500250%215.0=⨯⨯=bh ＞ρ（3）选配钢筋及绘配筋图查附表1-20，选用 20（A s =1256mm 2）。

截面配筋简图如图4-62所示。

习题4.1截面配筋简图4.2 已知钢筋混凝土挑檐板，安全等级为二级，处于一类环境，其厚度为80mm ，跨度l =1200mm ，如图4-59，板面永久荷载标准值为：防水层0.35kN/m 2，80mm 厚钢筋混凝土板（自重25kN/m 3），25mm 厚水泥砂浆抹灰（容重20kN/m 3），板面可变荷载标准值为：雪荷载0.4kN/m 2。

，板采用C25的混凝土，HRB335钢筋，试配置该板的受拉钢筋。

第四章 生产者行为理论一、单项选择题1.根据可变要素的总产量曲线、平均产量曲线和边际产量曲线之间的关系，可将生产划分为三个阶段，任何理性的生产者都会将生产选择在（ ）。

A.第Ⅰ阶段；B.第Ⅱ阶段；C.第Ⅲ阶段。

2.在维持产量水平不变的条件下，如果企业增加二个单位的劳动投入量就可以减少四个单位的资本投入量，则有（ ）。

A.RTS LK =2，且2=LK MP MP ； B.RTS LK =21，且2=L K MP MP ； C.RTS LK =2，且21=L K MP MP ； D ．RTS LK =21，且21=L K MP MP 。

3.在以横坐标表示劳动数量，纵坐标表示资本数量的平面坐标中所绘出的等成本线的斜率为（ ）。

A.γω；B.- γω；C.ωγ；D.- ωγ。

4.当边际产量大于平均产量时（ ）。

A.平均产量递减；B.平均产量递增；C.平均产量不变；D.总产量递减。

5.如图所示，厂商的理性决策应在( ) A ．0＜L ＜7；B.4.5＜L ＜7；C ．3＜L ＜4.5；D.0＜L ＜4.5。

6.已知某企业的生产函数Q=10K L （Q 为产量，L 和K 分别为劳动和资本），则（ ）。

A ．生产函数是规模报酬不变；B ．生产函数是规模报酬递增；C ．生产函数是规模报酬递减；D ．无法判断7.等成本曲线绕着它与纵轴Y的交点向外移动表明( )。

A.生产要素Y的价格下降了；B.生产要素x的价格上升了；C. 生产要素x的价格下降了；D. 生产要素Y的价格上升了。

8.总成本曲线与可变成本曲线之间的垂直距离（）。

A.随产量减少而减少；B.等于平均固定成本；C.等于固定成本；D.等于边际成本。

9.随着产量的增加，短期固定成本（）。

A．增加；B．减少；C．不变；D．先增后减。

10.已知产量为8个单位时，总成本为80元，当产量增加到9个单位时，平均成本为11元，那么，此时的边际成本为（）。

A．1元；B．19元；C．88元；D．20元。

第四章多组分系统热力学4.1有溶剂A与溶质B形成一定组成的溶液。

此溶液中B的浓度为c B，质量摩尔浓度为b B，此溶液的密度为。

以M A，M B分别代表溶剂和溶质的摩尔质量，若溶液的组成用B的摩尔分数x B表示时，试导出x B与c B，x B与b B之间的关系。

解：根据各组成表示的定义4.2D-果糖溶于水（A）中形成的某溶液，质量分数，此溶液在20℃时的密度。

求：此溶液中D-果糖的（1）摩尔分数；（2）浓度；（3）质量摩尔浓度。

解：质量分数的定义为4.3 在25℃，1 kg 水（A ）中溶有醋酸（B ），当醋酸的质量摩尔浓度b B 介于和之间时，溶液的总体积求：（1） 把水（A ）和醋酸（B ）的偏摩尔体积分别表示成b B 的函数关系。

（2）时水和醋酸的偏摩尔体积。

解：根据定义当时4.460℃时甲醇的饱和蒸气压是84.4 kPa ，乙醇的饱和蒸气压是47.0 kPa 。

二者可形成理想液态混合物。

若混合物的组成为二者的质量分数各50 %，求60℃时此混合物的平衡蒸气组成，以摩尔分数表示。

解：甲醇的摩尔分数为58980049465004232500423250....x B =+=4.580℃时纯苯的蒸气压为100 kPa，纯甲苯的蒸气压为38.7 kPa。

两液体可形成理想液态混合物。

若有苯-甲苯的气-液平衡混合物，80℃时气相中苯的摩尔分数，求液相的组成。

解：4.6在18℃，气体压力101.352 kPa下，1 dm3的水中能溶解O2 0.045 g，能溶解N2 0.02 g。

现将 1 dm3被202.65 kPa空气所饱和了的水溶液加热至沸腾，赶出所溶解的O2和N2，并干燥之，求此干燥气体在101.325 kPa，18℃下的体积及其组成。

设空气为理想气体混合物。

其组成体积分数为：，解：显然问题的关键是求出O2和N2的亨利常数。

4.7 20℃下HCl 溶于苯中达平衡，气相中HCl 的分压为101.325 kPa 时，溶液中HCl 的摩尔分数为0.0425。

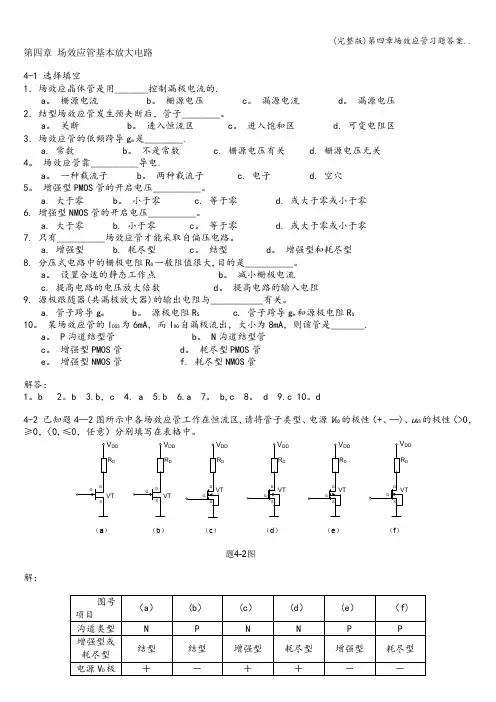
第四章 场效应管基本放大电路4-1 选择填空1．场效应晶体管是用_______控制漏极电流的.a 。

栅源电流b 。

栅源电压c 。

漏源电流d 。

漏源电压 2．结型场效应管发生预夹断后，管子________。

a 。

关断b 。

进入恒流区c 。

进入饱和区 d. 可变电阻区 3．场效应管的低频跨导g m 是________.a. 常数 b 。

不是常数 c. 栅源电压有关 d. 栅源电压无关 4。

场效应管靠__________导电.a 。

一种载流子b 。

两种载流子 c. 电子 d. 空穴 5。

增强型PMOS 管的开启电压__________。

a. 大于零 b 。

小于零 c. 等于零 d. 或大于零或小于零 6. 增强型NMOS 管的开启电压__________。

a. 大于零b. 小于零 c 。

等于零 d. 或大于零或小于零 7. 只有__________场效应管才能采取自偏压电路。

a. 增强型b. 耗尽型 c 。

结型 d 。

增强型和耗尽型 8. 分压式电路中的栅极电阻R G 一般阻值很大,目的是__________。

a 。

设置合适的静态工作点b 。

减小栅极电流c. 提高电路的电压放大倍数 d 。

提高电路的输入电阻 9. 源极跟随器(共漏极放大器)的输出电阻与___________有关。

a. 管子跨导g m b 。

源极电阻R S c. 管子跨导g m 和源极电阻R S 10。

某场效应管的I DSS 为6mA ，而I DQ 自漏极流出，大小为8mA ，则该管是_______.a 。

P 沟道结型管b 。

N 沟道结型管c 。

增强型PMOS 管d 。

耗尽型PMOS 管e 。

增强型NMOS 管 f. 耗尽型NMOS 管解答：1。

b 2。

b 3.b ，c 4. a 5.b 6.a 7。

b,c 8。

d 9.c 10。

d4-2 已知题4—2图所示中各场效应管工作在恒流区,请将管子类型、电源V DD 的极性（+、—)、u GS 的极性（>0，≥0，〈0,≤0，任意）分别填写在表格中。

习题4.1选择填空1、选用差分放大电路的原因是 A 。

A 、克服温漂B 、 提高输入电阻C 、稳定放入倍数2、用恒流源取代长尾式差分放大电路中的发射极电阻Re ，将使电路的 B 。

A 、差模放大倍数数值增大B 、抑制共模信号能力增强C 、差模输入电阻增大 3、差动放大器中的差模输入是指两输入端各加大小___相等_____、相位___相反____的信号。

4、设差放电路的两个输入端对地的电压分别为v i1和v i2，差模输入电压为v id ，共模输入电压为v ic ，则当v i1=50mV ，v i2=50mV 时，v id =_0mV __，v ic =_50mV __；当v i1=50mV ，v i2=-50mV 时，v id =_100mA __，v ic =_0mA__；当v i1=50mV ，v i2=0V 时，v id =_50mV __，v ic =_25mA __。

5、电流源常用于放大电路，作为_A ___（A.有源负载，B.电源，C.信号源），使得放大倍数__A __（A.提高，B.稳定）。

6、电压放大电路主要研究的指标是 a 、 b 、 c ；功率放大电路主要研究的指标是 d 、 e 、 f 、 g 、（a 电压放大倍数 b 输入电阻 c 输出电阻 d 输出功率 e 电源提供的功率 f 效率 g 管耗）7、功率放大电路中，___甲类____功率放大电路导通角最大；_____乙类___功率放大电路效率较高。

（甲类、乙类、甲乙类） 8、甲类功放效率低是因为 B 。

A 、只有一个功放管B 、 静态电流过大C 、管压降过大4.1对称差动放大电路如题图 4.1所示。

已知晶体管1T 和2T 的50=β，并设U BE (on )=0.7V,r bb ’=0,r ce =∞。

(1)求V 1和V 2的静态集电极电流I CQ 、U CQ 和晶体管的输入电阻r b’e 。

(2)求双端输出时的差模电压增益A ud ，差模输入电阻R id 和差模输出电阻R od 。

第四章公司法练习历年曾考试题一、单选题1.根据我国《公司法》的规定，有限责任公司全体股东的首次出资额不得低于注册资本的一定比例，该比例为( B )A.10％B.20％C.35％D.50％2.下列企业可以采用募集方式设立的是( D )A.个人独资企业B.合伙企业C.有限责任公司D.股份有限公司3.公司股东会作出下列决议后，依法不需要．．．通知并公告债权人的是( C )A.合并B.分立C.增加注册资本D.减少注册资本4.下列关于公司债券的说法正确的是( B )A.公司债券无风险B.公司债券利率固定C.可转换公司债券到期可以自动转为股票D.只有股份有限公司才能发行公司债券5.下列选项中不属于．．．债权人会议职权的是( C )A.核查债权B.决定继续或停止债务人的营业C.调查债务人财产状况，制作财产状况报告D.申请人民法院更换管理人，审查管理人的费用和报酬6.我国《公司法》规定，有限责任公司股东采用分期缴纳股款的，应当自公司成立之日起的一定年限内缴足，该年限为( B )A.1年B.2年C.3年D.4年7.有限责任公司股东向股东以外的人转让股权，依法应当经其他一定比例的股东同意，该比例为( B )A.过三分之一B.过二分之一C.过三分之二D.全体8.我国《公司法》规定，有限责任公司的股东人数不得超过( B )A.20人B.50人C.100人D.200人9.我国《公司法》规定，公司的法定公积金累计额为公司注册资本一定比例以上的，可以不再提取，该比例为( C )A.10％B.25％C.50％D.60％10.下列关于公司合并效力的表述不正确．．．的是（ B ）A.因合并而解散的公司，在解散时无须经过清算程序B.因合并而解散的公司，在解散时必须经过清算程序C.股东收容D.权利义务概括承受11.根据我国《公司法》的规定，下列事项不属于．．．股东会职权的是（ D ）A.决定公司的经营方针和投资计划B.对发行公司债券作出决议C.修改公司章程D.决定公司内部管理机构的设置12.某股份有限公司的股东大会拟对为公司的股东甲提供担保事项进行表决，下列有关该事项表决通过的表述中，符合《公司法》规定的是（ D ）A.该表决事项由公司全体股东所持表决权的过半数通过B.该表决事项由出席会议的股东所持表决权的过半数通过C.该表决事项由除甲以外股东所持表决权的过半数通过D.该表决事项由出席会议的除甲以外的股东所持表决权的过半数通过13.根据我国《公司法》的规定，一人有限责任公司注册资本的法定最低限额为人民币( B )A.3万元B.10万元C.50万元D.500万元14.我国《公司法》规定了有限责任公司和股份有限公司的最低注册资本额，但允许股东或发起人分期缴纳股款。

思考题：题4.1.1 按触发方式触发器可分为、和三类。

答：电平触发、主从触发、边沿触发。

题4.1.2 由与非门构成的RS锁存器输入信号不允许同时为。

答：0题4.1.3 触发器有个稳定状态，它可记录位二进制码，存储8位二进制信息需要个触发器。

答：2、1、8。

题 4.1.4 如果由或非门构成的RS锁存器输入信号同时为1，此时输出的原端Q和非端Q 为。

然后改变两输入信号为0，输出原端Q和非端Q为。

答：0、不定（0，1或1，0）题4.2.1 在图4.2.1（b）中将C1改为C2，当C2有效时，1S、1R和C2 。

答：无关。

题4.2.2 同步RS触发器和RS锁存器主要区别是。

答：触发信号。

题4.2.3 保证同步D触发器的输出稳定，要求输入有效信号的高电平至少需要。

答：4t pd。

题4.2.4 同步触发器的缺点是。

（A）抗干扰能力差（B）空翻现象（C）多次翻转（D）约束条件答：A、B、C、D。

题4.2.5 同步D触发器和同步RS触发器相同之处是，不同之处是。

（A）空翻现象，约束条件（B）同步信号，空翻现象（C）约束条件，空翻现象（D）时钟，同步信号答：A题4.3.1 具有约束条件的触发器有。

（A）主从RS触发器（B）由主从RS触发器组成D触发器（C）主从JK触发器（D）由主从JK触发器组成D触发器答：A题4.3.2 具有一次翻转特性的触发器有。

（A）主从RS触发器（B）由主从RS触发器组成D触发器（C）主从JK触发器（D）由主从JK触发器组成D触发器答：Ｃ、D题4.3.3 主从RS触发器不能完全克服多次翻转的原因是。

（A）主从RS触发器的主触发器工作原理和同步RS触发器相同（B）主从RS触发器的从触发器工作原理和同步RS触发器相同（C）输入信号R不稳定12（D ）异步复位或置位不考虑时钟的到来就将输出清零或置1 答：A题4.3.4 主从触发器的时钟在高电平时，将输入信号传递到 。

在低电平时，将信号传递到 。

第四章公司法练习历年曾考试题一、单选题1.根据我国《公司法》的规定，有限责任公司全体股东的首次出资额不得低于注册资本的一定比例，该比例为( B )A.10％B.20％C.35％D.50％2.下列企业可以采用募集方式设立的是( D )A.个人独资企业B.合伙企业C.有限责任公司D.股份有限公司3.公司股东会作出下列决议后，依法不需要．．．通知并公告债权人的是( C )A.合并B.分立C.增加注册资本D.减少注册资本4.下列关于公司债券的说法正确的是( B )A.公司债券无风险B.公司债券利率固定C.可转换公司债券到期可以自动转为股票D.只有股份有限公司才能发行公司债券5.下列选项中不属于．．．债权人会议职权的是( C )A.核查债权B.决定继续或停止债务人的营业C.调查债务人财产状况，制作财产状况报告D.申请人民法院更换管理人，审查管理人的费用和报酬6.我国《公司法》规定，有限责任公司股东采用分期缴纳股款的，应当自公司成立之日起的一定年限内缴足，该年限为( B )A.1年B.2年C.3年D.4年7.有限责任公司股东向股东以外的人转让股权，依法应当经其他一定比例的股东同意，该比例为( B )A.过三分之一B.过二分之一C.过三分之二D.全体8.我国《公司法》规定，有限责任公司的股东人数不得超过( B )A.20人B.50人C.100人D.200人9.我国《公司法》规定，公司的法定公积金累计额为公司注册资本一定比例以上的，可以不再提取，该比例为( C )A.10％B.25％C.50％D.60％10.下列关于公司合并效力的表述不正确．．．的是（ B ）A.因合并而解散的公司，在解散时无须经过清算程序B.因合并而解散的公司，在解散时必须经过清算程序C.股东收容D.权利义务概括承受11.根据我国《公司法》的规定，下列事项不属于．．．股东会职权的是（ D ）A.决定公司的经营方针和投资计划B.对发行公司债券作出决议C.修改公司章程D.决定公司内部管理机构的设置12.某股份有限公司的股东大会拟对为公司的股东甲提供担保事项进行表决，下列有关该事项表决通过的表述中，符合《公司法》规定的是（ D ）A.该表决事项由公司全体股东所持表决权的过半数通过B.该表决事项由出席会议的股东所持表决权的过半数通过C.该表决事项由除甲以外股东所持表决权的过半数通过D.该表决事项由出席会议的除甲以外的股东所持表决权的过半数通过13.根据我国《公司法》的规定，一人有限责任公司注册资本的法定最低限额为人民币( B )A.3万元B.10万元C.50万元D.500万元14.我国《公司法》规定了有限责任公司和股份有限公司的最低注册资本额，但允许股东或发起人分期缴纳股款。

第四章的习题及答案4-1 设有一台锅炉，水流入锅炉是之焓为62.7kJ ·kg -1，蒸汽流出时的焓为2717 kJ ·kg -1，锅炉的效率为70％，每千克煤可发生29260kJ 的热量，锅炉蒸发量为4.5t ·h -1，试计算每小时的煤消耗量。

解：锅炉中的水处于稳态流动过程，可由稳态流动体系能量衡算方程：Q W Z g u H s +=∆+∆+∆221体系与环境间没有功的交换：0=s W ，并忽 动能和位能的变化， 所以： Q H =∆设需要煤mkg ，则有：%7029260)7.622717(105.43⨯=-⨯m解得：kg m 2.583=4-2 一发明者称他设计了一台热机，热机消耗热值为42000kJ ·kg -1的油料0.5kg ·min -1,其产生的输出功率为170kW ，规定这热机的高温与低温分别为670K 与330K ，试判断此设计是否合理？解：可逆热机效率最大，可逆热机效率：507.06703301112max =-=-=T T η 热机吸收的热量：1m in210005.042000-⋅=⨯=kJ Q热机所做功为：1m in 102000m in)/(60)/(170-⋅-=⨯-=kJ s s kJ W该热机效率为：486.02100010200==-=Q W η 该热机效率小于可逆热机效率，所以有一定合理性。

4-3 1 kg 的水在1×105 Pa 的恒压下可逆加热到沸点，并在沸点下完全蒸发。

试问加给水的热量有多少可能转变为功？环境温度为293 K 。

解：查水蒸气表可得始态1对应的焓和熵为：H 1＝83.93kJ/kg, S 1=0.2962kJ/kg.K 末态2对应的焓和熵为：H 2＝2675.9kJ/kg, S 2=7.3609kJ/kg.K)/(0.259293.839.267512kg kJ H H Q =-=-=)/(0.522)2962.03609.7(15.2930.25920kg kJ S T H W sys id =-⨯-=∆-∆=4-4如果上题中所需热量来自温度为533 K 的炉子，此加热过程的总熵变为多少？由于过程的不可逆性损失了多少功？ 解：此时系统的熵变不变)./(0647.7K kg kJ S sys =∆炉子的熵变为)./(86.45330.2592K kg kJ T H T Q S sur -=-=∆-==∆ )./(205.286.40647.7K kg kJ S t =-=∆ )/(0.646205.215.2930kg kJ S T W t l =⨯=∆=4-5 1mol 理想气体，400K 下在气缸内进行恒温不可逆压缩，由0.1013MPa 压缩到1.013MPa 。

第四章分子结构习题1。

是非判断题1-1化学键是相邻原子与原子（或离子与离子）之间的强烈相互作用。

1—2 50Sn2+是18+2电子构型，50Sn4+是18电子构型。

1-3 Al3+，Ba2+,Si(IV）的电子构型都属于8电子构型.1-4具有未成对电子的两个原子相互接近时可以形成稳定的共价键.1—5原子形成共价键的数目等于基态原子的未成对电子数。

1-6σ键的特点是原子轨道沿键轴方向重叠,重叠部分沿键轴呈圆柱形对称。

1-7一般来说，σ键的键能比π键键能小。

1—8 s电子与s电子配对形成的键一定是σ键，p电子与p电子配对形成的键一定为π键.1—9两个σ键组成一个双键.1-10键的强度与键长无关。

1-11所有非金属元素之间形成的化合物都不是离子化合物。

1—12μ＝0的分子，其化学键一定是非极性键.1—13共价键具有饱和性的原因在于每个原子提供一定数目的自旋方向相反的未成对电子。

1—14原子核外有几个未成对电子，就能形成几个共价键。

1-15共价键类型可以分为σ键和π键，π键的键能小于σ键的键能,因此π键的稳定性弱于σ键. 1—16烷烃分子中C-H键的键能为413 KJ·mol -1，因此提供413KJ·mol -1的能量能使甲烷和乙烷分子中C-H键断裂。

1-17沿键轴方向的s轨道和p轨道进行重叠可形成π键。

1-18原子轨道相互重叠应满足最大重叠原理，所以沿键轴以“头碰头”方式才能成键。

1—19原子轨道之所以要发生杂化是因为能增大成键能力。

1—20 sp3杂化是,s轨道的主量子数和p轨道的主量子数可以是不同的，也可以是相同的。

1-21 1个s轨道和3个p轨道，形成1个sp3杂化轨道.1-22在sp,sp2，sp3杂化中，杂化轨道的成键能力随s轨道成分增多而增强。

1-23发生轨道杂化的原子轨道可以具有成对电子。

1-24原子轨道发生杂化，若轨道上有孤对电子存在,这类杂化是不等性的。

1-25 NH3和H2O分子中的中心原子都是发生sp3杂化,但氧原子的2对孤对电子占据2 个杂化轨道而产生更大的斥力，使O—H键键角大于氨分之中N—H键键角。

60解 E(Y) E(2X) 2E(X) 2 xe xdx 2,E(Z) E(e 2X ) e 2x e x dx 1.33. 游客乘电梯从底层到电视塔顶观光 , 电梯于每个整点的第 5 分钟、第 25 分钟和第 55分钟从底层起行 . 假设一游客在早八点的第 X 分钟到达底层侯梯处 , 且 X 在区间[0, 60] 上服从均匀分布 . 求该游客等候电梯时间的数学期望 . 解已知X 在[0,60] 上服从均匀分布 , 其概率密度为1X -20 2 P0.40.30.3E(X)；E(2－3 X); E(X 2)；2 E(3X 25).解 由定义和数学期望的性质知E(X) ( 2) 0.4 0 0.3 2 0.30.2;E(2 3X) 2 3E(X ) 2 3 (0 2) 2.6; E(X 2) ( 2)2 0.4 0 20.3220 3 2.8 ;E(3X 2 5) 3E(X 2)53 2.8 5 13.4. 2. 设随机变量 X 的概率密度为xe, x 0, 1. 设随机变量 X 的分布律为习题 4-1f (x)2X求Y 2X 和Z e 2X的数学期望 .0,x ≤0.0,其它.记Y 为游客等候电梯的时间,则5 X, 0 X ≤5,25 X,5 X ≤25,Y g(X)55 X, 25 X ≤55,65 X,55 X ≤60.160 因此, E(Y) E[g(X)] g(x) f (x)dxg(x)dxf (x) 60, 0≤x≤60,60(A) 若 X ~ B(n, p),则E(X) np.c a ， Yc,X 1, X 0.于是 E(Y) (c a) P{ X 1} c P{X 0} ap c .据题意有 ap c a 10% , 因此应要求顾客角保费 c (0.1 p)a .习题 4-21. 选择题(1) 已知 E(X ) 1,D(X)3 则 E[3(X2 2)2] ().(A) 9.(B) 6.(C) 30.(D)36解 E[3(X 2)2] 3E(X24X 4)3[E(X 2)4E(X)4]3{D(X) [E(X)]2 4E(X) 4}3 (3 14 4) 36 .可见，应选 (D).(2) 设 X ~ B(n, p),E(X )6,D(X) 3.6 , 则有 ( ).(A) n 10, p 0.6 . (B) n 20, p 0.3 (C) n 15, p 0.4 .(D) n 12, p 0.5解 因为 X ~ B(n, p), 所以 E(X)=np,D(X)=np(1-p), 得到 np=6, np(1-p)=3n=15 , p=0.4 . 可见，应选 (C).(3) 设 X 与 Y 相互独立，且都服从2N( , 2) , 则有 ( ).(A) E(X Y) E(X) E(Y). (B) E(X Y) 2 .(C) D(X Y) D(X)D(Y).(D) D(XY) 2 2.解 注意到 E(X Y) E(X) E(Y) 0.由于 X 与Y 相互独立 ,所以D(X Y) D(X) D(Y) 222. 选 (D).(4) 在下列结论中 , 错误的是 ().6 . 解之 ,1 5 25(5 x)dx (25 x)dx600 5=11.67(分钟 )..14. 某保险公司规定 , 如果在一年内顾客的投保事件 A 发生 , 该公司就赔偿顾客 a 元. 若一年内事件 A 发生的概率为 p, 为使该公司受益的期望值等于 a 的 10％, 该公司应该要求 顾客交多少保险费？解 设保险公司要求顾客交保费 55(55 x)dx60 (65 x)dx55c 元. 1， 0, 则 P{X 1} p, P{X 0} p . 引入随机变量 事件A 发生, 事件A 不发生. 保险公司的受益值(B) 若 X ~ U 1,1 ，则 D(X) 0 . (C) 若 X 服从泊松分布 , 则 D(X) E(X).(D) 若 X ~ N( , 1 2), 则 X~ N (0,1) .14.3 又 X 1, X 2 , X 3相互独立 , 所以D(Y) D(X 1 2X 2 3X 3) D(X 1) 4D(X 2) 9D(X 3)1 3 4 4 9 20.914. 设两个随机变量 X 和 Y 相互独立 , 且都服从均值为 0, 方差为 的正态分布 , 求2 |X Y |的的期望和方差 .11 解 记U X Y . 由于X ~ N(0, ),Y ~ N(0, ),所以22E(U) E(X) E(Y) 0, D(U) D(X) D(Y) 1. 由此 U ~ N (0,1) . 进而3203~ U( 1,1) , 则 D(X) (b a)122. 已知 X, Y 独立, E(X)= E(Y)=2, E(X 2)= E(Y 2)=5,解 由数学期望和方差的性质有E(3X- 2Y)= 3E(X)-2 E (Y)=3×2-2×2=2,D(3X 2Y) 9D(X) 4D(Y)9 {E(X 2) [E(X)]2} 9 (5 4) 4 (5 4) X 2, X 3 相 互独立 , 其 中 2X 2解X221. 选(B).312求 E(3X-2Y),D(3X-2Y).3. 设随 机变 量 2X 2 ~ N (0, 22), X 3解 由题设知X 1,~ P (3), 记 Y X 14 {E(Y 2) [E(Y)]2}13.X 1 服从区 间[0, 6]上的均匀分布, 3X 3 ,求 E(Y)和 D(Y) .E(X 1) 3, D(X 1) E(X 3)(6 0)2 3,12 113,D(X 3)E(X 2) 0,D(X 2 ) 4,由期望的性质可得E(Y) E(X 12X 2 3X 3) E(X 1) 2E(X 2 ) 3E(X 3)5. 设随机变量X ~U[ 1,2], 随机变量1, X 0,Y 0, X 0,1, X 0. 求期望E(Y) 和方差D(Y) .解因为X的概率密度为1, 1≤x≤2,f X (x) 3于是Y的分布率为P{Y 1} P{XP{YP{Y 1} P{ X因此0, 其它.0110}-f X(x)dx dx-133 0}P{ X 0} 0 ,+2120}0 f X (x)dx dx0033 21 x22 E(|X Y|) E(|U |) |x| e 2dx 0 xe E(|U |2) E(U2) D(U ) [E(U)]22x2 dx02故而D(|X Y|) D(|U|) E(|U|2) [E(|U |)]22e1.2212故有6. 设随机变量U1,X1,求E(X+Y), D(X+Y).E(Y)E(Y2 ) (1)20212D(Y) E(Y2 )[E(Y)]2321.389.在区间[-2, 2]上服从均匀分布若U ≤1, 若U1.9, 随机变量1, 若U≤1, Y 1,若U 1.解(1) 随机变量(X, Y) 的可能取值为(-1,- 1),(- 1,1),(1,- 1),(1,1).-11 1P{X 1,Y 1}P{U ≤ 1,U ≤ 1} P{U ≤ 1}dx-24 4P{ X 1,Y 1}P{U ≤ 1,U1} 0,111 P{ X 1,Y1}P{U1,U ≤1}14dx , 221 1 P{X 1,Y1}P{U1,U1}dx .144 于是得 X 和Y 的联合密度分布X+Y-2 0 21 1 1 P{ X+Y =k}424(X+Y)24P{ (X+Y)2=k}1 1 22由此可见2 2 2 E(X Y) 0;D(X Y) E[( X Y)2] 2. 44习题 4-31. 选择题(1) 在下列结论中 , ( )不是随机变量 X 与 Y 不相关的充分必要条件(A) E(XY)=E(X)E(Y). (B) D(X+Y)=D(X)+D(Y).(C) Cov(X,Y)=0.(D) X 与 Y 相互独立 .解 X 与 Y 相互独立是随机变量 X 与 Y 不相关的充分条件 ,而非必要条件 . 选(D).(2) 设随机变量 X 和 Y 都服从正态分布 , 且它们不相关 , 则下列结论中不正确的是(C) X 与 Y 未必独立 . (D) 解 对于正态分布不相关和独立是等价的 ).(A) X 与 Y 一定独立 . (B) (X, Y)服从二维正态分布 X+Y 服从一维正态分布 . 选 (A).(2) X(3) 设(X, Y)服从二元正态分布, 则下列说法中错误的是( ).(A) ( X, Y) 的边缘分布仍然是正态分布 . (B) X 与 Y 相互独立等价于 X 与 Y 不相关 . (C) (X, Y)是二维连续型随机变量 .(D)由(X, Y)的边缘分布可完全确定 (X, Y)的联合分布 .解 仅仅由 (X, Y)的边缘分布不能完全确定 (X, Y)的联合分布 . 选 (D) 2 设 D(X)=4, D(Y)=6, ρXY =0.6, 求 D(3X-2Y) .解 D(3X 2Y) 9D(X) 4D(Y) 12Cov( X,Y)9 4 4 6 12 XY D(X) D(Y)36 24 12 0.6 2 6 24.727 .3. 设随机变量 X, Y 的相关系数为 0.5, E(X) E(Y) 0, E(X2) E(Y 2) 2,2求 E[(X Y)2] .2 2 2 解 E[(X Y)2] E(X 2) 2E(XY) E(Y 2)4 2[Cov( X,Y) E(X)E(Y)] 4 2 XY D(X) D(Y) 4 2 0.5 2 6.4. 设随机变量 (X, Y)的分布律为1 0 0.42 0 a 1 1 0.2 2 1 b 0.2 2b0.1. 由此可得边缘分布律5. 已知随机变量 ( X ,Y ) ~ N (0.5, 4; 0.1, 9; 0) , Z=2X- Y, 试求方差D(Z), 协方差X 1 2 Y 01P{X i} 0.6 0.4 P{Y j} 0.5 0.5E(Y) 0 0.5 1 0.5 0.5. 0.5 0.1. E(X) 1 0.6 2 0.4 1.4 , Cov( X,Y) E(XY) E(X)E(Y) 0.8 1.4 0.8 E(XY) 得 b 0.3. 进而 a于是故 若 E(XY)=0.8, 求常数 解 首先由p ij 1 得 a b 0.4. 其次由i 1 j1Cov( X ,Z) , 相关系数 ρXZ .解 由于 X,Y 的相关系数为零 , 所以 X 和 Y 相互独立(因X 和Y 服从正态分布 ). 因此D(Z) D(2X Y) 4D(X) D(Y) 4 4 9 25 ,Cov( X,Z) Cov( X,2X Y)2Cov(X,X) Cov( X,Y) .1 X Y关系数XY , Z . 求: (1) E(Z), D(Z)； (2) X 与 Z 的相关系数 ρXZ ; (3)问 XY2 3 2 X 与 Z 是否相互独立 ?为什么? 22 解 (1) 由于 X ~ N (1,32 ) , Y ~ N(0,42) , 所以(3) 由 XZ 0知X 与Z 不相关, 又 X 与Z 均服从正态分布 , 故知 X 与 Z 相互独立 .7．证明: 对随机变量 (X, Y), E(XY)=E(X)E(Y)或者 D(X Y)=D(X)+D(Y)的充要条件是 X 与 Y 不相关 .证 首先我们来证明 E(XY) E(X)E(Y) 和D(X Y) D(X) D(Y)是等 价的. 事实上, 注意到 D(X Y) D(X) D(Y) 2Cov( X,Y) . 因此D(X Y) D(X) D(Y) Cov( X,Y) 0 E(XY) E(X)E(Y).因此2D(X) Cov( X,Z) D(X) D(Z) 6. 设随机变量 (X, Y)服从二维正态分布 : XXZ0880.8 . 2522~ N(1,32), Y ~N(0, 42);X 与 Y 的相因此E(Z)D(Z) (2) 由于Cov( X,Z)所以XZXYD(X) D(Y) 12 346.Y 2) 1 13E(X)1E(Y) 2 1 3 11 2 0 1 3 Y 1 111Y 2) D(X) 9 D(Y) 42Cov( 3 X , 12Y) 1 16 1 Cov( X,Y) 1 4 1( 6) 3.4 33Y1 11 1) D(X) Cov( X,Y)9( 6)2 323 2E(X) 1,D(X) 9,E(Y) 0,D(Y) 16,Cov( X,Y)9 X Cov( X, 3 E(X 3D(X 3 1 9Cov( X,Z)D(X) D(Z)0.0,其次证明必要性 . 假设 E(XY)=E(X)E(Y), 则Cov( X,Y) E(XY) E(X)E(Y) 0 .最后证明充分性 . 假设 X 与 Y 不相关, 即 XY 0, 则Cov( X,Y)E(XY) E(X)E(Y) .总习题四1. 设 X 和 Y 是相互独立且服从同一分布的两个随机变量 , 已知 X 的分布律为 1 P{X i} ,i 1,2,3 . 又设U max{ X ,Y}, V min{ X,Y} .3(1) 写出二维随机变量 (U, V)的分布律 ;(2) 求 E(U ). 解 (1) 下面实际计算一下 P{U 1,V 3}.注意到U max{ X,Y}, V min{ X ,Y} , 因此P{U 1,V 3} P{X 1,Y 3}P{X 1}P{Y 1111(2) 由的分布律可得关于 U 的边缘分布律进而XYCov( X,Y)D(X) D(Y)0, 即 X 与 Y 不相关 .0 . 由此知P{X 3,Y 1} 3} P{X 3}P{Y 1} 21 3 5 22 所以 E(U) 112 33 5 22. 99 9 92. 从学校乘汽车到火车站的途中有 3 个交通岗 . 假设在各个交通岗遇到红灯的事件是2相互独立的 , 并且概率是 . 设 X 为途中遇到红灯的次数 , 求随机变量 X 的分布律、 分布函5数和数学期望 .3. 设随机变量 (X,Y) 的概率密度为212y 2, 0≤ y ≤x ≤1, f(x,y) 0, 求E(X), E(Y), E(XY), E(X 2 Y 2).X0 1 2 3P2754 36 8125 125 125 1252754 36 8k} 0 1 2 3125125 125 125解 令 X 表示途中遇到红灯的次数 , 由题设知 X ~ B(3,2) . 即 X 的分布律为53从而 E(X) kP{Xk16 5其它. 解 E(X) xf ( x, y)dxdy 1dx12y 2dy4x 4dxE(X) yf ( x, y)dxdy 0dx 0y12y 2dy 03x 4dxE(XY)xyf(x,y)dxdy1 dx 0x0 xy 12 y 2dy3x 5dxE(X 2 Y 2)(x 2 y 2) f (x,y)dxdy4. 设随机变量(4x5 12 x 5)dx 05 (X,Y)的概率密度为1sin( x f(x,y) 20,2 325 30 1 dx16 15 .(x 2y 2)35 3 612y 2dyy),π0≤x ≤ π, 0≤y ≤22 其它.求E(X),D(X),E(Y),D(Y),E(XY)和Cov(X,Y).于是有1. 22 所以协方差Cov( X,Y) E(XY) E(X)E(Y) 1.2 1615. 设随机变量 X 与 Y 独立, 同服从正态分布 N(0, ) , 求2(1) E(X Y); D( X Y)；(2) E (max{ X ,Y}); E(min{ X,Y}) .11解 (1) 记 X Y .由于 X ~ N(0, ),Y ~ N(0, ),所以E( ) E(X) E(Y) 0, D( ) D(X) D(Y) 1. 由此 ~ N(0,1).所以解 E(X)122xf(x,y)dxdy 2 2 x sin( x y)dxdy2E(X 2)2x f (x, y)dxdy2y)dxdy 2. 2 0 2 0x 2 sin(x x 2 E(| X Y |) E(| |)12|x| 2 e 2dx 2 0xe x 22 dx82D(X)2E(X 2)2[E(X)]22.16 22利用对称性 ,有E(Y) 4,D(Y) 16 2. 2 又E(XY)1 xyf ( x, y)dxdy22xy sin( x y)dxdy 1 2 1 2 02 xdx 02 xdx 02ysin(x y)dy 2 y[sin x cos y cos xsin y]dyE(XY) xyf (x, y)dxdy2e x 22E(| |2) 0E( 2) D( ) [E( )]21 故而D(| X Y|) D(| 22|) E(| |2) [E(| |)]2 1021.221 2所以 (2) 注意到max( X , Y) (X Y) |X Y | , min( X , Y)X Y |X Y|E[max( X , Y)] 112{E(X) E(Y) E[| X Y|]} 12 12 212,1 12{E(X) 6. 设随机变量 (X,Y) 的联合概率密度为 x y, 0≤ x ≤2,0≤y ≤2,f (x, y) 8E[min( X,Y)] E(Y) E[| X Y|]} 0, 求: E(X), E(Y), Cov( X,Y), ρXY , D (X+Y ). 解 其它.注意到 f (x, y)只在区域 G:0≤x ≤2,0≤y ≤ 2上不为零,x x y dxdyG 82x(xE(X) xf(x,y)dxdy 因而所以E(X 2)2 dx 02dxD(X)21 0 x(x y)dy 42 x f (x,y)dxdy22 10x (x y)dy 4 22E(X 2) [E(X)]27 1)dx 7623(x 35 72 3 622x )dx11 3612 2 1 22 44 dx xy(x y)dy (x x)dx .8 0 0 4 0337 2 2 5 11E(X) , E(Y 2) E(X 2) , D(Y) D(X) . 6 3 364 491 Cov( X,Y) E(XY) E(X)E(Y) ,3 3636Cov( X,Y) 1XYD(X) D(Y) 11 5D(X Y) D(X) D(Y) 2Cov( X,Y) .917. 设A, B 为随机事件 , 且 P(A) ,P(B|A)41， A 发生 , XY 0， A 不发生 ,Y1P(AB)1111 解由P(B| A)得 P(AB)P(A) , 进而由3P(A)334 121P(AB)1P(A|B)得 P(B) 2P(AB). 在此基础上可以求得2P(B)6(1) P{ X1,Y 1} P(AB)112111P{X 0,Y 1}P(AB) P(B)P(AB)6 12 121 11P{ X 1,Y 0}P(AB)P(A) P(AB)412 6P{X 0,Y 0} P(AB)1 P(AUB) 1 [P(A)P(B) P(AB)]求: (1) 二维随机变量 (X, Y)的概率分布 ; (2) X 与Y 的相关系数XY111 21[111]2.4 6 12 3故(X, Y)的概率分布为由对称性知E(Y)这样，11,P(A|B) , 令 321， B 发生 , 0， B 不发生 .21312111612(2) 由(1)易得关于X 和Y的边缘分布律X0131P{X=k}44Y0151P{Y=k}66因此E(X)1,E(X2)1,4422113D(X) E(X 2)[E(X)]241616E(Y) 1,E(Y2) 1,D(Y) E(Y2)2[E(Y)]2 1 1 566 6 36 36又由(X, Y)的分布律可得21111 E(XY) 0 0 0 1 1 011.3121212 12故111E(XY) E(X)E(Y) 12 4615XY D(X) D(Y)3515.16 3601X。

第四章 模拟调制系统习题答案4-1 根据图P4-1所示的调制信号波形，试画出DSB 及AM 信号的波形图，并比较它们分别解由包络检波后波形可知：DSB 解调信号已严重失真，而AM 的解调信号不失真。

所以，AM 信号采用包络检波法解调，DSB 信号不能采用包络检波法解调。

4-2 设某信道具有均匀的双边噪声功率谱密度P n (f)=0.5×10-3 W/H Z ，在该信道中传输抑制载波的双边带信号，并设调制信号m(t)的频带限制在5kH Z ，而载波为100kH Z ，调制信号的功率为10kW 。

若接收机的输入信号在加至解调器之前，先经过带宽为10kH z 的一理想带通滤波器，试问（1） 该理想带通滤波器中心频率为多大？ （2） 解调器输入端的信噪功率比为多少？ （3） 解调器输出端的信噪功率比为多少？（4） 求出解调器输出端的噪声功率谱密度，并用图形表示出来。

解 （1）为了保证信号顺利通过和尽可能的滤除噪声，带通滤波器的带宽等于已调信号宽度，即B=2f m =2×5=10kH Z ,其中心频率应选信号的载波频率100kH Z ,带通滤波器特性为 ()⎩⎨⎧≤≤=其它010595Zz kH f kH k H ω(2) S i =10kWN i =2BP n (f)=2×10×103×0.5×10-3=10W故输入信噪比 S i ／N i ＝1000 (3) 因有G DSB ＝２，故输出信噪比 002210002000i iS SN N =⨯=⨯=(4) 根据双边带解调器的输出噪声与输入噪声功率之间的关系，有W N N i 5.2410410===故()()Zn Zm n kH f f p H W f N f P 521105.021/1025.010525.2233300≤=⨯⨯=⨯=⨯⨯==--双其双边谱如右图所示4-3某线性调制系统的输出信噪比为20dB ，输出噪声功率为10-9W ，由发射机输出端到解调器输入端之间总的传输损耗为100dB ，试求：⑴DSB/SC 时的发射机输出功率； ⑵SSB/SC 时的发射机输出功率。

第四章复式记账法习题一、应掌握的名词记账方法复式记账法借贷记账法对应账户账户对应关系会计分录试算平衡二、填空题１．记账方法分为单式记账法和复式记账法两类。

２．借贷记账法是以“借”“贷”两个字作为记账符号的。

３．资产类账户的借方记录资产的增加，贷方记录资产的减少，期末余额一般在借方。

４．负债及所有者权益类账户的贷方记录负债及所有者权益的增加额，借方记录负债及所有者权益的减少额，期末余额一般在贷方。

５．借贷记账法的记账规则是有借必有贷，借贷必相等。

６．账户之间的应借应贷关系，称为账户的对应关系。

７．会计分录分为简单会计分录复合会计分录两种。

８．损益类账户期末一般无余额。

９．简单分录是指一借一贷的会计分录。

三、判断题１．所有经济业务的发生，都会引起会计等式两边发生变化。

（ B ）２．会计记账从产生开始，一直都是采用复式记账法。

（ B ）３．单式记账法是指所有的经济业务都记一笔账。

（ B ）４．复式记账法造成账户之间没有对应关系。

（ B ）５．借贷记账法账户的基本结构是：每一个账户的左边均为借方，右边均为贷方。

（ A ）６．一个账户的借方如果用来记录增加额，其贷方一定用来记录减少额。

（ A ）７．一般地说，各类账户的期末余额与记录增加额的一方都在同一方向。

（ A ）四、单项选择题１．复式记账法对每一项经济业务都以相等的金额，在（ D ）中进行登记。

Ａ．一个账户Ｂ．所有账户Ｃ．两个账户Ｄ．两个或两个以上的账户２．存在着对应关系的账户，称为（ D ）。

Ａ．平衡账户Ｂ．“Ｔ”字账户Ｃ．相关账户Ｄ．对应账户３．下列各项属于简单会计分录的有（ A ）会计分录。

Ａ．一借一贷Ｂ．一借多贷Ｃ．一贷多借Ｄ．多借多贷４．损益收入类账户期末应（ A ）。

Ａ．无余额Ｂ．借贷方都有余额Ｃ．借方有余额Ｄ．贷方有余额５．损益收入类账户的结构与所有者权益类账户的结构（ C ）。

Ａ．完全相反Ｂ．完全一致Ｃ．基本相同Ｄ．没有关系６．预付给供货单位的货款，可视同为一种（ D ）。

第4章传输介质与网络设备一、填空题1.网卡又叫网络接口卡，也叫网络适配器，主要用于服务器与网络连接，是计算机和传输介质的接口。

2.网卡通常可以按传输速率、总线接口和连接器接口方式分类。

3.双绞线可分为非屏蔽双绞线和屏蔽双绞线。

4.根据光纤传输点模数的不同，光纤主要分为单模和多模两种类型。

5.双绞线是由 4 对8 芯线组成的。

6.集线器在OSI参考模型中属于物理层设备，而交换机是数据链路层设备。

7.MAC地址也称物理地址，是内置在网卡中的一组代码，由12 个十六进制数组成，总长48 bit。

8.交换机上的每个端口属于一个冲突域域，不同的端口属于不同的冲突域，交换机上所有的端口属于同一个广播域域。

9.路由器上的每个接口属于一个广播域域，不同的接口属于不同的广播域和的冲突域。

二、选择题1.下列不属于网卡接口类型的是 D 。

A．RJ45 B．BNC C．AUI D．PCI2.下列不属于传输介质的是 C 。

A．双绞线B．光纤C．声波D．电磁波3.下列属于交换机优于集线器的选项是 D 。

A．端口数量多B．体积大C．灵敏度高D．交换传输4.当两个不同类型的网络彼此相连时，必须使用的设备是 B 。

A．交换机B．路由器C．收发器D．中继器5.下列 D 不是路由器的主要功能。

A．网络互连B．隔离广播风暴C．均衡网络负载D．增大网络流量三、判断题1.网卡是工作在物理层的设备。

（×）2.集线器是工作在物理层的设备。

（√）3.交换机是工作在数据链路层的设备。

（√）4.MAC地址是内置在网卡中的一组代码，由6个十六进制数组成。

（×）5.交换机的各端口工作在一个广播域中。

（√）6.双绞线内各线芯的电气指标相同，可以互换使用。

（×）第4章传输介质与网络设备7.双绞线的线芯总共有4对8芯，通常只用其中的2对。

（√）8.路由器和交换机都可以实现不同类型局域网间的互连。

（×）9.卫星通信是是微波通信的特殊形式。

【最新整理，下载后即可编辑】 第四章习题 4.6 求下列周期信号的基波角频率Ω和周期T 。

（1）t j e 100 （2）)]3(2cos[-t π （3）)4sin()2cos(t t + （4）)5cos()3cos()2cos(t t t πππ++（5）)4sin()2cos(t t ππ+ （6）)5cos()3cos()2cos(t t t πππ++ 4.7 用直接计算傅里叶系数的方法，求图4-15所示周期函数的傅里叶系数（三角形式或指数形式）。

图4-154.10 利用奇偶性判断图4-18示各周期信号的傅里叶系数中所含有的频率分量。

图4-184-11 某1Ω电阻两端的电压)(t u 如图4-19所示，（1）求)(t u 的三角形式傅里叶系数。

（2）利用（1）的结果和1)21(=u ，求下列无穷级数之和 ......7151311+-+-=S （3）求1Ω电阻上的平均功率和电压有效值。

（4）利用（3）的结果求下列无穷级数之和 (7)151311222++++=S图4-194.17 根据傅里叶变换对称性求下列函数的傅里叶变换（1）∞<<-∞--=t t t t f ,)2()]2(2sin[)(ππ（2）∞<<-∞+=t t t f ,2)(22αα （3）∞<<-∞⎥⎦⎤⎢⎣⎡=t t t t f ,2)2sin()(2ππ4.18 求下列信号的傅里叶变换（1）)2()(-=-t e t f jt δ （2）)1(')()1(3-=--t e t f t δ（3）)9sgn()(2-=t t f （4）)1()(2+=-t e t f t ε（5）)12()(-=tt f ε4.19 试用时域微积分性质，求图4-23示信号的频谱。

图4-234.20 若已知)(j ])([ωF t f F =，试求下列函数的频谱：（1）)2(t tf （3）dt t df t )( （5）)-1(t)-(1t f （8）)2-3(t f e jt （9）tdt t df π1*)(4.21 求下列函数的傅里叶变换（1）⎩⎨⎧><=0,1,)(jωωωωωF（3）)(3cos2)(jωω=F（5）ωωωω1)(2n-2sin2)(j+=∑=jneF4.23 试用下列方式求图4-25示信号的频谱函数（1）利用延时和线性性质（门函数的频谱可利用已知结果）。

第4章存储器1. 解释概念：主存、辅存、Cache、RAM、SRAM、DRAM、ROM、PROM、EPROM、EEPROM、CDROM、Flash Memory。

答：主存：主存储器，用于存放正在执行的程序和数据。

CPU可以直接进行随机读写，访问速度较高。

辅存：辅助存储器，用于存放当前暂不执行的程序和数据，以及一些需要永久保存的信息。

Cache：高速缓冲存储器，介于CPU和主存之间，用于解决CPU和主存之间速度不匹配问题。

RAM：半导体随机存取存储器，主要用作计算机中的主存。

SRAM：静态半导体随机存取存储器。

DRAM：动态半导体随机存取存储器。

ROM：掩膜式半导体只读存储器。

由芯片制造商在制造时写入内容，以后只能读出而不能写入。

PROM：可编程只读存储器，由用户根据需要确定写入内容，只能写入一次。

EPROM：紫外线擦写可编程只读存储器。

需要修改内容时，现将其全部内容擦除，然后再编程。

擦除依靠紫外线使浮动栅极上的电荷泄露而实现。

EEPROM：电擦写可编程只读存储器。

CDROM：只读型光盘。

Flash Memory：闪速存储器。

或称快擦型存储器。

2. 计算机中哪些部件可以用于存储信息？按速度、容量和价格/位排序说明。

答：计算机中寄存器、Cache、主存、硬盘可以用于存储信息。

按速度由高至低排序为：寄存器、Cache、主存、硬盘；按容量由小至大排序为：寄存器、Cache、主存、硬盘；按价格/位由高至低排序为：寄存器、Cache、主存、硬盘。

3. 存储器的层次结构主要体现在什么地方？为什么要分这些层次？计算机如何管理这些层次？答：存储器的层次结构主要体现在Cache-主存和主存-辅存这两个存储层次上。

Cache-主存层次在存储系统中主要对CPU访存起加速作用，即从整体运行的效果分析，CPU访存速度加快，接近于Cache的速度，而寻址空间和位价却接近于主存。

主存-辅存层次在存储系统中主要起扩容作用，即从程序员的角度看，他所使用的存储器其容量和位价接近于辅存，而速度接近于主存。