配电网三相潮流计算程序

配电网潮流计算的数学模型可以描述为，对于N 个节点的配电网，已知配电网的电源点电压，各节点的有功负荷和无功负荷值，配电网的拓扑结构信息以及各个支路的阻抗。

求得各节点的节点电压以及流经各支路的功率、各支路的电流，系统的有功损耗以及其他电力系统分析量。

配电网潮流算法实质上可以看做初始条件为根节点（电源节点电压）和节点负荷功率已知的情况下，根据前代更新和回退更新确定配电网的功率分布和电压分布。

因为配电网为辐射状，电能流动具有单向性，所以从电源点出发，上游支路向下游各个支路提供电能。

以支路功率表示的前推回代法的基本计算步骤如下：
（1）初始化迭代的有关参数，设置根节点电压，并为其他节点电压赋值，置迭代次数k 为零
（2）从数据文件读取各个节点注入的有功负荷功率以及其无功负荷功率；（3）从整个树状配电网结构的叶子节点往根节点计算，先子支路后父支路，利用式（2-1）、式（2-2）计算配电网的功率分布；
（4）从根节点出发，先父节点后子节点，利用式(3)计算配电网的电压分布；（5）判断相邻两次迭代电压差幅值的电流最大值max|ΔVi|是否小于给定的收敛数值ε。

如果满足收敛条件，则停止计算；反之则置k=k+1，返回步骤(3)重新执行。

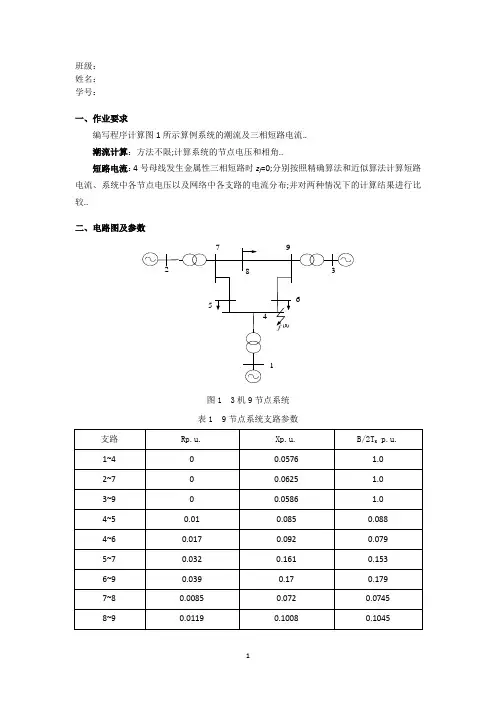
班级：姓名：学号：一、作业要求编写程序计算图1所示算例系统的潮流及三相短路电流..潮流计算：方法不限;计算系统的节点电压和相角..短路电流：4号母线发生金属性三相短路时z f=0;分别按照精确算法和近似算法计算短路电流、系统中各节点电压以及网络中各支路的电流分布;并对两种情况下的计算结果进行比较..二、电路图及参数图1 3机9节点系统表1 9节点系统支路参数表2 9节点系统发电机参数表3 9节点系统负荷参数三、计算步骤(1) 进行系统正常运行状态的潮流计算;求得(0)i U (2) 形成不含发电机和负荷的节点导纳矩阵Y N ；(3) 将发电机表示为电流源i I /i diE jx ''=和导纳i y 1/di jx '=的并联组合；节点负荷用恒阻抗的接地支路表示；形成包括所有发电机支路和负荷支路的节点导纳矩阵Y;即在Y N 中的发电机节点和负荷节点的自导纳上分别增加发电机导纳i y 和负荷导纳,LD i y *,,22LD i LDi LDiLD i i i S P jQ y V V -==； (4) 利用1Z Y-=;计算节点阻抗矩阵;从而得到阻抗矩阵中的第f 列；(5) 利用公式6-7或6-10计算短路电流；(6)利用公式6-8或6-11计算系统中各节点电压；(7)利用公式6-9计算变压器支路的电流；对输电线路利用П型等值电路计算支路电流..四、计算结果节点导纳矩阵Yn：Columns 1 through 50 -17.3611i 0 0 0 +17.3611i 00 0 -16.0000i 0 0 00 0 0 -17.0648i 0 00 +17.3611i 0 0 3.3074 -39.3089i -1.3652 +11.6041i0 0 0 -1.3652 +11.6041i 2.5528 -17.3382i0 0 0 -1.9422 +10.5107i 00 0 +16.0000i 0 0 -1.1876 + 5.9751i0 0 0 0 00 0 0 +17.0648i 0 0 Columns 6 through 90 0 0 00 0 +16.0000i 0 00 0 0 0 +17.0648i-1.9422 +10.5107i 0 0 00 -1.1876 + 5.9751i 0 03.2242 -15.8409i 0 0 -1.2820 + 5.5882i0 2.8047 -35.4456i -1.6171 +13.6980i 00 -1.6171 +13.6980i 2.7722 -23.3032i -1.1551 + 9.7843i-1.2820 + 5.5882i 0 -1.1551 + 9.7843i 2.4371 -32.1539i电压幅值：1.0400 1.0250 1.0250 1.0258 0.9956 1.0127 1.0258 1.0159 1.0324电压相角：0 0.1620 0.0814 -0.0387 -0.0696 -0.0644 0.0649 0.0127 0.0343节点有功：0.7164 1.6300 0.8500 0.0000 -1.2500 -0.9000 -0.0000 -1.0000 -0.0000节点无功：0.2705 0.0665 -0.1086 0.0000 -0.5000 -0.3000 -0.0000 -0.3500 -0.0000修正后的节点导纳矩阵Y：Columns 1 through 50 -20.6944i 0 0 0 +17.3611i 00 0 -19.3333i 0 0 00 0 0 -20.3982i 0 00 +17.3611i 0 0 3.3074 -39.3089i -1.3652 +11.6041i0 0 0 -1.3652 +11.6041i 3.8716 -17.6627i0 0 0 -1.9422 +10.5107i 00 0 +16.0000i 0 0 -1.1876 + 5.9751i0 0 0 0 00 0 0 +17.0648i 0 0 Columns 6 through 90 0 0 00 0 +16.0000i 0 00 0 0 0 +17.0648i-1.9422 +10.5107i 0 0 00 -1.1876 + 5.9751i 0 04.1321 -16.0184i 0 0 -1.2820 +5.5882i0 2.8047 -35.4456i -1.6171 +13.6980i 00 -1.6171 +13.6980i 3.7323 -23.6669i -1.1551 + 9.7843i-1.2820 + 5.5882i 0 -1.1551 + 9.7843i 2.4371 -32.1539i节点阻抗矩阵Z的第4列：0.0463 + 0.1252i0.0329 + 0.0693i0.0316 + 0.0707i0.0552 + 0.1493i0.0589 + 0.1204i0.0562 + 0.1226i0.0397 + 0.0838i0.0416 + 0.0814i0.0378 + 0.0845i精确计算结果：短路电流：模值：6.4459相角：-71.9365节点电压模值：0.1831 0.5687 0.5427 0.0000 0.1466 0.1506 0.4537 0.4463 0.4495支路电流：i j Iij1 4 0.5779-3.1264i2 7 1.3702-1.4433i3 9 0.64294-1.4808i4 5 -0.77968+1.5248i4 6 -0.6411+1.477i5 7 -0.89528+1.6436i6 9 -0.73353+1.5487i7 8 0.50734+0.10234i8 9 0.062766+0.056451i近似计算结果：短路电流：模值：6.2838相角：-69.7198节点电压模值：0.1611 0.5214 0.5157 0.0000 0.1827 0.1675 0.4227 0.4348 0.4217五、程序流程图六、程序及输入文件input_data.xls 文件：powerflow_cal.m 文件：l=9;%支路数n=9;%节点数m=6;%PQ节点数Yn=zerosn;%初始化节点导纳矩阵Y DATA1=xlsread'input_data.xls';1; %计算节点导纳矩阵Yfor k=1:li=DATA1k;1;j=DATA1k;2;R=DATA1k;3;X=DATA1k;4;B2=DATA1k;5;Yni;i=Yni;i+1i*B2+1/R+1i*X; Ynj;j=Ynj;j+1i*B2+1/R+1i*X; Yni;j=Yni;j-1/R+1i*X;Ynj;i=Ynj;i-1/R+1i*X;enddisp'节点导纳矩阵Yn：';dispYn;G=realYn;B=imagYn;DATA2=xlsread'input_data.xls';2;P=zeros1;n;Q=zeros1;n;U=ones1;n;P2:n=DATA22:n;3;Q4:n=DATA24:n;4;U1:3=DATA21:3;5;%设置节点电压初值e1=DATA21;5;e2:n=1.0;f1:n=0.0;%设置迭代次数t=0;tmax=10;while t<=tmax%计算fxa1:n=0.0;c1:n=0.0;for i=2:nfor j=1:nai=ai+Gi;j*ej-Bi;j*fj;ci=ci+Gi;j*fj+Bi;j*ej;endendfor i=2:ndeltaPi=Pi-ei*ai-fi*ci;endfor j=4:ndeltaQj=Qj-fj*aj+ej*cj;endfor k=2:3deltaU2k=Uk*Uk-ek*ek-fk*fk;endfx=deltaP2:n deltaQ4:n deltaU22:3';%计算雅克比矩阵Jfor i=2:nfor j=2:nif i~=jHi;j=-Gi;j*ei+Bi;j*fi;Ni;j=Bi;j*ei-Gi;j*fi;elseHi;j=-ai-Gi;i*ei+Bi;i*fi;Ni;j=-ci+Bi;i*ei-Gi;i*fi;endendendfor i=4:nfor j=2:nif i~=jMi;j=Bi;j*ei-Gi;j*fi;Li;j=Gi;j*ei+Bi;j*fi;elseMi;j=ci+Bi;i*ei-Gi;i*fi;Li;j=-ai+Gi;i*ei+Bi;i*fi;endendendfor i=2:3for j=2:nif i~=jRi;j=0;Si;j=0;elseRi;j=-2*ei;Si;j=-2*fi;endendendJ=H2:n;2:n N2:n;2:n;M4:n;2:n L4:n;2:n;R2:3;2:n S2:3;2:n;if maxabsfx<0.0001%输出结果break;else%求解修正方程获得dxdx=-J^-1*fx;dx=dx';e2:n=e2:n+dx1:n-1;f2:n=f2:n+dxn:2*n-1;t=t+1;endendif t>tmaxstr='潮流计算不收敛';dispstr;elsea1:n=0.0;c1:n=0.0;for i=1:nfor j=1:nai=ai+Gi;j*ej-Bi;j*fj; ci=ci+Gi;j*fj+Bi;j*ej;endendfor i=1:nUi=ei+1i*fi;ampi=absUi;argi=angleUi;Pi=ei*ai+fi*ci;Qi=fi*ai-ei*ci;enddisp'电压幅值：';dispamp;disp'电压相角：';disparg;disp'节点有功：';dispP;disp'节点无功：';dispQ;end%计算短路电流f=4;zf=0.0;%修正节点导纳矩阵Xd=DATA21:3;6;E=DATA21:3;7;for i=1:3Iii=Ei/1i*Xdi;endY=Yn;for i=1:3Yi;i=Yi;i+1/1i*Xdi;endfor j=4:nYj;j=Yj;j+-Pj+1i*Qj/Uj*Uj;enddisp'修正后的节点导纳矩阵Y：';Z=Y^-1;disp'节点阻抗矩阵Z的第4列：';dispZ:;4;%精确计算disp'精确计算结果：';U0=U;If=U0f/Zf;f+zf;amp=absIf;arg=atandimagIf/realIf;disp'短路电流：';disp'模值：';dispamp;disp'相角：';disparg;for i=1:nUi=U0i-Zi;f*If;amp=absU;enddisp'节点电压模值：';dispamp;disp'支路电流： ';str='i ''j '' Iij';dispstr;for k=1:li=DATA1k;1;j=DATA1k;2;r=DATA1k;3;x=DATA1k;4;z=r+1i*x;I=Ui-Uj/z;str=num2stri ' ' num2strj ' ' num2strI; dispstr;end%近似计算disp'近似计算结果：';U01:n=1.0;If=U0f/Zf;f+zf;amp=absIf;arg=atandimagIf/realIf;disp'短路电流：';disp'模值：';dispamp;disp'相角：';for i=1:nUi=U0i-Zi;f*If; amp=absU;enddisp'节点电压模值：'; dispamp;。

配电网三相潮流计算方法研究摘要：随着用户对供电可靠性及电能质量要求的提高，作为电力系统相对薄弱的配电网日益得到重视。

配网环网结构、辐射状运行，联络开关经常切换，运行方式多变，潮流计算作为电力系统分析最基本的计算，不仅可以计算网损、校验各种运行方式的合理性等，也可以为暂态计算提供初值，配电网基本潮流计算的重要性不言而喻。

关键词：配电网；三相潮流；计算方法1 配电网潮流计算的三相数学模型1.1 三相变压器模型基于相分量的适合配电网实际情况的变压器三相模型。

由于铁损与负载电流无关，基本上是一个恒定值，因此可以将铁损作为额外功率，并联在变压器等值电路的二次侧各相上。

变压器的节点电流向量和节点电压向量之间关系的变压器节点导纳矩阵YT，仍然可由变压器的原始导纳矩阵Y和变压器的节点-支路关联矩阵A共同表示为YT=AT×Y×A。

此时YT为6×6的矩阵。

但接线方式为Dyn11、Yyn0的变压器导纳矩阵中Y12和Y21是奇异的，而这对于前推回代算法来说，将不能进行正常的迭代。

将导纳矩阵用线分量和相分量混合表述，则可以解决这个问题。

1.2 单相变压器模型在实际生活中，配电网中的居民用户普遍采用的单相供电模式，是将单相变压器的高压侧连接在配电网的线电压上，然后从低压侧引出相线和零线对用户进行供电。

由此可建立单相变压器模型。

三相变压器的三相模型共考虑了两侧的六个节点，而单相变压器只有四个节点，故无法将求解三相变压器导纳矩阵的方法应用到单相变压器中。

对于单相变压器，本文采用了传统的T型等值电路。

实际上，对于基于电流的前推回代算法，进行反复迭代的主要根据是注入各个节点的电流和由其衍生的各支路电流。

而实践证明，采用双绕组变压器的传统型等值电路模型，完全可以得到准确有效的电流。

2 配电网潮流算法2.1 前推回代法前推回代法是配电网潮流计算中比较常用的方法，其基本思想是：首先将各节点电压设为额定电压值，并计算各节点的注入电流，然后从末端向首端前推求出配电网各支路电流；再依据各支路电流，从首端向末端回代求出各节点电压；反复进行前推回代计算，直至各节点的电压偏差满足迭代收敛条件为止。

电力系统潮流计算完整程序及详细理论说明——秦羽风在我刚开始学习潮流程序时,总是找不到一个正确的程序开始模仿学习。

后来经过多方努力，终于自己写出了一个结构清晰、完整的潮流程序。

此程序是一个通用的程序，只需要修改输入数据的子函数（PowerFlowsData_K)里面的母线、支路、发电机、负荷，就能算任意一个网络结构的交流系统潮流。

很适合初学者学习.为了帮助电力系统的同学一起学习,我将我编写的潮流计算程序分享下来给大家；此程序是在基于牛顿拉夫逊算法的基础上，编写的快速解耦算法。

每一个子程序我都有备注说明。

如果有不对的地方，希望大家指正！下文中呈现的顺序为：网络结构、子程序、主程序、运算结果、程序设计理论说明。

一、网络结构：5节点网络如下图。

二、子程序（共有9个子程序）子程序1：（其他系统，只需要修改Bus、Branch、Generator、Load,这四个矩阵就行了）function [Bus,Branch，Generator,Load］=PowerFlowsData_K％％节点数据% 类型:1-平衡节点；2-发电机PV节点；3—负荷PQ节点；4-发电机PQ节点;Bus=［% 类型电压相角1 1。

06 0；2 1 0；3 1 0;3 1 0；3 1 0]；％% 线路数据Branch=[% 发送接收电阻电感(电导电容)并联1 2 0.02 0.06 0 0.06；1 3 0。

08 0。

24 0 0。

05；2 3 0.06 0.18 0 0。

04;2 4 0。

06 0。

18 0 0.04;2 5 0.04 0.12 0 0。

03；3 4 0.01 0.03 0 0。

02;4 5 0.08 0.24 0 0.05］;%% 发电机数据Generator=［％节点定有功定无功(上限下限）无功1 0 0 5 —5;2 0。

4 03 —3];％％负载数据Load=［% 节点定有功定无功2 0.2 0.1；3 0。

中低压配电网的三项潮流计算方法作者：王耀贤来源：《科学与财富》2017年第25期摘要：配电网潮流计算是配电网分析的基础，配电网的网络重构，故障处理、无功优化和状态估计等都需要配电网潮流数据。

配电网的配电线路的总长度较输电线路要长且分支较多，配电线的线径比输电网细导致配电网的R/X比值较大，且线路的充电电容可以忽略。

正是由于配电线路的R/X较大，无法满足P， Q解耦条件X>R，所以在输电网中常用的快速解耦法（FDLF）在配电网中则常常难收敛。

关键词：潮流计算；中低配电网；程序设计；验证分析潮流计算是电力系统中应用最为广泛。

最基本和最重要的一种电气计算。

电力系统潮流计算的任务是根据给定的网络结构及其运行条件，求出整个网络的运行状态，其中包括各母线的电压、网络中的功率分布以及功率损耗等等。

潮流计算的结果，无论是对于现有系统运行方式的分析研究，还是对规划中供电方案的分析比较，都是必不可少的。

它为判别这些运行方式及规划设计方案的合理性、安全可靠性及经济性提供了定量分析的依据。

1.中低配电网的模型配电网中的元件有很多，如变压器、线路、电容器、调相机等。

1.1元件模型---电力线路的数学模型电力系统中线路模型是以电阻、电抗、电纳、电导来表示的等值电路。

在求得单位长度导线的电阻、电抗、电纳、电导后，就可作最原始的电力线路等值电路。

这是单相等值电路。

之所以用单相等值电路代表三相，一方面由于本设计中讨论的是三相对称运行方式，另一方面也因为设架空线路都已经整循环换位。

通常，由于线路的导线截面积选择，以晴朗天气不发生电晕为前提，而沿绝缘子的泄漏又很小。

短线路，就是指长度不超过100km的架空线路。

线路的电压不高时，这种线路导纳B的影响一般不大，可以忽略。

因此，这种线路的等值电路最简单。

中等长度线路，是指长度在 100-300km之间的架空线路，不超过100km的电力电缆线路。

这种线路的电纳一般不能省略。

这种线路的等值电路有П型等值电路和 T 型等值电路，其中，常用的是П型等值电路。

潮流计算程序(3.0版)说明1特点∙既可以用于高压输电网的潮流解算，又可以用于低压配电网的潮流解算，还可以同时解算输电网加配电网的混合潮流问题。

∙可以处理多平衡（机）节点问题，使用者只需输入各平衡节点的电压幅值和相位角，计算出的系统不平衡功率部分将自动在各平衡节点间进行分摊。

∙可以同时解算相互解列的几个子系统的潮流问题（只要每个子系统内均含有平衡节点），甚至某些子系统退化成孤立节点也不会影响其它子系统的潮流解算。

∙可以同时解算多配电馈线的潮流问题，而无需一个馈线一个馈线地分别计算。

∙由于该程序能够处理多平衡节点问题，故在解算具有多根节点和环状配电网潮流时，无需象以往方法那样只保留一个平衡节点，而将其余平衡节点全部人为地改成PV节点。

∙该版程序为PQ分解法。

2一般变量说明∙LINEMAX 程序所能处理的最大线路数，可以在#define说明语句中进行修改∙GENERA TORMAX 程序所能处理的最大发电机节点数，可以在#define说明语句中进行修改∙LOADMAX 程序所能处理的最大负荷节点数，可以在#define说明语句中进行修改∙NODEMAX 程序所能处理的最大系统节点总数，可以在#define说明语句中进行修改∙SWINGMAX 程序所能处理的最大平衡节点数，可以在#define说明语句中进行修改∙PVMAX 程序所能处理的最大PV节点数，可以在#define说明语句中进行修改∙NODEFACTOR 导纳矩阵的上三角阵中程序所能处理的最大非零非对角元素的个数相对于最大节点数（NODEMAX）的倍数∙Deg_to_Rad 度到弧度的转换系数，在#define说明语句中定义∙Rad_to_Deg 弧度到度的转换系数，在#define说明语句中定义∙Num_Line 系统的实际总线路数∙Num_Gen 系统的实际总发电机（节点）数∙Num_Load 系统的实际总负荷（节点）数∙Num_Node 系统的实际总节点数∙Num_Swing 系统的实际总平衡节点数∙Num_GPV 系统发电机节点中的PV节点数∙Num_GPQ 系统发电机节点中的PQ节点数∙Eps 节点功率失配量值收敛限值∙Iter_Max 迭代次数限值（在不满足电压收敛误差限值的条件下强行中止收敛的最大迭代次数）∙V olIni_Flag 是否读取电压初值标志：0-不读（以0-1启动）；1-读初值∙V olRes_Flag 是否将电压收敛值保存以备以后计算时当启动初值：0-不保存；1-保存3参数结构定义说明∙线路参数结构定义struct Line{int Node_No[2];int Flag;double RXBK[3];}LLine[LINEMAX]其中，Node_No[2]代表线路两端节点号：0—左节点号；1—右节点号。

随着配电网的发展和升级，三相潮流计算在配电网中的应用变得愈发重要。

在这篇论文中，我们将探讨三相潮流计算的概念、原理、应用和优点。

一、三相潮流计算的概念三相潮流计算是一种计算三相交流电路中电压、电流和功率等参数的方法。

这种方法在配电网中被广泛应用，因为配电网是由三相系统构成，并且三相系统具有相互独立的性质，即每个相位的电流和电压都是独立的。

因此，三相潮流计算可以非常方便地得出三相电路中各个参数的值，从而对配电网的运行进行有效的监控和管理。

二、三相潮流计算的原理三相潮流计算的原理基于电路分析和电力学原理。

通常情况下，三相潮流计算的基本方程可以表示为：S = 3VLIL*cos(phi) 其中S 为有功功率，VL 为相电压，IL 为相电流，phi 为电路的功率因数这个方程可以非常方便地用于计算三相电路中的有功功率和功率因数，从而为配电网管理提供有力支持。

此外，三相潮流计算还可以通过一些辅助的方程来计算无功功率和视在功率等参数。

三、三相潮流计算的应用三相潮流计算在配电网中的应用非常广泛。

以下是三相潮流计算在配电网中的主要应用：1. 配电网的稳态分析：三相潮流计算可以用于对配电网中的电路进行稳态分析，从而检查各分支电路的负荷和分配情况，为进一步的升级和优化提供重要依据。

2. 电网负荷预测：利用三相潮流计算方法，可以分析历史数据和未来负荷趋势，从而预测未来的配电网负载，为后续的电网规划和升级提供指导。

3. 潮流控制：利用三相潮流计算方法，可以对配电网进行全面的潮流控制，包括调节电压和保持一定的电网功率因数等。

4. 故障诊断：通过三相潮流计算方法，可以快速诊断故障点，从而提高配电网的运行效率。

5. 电压平衡控制：利用三相潮流计算方法，可以实现电压平衡控制，从而保证整个配电网的稳定运行。

四、三相潮流计算的优点使用三相潮流计算方法来处理配电网的数学模型可以带来许多好处。

下面是三相潮流计算方法的一些优点：1. 高精度：三相潮流计算方法可以提供高精度的计算结果，因为它可以对复杂的三相电路进行准确的数学模拟和计算。

潮流计算步骤
潮流计算是电力系统分析中的一种基本计算方法，用于确定电网中的电压分布和功率流动情况。

以下是潮流计算的基本步骤：
1、输入原始数据和信息：包括电网的结构信息、设备参数、负荷和电源的分布及大小等。

2、建立数学模型：根据电路理论和电力系统网络模型，建立描述电力系统中电压、电流和功率关系的数学模型。

3、形成节点导纳矩阵：根据电网结构，形成节点导纳矩阵，用于描述系统中各节点之间的电气联系。

4、确定待求状态变量初值：根据实际情况，为待求的状态变量（如节点电压）设定初值。

5、迭代求解：使用迭代法对数学模型进行求解，逐步更新状态变量的值，直到满足收敛条件为止。

6、计算节点电压：根据迭代求解的结果，计算出各节点的电压值。

7、计算功率分布：根据节点电压和网络参数，计算出各支路的功率流动情况。

8、结果分析：对计算结果进行整理和分析，评估电网的运行状态，为进一步优化和调整提供依据。

需要注意的是，潮流计算的具体步骤可能会因不同的计算方法和电力系统分析软件而有所差异。

在实际应用中，需要根据具体的软件
和要求进行操作。

潮流计算，电力学名词，指在给定电力系统网络拓扑、元件参数和发电、负荷参量条件下，计算有功功率、无功功率及电压在电力网中的分布。

潮流计算是根据给定的电网结构、参数和发电机、负荷等元件的运行条件，确定电力系统各部分稳态运行状态参数的计算。

通常给定的运行条件有系统中各电源和负荷点的功率、枢纽点电压、平衡点的电压和相位角。

待求的运行状态参量包括电网各母线节点的电压幅值和相角，以及各支路的功率分布、网络的功率损耗等。

潮流计算程序，相关的原始数据数据数据输入格式如下：%B1是支路参数矩阵，第一列和第二列是起始节点编号和终点节点编号%第三列、第四列、第五列、第六列、第七列、第八列分别为：支路电阻、电抗、电导、电纳、变压器变比、是否有变压器（1为有、0为无）。

%B2为节点参数矩阵，其中第一列到第六列为节点编号；为节点类型；注入有功、注入无功、电压幅值、电压相位。

%“1”为平衡节点，“2”为PQ节点，“3”为PV节点参数。

n=input('请输入节点数:n=');n1=input('请输入支路数:n1=');isb=input('请输入平衡节点号:isb=');pr=input('请输入误差精度:pr=');B1=input('请输入支路参数:B1=');B2=input('请输入节点参数:B2=');Y=zeros(n);N=1;%建立节点导纳矩阵for i=1:n1if B1(i,8)==0p=B1(i,1);q=B1(i,2);Y(p,q)=Y(p,q)-1/(B1(i,3)+B1(i,4))-B1(i,5);Y(q,p)=Y(p,q);Y(p,p)=Y(p,p)+1/(B1(i,3)+B1(i,4))+0.5*B1(i,6)+B1(i,5);Y(q,q)=Y(q,q)+1/(B1(i,3)+B1(i,4))+0.5*B1(i,6)+B1(i,5);elsep=B1(i,1);q=B1(i,2);Y(p,q)=Y(p,q)-1/((B1(i,3)+B1(i,4))*B1(i,7)) -B1(i,5);Y(q,p)=Y(p,q);Y(p,p)=Y(p,p)+1/(B1(i,3)+B1(i,4))+B1(i,5);Y(q,q)=Y(q,q)+1/(B1(i,7)^2*(B1(i,3)+B1(i,4)))+B1(i,5);endendYG=real(Y);B=imag(Y);PriS=zeros(2*n-2,1);ImbS=zeros(2*n-2,1);%创建PriS，用于存储初始功率参数h=0;j=0;for i=1:nif i~=isb&B2(i,2)==1h=h+1;for j=1:nPriS(2*h-1,1)=PriS(2*h-1,1)+B2(i,5)*(G(i,j)*B2(j,5)-B(i,j)*B2(j,6))+B2(i,6)*(G(i,j)*B2(j,6)+B(i, j)*B2(j,5));PriS(2*h,1)=PriS(2*h,1)+B2(i,6)*(G(i,j)*B2(j,5)-B(i,j)*B2(j,6))-B2(i,5)*(G(i,j)*B2(j,6)+B(i,j)*B 2(j,5));endendendfor i=1:nif i~=isb&B2(i,2)==2h=h+1;for j=1:nPriS(2*h-1,1)=PriS(2*h-1,1)+B2(i,5)*(G(i,j)*B2(j,5)-B(i,j)*B2(j,6))+B2(i,6)*(G(i,j)*B2(j,6)+B(i,j)*B2(j,5));PriS(2*h,1)=PriS(2*h,1)+B2(i,6)*(G(i,j)*B2(j,5)-B(i,j)*B2(j,6))-B2(i,5)*(G(i,j)*B2(j,6)+B(i,j)*B2(j,5))endendendPriSU3=zeros(n-h-1,2);%U3存储PV节点的初始电压t=0;for i=1:nif B2(i,2)==2t=t+1;U3(t,1)=B2(i,5);U3(t,2)=B2(i,6);endendU3%ImbS于存储有功功率、无功功率和电压幅值的不平衡量h=0;for i=1:nif i~=isb&B2(i,2)==1h=h+1;ImbS(2*h-1,1)=B2(i,3)-PriS(2*h-1,1);ImbS(2*h,1)=B2(i,4)-PriS(2*h,1);endendt=0;for i=1:nif i~=isb&B2(i,2)==2h=h+1;t=t+1;ImbS(2*h-1,1)=B2(i,3)-PriS(2*h-1,1);ImbS(2*h,1)=U3(t,1)^2+U3(t,2)^2-B2(i,5)^2-B2(i,6)^2;endendImbSI=zeros(n-1,1);%I，存储节点电流参数h=0;for i=1:nif i~=isbh=h+1;I(h,1)=(PriS(2*h-1,1)-PriS(2*h,1)*sqrt(-1))/conj(B2(i,5)+B2(i,6)*sqrt(-1));endendIJacbi=zeros(2*n-2);%Jacbi(雅可比矩阵)h=0;k=0;for i=1:nif B2(i,2)==1h=h+1;for j=1:nif j~=isbk=k+1;if i==jJacbi(2*h-1,2*k-1)=-B(i,j)*B2(i,5)+G(i,j)*B2(i,6)+imag(I(h,1));Jacbi(2*h-1,2*k)=G(i,j)*B2(i,5)+B(i,j)*B2(i,6)+real(I(h,1));Jacbi(2*h,2*k-1)=-Jacbi(2*h-1,2*k)+2*real(I(h,1));Jacbi(2*h,2*k)=Jacbi(2*h-1,2*k-1)-2*imag(I(h,1));elseJacbi(2*h-1,2*k-1)=-B(i,j)*B2(i,5)+G(i,j)*B2(i,6);Jacbi(2*h-1,2*k)=G(i,j)*B2(i,5)+B(i,j)*B2(i,6);Jacbi(2*h,2*k-1)=-Jacbi(2*h-1,2*k);Jacbi(2*h,2*k)=Jacbi(2*h-1,2*k-1);endif k==(n-1)k=0;endendendendendk=0;for i=1:nif B2(i,2)==2h=h+1;for j=1:nif j~=isbk=k+1;if i==jJacbi(2*h-1,2*k-1)= -B(i,j)*B2(i,5)+G(i,j)*B2(i,6)+imag(I(h,1));Jacbi(2*h-1,2*k)= G(i,j)*B2(i,5)+B(i,j)*B2(i,6)+real(I(h,1));Jacbi(2*h,2*k-1)=2*B2(i,6);Jacbi(2*h,2*k)=2*B2(i,5);elseJacbi(2*h-1,2*k-1)= -B(i,j)*B2(i,5)+G(i,j)*B2(i,6);Jacbi(2*h-1,2*k)= G(i,j)*B2(i,5)+B(i,j)*B2(i,6);Jacbi(2*h,2*k-1)=0;Jacbi(2*h,2*k)=0;endif k==(n-1)k=0;endendendendendJacbi%求解修正方程，获取节点电压的不平衡量ImbU=zeros(2*n-2,1);ImbU=inv(Jacbi)*ImbS;ImbU%修正节点电压j=0;for i=1:nif B2(i,2)==1j=j+1;B2(i,5)=B2(i,5)+ImbU(2*j,1);B2(i,6)=B2(i,6)+ImbU(2*j-1,1);endendfor i=1:nif B2(i,2)==2j=j+1;B2(i,5)=B2(i,5)+ImbU(2*j,1);B2(i,6)=B2(i,6)+ImbU(2*j-1,1);endendB2while abs(max(ImbU))>prPriS=zeros(2*n-2,1);h=0;j=0;for i=1:nif i~=isb&B2(i,2)==1h=h+1;for j=1:nPriS(2*h-1,1)=PriS(2*h-1,1)+B2(i,5)*(G(i,j)*B2(j,5)-B(i,j)*B2(j,6))+B2(i,6)*(G(i,j)*B2(j,6)+B(i, j)*B2(j,5));PriS(2*h,1)=PriS(2*h,1)+B2(i,6)*(G(i,j)*B2(j,5)-B(i,j)*B2(j,6))-B2(i,5)*(G(i,j)*B2(j,6)+B(i,j)*B 2(j,5));endendendfor i=1:nif i~=isb&B2(i,2)==2h=h+1;for j=1:nPriS(2*h-1,1)=PriS(2*h-1,1)+B2(i,5)*(G(i,j)*B2(j,5)-B(i,j)*B2(j,6))+B2(i,6)*(G(i,j)*B2(j,6)+B(i,j)*B2(j,5));PriS(2*h,1)=PriS(2*h,1)+B2(i,6)*(G(i,j)*B2(j,5)-B(i,j)*B2(j,6))-B2(i,5)*(G(i,j)*B2(j,6)+B(i,j)*B2(j,5))endendendPriS%创建ImbSh=0;for i=1:n %对PQ节点的处理if i~=isb&B2(i,2)==1h=h+1;ImbS(2*h-1,1)=B2(i,3)-PriS(2*h-1,1);ImbS(2*h,1)=B2(i,4)-PriS(2*h,1);endendt=0;for i=1:n %对PV节点的处理if i~=isb&B2(i,2)==2h=h+1;t=t+1;ImbS(2*h-1,1)=B2(i,3)-PriS(2*h-1,1);ImbS(2*h,1)=U3(t,1)^2+U3(t,2)^2-B2(i,5)^2-B2(i,6)^2;endendImbS%创建II=zeros(n-1,1);h=0;for i=1:nif i~=isbh=h+1;I(h,1)=(PriS(2*h-1,1)-PriS(2*h,1)*sqrt(-1))/conj(B2(i,5)+B2(i,6)*sqrt(-1));endendI%创建JacbiJacbi=zeros(2*n-2);h=0;k=0;for i=1:nif B2(i,2)==1h=h+1;for j=1:nif j~=isbk=k+1;if i==jJacbi(2*h-1,2*k-1)=-B(i,j)*B2(i,5)+G(i,j)*B2(i,6)+imag(I(h,1));Jacbi(2*h-1,2*k)=G(i,j)*B2(i,5)+B(i,j)*B2(i,6)+real(I(h,1));Jacbi(2*h,2*k-1)=-Jacbi(2*h-1,2*k)+2*real(I(h,1));Jacbi(2*h,2*k)=Jacbi(2*h-1,2*k-1)-2*imag(I(h,1));elseJacbi(2*h-1,2*k-1)=-B(i,j)*B2(i,5)+G(i,j)*B2(i,6);Jacbi(2*h-1,2*k)=G(i,j)*B2(i,5)+B(i,j)*B2(i,6);Jacbi(2*h,2*k-1)=-Jacbi(2*h-1,2*k);Jacbi(2*h,2*k)=Jacbi(2*h-1,2*k-1);endif k==(n-1)k=0;endendendendendk=0;for i=1:nif B2(i,2)==2h=h+1;for j=1:nif j~=isbk=k+1;if i==jJacbi(2*h-1,2*k-1)= -B(i,j)*B2(i,5)+G(i,j)*B2(i,6)+imag(I(h,1));Jacbi(2*h-1,2*k)= G(i,j)*B2(i,5)+B(i,j)*B2(i,6)+real(I(h,1));Jacbi(2*h,2*k-1)=2*B2(i,6);Jacbi(2*h,2*k)=2*B2(i,5);elseJacbi(2*h-1,2*k-1)= -B(i,j)*B2(i,5)+G(i,j)*B2(i,6);Jacbi(2*h-1,2*k)= G(i,j)*B2(i,5)+B(i,j)*B2(i,6);Jacbi(2*h,2*k-1)=0;Jacbi(2*h,2*k)=0;endif k==(n-1)k=0;endendendendendJacbiImbU=zeros(2*n-2,1);ImbU=inv(Jacbi)*ImbS;ImbU%修正节点电压j=0;for i=1:nif B2(i,2)==1j=j+1;B2(i,5)=B2(i,5)+ImbU(2*j,1);B2(i,6)=B2(i,6)+ImbU(2*j-1,1);endendfor i=1:nif B2(i,2)==2j=j+1;B2(i,5)=B2(i,5)+ImbU(2*j,1);B2(i,6)=B2(i,6)+ImbU(2*j-1,1);endendB2N=N+1; %迭代次数加1endN。

附表1：计算机计算潮流程序：%本程序的功能是用牛顿——拉夫逊法进行潮流计算% B1矩阵：1、支路首端号；2、末端号；3、支路阻抗；4、支路对地电纳% 5、支路的变比；6、支路首端处于K侧为1，1侧为0% B2矩阵：1、该节点发电机功率；2、该节点负荷功率；3、节点电压初始值% 4、PV节点电压V的给定值；5、节点所接的无功补偿设备的容量% 6、节点分类标号clear;n=13;%input('请输入节点数：n=');nl=13;%input('请输入支路数：nl=');isb=1;%input('请输入平衡母线节点号：isb=');pr=0.00001;%input('请输入误差精度：pr=');B1=[];%input('请输入由支路参数形成的矩阵：B1=');B2=[];%input('请输入各节点参数形成的矩阵：B2=');Y=zeros(n);e=zeros(1,n);f=zeros(1,n);V=zeros(1,n);sida=zeros(1,n);S1=zeros(nl); %－－－－－－－修改部分－－－－－－－－－－－－ym=0;SB=100;UB=220;%ym=input('您输入的参数是标么值？（若不是则输入一个不为零的数值）'); if ym~=0%SB=input('请输入功率基准值:SB=');%UB=input('请输入电压基准值:UB=');YB=SB./UB./UB;BB1=B1;BB2=B2;for i=1:nlB1(i,3)=B1(i,3)*YB;B1(i,4)=B1(i,4)./YB;enddisp('B1矩阵B1=');disp(B1)for i=1:nB2(i,1)=B2(i,1)./SB;B2(i,2)=B2(i,2)./SB;B2(i,3)=B2(i,3)./UB;B2(i,4)=B2(i,4)./UB;B2(i,5)=B2(i,5)./SB;enddisp('B2矩阵B2=');disp(B2)end% % %---------------------------------------------------for i=1:nl %支路数if B1(i,6)==0 %左节点处于低压侧p=B1(i,1);q=B1(i,2);elsep=B1(i,2);q=B1(i,1);endY(p,q)=Y(p,q)-1./(B1(i,3)*B1(i,5)); %非对角元Y(q,p)=Y(p,q);Y(q,q)=Y(q,q)+1./(B1(i,3)*B1(i,5)^2)+B1(i,4)./2; %对角元K侧Y(p,p)=Y(p,p)+1./B1(i,3)+B1(i,4)./2; %对角元1侧end%求导纳矩阵disp('导纳矩阵Y=');disp(Y)%----------------------------------------------------------G=real(Y);B=imag(Y); %分解出导纳阵的实部和虚部for i=1:n %给定各节点初始电压的实部和虚部e(i)=real(B2(i,3));f(i)=imag(B2(i,3));V(i)=B2(i,4); %PV节点电压给定模值endfor i=1:n %给定各节点注入功率S(i)=B2(i,1)-B2(i,2); %i节点注入功率SG-SLB(i,i)=B(i,i)+B2(i,5); %i节点无功补偿量end%=========================================================== ========P=real(S);Q=imag(S);ICT1=0;IT2=1;N0=2*n;N=N0+1;a=0;while IT2~=0IT2=0;a=a+1;for i=1:nif i~=isb %非平衡节点C(i)=0;D(i)=0;for j1=1:nC(i)=C(i)+G(i,j1)*e(j1)-B(i,j1)*f(j1);%Σ(Gij*ej-Bij*fj)D(i)=D(i)+G(i,j1)*f(j1)+B(i,j1)*e(j1);%Σ(Gij*fj+Bij*ej)endP1=C(i)*e(i)+f(i)*D(i);%节点功率P计算eiΣ(Gij*ej-Bij*fj)+fiΣ(Gij*fj+Bij*ej)Q1=C(i)*f(i)-e(i)*D(i);%节点功率Q计算fiΣ(Gij*ej-Bij*fj)-eiΣ(Gij*fj+Bij*ej)%求P',Q'V2=e(i)^2+f(i)^2; %电压模平方%========= 以下针对非PV节点来求取功率差及Jacobi矩阵元素=========if B2(i,6)~=3 %非PV节点DP=P(i)-P1; %节点有功功率差DQ=Q(i)-Q1; %节点无功功率差%=============== 以上为除平衡节点外其它节点的功率计算=================%================= 求取Jacobi矩阵===================for j1=1:nif j1~=isb&j1~=i %非平衡节点&非对角元X1=-G(i,j1)*e(i)-B(i,j1)*f(i); % dP/de=-dQ/dfX2=B(i,j1)*e(i)-G(i,j1)*f(i); % dP/df=dQ/deX3=X2; % X2=dp/df X3=dQ/deX4=-X1; % X1=dP/de X4=dQ/dfp=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X4;J(m,q)=X2;elseif j1==i&j1~=isb %非平衡节点&对角元X1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i);% dP/deX2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i);% dP/dfX3=D(i)+B(i,i)*e(i)-G(i,i)*f(i); % dQ/deX4=-C(i)+G(i,i)*e(i)+B(i,i)*f(i);% dQ/dfp=2*i-1;q=2*j1-1;J(p,q)=X3;J(p,N)=DQ;%扩展列△Qm=p+1;J(m,q)=X1;q=q+1;J(p,q)=X4;J(m,N)=DP;%扩展列△PJ(m,q)=X2;endendelse%=============== 下面是针对PV节点来求取Jacobi矩阵的元素===========DP=P(i)-P1; % PV节点有功误差DV=V(i)^2-V2; % PV节点电压误差for j1=1:nif j1~=isb&j1~=i %非平衡节点&非对角元X1=-G(i,j1)*e(i)-B(i,j1)*f(i); % dP/deX2=B(i,j1)*e(i)-G(i,j1)*f(i); % dP/dfX5=0;X6=0;p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;J(m,q)=X2;elseif j1==i&j1~=isb %非平衡节点&对角元X1=-C(i)-G(i,i)*e(i)-B(i,i)*f(i);% dP/deX2=-D(i)+B(i,i)*e(i)-G(i,i)*f(i);% dP/dfX5=-2*e(i);X6=-2*f(i);p=2*i-1;q=2*j1-1;J(p,q)=X5;J(p,N)=DV;m=p+1;J(m,q)=X1;J(m,N)=DP;q=q+1;J(p,q)=X6;J(m,q)=X2;endendendendend%========= 以上为求雅可比矩阵的各个元素===================== for k=3:N0 % N0=2*n （从第三行开始，第一、二行是平衡节点）k1=k+1;N1=N; % N=N0+1 即N=2*n+1扩展列△P、△Qfor k2=k1:N1 % 扩展列△P、△QJ(k,k2)=J(k,k2)./J(k,k); % 非对角元规格化endJ(k,k)=1; % 对角元规格化if k~=3 % 不是第三行%======================================================== ====k4=k-1;for k3=3:k4 % 用k3行从第三行开始到当前行前的k4行消去for k2=k1:N1 % k3行后各行下三角元素J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);%消去运算endJ(k3,k)=0;endif k==N0break;end%==========================================for k3=k1:N0for k2=k1:N1J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);%消去运算endJ(k3,k)=0;endelsefor k3=k1:N0for k2=k1:N1J(k3,k2)=J(k3,k2)-J(k3,k)*J(k,k2);%消去运算endJ(k3,k)=0;endendend%====上面是用线性变换方式将Jacobi矩阵化成单位矩阵=====for k=3:2:N0-1L=(k+1)./2;e(L)=e(L)-J(k,N); %修改节点电压实部k1=k+1;f(L)=f(L)-J(k1,N); %修改节点电压虚部end%------修改节点电压-----------for k=3:N0DET=abs(J(k,N));if DET>=pr %电压偏差量是否满足要求IT2=IT2+1; %不满足要求的节点数加1endendICT2(a)=IT2;ICT1=ICT1+1;end%用高斯消去法解"w=-J*V"disp('迭代次数：');disp(ICT1);disp('没有达到精度要求的个数：');disp(ICT2);for k=1:nV(k)=sqrt(e(k)^2+f(k)^2);sida(k)=atan(f(k)./e(k))*180./pi;E(k)=e(k)+f(k)*j;end%=============== 计算各输出量=========================== disp('各节点的实际电压标幺值E为(节点号从小到大排列)：');disp(E);EE=E*UB;disp(EE);disp('-----------------------------------------------------');disp('各节点的电压大小V为(节点号从小到大排列)：');disp(V);VV=V*UB;disp(VV);disp('-----------------------------------------------------');disp('各节点的电压相角sida为(节点号从小到大排列)：');disp(sida);for p=1:nC(p)=0;for q=1:nC(p)=C(p)+conj(Y(p,q))*conj(E(q));endS(p)=E(p)*C(p);enddisp('各节点的功率S为(节点号从小到大排列)：');disp(S);disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~');SS=S*SB;disp(SS);disp('-----------------------------------------------------');disp('各条支路的首端功率Si为(顺序同您输入B1时一致)：');for i=1:nlp=B1(i,1);q=B1(i,2);if B1(i,6)==0Si(p,q)=E(p)*(conj(E(p))*conj(B1(i,4)./2)+(conj(E(p)*B1(i,5))-conj(E(q)))*conj(1./( B1(i,3)*B1(i,5))));Siz(i)=Si(p,q);elseSi(p,q)=E(p)*(conj(E(p))*conj(B1(i,4)./2)+(conj(E(p)./B1(i,5))-conj(E(q)))*conj(1./( B1(i,3)*B1(i,5))));Siz(i)=Si(p,q);enddisp(Si(p,q));SSi(p,q)=Si(p,q)*SB;ZF=['S(',num2str(p),',',num2str(q),')=',num2str(SSi(p,q))];disp(ZF);%disp(SSi(p,q));disp('-----------------------------------------------------');enddisp('各条支路的末端功率Sj为(顺序同您输入B1时一致)：');for i=1:nlp=B1(i,1);q=B1(i,2);if B1(i,6)==0Sj(q,p)=E(q)*(conj(E(q))*conj(B1(i,4)./2)+(conj(E(q)./B1(i,5))-conj(E(p)))*conj(1./( B1(i,3)*B1(i,5))));Sjy(i)=Sj(q,p);elseSj(q,p)=E(q)*(conj(E(q))*conj(B1(i,4)./2)+(conj(E(q)*B1(i,5))-conj(E(p)))*conj(1./( B1(i,3)*B1(i,5))));Sjy(i)=Sj(q,p);enddisp(Sj(q,p));SSj(q,p)=Sj(q,p)*SB;ZF=['S(',num2str(q),',',num2str(p),')=',num2str(SSj(q,p))];disp(ZF);%disp(SSj(q,p));disp('-----------------------------------------------------');enddisp('各条支路的功率损耗DS为(顺序同您输入B1时一致)：');for i=1:nlp=B1(i,1);q=B1(i,2);DS(i)=Si(p,q)+Sj(q,p);disp(DS(i));DDS(i)=DS(i)*SB;ZF=['DS(',num2str(p),',',num2str(q),')=',num2str(DDS(i))];disp(ZF);%disp(DDS(i));disp('-----------------------------------------------------');endfigure(1);subplot(2,2,1);plot(V);xlabel('节点号');ylabel('电压标幺值');grid on;subplot(2,2,2);plot(sida);xlabel('节点号');ylabel('电压角度');grid on;subplot(2,2,3);bar(real(S));ylabel('节点注入有功');grid on;subplot(2,2,4);bar(Siz);ylabel('支路首端无功');grid on;1.冬季最大运行方式潮流计算结果:计算机运行的B1,B2阵如下：B1=[ 1 2 0.0318+0.0454*i 0.282*i 1 01 11 0.0114+0.0374*i 0.2332*i 1 011 3 0.001975+0.0695*i 0 1.025:1.1 11 12 0.0087+0.029*i 0.1788*i 1 012 4 0.0031+0.103*i 0 1:1.05 11 5 0.043+0.142*i 0.22*i 1 05 6 0.0031+0.103*i 0 1:1.05 15 7 0.043+0.142*i 0.22*i 1 01 7 0.051+0.168*i 0.26*i 1 07 8 0.00198+0.0695*i 0 1:1.1 17 13 0.01+0.033*i 0.204*i 1 013 9 0.0025+0.083*i 0 0.9956 11 10 0.00239+0.084*i 0 1.048 1]B2=[0 0 1.1 0 0 10 1.43+0.886*i 1.05 1.05 0 30 0.88+0.545*i 1 0 0 20 0.77+0.4772*i 1 0 0 20 0 1 0 0 20 0.77+0.4772*i 1 0 0 20 0 1 0 0 20 0.88+0.545*i 1 0 0 20.642+0.3817*i 0 1.05 1.05 0 31+0.75*i 0.2+0.1549*i 1.05 1.05 0 30 0 1 0 0 20 0 1 0 0 20 0 1 0 0 2]计算机运行结果如下表：节点号电压值相角值支路标号首端功率末端功率支路功率损耗1 242.0000 0 1-2 148.9391+3.327637i -143-27.45476i 5.93913-24.1271i2 231.0000 -3.0341 1-11 89.1956+37.193i -88.19803-61.4687i 0.997519-24.2757i3 227.4154 -4.4383 11-3 88.19803+61.4687i -88-54.5i 0.19803+6.9687i4 226.3304 -4.9004 1-12 77.8364+36.4186i -77.2404-55.7062i 0.596039-19.2876i5 229.8318 -3.9547 12-4 77.2404+55.7062i -77-47.72i 0.24036+7.9862i6 217.7226 -8.2720 1-5 63.5438+12.2204i -61.8773-32.0321i 1.66656-19.8116i7 234.9326 -3.1047 5-6 77.2597+56.3501i -77-47.72i 0.25974+8.6301i8 226.0991 -6.2429 5-7 15.3825-24.3181i 15.5354+0.274108i 0.152961-24.044i9 231.0000 0.5851 7-8 88.20085+61.55009i -88-54.5i 0.20085+7.0501i10 231.0000 3.4950 1-7 40.806-6.05737i -40.0647-22.0555i 0.741264-28.1128i11 236.1931 -1.3348 7-13 -63.6716-39.7687i 64.0965+17.5832i 0.424934-22.1855i12 237.9346 -0.8892 13-9 -64.0965-17.5832i 64.2+21.0187i 0.10348+3.4355i13 238.1868 -2.2028 1-10 79.8613+4.23546i 80+0.641048i 0.13875+4.8765i 计算机计算结果图形：2.冬季最小运行方式潮流计算结果：计算机运行的B1B2矩阵如下：B1=[ 1 2 0.0318+0.0454*i 0.282*i 1 01 11 0.0114+0.0374*i 0.2332*i 1 011 3 0.001975+0.0695*i 0 1.025:1.1 11 12 0.0087+0.029*i 0.1788*i 1 012 4 0.0031+0.103*i 0 1:1.05 11 5 0.043+0.142*i 0.22*i 1 05 6 0.0031+0.103*i 0 1:1.05 15 7 0.043+0.142*i 0.22*i 1 01 7 0.051+0.168*i 0.26*i 1 07 8 0.00198+0.0695*i 0 1:1.1 17 13 0.01+0.033*i 0.204*i 1 013 9 0.0025+0.083*i 0 0.9956 11 10 0.00239+0.084*i 0 1.048 1]B2=[0 0 1.1 0 0 10 1.43+0.886*i 1.05 1.05 0 30 0.616+0.3817*i 1 0 0 20 0.539+0.3817*i 1 0 0 20 0 1 0 0 20 0.539+0.334*i 1 0 0 20 0 1 0 0 20 0.539+0.334*i 1 0 0 20.642+0.3817*i 0 1.05 1.05 0 31+0.75*i 0.1+0.06197*i 1.05 1.05 0 30 0 1 0 0 20 0 1 0 0 20 0 1 0 0 2]电压调整措施：变电所1、4变压器变比：+2.5% 水电厂变压器变比：-2.5%5 234.2241 -2.0051 (12--4) 54.0234+42.2706i -53.9-38.17i 0.12342+4.1006i6 226.2159 -4.8577 (1--5) 34.1669+4.22856 -33.6427-28.276i 0.524165-24.0474i7 235.1128 -0.4737 (5--6) 54.0179+37.3169i -53.9-33.4i 0.11789+3.9169i8 223.9941 -2.4603 (5--7) -20.3752-9.04094i 20.5371-15.4558i 0.161947-24.4968i9 231.0000 3.4429 (1--7) 11.0013+1.45186i -10.8258-31.4513i 0.175442-29.9995i10 231.0000 3.9321 (7--8) 53.9768+36.0957i -53.9-33.4i 0.076797+2.6957i11 238.4187 -0.9561 (7--13) -63.6881+10.8115i 64.0874-32.7763i 0.39932-21.9648i12 239.1742 -0.6185 (13--9) -64.0874+32.7763i 64.2-29.0386i 0.11258+3.7377i13 234.9468 0.6942 (1--10) -89.8244+5.1673i 90+1.0049i 0.17561+6.1722i 计算机运行结果的图形：3.夏季最大运行方式计算机计算结果：计算机运行B1B2阵如下：B1=[ 1 2 0.0318+0.0454*i 0.282*i 1 01 11 0.0114+0.0374*i 0.2332*i 1 011 3 0.001975+0.0695*i 0 1.025:1.1 11 12 0.0087+0.029*i 0.1788*i 1 012 4 0.0031+0.103*i 0 1:1.05 11 5 0.043+0.142*i 0.22*i 1 05 6 0.0031+0.103*i 0 1:1.05 15 7 0.043+0.142*i 0.22*i 1 01 7 0.051+0.168*i 0.26*i 1 07 8 0.00198+0.0695*i 0 1:1.1 17 13 0.02+0.066*i 0.102*i 1 013 9 0.0025+0.083*i 0 0.9956 11 10 0.00239+0.084*i 0 1.048 1]B2=[0 0 1.1 0 0 10 1.26+0.7814*i 1.05 1.05 0 30 0.776+0.481*i 1 0 0 20 0.543+0.3367*i 1 0 0 20 0 1 0 0 20 0.543+0.3367*i 1 0 0 20 0 1 0 0 20 0.776+0.481*i 1 0 0 21.35+0.6538*i 0.2+0.124*i 1.05 1.05 0 31+0.75*i 0.25+0.1549*i 1.05 1.05 0 30 0 1 0 0 20 0 1 0 0 20 0 1 0 0 2]计算机运行结果如下表：10 231.0000 3.4950 (7,8) 77.7585+53.6634i -77.6-48.1i0.1585+5.5634i11 237.0938 -1.1858 (7,13) -113.4984+9.476406i 114.6926-28.38885i 1.19422-18.9124i12 239.1742 -0.6185 (13,9) -114.6926+28.38885 115-18.18369i0.307384+10.2052i13 233.3912 3.2303 (1,10) -79.8613+4.23546i 80+0.641048i 0.13875+4.8765i 计算机计算结果如图：4.夏季最小运行方式：计算机运行B1B2阵如下：B1=[ 1 2 0.0318+0.0454*i 0.282*i 1 01 11 0.0114+0.0374*i 0.2332*i 1 011 3 0.001975+0.0695*i 0 1.025:1.1 11 12 0.0087+0.029*i 0.1788*i 1 012 4 0.0031+0.103*i 0 1:1.05 11 5 0.043+0.142*i 0.22*i 1 05 6 0.0031+0.103*i 0 1:1.05 15 7 0.043+0.142*i 0.22*i 1 01 7 0.051+0.168*i 0.26*i 1 07 8 0.00198+0.0695*i 0 1:1.1 17 13 0.02+0.066*i 0.102*i 1 013 9 0.0025+0.083*i 0 0.9956 11 10 0.00239+0.084*i 0 1.048 1]B2=[0 0 1.1 0 0 10 1.26+0.7814*i 1.05 1.05 0 30 0.543+0.336*i 1 0 0 20 0.4753+0.2947*i 1 0 0 20 0 1 0 0 20 0.4753+0.2947*i 1 0 0 20 0 1 0 0 20 0.543+0.336*i 1 0 0 21.35+0.6538*i 0.2+0.124*i 1.05 1.05 0 31+0.75*i 0.25+0.1549*i 1.05 1.05 0 30 0 1 0 0 20 0 1 0 0 20 0 1 0 0 2]10 231.0000 3.9321 (7,8) 54.3735+36.2509i -54.3-33.67i 0.073528+2.5809i11 239.0099 -0.8518 (7,13) -113.4428+24.39707i 114.6754-43.79301i 1.23255-19.3959i12 239.8726 -0.5689 (13,9) -114.6754+43.79301i 115-33.01613i 0.324605+10.7769i13 235.9565 4.4510 (1,10) -89.8244+5.1673i 90+1.0049i 0.17561+6.1722i 计算机计算结果如图：5.夏季故障运行状态:调压及无功补偿措施如下:变电所3的变压器变比为-2.5%,无功补偿容量为20Mvar。

0、引言微积分的发明是人类科学史上一项伟大的成就，在科学技术中，积分是经常遇到的一个重要计算环节。

在一定条件下，虽然有Newton—Leibniz公式可以计算定积分的值，但在很多情况下,f(x)的原函数不易求得，或非常复杂。

此外，在实际工程中，函数f(x)是用函数表形式给出而没有解析表达式，这就更无法使用Newton—Leibniz公式了。

因此，探讨近似计算的数值积分方法是有明显的实际意义的，即有必要研究定积分的数值计算方法，以解决定积分的近似计算。

数值积分的计算方法很多，如Newton—Cotes方法、Romberg 方法、Gauss方法等. 其中Newton—Cotes方法是一种利用插值多项式来构造数值积分的常用方法，但是高阶的Newton—Cotes方法的收敛性没有保证，因此，在实际计算中很少使用高阶的Newton—Cotes公式。

Romberg方法收敛速度快、计算精度较高。

但是计算量较大。

Gauss方法积分精度高、数值稳定、收敛速度较快，但是节点与系数的计算较麻烦、而且要求已知积分函数f(x)。

近十年来，随着计算机的高速发展，数值积分环节在工程应用领域越来越广泛，国内外众多学者在数值积分应用领域提出了许多新方法,有效解决了许多工程实际问题。

本文对根据所学数值分析中的积分及迭代的方法对三相潮流计算进行了数据分析和计算。

1、配电网潮流计算相关背景1.1 问题的提出自从以电力广泛应用为代表的第二次工业革命以来，电能迅速发展成为人类社会生存和发展的基本能源。

随着信息技术的蓬勃兴起.电力事业得到了长足的进步。

二十一世纪的头十年，是我国实现第二战略目标向第三目标迈进的关键十年，在这时期，我国将建立比较完善的社会主义市场经济体制。

为保证我国国民经济保持持续健康的向前发展，作为重要能源基础的电力，受到了国家的高度重视，从而促进了电力基本理论的研究。

潮流计算是电力系统中应用最为广泛。

最基本和最重要的一种电气计算。

简单配电网的潮流计算电力系统正常运行状况下，运行、管理和调度人员需要知道在给定运行方式下各母线的电压是否满意要求，系统中的功率分布是否合理，元件是否过载，系统有功、无功损耗各是多少等等状况。

为了了解这些运行状况就需要进行潮流计算。

潮流计算：依据已知的负荷(功率）及电源电压计算出其它节点的电压和元件上的功率分布。

潮流计算是电力系统中最基本、最常用的一种汁算。

开式网：只有一端电源供电的网络。

一.计算中的两种类型：1.同一电压等级的开式网计算 2.不同电压等组的开式网计算二.计算中的三种状况：1.已知末端电压和功率，求首端电压和功率采纳将电压和功率由已知点向未知点逐段递推计算的方法。

即已知和，求和，见图1。

图1 已知末端电压和功率，求首端电压和功率(1)功率计算：2)电压计算：(3)对功率和电压交替计算，求和对于110kV及以下的网络，在计算电压损耗时常略去横重量，使计算进一步简化。

在计算时需留意变压器两侧参数与电压的归算。

2.已知首端电压和功率，求末端电压和功率即已知和，求和，这种状况的电路见图2。

图2 已知首端电压和功率，求末端电压和功率(1)功率计算：2.电压计算：(3)对功率和电压交替计算：求和3.已知末端功率和首端电压，求首端功率和末端电压（常见）即已知和，求末端和首端，这种状况的电路见图3。

图 3 已知末端功率和首端电压，求首端功率和末端电压近似计算（常用）：精确计算：不断迭代！(1)设定各节点电压等于其额定电压：(2)与第一种状况一样求出功率分布：(3)与其次种状况一样求出各节点电压分布：常见的状况是给出开式配电网的末端负荷与首端电压。

对于这种状况可进一步简化计算，不必进行反复递推。

设全网为额定电压（一般可将全网参数归算到同一个电压等级），由网络末端向首端推算各元件的功率损耗和功率分布，而不计算电压；待求得首端功率后，再由给定的首端电压与求得的首端功率、网络各处的功率分布，从首端向末端推算各元件电压损耗和各母线（节点）电压，此时不再重新计算功率损耗与功率分布。

电力系统潮流及短路电流计算程序以下是一个简单的电力系统潮流计算程序的框架：1.输入数据准备阶段：-输入潮流计算的电力系统拓扑结构，包括各节点之间的连接关系、导线电阻、电抗等信息。

-输入电力系统的负荷信息，包括负荷节点、负荷大小、负荷类型等。

-输入电力系统的发电机信息，包括发电机节点、发电机类型、发电机容量等。

2.潮流计算阶段：-初始条件设置：给定电力系统中各节点的初始电压、相角等信息。

-节点功率方程求解：根据电力系统的拓扑结构和发电机、负荷信息，建立节点功率方程。

-潮流计算迭代：使用牛顿-拉夫逊法等迭代算法求解节点功率方程，得到各节点的电压、相角等参数。

3.潮流计算结果输出阶段：-输出各节点的电压、相角、有功功率、无功功率等参数。

-输出各支路的电流、功率损耗等参数。

-输出系统的功率平衡情况。

4.短路电流计算阶段：-输入短路电流计算的电力系统拓扑结构。

-输入短路电流计算的负荷信息。

-输入短路电流计算的电源信息。

-使用KVL（电压法）或KCL（电流法）等方法计算各节点短路电流。

5.短路电流计算结果输出阶段：-输出各节点的短路电流大小。

-输出各支路的短路电流大小。

以上只是一个电力系统潮流及短路电流计算程序的大致流程框架，具体实现细节和算法选择还需要根据具体情况进行进一步的设计和开发。

在实际应用中，还需要考虑各种特殊情况和计算优化方法，以提高计算速度和准确性。

总之，电力系统潮流及短路电流计算程序是电力工程师在设计和运行电力系统中不可或缺的工具，它能够帮助工程师快速了解系统的运行状态和电流分布情况，以便进行系统优化和安全评估。

班级：之阳早格格创做姓名：教号：一、做业央供编写步调估计图1所示算例系统的潮流及三相短路电流.潮流估计：要领没有限，估计系统的节面电压战相角.短路电流：4号母线爆收金属性三相短路时（zf=0），分别依照透彻算法战近似算法估计短路电流、系统中各节面电压以及搜集中各支路的电流分散，并对于二种情况下的估计截止举止比较.二、电路图及参数图1 3机9节面系统表1 9节面系统支路参数支路R（p.u.）X（p.u.）B/2(TK) （p.u.）1~4 02~7 03~9 04~54~65~76~97~88~9表2 9节面系统收电机参数收电机编号节面典型PG（p.u.）VG（p.u.）（p.u.）（p.u.）1仄稳2PV3PV表3 9节面系统背荷参数节面编号节面典型Pi（p.u.）Qi（p.u.）4 PQ0 05 PQ6 PQ7 PQ 0 08 PQ 19 PQ 0 0三、估计步调(1)举止系统仄常运奇迹态的潮流估计，供得(2)产死没有含收电机战背荷的节面导纳矩阵YN；(3)将收电机表示为电流源()战导纳()的并联拉拢；节面背荷用恒阻抗的交天支路表示；产死包罗所有收电机支路战背荷支路的节面导纳矩阵Y，即正在YN 中的收电机节面战背荷节面的自导纳上分别减少收电机导纳战背荷导纳（）；(4)利用，估计节面阻抗矩阵，进而得到阻抗矩阵中的第f列；(5)利用公式(67)或者(610)估计短路电流；(6)利用公式(68)或者(611)估计系统中各节面电压；(7)利用公式(69)估计变压器支路的电流；对于输电线路利用П型等值电路估计支路电流.四、估计截止节面导纳矩阵Yn：Columns 1 through 50 17.3611i 0 0 0 +17.3611i 0 0 0 16.0000i 0 0 00 0 0 17.0648i 0 00 0 0 1.9422 +10.5107i 0 0 0 0 0 00 0 0 +17.0648i 0 0Columns 6 through 90 0 0 00 0 +16.0000i 0 01.9422 +10.5107i 0 0 00 1.1876 + 5.9751i 0 00 2.8047 35.4456i 1.6171 +13.6980i 0电压幅值：电压相角：节面有功：节面无功：建正后的节面导纳矩阵Y：Columns 1 through 50 20.6944i 0 0 0 +17.3611i 00 0 19.3333i 0 0 00 0 0 20.3982i 0 00 0 0 1.9422 +10.5107i 0 0 0 0 0 00 0 0 +17.0648i 0 0 Columns 6 through 90 0 0 00 0 +16.0000i 0 01.9422 +10.5107i 0 0 00 1.1876 + 5.9751i 0 00 2.8047 35.4456i 1.6171 +13.6980i 0节面阻抗矩阵Z的第4列：透彻估计截止：短路电流：模值：相角：节面电压模值：支路电流：i j Iij近似估计截止：短路电流：模值：节面电压模值：五、步调过程图六、步调及输进文献input_data.xls 文献：Sheet2powerflow_cal.m 文献：l=9;%支路数n=9;%节面数m=6;%PQ节面数Yn=zeros(n);%初初化节面导纳矩阵Y DATA1=xlsread('input_data.xls',1);%估计节面导纳矩阵Yfor k=1:li=DATA1(k,1);j=DATA1(k,2);R=DATA1(k,3);X=DATA1(k,4);B2=DATA1(k,5);Yn(i,i)=Yn(i,i)+1i*B2+1/(R+1i*X); Yn(j,j)=Yn(j,j)+1i*B2+1/(R+1i*X); Yn(i,j)=Yn(i,j)1/(R+1i*X);Yn(j,i)=Yn(j,i)1/(R+1i*X);enddisp('节面导纳矩阵Yn：');disp(Yn);G=real(Yn);B=imag(Yn);DATA2=xlsread('input_data.xls',2);P=zeros(1,n);Q=zeros(1,n);U=ones(1,n);P(2:n)=DATA2(2:n,3);Q(4:n)=DATA2(4:n,4);U(1:3)=DATA2(1:3,5);%树立节面电压初值e(1)=DATA2(1,5);e(2:n)=1.0;f(1:n)=0.0;%树立迭代次数t=0;tmax=10;while t<=tmax%估计f(x)a(1:n)=0.0;c(1:n)=0.0;for i=2:nfor j=1:na(i)=a(i)+G(i,j)*e(j)B(i,j)*f(j);c(i)=c(i)+G(i,j)*f(j)+B(i,j)*e(j);endendfor i=2:ndeltaP(i)=P(i)e(i)*a(i)f(i)*c(i);endfor j=4:ndeltaQ(j)=Q(j)f(j)*a(j)+e(j)*c(j);endfor k=2:3deltaU2(k)=U(k)*U(k)e(k)*e(k)f(k)*f(k); endfx=[deltaP(2:n) deltaQ(4:n) deltaU2(2:3)]'; %估计俗克比矩阵Jfor i=2:nfor j=2:nif i~=jH(i,j)=(G(i,j)*e(i)+B(i,j)*f(i));N(i,j)=B(i,j)*e(i)G(i,j)*f(i);elseH(i,j)=a(i)(G(i,i)*e(i)+B(i,i)*f(i)); N(i,j)=c(i)+(B(i,i)*e(i)G(i,i)*f(i)); endendendfor i=4:nfor j=2:nif i~=jM(i,j)=B(i,j)*e(i)G(i,j)*f(i);L(i,j)=G(i,j)*e(i)+B(i,j)*f(i);elseM(i,j)=c(i)+(B(i,i)*e(i)G(i,i)*f(i)); L(i,j)=a(i)+(G(i,i)*e(i)+B(i,i)*f(i)); endendendfor i=2:3for j=2:nif i~=jR(i,j)=0;S(i,j)=0;elseR(i,j)=2*e(i);S(i,j)=2*f(i);endendendJ=[H(2:n,2:n) N(2:n,2:n);M(4:n,2:n) L(4:n,2:n);R(2:3,2:n) S(2:3,2:n)];%输出截止break;else%供解建正圆程赢得dxdx=J^(1)*fx;dx=dx';e(2:n)=e(2:n)+dx(1:n1);f(2:n)=f(2:n)+dx(n:2*(n1));t=t+1;endendif t>tmaxstr='潮流估计没有支敛';disp(str);elsea(1:n)=0.0;c(1:n)=0.0;for i=1:nfor j=1:na(i)=a(i)+G(i,j)*e(j)B(i,j)*f(j); c(i)=c(i)+G(i,j)*f(j)+B(i,j)*e(j); endendfor i=1:nU(i)=e(i)+1i*f(i);amp(i)=abs(U(i));arg(i)=angle(U(i));P(i)=e(i)*a(i)+f(i)*c(i);Q(i)=f(i)*a(i)e(i)*c(i);disp('电压幅值：');disp(amp);disp('电压相角：');disp(arg);disp('节面有功：');disp(P);disp('节面无功：');disp(Q);end%估计短路电流f=4;zf=0.0;%建正节面导纳矩阵Xd=DATA2(1:3,6);E=DATA2(1:3,7);for i=1:3Ii(i)=E(i)/(1i*Xd(i));endY=Yn;for i=1:3Y(i,i)=Y(i,i)+1/(1i*Xd(i));for j=4:nY(j,j)=Y(j,j)+(P(j)+1i*Q(j))/(U(j)*U(j)); enddisp('建正后的节面导纳矩阵Y：');disp(Y);Z=Y^(1);disp('节面阻抗矩阵Z的第4列：');disp(Z(:,4));%透彻估计disp('透彻估计截止：');U0=U;If=U0(f)/(Z(f,f)+zf);amp=abs(If);arg=atand(imag(If)/real(If));disp('短路电流：');disp('模值：');disp(amp);disp('相角：');disp(arg);for i=1:nU(i)=U0(i)Z(i,f)*If;amp=abs(U);enddisp('节面电压模值：');disp(amp);disp('支路电流： ');str=['i ''j '' Iij'];disp(str);for k=1:li=DATA1(k,1);j=DATA1(k,2);r=DATA1(k,3);x=DATA1(k,4);z=r+1i*x;I=(U(i)U(j))/z;str=[num2str(i) ' ' num2str(j) ' ' num2str(I)]; disp(str);end%近似估计disp('近似估计截止：');U0(1:n)=1.0;If=U0(f)/(Z(f,f)+zf);amp=abs(If);arg=atand(imag(If)/real(If)); disp('短路电流：');disp('模值：');disp(amp);disp('相角：');disp(arg);for i=1:nU(i)=U0(i)Z(i,f)*If;amp=abs(U);enddisp('节面电压模值：'); disp(amp);。