气体摩尔体积的计算共17页

化学习题范例气体的摩尔体积计算问题化学习题范例：气体的摩尔体积计算问题摩尔体积是化学中一个重要的概念，它指的是一摩尔气体所占据的体积。

在许多化学计算中，需要用到气体的摩尔体积来解决问题。

本文将以一些典型的化学习题为例，介绍气体摩尔体积的计算方法。

1. 摩尔体积的定义摩尔体积是指在一定的温度和压力下，1摩尔气体所占据的体积，通常用标准状况下的摩尔体积进行计算。

标准状况是指温度为273.15K （0℃）和压力为标准大气压下（1 atm，或约为101.3 kPa）。

2. 摩尔体积的计算公式根据理想气体状态方程PV = nRT，摩尔体积计算公式为V = (RT)/P，其中V为摩尔体积，R为气体常量（8.314 J/(mol·K)），T为温度（K），P为压力（Pa）。

3. 气体摩尔体积的计算实例3.1 问题一：求氢气的摩尔体积根据题目给出的条件，假设温度为25℃（即298K），压力为1 atm。

代入计算公式，可得V = (8.314 J/(mol·K) × 298K) / (1 atm × 101.3kPa/atm) ≈ 24.47 L/mol。

因此，氢气的摩尔体积约为24.47升/摩尔。

3.2 问题二：求氧气的摩尔体积假设温度为27℃（即300K），压力为1.5 atm。

根据计算公式，可得V = (8.314 J/(mol·K) × 300K) / (1.5 atm × 101.3 kPa/atm) ≈ 16.40 L/mol。

因此，氧气的摩尔体积约为16.40升/摩尔。

4. 摩尔体积与气体的物理特性摩尔体积与气体的物理特性密切相关。

不同气体在相同的温度和压力下，其摩尔体积可能不同。

根据理想气体状态方程，摩尔体积与气体分子的质量有关，分子质量越大，摩尔体积越大。

5. 摩尔体积的应用摩尔体积的计算在化学实验和工业生产中具有重要的应用价值。

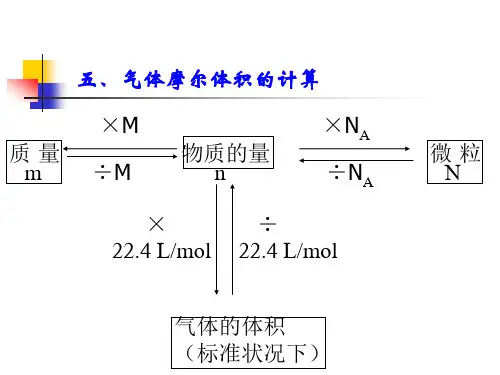
气体摩尔体积
气体摩尔体积通常用Vm表示，计算公式n=V/Vm，Vm表示气体摩尔体积，V表示体积，n表示物质的量。

1、定义：单位物质的量的气体所占的体积叫做气体摩尔体积。

2、公式：Vn=V/n，摩尔体积等于体积除以摩尔质量，但是注意在标准状况（0℃、101kPa）下，气体摩尔体积（Vm）约为22.4L/mol。

对1mol任何气体所占的体积都约是22.4 L的理解：
（1）标准状况（简称标况）：指气体在0℃、100 kPa下的状态。

温度越高，体积越大；压强越大，体积越小。

故在非标况下，其值不一定就是“22.4 L”。

但若同时增大压强，升高温度，或是降低压强和温度，1摩尔任何气体所占的体积有可能为22.4升。

（2）1mol气体在非标准状况下，其体积可能为22.4 L，也可能不为22.4 L。

如在室温（20℃，一个大气压）的情况下气体的体积是24L。

（3）气体分子间的平均距离比分子的直径大得多，因而气体体积主要决定于分子间的平均距离。

在标准状况下，不同气体的分子间的平均距离几乎是相等的，所以任何气体在标准状况下气体摩尔体积都约是22.4 L/mol。

（4）此概念应注意：气态物质；物质的量为1mol；气体状态为0℃和100 kPa（标况）；22.4 L体积是近似值；Vm的单位为L/mol和m3/mol。

（5）适用对象：纯净气体与混合气体均可。

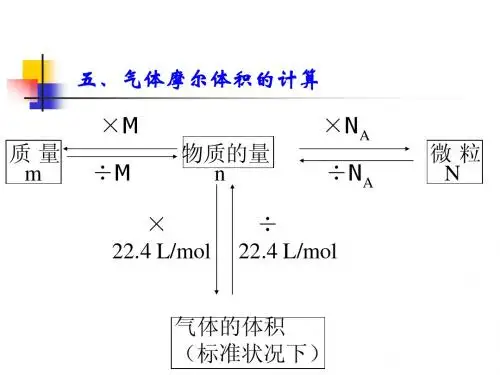
气体的摩尔体积与分压计算在化学和物理学领域中，气体的摩尔体积与分压是两个重要的概念。

摩尔体积指的是单位摩尔气体所占据的体积，而分压则是指在混合气体中每种气体所产生的压力。

在本文中，我们将详细讨论气体摩尔体积与分压的计算方法和相关理论。

一、摩尔体积的计算气体的摩尔体积可以通过摩尔体积公式进行计算。

根据理想气体状态方程，摩尔体积公式可以表示为V = V_0/n，其中V表示气体的体积，V_0表示标准摩尔体积，n表示气体的摩尔数。

标准摩尔体积是指在标准条件下，1摩尔气体所占据的体积，通常情况下为22.4升。

因此，如果我们知道气体的摩尔数，就可以通过将所给的气体体积除以摩尔数来计算摩尔体积。

需要注意的是，以上摩尔体积计算方法仅适用于理想气体的情况。

对于实际气体，由于气体分子之间存在相互作用力，摩尔体积会受到修正。

实际气体的摩尔体积可以通过实验方法获得，例如通过温度、压力和气体间距离的测量来计算。

二、分压的计算在混合气体中，每种气体所产生的压力称为分压。

分压可以通过分压公式来计算。

分压公式可以表示为P_i = P * X_i，其中P_i表示气体i的分压，P表示总压力，X_i表示气体i的摩尔分数。

摩尔分数是指气体i的摩尔数与混合气体总摩尔数之比。

如果我们知道每种气体的摩尔数和总压力，就可以通过将气体i的摩尔数除以总摩尔数，再乘以总压力来计算分压。

需要注意的是，以上分压计算方法同样适用于理想气体的情况。

对于实际气体，同样需要考虑气体分子之间的相互作用力，分压会受到修正。

三、摩尔体积与分压的关系摩尔体积与分压之间存在着一定的关系。

根据道尔顿分压定律和理想气体状态方程，可以得到P_iV_i = n_iRT，其中P_i表示气体i的分压，V_i表示气体i的摩尔体积，n_i表示气体i的摩尔数，R为气体常数，T表示温度。

由于摩尔体积V_i = V_0/n_i，将摩尔体积代入上述公式中，可以得到P_iV_0 = RT。

这个公式说明，在相同的温度和压力下，不同气体的摩尔体积是相等的。

气体的摩尔体积公式好嘞，以下是为您生成的关于“气体的摩尔体积公式”的文章：在我们学习化学的奇妙世界里，有一个非常重要的概念，那就是气体的摩尔体积公式。

这玩意儿就像是一把神奇的钥匙，能帮我们打开理解气体行为的大门。

咱先来说说啥是气体的摩尔体积。

想象一下，气体分子就像一群调皮的小精灵，在空间里自由自在地飞来飞去。

它们之间的距离相对较大，不像固体和液体那样紧密排列。

而气体的摩尔体积呢，简单说就是在特定条件下，一摩尔气体所占的体积。

那气体的摩尔体积公式到底是啥呢？它就是 Vm = V / n 。

这里的Vm 表示气体摩尔体积，V 是气体的体积，n 是气体的物质的量。

还记得我之前给学生们讲这部分内容的时候，有个小同学瞪着大眼睛，一脸迷茫地问我：“老师，这公式到底咋用啊？”我笑着跟他说：“别着急，咱们一起来看看。

”比如说，咱们知道了某气体的体积是 22.4 升，物质的量是 1 摩尔，那用这个公式一计算，气体的摩尔体积不就正好是 22.4 升/摩尔嘛。

这就像是你知道了走的路程和花费的时间，就能算出速度一样。

咱们再深入点说，这个公式在实际生活中也挺有用的。

就拿给气球充气来说吧。

假设你要给一个大气球充满氢气，让它能飘起来。

你得先知道需要多少氢气，这时候就得用气体的摩尔体积公式来算一算啦。

还有啊，在化学实验里，要是想控制气体的产生量或者消耗量，也得靠这个公式来帮忙。

说到这，我想起有一次在实验室里，同学们分组做实验，计算某种气体产生的体积。

有一组同学怎么算都不对，急得满头大汗。

我过去一看，原来是他们把物质的量给算错了。

我引导他们重新梳理思路，最后终于得出了正确的结果，那几个孩子高兴得直拍手。

总之，气体的摩尔体积公式虽然看起来简单，但是作用可大着呢。

只要咱们认真理解，多多练习，就能用它解决好多和气体相关的问题。

所以啊，同学们，可别小看这个公式，它就像是我们在化学世界里的好帮手，能让我们更清楚地了解气体的奥秘。

好好掌握它，咱们就能在化学的知识海洋里畅游得更畅快啦！。

高中化学气体摩尔体积大家好呀！今天咱们来聊聊高中化学里的一个有意思的概念——气体摩尔体积。

这可不是什么高深莫测的东西，其实就是说，同样体积下各种气体里的粒子数目是一样的这么一个规律。

反正就是就是说，不管是哪一种气体，只要占据的体积一样，那它们里面的小分子个数是相等的。

有点像是我们小时候玩的“别人的东西总比自己的多”，哈哈哈！其实这个概念也挺好理解的。

咱们都知道，气体分子之间距离比较远，所以它们的体积并不是由分子自己撑开的，而是由它们所占的空间来决定的。

就好像人多了，房子还是那个房子，不会自己长大变大。

同理，气体摩尔体积就是说，房子不变，但人多了，变成了挤挤挨挨的状态。

1. 什么是气体摩尔体积1.1 气体摩尔体积的概念1.2 摩尔体积的规律那摩尔体积的规律是什么呢？其实很简单嘛，就是说在相同的温度和压力下，不管是哪种气体，它们的摩尔体积都是一样的。

就好像是大家一起排队上车，每个人都占了一样的位置，也不会有人多占少占的情况。

所以摩尔体积这个规律也是符合常理的。

2. 气体摩尔体积的应用2.1 摩尔体积的计算2.2 摩尔体积的实际意义摩尔体积的计算呢，其实也不是什么难事。

只要知道气体的摩尔数和它所占的体积，那摩尔体积就出来了。

有点像是要知道车上有几个人，就数数一下就行了。

而摩尔体积的实际意义嘛，其实就是告诉我们，不同种类的气体在相同的条件下是平等的。

就好像是人在法律面前是一样的，不分贵贱，这样才能保证公平嘛！3. 气体摩尔体积的意义3.1 了解气体的特性3.2 探索气体的奥秘其实，懂得摩尔体积的概念和规律，对我们来说还是挺重要的。

可以帮助我们了解气体的特性，而且在一定程度上也探索了气体的奥秘。

就好像是学会了科学的游戏规则，才能更好地去探索未知的世界嘛！所以，气体摩尔体积这个概念，不管是在学习上还是在生活中，都有着重要的意义。

所以，就这样，今天我们就来聊了聊高中化学里的气体摩尔体积，希望大家能有所收获。

学问就像是一片海洋，只有不断地探索，才能收获更多的宝藏。

标准状态下气体的摩尔体积气体是物质存在的一种状态，它具有可压缩性、扩散性和容易受温度影响的特点。

在一定的条件下，气体的摩尔体积是研究气体性质的重要参数之一。

本文将围绕标准状态下气体的摩尔体积展开讨论。

首先，我们需要了解什么是标准状态。

标准状态是指气体的温度为0摄氏度（273.15K），压强为1标准大气压（101.325kPa）时的状态。

在这种状态下，气体的摩尔体积被称为标准摩尔体积。

标准摩尔体积的大小是一个固定值，对于理想气体来说，其标准摩尔体积为22.414L/mol。

接下来，我们来探讨气体摩尔体积的计算方法。

根据理想气体状态方程PV=nRT（P为气体压强，V为气体体积，n为气体摩尔数，R为气体常数，T为气体温度），我们可以推导出气体摩尔体积的计算公式为V=nRT/P。

在标准状态下，压强P=1标准大气压，温度T=0摄氏度，代入公式中可得V=nR。

由此可见，标准状态下气体的摩尔体积与气体的摩尔数成正比。

那么，气体摩尔体积的大小受到哪些因素的影响呢？首先是气体的摩尔数，摩尔数越大，气体摩尔体积也越大。

其次是气体的温度，根据理想气体状态方程可知，温度越高，气体摩尔体积越大。

最后是气体的压强，压强越大，气体摩尔体积越小。

这些因素共同影响着气体的摩尔体积，使得气体在不同条件下具有不同的摩尔体积。

除了理想气体，实际气体在标准状态下的摩尔体积也有所不同。

由于实际气体分子之间存在一定的相互作用力，导致实际气体的摩尔体积略小于理想气体。

因此，在实际应用中，需要对气体的摩尔体积进行修正，以得到更准确的结果。

总结一下，标准状态下气体的摩尔体积是指气体在0摄氏度、1标准大气压下的摩尔体积。

通过理想气体状态方程，我们可以计算出气体的摩尔体积，并了解到摩尔体积受到摩尔数、温度和压强的影响。

在实际应用中，需要注意实际气体摩尔体积与理想气体的差异，并进行修正。

通过对标准状态下气体摩尔体积的研究，我们可以更深入地了解气体的性质和行为，为相关领域的研究和应用提供理论支持。

气体摩尔体积公式是什么有哪些应用
气体摩尔体积公式是n=V/Vm，气体摩尔体积通常用Vm表示，Vm表示气体摩尔体积，V表示体积，n表示物质的量。

摩尔体积等于体积除以摩尔质量，但是注意在标准状况（0℃、101kPa）下，气体摩尔体积（Vm）约为22.4L/mol。

气体摩尔体积公式是什么
气体摩尔体积通常用Vm表示，计算公式n=V/Vm，Vm表示气体摩尔体积，V表示体积，n表示物质的量。

1、定义：单位物质的量的气体所占的体积叫做气体摩尔体积。

2、公式：Vn=V/n，摩尔体积等于体积除以摩尔质量，但是注意在标准状况（0℃、101kPa）下，气体摩尔体积（Vm）约为22.4L/mol。

气体摩尔体积的应用
标准状况下1mol气体为22.4L，即可导出其质量便是该气体的摩尔质量。

据此可求出未知化学式的气体摩尔质量和相对分子质量，也可求出1L气体的质量即气体密度。

反之也可由气体密度求摩尔质量。

同温同压下两气体的密度比叫气体的相对密度，可据以由气体的相对密度求气体的摩尔质量，如某气体对氢气（H2）的相对密度为15，则其相对分子质量为30。

气体的摩尔体积与摩尔质量计算气体是物质存在的一种形态，其性质与常见的固体和液体有所不同。

在研究和应用气体时，了解其摩尔体积和摩尔质量的计算方法是非常重要的。

本文将介绍气体的摩尔体积和摩尔质量的定义、计算公式以及相关实例，帮助读者更好地理解和运用这些概念。

一、摩尔体积的定义与计算方法摩尔体积是指在标准条件下，1摩尔气体所占据的体积。

通常情况下，标准条件是指温度为273.15K（0摄氏度）和压强为标准大气压（760毫米汞柱）的状态。

摩尔体积的计算可以通过理想气体状态方程来实现，即PV = nRT。

其中，P是气体的压强，V是气体所占据的体积，n是气体的摩尔数，R是气体常数，T是气体的绝对温度。

根据该方程，摩尔体积可以通过测量气体的压强和体积，以及知道气体的摩尔数和温度来计算。

举个例子，假设我们有2摩尔的氧气在标准条件下，气体所占据的体积为V。

现在，我们将温度保持不变，但是将氧气的摩尔数增加到4摩尔。

根据理想气体状态方程，我们可以得到：P × V = n × R × T由于温度和气体常数不变，可以得到：P1 × V = n1 × R × TP2 × V = n2 × R × T通过以上两个方程可以推导得到：P1 × V = P2 × V因此，气体的摩尔体积在保持温度不变的情况下是相等的。

这说明，摩尔体积与摩尔数成正比。

二、摩尔质量的定义与计算方法摩尔质量是指1摩尔物质的质量。

对于气体，摩尔质量与其摩尔质量相关联，可以通过元素的相对原子质量计算得出。

元素的相对原子质量是指元素原子质量与碳12的质量比值。

举个例子，假设我们要计算氧气（O2）的摩尔质量。

根据元素的相对原子质量，氧的相对原子质量为16。

由于氧气由两个氧原子组成，所以氧气的摩尔质量为2乘以氧的相对原子质量，即32克/摩尔。

得知气体的摩尔质量后，我们就能够利用摩尔质量与摩尔体积之间的关系，计算气体的体积。