普通年金和期初年金
- 格式:ppt
- 大小:374.00 KB
- 文档页数:47

《财务管理》综合复习题一. 单项选择题1、财务管理区别于企业其它管理的主要特征在于它是一种( B )。
A、财务管理B、价值管理C、企业管理D、使用价值管理2、作为企业财务管理目标,权益资本利润率最大化目标较之利润最大化目标的优点在于( B )。
A、考虑了资金时间价值因素B、考虑了风险价值因素C、反映了利润与资本之间的关系D、能够避免企业的短期行为3、财务关系是指企业在组织财务活动时与有关方面发生的各种( C )A、货币关系B、结算关系C、经济利益关系D、往来关系4、财务管理的最优目标是( D )A、利润最大化B、每股盈余最大化C、权益资本净利率最大化D、股东财富最大化或企业价值最大化5、在下列经济活动中,能够体现企业与其投资者之间财务关系的是( A )。
A、企业向国有资产投资公司支付利润B、企业向国家税务机关缴纳税款C、企业向其它企业支付货款D、企业向职工支付工资6、在利息不断资本化的条件下,货币时间价值计算的基础是( B )。
A、单利B、复利C、年金D、现值7、一定时期内每期期末等额收付的系列款项是( D )。
A、即付年金B、永续年金C、递延年金D、普通年金8、一定时期内每期期初等额收付的系列款项是( A )。
A、即付年金B、永续年金C、递延年金D、普通年金9、某企业拟进行一项投资,有甲、乙两个方案可供选择:已知甲方案的标准离差为300万元;乙方案的标准离差为330万元;两个方案的预期值相同。
下列结论中正确的是( B )。
A、甲方案的风险等于乙方案B、甲方案的风险大于乙方案C、甲方案的风险小于乙方案D、无法评价10、若某股票的β系数等于1,则下列表述正确的是( C )。
A、该股票的市场风险大于整个市场股票的风险B、该股票的市场风险小于整个市场股票的风险C、该股票的市场风险等于整个市场股票的风险D、该股票的市场风险与整个市场股票的风险无关11、投资者甘愿冒风险进行投资,是因为:( D )。
A、可以获得收入B、可以获得利润C、可以获得时间价值D、可以获得超过时间价值以上的报酬12、下列权利中,不属于普通股股东权利的是( D )。




关于年金的总结1.单利现值P=F/(1+n*i) , 单利现值系数1/(1+n*i)。
2.单利终值F=P*(1+n*i) , 单利终值系数(1+n*i)。
3.复利现值P=F/ (1+i )n =F*(P/F ,i ,n) ,复利现值系数1/(1+i )n ,记作(P/F ,i ,n)。
4.复利终值F=P*(1+i )n =P*(F/P ,i ,n ),复利终值系数(1+i )n , 记作(F/P ,i ,n )。
结论(一)复利终值与复利现值互为逆运算。
(二)复利终值系数 1/(1+i )n 与复利现值系数 (1+i )n 互为倒数。
即 复利终值系数(F/P ,i ,n )与 复利现值系数(P/F ,i ,n)互为倒数。
可查“复利终值系数表”与“复利现值系数表”!5.普通年金终值F=A*(1)1n i i +-=A*(F/A ,i ,n) ,年金终值系数(1)1n i i+-,记作(F/A ,i ,n)。
可查“年金终值系数表”(1)在普通年金终值公式中解出A ,这个A 就是“偿债基金”。
偿债基金A=F*(1)1n i i +-=F*( A/F ,i ,n),偿债基金系数(1)1n i i +-,记作( A/F ,i ,n)。
结论(一)偿债基金 与 普通年金终值 互为逆运算。
(二)偿债基金系数(1)1n i i +-与 普通年金系数(1)1n i i +- 互为倒数。
即 偿债基金系数( A/F ,i ,n) 与 普通年金系数(F/A ,i ,n)互为倒数。
6.普通年金现值P=A*1(1)n i i --+=A*(P/A ,i ,n) , 年金现值系数1(1)n i i--+,记作(P/A ,i ,n )。
可查“年金现值系数表”(1).在普通年金现值公式中解出A ,这个A 就是“年资本回收额”。
年资本回收额A=P* 1(1)n i i --+=P*(A/P ,i ,n) , 资本回收系数1(1)ni i --+,记作(A/P ,i ,n)。

例如:本金为50000元,利率或者投资回报率为3%,投资年限为30年,那么,30年后所获得的利息收入,按复利计算公式来计算就是:50000×(1+3%)30由于,通胀率和利率密切关联,就像是一个硬币的正反两面,所以,复利终值的计算公式也可以用以计算某一特定资金在不同年份的实际价值。
只需将公式中的利率换成通胀率即可。
这均是时间价值问题,简单来讲,今天的100元不等于5年后的100元,那5年后的100元相当于今天的多少呢?这就需要贴现,即用100乘以期限为5,相应利率的复利现值系数,而如果要知道今天的100元相当于5年后的多少呢?则用100乘以复利终值系数,也就是求本利和。
这里的复利终值系数和复利现值系数都是在复利计算下推出的。
(一次性收付款)年金是每隔相同时间就发生相等金额的收付款,比如房租,如果发生时间在每期期末,则称为普通年金,如果以后5年中每年末可以得到100元,相当于今天能得多少(从时间价值考虑,肯定不是500元)就要用100乘以普通年金现值系数 ,反之,比如每年末存银行100元,在复利下5年能得到多少?则用100乘以年金终值系数复利终值系数、复利现值系数是针对一次性收付款,而年金终值系数和年金现值系数是系列收付款,而且是特殊的系列收付款不知道明白没有,最好能看看财务管理中时间价值章节终值的计算终值是指货币资金未来的价值,即一定量的资金在将来某一时点的价值,表现为本利和。
单利终值的计算公式:f=p(1+r×n)n复利终值的计算公式:f = p(1+r)式中f表示终值;p表示本金;r表示年利率;n表示计息年数其中,(1+r)n称为复利终值系数,记为fvr,n,可通过复利终值系数表查得。
现值的计算现值是指货币资金的现在价值,即将来某一时点的一定资金折合成现在的价值。
单利现值的计算公式:复利现值的计算公式:式中p表示现值;f表示未来某一时点发生金额;r表示年利率;n表示计息年数其中称为复利现值系数,记为pvr,n,可通过复利现值系数表查得。




期末年金的计算公式一、年金定义年金(Annuity)是指一定时期内每次等额收付的系列款项,通常用A来表示。
年金最初就是指一年一次的付款,但是后来有很多跟年金一样的性质的付款出现,但是其时间间隔不是一年,还有的是一年一次的收款,慢慢的,年金的指代的范围就扩大了,虽然现在年金所指代的范围扩大了,但是依然沿用年金这个叫法;年金的特点在于等额、等期、等息,是一种理想化的收付款项,等额是指每次收付款的金额相等,等期是指经过相同的时间间隔就会发生一次收付款,等息是指年金整个收支过程,利率是保持不变的。
二、年金的分类按照年金收付款时间点和其他收付条件的不同,年金分为普通年金、预付年金、递延年金和永续年金;普通年金:又称为后付年金,是指从第一期起,在连续间隔期相等的多个时期中,每期期末收付等额年金的年金;预付年金:又称先付年金、即付本金或期初年金,是指从第一期起,在连续间隔期相等的多个时期中,每期期初等额收付的系列款项,预付年金与普通年金的区别仅在于收付款时间点不同,普通年金发生在期末,而预付年金发生在期初。
递延年金:是指在第一期开始,递延一定时期后,开始在在连续间隔期相等的多个时期中,每期期末支付等额年金的年金,递延年金是普通年金的一种特殊形式;永续年金:是等额收付年金的期限无限的一种特殊的普通年金。
三、年金的计算年金是一种特殊形式的收付款项,核算年金的目的是帮助使用者衡量收支,所以年金的应用在于计算年金的终值F(Future Value或者Final Value,也叫本利和,即本金和利息的和)和现值P(Present Value),当然有时候也会要计算收付次数n(n也代表年金收支的期数)、利率i、年金A。
计算年金的时候,不是站在收款方或者付款方的角度,而是站在一个与年金收付无关系的第三方角度,来计算年金的现值和终值;因为年金现值和终值的计算基础是资金的复利计算,所以先介绍资金在复利情况下现值和终值的计算:复利现值:P=F*(1+i)^-n,(1+i)^-n也称为复利现值系数,记作(P/F,i,n)复利终值:F=P*(1+i)ⁿ,(1+i)ⁿ也称为为复利终值系数,记作(F/P,i,n)普通年金现值和终值的计算普通年金现值和终值的计算也就是将每一次的收付款按复利计算现值或终值,然后在再加总求和;原始公式:P=A(1+i)^-1+A(1+i)^-2+……+A(1+i)^-nF=A(1+i)^1+A(1+i)^2+……+A(1+i)^(n-1)公式中的每一项对应的就是年金中的一次收付款,通过将每一次收付款按照复利现值(复利终值)公式算出现值(终值)之后,再求和,就得到年金现值(年金终值)的公式了;如果使用该公式计算,年金收付次数较多时,计算起来很繁琐,为了方便计算,通过推导可以将公式简化如下:P=A*[1-(1+i)^-n]/iF=A*[(1+i)^n-1]/i将公式右边年金以外部分视为系数(分别称作年金现值系数和年金终值系数),通过查询相关系数表找出对应的值,可以进一步简化计算;P=A*(P/A,i,n)F=A*(F/A,i,n)例题:2020年初张某因工作原因要出国工作三年,拟在银行存入一笔款项请家人分次取出正好付清三年房屋物业费,每年支付两次,一次是6月末一次是12月末,每次3000元,若存款年利率是6%,那么张某出国前应存入银行多少钱?((P/A,3%,6)=5.4172)该题中求的是普通年金现值,因为每年支付两次,三年就是6次,收付款次数n=6,利率也要与收付款间隔期对应,所以利率i=3%;可以使用原始公式进行计算,就是将每一次支付的物业费按其支付的时间点折现到2020年初,然后再将所有现值的和加起来,就可以得到年金现值,在这里十三就不详细列出原始公式计算过程了;用年金现值系数可以算出P=3000*(P/A,3%,6)=16251.60预付年金现值和终值的计算原始公式:P=A(1+i)^-1+A(1+i)^-2+……+A(1+i)^-(n-1)F=A(1+i)^2+A(1+i)^3+……+A(1+i)^(n)和普通年金的原始公式计算的原理相同,公式中的每一项对应的是预付年金中的一次收付款,通过将每一次收付款按照复利现值(终值)公式算出现值(终值)之后,再求和,就得到预付年金现值(终值)的公式了;预付年金同样可以通过推导进行简化,但是还有一个更加简便的方法,预付年金和普通年金的区别在于收付款的时间点,普通年金收付款的时间点在每期的期末,而预付年金的收付款时间点在每期的期初,这个差异就导致预付年金每一次收付款的现值要比普通年金收付款的现值少折现一次,也就是少除以一次(1+i),所以预付年金的现值可由普通年金现值公式算出:P=A*(P/A,i,n)*(1+i)同样的原理,对于预付年金的终值,每一次收付款的终值要比普通年金多算一次利息,也就是多乘以一次(1+i),所以预付年金的终值就等于F=A*(F/A,i,n)*(1+i)如此一来,预付年金的现值和终值都等于普通年金的现值和终值乘以(1+i),对于预付年金的计算就转化成了普通年金的计算;例题:某公司拟在5年后还清100万元债务,从现在起每年年初存入银行一笔款项。
年金知识讲解
1.年金的含义
年金(annuity)是指间隔期相等的系列等额收付款。
同时具备三个要素:①每次金额相等;②固定间隔期;③多笔。
2.年金的种类
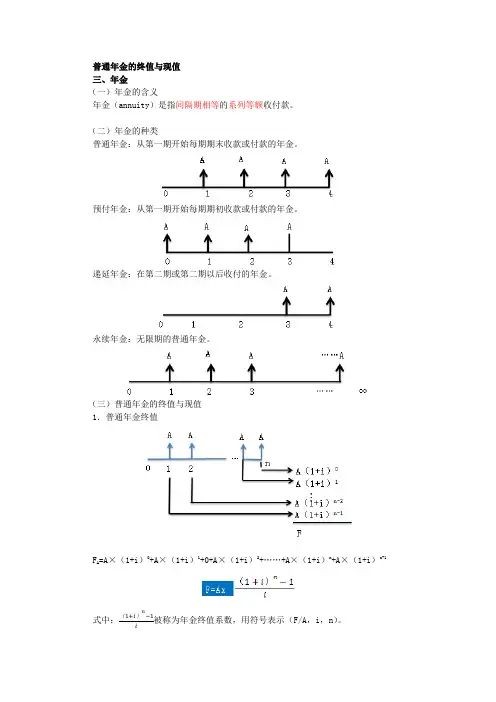
普通年金:从第一期开始每期期末收款或付款的年金。
预付年金:从第一期开始每期期初收款或付款的年金。
递延年金:在第二期或第二期以后收付的年金。
永续年金:无限期的普通年金。
(四)年金的终值和现值
1.普通年金的终值与现值
(1)普通年金终值
式中:被称为年金终值系数,用符号表示(
经计算可得:
式中:被称为年金现值系数,。