克莱姆法则课后习题

格式：ppt
大小：1.38 MB
文档页数：43

下载文档原格式

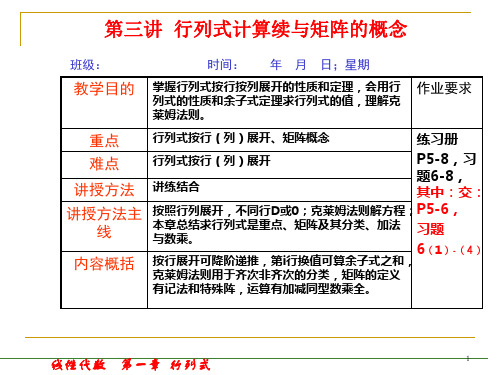
克莱姆法则解线性方程组三

或
D a ij Aij a1 j A1 j a 2 j A2 j a nj Anj j 1,2,, n
i 1
n
一、行列式计算（续） 1.递推行列式例1：计算下列行列式
1 1 0 0 1 1 Dn 0 0 0 0 0 1 1 1
线性代数
0 0 0 0 1 1 0 1 1 1 1
内容概括讲练结合讲授方法行列式按行列展开难点行列式按行列展开矩阵概念重点作业要求掌握行列式按行按列展开的性质和定理会用行列式的性质和余子式定理求行列式的值理解克莱姆法则
第三讲行列式计算续与矩阵的概念
班级：时间：年月日；星期
教学目的重点
掌握行列式按行按列展开的性质和定理，会用行列式的性质和余子式定理求行列式的值，理解克莱姆法则。行列式按行（列）展开、矩阵概念
2 5 0 2 4.
2 5
线性代数
第一章行列式
17
第三讲行列式计算续与矩阵的概念
例3（2001.4）设行列式
3 0 4 2 2 2 D 0 7 0 5 3 2
0 2 0 2
则第4行各元素余子式之和的值为_____
分析：本题求得是余子式，可将其转换为代数余子式求解，即
M41 M42 M43 M44 A41 A42 A43 A44
a11 a1n
a11 Ai 1 a12 Ai 2 a1n Ain

a11 a1n a j1
线性代数第一章行列式
0 a jn
13
an1 ann
第三讲行列式计算续与矩阵的概念
同理，用第j行元素对应取代第i行元素，则由于行列式两行元素相等，得0值。 a11 a1n

线性代数课后习题与答案

《线性代数》课程习题第1章行列式习题 1.11．计算下列二阶行列式：（1）2345 （2）2163- （3）xxx x cos sin sin cos - （4）11123++-x x x x（5）2232ab b a a （6）ββααcos sin cos sin （7）3log log 1a b b a2．计算下列三阶行列式：（1）341123312-- （2）00000d c b a （3）d c e ba 0000 （4）zy y x x 00002121（5）369528741 （6）01110111-- 3．用定义计算行列式：（1）4106705330200100 （2）1014300211321221---（3）5000000004000300020001000 (4)dcb a 100110011001---.4.用方程组求解公式解下列方程组:(1) ⎪⎩⎪⎨⎧=-+=--=--0520322321321321x x x x x x x x x (2)⎪⎩⎪⎨⎧=+-=-+=++232120321321321x x x x x x x x x习题 1.21．计算下列行列式：（1）123112101 (2)15810644372---- （3）3610285140 （4）6555655562.计算行列式（1）2341341241231234（2）12114351212734201----- （3）524222425-----a a a（4）322131399298203123- （5）0532004140013202527102135---- 3.用行列式的性质证明：（1）322)(11122b a b b a a b ab a -=+（2）3332221113333332222221111112c b a c b a c b a a c c b b a a c c b b a a c c b b a =+++++++++ 4.试求下列方程的根：（1）022223356=-+--λλλ（2）0913251323221321122=--x x5.计算下列行列式（1）8364213131524273------ （2）efcfbfde cd bdae ac ab---（3）2123548677595133634424355---------- （4）111110000000002211n n a a a a a a ---（5）xaaa x a a a x（6）abb a b a b a 000000000000习题 1.31．解下列方程组（1）⎪⎩⎪⎨⎧-=++=+--=++1024305222325321321321x x x x x x x x x （2）⎪⎪⎩⎪⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x2． k 取何值时，下列齐次线性方程组可能有非零：(1) ⎪⎩⎪⎨⎧=+-=++-=++0200321321321x x x x kx x kx x x (2)⎪⎩⎪⎨⎧=+-=++=++0300321321321x x x x kx x x x kx 习题五1.41．计算下列行列式（1）3010002113005004，（2）113352063410201-- （3）222111c b a c b a（4）335111243152113------，（5）nn n n n b a a a a a b a a a a D ++=+212112111112．用克莱姆法则解线性方程（1）⎪⎩⎪⎨⎧=+-=-+=--114231124342321321321x x x x x x x x x (2)⎪⎪⎩⎪⎪⎨⎧=++=+-+=+-+=++3322212543143214321321x x x x x x x x x x x x x x3．当λ为何值时，方程组⎪⎩⎪⎨⎧=+-=+-=++0020321321321x x x x x x x x x λλ可能存在非零解？4.证明下列各等式(1) 222)(11122b a b b a a b ab a -=+(2) ))()((4)2()1()2()1()2()1(222222222c b a c a b c c c b b ba a a ---=++++++ (3) ))()()()()()((111144442222d c b a d c d b c b d a c a b a d c b a d c b a d c b a+++------=5.试求一个2次多项式)(x f ,满足1)2(,1)1(,0)1(-==-=f f f .第2章矩阵习题 2.21．设 ⎥⎦⎤⎢⎣⎡=530142A ， ⎥⎦⎤⎢⎣⎡-=502131B ， ⎥⎦⎤⎢⎣⎡--=313210C ，求3A -2B +C 。

线性代数第3版习题全解（上海交通大学）

习题1.11. 计算下列行列式：(1) 7415； ()()c o s s i n 2;3s i n c o s xy z x x zx y x x yzx-； ()2cos 1412cos 1012cos x x x；(5)xy x y yx y x x yxy+++。

解：(1)7415=7×5−1×4=31；(2) 1D =；(3) ()111x y zy zyz D x y zx y x y z x y x y zz x z x++=++=++++ ()3331030yzx y z x yy z x y z xyz z yx z=++--=++---。

(4)22cos 10014cos 2cos 12cos 112cos 1012cos 012cos x x x x x xx--=2314cos 2cos 8cos 4cos 12cos x xx x x--=-=-。

(5) xy x y y x y x x yx y+++=2()()()()()x x y y yx x y yx x y x y x y +++++-++33y x --3322x y =--2. 用行列式方法求解下列线性方程组：(1) 31528x y x y +=-⎧⎨+=⎩； (2)1231231323142543x x x x x x x x -+=⎧⎪++=⎨⎪+=⎩。

解：(1) 123111311,10,29528258D D D --====-==, 121210,29D Dx x D D==-== (2) 12131134253,42527,10131D D --==-==- 242132114453,42418131103D D -====，3121239,1,6D D Dx x x D D D====-==-。

3．求下列各排列的逆序数：(1) 34215； (2) 13…(2n −1)(2n )(2n −2)…2。

行列式性质计算克莱姆法则

问题：当aij与Akj的脚标不一样时，
ai1Ak1+ai2Ak2+...+ainAkn=？
☺ 恰好 A 中第 k 行用第 i 行代替！
克莱姆法则
当 i=k 时，
ai1Ak1+ai2Ak2+...+ainAkn=det A
当 i≠k 时，
ai1Ak1+ai2Ak2+...+ainAkn=0
若按列展开，有类似的结论
行列式的性质和计算
行初等变换
交换矩阵 A 第 i、j 行（ri rj ）
第 i 行乘数 k （kri）
第 j 行乘 k 加到第 i 行（ri+krj ）
行初等变换
交换矩阵 A 第 i、j 行（ri rj ）
第 i 行乘数 k （kri）
第 j 行乘 k 加到第 i 行（ri+krj ）
=(-1)n det A 由于 n 为奇数，det A=0
例4 求 det D
a b b b a b D b b b
b b a
例4 求 det D
a b b b a b D b b b
b b a
注意 D 的行之间具有“循环”性质将其他行加到第一行，第一行相等
A21 A22 A2 n
An1 An 2 Ann
则 AA*=det A En ，称A*伴随矩阵 1 1 若 A 可逆，则 A A* det A
克莱姆法则
对于线性方程组
a11 x1 a12 x2 a1n xn b1 a x a x a x b 21 1 22 2 2n n 2 an1 x1 an 2 x2 ann xn bn

线性代数第3版习题全解上海交通大学

线性代数第3版习题全解上海交通大学(总85页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题1. 计算下列行列式：(1)7415； ()()cos sin 2;3sin cos x y z x x zx y x xyzx-； ()2cos 10412cos 1012cos x x x； (5)xy x y yx y x x yxy+++。

解：(1)7415=7×5−1×4=31；(2) 1D =；(3) ()111x y zy zyz D x y zx y x y z x y x y zzx zx++=++=++++()3331030y zx y z x yy z x y z xyz z yx z=++--=++---。

(4) 22cos 10014cos 2cos 12cos 112cos 1012cos 012cos x x x x x xx--=2314cos 2cos 8cos 4cos 12cos x xx x x--=-=-。

(5)xy x y y x y x x yxy+++=2()()()()()x x y y yx x y yx x y x y x y +++++-++33y x --3322x y =--2. 用行列式方法求解下列线性方程组：(1) 31528x y x y +=-⎧⎨+=⎩； (2) 1231231323142543x x x x x x x x -+=⎧⎪++=⎨⎪+=⎩。

解：(1) 123111311,10,29528258D D D --====-==,121210,29D Dx x D D==-== (2) 12131134253,42527,10131D D --==-==- 242132114453,42418131103D D -====， 3121239,1,6D D Dx x x D D D====-==-。

线性代数—克莱姆法则

8
取何值时，例2 问 λ 取何值时，齐次线性方程组 λ x 1 + x 2 + x 3 = 0 有非零解？有非零解？ x1 + λx 2 + x 3 = 0 x + x + λx = 0 2 3 1 解
1 1 1 λ+2 1 1 D = 1 λ 1 = λ + 2 λ 1 = ( λ + 2) ⋅ 1 λ 1 1 1 λ λ+2 1 λ 1 1 λ 1 1 1 1 1 0 = (λ + 2)(λ − 1) 2 , = ( λ + 2) ⋅ 0 λ − 1 0 0 λ −1
解

2 1 −5 1 1 −3 0 −6 D= 0 2 −1 2 1 4 −7 6
r1 − 2r2 r4 − r2
− 5 13 1 −3 0 −6 0 2 −1 2 0 7 0 7 −7 12
4
− 5 13 7 − 5 13 1 −3 0 −6 = −2 −1 2 = 0 2 −1 2 7 − 7 12 0 7 − 7 12 0 7
第四节
音乐
如果线性方程组
a11 x1 + a12 x 2 + L + a1n x n = b1 a x + a x + L + a x = b 21 1 22 2 2n n 2 LLLLLLLLLLLL a n1 x1 + a n 2 x 2 + L + a nn x n = bn
λ
所以当 λ = −2 或 λ = 1 时,方程组有非零解. 方程组有非零解.
9
练习：练习：
P28 习题一
10
END

习题1-5-克莱姆法则

1、用克莱姆法则解下列线性方程组：()1251372x y x y +=⎧⎨+=⎩；【解】方程组系数矩阵为2537D =141510=-=-≠，方程组有惟一解，由于115710327D ==-=-；22143132D ==-=，得方程组惟一解为 1331D x D -===-，2111D y D ===--。

()2121264105729x x x x -=⎧⎨+=⎩。

【解】方程组系数矩阵为64422062057D -==+=≠，方程组有惟一解，由于110470116186297D -==+=；261017450124529D ==-=，得方程组惟一解为 11186362D x D ===，22124262D x D ===。

2、用克莱姆法则解下列线性方程组：()123527222544x y z x y z x y z +-=-⎧⎪-+=⎨⎪-+=⎩；【解】方程组系数矩阵为112527254D -=--21312c c c c -+1005717278--23 r r -100309278-1 r 按展开 0978-630=≠，知方程组有惟一解，由于13122227454D --=--12323 2c c c c ++01016231156----1 r 按展开 163116---63=；21325227244D --=21323 2c c c c ++1005371721081 r 按展开 3717108126=， 31135222254D -=--21313c c c c -+157372710--1 r 按展开 737710--189=，得方程组惟一解为163163D x D ===，2126263D y D ===，3189363D z D ===。

()2 20230 0bx ay ab cy bz bc cx az -+=⎧⎪-+-=⎨⎪+=⎩，其中0abc ≠。

【解】方程组按标准形整理为 2 23 0bx ay ab cy bz bc cx az -=-⎧⎪-+=⎨⎪+=⎩，于是得系数矩阵为0230ba D cb ca-=-203000abc abc =-+----50abc =-≠，知方程组有惟一解，由于1202300ab a D bcc b a--=-2240000a bc a bc =++--+25a bc =； 22030b ab D bc b ca -=226000abc ab c =-+--25ab c =-；32020baab D cbc c --=-2200400abc abc =+----25abc =-，得方程组惟一解为2155D a bc x a D abc ===--，2255D ab c y b D abc -===-，2355D abc z c D abc-===-。

克莱姆法则汇总

4. 计算行列式（考题，3分）设m阶行列式|A|=a, n阶行列式|B|=b,
a11 a1m C am1 b11 b1n bn1 bnn 0 amm
A
B 0
, 则C
解
将第n+1列作n次相邻交换，到第1列，…，将第 n+m列作n次相邻交换，到第m列,共作了mn次列交换，得：
xn (a1n A1 j a2 n A2 j ann Anj ) b1 A1 j b2 A2 j bn Anj
j 1： x1 D D1
j 2： x2 D D2
j n ： x n D Dn
xj
由定理4和定理5

Dj D
j 1,2, , n 证毕
解法二：化成三角形行列式
解法三：按第一行展开
2.计算行列式（考题）
a2 1
ab 1
b2 1
D 2a a b 2b
解法一：
(a b)2 0 0
D
2l2 l1 , l3 l1
a b 2b (a b)2 a b 2b 1 1 1 1
ab b 2
(a b)3
x1 (a11 A1 j a21 A2 j an1 Anj )

用D的第j列元素的代数余子式乘两边对应相加整理
x2 (a12 A1 j a22 A2 j an 2 Anj )
xn (a1n A1 j a2 n A2 j ann Anj )
4. 计算行列式（考题，3分）
设m阶行列式|A|=a, n阶行列式|B|=b,
a11 a1m C am1 b11 b1n bn1 bnn

克拉默法则及习题课

机动目录上页下页返回结束
例２解
解设 D5中第1,2,3,4,5行的元素分别为a1 p1 , a2 p2 , a3 p3 , a4 p4 , a5 p5 , 那么，由D5中第1,2,3,4,5行可能的非零元素分别得到
p1 2,3;
p 1,2,3,4,5; 2
p3 1,2,3,4,5;
典型例题
典型例题
一、计算排列的逆序数二、计算（证明）行列式三、克拉默法则
机动目录上页下页返回结束
一、计算排列的逆序数（例１）
一、计算排列的逆序数
例１求排列 2k12k 122k 232k 3
k 1k 的逆序数,并讨论奇偶性.
解 2k排在首位,故逆序数为0; 1的前面比1大的数有一个(2k ), 故逆序数为1; (2k 1)的前面比(2k 1)大的数有一个(2k),故
§7 克拉默（克莱姆）法则
一、克拉默法则
a11 x1 a12 x2 a1n xn b1
若线性方程组
a21 x1 a22 x2 a2n xn b2
(8)
an1 x1 an2 x2 ann xn bn
的系数行列式不等于零，即
a11 a12 a1n
D
a21
a22
cd bd ad
把上面右端行列式第2行加到第1行，再从第1行
中提取公因子a b c d，得
D４ (a b c d )(a b c d ) 110
• dc ac bc, cd bd ad
机动目录上页下页返回结束
再将第2列减去第1列，得 D4 (a b c d )(a b c d )
5 2 2 D 2 6 0
2 0 4
5 6 4 44 46

克莱姆法则

2 12
1 4 7 6 0 7 7 12
3 0
7
5 1 7
3 3
机动目录上页下页返回结束
定理1 设线性非齐次方程组(*)的系数行列式
a11 L a1n
D M
M0
an1 L ann
则(*)有唯一解
x1

D1 D
,
x2

D2 D
,L
,
xn

Dn D
即:
xj

Dj D
其中,
a11 L
Dj M an1 L
a1, j1 b1 a1, j1 L MMM
a11 x1 a12 x2 L a1n xn b1
a21 x1 a22 x2 L a2n xn b2 (*)

M
an1 x1 an2 x2 L ann xn bn
或表示为 n
aij x j bi
j 1
i 1, 2,L , n
n个未知量n个方程的线性方程组, 在系数行列式不为零时的行列式解法, 称为克莱姆 (Cramer)法则.
j1

1 D bi D
＝bi ( i＝1, 2, …, n)

Q
n
aij Akj
j 1

D, 0,
ki ki

a11 L a1, j1 b1 a1, j1 L a1n
Dj M an1 L
MMM an, j1 bn an, j1 L
M 将Dj按第j列展开 ann
有非零解, 则 D＝0
(定理2的逆否命题)
注:定理3说明D＝0是齐次线性方程组有非零解的必要条件.

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

17
2(2)证明
c a d a c d a c b c a b
b b d d
=0
=
c−a a−c 0 a c d
0 b
a−c c−a 0 0 c a b d
=
0 a
0 c
0 d
0 b
a−c c−a 0 0 c a b d
=0
18
P 5(1) 18
a 0 L 1 0 a L 0 O 1 0 L a
M M L x−a
= [ x + ( n − 1)a ]( x − a ) n−1
20
利用行列式的性质使得行列式中零尽量的多
x a 计算Dn = M a
a L a x L a M M M a L x a L a 1 a L a x L a 1 x L a = ( x + ( n − 1)a ) M M M M M M M a L x
Dx j = Dj ( j = 1,2,L, n).
(2)
9
机动目录上页下页返回结束
a11 x1 + a12 x 2 + L + a1n x n = b1
a 21 x1 + a 22 x 2 + L + a 2 n x n = b 2
(4.1)
a n1 x1 + a n 2 x 2 + L + a nn x n = b n 克莱姆法则可叙述为：克莱姆法则可叙述为：
i=(1, 2, …, n )
a1, i +1 M a1n M M M a n, i +1 M a nn
7
证明
j A 用D中第列元素的代数余子式 1 j , A2 j ,L, Anj
( , 依次乘方程组1)的n个方程得
(a11 x1 + a12 x2 + L+ a1n xn ) A1 j = b1 A1 j (a x + a x + L+ a x ) A = b A 21 1 22 2 2n n 2j 2 2j L L L L L L L L L L L L (an1 x1 + an2 x2 + L+ ann xn ) Anj = bn Anj
1 0 M 0 L a x−a L M 0 a 0
解二：
c1 + c 2 +Lc n
x + ( n − 1)a = x + ( n − 1)a M x + ( n − 1)a
Dn
1 a L x
ri − r1
i = 2Ln
= ( x + ( n − 1)a )
M M L x−a
= [ x + ( n − 1)a ]( x 3; a12 x2 + L + a1n xn = 0
a 21 x1 + a 22 x 2 + L + a 2n x n = 0
(4.2)
…
a n1 x1 + a n 2 x 2 + L + a nn xn = 0
为齐次线性方程组，而(4.1)称为非齐次的线性方程组. 显然 x1= x2 = … = xn = 0 是 (4.2) 的解(零解).
非齐次线性方程组; 非齐次线性方程组若常数项b1 , b2 ,L, bn 全为零 , 此时称方程组为齐次线性方程组此时称方程组为齐次线性方程组. 齐次线性方程组
5
机动目录上页下页返回结束
克莱姆法则) 定理1 克莱姆法则定理 (克莱姆法则设 n 个变量 n 个方程的线性方程组为
a11 x1 + a12 x 2 + L + a1n x n = b1
−3 −5 3 − 0 −1 0 −7 −7 −2
−3 3 = = 27, −7 −2
1 −5 1 −3 0 −6 D1 = − 5 2 −1 2 0 4 −7 6 8 9
−5 1 0 −6 D2 = 0 − 5 −1 2 1 0 −7 6 2 1 8 9
= 81,
= −108,
15
机动目录上页下页返回结束
(i = 1, 2, L , n) D = a1 j A1 j + a 2 j A2 j + L + a nj Anj = ( j = 1, 2, L , n)
k =1
n
Σ aik Aik
n
k =1
Σ akj Akj
1
关于代数余子式, 还有下列定理行列式的任一行(列的所有元素与另行列式的任一行列 )的所有元素与另一行(列的对应元素的代数余子式乘一行列 )的对应元素的代数余子式乘积之各等于零. 积之各等于零
行（列）和相等
21
P 5(3) 18
3计算
2 1 1 2 0 1 0 0 0 0
0 0 L 0 1 0 L 0 2 1 L 0 L L 0 0 L L 2 1 1 2
1
0
0
L 0
2 1 1 2 0 1
0
0
L 0
1 0 L 0 2 1 L 0 1 2 1 L 0 = L L L L 0 0 L 2 1 0 0 0 L 2 1 0 0 L 1 2 0 0 0 L 1 2 n−2
Dn xn = D
则方程组(4.1)有唯一解,且解可表示为
D1 x1 = , D
D2 , x2 = D
L,
6
其中 Di ( i = 1, 2, …, n)是用常数项 b1, b2,…, bn代替 D 中第 i列各元素而得到的 n 阶行列式, 即
a11 M a1, i −1 b1 Di = M M M M a n1 M a n, i −1 bn
D4 27 x4 = = = 1. D 27
16
机动目录上页下页返回结束
例3 问
λ
为何值时，为何值时，齐次线性方程组
(5 − λ ) x + 2 y + 2 z = 0 2 x + (6 − λ ) y = 0 2 x + (4 − λ ) z = 0
有非零解? 有非零解?
x1 + x 2 − 2 x3 + x 4 = 1
x1 + x 2 + x 4 = 2
x1 + x3 − x 4 = 1
1 −1 1 21 − 1 1 1 −D = 1 18 1D 2 − D = − 10 2 1 2 1 1 D 0 −1 1 4 8 1 = 1= − 1 = 0 故 1 x1 0 1 D − 10 5
按第一列展开
1计算
按第一行展开
a 0 L 0 0 a L 0 O 0 0 L a n −1
0 a 0L 0 + (−1)
n +1
=a
0 0 aL 0 O 1 0 0L 0
a 0 L 0 n +1 n 0 a L 0 n n−2 n = a −a = a + (−1) ⋅ (−1) O 0 0 L a n−2
n −1
按第一列展开
0 0 L 0 1 0 L 0 2 1 L 0 − =2 L L 0 0 0 L 2 1 0 0 0 L 1 2 n −1 2 1 1 2 0 1
1 2
− 2 9 1D = −5 D = −3 =− 3 4 0 1
D2 9 = 1 x2 − 1 = D 10
D4 3 x4 = = D 10
D3 − 5 1 x3 = = = D − 10 2
13
例2.
用克莱姆法则解方程组
2x1 + x2 − 5x3 + x4 = 8, x − 3x − 6x = 9, 1 2 4 2x2 − x3 + 2x4 = −5, x1 + 4x2 − 7x3 + 6x4 = 0.
a 21 x1 + a 22 x 2 + L + a 2 n x n = b 2
(4.1)
a n1 x1 + a n 2 x 2 + L + a nn x n = b n 如果系数行列式
………………
D=
a11 a 21 L a n1
a12 L a1n a 22 L a 2n ≠0 L L L a n 2 L a nn
19
P 5(2) 18
.
x a L a a 2计算Dn = M x L a M M M
a L x−a L M 0
a a L x
解一：
Dn =
ri − r1
x a− x M a− x
a 0
i = 2Ln
M M L x−a L a x−a L M 0 a 0
c1 + c 2 +Lc n
=
x + ( n − 1)a 0 M 0
………………
结论1. 若线形方程组（4.1)系数行列式 ≠ 0，系数行列式D 结论1 若线形方程组（系数行列式，则它一定有唯一解. 则它一定有唯一解线形方程组（等价若线形方程组（4.1)无解或有两个不同无解或有两个不同解，则必有系数行列式D = 0. 则必有系数行列式
10
在方程组(4.1)中, 若b1=b2=…=bn=0, 即
阶行列式，引理一个 n阶行列式，如果其中第 i 行所有元素除 aij外都为零，那末这行列式等于 aij与它的外都为零，代数余子式的乘积，代数余子式的乘积，即 D = aij Aij ．展开定理) 定理(Laplace展开定理行列式等于它的展开定理任一行(列任一行列) 的各元素与其对应的代数余子式乘积之和. 子式乘积之和 D = ai1 Ai1 + ai 2 Ai 2 + L + ain Ain =