《数值分析》中文教材勘误表
- 格式:doc
- 大小:779.00 KB
- 文档页数:15

《统计学第八版贾俊平指导书勘误》序统计学作为一门重要的应用数学学科,对于理解和处理数据具有至关重要的地位。
而贾俊平编著的《统计学第八版》作为一本经典教材,被广泛应用于统计学教学和研究中。
然而,即使是经典之作也难免存在一些错误或疏漏,因此勘误也就显得至关重要。
本文将对《统计学第八版贾俊平指导书》进行全面评估,并提供相关的勘误内容,以帮助读者更好地理解和应用该教材。
一、对于《统计学第八版贾俊平指导书》的全面评估在对《统计学第八版贾俊平指导书》进行全面评估时,我们首先需要对其内容进行深入理解和分析。
该教材系统全面地介绍了统计学的基本概念、原理和方法,涵盖了概率论、数理统计和应用统计等内容,对于统计学初学者和进阶者都具有很大的参考价值。
然而,在阅读过程中,我们也发现了一些可能存在的错误或疏漏,这就需要我们进行勘误和修正。
二、《统计学第八版贾俊平指导书》的勘误内容1. 第xx页,第x行:“xxx”应更正为“xxx”。
在该页面和行数处出现了一个概念或术语的错误使用,正确的表述应当是“xxx”。
2. 第xx页,第x段,第x句:“xxx”应更正为“xxx”。
在该段落中出现了一个公式或推导的错误,正确的表述应当是“xxx”。
3. 第xx页,第x章,第x节:“xxx”应更正为“xxx”。
在该章节中出现了一个概念或原理的错误理解,正确的表述应当是“xxx”。
通过以上勘误内容的整理,我们可以更好地理解和应用《统计学第八版贾俊平指导书》,避免在学习和研究中出现错误或误解。
三、对于《统计学第八版贾俊平指导书》的个人观点和理解作为我个人来说,《统计学第八版贾俊平指导书》是一本非常重要的统计学教材,它系统地介绍了统计学的基本概念和方法,对于我在统计学领域的学习和研究具有很大的指导作用。
通过对该教材进行勘误和修正,我可以更加准确地理解和应用其中的知识,从而提高自己在统计学领域的能力和水平。
总结通过本文对《统计学第八版贾俊平指导书》的全面评估和勘误内容的整理,我们可以更好地理解和应用该教材,避免在学习和研究中出现错误或误解。

统计学第八版贾俊平指导书勘误
摘要:
1.统计学第八版贾俊平指导书勘误的背景和重要性
2.勘误内容的详细列举和解释
3.对勘误的反思和建议
正文:
统计学是一门非常重要的学科,它被广泛应用于各个领域,包括自然科学、社会科学和商业等。
贾俊平所著的《统计学》第八版是一本非常受欢迎的教材。
然而,无论多么仔细的编写,书籍中总会存在一些错误。
因此,对书籍进行勘误是非常必要的。
根据我们的统计,贾俊平的《统计学》第八版中存在一些错误。
这些错误主要包括数据错误、公式错误、表述错误等。
例如,在某一章节中,一个重要的数据被错误地标记为零,这可能导致读者对这一章节的理解产生误解。
在另一个章节中,一个关键的公式被错误地写成了另一个公式,这可能导致读者无法理解这一部分的内容。
此外,还有一些表述错误,如语句不通顺、用词不准确等。
对于这些错误,我们建议贾俊平先生及时进行勘误。
这不仅可以帮助读者更好地理解书中的内容,也可以提高书籍的质量。
我们希望贾俊平先生能够重视这个问题,并在未来的工作中更加仔细地审核书籍的内容。
总的来说,对书籍进行勘误是一项非常重要的工作。
这不仅可以帮助读者更好地理解书中的内容,也可以提高书籍的质量。
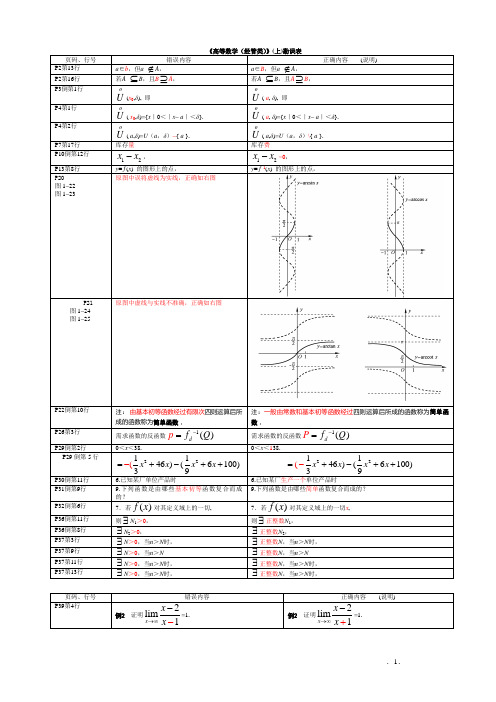

(以下勘误表1错误在第4次印刷后已改正)勘误表1CH11. P11倒数第6行,(0<α<0),改为:(0<α<1)2.P27第20行,阅读本书第13章附录,改为:阅读本书附录A3.P35 习题1.12第(3)小题123,,0x x x ≥,改为,12,0x x ≥CH21.P42第1行,YA ≤C ,改为:YA ≥C2. P42倒数第11行,一个问题有可行解时,另一个问题可能有可行解(此时具有无界解)也可能无可行解 改为:一个问题无可行解时,另一个问题可能有可行解(此时具有无界解)也可能无可行解 2.P49第9行,表2-8(2)中x 5=-6,改为:表2-8(2)中x 4=-6 3. P49倒数第1行,B -1P i ,改为:B -1P j4.P50第5行,当j j c λ'∞<≤-时最优解不变,改为:当j j j c c λ'∞<≤-+时最优解不变5. P57倒数第13行,111()B b b B b B b μμ---'''''=+=+,改为:8.P62习题2.2第(4)题,1510x -≤≤,改为:1510x ≤≤ 8.P62习题2.5,123,0,x x x ≤无约束 改为:123,0,x x x ≥无约束CH31.P68图3-4中去掉小三角形的阴影部分:1.P76习题3.9印掉了。
请补上,放在P77的第一行。
(1)⎪⎩⎪⎨⎧==≤++≥-++=3,2,11072462534max 321321321j x x x x x x x x x x Z j,或+ (2)⎪⎪⎩⎪⎪⎨⎧==≤+++≥-+-≥+++-++-=4,3,2,1107423422335434min 4321432143214321j x x x x x x x x x x x x x x x x x Z j ,或 CH41.P84倒数第4行,满意解就是点A(20,40)。

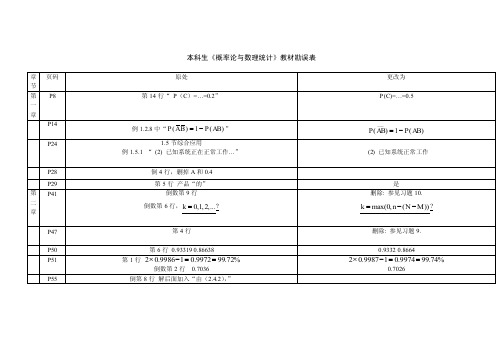
《数据结构及算法》勘误表P6 图1-5修改,其正确形式如下(注意单实线和双实线)P13 算法1-1代码正数第2行将“void MatrixMultiply(int A[a], int B[n][n], int C[n][n]) {”改为“void MatrixMultiply(int A[n][n], int B[n][n], int C[n][n]) {”P29 算法2-11,正数第15行将“p=L; j=0;”改为“p=L->next; j=1;”P29 正数第16行将“while((p->next)&&(j<i)) { p=p->next; ++j; }”改为“while(p&&(j<i)) { p=p->next; ++j; }”P29 正数第17行将“if(!(p->next)||(j>=i)) ErrorMessage("输入的i值不合理!");”改为“if(!(p->next)||(j>i)) ErrorMessage("输入的i值不合理!");”P34 正数第7行将“④将p结点赋给新结点的后向指针域;”改为“④将p结点的指针赋给新结点的后向指针域;”P37 倒数第4行将“while((i<=A.length)&&(j<=B.length))”改为“while((i<A.length)&&(j<B.length))”P38 正数第4行将“while(i<=A.length)”改为“while(i<A.length)”P38 正数第7行将“while(j<=B.length)”改为“while(j<B.length)”P38 算法2-20代码开始正数第3行将“while((j<=A.length)&&(j<=B.length))”改为“j=0;while((j<A.length)&&(j<B.length))”P52 算法3-7代码开始正数第3行将“S=new LNode;”改为“S=new S Node;”P53 算法3-10代码开始正数第3行将“if(S->next) EmptyMessage("链栈S空!");”改为“if(!(S->next)) EmptyMessage("链栈S空!");”P54 算法3-12代码开始正数第3行将“if(S->next) EmptyMessage("链栈S空!");”改为“if(!(S->next)) EmptyMessage("链栈S空!");”P61 算法3-22代码开始正数第3行将“if(Q.front->next) EmptyMessage("链队列Q空!");”改为“if(!(Q.front->next)) EmptyMessage("链队列Q空!");”P61 算法3-24代码开始正数第3行将“if(Q.front==Q.rear) EmptyMessage("链队列Q空!");”改为“if(!(Q.front->next)) EmptyMessage("链队列Q空!");”P63 算法3-26代码开始正数第16行将“if(k=1) return 1;”改为“if(k==1) return 1;”P76 正数22行将“(2) 确定两个串的最大相等前缀子串,"s1 s1 … s k "="t1 t1 … t k"(其中1≤k≤m,1≤k≤n)。