北邮-作业-高等数学

北京邮电大学高等数学答案一、单项选择题（共20道小题，共100.0分）设的定义域为则的定义域为___________.函数是定义域内的____________.A.周期函数B.单调函数C.有界函数D.无界函数设，则__________.函数设与分别是同一变化过程中的两个无穷大量，则时与无穷小时,与为等价无穷小则__________.____________._________.M.0N. 1下列计算极限的过程，正确的是____________.设在处连续,则_________.Q. 2设 ,则（）设且可导，则（）已知，则（）R. 1设，则（）设设则曲线处的切线方程为设存在，则等于（设函数可导，则（函数函数的周期是___________.是____________.A.单调函数B.周期函数C.D.函数是___________.E.F.G.非奇非偶函数H.既是奇函数又是偶函数设（为常数），则___________.设，则__________.下列各对函数相同的是________.I.与J.与与设与分别是同一变化过程中的两个无穷大量，则存在是W.无关的条件设在处连续，且时，，则_________.AA.2设函数，则的连续区间为______________.设且可导，则（）设，则（）设则( )设，则（）设,且,则( )设设则的定义域为函数函数F.周期函数G.H.函数是___________.I.J.K.L.既是奇函数又是偶函数下列函数中为奇函数的是__________.设（为常数），则___________.函数的定义域是____________._____________.O. 2____________.设在处连续，且，则_________.设函数，则的连续区间为设且可导，则（设则(设,且,则( )W. 1设,则( )X.99Y.99!曲线在点(0,1)处的切线方程为( )设曲线在点M处的切线斜率为3，则点M的坐标为（）CC.(1,1)设函数可导，则（）一、单项选择题（共20道小题，共100.0分）1.若设则的定义域为2.函数G.有界函数3.(错误)下列函数中为奇函数的是__________.4.(错误)当时，与比较是______________.A.高阶无穷小C.非等价的同阶无穷小D.低阶无穷小5._________.A.0B. 16.(错误)下列计算极限的过程，正确的是____________.7.(错误)下列变量在给定的变化过程中为无穷小量的是_____________.8.(设9.(存在是在处连续的10.(错误)设函数，则的连续区间为______________.11.(错误)函数的连续区间为___________.12.设且可导，则（）13.(错误)设则（）14.(错误)设则( )15.(错误)16.(设存在，则等于（17.设在点可导，则（1.(若，，则___________.2.函数的反函数是____________.3.(错误)函数的周期是___________.4.(错误)函数是定义域内的____________.A.周期函数5.下列函数中为奇函数的是__________.6.(错误)设（为常数），则___________.7.(错误)8.(的定义域为9.(与与与与10.(_____________.C. 211.(错误)____________.A. 112.(错误)___________.A.0B. 113.存在是在处连续的_________.D.无关的条件14.(错误)设 ,则（）15.(错误)设则( )16.(17.(设则18.(处的切线方程为(19.(设曲线在点20.(设函数可导，则（）。

高等数学北邮第2版介绍《高等数学北邮第2版》是由北京邮电大学出版社出版的教材，主要面向高等院校的理工科专业学生。

本教材是高等数学领域的经典教材之一，经过多年的使用和改进，逐渐发展成为一本综合性的高等数学教材。

本教材分为多个部分，涵盖了高等数学的各个方面，包括数列与极限、函数与连续、导数与微分、定积分与定积分应用、常微分方程等内容。

每个章节都以理论知识和例题相结合的形式，旨在帮助学生深入理解高等数学的概念和原理，并培养学生的数学思维和解题能力。

目录1.数列与极限2.函数与连续3.导数与微分4.定积分与定积分应用5.常微分方程6.二重积分与曲线积分7.空间解析几何数列与极限在数学中，数列是将自然数映射到数域的一个函数。

数列的极限是数列中接近某一特定值的值。

数列与极限是高等数学中的重要概念，它们贯穿了高等数学的各个领域。

本章介绍了数列的基本概念和性质，包括数列的定义、极限的定义和性质、极限存在准则等等。

通过学习本章，学生将掌握数列的极限计算方法，并能够应用数列的极限解决实际问题。

函数与连续函数是数学中的一个基本概念，它描述了两个数集之间的对应关系。

连续是函数在某一点处没有跳跃或间断的特性，连续性是函数中的一个重要概念。

本章介绍了函数的基本概念和性质，包括函数的定义、函数的运算、反函数与复合函数等。

同时，本章还介绍了连续函数的定义和性质，并通过例题讲解了如何判断函数的连续性以及如何应用连续函数解决实际问题。

导数与微分导数是函数在某一点处的变化率，微分是函数在某一点处的近似变化量。

导数与微分是高等数学中的核心概念，它们在数学和物理等领域具有广泛的应用。

本章介绍了导数的定义和性质，包括导数的计算公式、导数的几何意义、高阶导数等。

同时，本章还介绍了微分的定义和性质，包括微分的近似计算、微分中值定理等。

通过学习本章，学生将掌握导数和微分的计算方法，并能够应用导数和微分解决实际问题。

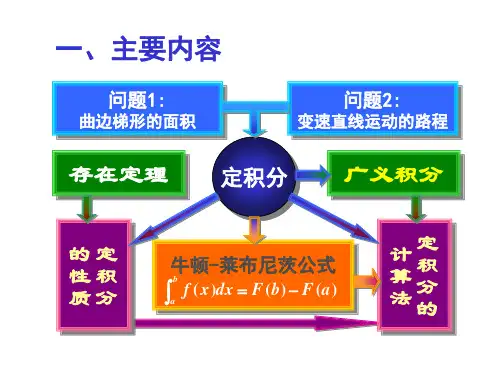
定积分与定积分应用定积分是计算曲线下面积的数学工具，定积分应用是将定积分应用于实际问题的过程。

北邮大一高等数学教材高等数学是大学数学的一门基础课程，对于计算机科学与技术专业的学生来说尤为重要。

北邮是国内知名的信息科学与技术高校之一，其大一高等数学教材的编写是经过精心策划和整理的。

下面将对北邮大一高等数学教材的内容进行简要介绍，并探讨其在培养学生数学思维和解决实际问题能力方面的优势。

【第一章：极限与连续】该章节是高等数学中的重要概念，也是后续学习的基石。

从基本的函数极限与趋近性开始，逐渐引入函数的连续性与间断点等内容。

此外，该教材在讲解定积分的概念时，强调与极限的联系，为后续章节的学习打好基础。

【第二章：微分学】微分学是高等数学中的经典部分，也是大学数学中的难点之一。

北邮的教材紧密围绕求导原理与法则展开，注重引入相关函数的导数与微分，并着重解释微分的几何意义。

通过数学公式的推导和实际问题的应用，教材在培养学生的推理能力和问题解决能力方面具有明显的优势。

【第三章：数值级数与函数级数】数值级数与函数级数是高等数学中的重要内容之一。

北邮的教材着重讲解级数的收敛性和敛散判别法则，并以实际问题为例，引导学生在解决实际问题时灵活运用级数概念。

此外，教材还对一些常用的基本级数进行了详细的介绍，为学生的数学运算提供了便利。

【第四章：多元函数微分学与多重积分】多元函数的微分学与多重积分是数学中的重要分支。

北邮的教材从函数的极限与连续开始，引入了多元函数的偏导数与全微分的定义，为后续的多元函数微分学打下了基础。

同时，教材对二重积分和三重积分进行了详细的解释与实例讲解，帮助学生理解积分的几何和物理意义。

【第五章：曲线积分与曲面积分】曲线积分与曲面积分是高等数学中的重要概念，并在物理学和工程学等学科中得到广泛应用。

北邮的教材在这一章节中详细介绍了曲线积分和曲面积分的概念、性质及相关公式，并给出了一些常见的曲线积分和曲面积分的计算方法，培养学生的应用能力和解决实际问题的能力。

总之，北邮大一高等数学教材在内容编排和讲解方式上都非常合理和专业。

北邮高数考试题库及答案一、选择题（每题4分，共20分）1. 函数f(x)=x^2+2x+1的导数为：A. 2x+2B. 2x+1C. 2xD. x^2+2答案：A2. 极限lim(x→0) (sin(x)/x)的值为：A. 1B. 0C. -1D. ∞答案：A3. 以下哪个函数是偶函数：A. f(x) = x^2B. f(x) = x^3C. f(x) = x^2 + xD. f(x) = x^2 - x答案：A4. 定积分∫(0,1) x^2 dx的值为：A. 1/3B. 1/2C. 1D. 2答案：A5. 以下哪个级数是收敛的：A. 1 + 1/2 + 1/4 + 1/8 + ...B. 1 + 1/2 + 1/3 + 1/4 + ...C. 1 - 1/2 + 1/4 - 1/8 + ...D. 1 + 2 + 3 + 4 + ...答案：C二、填空题（每题4分，共20分）6. 函数f(x)=x^3-3x的二阶导数为______。

答案：6x-37. 极限lim(x→∞) (x^2-3x+2)/(x^3+2x^2-5)的值为______。

答案：08. 函数f(x)=e^x的不定积分为______。

答案：e^x + C9. 定积分∫(-1,1) (x^2-2x+1) dx的值为______。

答案：2/310. 级数1/2 + 1/4 + 1/8 + ...的和为______。

答案：1三、计算题（每题10分，共30分）11. 求函数f(x)=x^2-4x+3的极值点。

解：首先求导数f'(x)=2x-4，令f'(x)=0，解得x=2。

将x=2代入原函数，得到极小值点(2, -1)。

12. 计算极限lim(x→0) (x^2+3x-2)/(x^3-x+1)。

解：分子分母同时除以x^3，得到lim(x→0) (1+3/x^2-2/x^3)/(1-1/x^2+1/x^3)。

当x→0时，极限不存在。

北京邮电大学高等数学教材高等数学是大学理科类专业中的一门重要课程，对于学生的数学素养和理解能力具有重要的意义。

作为北京邮电大学的学生，我们需要学习并掌握高等数学的基本知识和方法，以便在今后的学习和科研工作中能够有所作为。

北京邮电大学的高等数学教材是经过精心编撰和审定，专门为我们学校的学生设计的。

该教材从理论与实践相结合的角度出发，将重点放在基本概念及其应用、定积分与定积分的应用、微分方程等内容上，以全面提升学生的数学素养。

以下将对北京邮电大学高等数学教材的特点和优势进行介绍。

首先，北京邮电大学高等数学教材注重理论与实践的结合。

教材中不仅包含了丰富的理论知识，还通过大量的例题和习题对知识进行了实际运用，使学生能够更好地理解和掌握数学的基本概念和方法。

同时，教材还结合了实际问题的解决方法，帮助学生将抽象的数学理论与实际问题相结合，培养学生的应用能力。

其次，教材的内容设计合理、层次清晰。

教材分为多个章节，每个章节都按照一定的逻辑顺序进行布局，使学生能够系统地学习和理解高等数学的各个知识点。

每个章节的开篇部分均有一段简短的引言，引导学生对本章内容的整体把握，同时对与以往章节的联系进行了明确说明，使学生能够更好地掌握所学知识。

教材还设置了许多习题，供学生进行巩固和拓展，以帮助学生全面掌握所学内容。

第三，教材的语言简练易懂。

教材在内容的讲解中使用了通俗易懂的语言，避免使用过于复杂的数学术语和推导过程。

同时，教材中穿插了一些生动的例子，使抽象的数学理论更加具体形象，有助于学生的理解和记忆。

教材的语言风格优美流畅，条理清晰，有助于学生更加容易地掌握高等数学的知识。

综上所述，北京邮电大学高等数学教材具有理论与实践相结合、内容设计合理、语言简练易懂等优势。

它不仅能够帮助学生全面掌握高等数学的基本知识和方法，还能够培养学生的应用能力和解决实际问题的能力。

相信通过学习这本教材，我们将能够在高等数学中取得优异的学习成绩，为今后的学习和科研工作打下坚实的基础。

习题选解第一章 习题选解.习 题 1－11．若2(+1)x +3x 5f x =+，求 ()f x ．解： 因为 ()22(+1)x +3x 5=1(1)3f x x x =+++++， 所以 2()3f x x x =++.2．下列各题中，函数)(x f 与)(x g 是否相同？为什么？（1） 24)(2--=x x x f ，2)(+=x x g ； 解：因为)(x f 的定义域为(,2)(2,)-∞⋃+∞，而()g x 的定义域为(,)-∞+∞，所以()f x 与()g x 定义域不同，因此()f x 与()g x 不相同．（2） 2)13()(-=x x f ，13)(-=x x g ；解：因为()f x 与()g x 定义域相同，对应法则相同，故()f x 与()g x 相同．（3） 11ln )(-+=x x x f ，)1ln()1ln()(--+=x x x g ； 解：由10101x x x -≠⎧⎪+⎨>⎪-⎩解出()f x 的定义域为(,1)(1,)-∞-⋃+∞，而由1010x x +>⎧⎨->⎩解出()g x 的定义域为(1,)+∞，所以()f x 与()g x 定义域不同，因此()f x 与()g x 不相同． （4） 11ln )(2++=x x x f ，)1ln()1ln()(2+-+=x x x g ． 解：因为()f x 与()g x 定义域相同，对应法则相同，故()f x 与()g x 相同．3．设⎩⎨⎧>+≤-=11121)(2x x x x x f ， ， ，求 )0(f ，)1(f ，)1(-f ，)23(f ，)23(-f ． 解：(0)1f =，(1)1f =-，(1)3f -=，313()24f =，313()24f -=． 4．设函数y()f x =是以T>0为周期的周期函数，证明(a )(0为常数)f x a >是以a T为周期的周期函数，并求出函数y sin 3cos 2x x =+的周期．证：因为 a (+)()()=+=⎡⎤⎣⎦T f a x f ax T f ax ，所以(a )f x 是以aT 为周期的周期函数。

北邮新编高等数学教材答案第一章：导数和微分1.求下列函数的导数：(1) f(x) = x^3 + 2x^2 - 3x + 1(2) f(x) = sin(x) + cos(x)(3) f(x) = e^x / (1 + e^x)第二章：定积分1.计算下列定积分：(1) ∫(0 to π) sin(x) dx(2) ∫(-∞ to ∞) e^(-x^2) dx(3) ∫(1 to 2) ln(x) dx第三章：多元函数微分学1.求下列函数的偏导数：(1) f(x, y) = x^2 + y^2 - xy(2) f(x, y) = e^x sin(y)第四章：多元函数的极限与连续性1.计算下列函数的极限：(1) lim (x, y)→(0, 0) (x^2 + y^2) / sqrt(x^2 + y^2)(2) lim (x, y)→(1, 1) (x^2 + y^2) / (x + y - 2)第五章：一阶常微分方程1.求解下列一阶常微分方程：(1) dy/dx + y = x(2) dy/dx = y/x第六章：多元函数的极值与条件极值1.求函数 f(x, y) = x^2 + xy + y^2 在D={(x,y)|x^2 + y^2 ≤ 4} 上的极值。

第七章：重积分1.计算下列二重积分：(1) ∬(D) x^2 + y^2 dA, D = { (x, y) | x^2 + y^2 ≤ 1 }(2) ∬(D) e^(-x^2-y^2) dA, D = { (x, y) | x^2 + y^2 ≤ 2, x ≥ 0, y ≥ 0 }第八章：二阶常微分方程1.求解二阶常微分方程：(1) d^2y/dx^2 + 2dy/dx + 2y = 0(2) d^2y/dx^2 + 4dy/dx + 4y = sin(x)第九章：无穷级数1.求下列级数的和：(1) ∑(n=1 to ∞) 2^n / 3^n(2) ∑(n=0 to ∞) n/(n^2+4)第十章：傅里叶级数与傅里叶变换1.求函数 f(x) = x 在[-π, π] 上的傅里叶级数展开式。