2020年中考数学专题训练：圆(含答案)

2020年九年级中考数学压轴题专项训练：圆的综合卷（含答案）1．如图，点O为Rt△ABC斜边AB上的一点，∠C＝90°，以OA为半径的⊙O与BC交于点D，与AC交于点E，连接AD且AD平分∠BAC．（1）求证：BC是⊙O的切线；（2）若∠BAC＝60°，OA＝2，求阴影部分的面积（结果保留π）（1）证明：连接OD，∵AD平分∠BAC，∴∠BAD＝∠DAC，∵AO＝DO，∴∠BAD＝∠ADO，∴∠CAD＝∠ADO，∴AC∥OD，∵∠ACD＝90°，∴OD⊥BC，∴BC与⊙O相切；（2）解：连接OE，ED，∵∠BAC＝60°，OE＝OA，∴△OAE为等边三角形，∴∠AOE＝60°，∴∠ADE＝30°，又∵∠OAD＝∠BAC＝30°，∴∠ADE＝∠OAD，∴ED∥AO，∴四边形OAED是菱形，∴OE⊥AD，且AM＝DM，EM＝OM，∴S△AED ＝S△AOD，∴阴影部分的面积＝S扇形ODE＝＝π．2．如图，已知AB是⊙O的直径，AC是⊙O的弦，点E在⊙O外，连接CE，∠ACB的平分线交⊙O于点D．（1）若∠BCE＝∠BAC，求证：CE是⊙O的切线；（2）若AD＝4，BC＝3，求弦AC的长．（1）证明：连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠ACO+∠BCO＝90°，∵OA＝OC，∴∠OAC＝∠OCA，∵∠BAC＝∠BCE，∴∠ACO＝∠BCE，∴∠BCE+∠BCO＝90°，∴∠OCE＝90°，∴CE是⊙O的切线；（2）解：连接BD，∵∠ACB的平分线交⊙O于点D，∴∠ACD＝∠BCD，∴＝，∴AD＝BD，∵AB是⊙O的直径，∴∠ADB＝90°，∴△ADB是等腰直角三角形，∴AB＝AD＝4，∵BC＝3，∴AC＝＝＝．3．如图，AB是⊙O的直径，AE平分∠BAF，交⊙O于点E，过点E作直线ED⊥AF，交AF的延长线于点D，交AB的延长线于点C．（1）求证：CD是⊙O的切线；（2）∠C＝45°，⊙O的半径为2，求阴影部分面积．（1）证明：连接OE ．∵OA ＝OE ，∴∠OAE ＝∠OEA ，又∵∠DAE ＝∠OAE ，∴∠OEA ＝∠DAE ，∴OE ∥AD ，∴∠ADC ＝∠OEC ，∵AD ⊥CD ，∴∠ADC ＝90°，故∠OEC ＝90°．∴OE ⊥CD ，∴CD 是⊙O 的切线；（2）解：∵∠C ＝45°，∴△OCE 是等腰直角三角形，∴CE ＝OE ＝2，∠COE ＝45°，∴阴影部分面积＝S △OCE ﹣S 扇形OBE ＝2×2﹣＝2﹣．4．如图①，BC 是⊙O 的直径，点A 在⊙O 上，AD ⊥BC 垂足为D ，弧AE ＝弧AB ，BE 分别交AD 、AC 于点F 、G ．（1）判断△FAG的形状，并说明理由；（2）如图②若点E与点A在直径BC的两侧，BE、AC的延长线交于点G，AD的延长线交BE于点F，其余条件不变（1）中的结论还成立吗？请说明理由．（3）在（2）的条件下，若BG＝26，DF＝5，求⊙O的直径BC．解：（1）△FAG等腰三角形；理由：∵BC为直径，∴∠BAC＝90°，∴∠ABE+∠AGB＝90°，∵AD⊥BC，∴∠ADC＝90°，∴∠ACD+∠DAC＝90°，∵弧AE＝弧AB，∴∠ABE＝∠ACD，∴∠DAC＝∠AGB，∴FA＝FG，∴△FAG是等腰三角形；（2）成立；∵BC为直径，∴∠BAC＝90°∴∠ABE+∠AGB＝90°∵AD⊥BC，∴∠ADC＝90°，∴∠ACD+∠DAC＝90°，∵弧AE＝弧AB，∴∠ABE＝∠ACD，∴∠DAC＝∠AGB，∴FA＝FG，∴△FAG是等腰三角形；（3）由（2）知∠DAC＝∠AGB，且∠BAD+∠DAC＝90°，∠ABG+∠AGB＝90°，∴∠BAD＝∠ABG，∴AF＝BF，又∵AF＝FG，∴F为BG的中点∵△BAG为直角三角形，∴AF＝BF＝BG＝13，∵DF＝5，∴AD＝AF﹣DF＝13﹣5＝8，∴在Rt△BDF中，BD＝＝12，∴在Rt△BDA中，AB＝＝4，∵∠ABC＝∠DBA，∠BAC＝∠ADB＝90°∴△ABC∽△DBA，∴＝，∴＝，∴BC＝，∴⊙O的直径BC＝．5．如图，已知矩形ABCD的边AB＝6，BC＝4，点P、Q分别是AB、BC边上的动点．（1）连接AQ、PQ，以PQ为直径的⊙O交AQ于点E．①若点E恰好是AQ的中点，则∠QPB与∠AQP的数量关系是∠QPB＝2∠AQP；②若BE＝BQ＝3，求BP的长；（2）已知AP＝3，BQ＝1，⊙O是以PQ为弦的圆．①若圆心O恰好在CB边的延长线上，求⊙O的半径；②若⊙O与矩形ABCD的一边相切，求⊙O的半径．解：（1）①∵点E恰好是AQ的中点，∠ABQ＝90°，∴BE＝AE＝EQ，∴∠EAB＝∠EBA，∴∠QEB＝2∠EBP，∵以PQ为直径的⊙O交AQ于点E，∴∠QPB＝∠QEB，∠PBE＝∠PQA，∴∠QPB＝2∠AQP，故答案为：∠QPB＝2∠AQP；②∵BE＝BQ，∴∠BEQ＝∠BQE，且∠BPQ＝∠BEQ，∴∠BPQ＝∠BQE，∴tan∠BPQ＝tan∠BPQ，∴，∴，∴BP＝（2）①如图1，过点O作OE⊥PQ，∵AP＝3，AB＝6，∴BP＝3，∴PQ＝＝＝，∵OE⊥PQ，∴QE＝PE＝，∵cos∠PQB＝＝，∴＝∴OQ＝5，∴⊙O的半径为5；②如图2，若⊙O与BC相切于点Q，连接OQ，过点O作OE⊥PQ于E，∴EQ＝PE＝，∵BC是⊙O切线，∴OQ⊥BC，且AB⊥BC，∴OQ∥AB，∴∠OQP＝∠BPQ，∴cos∠OQP＝cos∠BPQ，∴，∴∴OQ＝；如图3，若⊙O与AB相切于点P，连接OP，过点O作OE⊥PQ于E，∴EQ＝PE＝，∵AB是⊙O切线，∴OP⊥AB，且AB⊥BC，∴OP∥BC，∴∠OPQ＝∠PQB，∴cos∠OPQ＝cos∠PQB，∴∴，∴OP＝5；如图4，若⊙O与AD相切于点M，连接OM，OQ，OP，延长MO交BC于F，作OH⊥AB于H 点，∴OM⊥AD，且BC∥AD，∴OF⊥BC，∵∠A＝∠B＝∠AMO＝∠OFB＝∠OHB＝90°，∴四边形AHOM，OHBF是矩形，∴OM＝AH，OH＝BF，∵OQ2＝OF2+FQ2，OP2＝OH2+PH2，∴OQ2＝（6﹣OQ）2+（BF﹣1）2，OQ2＝BF2+（OQ﹣3）2，∴OQ＝5﹣若图5，若⊙O与CD相切于点N，连接ON，OQ，OP，延长NO交BC于E，作OH⊥BC于H 点，同理可得：OP2＝PE2+OE2，OQ2＝OH2+QH2，∴OQ2＝（3﹣OH）2+（4﹣OQ）2，OQ2＝OH2+（4﹣OQ﹣1）2，∴OQ＝35﹣6．6．如图，在矩形ABCD中，E是BC上一点，连接AE，将矩形沿AE翻折，使点B落在CD边F处，连接AF，在AF上取一点O，以点O为圆心，OF为半径作⊙O与AD相切于点P．AB ＝6，BC＝，（1）求证：F是DC的中点．（2）求证：AE＝4CE．（3）求图中阴影部分的面积．（1）证明：由折叠的性质可知，AF＝AB＝6，在Rt△ADF中，DF＝＝＝3，∴CF＝DC﹣DF＝3，∴DF＝FC，即F是CD的中点；（2）证明：在Rt△ADF中，DF＝3，AF＝6，∴∠DAF＝30◦，∴∠BAF＝60◦，由折叠的性质可知，∠EAF＝∠EAB，∠AFE＝∠B＝90°，∴∠EAF＝∠EAB＝30°，∴AE＝2EF，∠EFC＝180°﹣∠AFD﹣∠AFE＝30◦，∴EF＝2CE，∴AE＝4CE；（3）解：连接OP、OH、PH，∵⊙O与AD相切于点P，∴OP⊥AD，∴OP∥DF，∵∠DAF＝30°，∴∠AOP＝90°﹣∠DAF＝60°，OF＝OP＝OA，∴∠OFH＝∠AOP＝60°，OP＝OF＝2，∴AP＝＝2，∴DP＝AD﹣AP＝，∵∠OFH＝60°，OH＝OF，∴△OHF为等边三角形，∴∠FOH＝∠OHF＝60°，HF＝OF＝2，∴DH＝DF﹣HF＝1，∵OP∥DF，∴∠POH＝∠OHF＝60°，∴∠POH＝∠HOF，∴＝，∴阴影部分的面积＝△PDH的面积＝×DH×DP＝．7．如图，Rt△ABC中，∠ABC＝90°，以AB为直径作⊙O交AC于点D，连接BD．（1）求证：∠A＝∠CBD．（2）若AB＝10，AD＝6，M为线段BC上一点，请写出一个BM的值，使得直线DM与⊙O 相切，并说明理由．（1）证明：∵AB为⊙O直径，∴∠ADB＝90°，∴∠A+∠ABD＝90°．∵∠ABC＝90°，∴∠CBD+∠ABD＝90°，∴∠A＝∠CBD；（2）BM＝．理由如下：如图，连接OD，DM，∵∠ADB＝90°，AB＝10，AD＝6，∴BD＝＝8，OA＝5，∵∠A＝∠CBD，∵Rt△CBD∽Rt△BAD，∴＝，即＝，解得BC＝取BC的中点M，连接DM、OD，如图，∵DM为Rt△BCD斜边BC的中线，∴DM＝BM，∵∠2＝∠4，∵OB＝OD，∴∠1＝∠3，∴∠1+∠2＝∠3+∠4＝90°，即∠ODM＝90°，∴OD⊥DM，∴DM为⊙O的切线，此时BM＝BC＝．8．如图，AB是⊙O的直径，直线MC与⊙O相切于点C．过点A作MC的垂线，垂足为D，线段AD与⊙O相交于点E．（1）求证：AC是∠DAB的平分线；（2）若AB＝10，AC＝4，求AE的长．（1）证明：连接OC，∵直线MC与⊙O相切于点C，∴∠OCM＝90°，∵AD⊥CD，∴∠ADM＝90°，∴∠OCM＝∠ADM，∴OC∥AD，∴∠DAC＝∠ACO，∵OA＝OC，∴∠ACO＝∠CAO，∴∠DAC＝∠CAB，即AC是∠DAB的平分线；（2）解：连接BC，连接BE交OC于点F，∵AB是⊙O的直径，∴∠ACB＝∠AEB＝90°，∵AB＝10，AC＝4，∴BC＝＝＝2，∵OC∥AD，∴∠BFO＝∠AEB＝90°，∴∠CFB＝90°，F为线段BE中点，∵∠CBE＝∠EAC＝∠CAB，∠CFB＝∠ACB，∴△CFB∽△BCA．∴＝，即＝，解得，CF＝2，∴OF＝OC﹣CF＝3．∵O为直径AB中点，F为线段BE中点，∴AE＝2OF＝6．9．如图，AB是⊙O的直径，点C是圆上一点，点D是半圆的中点，连接CD交OB于点E，点F是AB延长线上一点，CF＝EF．（1）求证：FC是⊙O的切线；（2）若CF＝5，tan A＝，求⊙O半径的长．（1）证明：如图，连接OD．∵点D是半圆的中点，∴∠AOD＝∠BOD＝90°，∴∠ODC+∠OED＝90°，∵OD＝OC，∴∠ODC＝∠OCD．又∵CF＝EF，∴∠FCE＝∠FEC．∵∠FEC＝∠OED，∴∠FCE＝∠OED．∴∠FCE+∠OCD＝∠OED+∠ODC＝90°，即FC⊥OC，∴FC是⊙O的切线；（2）解：∵tan A＝，∴在Rt△ABC中，＝，∵∠ACB＝∠OCF＝90°，∴∠ACO＝∠BCF＝∠A，∵△ACF∽△CBF，∴＝＝＝．∴AF＝10，∴CF2＝BF•AF．∴BF＝．∴AO＝＝．10．如图，AB是⊙O的直径，弦DE垂直半径OA，C为垂足，DE＝6，连接DB，∠B＝30°，过点E作EM∥BD，交BA的延长线于点M．（1）求的半径；（2）求证：EM是⊙O的切线；（3）若弦DF与直径AB相交于点P，当∠APD＝45°时，求图中阴影部分的面积．解：（1）连结OE，∵DE垂直OA，∠B＝30°，∴CE＝DE＝3，，∴∠AOE＝2∠B＝60°，∴∠CEO＝30°，OC＝OE，由勾股定理得OE＝2；（2）∵EM∥BD，∴∠M＝∠B＝30°，∠M+∠AOE＝90°，∴∠OEM＝90°，即OE⊥ME，∴EM是⊙O的切线；（3）再连结OF，当∠APD＝45°时，∠EDF＝45°，∴∠EOF＝90°，S＝π（2）2﹣（2）2＝3π﹣6．阴影11．如图，Rt△ABC中，∠C＝90°．BE平分∠ABC交AC于点D，交△ABC的外接圆于点E，过点E作EF⊥BC交BC的延长线于点F．请补全图形后完成下面的问题：（1）求证：EF是△ABC外接圆的切线；（2）若BC＝5，sin∠ABC＝，求EF的长．（1）证明：补全图形如图所示，∵△ABC是直角三角形，∴△ABC的外接圆圆心O是斜边AB的中点．连接OE，∴OE＝OB．∴∠2＝∠3，∵BE平分∠ABC，∴∠1＝∠2，∴∠1＝∠3．∴OE∥BF．∵EF⊥BF，∴EF⊥OE，∴EF是△ABC外接圆的切线；（2）解：在Rt△ABC中，BC＝5，sin∠ABC＝，∴＝．∵AC2+BC2＝AB2，∴AC＝12．∵∠ACF＝∠CFE＝∠FEH＝90°，∴四边形C FEH是矩形．∴EF＝HC，∠EHC＝90°．∴EF＝HC＝AC＝6．12．我们定义：如果圆的两条弦互相垂直，那么这两条弦互为“十字弦”，也把其中的一条弦叫做另一条弦的“十字弦”．如：如图，已知⊙O的两条弦AB⊥CD，则AB、CD互为“十字弦”，AB是CD的“十字弦”，CD也是AB的“十字弦”．（1）若⊙O的半径为5，一条弦AB＝8，则弦AB的“十字弦”CD的最大值为10 ，最小值为 6 ．（2）如图1，若⊙O的弦CD恰好是⊙O的直径，弦AB与CD相交于H，连接AC，若AC＝12，DH＝7，CH＝9，求证：AB、CD互为“十字弦”；（3）如图2，若⊙O的半径为5，一条弦AB＝8，弦CD是AB的“十字弦”，连接AD，若∠ADC＝60°，求弦CD的长．解：（1）如图a，当CD是直径时，CD的长最大，则CD的最大值为10；如图b，当点D与点A重合时，CD有最小值，过点O作OE⊥CD于E，OF⊥AB于F，∴AF＝BF＝4，DE＝CE，∴OF＝＝＝3，∵OE⊥CD，OF⊥AB，∠CDB＝90°，∴四边形CEOF是矩形，∴CE＝OF＝3，∴CD＝6，∴CD最小值为6，故答案为：10，6；（2）如图1，连接AD，∵DH＝7，CH＝9，∴CD＝16，∵CD是直径，∴∠CAD＝90°，∴AD＝＝＝4，∵，＝，∴，∠ADH＝∠ADC，∴△ADH∽△CDA，∴∠AHD＝∠CAD＝90°，∴AB⊥CD，∴AB、CD互为“十字弦”；（3）如图2，过点O作OE⊥CD于E，过点O作OF⊥AB于点F，连接AO，CO，过点O作ON⊥AC于N，∵∠ADC＝60°，AB⊥CD，∴AF＝DF，∵OE⊥CD，OF⊥AB，AB⊥CD，∴四边形OEHF是矩形，AF＝BF＝4，CE＝ED，∴OF＝EH，∵OF＝＝＝3，∴EH＝3，∴ED＝CE＝3+DH，∴CF＝3+2DH，∵∠AOC＝2∠ADC＝120°，且AO＝CO＝5，ON⊥AC，∴∠CAO＝30°，AN＝CN，∴NO＝，AN＝，∴AC＝5，∵AH2+CH2＝AC2，∴75＝3DH2+（3+2DH）2，∴DH＝2﹣，∴CD＝2CE＝2（3+2﹣）＝．13．如图，AB是⊙O的弦，AB＝4，点P在上运动（点P不与点A、B重合），且∠APB ＝30°，设图中阴影部分的面积为y．（1）⊙O的半径为 4 ；（2）若点P到直线AB的距离为x，求y关于x的函数表达式，并直接写出自变量x的取值范围．解：（1）∵∠AOB＝2∠APB＝2×30°＝60°，而OA＝OB，∴△OAB为等边三角形，∴OA＝AB＝4，即⊙O的半径为4；故答案为4；（2）过点O作OH⊥AB，垂足为H，如图，则∠OHA＝∠OHB＝90°∵∠APB＝30°∴∠AOB＝2∠APB＝60°，∵OA＝OB，OH⊥AB，∴AH＝BH＝AB＝2，在Rt△AHO中，∠AHO＝90°，AO＝4，AH＝2，∴OH＝＝2，∴y＝﹣×4×2+×4×x＝2x+π﹣4（0＜x≤2+4）．14．如图，四边形ABCD内接于⊙O，AC为⊙O的直径，D为的中点，过点D作DE∥AC，交BC的延长线于点E．（1）判断DE与⊙O的位置关系，并说明理由；（2）若CE＝，AB＝6，求⊙O的半径．（1）解：结论：DE与⊙O相切证：连接OD在⊙O中，∵D为的中点，∴＝，∴AD＝DC，∵AD＝DC，点O是AC的中点，∴OD⊥AC，∴∠DOA＝∠DOC＝90°，∵DE∥AC，∴∠DOA＝∠ODE＝90°，∵∠ODE＝90°，∴OD⊥DE，∵OD⊥DE，DE经过半径OD的外端点D，∴DE与⊙O相切．（2）解：连接BD．∵四边形ABCD是⊙O的内接四边形，∴∠DAB+∠DCB＝180°，又∵∠DCE+∠DCB＝180°，∴∠DAB＝∠DCE，∵AC为⊙O的直径，点D、B在⊙O上，∴∠ADC＝∠ABC＝90°，∵＝，∴∠ABD＝∠CBD＝45°，∵AD＝DC，∠ADC＝90°，∴∠DAC＝∠DCA＝45°，∵DE∥AC，∴∠DCA＝∠CDE＝45°，在△ABD和△CDE中，∵∠DAB＝∠DCE，∠ABD＝∠CDE＝45°，∴△ABD∽△CDE，∴＝，∴＝，∴AD＝DC＝4，在Rt△ADC中，∠ADC＝90°，AD＝DC＝4，∴AC＝＝＝8，∴⊙O的半径为4．15．（1）如图①，点A，B，C在⊙O上，点D在⊙O外，比较∠A与∠BDC的大小，并说明理由；（2）如图②，点A，B，C在⊙O上，点D在⊙O内，比较∠A与∠BDC的大小，并说明理由；（3）利用上述两题解答获得的经验，解决如下问题：在平面直角坐标系中，如图③，已知点M（1，0），N（4，0），点P在y轴上，试求当∠MPN度数最大时点P的坐标．解：（1）∠A＞∠BDC，理由如下：设CD交⊙O于E，连接BE，如图1所示：∠BEC＝∠BDC+∠DBE，∴∠BEC＞∠BDC，∵∠A＝∠BEC，∴∠A＞∠BDC；（2）∠A＜∠BDC，理由如下：延长CD交⊙O于点F，连接BF，如图2所示：∵∠BDC＝∠BFC+∠FBD，∴∠BDC＞∠BFC，又∵∠A＝∠BFC，∴∠A＜∠BDC；（3）由（1）、（2）可得：当点P是经过M、N两点的圆和y轴相切的切点时，∠MPN度数最大，①当点P在y轴的正半轴上时，如图3所示：设⊙O′为点P是经过M、N两点的圆和y轴相切的切点的圆，连接O′P、O′M、O′N，作O′H⊥MN于H，则四边形OPO′H是矩形，MH＝HN，∴OP＝O′H，O′P＝OH＝O′M，∵M（1，0），N（4，0），∴OM＝1，MN＝3，∴MH＝HN＝MN＝，设O′P＝OH＝O′M＝x，MH＝OH﹣OM＝x﹣1，∴x﹣1＝，∴x＝，∴O′H＝＝＝2，∴OP＝2，∴点P的坐标为（0，2）；②当点P在y轴的负半轴上时，如图4所示：同理可得O′H＝OP＝2，∴点P的坐标为（0，﹣2）；综上所述，当∠MPN度数最大时点P的坐标为（0，2）或（0，﹣2）．。

2020年中考数学复习专题练：《圆的综合》1．如图，△ABC内接于⊙O，AB是直径，过点A作直线MN，且∠MAC＝∠ABC．（1）求证：MN是⊙O的切线．（2）设D是弧AC的中点，连结BD交AC于点G，过点D作DE⊥AB于点E，交AC于点F．①求证：FD＝FG．②若BC＝3，AB＝5，试求AE的长．2．如图，已知BC⊥AC，圆心O在AC上，点M与点C分别是AC与⊙O的交点，点D是MB 与⊙O的交点，点P是AD延长线与BC的交点，且AD•AO＝AM•AP．（1）连接OP，证明：△ADM∽△APO；（2）证明：PD是⊙O的切线；（3）若AD＝12，AM＝MC，求PB和DM的值．3．已知正方形ABCD内接于⊙O，点E为上一点，连接BE、CE、DE．（1）如图1，求证：∠DEC+∠BEC＝180°；（2）如图2，过点C作CF⊥CE交BE于点F，连接AF，M为AE的中点，连接DM并延长交AF于点N，求证：DN⊥AF；（3）如图3，在（2）的条件下，连接OM，若AB＝10，tan∠DCE＝，求OM的长．4．△ABC内接于⊙O，D为的中点，连接OD，交BC边于点E，且OE＝DE．（1）如图1，求∠BAC的度数；（2）如图2，作AF⊥BC于点F，BG⊥AC于点G，AF、BG交于点H，求证：AH＝OD；（3）如图3，在（2）的条件下，连接OH，若AC＝4OH，EF＝3，求线段GH的长．5．如图，以点O为圆心，OE为半径作优弧EF，连接OE，OF，且OE＝3，∠EOF＝120°，在弧EF上任意取点A，B（点B在点A的顺时针方向）且使AB＝2，以AB为边向弧内作正三角形ABC．（1）发现：不论点A在弧上什么位置，点C与点O的距离不变，点C与点O的距离是；点C到直线EF的最大距离是．（2）思考：当点B在直线OE上时，求点C到OE的距离，在备用图1中画出示意图，并写出计算过程．（3）探究：当BC与OE垂直或平行时，直接写出点C到OE的距离．6．已知，AB、AC为圆O的弦，连接CO并延长，交AB于点D，且∠ADC＝2∠C；（1）如图1，求证：AD＝CO；（2）如图2，取弧BC上一点E，连接EB、EC、ED，且∠EDA＝∠ECA，延长EB至点F，连接FD，若∠EDF﹣∠F＝60°，求∠BDF的度数；（3）如图3，在（2）的条件下，若CD＝10，EF＝6，求AC的长度．7．如图，AB是⊙O的直径，AC⊥AB，BC交⊙O于点D，点E在劣弧BD上，DE的延长线交AB的延长线于点F，连接AE交BD于点G．（1）求证：∠AED＝∠CAD；（2）若点E是劣弧BD的中点，求证：ED2＝EG•EA；（3）在（2）的条件下，若BO＝BF，DE＝2，求EF的长．8．如图，点O为Rt△ABC斜边AB上的一点，以OA为半径的⊙O与BC切于点D，与AC交于点E，连接AD．（1）求证：AD平分∠BAC；（2）若∠B＝30°，OA＝2，求阴影部分的面积．（结果保留π）9．如图，在等腰△ABC中，AC＝BC，以BC为直径的⊙O与底边AB交于点D，过D作⊙O的切线交AC于点E．（1）证明：DE⊥AC．（2）若BC＝8，AD＝6，求AE的长．10．如图，已知AB是⊙O的直径，点P是弦BC上一动点（不与端点重合），过点P作PE ⊥AB于点E，延长EP交于点F，交过点C的切线于点D．（1）求证：△DCP是等腰三角形；（2）若OA＝6，∠CBA＝30°．①当OE＝EB时，求DC的长；②当的长为多少时，以点B，O，C，F为顶点的四边形是菱形？11．如图，AB是⊙O的直径，AE是弦，C是弧AE的中点，过点C作⊙O的切线交BA的延长线于点G，过点C作CD⊥AB于点D，交AE于点F．（1）求证：GC∥AE；（2）若sin∠EAB＝，OD＝3，求AE的长．12．如图，AB是⊙O的直径，过点B作⊙O的切线BM，点C为BM上一点，连接AC与⊙O交于点D，E为⊙O上一点，且满足∠EAC＝∠ACB，连接BD，BE．（1）求证：∠ABE＝2∠CBD；（2）过点D作AB的垂线，垂足为F，若AE＝6，BF＝，求⊙O的半径长．13．如图，以矩形ABCD的边CD为直径作⊙O，点E是AB的中点，连接CE交⊙O于点F，连接AF并延长交BC于点H．（1）若连接AO，试判断四边形AECO的形状，并说明理由；（2）求证：AH是⊙O的切线；（3）若AB＝6，CH＝2，则AH的长为．14．如图，在平面直角坐标系xOy中，A（0，8），B（6，0），C（0，3），点D从点A运动到点B停止，连接CD，以CD长为直径作⊙P．（1）若△ACD∽△AOB，求⊙P的半径；（2）当⊙P与AB相切时，求△POB的面积；（3）连接AP、BP，在整个运动过程中，△PAB的面积是否为定值，如果是，请直接写出面积的定值，如果不是，请说明理由．15．如图，点A，P，B，C是⊙O上的四个点，∠DAP＝∠PBA．（1）求证：AD是⊙O的切线；（2）若∠APC＝∠BPC＝60°，试探究线段PA，PB，PC之间的数量关系，并证明你的结论；（3）在第（2）问的条件下，若AD＝2，PD＝1，求线段AC的长．16．如图，A，B，C，D四点都在OO上，弧AC＝弧BC，连接AB，CD、AD，∠ADC＝45°．（1）如图1，AB是⊙O的直径；（2）如图2，过点B作BE⊥CD于点E，点F在弧AC上，连接BF交CD于点G，∠FGC＝2∠BAD，求证：BA平分∠FBE；（3）如图3，在（2）的条件下，MN与⊙O相切于点M，交EB的延长线于点N，连接AM，若2∠MAD+∠FBA＝135°，MN＝AB，EN＝26，求线段CD的长．17．对于平面内⊙C和⊙C外一点P，若过点P的直线l与⊙C有两个不同的公共点M，N，点Q为直线l上的另一点，且满足（如图1所示），则称点Q是点P关于的密切点已知在平面直角坐标系xOy中，⊙O的半径为2，点P（4，0）．（1）在点D（2，1），E（1，0），F（3，）中，是点P关于⊙O的密切点的为．（2）设直线l方程为y＝kx+b，如图2所示，①k＝﹣时，求出点P关于O的密切点Q的坐标；②⊙T的圆心为T（t，0），半径为2，若⊙T上存在点P关于⊙O的密切点，直接写出t的取值范围．18．如图，在△AOB中，∠AOB＝90°，AO＝6，BO＝6，以点O为圆心，以2为半径作优弧，交AO于点D，交BO于点E．点M在优弧上从点D开始移动，到达点E时停止，连接AM．（1）当AM＝4时，判断AM与优弧的位置关系，并加以证明；（2）当MO∥AB时，求点M在优弧上移动的路线长及线段AM的长；（3）连接BM，设△ABM的面积为S，直接写出S的取值范围．19．如图，四边形ABCD为菱形，以AD为直径作⊙O交AB于点F，连接DB交⊙O于点H，E 是BC上的一点，且BE＝BF，连接DE．（1）求证：△DAF≌△DCE．（2）求证：DE是⊙O的切线．（3）若BF＝2，DH＝，求四边形ABCD的面积．20．如图1，已知AB是⊙O的直径，点D是弧AB上一点，AD的延长线交⊙O的切线BM于点C，点E为BC的中点，（1）求证：DE是⊙O的切线；（2）如图2，若DC＝4，tan∠A＝，延长OD交切线BM于点H，求DH的值；（3）如图3，若AB＝8，点F是弧AB的中点，当点D在弧AB上运动时，过F作FG⊥AD 于G，连接BG，求BG的最小值．参考答案1．（1）证明：∵AB是直径，∴∠ACB＝90°，∴∠CAB+∠ABC＝90°；∵∠MAC＝∠ABC，∴∠MAC+∠CAB＝90°，即MA⊥AB，∴MN是⊙O的切线；（2）①证明：∵D是弧AC的中点，∴∠DBC＝∠ABD，∵AB是直径，∴∠CBG+∠CGB＝90°，∵DE⊥AB，∴∠FDG+∠ABD＝90°，∵∠DBC＝∠ABD，∴∠FDG＝∠CGB＝∠FGD，∴FD＝FG；②解：连接AD、CD，作DH⊥BC，交BC的延长线于H点．∵∠DBC＝∠ABD，DH⊥BC，DE⊥AB，∴DE＝DH，在Rt△BDE与Rt△BDH中，，∴Rt△BDE≌Rt△BDH（HL），∴BE＝BH，∵D是弧AC的中点，∴AD＝DC，在Rt△ADE与Rt△CDH中，，∴Rt△ADE≌Rt△CDH（HL）．∴AE＝CH．∴BE＝AB﹣AE＝BC+CH＝BH，即5﹣AE＝3+AE，∴AE＝1．2．（1）证明：连接OD、OP、CD．∵AD•AO＝AM•AP，∴，∠A＝∠A，∴△ADM∽△APO．（2）证明：∵△ADM∽△APO，∴∠ADM＝∠APO，∴MD∥PO，∴∠DOP＝∠MDO，∠POC＝∠DMO，∵OD＝OM，∴∠DMO＝∠MDO，∴∠DOP＝∠POC，∵OP＝OP，OD＝OC，∴△ODP≌△OCP（SAS），∴∠ODP＝∠OCP，∵BC⊥AC，∴∠OCP＝90°，∴OD⊥AP，∴PD是⊙O的切线．（3）解：连接CD．由（1）可知：PC＝PD，∵AM＝MC，∴AM＝2MO＝2R，在Rt△AOD中，OD2+AD2＝OA2，∴R2+122＝9R2，∴R＝3，∴OD＝3，MC＝6，∵，∴，∴AP＝18，∴DP＝AP﹣AD＝18﹣12＝6，∵O是MC的中点，∴，∴点P是BC的中点，∴PB＝CP＝DP＝6，∵MC是⊙O的直径，∴∠BDC＝∠CDM＝90°，在Rt△BCM中，∵BC＝2DP＝12，MC＝6，∴BM＝＝＝6，∵△BCM∽△CDM，∴，即，∴DM＝2．3．（1）证明：连接BD，OC，∵四边形ABCD为正方形，∴∠A＝90°，BC＝CD，∴BD为⊙O的直径，∵OB＝OD，∴OC⊥BD，∴∠BOC＝90°，∴∠BEC＝∠BOC＝45°，∵正方形ABED是圆O的内接四边形，∴∠A+∠DEB＝180°，∴∠DEB＝90°，∴∠DEC+∠BEC＝∠DEB+∠BEC+∠BEC＝180°；（2）证明：如图2，延长ED至G，使ED＝DG，连接AG，∵CE⊥CF，∴∠ECF＝90°，∵∠CEF＝45°，∴∠CEF＝∠CFE＝45°，∴CE＝CF，∵∠BCD＝∠ECF＝90°，∴∠BCF＝∠DCF，∵BC＝CD，∴△BFC≌△DEC（SAS），∴BF＝DE，∵DE＝DG，∴BF＝DG，∵四边形ABED为圆O的内接四边形，∴∠ABE+∠ADE＝180°，∵∠ADE+∠ADG＝180°，∴∠ABE＝∠ADG，∵AB＝AD，∴△ABF≌△ADG（SAS），∴∠BAF＝∠DAC，∵∠BAF+∠FAD＝∠BAD＝90°，∴∠DAG+∠FAD＝90°，∴∠FAG＝90°，∵M为AE的中点，∴DM为△AEG的中位线，∴DM∥AG，∴∠DNF＝∠FAG＝90°，∴DN⊥AF，（3）解：如图3，连接BD，OC，过点B作BK⊥CF交CF的延长线于点K，过点B作BT⊥AE于点T，由（1）知∠BOC＝90°，∴OB＝OC＝，由（1）知BD为⊙O的直径，在Rt△ABD中，BD＝AB＝10，∵，∴∠DBE＝∠DCE，∴tan∠DCE＝tan∠DBE＝，∴，设DE＝x，则BE＝7x，在Rt△BDE中，BD＝＝5x，∴，∴x＝2，∴DE＝2，∴BF＝2，∵∠EFC＝45°，∴∠BFK＝∠EFC＝45°，∴∠KBF＝∠BFK＝45°，∴，由（2）知∠BCF＝∠DCE，∴tan∠BCF＝tan∠DCE＝，∴，∴，∴，在Rt△ECF中，EF＝CF＝12，∴BE＝EF+BF＝14，∵∠AEB＝∠AEC﹣∠BEC＝90°﹣45°＝45°，∴∠TBE＝∠TEB，∴TB＝TE＝，∴＝，∴，∴，∵M为AE的中点，∴OM⊥AE，在Rt△OME中，OM＝＝3．4．解：（1）连接OB，OC，如图所示：∵OE＝DE，∴OB＝2OE，∴，∴∠OBC＝30°，∵OB＝OC，∴∠OCB＝30°，∴∠BOC＝120°，（2）证明：连接OA，过O做OM⊥AB，垂足为M，连接AD，如图所示：∵∠BAC＝60°．∠AGB＝90°，∴∠ABG＝30°，∴，∵OM⊥AB，∴，∴AM＝AG，∵D为弧中点，∴∠BAD＝∠CAD，∴OD⊥BC，∴OD∥AF，∴∠ODA＝∠OAD＝∠FAD，∴∠OAM＝∠HAG，∴△OAM≌△HAG（AAS），∴AH＝AO＝OD．∴AH＝OD；（3）连接DA，DB，DC，DH，延长AC至N，使AN＝AB，连接DN．如图所示：由（2）可知，DO＝DH，∴△ABD≌△AND（SAS），∴DN＝DB＝DC＝DO＝DH．∴△OBD为等边三角形，∴∠OBD＝∠ODB＝60°，设∠HBF＝α，则∠CAF＝α，∠DAF＝30°﹣α，∴∠ODH＝60°﹣2α，∵四边形ABDC内接于⊙O，∠DCN＝DBA＝∠N＝60°+α，∴∠CDN＝60°﹣2α＝∠ODH，∴△DOH≌△DCN（SAS），∴OH＝CN，∴AC+OH＝AB．设OH＝2a，∵AC＝4OH，∴AC＝8a，AB＝10a，∵∠AGB＝90°，∠ABG＝30°，∴AG＝5a，CG＝3a，∴BG＝＝5a，∴BC＝＝2a，∴，∵△OBD为等边三角形，∴，由勾股定理得：GH＝＝a，∴，∵cos∠HBF＝cos∠HAG，∴＝，∴BF＝×BH＝×4a＝a，又∵EF＝3，∴，解得，∴GH＝×＝．∴线段GH的长为．5．解：（1）如图1，连接OA、OB、OC，延长OC交AB于点G，在正三角形ABC中，AB＝BC＝AC＝2，∵OA＝OB，AC＝BC，∴OC垂直平分AB，∴AG＝AB＝1，∴在Rt△AGC中，由勾股定理得：CG＝＝＝，在Rt△AGO中，由勾股定理得：OG＝＝＝2，∴OC＝2﹣；如图2，延长CO交EF于点H，当CO⊥EF时，点C到直线EF的距离最大，最大距离为CH的长，∵OE＝OF，CO⊥EF，∴CO平分∠EOF，∵∠EOF＝120°，∴∠EOH＝∠EOF＝60°，在Rt△EOH中，cos∠EOH＝，∴cos60°＝＝，∴OH＝，∴CH＝CO+OH＝，∴点C到直线EF的最大距离是．故答案为：2﹣；．（2）如图3，当点B在直线OE上时，由OA＝OB，CA＝CB可知，点O，C都在线段AB的垂直平分线上，过点C作AB的垂线，垂足为G，则G为AB中点，直线CG过点O．∴由∠COM＝∠BOG，∠CMO＝∠BGO∴△OCM∽△OBG，∴＝，∴＝，∴CM＝，∴点C到OE的距离为．（3）如图4，当BC⊥OE时，设垂足为点M，∵∠EOF＝120°，∴∠COM＝180°﹣120°＝60°，∴在Rt△COM中，sin∠COM＝，∴sin60°＝＝，∴CM＝CO＝（2﹣）＝﹣；如图5，当BC∥OE时，过点C作CN⊥OE，垂足为N，∵BC∥OE，∴∠CON＝∠GCB＝30°，∴在Rt△CON中，sin∠CON＝，∴sin30°＝＝，∴CN＝CO＝（2﹣）＝﹣；综上所述，当BC与OE垂直或平行时，点C到OE的距离为﹣或﹣．6．解：（1）如图1，连接AO，则∠DCA＝∠OAC，∵∠DOA＝∠DCA+∠OAC＝2∠C，而∠ADC＝2∠C，∴∠ADC＝∠DOA，∴AD＝AO＝CO；（2）设∠F＝x，则∠EDF＝60°+x，∴∠FED＝180°﹣x﹣（60°+x）＝120°﹣2x，∵∠EDA＝∠ECA，∴∠EBD＝∠EDB＝（180°﹣120+2x）＝30°+x，∴∠BDF＝∠EDF﹣∠EDB＝60°+x﹣30°﹣x＝30°；（3）延长ED交圆于点G，连接OG、OA、AG、BG，作AM⊥OD于点M，作ON⊥BG于点N，∵∠BEG＝∠BAG＝120°﹣2x，∠ADG＝∠EDB＝∠EBD＝∠AGD＝30°+x，∴AG＝AD＝OG＝OA，∴△OGA为等边三角形，则∠ABG＝AOG＝30°＝∠BDF，∵EB＝ED，∠FED＝∠GEB，∴△FED≌△GEB（AAS），∴EG＝EF＝6，∴NG＝NE＝3，∵∠OAD＝∠OAG﹣∠DAG＝60°﹣（120°﹣2x）＝2x﹣60°，AD＝AO，∴∠ADO＝∠AOD＝120°﹣x，∴∠NDO＝180°﹣∠ADO﹣∠ADG＝180°﹣（120°﹣x）﹣（30°﹣x）＝30°，∴ON＝OD＝DM＝OM＝a，∴OC＝OG＝10﹣2a，在Rt△NOG中，由勾股定理得：（10﹣2a）2+a2+（3）2，解得：a＝1或（舍去，此时OC＝10﹣2a＜0），∴CM＝10﹣1＝9，AM＝3，则AC＝＝12．7．（1）证明：∵AB是⊙O的直径，∴∠ADB＝90°，∵AC⊥AB，∴∠CAB＝90°，∴∠ABD＝∠CAD，∵＝，∴∠AED＝∠ABD，∴∠AED＝∠CAD；（2）证明：∵点E是劣弧BD的中点，∴＝，∴∠EDB＝∠DAE，∵∠DEG＝∠AED，∴△EDG∽△EAD，∴，∴ED2＝EG•EA；（3）解：连接OE，∵点E是劣弧BD的中点，∴∠DAE＝∠EAB，∵OA＝OE，∴∠OAE＝∠AEO，∴∠AEO＝∠DAE，∴OE∥AD，∴，∵BO＝BF＝OA，DE＝2，∴，∴EF＝4．8．（1）证明：∵⊙O切BC于D，∴OD⊥BC，∵AC⊥BC，∴AC∥OD，∴∠CAD＝∠ADO，∵OA＝OD，∴∠OAD＝∠ADO，∴∠OAD＝∠CAD，即AD平分∠BAC；（2）解：设EO与AD交于点M，连接ED．∵∠B＝30°，∠ACB＝90°，∴∠BAC＝60°，∵OA＝OE，∴△AEO是等边三角形，∴AE＝OA，∠AOE＝60°，∴AE＝AO＝OD，又由（1）知，AC∥OD即AE∥OD，∴四边形AEDO是菱形，则△AEM≌△DMO，∠EOD＝60°，∴S△AEM ＝S△DMO，∴S阴影＝S扇形EOD＝＝．9．解：（1）如图，连接OD，∵DE是⊙O的切线，∴∠ODE＝90°，∵OB＝OD，∴∠OBD＝∠ODB，∵AC＝BC，∴∠OBD＝∠A，∴∠A＝∠ODB，∴OD∥AC，∴∠DEC＝90°，即DE⊥AC．（2）连接CD，∵BC为直径，∴∠BDC＝∠CDA＝90°，∴∠DEA＝∠CDA＝90°，∵∠A＝∠A，∴△ADE∽△ACD，∴＝，即＝，∴AE＝．10．（1）证明：连接OC，如图1，∵CD为⊙O的切线，∴OC⊥CD，∴∠OCD＝90°，即∠OCB+∠BCD＝90°，∵OB＝OC，∴∠OCB＝∠OBC，∵PE⊥AB，∴∠B+∠BPE＝90°，而∠BPE＝∠DPC，∴∠OCB+∠DPC＝90°，∴∠DPC＝∠BCD，∴DC＝DP，∴△DCP是等腰三角形；（2）解：①如图1，连接AC，∵AB是⊙O的直径，AB＝2AO＝12，∴∠ACB＝90°，∵∠ABC＝30°，∴AC＝AB＝6，BC＝6，Rt△PEB中，∵OE＝BE＝3，∠ABC＝30°，∴PE＝，PB＝2，∴CP＝BC﹣PB＝6﹣2＝4，∵∠DCP＝∠CPD＝∠EPB＝60°，∴△PCD为等边三角形，∴CD＝PC＝4；②当F是弧BC的中点，即弧FB所对的圆周角为60°时，此时的长：＝2π，以点B，O，C，F为顶点的四边形是菱形；理由如下：如图2，连接OF，AC，∵AB是⊙O的直径，∴∠ACB＝90°，∵∠CBA＝30°，∴∠A＝60°，∴△OAC为等边三角形，∴∠BOC＝120°，当F是弧BC的中点时，∠BOF＝∠COF＝60°，∴△BOF与△COF均为等边三角形，∴OB＝OC＝CF＝BF，∴四边形OCFB为菱形，则当的长为2π时，以点B，O，C，F为顶点的四边形是菱形．11．（1）证明：连接OC，交AE于点H．∵C是弧AE的中点，∴OC⊥AE．∵GC是⊙O的切线，∴OC⊥GC，∴∠OHA＝∠OCG＝90°，∴GC∥AE；（2）解：OC⊥AE，CD⊥AB，∴∠OCD＝∠EAB．∴．在Rt△CDO中，OD＝3，∴OC＝5，∴AB＝10，连接BE∵AB是⊙O的直径，∴∠AEB＝90°．在Rt△AEB中，∵，∴BE＝6，∴AE＝8．12．解：（1）∵AB是⊙O的直径，∴∠ADB＝90°，即∠DAB+∠DBA＝90°，∵BM是⊙O的切线，∴AB⊥BC，∴∠ABC＝90°，即∠CBD+∠DBA＝90°，∴∠DAB＝∠CBD，∵∠ABC＝90°，∴∠ACB＝90°﹣∠BAC，∵∠EAC＝∠ACB，∴∠EAC＝90°﹣∠BAC＝90°﹣（∠EAC﹣∠BAE），∴∠BAE＝2∠EAC﹣90°，∵AB是直径，∴∠AEB＝90°，∴∠ABE＝90°﹣∠BAE＝90°﹣（2∠EAC﹣90°）＝2（90°﹣∠EAC）＝2（90°﹣∠ACB）＝2∠CAB＝2∠CBD．∴∠ABE＝2∠CBD；（2）如图，连接DO并延长交AE于点G，∵∠DOB＝2∠BAD，∠ABE＝2∠CAB，∴∠DOB＝∠ABE，∴DG∥BE，∴∠AGO＝∠AEB＝90°，∴AG＝EG＝AE＝3，∠AOG＝∠DOF，OA＝OD，∴△AOG≌△DOF（AAS）∴DF＝AG＝3，又OF＝OB﹣BF＝OD﹣，在Rt△DOF中，根据勾股定理，得OD2＝DF2+OF2，即OD2＝32+（OD﹣）2，解得OD＝．答：⊙O的半径长为．13．（1）解：连接AO，四边形AECO是平行四边形．∵四边形ABCD是矩形，∴AB∥CD，AB＝CD．∵E是AB的中点，∴AE＝AB．∵CD是⊙O的直径，∴OC＝CD．∴AE∥OC，AE＝OC．∴四边形AECO为平行四边形．（2）证明：由（1）得，四边形AECO为平行四边形，∴AO∥EC∴∠AOD＝∠OCF，∠AOF＝∠OFC．∵OF＝OC∴∠OCF＝∠OFC．∴∠AOD＝∠AOF．∵在△AOD和△AOF中，AO＝AO，∠AOD＝∠AOF，OD＝OF ∴△AOD≌△AOF（SAS）．∴∠ADO＝∠AFO．∵四边形ABCD是矩形，∴∠ADO＝90°．∴∠AFO＝90°，即AH⊥OF．∵点F在⊙O上，∴AH是⊙O的切线．（3）∵CD为⊙O的直径，∠ADC＝∠BCD＝90°，∴AD，BC为⊙O的切线，又∵AH是⊙O的切线，∴CH＝FH，AD＝AF，设BH＝x，∵CH＝2，∴BC＝2+x，∴BC＝AD＝AF＝2+x，∴AH＝AF+FH＝4+x，在Rt△ABH中，∵AB2+BH2＝AH2，∴62+x2＝（4+x）2，解得x＝．∴．故答案为：．14．解：（1）如图1，∵A（0，8），B（6，0），C（0，3），∴OA＝8，OB＝6，OC＝3，∴AC＝5，∵△ACD∽△AOB，∴，∴∴CD的＝，∴⊙P的半径为；（2）在Rt△AOB中，OA＝8，OB＝6，∴＝＝10，如图2，当⊙P与AB相切时，CD⊥AB，∴∠ADC＝∠AOB＝90°，∠CAD＝∠BAO，∴△ACD∽△ABO，∴，即，∴AD＝4，CD＝3，∵CD为⊙P的直径，∴CP＝，过点P作PE⊥AO于点E，∵∠PEC＝∠ADC＝90°，∠PCE＝∠ACD，∴△CPE∽△CAD，∴，即，∴，∴，∴△POB的面积＝＝；（3）①如图3，若⊙P与AB只有一个交点，则⊙P与AB相切，由（2）可知PD⊥AB，PD＝，∴△PAB的面积＝．②如图4，若⊙P与AB有两个交点，设另一个交点为F，连接CF，可得∠CFD＝90°，由（2）可得CF＝3，过点P作PG⊥AB于点G，则DG＝，则PG为△DCF的中位线，PG＝，∴△PAB的面积＝＝．综上所述，在整个运动过程中，△PAB的面积是定值，定值为．15．（1）证明：先作⊙O的直径AE，连接PE，∵AE是直径，∴∠APE＝90°．∴∠E+∠PAE＝90°．又∵∠DAP＝∠PBA，∠E＝∠PBA，∴∠DAP＝E，∴∠DAP+∠PAE＝90°，即AD⊥AE，∴AD是⊙O的切线；（2）PA+PB＝PC，证明：在线段PC上截取PF＝PB，连接BF，∵PF＝PB，∠BPC＝60°，∴△PBF是等边三角形，∴PB＝BF，∠BFP＝60°，∴∠BFC＝180°﹣∠PFB＝120°，∵∠BPA＝∠APC+∠BPC＝120°，∴∠BPA＝∠BFC，在△BPA和△BFC中，，∴△BPA≌△BFC（AAS），∴PA＝FC，AB＝CB，∴PA+PB＝PF+FC＝PC；（3）过点D作DH⊥AB于H，由已知可得，∠DAB＝∠ACB＝60°．在Rt△ADH中，可求得AH＝1，DH＝．在Rt△BDH中，由BD＝4，DH＝，可求得BH＝，所以AC＝AB＝AH+BH＝1+．16．解（1）如图1，连接BD．∵＝，∴∠BDC＝∠ADC＝45°，∴∠ADB＝90°，∴AB是圆O的直径．（2）如图2，连接OG、OD、BD．则OA＝OD＝OB，∴∠OAD＝∠ODA，∠OBD＝∠ODB，∴∠DOB＝∠OAD+∠ODA＝2∠BAD，∵∠FGC＝2∠BAD，∴∠DOB＝∠FGC＝∠BGD，∴B、G、O、D四点共圆，∴∠ODE＝∠OBG，∵BE⊥CD，∠BDC＝45°，∴∠EBD＝45°＝∠EDB，∴∠OBE＝∠ODE＝∠OBG，∴BA平分∠FBE．（3）如图3，连接AC、BC、CO、DO、EO、BD．∵AC＝BC，∴AC＝BC，∵AB为直径，∴∠ACB＝90°，∠CAB＝∠CBA＝45°，CO⊥AB，延长CO交圆O于点K，则∠DOK＝∠OCD+∠ODC＝2∠ODC＝2∠OBE＝2∠FBA，连接DM、OM，则∠MOD＝2∠MAD，∵2∠MAD+∠FBA＝135°，∴∠MOD+∠FBA＝135°，∴2∠MOD+2∠FBA＝270°，∴2∠MOD+∠DOK＝270°，∵∠AOM+∠DOM+∠KOK＝270°，∴∠AOM＝∠DOM，∴AM＝DM，连接MO并延长交AD于H，则∠MHA＝∠MHD＝90°，AH＝DH，设MH与BC交于点R，连接AR，则AR＝DR，∵∠ADC＝45°，∴∠ARD＝∠ARC＝90°，△ADR是等腰直角三角形，∴∠BRH＝∠ARH＝45°∵∠ACR+∠BCE＝∠BCE+∠CBE＝90°，∴∠ACR＝∠CBE，∴△ACR≌△CBE（AAS），∴CR＝BE＝ED，作EQ⊥MN于Q，则∠EQN＝∠EQM＝90°，连接OE，则OE垂直平分BD，∴OE∥AD∥MN，∴四边形OEQM是矩形，∴OM＝EQ，OE＝MQ，延长DB交MN于点P，∵∠PBN＝∠EBD＝45°，∴∠BNP＝45°，∴△EQN是等腰直角三角形，∴EQ＝QN＝EN＝13，∴OA＝OB＝OC＝OD＝OM═13，AB＝2OA＝26，∴BC＝OC＝26，∵MN＝AB＝20，∴OE＝MQ＝MN﹣QN＝20﹣13＝7，∵∠ORE＝45°，∠EOR＝90°，∴△OER是等腰直角三角形，∴RE＝OE＝14，设BE＝CR＝x，则CE＝14+x，在Rt△CBE中：BC2＝CE2+BE2，∴262＝（x+14）2+x2，解得x＝10，∴CD＝CR+RE+DE＝10+14+10＝34．17．解：（1）当圆心在坐标原点时，直线l为y＝0时，∵⊙O的半径为2，点P（4，0）．∴M（2，0），N（﹣2，0），PM＝2，PN＝6，＝，∵，∴＝，设Q点坐标为（x，y），则QM＝|2﹣x|，QN＝|x﹣（﹣2）|＝|x+2|，∴＝，∴|2+x|＝3|2﹣x|，∴2+x＝6﹣3x，或2+x＝3x﹣6，∴x＝1，或x＝4，∴E（1，0）是点P关于⊙O的密切点．故答案为：E．（2）①依题意直线l：y＝kx+b过定点P（4，0），∵k＝﹣∴将P（4，0）代入y＝﹣x+b得：0＝﹣×4+b，∴b＝，∴y＝﹣x+．如图，作MA⊥x轴于点A，NB垂直x轴于点B，设M（x，﹣x+），由OM＝2得：x2+＝4，∴5x2﹣4x﹣10＝0，则M，N两点的横坐标x M，x N是方程5x2﹣4x﹣10＝0的两根，解得x M＝，x N＝，∴AB＝，PA＝，PB＝，∵，∴＝，＝，∴＝，∴HA＝，∴OH＝OA﹣HA＝﹣＝1，∴Q（1，1）．②点P关于⊙O的密切点的轨迹为切点弦ST（不含端点），如图所示：∴﹣1≤t＜0或2＜t≤3．18．解：（1）结论；AM与优弧相切．理由如下：∵AO＝6，OM＝2，AM＝，∴OM2+AM2＝OA2，∴∠AMO＝90°，∴AM与优弧相切．（2）在△AOB中，∠AOB＝90°，AO＝6，BO＝6，∴tan∠OAB＝，∴∠OAB＝60°，∠ABO＝30°，当MO∥AB时，M点位置有两种情况：Ⅰ．如解图1，过M点作MF⊥AO，交AO于F，∴∠FOM＝60°，∵OM＝2，∴OF＝OM•cos60°＝2×＝1，MF＝OM•sin60°＝＝，∴AF＝OA﹣OF＝5，∴AM＝＝＝．的弧长＝，Ⅱ．如解图2，过M点作MF⊥AO，交AO延长线于F，同理可得：∠MOF＝60°，OF＝1，MF＝，AM＝7，∴AM＝＝＝．∴.的弧长＝，综上所述：当MO∥AB时，点M在优弧上移动的路线长为时，线段AM的长＝；点M在优弧上移动的路线长为时，线段AM的长＝；（3）由（2）可知∠OAB＝60°，∠ABO＝30°，AB＝12．如解图3，Ⅰ．由图可知，△ABM的AB边最小高为M在D时，∵OD＝2，AO＝6，∴AD＝4＝AD•sin∠OAB＝，∴DH1∴△ABM的面积为S的最小值为＝＝．Ⅱ．M在过O垂直于AB的直线上，△ABM的AB边的高最大，OH2＝OA•sin∠OAB＝，∴△ABM的AB边的高最大值为OM+OH2＝2+3，∴△ABM的面积为S的最大值为＝＝＝12+18．∴△ABM的面积为S取值范围为：．19．（1）证明：如图，连接DF，∵四边形ABCD为菱形，∴AB＝BC＝CD＝DA，AD∥BC，∠DAB＝∠C，∵BF＝BE，∴AB﹣BF＝BC﹣BE，即AF＝CE，∴△DAF≌△DCE（SAS）；（2）由（1）知，△DAF≌△DCE，则∠DFA＝∠DEC．∵AD是⊙O的直径，∴∠DFA ＝90°，∴∠DEC ＝90° ∵AD ∥BC ，∴∠ADE ＝∠DEC ＝90°， ∴OD ⊥DE ， ∵OD 是⊙O 的半径， ∴DE 是⊙O 的切线；（2）解：如图，连接AH ， ∵AD 是⊙O 的直径， ∴∠AHD ＝∠DFA ＝90°， ∴∠DFB ＝90°， ∵AD ＝AB ，DH ＝， ∴DB ＝2DH ＝2，在Rt △ADF 和Rt △BDF 中， ∵DF 2＝AD 2﹣AF 2，DF 2＝BD 2﹣BF 2， ∴AD 2﹣AF 2＝DB 2﹣BF 2， ∴AD 2﹣（AD ﹣BF ）2＝DB 2﹣BF 2， ∴AD 2﹣（AD ﹣2）2＝（2）2﹣22，∴AD ＝5． ∴AH ＝＝＝2∴S 四边形ABCD ＝2S △ABD ＝2וAH ＝BD •AH ＝2×2＝20．即四边形ABCD 的面积是20．20．（1）证明：如图，连接OD ，BD ，∵AB是⊙O的直径，∴∠ADB＝∠CDB＝90°，∵BM是⊙O的切线，∴∠ABC＝90°，∵点E是BC的中点，∴DE＝BC＝BE＝CE，∴∠EDB＝∠EBD，又∵OD＝OB，∴∠ODB＝∠OBD，∴∠ODB+∠EDB＝∠OBD+∠EBD＝90°，即∠ODE＝90°，∴OD⊥DE，∴DE是⊙O的切线；（2）解：如图2，连接BD，∵∠A+∠ABD＝∠ABD+∠CBD＝90°，∴∠A＝∠CBD，∵DC＝4，tan∠A＝，∴tan∠CBD＝tan∠A＝，∴BD＝8，∴BC＝＝4，∴DE＝，∴AB＝，∴BO＝OD＝4，又∵DE是⊙O的切线，∴∠HDE＝90°，∴tan∠DHE＝＝，设DH＝x，则，∴BH＝2x，在Rt△BOH中，OB2+BH2＝OH2，即，解得：x＝或x＝0（舍去），∴DH＝；（3）解：如图3，连接BF，取AF中点N，构造圆N，连接NG，∵FG⊥AD于点G，∴当点D在弧AB上运动时，点G在圆N上运动，∴当点N、G、B三点共线时，BG有最小值，∵AB＝8，点F是弧AB的中点，∴∠AFB＝90°，AF＝BF＝，∴NG＝NF＝，BN＝＝＝2，∴BG＝BN﹣NG＝2．。

2020年九年级中考数学压轴题专项训练：圆的综合卷（含答案）1．如图，点O为Rt△ABC斜边AB上的一点，∠C＝90°，以OA为半径的⊙O与BC交于点D，与AC交于点E，连接AD且AD平分∠BAC．（1）求证：BC是⊙O的切线；（2）若∠BAC＝60°，OA＝2，求阴影部分的面积（结果保留π）（1）证明：连接OD，∵AD平分∠BAC，∴∠BAD＝∠DAC，∵AO＝DO，∴∠BAD＝∠ADO，∴∠CAD＝∠ADO，∴AC∥OD，∵∠ACD＝90°，∴OD⊥BC，∴BC与⊙O相切；（2）解：连接OE，ED，∵∠BAC＝60°，OE＝OA，∴△OAE为等边三角形，∴∠AOE＝60°，∴∠ADE＝30°，又∵∠OAD＝∠BAC＝30°，∴∠ADE＝∠OAD，∴ED∥AO，∴四边形OAED是菱形，∴OE⊥AD，且AM＝DM，EM＝OM，∴S△AED ＝S△AOD，∴阴影部分的面积＝S扇形ODE＝＝π．2．如图，已知AB是⊙O的直径，AC是⊙O的弦，点E在⊙O外，连接CE，∠ACB的平分线交⊙O于点D．（1）若∠BCE＝∠BAC，求证：CE是⊙O的切线；（2）若AD＝4，BC＝3，求弦AC的长．（1）证明：连接OC，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠ACO+∠BCO＝90°，∵OA＝OC，∴∠OAC＝∠OCA，∵∠BAC＝∠BCE，∴∠ACO＝∠BCE，∴∠BCE+∠BCO＝90°，∴∠OCE＝90°，∴CE是⊙O的切线；（2）解：连接BD，∵∠ACB的平分线交⊙O于点D，∴∠ACD＝∠BCD，∴＝，∴AD＝BD，∵AB是⊙O的直径，∴∠ADB＝90°，∴△ADB是等腰直角三角形，∴AB＝AD＝4，∵BC＝3，∴AC＝＝＝．3．如图，AB是⊙O的直径，AE平分∠BAF，交⊙O于点E，过点E作直线ED⊥AF，交AF的延长线于点D，交AB的延长线于点C．（1）求证：CD是⊙O的切线；（2）∠C＝45°，⊙O的半径为2，求阴影部分面积．（1）证明：连接OE ．∵OA ＝OE ，∴∠OAE ＝∠OEA ，又∵∠DAE ＝∠OAE ，∴∠OEA ＝∠DAE ，∴OE ∥AD ，∴∠ADC ＝∠OEC ，∵AD ⊥CD ，∴∠ADC ＝90°，故∠OEC ＝90°．∴OE ⊥CD ，∴CD 是⊙O 的切线；（2）解：∵∠C ＝45°，∴△OCE 是等腰直角三角形，∴CE ＝OE ＝2，∠COE ＝45°，∴阴影部分面积＝S △OCE ﹣S 扇形OBE ＝2×2﹣＝2﹣．4．如图①，BC 是⊙O 的直径，点A 在⊙O 上，AD ⊥BC 垂足为D ，弧AE ＝弧AB ，BE 分别交AD 、AC 于点F 、G ．（1）判断△FAG的形状，并说明理由；（2）如图②若点E与点A在直径BC的两侧，BE、AC的延长线交于点G，AD的延长线交BE于点F，其余条件不变（1）中的结论还成立吗？请说明理由．（3）在（2）的条件下，若BG＝26，DF＝5，求⊙O的直径BC．解：（1）△FAG等腰三角形；理由：∵BC为直径，∴∠BAC＝90°，∴∠ABE+∠AGB＝90°，∵AD⊥BC，∴∠ADC＝90°，∴∠ACD+∠DAC＝90°，∵弧AE＝弧AB，∴∠ABE＝∠ACD，∴∠DAC＝∠AGB，∴FA＝FG，∴△FAG是等腰三角形；（2）成立；∵BC为直径，∴∠BAC＝90°∴∠ABE+∠AGB＝90°∵AD⊥BC，∴∠ADC＝90°，∴∠ACD+∠DAC＝90°，∵弧AE＝弧AB，∴∠ABE＝∠ACD，∴∠DAC＝∠AGB，∴FA＝FG，∴△FAG是等腰三角形；（3）由（2）知∠DAC＝∠AGB，且∠BAD+∠DAC＝90°，∠ABG+∠AGB＝90°，∴∠BAD＝∠ABG，∴AF＝BF，又∵AF＝FG，∴F为BG的中点∵△BAG为直角三角形，∴AF＝BF＝BG＝13，∵DF＝5，∴AD＝AF﹣DF＝13﹣5＝8，∴在Rt△BDF中，BD＝＝12，∴在Rt△BDA中，AB＝＝4，∵∠ABC＝∠DBA，∠BAC＝∠ADB＝90°∴△ABC∽△DBA，∴＝，∴＝，∴BC＝，∴⊙O的直径BC＝．5．如图，已知矩形ABCD的边AB＝6，BC＝4，点P、Q分别是AB、BC边上的动点．（1）连接AQ、PQ，以PQ为直径的⊙O交AQ于点E．①若点E恰好是AQ的中点，则∠QPB与∠AQP的数量关系是∠QPB＝2∠AQP；②若BE＝BQ＝3，求BP的长；（2）已知AP＝3，BQ＝1，⊙O是以PQ为弦的圆．①若圆心O恰好在CB边的延长线上，求⊙O的半径；②若⊙O与矩形ABCD的一边相切，求⊙O的半径．解：（1）①∵点E恰好是AQ的中点，∠ABQ＝90°，∴BE＝AE＝EQ，∴∠EAB＝∠EBA，∴∠QEB＝2∠EBP，∵以PQ为直径的⊙O交AQ于点E，∴∠QPB＝∠QEB，∠PBE＝∠PQA，∴∠QPB＝2∠AQP，故答案为：∠QPB＝2∠AQP；②∵BE＝BQ，∴∠BEQ＝∠BQE，且∠BPQ＝∠BEQ，∴∠BPQ＝∠BQE，∴tan∠BPQ＝tan∠BPQ，∴，∴，∴BP＝（2）①如图1，过点O作OE⊥PQ，∵AP＝3，AB＝6，∴BP＝3，∴PQ＝＝＝，∵OE⊥PQ，∴QE＝PE＝，∵cos∠PQB＝＝，∴＝∴OQ＝5，∴⊙O的半径为5；②如图2，若⊙O与BC相切于点Q，连接OQ，过点O作OE⊥PQ于E，∴EQ＝PE＝，∵BC是⊙O切线，∴OQ⊥BC，且AB⊥BC，∴OQ∥AB，∴∠OQP＝∠BPQ，∴cos∠OQP＝cos∠BPQ，∴，∴∴OQ＝；如图3，若⊙O与AB相切于点P，连接OP，过点O作OE⊥PQ于E，∴EQ＝PE＝，∵AB是⊙O切线，∴OP⊥AB，且AB⊥BC，∴OP∥BC，∴∠OPQ＝∠PQB，∴cos∠OPQ＝cos∠PQB，∴∴，∴OP＝5；如图4，若⊙O与AD相切于点M，连接OM，OQ，OP，延长MO交BC于F，作OH⊥AB于H 点，∴OM⊥AD，且BC∥AD，∴OF⊥BC，∵∠A＝∠B＝∠AMO＝∠OFB＝∠OHB＝90°，∴四边形AHOM，OHBF是矩形，∴OM＝AH，OH＝BF，∵OQ2＝OF2+FQ2，OP2＝OH2+PH2，∴OQ2＝（6﹣OQ）2+（BF﹣1）2，OQ2＝BF2+（OQ﹣3）2，∴OQ＝5﹣若图5，若⊙O与CD相切于点N，连接ON，OQ，OP，延长NO交BC于E，作OH⊥BC于H 点，同理可得：OP2＝PE2+OE2，OQ2＝OH2+QH2，∴OQ2＝（3﹣OH）2+（4﹣OQ）2，OQ2＝OH2+（4﹣OQ﹣1）2，∴OQ＝35﹣6．6．如图，在矩形ABCD中，E是BC上一点，连接AE，将矩形沿AE翻折，使点B落在CD边F处，连接AF，在AF上取一点O，以点O为圆心，OF为半径作⊙O与AD相切于点P．AB ＝6，BC＝，（1）求证：F是DC的中点．（2）求证：AE＝4CE．（3）求图中阴影部分的面积．（1）证明：由折叠的性质可知，AF＝AB＝6，在Rt△ADF中，DF＝＝＝3，∴CF＝DC﹣DF＝3，∴DF＝FC，即F是CD的中点；（2）证明：在Rt△ADF中，DF＝3，AF＝6，∴∠DAF＝30◦，∴∠BAF＝60◦，由折叠的性质可知，∠EAF＝∠EAB，∠AFE＝∠B＝90°，∴∠EAF＝∠EAB＝30°，∴AE＝2EF，∠EFC＝180°﹣∠AFD﹣∠AFE＝30◦，∴EF＝2CE，∴AE＝4CE；（3）解：连接OP、OH、PH，∵⊙O与AD相切于点P，∴OP⊥AD，∴OP∥DF，∵∠DAF＝30°，∴∠AOP＝90°﹣∠DAF＝60°，OF＝OP＝OA，∴∠OFH＝∠AOP＝60°，OP＝OF＝2，∴AP＝＝2，∴DP＝AD﹣AP＝，∵∠OFH＝60°，OH＝OF，∴△OHF为等边三角形，∴∠FOH＝∠OHF＝60°，HF＝OF＝2，∴DH＝DF﹣HF＝1，∵OP∥DF，∴∠POH＝∠OHF＝60°，∴∠POH＝∠HOF，∴＝，∴阴影部分的面积＝△PDH的面积＝×DH×DP＝．7．如图，Rt△ABC中，∠ABC＝90°，以AB为直径作⊙O交AC于点D，连接BD．（1）求证：∠A＝∠CBD．（2）若AB＝10，AD＝6，M为线段BC上一点，请写出一个BM的值，使得直线DM与⊙O 相切，并说明理由．（1）证明：∵AB为⊙O直径，∴∠ADB＝90°，∴∠A+∠ABD＝90°．∵∠ABC＝90°，∴∠CBD+∠ABD＝90°，∴∠A＝∠CBD；（2）BM＝．理由如下：如图，连接OD，DM，∵∠ADB＝90°，AB＝10，AD＝6，∴BD＝＝8，OA＝5，∵∠A＝∠CBD，∵Rt△CBD∽Rt△BAD，∴＝，即＝，解得BC＝取BC的中点M，连接DM、OD，如图，∵DM为Rt△BCD斜边BC的中线，∴DM＝BM，∵∠2＝∠4，∵OB＝OD，∴∠1＝∠3，∴∠1+∠2＝∠3+∠4＝90°，即∠ODM＝90°，∴OD⊥DM，∴DM为⊙O的切线，此时BM＝BC＝．8．如图，AB是⊙O的直径，直线MC与⊙O相切于点C．过点A作MC的垂线，垂足为D，线段AD与⊙O相交于点E．（1）求证：AC是∠DAB的平分线；（2）若AB＝10，AC＝4，求AE的长．（1）证明：连接OC，∵直线MC与⊙O相切于点C，∴∠OCM＝90°，∵AD⊥CD，∴∠ADM＝90°，∴∠OCM＝∠ADM，∴OC∥AD，∴∠DAC＝∠ACO，∵OA＝OC，∴∠ACO＝∠CAO，∴∠DAC＝∠CAB，即AC是∠DAB的平分线；（2）解：连接BC，连接BE交OC于点F，∵AB是⊙O的直径，∴∠ACB＝∠AEB＝90°，∵AB＝10，AC＝4，∴BC＝＝＝2，∵OC∥AD，∴∠BFO＝∠AEB＝90°，∴∠CFB＝90°，F为线段BE中点，∵∠CBE＝∠EAC＝∠CAB，∠CFB＝∠ACB，∴△CFB∽△BCA．∴＝，即＝，解得，CF＝2，∴OF＝OC﹣CF＝3．∵O为直径AB中点，F为线段BE中点，∴AE＝2OF＝6．9．如图，AB是⊙O的直径，点C是圆上一点，点D是半圆的中点，连接CD交OB于点E，点F是AB延长线上一点，CF＝EF．（1）求证：FC是⊙O的切线；（2）若CF＝5，tan A＝，求⊙O半径的长．（1）证明：如图，连接OD．∵点D是半圆的中点，∴∠AOD＝∠BOD＝90°，∴∠ODC+∠OED＝90°，∵OD＝OC，∴∠ODC＝∠OCD．又∵CF＝EF，∴∠FCE＝∠FEC．∵∠FEC＝∠OED，∴∠FCE＝∠OED．∴∠FCE+∠OCD＝∠OED+∠ODC＝90°，即FC⊥OC，∴FC是⊙O的切线；（2）解：∵tan A＝，∴在Rt△ABC中，＝，∵∠ACB＝∠OCF＝90°，∴∠ACO＝∠BCF＝∠A，∵△ACF∽△CBF，∴＝＝＝．∴AF＝10，∴CF2＝BF•AF．∴BF＝．∴AO＝＝．10．如图，AB是⊙O的直径，弦DE垂直半径OA，C为垂足，DE＝6，连接DB，∠B＝30°，过点E作EM∥BD，交BA的延长线于点M．（1）求的半径；（2）求证：EM是⊙O的切线；（3）若弦DF与直径AB相交于点P，当∠APD＝45°时，求图中阴影部分的面积．解：（1）连结OE，∵DE垂直OA，∠B＝30°，∴CE＝DE＝3，，∴∠AOE＝2∠B＝60°，∴∠CEO＝30°，OC＝OE，由勾股定理得OE＝2；（2）∵EM∥BD，∴∠M＝∠B＝30°，∠M+∠AOE＝90°，∴∠OEM＝90°，即OE⊥ME，∴EM是⊙O的切线；（3）再连结OF，当∠APD＝45°时，∠EDF＝45°，∴∠EOF＝90°，S＝π（2）2﹣（2）2＝3π﹣6．阴影11．如图，Rt△ABC中，∠C＝90°．BE平分∠ABC交AC于点D，交△ABC的外接圆于点E，过点E作EF⊥BC交BC的延长线于点F．请补全图形后完成下面的问题：（1）求证：EF是△ABC外接圆的切线；（2）若BC＝5，sin∠ABC＝，求EF的长．（1）证明：补全图形如图所示，∵△ABC是直角三角形，∴△ABC的外接圆圆心O是斜边AB的中点．连接OE，∴OE＝OB．∴∠2＝∠3，∵BE平分∠ABC，∴∠1＝∠2，∴∠1＝∠3．∴OE∥BF．∵EF⊥BF，∴EF⊥OE，∴EF是△ABC外接圆的切线；（2）解：在Rt△ABC中，BC＝5，sin∠ABC＝，∴＝．∵AC2+BC2＝AB2，∴AC＝12．∵∠ACF＝∠CFE＝∠FEH＝90°，∴四边形C FEH是矩形．∴EF＝HC，∠EHC＝90°．∴EF＝HC＝AC＝6．12．我们定义：如果圆的两条弦互相垂直，那么这两条弦互为“十字弦”，也把其中的一条弦叫做另一条弦的“十字弦”．如：如图，已知⊙O的两条弦AB⊥CD，则AB、CD互为“十字弦”，AB是CD的“十字弦”，CD也是AB的“十字弦”．（1）若⊙O的半径为5，一条弦AB＝8，则弦AB的“十字弦”CD的最大值为10 ，最小值为 6 ．（2）如图1，若⊙O的弦CD恰好是⊙O的直径，弦AB与CD相交于H，连接AC，若AC＝12，DH＝7，CH＝9，求证：AB、CD互为“十字弦”；（3）如图2，若⊙O的半径为5，一条弦AB＝8，弦CD是AB的“十字弦”，连接AD，若∠ADC＝60°，求弦CD的长．解：（1）如图a，当CD是直径时，CD的长最大，则CD的最大值为10；如图b，当点D与点A重合时，CD有最小值，过点O作OE⊥CD于E，OF⊥AB于F，∴AF＝BF＝4，DE＝CE，∴OF＝＝＝3，∵OE⊥CD，OF⊥AB，∠CDB＝90°，∴四边形CEOF是矩形，∴CE＝OF＝3，∴CD＝6，∴CD最小值为6，故答案为：10，6；（2）如图1，连接AD，∵DH＝7，CH＝9，∴CD＝16，∵CD是直径，∴∠CAD＝90°，∴AD＝＝＝4，∵，＝，∴，∠ADH＝∠ADC，∴△ADH∽△CDA，∴∠AHD＝∠CAD＝90°，∴AB⊥CD，∴AB、CD互为“十字弦”；（3）如图2，过点O作OE⊥CD于E，过点O作OF⊥AB于点F，连接AO，CO，过点O作ON⊥AC于N，∵∠ADC＝60°，AB⊥CD，∴AF＝DF，∵OE⊥CD，OF⊥AB，AB⊥CD，∴四边形OEHF是矩形，AF＝BF＝4，CE＝ED，∴OF＝EH，∵OF＝＝＝3，∴EH＝3，∴ED＝CE＝3+DH，∴CF＝3+2DH，∵∠AOC＝2∠ADC＝120°，且AO＝CO＝5，ON⊥AC，∴∠CAO＝30°，AN＝CN，∴NO＝，AN＝，∴AC＝5，∵AH2+CH2＝AC2，∴75＝3DH2+（3+2DH）2，∴DH＝2﹣，∴CD＝2CE＝2（3+2﹣）＝．13．如图，AB是⊙O的弦，AB＝4，点P在上运动（点P不与点A、B重合），且∠APB ＝30°，设图中阴影部分的面积为y．（1）⊙O的半径为 4 ；（2）若点P到直线AB的距离为x，求y关于x的函数表达式，并直接写出自变量x的取值范围．解：（1）∵∠AOB＝2∠APB＝2×30°＝60°，而OA＝OB，∴△OAB为等边三角形，∴OA＝AB＝4，即⊙O的半径为4；故答案为4；（2）过点O作OH⊥AB，垂足为H，如图，则∠OHA＝∠OHB＝90°∵∠APB＝30°∴∠AOB＝2∠APB＝60°，∵OA＝OB，OH⊥AB，∴AH＝BH＝AB＝2，在Rt△AHO中，∠AHO＝90°，AO＝4，AH＝2，∴OH＝＝2，∴y＝﹣×4×2+×4×x＝2x+π﹣4（0＜x≤2+4）．14．如图，四边形ABCD内接于⊙O，AC为⊙O的直径，D为的中点，过点D作DE∥AC，交BC的延长线于点E．（1）判断DE与⊙O的位置关系，并说明理由；（2）若CE＝，AB＝6，求⊙O的半径．（1）解：结论：DE与⊙O相切证：连接OD在⊙O中，∵D为的中点，∴＝，∴AD＝DC，∵AD＝DC，点O是AC的中点，∴OD⊥AC，∴∠DOA＝∠DOC＝90°，∵DE∥AC，∴∠DOA＝∠ODE＝90°，∵∠ODE＝90°，∴OD⊥DE，∵OD⊥DE，DE经过半径OD的外端点D，∴DE与⊙O相切．（2）解：连接BD．∵四边形ABCD是⊙O的内接四边形，∴∠DAB+∠DCB＝180°，又∵∠DCE+∠DCB＝180°，∴∠DAB＝∠DCE，∵AC为⊙O的直径，点D、B在⊙O上，∴∠ADC＝∠ABC＝90°，∵＝，∴∠ABD＝∠CBD＝45°，∵AD＝DC，∠ADC＝90°，∴∠DAC＝∠DCA＝45°，∵DE∥AC，∴∠DCA＝∠CDE＝45°，在△ABD和△CDE中，∵∠DAB＝∠DCE，∠ABD＝∠CDE＝45°，∴△ABD∽△CDE，∴＝，∴＝，∴AD＝DC＝4，在Rt△ADC中，∠ADC＝90°，AD＝DC＝4，∴AC＝＝＝8，∴⊙O的半径为4．15．（1）如图①，点A，B，C在⊙O上，点D在⊙O外，比较∠A与∠BDC的大小，并说明理由；（2）如图②，点A，B，C在⊙O上，点D在⊙O内，比较∠A与∠BDC的大小，并说明理由；（3）利用上述两题解答获得的经验，解决如下问题：在平面直角坐标系中，如图③，已知点M（1，0），N（4，0），点P在y轴上，试求当∠MPN度数最大时点P的坐标．解：（1）∠A＞∠BDC，理由如下：设CD交⊙O于E，连接BE，如图1所示：∠BEC＝∠BDC+∠DBE，∴∠BEC＞∠BDC，∵∠A＝∠BEC，∴∠A＞∠BDC；（2）∠A＜∠BDC，理由如下：延长CD交⊙O于点F，连接BF，如图2所示：∵∠BDC＝∠BFC+∠FBD，∴∠BDC＞∠BFC，又∵∠A＝∠BFC，∴∠A＜∠BDC；（3）由（1）、（2）可得：当点P是经过M、N两点的圆和y轴相切的切点时，∠MPN度数最大，①当点P在y轴的正半轴上时，如图3所示：设⊙O′为点P是经过M、N两点的圆和y轴相切的切点的圆，连接O′P、O′M、O′N，作O′H⊥MN于H，则四边形OPO′H是矩形，MH＝HN，∴OP＝O′H，O′P＝OH＝O′M，∵M（1，0），N（4，0），∴OM＝1，MN＝3，∴MH＝HN＝MN＝，设O′P＝OH＝O′M＝x，MH＝OH﹣OM＝x﹣1，∴x﹣1＝，∴x＝，∴O′H＝＝＝2，∴OP＝2，∴点P的坐标为（0，2）；②当点P在y轴的负半轴上时，如图4所示：同理可得O′H＝OP＝2，∴点P的坐标为（0，﹣2）；综上所述，当∠MPN度数最大时点P的坐标为（0，2）或（0，﹣2）．。

2020年九年级数学典型中考压轴题专练：圆有关题型1、如图，已知⊙O的直径AB=10，弦AC=6，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC 交AC的延长线于点E．（1）求证：DE是⊙O的切线．（2）求DE的长．2、如图，AB为⊙O的直径，弦CD⊥AB，垂足为点P，直线BF与AD的延长线交于点F，且∠AFB=∠ABC．（1）求证：直线BF是⊙O的切线．（2）若CD=2，OP=1，求线段BF的长．3、如图，已知AB为⊙O的直径，AC为⊙O的切线，OC交⊙O于点D，BD的延长线交AC于点E．（1）求证：∠1=∠CAD；（2）若AE=EC=2，求⊙O的半径．4、如图，在四边形ABCD 中，AB=6，BC=8，CD=24，AD=26，∠B=90°，以AD 为直径作圆O ，过点D 作DE ∥AB 交圆O 于点E（1）证明点C 在圆O 上；（2）求tan ∠CDE 的值；（3）求圆心O 到弦ED 的距离．5、如图，AB 是半圆O 的直径，点P 是BA 延长线上一点，PC 是⊙O 的切线，切点为C. 过点B 作BD ⊥PC 交PC 的延长线于点D ，连接BC. 求证：（1）∠PBC =∠CBD;（2）BC 2=AB ·BD6、如图，AB 是⊙O 的直径，点P 是弦AC 上一动点(不与A 、C 重合)，过点P 作PE ⊥AB,垂足为E ，弧AC 射线EP 交于点F ，交过点C 的切线于点D.(1)求证DC=DP(2)若∠CAB=30°，当F 是 的中点时，判断以A 、O 、C 、F 为顶点的四边形是什么特殊四边形？说明理由；7、如图，在△ABC 中，∠C=90°，D 是BC 边上一点，以DB 为直径的⊙O 经过AB 的中点E ，交AD 的延长线于点F ，连结EF ．AC（1）求证：∠1=∠F．（2）若sinB=，EF=2，求CD的长．8、如图，已知四边形ABCD内接于⊙O，A是的中点，AE⊥AC于A，与⊙O及CB的延长线交于点F、E，且．（1）求证：△ADC∽△EBA；（2）如果AB=8，CD=5，求tan∠CAD的值．9、如图1，AB为半圆O的直径，D为BA的延长线上一点，DC为半圆O的切线，切点为C．（1）求证：∠ACD=∠B；（2）如图2，∠BDC的平分线分别交AC，BC于点E，F；①求tan∠CFE的值；②若AC=3，BC=4，求CE的长．10、如图，已知⊙O是△ABC的外接圆，AD是⊙O的直径，且BD=BC，延长AD 到E，且有∠EBD=∠CAB．（1）求证：BE是⊙O的切线；（2）若BC=，AC=5，求圆的直径AD及切线BE的长．11、已知：如图，⊙O是△ABC的外接圆， =，点D在边BC上，AE∥BC，AE=BD．（1）求证：AD=CE；（2）如果点G在线段DC上（不与点D重合），且AG=AD，求证：四边形AGCE是平行四边形．12、如图，△ABC中，∠BAC=120°，AB=AC=6．P是底边BC上的一个动点（P与B、C不重合），以P为圆心，PB为半径的⊙P与射线BA交于点D，射线PD交射线CA于点E．（1）若点E在线段CA的延长线上，设BP=x，AE=y，求y关于x的函数关系式，并写出x 的取值范围．（2）当BP=2时，试说明射线CA与⊙P是否相切．（3）连接PA，若S△APE=S△ABC，求BP的长．13、如图，AB是⊙O的弦，点C为半径OA的中点，过点C作CD⊥OA交弦AB于点E，连接BD，且DE=DB．（1）判断BD与⊙O的位置关系，并说明理由；（2）若CD=15，BE=10，tanA=，求⊙O的直径．14、如图，直线AB经过⊙O上的点C，直线AO与⊙O交于点E和点D，OB与⊙O交于点F，连接DF、DC．已知OA=OB，CA=CB，DE=10，DF=6．（1）求证：①直线AB是⊙O的切线；②∠FDC=∠EDC；（2）求CD的长．15、如图1是一个用铁丝围成的篮框，我们来仿制一个类似的柱体形篮框．如图2，它是由一个半径为r、圆心角90°的扇形A2OB2，矩形A2C2EO、B2D2EO，及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、A n B n C n D n，OEFG围成，其中A1、G、B1在上，A2、A3…、A n与B2、B3、…B n分别在半径OA2和OB2上，C2、C3、…、C n和D2、D3…D n分别在EC2和ED2上，EF⊥C2D2于H2，C1D1⊥EF于H1，FH1=H1H2=d，C1D1、C2D2、C3D3、C n D n依次等距离平行排放（最后一个矩形状框的边C n D n与点E间的距离应不超过d），A1C1∥A2C2∥A3C3∥…∥A n C n（1）求d的值；（2）问：C n D n与点E间的距离能否等于d？如果能，求出这样的n的值，如果不能，那么它们之间的距离是多少？16、在平面直角坐标中，△ABC三个顶点坐标为A（﹣，0）、B（，0）、C（0，3）．（1）求△ABC内切圆⊙D的半径．（2）过点E（0，﹣1）的直线与⊙D相切于点F（点F在第一象限），求直线EF的解析式．（3）以（2）为条件，P为直线EF上一点，以P为圆心，以2为半径作⊙P．若⊙P上存在一点到△ABC三个顶点的距离相等，求此时圆心P的坐标．答案:1、【解答】证明：（1）连接OD，∵AD平分∠BAC，∴∠DAE=∠DAB，∵OA=OD，∴∠ODA=∠DAO，∴∠ODA=∠DAE，∴OD∥AE，∵DE⊥AC，∴OD⊥DE，∴DE是⊙O切线．（2）过点O作OF⊥AC于点F，∴AF=CF=3，∴OF===4．∵∠OFE=∠DEF=∠ODE=90°，∴四边形OFED是矩形，∴DE=OF=4．2、【解答】（1）证明：∵∠AFB=∠ABC，∠ABC=∠ADC，∴∠AFB=∠ADC，∴CD∥BF，∴∠AFD=∠ABF，∵CD⊥AB，∴AB⊥BF，∴直线BF是⊙O的切线．（2）解：连接OD，∵CD⊥AB，∴PD=CD=，∵OP=1，∴OD=2，∵∠PAD=∠BAF，∠APO=∠ABF，∴△APD∽△ABF，∴=，∴=，∴BF=．3、【解答】（1）证明：∵AB为⊙O的直径，∴∠ADB=90°，∴∠ADO+∠BDO=90°，∵AC为⊙O的切线，∴OA⊥AC，∴∠OAD+∠CAD=90°，∵OA=OD，∴∠OAD=∠ODA，∵∠1=∠BDO，∴∠1=∠CAD；（2）解：∵∠1=∠CAD，∠C=∠C，∴△CAD∽△CDE，∴CD：CA=CE：CD，∴CD2=CA•CE，∵AE=EC=2，∴AC=AE+EC=4，∴CD=2，设⊙O的半径为x，则OA=OD=x，则Rt△AOC中，OA2+AC2=OC2，∴x2+42=（2+x）2，解得：x=．∴⊙O的半径为．4、【解答】（1）证明：如图1，连结CO．∵AB=6，BC=8，∠B=90°，∴AC=10．又∵CD=24，AD=26，102+242=262，∴△ACD是直角三角形，∠C=90°．∵AD为⊙O的直径，∴AO=OD，OC为Rt△ACD斜边上的中线，∴OC=AD=r，∴点C在圆O上；（2）解：如图2，延长BC、DE交于点F，∠BFD=90°．∵∠BFD=90°，∴∠CDE+∠FCD=90°，又∵∠ACD=90°，∴∠ACB+∠FCD=90°，∴∠CDE=∠ACB．在Rt△ABC中，tan∠ACB==，∴tan∠CDE=tan∠ACB=；（3）解：如图3，连结AE，作OG⊥ED于点G，则OG∥AE，且OG=AE．易证△ABC∽△CFD，∴=，即=，∴CF=，∴BF=BC+CF=8+=．∵∠B=∠F=∠AE D=90°，∴四边形ABFE是矩形，∴AE=BF=，∴OG=AE=，即圆心O到弦ED的距离为．5、【解答】证明：（1）连接OC，∵PC是⊙O的切线，∴∠OCD=90°.又∵BD⊥PC∴∠BDP=90°∴OC∥BD.∴∠CBD=∠OCB.∴OB=OC .∴∠OCB=∠PBC.∴∠PBC=∠CBD.（2）连接AC∵AB 是直径，∴∠BDP=90°.又∵∠BDC=90°，∴∠ACB=∠BDC.∵∠PBC=∠CBD,∴△ABC ∽△CBD. ∴BC AB =BD BC .∴BC 2=AB ·BD6、【解析】 (1) 如图连接OC, ∵CD 是⊙O 的切线，∴ OC ⊥CD ∴∠OCD=90º，∴∠DCA= 90º－∠OCA .又PE⊥AB ，点D在EP的延长线上，∴∠DEA=90º，∴∠DPC=∠APE=90º－∠OAC.∵OA=OC , ∴∠OCA=∠OAC.∴∠DCA=∠DPC ,∴DC=DP.(2) 如图四边形AOCF是菱形.连接CF、AF，∵F是弧AC的中点，∴弧AF=弧CF ∴ AF=FC .∵∠BAC=30º，∴弧BC =60º，又AB是⊙O的直径，∴弧ACB =120º，∴弧AF=弧CF= 60º，∴∠ACF=∠FAC =30º .∵OA=OC, ∴∠OCA=∠BAC=30º,∴⊿OAC≌⊿FAC (ASA) , ∴AF=OA ,∴AF=FC=OC=OA , ∴四边形AOCF是菱形.7、【解答】解：（1）证明：连接DE，∵BD是⊙O的直径，∴∠DEB=90°，∵E是AB的中点，∴DA=DB，∴∠1=∠B，∵∠B=∠F，∴∠1=∠F；（2）∵∠1=∠F，∴AE=EF=2，∴AB=2AE=4，在Rt△ABC中，AC=AB•sinB=4，∴BC==8，设CD=x，则AD=BD=8﹣x，∵AC2+CD2=AD2，即42+x2=（8﹣x）2，∴x=3，即CD=3．8、【解答】（1）证明：∵四边形ABCD内接于⊙O，∴∠CDA=∠ABE．∵，∴∠DCA=∠BAE．∴△ADC∽△EBA；（2）解：∵A是的中点，∴∴AB=AC=8，∵△ADC∽△EBA，∴∠CAD=∠AEC，，即，∴AE=，∴tan∠CAD=tan∠AEC===．9、【解答】（1）证明：如图1中，连接OC．∵OA=OC，∴∠1=∠2，∵CD是⊙O切线，∴OC⊥CD，∴∠DCO=90°，∴∠3+∠2=90°，∵AB是直径，∴∠1+∠B=90°，∴∠3=∠B．（2）解：①∵∠CEF=∠ECD+∠CDE，∠CFE=∠B+∠FDB，∵∠CDE=∠FDB，∠ECD=∠B，∴∠CEF=∠CFE，∵∠ECF=90°，∴∠CEF=∠CFE=45°，∴tan∠CFE=tan45°=1．②在RT△ABC中，∵AC=3，BC=4，∴AB==5，∵∠CDA=∠BDC，∠DCA=∠B，∴△DCA∽△DBC，∴===，设DC=3k，DB=4k，∵CD2=DA•DB，∴9k2=（4k﹣5）•4k，∴k=，∴CD=，DB=，∵∠CDE=∠BDF，∠DCE=∠B，∴△DCE∽△DBF，∴=，设EC=CF=x，∴=，∴x=．∴CE=．10、【解答】解：如图，连接OB，∵BD=BC，∴∠CAB=∠BAD，∵∠EBD=∠CAB，∴∠BAD=∠EBD，∵AD是⊙O的直径，∴∠ABD=90°，OA=BO，∴∠BAD=∠ABO，[来源:学科网]∴∠EBD=∠ABO，∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°，∵点B在⊙O上，∴BE是⊙O的切线，（2）如图2，设圆的半径为R，连接CD，∵AD为⊙O的直径，∴∠ACCD=90°，∵BC=BD，∴OB⊥CD，∴OB∥AC，∵OA=OD，∴OF=AC=，∵四边形ACBD是圆内接四边形，∴∠BDE=∠ACB，∵∠DBE=∠ACB，∴△DBE∽△CAB，∴，∴，∴DE=，∵∠OBE=∠OFD=90°，∴DF∥BE，∴，∴，∵R＞0，∴R=3，∵BE是⊙O的切线，∴BE===．11、【解答】证明：（1）在⊙O中，∵=，∴AB=AC，∴∠B=∠ACB，∵AE∥BC，∴∠EAC=∠ACB，∴∠B=∠EAC，在△ABD和△CAE中，，∴△ABD≌△CAE（SAS），∴AD=CE；（2）连接AO并延长，交边BC于点H，∵=，OA为半径，∴AH⊥BC，∴BH=CH，∵AD=AG，∴DH=HG，∴BH﹣DH=CH﹣GH，即BD=CG，∵BD=AE，∴CG=AE，∵CG∥AE，∴四边形AGCE是平行四边形．12、【解答】解：（1）过A作AF⊥BC于F，过P作PH⊥AB于H，∵∠BAC=120°，AB=AC=6，∴∠B=∠C=30°，∵PB=PD，∴∠PDB=∠B=30°，CF=AC•cos30°=6×=3，∴∠ADE=30°，∴∠DAE=∠CPE=60°，∴∠CEP=90°，∴CE=AC+AE=6+y，∴PC==，∵BC=6，∴PB+CP=x+=6，∴y=﹣x+3，∵BD=2BH=x＜6，∴x＜2，∴x的取值范围是0＜x＜2；（2）∵BP=2，∴CP=4，∴PE=PC=2=PB，∴射线CA与⊙P相切；（3）当D点在线段BA上时，连接AP，∵S△ABC=BC•AF=××3=9，∵S△APE=AE•PE=y•×（6+y）=S△ABC=，解得：y=，代入y=﹣x+3得x=4﹣．当D点BA延长线上时，PC=EC=（6﹣y），∴PB+CP=x+（6﹣y）=6，∴y=x﹣3，∵∠PEC=90°，∴PE===（6﹣y），∴S△APE=AE•PE=x•=y•（6﹣y）=S△ABC=，解得y=或，代入y=x﹣3得x=3或5．综上可得，BP的长为4﹣或3或5．13、【解答】（1）证明：连接OB，∵OB=OA，DE=DB，∴∠A=∠OBA，∠DEB=∠ABD，又∵CD⊥OA，∴∠A+∠AEC=∠A+∠DEB=90°，∴∠OBA+∠ABD=90°，∴OB⊥BD，∴BD是⊙O的切线；（2）如图，过点D作DG⊥BE于G，∵DE=DB，∴EG=BE=5，∵∠ACE=∠DGE=90°，∠AEC=∠GED，∴∠GDE=∠A，∴△ACE∽△DGE，∴sin∠EDG=sinA==，即CE=13，在Rt△ECG中，∵DG==12，∵CD=15，DE=13，∴DE=2，∵△ACE∽△DGE，∴=，∴AC=•DG=，∴⊙O的直径2OA=4AD=．4、【解答】（1）①证明：连接OC．∵OA=OB，AC=CB，∴OC⊥AB，∵点C在⊙O上，∴AB是⊙O切线．②证明：∵OA=OB，AC=CB，∴∠AOC=∠BOC，∵OD=OF，∴∠ODF=∠OFD，∵∠AOB=∠ODF+∠OFD=∠AOC+∠BOC，∴∠BOC=∠OFD，∴OC∥DF，∴∠CDF=∠OCD，∵OD=OC，∴∠ODC=∠OCD，∴∠ADC=∠CDF．（2）作ON⊥DF于N，延长DF交AB于M．∵ON⊥DF，∴DN=NF=3，在RT△ODN中，∵∠OND=90°，OD=5，DN=3，∴ON==4，∵∠OCM+∠CMN=180°，∠OCM=90°，∴∠OCM=∠CMN=∠MNO=90°，∴四边形OCMN是矩形，∴ON=CM=4，MN=OC=5，在RT△CDM中，∵∠DMC=90°，CM=4，DM=DN+MN=8，∴CD===4．15、【解答】解：（1）在RT△D2EC2中，∵∠D2EC2=90°，EC2=ED2=r，EF⊥C2D2，∴EH1=r，FH1=r﹣r，∴d=（r﹣r）=r，（2）假设C n D n与点E间的距离能等于d，由题意•r=r，这个方程n没有整数解，所以假设不成立．∵r÷r=2+2≈4.8，∴n=6，此时C n D n与点E间的距离=r﹣4×r=r．16、【解答】解：（1）连接BD，∵B（，0），C（0，3），∴OB=，OC=3，∴tan∠CBO==，∴∠CBO=60°∵点D是△ABC的内心，∴BD平分∠CBO，∴∠DBO=30°，∴tan∠DBO=，∴OD=1，∴△ABC内切圆⊙D的半径为1；（2）连接DF，过点F作FG⊥y轴于点G，∵E（0，﹣1）∴OE=1，DE=2，∵直线EF与⊙D相切，∴∠DFE=90°，DF=1，∴sin∠DEF=，∴∠DEF=30°，∴∠GDF=60°，∴在Rt△DGF中，∠DFG=30°，∴DG=，由勾股定理可求得：GF=，∴F（，），设直线EF的解析式为：y=kx+b，∴，∴直线EF的解析式为：y=x﹣1；（3）∵⊙P上存在一点到△ABC三个顶点的距离相等，∴该点必为△ABC外接圆的圆心，由（1）可知：△ABC是等边三角形，∴△ABC外接圆的圆心为点D∴DP=2，设直线EF与x轴交于点H，∴令y=0代入y=x﹣1，∴x=，∴H（，0），∴FH=，当P在x轴上方时，过点P1作P1M⊥x轴于M，由勾股定理可求得：P1F=3，∴P1H=P1F+FH=，∵∠DEF=∠HP1M=30°，∴HM=P1H=，P1M=5，∴OM=2，∴P1（2，5），当P在x轴下方时，过点P2作P2N⊥x轴于点N，由勾股定理可求得：P2F=3，∴P2H=P2F﹣FH=，∴∠DEF=30°∴∠OHE=60°∴sin∠OHE=，∴P2N=4，令y=﹣4代入y=x﹣1，∴x=﹣，∴P2（﹣，﹣4），综上所述，若⊙P上存在一点到△ABC三个顶点的距离相等，此时圆心P的坐标为（2，5）或（﹣，﹣4）．。

2020届中考数学 几何专题：与圆有关的性质（含答案）一、选择题1.如图，⊙O 是△ABC 的外接圆，已知∠B ＝60°，则∠CAO 的度数是( )A ．15°B ．30°C ．45°D ．60°2.如图，⊙O 的半径为1，AB 是⊙O 的一条弦，且AB＝，则弦AB 所对圆周角的度数为（）A.30°B.60° C.30°或150° D.60°或120°3.如图，⊙P 内含于⊙O ，⊙O 的弦AB 切⊙P 于点C ，且AB ∥OP ．若阴影部分的面积为，则弦AB 的长为（ ）A ．3B ．4C ．6D ．94.如图，△ABC 内接于⊙O ，若∠OAB ＝28°，则∠C 的大小为（ ）A ．28°B ．56°C ．60°D ．62°5.如图，弦CD 垂直于⊙O 的直径AB ，垂足为H ，且CD ＝BD ，则AB 的长为（ ） A ．2 B ．3 C ．4 D ．53 96.如图，∠AOB 是⊙0的圆心角，∠AOB ＝80°，则弧AB 所对圆周角∠ACB 的度数是( )A ．40°B ．45°C ．50°D ．80°7.如图，已知⊙O 的两条弦AC ，BD 相交于点E ，∠A ＝70o ，∠C ＝50o，那么sin ∠AEB 的值为( )A. B. C. D.8.如图，某公园的一座石拱桥是圆弧形（劣弧），其跨度为24米， 拱的半径为13米，则拱高为( ) A ．5米 B ．8米 C ．7米 D ．5米9.如图，△ABC 内接于⊙O ，连结OA 、OB ，若∠ABO＝25°，则∠C 的度数为（ ）A ．55°B ．60°C ．65°D ．70°10.一根水平放置的圆柱形输水管道横截面如图所示，其中有水部分水面宽0.8米，最深处水深0.2米，则此输水管道的直径是（ ）．213322233A ．0.4米B ．0.5米C ．0.8米D ．1米11.如图，AB 是半圆O 的直径，点P 从点O 出发，沿的路径运动一周．设为，运动时间为，则下列图形能大致地刻画与之间关系的是（ ）12.如图，AB 是⊙O 的弦，OD ⊥AB 于D 交⊙O 于E ，则下列说法错误．．的是（ ）A ．AD ＝BDB ．∠ACB ＝∠AOEC ．D ．OD ＝DE13.如图，⊙O 的直径AB 垂直弦CD 于点P ，且P 是半径OB 的中点，CD ＝6cm ，则直径AB 的 长是（ ）A ．B ．C ．D ．14．如图，⊙O 的弦AB ＝6，M 是AB 上任意一点，且OM 最小值为4，则⊙O 的半径为（ ）A ．5B ．4C ．3D ．2OA AB BO --OP s t s t AE BE =O A ． B ．C ．D ．15．如图，⊙O 的半径为5，弦AB ＝8，M 是弦AB 上的动点，则OM 不可能为（ ）A ．2B ．3C ．4D ．516．如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∠CDB ＝30°,⊙O的半径为，则弦CD 的长为（ ）A ．B ．C ．D ．二、填空题1.如图，AB 为半圆O 的直径，延长AB 到点P ，使BP ＝AB ，PC 切半圆O 于点C ，点D 是上和点C 不重合的一点，则的度数为 .2.如图，在⊙O 中，∠ACB ＝20°，则∠AOB ＝______度.3.如图所示，A 、B 、C 、D 是圆上的点，则 度． cm 33cm 23cm 9cm 12AC D ∠17040A ∠=∠=°，°，C ∠=4.在⊙O 中，已知⊙O 的直径AB 为2，弦AC 长为，弦AD 长为．则DC 2＝______5.如图，AB 是⊙O 的直径，点C 在⊙O 上 ，OD∥AC ，若BD ＝1，则BC 的长为6.已知的直径为上的一点，，则＝ _ ．7.如图，的半径弦点为弦上一动点，则点到圆心的最短距离是 cm ．8.如图，AB 为⊙O 的直径，弦CD ⊥AB ，E 为上一点，若∠CEA ＝，则∠ABD ＝°.9.如图，AB 是⊙O 的直径，AC 是弦，若∠A CO ＝32°，则∠COB 的度数等于 ． 32O ⊙8cm AB C =，O ⊙30BAC ∠=°BC cm O 5cm OA =，8cm AB =，P AB P O BC 28BABCD 1三、解答题1.如图，AB 是⊙O 的直径，C 是弧BD 的中点，CE⊥AB，垂足为E ，BD 交CE 于点F ．（1）求证：CF ＝BF ；（2）若AD ＝2，⊙O 的半径为3，求BC 的长．2.已知：如图，⊙O 1与坐标轴交于A （1，0）、B （5，0）两点，点O 1的纵坐标为．求⊙O 1的半径．3.已知：如图，⊙O 的直径AD ＝2，，∠BAE ＝90°．(1)求△CAD 的面积；(2)如果在这个圆形区域中，随机确定一个点P ，那么点P 落在四边形ABCD 区域的概率是多少？5图2 BC CD DE ==4.如图，已知AB 是⊙O 的直径，点C 是⊙O 上一点，连结BC ，AC ，过点C 作直线CD⊥AB 于点D ，点E 是AB 上一点，直线CE 交⊙O 于点F ，连结BF ，与直线CD 交于点G ．求证：.【参考答案】选择题1. B2.DBF BG BC ⋅=23. C4. D5. B6. A7. D8. B9. C10. D11. C12. D13. D14. A15. A16. B填空题1. 30°2. 403. 304.5. 26. 47. 38. 289. 64º解答题1. 证明：（1） 连结AC ，如图。

备考2020年中考数学复习专题《圆》综合练习题一．选择题1．如图，一个小圆沿着一个五边形的边滚动，如果五边形的各边长都和小圆的周长相等，那么当小圆滚动到原来位置时，小圆自身滚动的圈数是（）A．4 B．5 C．6 D．102．如图，在⊙O中，弦AB长6cm，圆心O到AB的距离是3cm，⊙O的半径是（）A．3cm B．C．4cm D．3．如图为球形灯笼的截面图，过圆心的CD垂直弦AB于D，AB＝2dm，CD＝4dm，则⊙O半径为（）A．2dm B．dm C．dm D．dm4．下列判断中不正确的是（）A．半圆是弧，但弧不一定是半圆B．平分弦的直径垂直于弦C．在平面内，到圆心的距离等于半径的点都在圆上D．在同圆或等圆中，相等的圆心角所对的弦相等5．如图，点A、B、C在⊙O上，D是的中点，若∠ACD＝20°，则∠AOB的度数为（）A．60°B．70°C．80°D．90°6．在菱形ABCD中，记∠ABC＝∠α（0°＜∠α＜90°），菱形的面积记作S，菱形的周长记作C，若AD＝2，则（）A．C与∠α的大小有关B．当∠α＝45°时，S＝C．A，B，C，D四个点可以在同一个圆上D．S随∠α的增大而增大7．如图在一次游园活动中有个投篮游戏，活动开始时四个人A、B、C、D在距篮筐P都是5米处站好，篮球放在AC和BD的交点O处，已知取篮球时A要走6米，B要走3米，C要走2米，则D要走（）A．2米B．3米C．4米D．5米8．⊙O半径为5，圆心O的坐标为（0，0），点P的坐标为（3，4），则点P与⊙O的位置关系是（）A．点P在⊙O内B．点P在⊙O上C．点P在⊙O外D．点P在⊙O上或外9．给定下列条件可以确定一个圆的是（）A．已知圆心B．已知半径C．已知直径D．不在同一直线上三点10．如图，△ABC是⊙O的内接三角形，半径OE⊥AB，垂足为点F，连结弦AE，已知OE ＝1，则下面的结论：①AE2+BC2＝4 ②sin∠ACB＝③cos∠B＝，其中正确的是（）A．①②B．①③C．②③D．②11．若半径为5m的圆，其圆心到直线的距离是5m，则直线和圆的位置关系为（）A．相离B．相交C．相切D．无法确定12．如图，圆上有A、B、C三点，直线l与圆相切于点A，CD平分∠ACB，且与l交于点D，若＝80°，＝60°，则∠ADC的度数为（）A．80°B．85°C．90°D．95°二．填空题13．如图，在正方形纸片ABCD中，EF∥AD，M，N是线段EF的六等分点，若把该正方形纸片卷成一个圆柱，使点A与点D重合，此时，底面圆的半径为2cm，则此时M、N两点间的距离是cm．14．如图，⊙O的半径OA垂直于弦BC，垂足是D，OA＝5，AD：OD＝1：4，则BC的长为．15．在我国古代数学著作《九章算术》中记载了这样一个问题：“今有圆材，埋在墙壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”问题题意为：如图，有一圆柱形木材埋在墙壁中，不知其直径大小．用锯去锯这木材，锯口深1寸（即CD＝1寸），锯道长1尺（即AB＝1尺），问这圆形木材直径是多少？（注：1尺＝10寸）由此，可求出这圆形木材直径为为寸．16．′如图，在平面直角坐标系xOy中，扇形OAB的圆心角∠AOB＝60°，点A在x轴正半轴上且OA＝2，带你C为弧AB的中点，D为半径OA上一点，点A关于直线CD的对称点为E，若点E落在扇形OAB内（不含边界），则点E的横坐标x取值范围为．17．如图，以等边△ABC的一边AB为直径的半圆O交AC于点D，交BC于点E，若AB ＝4，则阴影部分的面积是．18．在一个圆内接四边形ABCD中，已知∠A＝100°，则∠C的度数为．三．解答题19．如图AB＝3cm，用图形表示：到点A的距离小于2cm，且到点B的距离不小于2cm 的所有点的集合（用阴影表示，注意边界上的点是否在集合中，如果在，用实线表示，如果不在，则用虚线表示）．20．如图，⊙O直径AB和弦CD相交于点E，AE＝2，EB＝6，∠DEB＝30°，求弦CD长．21．一条排水管的截面如图所示，已知排水管的半径OA＝10m，水面宽AB＝12m，某天下雨后，水管水面上升了2m，求此时排水管水面的宽CD．22．如图，已知⊙O的弦AB，E，F是弧AB上两点，＝，OE、OF分别交于AB于C、D两点，求证：AC＝BD．23．如图，CD为⊙O的弦，P为⊙O上一点，OP∥CD，∠PCD＝15°（1）求∠POC的度数；（2）若＝，AB⊥CD，点A在CD的上方，直接写出∠BPA的度数．24．如图，四边形ABCD内接于⊙O，∠ABC＝135°，AC＝4，求⊙O的半径长．25．已知圆O，弦AB、CD相交于点M．（1）求证：AM•MB＝CM•MD；（2）若M为CD中点，且圆O的半径为3，OM＝2，求AM•MB的值．参考答案一．选择题1．解：因为五边形的各边长都和小圆的周长相等，所以小圆在每一边上滚动正好一周，在五条边上共滚动了5周．由于每次小圆从五边形的一边滚动到另一边时，都会翻转72°，所以小圆在五个角处共滚动一周．因此，总共是滚动了6周．故选：C．2．解：如图所示，由题意知OC＝3，且OC⊥AB，∵AB＝6，∴AC＝AB＝3，则OA＝＝＝3，故选：B．3．解：∵过圆心的CD垂直弦AB于D，AB＝2dm，CD＝4dm，∴BD＝AD＝1dm，在Rt△ODB中，OD2+DB2＝OB2，即（4﹣r）2+12＝r2，解得：r＝dm，故选：C．4．解：A、半圆是弧，但弧不一定是半圆，正确；B、平分弦的直径垂直于弦，不正确．需要添加条件：此弦非直径；C、在平面内，到圆心的距离等于半径的点都在圆上，正确；D、在同圆或等圆中，相等的圆心角所对的弦相等，正确，故选：B．5．解：连接OD，∴∠AOD＝2∠ACD，∵D是的中点，∴∠AOB＝2∠AOD＝4∠ACD＝80°，故选：C．6．【解答】解：A、错误．菱形的周长＝8，与∠α的大小无关；B、错误，∠α＝45°时，菱形的面积＝2•2•sin45°＝2；C、错误，A，B，C，D四个点不在同一个圆上；D、正确．∵0°＜α＜90°，S＝菱形的面积＝2•2•sinα，∴菱形的面积S随α的增大而增大．故选：D．7．解：根据题意得：A、B、C、D在以P为圆心，半径是5米的圆上．∴OA•OC＝OB•OD，即6×2＝3×OD．解得OD＝4．故选：C．8．解：∵点P的坐标为（3，4），∴由勾股定理得，点P到圆心O的距离＝＝5，∴点P在⊙O上，故选B．9．解：A、不能确定．因为半径不确定，故不符合题意；B、不能确定．因为圆心的位置不确定，故不符合题意；C、不能确定，因为圆心的位置不确定，故不符合题意；D．不在同一直线上三点可以确定一个圆．故符合题意；故选：D．10．解：连接AO，延长AO交⊙O于M，连接BM、CM、EM．∵AM是直径，∴∠AEM＝90°，∴AE2+EM2＝AM2，∴AE2+EM2＝4，显然无法判定BC＝EM，故①错误，∵∠ACB＝∠AMB，∴sin∠ACB＝sin∠AMB＝＝，故②正确，∵∠ABC＝∠AMC，∴cos∠ABC＝cos∠AMC＝＝，显然无法判断CM＝AE，故③错误，故选：D．11．解：根据圆心到直线的距离等于圆的半径，则直线和圆相切．故选：C．12．解：设圆心为O，连接OA、OC，∵＝80°，＝60°，∴∠AOC＝140°，∠ACB＝40°，∵OA＝OC，∴∠OAC＝20°，∵直线l与圆相切于点A，∴OA⊥l，∴∠OAD＝90°，∴∠CAD＝70°，∵CD平分∠ACB，∴∠ACD＝∠ACB＝20°，∴∠ADC＝180°﹣∠CAD﹣∠ACD＝90°，故选：C．二．填空题（共6小题）13．解：根据题意得：EF＝BC，MN＝EF，把该正方形纸片卷成一个圆柱，使点A与点D重合，则线段BC形成一半径为2cm的圆，线段BC是圆的周长，BC＝EF＝2π×2＝4π，∴的长＝EF＝＝，∴n＝120°，即∠MON＝120°，∵OM＝ON，∴∠M＝30°，过O作OG⊥MN于G，∵OM＝2，∴OG＝1，MG＝，∴MN＝2MG＝2，故答案为：2．14．解：连接OB，∵OA＝5，AD：OD＝1：4，∴AD＝1，OD＝4，OB＝5，在Rt△ODB中，由勾股定理得：OB2＝OD2+BD2，52＝42+BD2，解得：BD＝3，∵OD⊥BC，OD过O，∴BC＝2BD＝6，故答案为：6．15．解：延长CD，交⊙O于点E，连接OA，由题意知CE过点O，且OC⊥AB，则AD＝BD＝AB＝5（寸），设圆形木材半径为r，则OD＝r﹣1，OA＝r，∵OA2＝OD2+AD2，∴r2＝（r﹣1）2+52，解得r＝13，所以⊙O的直径为26寸，故答案为：26．16．解：当点E落在半径OA上时，连接OC，如下图1所示，∵∠ADC＝90°，∠AOB＝60°，点C为弧AB的中点，点A（2，0），∴∠COD＝30°，OA＝OC＝2，∴CD＝OC•sin30°＝2×＝1，∴OD＝O C•cos30°＝2×＝，∴AD＝OA﹣OD＝2﹣，∵DE＝DA，∴OE＝OD﹣OE＝﹣（2﹣）＝2﹣2，即点E的坐标为（2﹣2，0）；当点E落在半径OB上时，连接OC，CD，如图2所示，由已知可得，CE＝CA＝CB，由上面的计算可知，OE＝2﹣2，∴点E的横坐标为：（2﹣2）×cos60°＝﹣1，点E的纵坐标为：（2﹣2）×sin60°＝3﹣，∴E（﹣1，3﹣），∴满足条件的点E的横坐标x取值范围为﹣1＜x＜2﹣2．故答案为﹣1＜x＜2﹣2．17．解：如图，连接OD，OE，DE．∵△ABC是等边三角形，∴∠A＝∠B＝60°，∵OA＝OD＝OB＝OE＝2，∴△AOD，∠EOB都是等边三角形，∴∠AOD＝∠EOB＝60°，∴∠DOE＝60°，△DOE是等边三角形，∴∠DOE＝∠EOB，∴弓形DE与弓形BE的面积相等，∵CD＝DE＝CE＝2，∴△CDE是等边三角形，∴S阴＝S△CDE＝×22＝，故答案为．18．解：∵四边形ABCD是⊙O的内接四边形，∴∠C+∠A＝180°，∴∠C＝180°﹣100°＝80°．故答案为：80°三．解答题（共7小题）19．解：到点A的距离小于2cm，且到点B的距离不小于2cm的所有点的集合如图所示：20．解：过O作OF⊥CD，交CD于点F，连接OD，∴F为CD的中点，即CF＝DF，∵AE＝2，EB＝6，∴AB＝AE+EB＝2+6＝8，∴OA＝4，∴OE＝OA﹣AE＝4﹣2＝2，在Rt△OEF中，∠DEB＝30°，∴OF＝OE＝1，在Rt△ODF中，OF＝1，OD＝4，根据勾股定理得：DF＝＝，则CD＝2DF＝2．21．解：如图：作OE⊥AB于E，交CD于F，∵AB＝12m，OE⊥AB，OA＝1m，∴OE＝8m．∵水管水面上升了2m，∴OF＝8﹣2＝6m，∴CF＝＝8m，∴CD＝16m．22．证明：连接OA、OB，∵OA＝OB，∴∠A＝∠B，∵＝，∴∠AOC＝∠BOD，在△AOC和△BOD中，，∴△AOC≌△BOD，∴AC＝BD．23．解：（1）∵OP∥CD，∴∠OPC＝∠PCD＝15°，∵OP＝OC，∴∠OPC＝∠OCP＝15°，∴∠OCD＝30°．（2）①如图1中，当AB在点O的左侧时，连接PA，PB，OD，OA，OB．∵OC＝OD，∴∠OCD＝∠ODC＝30°，∴∠COD＝120°，∵＝，∴∠AOB＝∠COD＝120°，∴∠APB＝∠AOB＝60°．②如图2中，当AB在点O的右侧时，同法可得∠ACB＝60°，∵∠APB+∠ACB＝180°，∴∠APB＝120°，综上所述，∠APB＝60°或120°．24．解：∵四边形ABCD内接于⊙O，∠ABC＝135°，∴∠D＝180°﹣∠ABC＝45°，∴∠AOC＝2∠D＝90°，∵OA＝OC，且AC＝4，∴OA＝OC＝AC＝2，即⊙O的半径长为2．25．解：（1）连接AD、BC．∵∠A＝∠C，∠D＝∠B，∴△ADM∽△CBM∴即AM•MB＝CM•MD．（2）连接OM、OC．∵M为CD中点，∴OM⊥CD在Rt△OMC中，∵OC＝3，OM＝2 ∴CD＝CM＝＝＝由（1）知AM•MB＝CM•MD．∴AM•MB＝•＝5．。

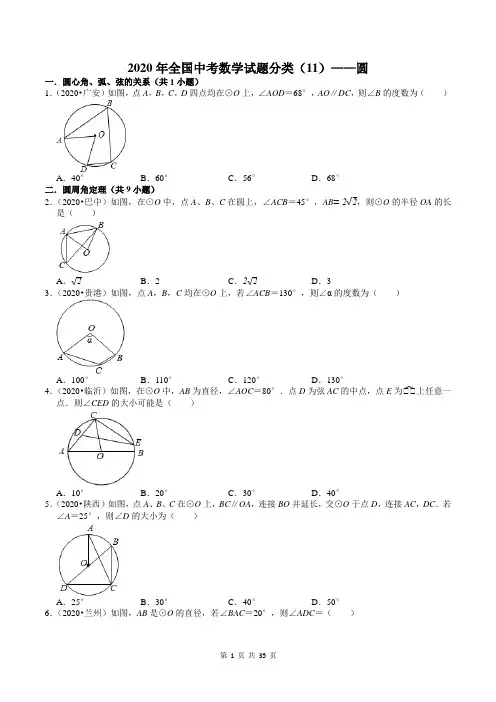
2020年全国中考数学试题分类（11）——圆一．圆心角、弧、弦的关系（共1小题）1．（2020•广安）如图，点A，B，C，D四点均在⊙O上，∠AOD＝68°，AO∥DC，则∠B的度数为（）A．40°B．60°C．56°D．68°二．圆周角定理（共9小题）2．（2020•巴中）如图，在⊙O中，点A、B、C在圆上，∠ACB＝45°，AB=2√2，则⊙O的半径OA的长是（）A．√2B．2 C．2√2D．33．（2020•贵港）如图，点A，B，C均在⊙O上，若∠ACB＝130°，则∠α的度数为（）A．100°B．110°C．120°D．130°̂上任意一4．（2020•临沂）如图，在⊙O中，AB为直径，∠AOC＝80°．点D为弦AC的中点，点E为BB 点．则∠CED的大小可能是（）A．10°B．20°C．30°D．40°5．（2020•陕西）如图，点A、B、C在⊙O上，BC∥OA，连接BO并延长，交⊙O于点D，连接AC，DC．若∠A＝25°，则∠D的大小为（）A．25°B．30°C．40°D．50°6．（2020•兰州）如图，AB是⊙O的直径，若∠BAC＝20°，则∠ADC＝（）A ．40°B ．60°C ．70°D ．80°7．（2020•阜新）如图，AB 为⊙O 的直径，C ，D 是圆周上的两点，若∠ABC ＝38°，则锐角∠BDC 的度数为（ ）A ．57°B ．52°C ．38°D ．26°8．（2020•赤峰）如图，⊙A 经过平面直角坐标系的原点O ，交x 轴于点B （﹣4，0），交y 轴于点C （0，3），点D 为第二象限内圆上一点．则∠CDO 的正弦值是（ ）A ．35B ．−34C ．34D ．45 9．（2020•眉山）如图，四边形ABCD 的外接圆为⊙O ，BC ＝CD ，∠DAC ＝35°，∠ACD ＝45°，则∠ADB的度数为（ ）A ．55°B ．60°C ．65°D ．70°10．（2020•河池）如图，AB 是⊙O 的直径，点C ，D ，E 都在⊙O 上，∠1＝55°，则∠2＝ °．三．圆内接四边形的性质（共2小题）11．（2020•广西）如图，已知四边形ABCD 为⊙O 的内接四边形，BD 平分∠ABC ，DH ⊥AB 于点H ，DH =√3，∠ABC＝120°，则AB+BC的值为（）A．√2B．√3C．2 D．√512．（2020•雅安）如图，四边形ABCD内接于圆，∠ABC＝60°，对角线BD平分∠ADC．（1）求证：△ABC是等边三角形；（2）过点B作BE∥CD交DA的延长线于点E，若AD＝2，DC＝3，求△BDE的面积．四．点与圆的位置关系（共1小题）13．（2020•广东）有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉．把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图，∠ABC ＝90°，点M，N分别在射线BA，BC上，MN长度始终保持不变，MN＝4，E为MN的中点，点D到BA，BC的距离分别为4和2．在此滑动过程中，猫与老鼠的距离DE的最小值为．五．三角形的外接圆与外心（共3小题）14．（2020•赤峰）如图，△ABC中，AB＝AC，AD是∠BAC的平分线，EF是AC的垂直平分线，交AD于点O．若OA＝3，则△ABC外接圆的面积为（）A．3πB．4πC．6πD．9π̂的长为．15．（2020•锦州）如图，⊙O是△ABC的外接圆，∠ABC＝30°，AC＝6，则BB16．（2020•黄石）如图，在6×6的方格纸中，每个小方格都是边长为1的正方形，其中A、B、C为格点，̂的长等于．作△ABC的外接圆，则BB六．直线与圆的位置关系（共1小题）17．（2020•泰州）如图，直线a⊥b，垂足为H，点P在直线b上，PH＝4cm，O为直线b上一动点，若以1cm为半径的⊙O与直线a相切，则OP的长为．七．切线的性质（共4小题）18．（2020•桂林）如图，AB是⊙O的弦，AC与⊙O相切于点A，连接OA，OB，若∠O＝130°，则∠BAC 的度数是（）A．60°B．65°C．70°D．75°19．（2020•眉山）如图，点P为⊙O外一点，过点P作⊙O的切线P A、PB，点A、B为切点，连接AO并延长交PB的延长线于点C，过点C作CD⊥PO，交PO的延长线于点D．已知P A＝6，AC＝8，则CD的长为．20．（2020•呼和浩特）已知AB为⊙O的直径且长为2r，C为⊙O上异于A，B的点，若AD与过点C的⊙O的切线互相垂直，垂足为D．①若等腰三角形AOC的顶角为120度，则CD=12r，②若△AOC为正三角形，则CD=√32r，③若等腰三角形AOC的对称轴经过点D，则CD＝r，④无论点C在何处，将△ADC沿AC折叠，点D一定落在直径AB上，其中正确结论的序号为．21．（2020•济南）如图，AB为⊙O的直径，点C是⊙O上一点，CD与⊙O相切于点C，过点A作AD⊥DC，连接AC，BC．（1）求证：AC是∠DAB的角平分线；（2）若AD＝2，AB＝3，求AC的长．八．切线的判定与性质（共9小题）22．（2020•兰州）如图，在Rt△AOB中，∠AOB＝90°，OA＝OB，点C是AB的中点，以OC为半径作⊙O．（1）求证：AB是⊙O的切线；（2）若OC＝2，求OA的长．23．（2020•西藏）如图所示，AB是⊙O的直径，AD和BC分别切⊙O于A，B两点，CD与⊙O有公共点E，且AD＝DE．（1）求证：CD是⊙O的切线；（2）若AB＝12，BC＝4，求AD的长．24．（2020•葫芦岛）如图，四边形ABCD内接于⊙O，AC是直径，AB＝BC，连接BD，过点D的直线与CA的延长线相交于点E，且∠EDA＝∠ACD．（1）求证：直线DE是⊙O的切线；（2）若AD＝6，CD＝8，求BD的长．25．（2020•镇江）如图，▱ABCD 中，∠ABC 的平分线BO 交边AD 于点O ，OD ＝4，以点O 为圆心，OD 长为半径作⊙O ，分别交边DA 、DC 于点M 、N ．点E 在边BC 上，OE 交⊙O 于点G ，G 为BB̂的中点． （1）求证：四边形ABEO 为菱形；（2）已知cos ∠ABC =13，连接AE ，当AE 与⊙O 相切时，求AB 的长． 26．（2020•宁夏）如图，在△ABC 中，∠B ＝90°，点D 为AC 上一点，以CD 为直径的⊙O 交AB 于点E ，连接CE ，且CE 平分∠ACB ．（1）求证：AE 是⊙O 的切线；（2）连接DE ，若∠A ＝30°，求BB BB ．27．（2020•烟台）如图，在▱ABCD 中，∠D ＝60°，对角线AC ⊥BC ，⊙O 经过点A ，B ，与AC 交于点M ，连接AO 并延长与⊙O 交于点F ，与CB 的延长线交于点E ，AB ＝EB ．（1）求证：EC 是⊙O 的切线；（2）若AD ＝2√3，求BB ̂的长（结果保留π）．28．（2020•广东）如图1，在四边形ABCD 中，AD ∥BC ，∠DAB ＝90°，AB 是⊙O 的直径，CO 平分∠BCD ．（1）求证：直线CD 与⊙O 相切；（2）如图2，记（1）中的切点为E ，P 为优弧BB̂上一点，AD ＝1，BC ＝2．求tan ∠APE 的值．29．（2020•株洲）AB是⊙O的直径，点C是⊙O上一点，连接AC、BC，直线MN过点C，满足∠BCM＝∠BAC＝α．（1）如图①，求证：直线MN是⊙O的切线；（2）如图②，点D在线段BC上，过点D作DH⊥MN于点H，直线DH交⊙O于点E、F，连接AF并延长交直线MN于点G，连接CE，且CE=53，若⊙O的半径为1，cosα=34，求AG•ED的值．30．（2020•潍坊）如图，AB为⊙O的直径，射线AD交⊙O于点F，点C为劣弧BB̂的中点，过点C作CE ⊥AD，垂足为E，连接AC．（1）求证：CE是⊙O的切线；（2）若∠BAC＝30°，AB＝4，求阴影部分的面积．九．三角形的内切圆与内心（共1小题）31．（2020•随州）设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R，则下列结论不正确的是（）A．h＝R+r B．R＝2r C．r=√34a D．R=√3 3a一十．正多边形和圆（共7小题）32．（2020•济南）如图，在正六边形ABCDEF中，分别以C，F为圆心，以边长为半径作弧，图中阴影部分的面积为24π，则正六边形的边长为．33．（2020•黄石）匈牙利著名数学家爱尔特希（P．Erdos，1913﹣1996）曾提出：在平面内有n个点，其中每三个点都能构成等腰三角形，人们将具有这样性质的n个点构成的点集称为爱尔特希点集．如图，是由五个点A、B、C、D、O构成的爱尔特希点集（它们为正五边形的任意四个顶点及正五边形的中心构成），则∠ADO的度数是．34．（2020•株洲）据《汉书律历志》记载：“量者，龠（yuè）、合、升、斗、斛（hú）也”斛是中国古代的一种量器，“斛底，方而圜（huán）其外，旁有庣（tiāo）焉”．意思是说：“斛的底面为：正方形外接一个圆，此圆外是一个同心圆”，如图所示．问题：现有一斛，其底面的外圆直径为两尺五寸（即2.5尺），“庣旁”为两寸五分（即两同心圆的外圆与内圆的半径之差为0.25尺），则此斛底面的正方形的周长为尺．（结果用最简根式表示）35．（2020•南京）如图，在边长为2cm的正六边形ABCDEF中，点P在BC上，则△PEF的面积为cm2．̂上一点（点P与点D，点E不重合），连36．（2020•绥化）如图，正五边形ABCDE内接于⊙O，点P为BB接PC、PD，DG⊥PC，垂足为G，∠PDG等于度．37．（2020•成都）如图，六边形ABCDEF是正六边形，曲线F A1B1C1D1E1F1…叫做“正六边形的渐开线”，BB 1̂，B 1B 1̂，B 1B 1̂，B 1B 1̂，B 1B 1̂，B 1B 1̂，…的圆心依次按A ，B ，C ，D ，E ，F 循环，且每段弧所对的圆心角均为正六边形的一个外角．当AB ＝1时，曲线F A 1B 1C 1D 1E 1F 1的长度是 ．38．（2020•通辽）中心为O 的正六边形ABCDEF 的半径为6cm ，点P ，Q 同时分别从A ，D 两点出发，以1cm /s 的速度沿AF ，DC 向终点F ，C 运动，连接PB ，PE ，QB ，QE ，设运动时间为t （s ）．（1）求证：四边形PBQE 为平行四边形；（2）求矩形PBQE 的面积与正六边形ABCDEF 的面积之比．一十一．弧长的计算（共4小题）39．（2020•盘锦）如图，在△ABC 中，AB ＝BC ，∠ABC ＝90°，以AB 为直径的⊙O 交AC 于点D ，点E 为线段OB 上的一点，OE ：EB ＝1：√3，连接DE 并延长交CB 的延长线于点F ，连接OF 交⊙O 于点G ，若BF ＝2√3，则BB̂的长是（ ） A ．B 3 B ．B 2 C ．2B 3 D ．3B 440．（2020•沈阳）如图，在矩形ABCD 中，AB =√3，BC ＝2，以点A 为圆心，AD 长为半径画弧交边BC 于点E ，连接AE ，则BB̂的长为（ ） A ．4B 3 B ．π C ．2B 3 D ．B 3 41．（2020•潍坊）如图，四边形ABCD 是正方形，曲线DA 1B 1C 1D 1A 2…是由一段段90度的弧组成的．其中：BB 1̂的圆心为点A ，半径为AD ；B 1B 1̂的圆心为点B ，半径为BA 1；B 1B 1̂的圆心为点C ，半径为CB 1；B 1B 1̂的圆心为点D ，半径为DC 1；⋯BB 1̂，B 1B 1̂，B 1B 1̂，B 1B 1̂，…的圆心依次按点A ，B ，C ，D 循环．若正方形ABCD 的边长为1，则B 2020B 2020̂的长是 ．42．（2020•河南）如图，在扇形BOC 中，∠BOC ＝60°，OD 平分∠BOC 交BB̂于点D ，点E 为半径OB 上一动点．若OB ＝2，则阴影部分周长的最小值为 ．一十二．扇形面积的计算（共6小题）43．（2020•山西）中国美食讲究色香味美，优雅的摆盘造型也会让美食锦上添花．图①中的摆盘，其形状是扇形的一部分，图②是其几何示意图（阴影部分为摆盘），通过测量得到AC ＝BD ＝12cm ，C ，D 两点之间的距离为4cm ，圆心角为60°，则图中摆盘的面积是（ ）A ．80πcm 2B ．40πcm 2C ．24πcm 2D ．2πcm 244．（2020•日照）如图，AB 是⊙O 的直径，CD 为⊙O 的弦，AB ⊥CD 于点E ，若CD ＝6√3，AE ＝9，则阴影部分的面积为（ ） A ．6π−92√3 B ．12π﹣9√3C ．3π−94√3D ．9√3 45．（2020•西藏）如图，AB 为半圆O 的直径，C 为半圆上的一点，OD ⊥AC ，垂足为D ，延长OD 与半圆O 交于点E ．若AB ＝8，∠CAB ＝30°，则图中阴影部分的面积为（ ）A ．43π−√3B ．43π﹣2√3C ．83π−√3D ．83π﹣2√3 46．（2020•呼伦贝尔）若一个扇形的弧长是2πcm ，面积是6πcm 2，则扇形的圆心角是 度．47．（2020•鄂尔多斯）如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足为E ，∠BCD ＝30°，CD ＝2√3，则阴影部分面积S 阴影＝ ．48．（2020•福建）一个扇形的圆心角是90°，半径为4，则这个扇形的面积为 ．（结果保留π）一十三．圆锥的计算（共1小题）49．（2020•广东）如图，从一块半径为1m 的圆形铁皮上剪出一个圆周角为120°的扇形ABC ，如果将剪下来的扇形围成一个圆锥，则该圆锥的底面圆的半径为 m ．一十四．圆的综合题（共1小题）50．（2020•呼和浩特）某同学在学习了正多边形和圆之后，对正五边形的边及相关线段进行研究，发现多处出现著名的黄金分割比√5−12≈0.618．如图，圆内接正五边形ABCDE ，圆心为O ，OA 与BE 交于点H ，AC 、AD 与BE 分别交于点M 、N ．根据圆与正五边形的对称性，只对部分图形进行研究．（其它可同理得出）（1）求证：△ABM 是等腰三角形且底角等于36°，并直接说出△BAN 的形状；（2）求证：BB BB =BB BB ，且其比值k =√5−12；（3）由对称性知AO ⊥BE ，由（1）（2）可知BB BB 也是一个黄金分割数，据此求sin18°的值．2020年全国中考数学试题分类（11）——圆参考答案与试题解析一．圆心角、弧、弦的关系（共1小题）1．【解答】解：如图，连接OC，∵AO∥DC，∴∠ODC＝∠AOD＝68°，∵OD＝OC，∴∠ODC＝∠OCD＝68°，∴∠COD＝44°，∴∠AOC＝112°，∴∠B=12∠AOC＝56°．故选：C．二．圆周角定理（共9小题）2．【解答】解：根据圆周角定理得：∠AOB＝2∠ACB，∵∠ACB＝45°，∴∠AOB＝90°，∵AB＝2√2，OA＝OB，∴2OA2＝AB2，∴OA＝OB＝2，故选：B．3．【解答】解：在优弧AB上任意找一点D，连接AD，BD．∵∠D＝180°﹣∠ACB＝50°，∴∠AOB＝2∠D＝100°，故选：A．4．【解答】解：连接OD、OE，∵OC＝OA，∴△OAC是等腰三角形，∵点D为弦AC的中点，∴∠DOC＝40°，∠BOC＝100°，设∠BOE ＝x ，则∠COE ＝100°﹣x ，∠DOE ＝100°﹣x +40°， ∵OC ＝OE ，∠COE ＝100°﹣x ，∴∠OEC ＝∠OCE ＝40°+12x ，∵OD ＜OE ，∠DOE ＝100°﹣x +40°＝140°﹣x ，∴∠OED ＜20°+12x ， ∴∠CED ＝∠OEC ﹣∠OED ＞（40°+12x ）﹣（20°+12x ）＝20°，∵∠CED ＜∠ABC ＝40°，∴20°＜∠CED ＜40°故选：C ．5．【解答】解：∵BC ∥OA ，∴∠ACB ＝∠A ＝25°，∠B ＝∠AOB ＝2∠ACB ＝50°，∵BD 是⊙O 的直径，∴∠BCD ＝90°，∴∠D ＝90°﹣∠B ＝90°﹣50°＝40°，故选：C ．6．【解答】解：∵AB 是直径，∴∠ACB ＝90°，∵∠BAC ＝20°，∴∠ABC ＝90°﹣20°＝70°，∴∠ADC ＝∠ABC ＝70°，故选：C ．7．【解答】解：连接AC ，∵AB 是⊙O 的直径，∴∠ACB ＝90°，∵∠ABC ＝38°，∴∠BAC ＝90°﹣∠ABC ＝52°，∴∠BDC ＝∠BAC ＝52°．故选：B ．8．【解答】解：连接BC ，如图，∵B （﹣4，0），C （0，3），∴OB ＝4，OC ＝3，∴BC =√32+42=5，∴sin ∠OBC =BB BB =35， ∵∠ODC ＝∠OBC ，∴sin ∠CDO ＝sin ∠OBC =35．故选：A ．9．【解答】解：∵BC ＝CD ， ∴BB̂=BB ̂， ∵∠ABD 和∠ACD 所对的弧都是BB̂， ∴∠BAC ＝∠DAC ＝35°，∵∠ABD ＝∠ACD ＝45°，∴∠ADB ＝180°﹣∠BAD ﹣∠ABD ＝180°﹣70°﹣45°＝65°． 故选：C ．10．【解答】解：如图，连接AD ．∵AB 是直径，∴∠ADB ＝90°，∵∠1＝∠ADE ，∴∠1+∠2＝90°，∵∠1＝55°，∴∠2＝35°，故答案为35．三．圆内接四边形的性质（共2小题）11．【解答】解：延长BA 到E ，使AE ＝BC ，连接DE ，如图，∵BD 平分∠ABC ，∴∠ABD ＝∠CBD =12∠ABC =12×120°＝60°，∵∠DAC ＝∠DBC ＝60°，∠DCA ＝∠DBA ＝60°，∴△DAC 为等边三角形，∴DA ＝DC ，在△ADE 和△BCD 中，{BB =BB BBBB =BBBB BB =BB ，∴△ADE ≌△BCD （SAS ），∴∠E ＝∠DBC ＝60°，而∠DBA ＝60°，∴△DBE 为等边三角形，∵DH ⊥AB ，∴BH ＝EH ，在Rt △BDH 中，BH =√33DH =√33×√3=1，∴BE ＝2BH ＝2，∴AB +BC ＝2．故选：C ．12．【解答】（1）证明：∵四边形ABCD 内接于圆．∴∠ABC +∠ADC ＝180°，∵∠ABC ＝60°，∴∠ADC ＝120°，∵DB 平分∠ADC ，∴∠ADB ＝∠CDB ＝60°，∴∠ACB ＝∠ADB ＝60°，∠BAC ＝∠CDB ＝60°，∴∠ABC ＝∠BCA ＝∠BAC ，∴△ABC 是等边三角形．（2）过点A 作AM ⊥CD ，垂足为点M ，过点B 作BN ⊥AC ，垂足为点N ． ∴∠AMD ＝90°，∵∠ADC ＝120°，∴∠ADM ＝60°，∴∠DAM ＝30°，∴DM =12AD ＝1，AM =√BB 2−BB 2=√22−12=√3，∵CD ＝3，∴CM ＝CD +DM ＝1+3＝4，∴S △ACD =12CD •AM =12×3×√3=3√32，Rt △AMC 中，∠AMD ＝90°，∴AC =√BB 2+BB 2=√3+16=√19，∵△ABC 是等边三角形，∴AB ＝BC ＝AC =√19，∴BN =√32BC =√572，∴S △ABC =12×√19×√572=19√34， ∴四边形ABCD 的面积=19√34+3√32=25√34， ∵BE ∥CD ，∴∠E +∠ADC ＝180°，∵∠ADC ＝120°，∴∠E ＝60°，∴∠E ＝∠BDC ，∵四边形ABCD 内接于⊙O ，∴∠EAB ＝∠BCD ，在△EAB 和△DCB 中，{∠B =∠BBBBBBB =BBBB BB =BB，∴△EAB ≌△DCB （AAS ），∴△BDE 的面积＝四边形ABCD 的面积=25√34． 四．点与圆的位置关系（共1小题）13．【解答】解：如图，连接BE ，BD ．由题意BD =√22+42=2√5，∵∠MBN ＝90°，MN ＝4，EM ＝NE ，∴BE =12MN ＝2，∴点E 的运动轨迹是以B 为圆心，2为半径的弧， ∴当点E 落在线段BD 上时，DE 的值最小，∴DE 的最小值为2√5−2．（也可以用DE ≥BD ﹣BE ，即DE ≥2√5−2确定最小值） 故答案为2√5−2．五．三角形的外接圆与外心（共3小题）14．【解答】解：∵AB ＝AC ，AD 是∠BAC 的平分线， ∴BD ＝CD ，AD ⊥BC ，∵EF 是AC 的垂直平分线，∴点O 是△ABC 外接圆的圆心，∵OA ＝3，∴△ABC 外接圆的面积＝πr 2＝π×32＝9π．故选：D ．15．【解答】解：连接OC ，OA ．∵∠AOC ＝2∠ABC ，∠ABC ＝30°，∴∠AOC ＝60°，∵OA ＝OC ，∴△AOC 是等边三角形，∴OA ＝OC ＝AC ＝6，∴BB ̂的长=60⋅B ⋅6180=2π， 故答案为2π．16．【解答】解：∵每个小方格都是边长为1的正方形， ∴AB ＝2√5，AC =√10，BC =√10，∴AC 2+BC 2＝AB 2，∴△ACB 为等腰直角三角形，∴∠A ＝∠B ＝45°，∴连接OC ，则∠COB ＝90°，∵OB =√5，∴BB̂的长为：90⋅B ×√5180=√52π， 故答案为：√52π． 六．直线与圆的位置关系（共1小题）17．【解答】解：∵直线a ⊥b ，O 为直线b 上一动点， ∴⊙O 与直线a 相切时，切点为H ，∴OH ＝1cm ，当点O 在点H 的左侧，⊙O 与直线a 相切时，如图1所示：OP ＝PH ﹣OH ＝4﹣1＝3（cm ）；当点O 在点H 的右侧，⊙O 与直线a 相切时，如图2所示：OP ＝PH +OH ＝4+1＝5（cm ）；∴⊙O 与直线a 相切，OP 的长为3cm 或5cm ，故答案为：3cm 或5cm ．七．切线的性质（共4小题）18．【解答】解：∵AC 与⊙O 相切于点A ，∴AC ⊥OA ，∴∠OAC ＝90°，∵OA ＝OB ，∴∠OAB ＝∠OBA ．∵∠O ＝130°，∴∠OAB=180°−BB2=25°，∴∠BAC＝∠OAC﹣∠OAB＝90°﹣25°＝65°．故选：B．19．【解答】解：连接OB，如图，∵P A、PB为⊙O的切线，∴PB＝P A＝6，OB⊥PC，OA⊥P A，∴∠CAP＝∠CBO＝90°，在Rt△APC中，PC=√BB2+BB2=√62+82=10，∴BC＝PC﹣PB＝4，设⊙O的半径为r，则OA＝OB＝r，OC＝8﹣r，在Rt△BCO中，42+r2＝（8﹣r）2，解得r＝3，∴OA＝3，OC＝5，在Rt△OP A中，OP=√BB2+BB2=√32+62=3√5，∵CD⊥PO，∴∠CDO＝90°，∵∠COD＝∠POA，∠CDO＝∠P AO，∴△COD∽△POA，∴CD：P A＝OC：OP，即CD：6＝5：3√5，∴CD＝2√5．故答案为2√5．20．【解答】解：①如图1，∵∠AOC＝120°，∴∠CAO＝∠ACO＝30°，∵CD和圆O相切，AD⊥CD，∴∠OCD＝90°，AD∥CO，∴∠ACD＝60°，∠CAD＝30°，∴CD=12AC，∵C为⊙O上异于A，B的点，∴AC＜AB，∴CD≠12r，故①错误；②如图2，过点A作AE⊥OC，垂足为E，若△AOC为正三角形，∠AOC＝∠OAC＝60°，AC＝OC＝OA＝r，∴∠OAE＝30°，∴OE=12AO，AE=√32AO=√32r，∵四边形AECD为矩形，∴CD＝AE=√32r，故②正确；③若等腰三角形AOC的对称轴经过点D，如图3，∴AD＝CD，而∠ADC＝90°，∴∠DAC＝∠DCA＝45°，又∠OCD＝90°，∴∠ACO＝∠CAO＝45°∴∠DAO＝90°，∴四边形AOCD为矩形，∴CD＝AO＝r，故③正确；④如图4，过点C作CE⊥AO，垂足为E，连接DE，∵OC⊥CD，AD⊥CD，∴OC∥AD，∴∠CAD＝∠ACO，∵OC＝OA，∴∠ACO＝∠CAO，∴∠CAD＝∠CAO，∴CD＝CE，在△ADC和△AEC中，∠ADC＝∠AEC＝90°，CD＝CE，AC＝AC，∴△ADC≌△AEC（HL），∴AD＝AE，∴AC垂直平分DE，则点D和点E关于AC对称，即点D一定落在直径上，故④正确．故正确的序号为：②③④，故答案为：②③④．21．【解答】解：（1）证明：连接OC，如图，∵CD与⊙O相切于点C，∴∠OCD ＝90°，∴∠ACD +∠ACO ＝90°，∵AD ⊥DC ，∴∠ADC ＝90°，∴∠ACD +∠DAC ＝90°，∴∠ACO ＝∠DAC ，∵OA ＝OC ，∴∠OAC ＝∠OCA ，∴∠DAC ＝∠OAC ，∴AC 是∠DAB 的角平分线；（2）∵AB 是⊙O 的直径，∴∠ACB ＝90°，∴∠D ＝∠ACB ＝90°，∵∠DAC ＝∠BAC ，∴Rt △ADC ∽Rt △ACB ，∴BB BB =BB BB ，∴AC 2＝AD •AB ＝2×3＝6，∴AC =√6．八．切线的判定与性质（共9小题）22．【解答】（1）证明：∵OA ＝OB ，点C 是AB 的中点，∴OC ⊥AB ，∵OC 为⊙O 的半径，∴AB 是⊙O 的切线；（2）∵△AOB 是等腰直角三角形，点C 是AB 的中点，∴OC ⊥AB ，AB ＝2OC ＝4，∵12OA 2=12BB ⋅BB ， ∴OA =√2×4=2√2．23．【解答】（1）证明：连接OD ，OE ，∵AD 切⊙O 于A 点，AB 是⊙O 的直径，∴∠DAB ＝90°，∵AD ＝DE ，OA ＝OE ，OD ＝OD ，∴△ADO ≌△EDO （SSS ），∴∠OED ＝∠OAD ＝90°，∴CD 是⊙O 的切线；（2）解：过C 作CH ⊥AD 于H ，∵AB 是⊙O 的直径，AD 和BC 分别切⊙O 于A ，B 两点，∴∠DAB ＝∠ABC ＝∠CHA ＝90°，∴四边形ABCH 是矩形，∴CH ＝AB ＝12，AH ＝BC ＝4，∵CD 是⊙O 的切线，∴AD ＝DE ，CE ＝BC ，∴DH ＝AD ﹣BC ＝AD ﹣4，CD ＝AD +4，∵CH 2+DH 2＝CD 2，∴122+（AD ﹣4）2＝（AD +4）2，∴AD ＝9．24．【解答】（1）证明：连接OD，∵OC＝OD，∴∠OCD＝∠ODC，∵AC是直径，∴∠ADC＝90°，∵∠EDA＝∠ACD，∴∠ADO+∠ODC＝∠EDA+∠ADO＝90°，∴∠EDO＝∠EDA+∠ADO＝90°，∴OD⊥DE，∵OD是半径，∴直线DE是⊙O的切线．（2）解法一：过点A作AF⊥BD于点F，则∠AFB＝∠AFD＝90°，∵AC是直径，∴∠ABC＝∠ADC＝90°，∵在Rt△ACD中，AD＝6，CD＝8，∴AC2＝AD2+CD2＝62+82＝100，∴AC＝10，∵在Rt△ABC中，AB＝BC，∴∠BAC＝∠ACB＝45°，∵BBB∠BBB=BB BB，∴BB=BBB45°⋅BB=5√2，∵∠ADB＝∠ACB＝45°，∵在Rt△ADF中，AD＝6，∵BBB∠BBB=BB BB，∴BB=BBB45°⋅BB=3√2，∴BB=BB=3√2，在Rt△ABF中，BB2=BB2−BB2=(5√2)2−(3√2)2=32，∴BB=4√2，∴BB=BB+BB=7√2．解法二：过点B作BH⊥BD交DC延长线于点H．∴∠DBH＝90°，∵AC是直径，∴∠ABC＝90°，∵∠ABD＝90°﹣∠DBC，∠CBH＝90°﹣∠DBC，∴∠ABD＝∠CBH，∵四边形ABCD内接于⊙O，∴∠BAD+∠BCD＝180°，∵∠BCD+∠BCH＝180°，∴∠BAD＝∠BCH，∵AB＝CB，∴△ABD≌△CBH（ASA），∴AD ＝CH ，BD ＝BH ，∵AD ＝6，CD ＝8，∴DH ＝CD +CH ＝14，在Rt △BDH 中，∵BD 2＝DH 2﹣BH 2，BD ＝BH ，则BD 2＝98．∴BB =7√2．25．【解答】解：（1）证明：∵G 为BB̂的中点， ∴∠MOG ＝∠MDN ．∵四边形ABCD 是平行四边形．∴AO ∥BE ，∠MDN +∠A ＝180°，∴∠MOG +∠A ＝180°，∴AB ∥OE ，∴四边形ABEO 是平行四边形．∵BO 平分∠ABE ，∴∠ABO ＝∠OBE ，又∵∠OBE ＝∠AOB ，∴∠ABO ＝∠AOB ，∴AB ＝AO ，∴四边形ABEO 为菱形；（2）如图，过点O 作OP ⊥BA ，交BA 的延长线于点P ，过点O 作OQ ⊥BC 于点Q ，设AE 交OB 于点F ，则∠P AO ＝∠ABC ，设AB ＝AO ＝OE ＝x ，则∵cos ∠ABC =13，∴cos ∠P AO =13，∴BB BB =13，∴P A =13x ， ∴OP ＝OQ =2√23x当AE 与⊙O 相切时，由菱形的对角线互相垂直，可知F 为切点，∴在Rt △OBQ 中，由勾股定理得：(43B )2+(2√23B )2=82， 解得：x ＝2√6（舍负）．∴AB 的长为2√6．26．【解答】（1）证明：连接OE ，如图1所示：∵CE 平分∠ACB ，∴∠ACE ＝∠BCE ，又∵OE ＝OC ，∴∠ACE ＝∠OEC ，∴∠BCE ＝∠OEC ，∴OE ∥BC ，∴∠AEO ＝∠B ，又∵∠B ＝90°，∴∠AEO ＝90°，即OE ⊥AE ，∵OE 为⊙O 的半径，∴AE 是⊙O 的切线；（2）解：连接DE ，如图2所示：∵CD 是⊙O 的直径，∴∠DEC ＝90°，∴∠DEC ＝∠B ，又∵∠DCE ＝∠ECB ，∴△DCE ∽△ECB ，∴BB BB =BB BB ，∵∠A ＝30°，∠B ＝90°，∴∠ACB ＝60°，∴∠DCE =12∠ACB =12×60°＝30°，∴BB BB =cos ∠DCE ＝cos30°=√32，∴BB BB =√32．27．【解答】（1）证明：连接OB ，连接OM ，∵四边形ABCD 是平行四边形，∴∠ABC ＝∠D ＝60°，∵AC ⊥BC ，∴∠ACB ＝90°，∵BE ＝AB ，∴∠E ＝∠BAE ，∵∠ABC ＝∠E +∠BAE ＝60°，∴∠E ＝∠BAE ＝30°，∵OA ＝OB ，∴∠ABO ＝∠OAB ＝30°，∴∠OBC ＝30°+60°＝90°，∴OB ⊥CE ，∴EC 是⊙O 的切线；（2）解：∵四边形ABCD 是平行四边形，∴BC ＝AD ＝2√3，过O 作OH ⊥AM 于H ，则四边形OBCH 是矩形，∴OH ＝BC ＝2√3，∴OA =BB BBB60°=4，∠AOM ＝2∠AOH ＝60°，∴BB ̂的长度=60⋅B ×4180=4B 3． 28．【解答】（1）证明：作OE ⊥CD 于E ，如图1所示：则∠OEC ＝90°，∵AD ∥BC ，∠DAB ＝90°，∴∠OBC ＝180°﹣∠DAB ＝90°，∴∠OEC ＝∠OBC ，∵CO 平分∠BCD ，∴∠OCE ＝∠OCB ，在△OCE 和△OCB 中，{∠BBB =∠BBBBBBB =BBBB BB =BB，∴△OCE ≌△OCB （AAS ），∴OE ＝OB ，又∵OE ⊥CD ，∴直线CD 与⊙O 相切；（2）解：作DF ⊥BC 于F ，连接BE ，如图2所示：则四边形ABFD 是矩形，∴AB ＝DF ，BF ＝AD ＝1，∴CF ＝BC ﹣BF ＝2﹣1＝1，∵AD ∥BC ，∠DAB ＝90°，∴AD ⊥AB ，BC ⊥AB ，∴AD 、BC 是⊙O 的切线，由（1）得：CD 是⊙O 的切线，∴ED ＝AD ＝1，EC ＝BC ＝2，∴CD ＝ED +EC ＝3，∴DF =√BB 2−BB 2=√32−12=2√2，∴OB=√2，∵CO平分∠BCD，∴CO⊥BE，∴∠BCH+∠CBH＝∠CBH+∠ABE＝90°，∴∠ABE＝∠BCH，∵∠APE＝∠ABE，∴∠APE＝∠BCH，∴tan∠APE＝tan∠BCH=BBBB=√22．29．【解答】（1）证明：连接OC，如图①，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠A+∠B＝90°，∵OC＝OB，∴∠B＝∠OCB，∵∠BCM＝∠A，∴∠OCB+∠BCM＝90°，即OC⊥MN，∴MN是⊙O的切线；（2）解：如图②，∵AB是⊙O的直径，⊙O的半径为1，∴AB＝2，∵cos∠BAC=BBBB=BBBB=34，即BB2=34，∴BB=3 2，∵∠AFE＝∠ACE，∠GFH＝∠AFE，∴∠GFH＝∠ACE，∵DH⊥MN，∴∠GFH+∠AGC＝90°，∵∠ACE+∠ECD＝90°，∴∠ECD＝∠AGC，又∵∠DEC＝∠CAG，∴△EDC∽△ACG，∴BB BB =BB BB ，∴BB ⋅BB =BB ⋅BB =32×53=52．30．【解答】解：（1）连接BF ，OC ，∵AB 是⊙O 的直径，∴∠AFB ＝90°，即BF ⊥AD ，∵CE ⊥AD ，∴BF ∥CE ，连接OC ，∵点C 为劣弧BB ̂的中点，∴OC ⊥BF ，∵BF ∥CE ，∴OC ⊥CE ，∵OC 是⊙O 的半径，∴CE 是⊙O 的切线；（2）连接OF ，CF ，∵OA ＝OC ，∠BAC ＝30°，∴∠BOC ＝60°，∵点C 为劣弧BB ̂的中点，∴BB ̂=BB ̂，∴∠FOC ＝∠BOC ＝60°，∵OF ＝OC ，∴∠OCF ＝∠COB ，∴CF ∥AB ，∴S △ACF ＝S △COF ，∴阴影部分的面积＝S 扇形COF ，∵AB ＝4，∴FO ＝OC ＝OB ＝2，∴S 扇形FOC =60⋅B ×22360=23B ， 即阴影部分的面积为：23B ． 九．三角形的内切圆与内心（共1小题）31．【解答】解：如图，∵△ABC 是等边三角形，∴△ABC 的内切圆和外接圆是同心圆，圆心为O ，设OE ＝r ，AO ＝R ，AD ＝h ，∴h ＝R +r ，故A 正确；∵AD ⊥BC ，∴∠DAC =12∠BAC =12×60°＝30°，在Rt △AOE 中，∴R ＝2r ，故B 正确；∵OD ＝OE ＝r ，∵AB ＝AC ＝BC ＝a ，∴AE =12AC =12a ，∴（12a ）2+r 2＝（2r ）2，（12a ）2+（12R ）2＝R 2， ∴r =√3B 6，R =√33a ，故C 错误，D 正确；故选：C ．一十．正多边形和圆（共7小题）32．【解答】解：∵正六边形的内角是120度，阴影部分的面积为24π，设正六边形的边长为r ，∴120B ×B 2360×2＝24π，解得r ＝6．则正六边形的边长为6．33．【解答】解：由题意知点A 、B 、C 、D 为正五边形任意四个顶点，且O 为正五边形中心， ∴∠AOB ＝∠BOC ＝∠COD =360°5=72°，∴∠AOD ＝360°﹣3∠AOB ＝144°，又∵OA ＝OD ，∴∠ADO =180°−BBBB 2=180°−144°2=18°， 故答案为：18°．34．【解答】解：如图，∵四边形CDEF为正方形，∴∠D＝90°，CD＝DE，∴CE为直径，∠ECD＝45°，由题意得AB＝2.5，∴CE＝2.5﹣0.25×2＝2，∴CD＝CE⋅BBB∠BBB=2×√22=√2，∴正方形CDEF周长为4√2尺．故答案为：4√2．35．【解答】解：连接BF，BE，过点A作AT⊥BF于T∵ABCDEF是正六边形，∴CB∥EF，AB＝AF，∠BAF＝120°，∴S△PEF＝S△BEF，∵AT⊥BF，AB＝AF，∴BT＝FT，∠BAT＝∠F AT＝60°，∴BT＝FT＝AB•sin60°=√3，∴BF＝2BT＝2√3，∵∠AFE＝120°，∠AFB＝∠ABF＝30°，∴∠BFE＝90°，∴S△PEF＝S△BEF=12•EF•BF=12×2×2√3=2√3，故答案为2√3．36．【解答】解：连接OC、OD，如图所示：∵ABCDE是正五边形，∴∠COD=360°5=72°，∴∠CPD=12∠COD＝36°，∵DG⊥PC，∴∠PGD＝90°，∴∠PDG＝90°﹣∠CPD＝90°﹣36°＝54°，故答案为：54．37．【解答】解：BB 1̂的长=60⋅B ⋅1180=B 3，B 1B 1̂的长=60⋅B ⋅2180=2B 3， B 1B 1̂的长=60⋅B ⋅3180=3B 3，B 1B 1̂的长=60⋅B ⋅4180=4B 3，B 1B 1̂的长=60⋅B ⋅5180=5B 3， B 1B 1̂的长=60⋅B ⋅6180=6B 3，∴曲线F A 1B 1C 1D 1E 1F 1的长度=B 3+2B 3+⋯+6B 3=21B 3=7π， 故答案为7π．38．【解答】（1）证明：∵六边形ABCDEF 是正六边形，∴AB ＝BC ＝CD ＝DE ＝EF ＝F A ，∠A ＝∠ABC ＝∠C ＝∠D ＝∠DEF ＝∠F ，∵点P ，Q 同时分别从A ，D 两点出发，以1cm /s 速度沿AF ，DC 向终点F ，C 运动， ∴AP ＝DQ ＝t ，PF ＝QC ＝6﹣t ，在△ABP 和△DEQ 中，{BB =BBBB =BB BB =BB ，∴△ABP ≌△DEQ （SAS ），∴BP ＝EQ ，同理可证PE ＝QB ，∴四边形PEQB 为平行四边形．（2）解：连接BE 、OA ，则∠AOB =360°6=60°，∵OA ＝OB ，∴△AOB 是等边三角形，∴AB ＝OA ＝6，BE ＝2OB ＝12，当t ＝0时，点P 与A 重合，Q 与D 重合，四边形PBQE 即为四边形ABDE ，如图1所示： 则∠EAF ＝∠AEF ＝30°，∴∠BAE ＝120°﹣30°＝90°，∴此时四边形ABDE 是矩形，即四边形PBQE 是矩形．当t ＝6时，点P 与F 重合，Q 与C 重合，四边形PBQE 即为四边形FBCE ，如图2所示： 同法可知∠BFE ＝90°，此时四边形PBQE 是矩形．综上所述，t ＝0s 或6s 时，四边形PBQE 是矩形，∴AE =√122−62=6√3，∴矩形PBQE 的面积＝矩形ABDE 的面积＝AB ×AE ＝6×6√3=36√3；∵正六边形ABCDEF 的面积＝6△AOB 的面积＝6×14矩形ABDE 的面积＝6×14×36√3=54√3， ∴矩形PBQE 的面积与正六边形ABCDEF 的面积之比=23．一十一．弧长的计算（共4小题）39．【解答】解：连接OD 、BD ，∵在△ABC 中，AB ＝BC ，∠ABC ＝90°，∴∠A ＝∠C ＝45°，∵AB 是直径，∴∠ADB ＝90°，∵OA ＝OB ，∴OD ⊥AB ，∴∠AOD ＝90°，∴∠AOD ＝∠ABC ，∴OD ∥FC ，∴△DOE ∽△FBE ，∴BB BB =BB BB ，∵OB ＝OD ，OE ：EB ＝1：√3，∴tan ∠BOF =BB BB =√3， ∴∠BOF ＝60°，∴BF ＝2√3，∴OB ＝2，∴BB̂的长=60B ×2180=23π， 故选：C ．40．【解答】解：∵四边形ABCD 是矩形，∴AD ＝BC ＝2，∠B ＝90°，∴AE ＝AD ＝2，∵AB =√3，∴cos ∠BAE =BB BB =√32， ∴∠BAE ＝30°，∴∠EAD ＝60°，∴BB̂的长=60⋅B ×2180=2B 3， 故选：C ．41．【解答】解：由图可知，曲线DA 1B 1C 1D 1A 2…是由一段段90度的弧组成的，半径每次比前一段弧半径+1，AD ＝AA 1＝1，BA 1＝BB 1＝2，……，AD n ﹣1＝AA n ＝4（n ﹣1）+1，BA n ＝BB n ＝4（n ﹣1）+2，故B 2020B 2020̂的半径为BA 2020＝BB 2020＝4（2020﹣1）+2＝8078，B 2020B 2020̂的弧长=90180×8078B =4039B ． 故答案为：4039π．42．【解答】解：如图，作点D 关于OB 的对称点D ′，连接D ′C 交OB 于点E ′，连接E ′D 、OD ′， 此时E ′C +E ′D 最小，即：E ′C +E ′D ＝CD ′，由题意得，∠COD ＝∠DOB ＝∠BOD ′＝30°，∴∠COD ′＝90°，∴CD ′=√BB 2+BB′2=√22+22=2√2，BB ̂的长l =30B ×2180=B 3， ∴阴影部分周长的最小值为2√2+B 3=6√2+B 3． 故答案为：6√2+B 3．一十二．扇形面积的计算（共6小题）43．【解答】解：如图，连接CD ．∵OC ＝OD ，∠O ＝60°，∴△COD 是等边三角形，∴OC ＝OD ＝CD ＝4cm ，∴S 阴＝S 扇形OAB ﹣S 扇形OCD =60⋅B ⋅162360−60⋅B ⋅42360=40π（cm 2）， 故选：B ．44．【解答】 解：∵AB 是⊙O 的直径，CD 为⊙O 的弦，AB ⊥CD 于点E ， ∴CE ＝DE =12BB =3√3． 设⊙O 的半径为r ，在直角△OED 中，OD 2＝OE 2+DE 2，即B 2=(9−B )2+(3√3)2， 解得，r ＝6，∴OE ＝3，∴cos ∠BOD =BB BB =36=12，∴∠EOD ＝60°，∴B 扇形BBB =16B ×36=6B ，B BB △BBB =12×3×3√3=92√3，∴B 阴影=6B −92√3，故选：A ．45．【解答】解：∵OD ⊥AC ， ∴∠ADO ＝90°，BB̂=BB ̂，AD ＝CD ， ∵∠CAB ＝30°，OA ＝4，∴OD =12OA ＝2，AD =√32OA ＝2√3， ∴图中阴影部分的面积＝S 扇形AOE ﹣S △ADO =60⋅B ×42360−12×2√3×2=8B 3−2√3，故选：D ．46．【解答】解：设圆心角都度数为n 度，扇形的面积=12BB =6π，解得：r ＝6，又∵B =BB ×6180=2π， ∴n ＝60．故答案为：60．47．【解答】解：连接OC ．∵AB ⊥CD ，∴BB̂=BB ̂，CE ＝DE =√3， ∴∠COB ＝∠BOD ，∵∠BOD ＝2∠BCD ＝60°，∴∠COB ＝60°，∵OC ＝OB ＝OD ，∴△OBC ，△OBD 都是等边三角形，∴OC ＝BC ＝BD ＝OD ，∴四边形OCBD 是菱形，∴OC ∥BD ，∴S △BDC ＝S △BOD ，∴S 阴＝S 扇形OBD ，∵OD =BB BBB60°=2，∴S 阴=60⋅B ⋅22360=2B 3，故答案为2B 3． 48．【解答】解：S 扇形=90⋅B ⋅42360=4π， 故答案为：4π．一十三．圆锥的计算（共1小题）49．【解答】解：如图，连接OB ，OC ，OA ，∵OB ＝OA ，OA ＝OC ，AB ＝AC ，∴△ABO ≌△ACO （SSS ），∴∠BAO ＝∠CAO ＝60°，∵AO ＝BO ，∴△ABO 是等边三角形，∴AB ＝AO ＝1，由题意得，阴影扇形的半径为1m ，圆心角的度数为120°， 则扇形的弧长为：120B ×1180， 而扇形的弧长相当于围成圆锥的底面周长，因此有： 2πr =120B ×1180， 解得，r =13，故答案为：13． 一十四．圆的综合题（共1小题）50．【解答】解：（1）连接圆心O 与正五边形各顶点， 在正五边形中，∠AOE ＝360°÷5＝72°，∴∠ABE =12∠AOE ＝36°，同理∠BAC =12×72°＝36°，∴AM ＝BM ，∴△ABM 是等腰三角形且底角等于36°，∵∠BOD ＝∠BOC +∠COD ＝72°+72°＝144°，∴∠BAD =12∠BOD ＝72°， ∴∠BNA ＝180°﹣∠BAD ﹣∠ABE ＝72°，∴AB ＝NB ，即△ABN 为等腰三角形；（2）∵∠ABM ＝∠ABE ，∠AEB =12∠AOB ＝36°＝∠BAM ， ∴△BAM ∽△BEA ，∴BB BB =BB BB ，而AB ＝BN ， ∴BB BB =BB BB ，设BM ＝y ，AB ＝x ，则AM ＝AN ＝y ，AB ＝AE ＝BN ＝x ，∵∠AMN ＝∠MAB +∠MBA ＝72°＝∠BAN ，∠ANM ＝∠ANB ， ∴△AMN ∽△BAN ，∴BB BB =BB BB ，即B B =B −B B ，则y 2＝x 2﹣xy ，两边同时除以x 2，得：(B B )2=1−B B ，设B B=t ， 则t 2+t ﹣1＝0，解得：t =√5−12或−1−√52（舍）， ∴BB BB =BB BB =B B =√5−12； （3）∵∠MAN ＝36°，根据对称性可知：∠MAH ＝∠NAH =12∠MAN ＝18°， 而AO ⊥BE ，∴sin18°＝sin ∠MAH =BB BB =12BB BB =12(B −B )B =B −B 2B =12×B B −12=12×√5−1−12=√5−14．。

2020年中考数学复习：《圆》解答题压轴专题训练1．如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于E，过点A作AF⊥AC于F 交⊙O于D，连接DE，BE，BD（1）求证：∠C＝∠BED；（2）若AB＝12，tan∠BED＝，求CF的长．（1）证明：∵AB是⊙O的直径，CA切⊙O于A，∴∠C+∠AOC＝90°；又∵OC⊥AD，∴∠OFA＝90°，∴∠AOC+∠BAD＝90°，∴∠C＝∠BAD．又∵∠BED＝∠BAD，∴∠C＝∠BED．（2）解：由（1）知∠C＝∠BAD，tan∠BED＝，∴tan∠C＝，∴tan∠C＝＝，且OA＝AB＝6，∴，解得AC＝8，∴＝10，∵OC•AF＝OA•AC，∴．∴＝＝．2．如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D 为弧BE的中点，连接AD交BC于F，AC＝FC，连接BD．（1）求证：AC是⊙O的切线；（2）已知⊙O的半径R＝5cm，AB＝8cm，求△ABD的面积．（1）证明：连接OA，OD．∵点D是弧BE的中点，∴∠BOD＝∠EOD＝90°，∴∠ODF+∠OFD＝90°又∵∠OFD＝∠AFC，∴∠ODF+∠AFC＝90°又∵AC＝FC，∴∠AFC＝∠CAF，∵OA＝OD，∴∠ODF＝∠OAF，∴∠OAF+∠CAF＝90°，即∠OAC＝90°，故AC是⊙O的切线；（2）解：过点B作BG⊥AD于G，∵∠BOD＝90°，OB＝OD＝R＝5，∴，∵点D是弧BE的中点，∴∠BAD＝45°，∵∠AGB＝90°，∴∠ABG＝∠BAD＝45°，即BG＝AG．∴又∵，∴＝AD•BG＝＝28（cm2）．故S△ABD3．如图所示，以△ABC的边AB为直径作⊙O，点C在⊙O上，BD是⊙O的弦，∠A＝∠CBD，过点C作CF⊥AB于点F，交BD于点G过C作CE∥BD交AB的延长线于点E．（1）求证：CE是⊙O的切线；（2）求证：CG＝BG；（3）若∠DBA＝30°，CG＝8，求BE的长．（1）证明：连接OC，∵∠A＝∠CBD，∴＝，∴OC⊥BD，∵CE∥BD，∴OC⊥CE，∴CE是⊙O的切线；（2）证明：∵AB为直径，∵CF⊥AB，∴∠ACB＝∠CFB＝90°，∵∠ABC＝∠CBF，∴∠A＝∠BCF，∵∠A＝∠CBD，∴∠BCF＝∠CBD，∴CG＝BG；（3）解：连接AD，∵AB为直径，∴∠ADB＝90°，∵∠DBA＝30°，∴∠BAD＝60°，∵＝，∴∠DAC＝∠BAC＝∠BAD＝30°，∴＝tan30°＝，∵CE∥BD，∴∠E＝∠DBA＝30°，∴AC＝CE，∴＝，∵∠A＝∠BCF＝∠CBD＝30°，∴∠BCE＝30°，∴BE＝BC，∴△CGB∽△CBE，∴＝＝，∵CG＝8，∴BC＝8，∴BE＝8．4．如图，B，E是⊙O上的两个定点，A为优弧BE上的动点，过点B作BC⊥AB交射线AE于点C，过点C作CF⊥BC，点D在CF上，且∠EBD＝∠A．（1）求证：BD与⊙O相切；（2）已知∠A＝30°．①若BE＝3，求BD的长；②当O，C两点间的距离最短时，判断A，B，C，D四点所组成的四边形的形状，并说明理由．（1）证明：如图1，作直径BG，连接GE，则∠GEB＝90°，∴∠G+∠GBE＝90°，∵∠A＝∠EBD，∠A＝∠G，∴∠EBD＝∠G，∴∠EBD+∠GBE＝90°，∴∠GBD＝90°，∴BD⊥OB，∴BD与⊙O相切；（2）解：如图2，连接AG，∵BC⊥AB，∴∠ABC＝90°，由（1）知∠GBD＝90°，∴∠GBD＝∠ABC，∴∠GBA＝∠CBD，又∵∠GAB＝∠DCB＝90°，∴△BCD∽△BAG，∴＝＝tan30°＝，又∵Rt△BGE中，∠BGE＝30°，BE＝3，∴BG＝2BE＝6，∴BD＝6×＝2；（3）解：四边形ABCD是平行四边形，理由如下，由（2）知＝，＝，∴＝，∵B，E为定点，BE为定值，∴BD为定值，D为定点，∵∠BCD＝90°，∴点C在以BD为直径的⊙M上运动，∴当点C在线段OM上时，OC最小，此时在Rt△OBM中，＝＝，∴∠OMB＝60°，∴MC＝MB，∴∠MDC＝∠MCD＝30°＝∠A，∵AB⊥BC，CD⊥BC，∴∠ABC＝∠DCB＝90°，∴AB∥CD，∴∠A+∠ACD＝180°，∴∠BDC+∠ACD＝180°，∴AC∥BD，∴四边形ABCD为平行四边形．5．如图，在△ABC中，A B＝AC，⊙O是△ABC的外接圆，连结OA、OB、OC，延长BO与AC 交于点D，与⊙O交于点F，延长BA到点G，使得∠BGF＝∠GBC，连接FG．（1）求证：FG是⊙O的切线；（2）若⊙O的径为4．①当OD＝3，求AD的长度；②当△OCD是直角三角形时，求△ABC的面积．（1）证明：连接AF，∵BF为⊙O的直径，∴∠BAF＝90°，∠FAG＝90°，∴∠BGF+∠AFG＝90°，∵AB＝AC，∴∠ABC＝∠ACB，∵∠ACB＝∠AFB，∠BGF＝∠ABC，∴∠BGF＝∠AFB，∴∠AFB+∠AFG＝90°，即∠OFG＝90°，又∵OF为半径，∴FG是⊙O的切线；（2）解：①连接CF，则∠ACF＝∠ABF，∵AB＝AC，AO＝AO，BO＝CO，∴△ABO≌△ACO（SSS），∴∠ABO＝∠BAO＝∠CAO＝∠ACO，∴∠CAO＝∠ACF，∴AO∥CF，∴＝，∵半径是4，OD＝3，∴DF＝1，BD＝7，∴＝＝3，即CD＝AD，∵∠ABD＝∠FCD，∠ADB＝∠FDC，∴△ADB∽△FDC，∴＝，∴AD•CD＝BD•DF，∴AD•CD＝7，即AD2＝7，∴AD＝（取正值）；②∵△ODC为直角三角形，∠DCO不可能等于90°，∴存在∠ODC＝90°或∠COD＝90°，当∠ODC＝90°时，∵∠ACO＝∠ACF，∴OD＝DF＝2，BD＝6，∴AD＝CD，∴AD•CD＝AD2＝12，∴AD＝2，AC＝4，＝×4×6＝12；∴S△ABC当∠COD＝90°时，∵OB＝OC＝4，∴△OBC是等腰直角三角形，∴BC＝4，延长AO交BC于点M，则AM⊥BC，∴MO＝2，∴AM＝4+2，＝×4×（4+2）＝8+8，∴S△ABC∴△ABC的面积为12或8+8．6．如图⊙O的直径AB＝10cm，弦BC＝6cm，∠ACB的平分线交⊙O于D，交AB于E，P是AB 延长线上一点，且PC＝PE．（l）求证：PC是⊙O的切线；（2）求AC、AD的长．（1）证明：连结OC，如图所示：∵PC＝PE，∴∠PCE＝∠PEC，∵∠PEC＝∠EAC+∠ACE＝∠EAC+45°，而∠CAB＝90°﹣∠ABC，∠ABC＝∠OCB，∴∠PCE＝90°﹣∠OCB+45°＝90°﹣（∠OCE+45°）+45°，∴∠OCE+∠PCE＝90°，即∠PCO＝90°，∴OC⊥PC，∴PC为⊙O的切线；（2）连结BD，如图所示，∵AB为直径，∴∠ACB＝90°，在Rt△ACB中，AB＝10cm，BC＝6cm，∴AC＝＝8（cm）；∵DC平分∠ACB，∴∠ACD＝∠BCD＝45°，∴∠DAB＝∠DBA＝45°∴△ADB为等腰直角三角形，∴AD＝AB＝5（cm）．7．如图，在Rt△ABC中，∠BAC＝90°，CD平分∠ACB，交AB于点D，以点D为圆心，DA 为半径的圆与AB相交于点E，与CD交于点F．（1）求证：BC是⊙D的切线；（2）若EF∥BC，且BC＝6，求图中阴影部分的面积．（1）证明：过D作DG⊥BC于G，∵DA⊥AC，∠ACD＝∠BCD，∴DG＝DA，∴BC是⊙D的切线；（2）解：连接EF，∵EF∥BC，由（1）DG⊥BC，∴DG⊥EF，∴＝．∴∠EDG＝∠CDG．由（1）∠ACD＝∠BCD，∠ACD+∠ADC＝∠BCD+∠CDG＝90°，∴∠CDG＝∠ADC，∴∠CDG＝∠ADC＝∠BDG＝60°．∵EF∥BC，∴∠DEF＝∠B，∠DFE＝∠DCB，在⊙D中，DE＝DF，∴∠DFE＝∠DEF．∴∠B＝∠DCB，∴DB＝DC．∵DG⊥BC，∴CG＝BC＝3．在Rt△DCG中，D G＝CG/＝．∴S＝×3×﹣π（）2＝﹣．阴影8．请阅读下列材料，并完成相应的任务．人类会作圆并且真正了解圆的性质是在2000多年前，由我国的墨子给出圆的概念：“一中同长也．”．意思说，圆有一个圆心，圆心到圆周的长都相等．这个定义比希腊数学家欧几里得给圆下的定义要早100年．与圆有关的定理有很多，弦切角定理就是其中之一．我们把顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角．弦切角定理：弦切角的度数等于它所夹弧所对的圆周角度数．下面是弦切角定理的部分证明过程：证明：如图①，AB与⊙O相切于点A．当圆心O在弦AC上时，容易得到∠CAB＝90°，所以弦切角∠BAC的度数等于它所夹半圆所对的圆周角度数．如图②，AB与⊙O相切于点A，当圆心O在∠BAC的内部时，过点A作直径AD交⊙O于点D，在上任取一点E，连接EC，ED，EA，则∠CED＝∠CAD．任务：（1）请按照上面的证明思路，写出该证明的剩余部分；（2）如图③，AB与⊙O相切于点A．当圆心O在∠BAC的外部时，请写出弦切角定理的证明过程．解：（1）如图②，∵AD是⊙O直径，∴∠DEA＝90°．∵AB与⊙O相切于点A，∴∠DAB＝90°．∴∠CED+∠DEA＝∠CAD+∠DAB，即∠CEA＝∠CAB，∴弦切角的度数等于它所夹弧所对的圆周角度数；（2）证明：如图③，过点A作直径AF交⊙O于点F，连接FC，∵AF是直径，∴∠ACF＝90°，∴∠CFA+∠FAC＝90°，∵AB与⊙O相切于点A，∴∠FAB＝90°，∴∠CAB+∠FAC＝90°，∴∠CAB＝∠CFA，即弦切角的度数等于它所夹弧所对的圆周角度数．9．【问题背景】（1）如图1，⊙O与∠P的两边分别切与A，B两点．求证：PA＝PB．【深入探究】（2）在（1）的条件下，若∠APB＝60°，连接PO，以PO为一条边向上作等边三角形POQ，连接AO，AQ．求证：AO＝AQ．（3）若在（1）的条件下，以OP为斜边向上作等腰直角三角形POQ，取OP中点M，连接MB，MQ，BQ，求证：∠MQB＝∠MBQ．【拓展延伸】在（3）的条件下，连接AO，AQ，探索AO，AQ，AP之间的数量关系．解：【问题背景】（1）连接OA，OB，OP，∵PA、PB是切线，∴PA⊥OA，PB⊥OB，∴∠PAO＝∠PBO＝90°，在Rt△PAO和Rt△PBO中，，∴Rt△PAO≌Rt△PBO（HL），∴PA＝PB；【深入探究】（2）∵Rt△PAO≌Rt△PBO，∴∠APO＝∠BPO，∵∠APB＝60°，∴∠APO＝∠BPO＝30°，∵△POQ是等边三角形，∴∠OPQ＝60°，PO＝PQ，∴∠APQ＝∠APO＝30°，且PO＝PQ，∴PA垂直平分OQ，∴AO＝AQ；（3）如图3，连接OB，∵PB是⊙O是切线，∴PB⊥OB，且点M是OP的中点，∴BM＝PO，∵△OPQ是等腰直角三角形，且点M是OP的中点，∴QM＝OP，∴QM＝BM，∴∠MQB＝∠MBQ；拓展延伸】AO+AQ＝AP，理由如下：过点Q作QH⊥AQ交AP于点H，∴∠AQH＝∠PQO＝90°，∴∠AQO＝∠PQH，∵∠QPO+∠QOP＝90°，∠AOP+∠APO＝90°，∴∠APQ+∠APO＝∠APO+∠AOQ，∴∠APQ＝∠AOP，且∠AQO＝∠PQH，QP＝OQ，∴△AOQ≌△HPQ（ASA）∴QH＝AQ，AO＝PH，∴AH＝AQ，∵AP＝PH+AH，∴AO+AQ＝AP．10．如图，AB、CE是⊙O的直径，过点C的切线与AB的延长线交于点P，AD⊥PC于D，连接AC、OD、PE．（1）求证：AC是∠DAP的角平分线；（2）求证：PC2＝PA•PB；（3）若AD＝3，PE＝2DO，求⊙O的半径．证明：（1）∵PC是圆的切线，AD⊥PD，∴AD∥OC，∴∠DAC＝∠ACO，∵AO＝CO，∴∠CAO＝∠ACO，∴∠DAC＝∠CAO，∴AC是∠DAP的平分线；（2）如右图，连接BC，∵OC＝OB，∴∠OCB＝∠OBC，∵AB为⊙O的直径，∴∠ACB＝90°，∴∠CAB+∠OBC＝90°，∵PC是⊙O的切线，∴∠OCB+∠BCP＝90°，∴∠CAB＝∠BCP，又∵∠CPB＝∠APC，∴△CPB∽△APC，∴＝，∴PC2＝PA•PB；（3）设半径为r，在Rt△PCE中，PE2＝（2r）2+PC2＝4r2+PC2，∵PE＝2DO，∴4DO2＝4r2+PC2，∴4（DO2﹣r2）＝PC2，∴4DC2＝PC2，∴PC＝2CD，∵AD∥OC，∴△PCO∽△PDA，∴＝，∴＝，∴r＝2．11．如图，AB是直经，D是的中点，DE⊥AC交AC的延长线于E，⊙O的切线BF交AD的延长线于点F．（1）求证：DE是⊙O的切线．（2）试探究AE，AD，AB三者之间的等量关系．（3）若DE＝3，⊙O的半径为5，求BF的长．（1）证明：如图1，连接OC，OD，BC，∵AB是直径，∵DE⊥AC于E，∴∠E＝90°，∴∠ACB＝∠E，∴BC∥DE，∵点D是的中点，∴，∴∠COD＝∠BOD，又∵OC＝OB，∴OD垂直平分BC，∵BC∥DE，∴OD⊥DE，∴DE是⊙O的切线；（2）AD2＝AE•AB，理由如下：如图2，连接BD，由（1）知，，∴∠EAD＝∠DAB，∵AB为直径，∴∠ADB＝∠E＝90°，∴△AED∽△ADB，∴＝，即AD2＝AE•AB；（3）由（1）知，∠E＝∠ECH＝∠CHD＝90°，∴四边形CHDE为矩形，∴ED＝CH＝BH＝3，∴OH＝＝＝4，∴CE＝HD＝OD﹣OH＝5﹣4＝1，AC＝＝＝8，∵BF是⊙O的切线，∴∠FBA＝∠E＝90°，又∵∠EAD＝∠DAB，∴△EAD∽△BAF，∴＝，即＝，∴BF＝．12．如图1，在直角坐标系中，直线l与x、y轴分别交于点A（2，0）、B（0，）两点，∠BAO的角平分线交y轴于点D．点C为直线l上一点，以AC为直径的⊙G经过点D，且与x轴交于另一点E．（1）求出⊙G的半径r，并直接写出点C的坐标；（2）如图2，若点F为⊙G上的一点，连接AF，且满足∠FEA＝45°，请求出EF的长？解：（1）连接GD，EC．∵∠OAB的角平分线交y轴于点D，∴∠GAD＝∠DAO，∵GD＝GA，∴∠GDA＝∠GAD，∴∠GDA＝∠DAO，∴GD∥OA，∴∠BDG＝∠BOA＝90°，∵GD为半径，∴y轴是⊙G的切线；∵A（2，0），B（0，），∴OA＝2，OB＝，在Rt△AOB中，由勾股定理可得：AB＝＝＝设半径GD＝r，则BG＝﹣r，∵GD∥OA，∴△BDG∽△BOA，∴＝，∴r＝2（﹣r），∴r＝，∵AC是直径，∴∠AEC＝∠AOB＝90°，∴EC∥OB，∴＝＝，∴＝＝，∴EC＝2，AE＝，∴OE＝2﹣＝，∴C的坐标为（，2）；（2）过点A作AH⊥EF于H，连接CE、CF，∵AC是直径，∴AC＝2×＝∴∠AEC＝∠AFC＝90°∵∠FEA＝45°∴∠FCA＝45°∴在Rt△AEH中，由勾股定理可知：AF＝CF＝，设OE＝a∴AE＝2﹣a∵CE∥OB∴△ACE∽△ABO∴＝，∴CE＝，∵CE2+AE2＝AC2，∴（2﹣a）2+（2﹣a）2＝∴a＝或a＝（不合题意，舍去）∴AE＝∴在Rt△AEH中，由勾股定理可得，AH＝EH＝，∴在Rt△AEH中，由勾股定理可知：FH2＝AF2﹣AH2＝（）2﹣（）2＝2，∴FH＝，∴EF＝EH+FH＝．13．如图I，四边形ADBC内接于⊙O，E为BD延长线上一点，AD平分∠EDC，（1）求证：AB＝AC；（2）如图2，若CD为直径，过A点的圆的切线交BD延长线于E，若DE＝1，AE＝2．求⊙O的半径．（1）证明：∵四边形ADBC内接于⊙O，∴∠EDA＝∠ACB，由圆周角定理得，∠CDA＝∠ABC，∵AD平分∠EDC，∴∠EDA＝∠CDA，∴∠ABC＝∠ACB，∴AB＝AC；（2）解：连接AO并延长交BC于H，AM⊥CD于M，∵AB＝AC，∴AH⊥BC，又AH⊥AE，∴AE∥BC，∵CD为⊙O的直径，∴∠DBC＝90°，∴∠E＝∠DBC＝90°，∴四边形AEBH为矩形，∴BH＝AE＝2，∴BC＝4，∵AD平分∠EDC，∠E＝90°，AM⊥CD，∴DE＝DM＝1，AE＝AM＝2，在Rt△ABE和Rt△ACM中，∴Rt△ABE≌Rt△ACM（HL），∴BE＝CM，设BE＝x，CD＝x+2，在Rt△BDC中，x2+42＝（x+2）2，解得，x＝3，∴CD＝5，∴⊙O的半径为2.5．14．如图，AB为⊙O的直径，弦CD⊥AB，垂足为F，CG⊥AE，交弦AE的延长线于点G，且CG＝CF．（1）求证：CG是⊙O的切线；（2）若AE＝2，EG＝1，求由弦BC和所围成的弓形的面积．解：（1）证明：连接OC．∵CD⊥AB，CG⊥AE，CG＝CF，∴∠CAG＝∠BAC，∠AFC＝∠G＝90°，∵OA＝OC，∴∠ACO＝∠BAC．∴∠CAG＝∠ACO，∴OC∥AG，∴∠OCG＝180°﹣∠G＝90°，∴CG是⊙O的切线；（2）过点O作OM⊥AE，垂足为M，则AM＝ME＝AE＝1，∠OMG＝∠OCG＝∠G＝90°．∴四边形OCGM为矩形，∴OC＝MG＝ME+EG＝2．在Rt△AGC和Rt△AFC中∴Rt△AGC≌Rt△AFC（HL），∴AF＝AG＝AE+EG＝3，∴OF＝AF﹣OA＝1，在Rt△COF中，∵cos∠COF＝＝．∴∠COF＝60°，CF＝OC•sin∠COF＝2×＝，＝﹣×2×＝π﹣．∴S弓形BC15．如图，AB、AC是⊙O的两条弦，M是的中点，N是的中点，弦MN分别交AB、AC 于点P、D．（1）求证：AP＝AD；（2）连接PO，当AP＝3，OP＝，⊙O的半径为5，求MP的长．（1）证明：连AM，AN，∵＝，＝，∴∠BAM＝∠ANM，∠AMN＝∠CAN，∵∠APD＝∠AMN+∠BAM，∠ADP＝∠CAN+∠ANM，∴∠APD＝∠ADP，∴AP＝AD．（2 ）解：连AO，OM交AB于E，设PE＝x，∵＝，∴OM⊥AB，∴∠AEO＝90°，∵OE2＝OA2﹣AE2＝OP2﹣PE2∴52﹣（x+3）2＝（）2﹣x2，∴x＝1，∴AE＝4，OE＝3，ME＝2，∴MP＝＝＝．16．如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（0，4），点B的坐标为（4，0），点C的坐标为（﹣4，0），点P在AB上，连结CP与y轴交于点D，连结BD．过P，D，B三点作⊙Q与y轴的另一个交点为E，延长DQ交⊙Q于点F，连结EF，BF．（1）求直线AB的函数解析式；（2）求证：∠BDE＝∠ADP；（3）设DE＝x，DF＝y．请求出y关于x的函数解析式．解：（1）设直线AB的函数解析式为y＝kx+4，将点B（4，0）代入y＝kx+4，得：4k+4＝0，解得：k＝﹣1，则直线AB的函数解析式为y＝﹣x+4；（2）由已知得：OB＝OC，∠BOD＝∠COD＝90°，又∵OD＝OD，∴△BOD≌△COD（SAS），∴∠BDO＝∠CDO，∵∠CDO＝∠ADP，∴∠BDE＝∠ADP；（3）如图2，连结PE，∵∠ADP是△DPE的一个外角，∴∠ADP＝∠DEP+∠DPE，∵∠BDE是△ABD的一个外角，∴∠BDE＝∠ABD+∠OAB，∵∠ADP＝∠BDE，∠DEP＝∠ABD，∴∠DPE＝∠OAB，∵OA＝OB＝4，∠AOB＝90°，∴∠OAB＝45°，∴∠DPE＝45°，∴∠DFE＝∠DPE＝45°，∵DF是⊙Q的直径，∴∠DEF＝90°，∴△DEF是等腰直角三角形，∴DF＝DE，即y＝x．17．如图1，AB为⊙O的弦，弧AC＝弧BC，G为弧BC上一点，连接AG交BC于点D，连接CG、BG．（1）求证：∠GCB+∠GBC＝∠CBA；（2）如图2，若AB为⊙O的直径，求证：AG＝CG+BG；（3）如图3，在（2）的条件下，F为圆上一点，连接CF交AB于点E，若CD：DB＝5：7，∠ACF＝∠CAG，AE＝，求线段CG的长．证明：（1）∵＝，∴∠CAB＝∠CBA，∵∠GCB＝∠GAB，∠CBG＝∠CAG，∴∠GCB+∠GBC＝∠GAB+∠CAG＝∠CAB＝∠CBA；（2）如图2，过点C作CH⊥CG交AG于点H，∵AB为⊙O的直径，∴∠AGB＝∠ACB＝90°，且AC＝BC，∴∠ABC＝∠BAC＝45°．∵∠AGC＝∠ABC，∴∠AGC＝45°，且CH⊥CG，∴∠CHG＝∠AGC＝45°，∴CH＝CG，∠AHC＝135°∴GH＝CG．∵∠CGB＝∠CGA+∠AGB＝135°，∴∠AHC＝∠CGB，CH＝CG，∠CAH＝∠CBG，∴△ACH≌△BCG（AAS）∴AH＝BG，∴AG＝CG+BG；（3）∵CD：DB＝5：7，∴设CD＝5a，DB＝7a，∴BC＝AC＝12a，∴AD＝＝＝13a．如图3，过点E作EH⊥AC于H，作AP平分∠GAC，交BC于P，作PQ⊥AD于Q，∴∠CAP＝∠DAP＝∠CAG，∠PQA＝90°＝∠ACB，且AP＝AP，∴△CAP≌△QAP（AAS）∴AC＝AQ＝12a，CP＝PQ，∴QD＝AD﹣AQ＝a．∵PD2＝PQ2+QD2，∴（5﹣PQ）2＝PQ2+a2，∴PQ＝a，∴CP＝a，∵HE⊥AC，∠CAB＝45°，∴∠HEA＝∠CAB＝45°，∴AH＝HE，∵AE2＝AH2+HE2＝（3）2，∴AH＝HE＝3，∵∠ACF＝∠CAG，∠CAP＝∠DAP＝∠CAG，∴∠ACF＝∠CAP，∴tan∠CAP＝tan∠ACF＝，∴∴CH＝15，∴AC＝3+15＝18＝12a，∴a＝，∴CD＝，BD＝，AD＝．∵∠ACD＝∠AGB＝90°，∠CAD＝∠DBG，∴△ACD∽△BGD，∴，∴，∴BG＝，DG＝，∴AG＝AD+DG＝+＝，∵AG＝CG+BG，∴＝＝CG，∴CG＝．18．如图1，在△ABC中，∠ACB＝90°，∠ABC的角平分线交AC上点E，过点E作BE的垂线交AB于点F，△BEF的外接圆⊙O与CB交于点D．（1）求证：AC是⊙O的切线；（2）若BC＝9，EH＝3，求⊙O的半径长；（3）如图2，在（2）的条件下，过C作CP⊥AB于P，求CP的长．（1）证明：连接OE．如图1所示：∵BE⊥EF，∴∠BEF＝90°，∴BF是圆O的直径，∴OB＝OE，∴∠OBE＝∠OEB，∵BE平分∠ABC，∴∠CBE＝∠OBE，∴∠OEB＝∠CBE，∴OE∥BC，∴∠AEO＝∠C＝90°，∴AC⊥OE，∴AC是⊙O的切线；（2）解：∵∠ACB＝90°，∴EC⊥BC，∵BE平分∠ABC，EH⊥AB，∴EH＝EC，∠BHE＝90°，在Rt△BHE和Rt△BCE中，，∴Rt△BHE≌Rt△BCE（HL），∴BH＝BC＝9，∵BE⊥EF，∴∠BEF＝90°＝∠BHE，BF是圆O的直径，∴BE＝＝＝3，∵∠EBH＝∠FBE，∴△BEH∽△BFE，∴＝，即＝，解得：BF＝10，∴⊙O的半径长＝BF＝5；（3）解：连接OE，如图2所示：由（2）得：OE＝OF＝5，EC＝EH＝3，∵EH⊥AB，∴OH＝＝＝4，在Rt△OHE中，cos∠EOA＝＝，在Rt△EOA中，cos∠EOA＝＝，∴OA＝OE＝，∴AE＝＝＝，∴AC＝AE+EC＝+3＝，，∵AB＝OB+OA＝5+＝，∠ACB＝90°，∴△ABC的面积＝AB×CP＝BC×AC，∴CP＝＝＝．19．△ABC内接于⊙O，弦BD与AC相交于点E，连接BO，且AC⊥BD．（1）如图1，求证：∠OBC＝∠ABD；（2）如图2，作CG⊥AB于G，交BD于F，若∠BAC＝∠ABO+30°，求证：BO＝BF；（3）如图3，在（2）的条件下，直线OF与AB相交于点M，与BC相交于点N，若NC：MA＝5：3，且S＝16，求线段AE的长．△BMN解：（1）延长BO交⊙O于点K，连接CK，则BK为⊙O的直径，∴∠BCK＝90°，∴∠OBC+∠K＝90°，∵AC⊥BD，∴∠AEB＝90°，∴∠ABE+∠A＝90°，∵，∴∠A＝∠K∴∠OBC＝∠ABD；（2）作OH⊥BC于H，则BC＝2BH，∵∠K+∠KBC＝90°，∴∠BAC+∠KBC＝90°，∴∠ABO+30°+∠KBC＝90°，∴∠ABC＝60°∴BC＝2BG，∴BG＝BH，且∠ABD＝∠OBC，∠BGF＝∠BHO＝90°，∴△BFG≌△BOH（AAS）∴BO＝BF；（3）作OH⊥BC于H，∵△BFG≌△BOH，∴BF＝BO，∴∠MFB＝∠BON，且BF＝BO，∠ABD＝∠OBN，∴△BFM≌△BON（ASA）∴BM＝BN，且∠ABC＝60°，∴△MBN为等边三角形，∴S＝BM2＝16，△BMN∴BM＝BN＝8，∵NC：MA＝5：3，∴设NC＝5x，AM＝3x，∴BC＝8+5x，BH＝＝BG，CG＝BG＝•（）∴GM＝HN＝8﹣＝，∵∠MNB＝60°，∴OH＝HN＝•（），∵∠OBC＝∠ABD＝∠ACG，∴tan∠OBC＝tan∠ACG，∴，∴＝，∴x＝1，∴AM＝3，CN＝5，HN＝GM＝，OH＝，BH＝∴OB＝＝＝7，∵sin∠OBH＝sin∠ABD，∴∴AE＝＝．20．如图1，AB为⊙O的直径，BC为⊙O的切线，过点B作OC的垂线与⊙O的另一交点为点E，连接CE．（1）求证：CE为⊙O的切线；（2）如图2，过点C作BC的垂线交AE的延长线于点F，若BC＝AB，求的值．解：（1）证明：如图，连接OE，设OC与BE的交点为M∵OB＝OE∠OBM＝∠OEM∵BE⊥OC∴∠BMO＝∠EMO∴∠BOC＝∠EOC∴在△OBC和△OEC中∴△OBC≌△OEC（SAS）∴∠OEC＝∠OBC∵BC为⊙O的切线∴OB⊥BC∴∠OBC＝90°∴∠OEC＝90°∴CE为⊙O的切线；（2）∵AB为⊙O的直径，∴∠BEA＝90°∵OB⊥BC∴AF∥OC∵AB⊥BC，CF⊥BC∴AO∥CF∴四边形AOCF为平行四边形∴AF＝OC∵BC＝AB∴设BC＝AB＝2k，则OB＝OA＝k在Rt△OBC中，由勾股定理得：OC＝＝k∴AF＝k∵∠ABE+∠CBE＝90°，∠CBE+∠BCO＝90°∴∠ABE＝∠BCO∴sin∠ABE＝sin∠BCO∵＝sin∠BCO＝＝∴＝sin∠ABE＝∴AE＝×2k＝∴EF＝AF﹣AE＝∴＝．。

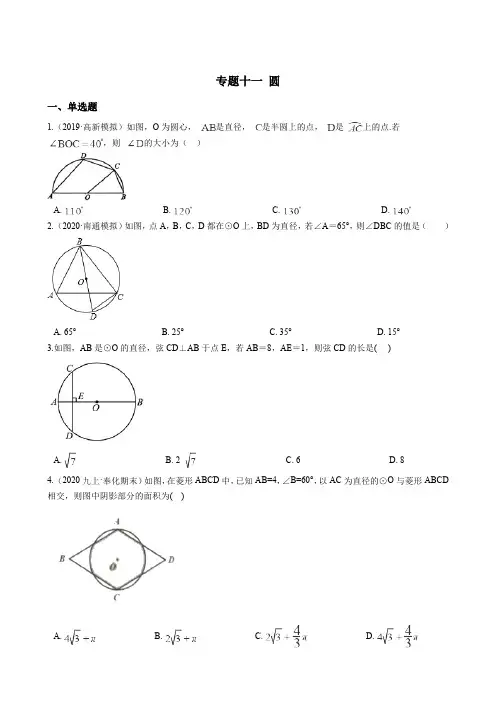
专题十一圆一、单选题1.（2019·高新模拟）如图，O为圆心，是直径，是半圆上的点，是上的点.若，则的大小为（）A. B. C. D.2.（2020·南通模拟）如图，点A，B，C，D都在⊙O上，BD为直径，若∠A＝65°，则∠DBC的值是（ ）A. 65°B. 25°C. 35°D. 15°3.如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB＝8，AE＝1，则弦CD的长是( )A. B. 2 C. 6 D. 84.（2020九上·奉化期末）如图，在菱形ABCD中，已知AB=4，∠B=60°，以AC为直径的⊙O与菱形ABCD 相交，则图中阴影部分的面积为( )A. B. C. D.5.（2019九上·温州月考）如图，△ABC内接于⊙O中，AB=AC，=60°，则∠B=( )A. 30°B. 45°C. 60°D. 75°6.（2020九上·中山期末）如图，AD是半圆的直径，点C是弧BD的中点，∠ADC=55°，则∠BAD等于（）A. 50°B. 55°C. 65°D. 70°7.（2020九上·海曙期末）平面直角坐标系中，⊙P的圆心坐标为(-4，-5)，半径为5，那么⊙P与y轴的位置关系是（）A. 相交B. 相离C. 相切D. 以上都不是8.（2019九上·驻马店期末）如图，直径AB为3的半圆，绕A点逆时针旋转60°，此时点B到了点B′处，则图中阴影部分的面积是（）A. 3πB.C. 6πD. 24π9.（2020九上·北仑期末）下列四个结论，不正确的是（）①过三点可以作一个圆；②圆内接四边形对角相等③平分弦的直径垂直于弦；④相等的圆周角所对的弧也相等A. ②③B. ①③④C. ①②④D. ①②③④10.（2020九上·诸暨期末）如图，是圆内接四边形的一条对角线，点关于的对称点在边上，连接.若，则的度数为（）A. 106°B. 116°C. 126°D. 136°11.（2019九上·武汉月考）如图，O的半径为1，弦AB＝1，点P为优弧AB上一动点，AC⊥AP交直线PB 于点C，则△ABC的最大面积是（）A. B. C. D.12.如图，在⊙O中，点C在优弧AB上，将弧BC沿BC折叠后刚好经过AB的中点D. 若⊙O的半径为，AB=8，则BC的长是（）A. B. C. D.13.（2019九上·如皋期末）如图，▱ABCD中，，，，是边AB上的两点，半径为2的过点A，半径为1的过点、E、F分别是边CD，和上的动点则的最小值等于A. B. 6 C. D. 914.（2019·武汉模拟）点G为△ABC的重心（△ABC三条中线的交点），以点G为圆心作⊙G与边AB，AC相切，与边BC相交于点H，K，若AB＝4，BC＝6，则HK的长为（）A. B. C. D.15.（2019·武汉模拟）如图，⊙O内切于正方形ABCD，边AD，CD分别与⊙O切于点E，F，点M、N 分别在线段DE，DF上，且MN与⊙O相切，若△MBN的面积为8，则⊙O的半径为（）A. B. 2 C. D. 216.（2020·长兴模拟）如图，AB为☉O的直径，P为弦BC上的点，∠ABC=30°，过点P作PD⊥OP交☉O 于点D，过点D作DE∥AB交AB的延长线于点E.若点C恰好是的中点，BE=6，则PC的长是（）A. -8B. -3C. 2D. 12-17.（2019九上·宜兴月考）在平面直角坐标系中，直线经过点A（－3，0），点B（0，），点P的坐标为（1，0），与轴相切于点O，若将⊙P沿轴向左平移，平移后得到（点P的对应点为点P′），当⊙P′与直线相交时，横坐标为整数的点P′共有（）A. 1个B. 2个C. 3个D. 4个18.（2019·海州模拟）如图，菱形ABCD的边AB=5，面积为20，∠BAD＜90°，⊙O与边AB、AD都相切，AO=2，则⊙O的半径长等于（）A. B. C. D.19.（2019·高台模拟）如图，AB与⊙O相切于点C，OA＝OB，⊙O的直径为6cm，AB＝6 cm，则阴影部分的面积为（）A. B. C. D.20.（2019九下·深圳月考）如图，△ABC内接于圆O，∠BOC=120°，AD为圆O的直径．AD交BC于P 点且PB=1，PC=2，则AC的长为( )A. B. C. 3 D. 2二、填空题21.（2019·嘉定模拟）如图，的半径长为5cm，内接于，圆心O在的内部，如果，cm，那么的面积为________cm22.（2019九上·黄石期末）如图，PA，PB是⊙O的切线，A，B为切点，AC是⊙O的直径，∠BAC=25°.求∠P的度数________.23.（2020九上·东台期末）如图，⊙O是△ABC的外接圆，已知∠ABO=40°，则∠ACB的大小为________．24.（2019·台江模拟）如图，⊙O是Rt△ABC的外接圆，∠ACB＝90°，∠A＝25°，过点C作圆O的切线，交AB的延长线于点D，则∠D的度数是________．25.（2019九上·道里期末）如图，已知，在中，，，，是ABC的内切圆，则这个圆的半径是________．26.（2020九上·北仑期末）如图，四边形ABCD中，∠BAD=∠BCD=90°，∠B=45°，DE⊥AC于E交AB 于F，若BC=2CD，AE=2，则线段BF=________。