各拟合指数一览

结构方程模型中拟合度指标的选择与评价方法摘要：结构方程模型是一种常用的统计分析方法，用于研究变量之间的关系。

在进行结构方程模型分析时，需要选择合适的拟合度指标来评价模型的拟合程度。

本文介绍了常见的拟合度指标及其评价方法，并探讨了在选择拟合度指标时需要考虑的因素。

关键词：结构方程模型；拟合度指标；评价方法；选择因素一、引言结构方程模型是一种常用的多变量统计分析方法，可以用于研究变量之间的关系。

结构方程模型可以分为两类：一类是指标式结构方程模型，另一类是路径式结构方程模型。

指标式结构方程模型又称为测量模型，它用于研究测量变量之间的关系；路径式结构方程模型用于研究变量之间的因果关系。

无论是指标式结构方程模型还是路径式结构方程模型，都需要进行模型拟合度检验。

模型拟合度指的是模型与实际数据的吻合程度，模型拟合度检验的目的是评估模型的可靠性和有效性。

本文将介绍常见的拟合度指标及其评价方法，并探讨在选择拟合度指标时需要考虑的因素。

二、常见的拟合度指标及其评价方法1.卡方检验卡方检验是最常用的结构方程模型拟合度检验方法之一。

卡方检验的原理是比较实际数据和模型预测数据之间的差异，如果差异较小，则说明模型拟合度较好。

卡方检验的统计量是卡方值，卡方值越小，说明实际数据与模型预测数据之间的差异越小，模型拟合度越好。

卡方检验的显著性水平通常设定为0.05或0.01。

如果卡方值小于设定的显著性水平，则说明模型拟合度良好。

卡方检验的缺点是它对样本量和指标个数非常敏感。

当样本量较大或指标个数较多时，卡方值往往会偏大，导致模型拟合度被低估。

因此，在使用卡方检验时，需要同时考虑其他拟合度指标。

2.均方根误差（Root Mean Square Error of Approximation，RMSEA）均方根误差是一种常用的结构方程模型拟合度指标。

均方根误差的计算方法为：$$ RMSEA =sqrt{frac{sum_{i=1}^{n}(y_i-hat{y_i})^2}{df(n-1)}} $$ 其中，$y_i$是实际数据，$hat{y_i}$是模型预测数据，$n$是样本量，$df$是自由度。

指数函数曲线拟合公式
指数函数曲线拟合公式是一种用于拟合指数函数曲线的数学公式。

指数函数是
一种常见的数学函数形式，其特点是自变量的指数部分增长或减小得十分迅速，适用于描述呈现指数增长或衰减趋势的数据。

拟合指数函数曲线的目的是找到最佳的数学公式来描述一组数据点，使得模型
与实际数据尽可能吻合。

这样可以通过拟合曲线来预测未知数据的趋势或进行数据分析。

常见的指数函数曲线拟合公式是指数函数的一般形式：
y = a * e^(bx)
其中，y表示因变量，x表示自变量，a和b是拟合参数，e表示自然对数的底。

为了得到最佳的拟合结果，可以利用最小二乘法进行拟合。

最小二乘法是一种
常用的拟合方法，通过最小化实际数据点与拟合曲线之间的误差平方和来确定最佳拟合参数。

在实际应用中，可以利用数学软件或编程语言进行指数函数曲线拟合。

例如，
使用Python编程语言可以使用SciPy库中的curve_fit函数进行指数函数曲线拟合。

该函数可以根据给定的数据点和适当的初始参数估计，自动调整参数值以获得最佳的拟合结果。

总之，指数函数曲线拟合公式是一种用于拟合指数函数曲线的数学公式。

通过
拟合曲线，我们可以获得数据的趋势信息，进行未知数据的预测和数据分析。

拟合过程可以利用最小二乘法等方法进行，以获得最佳的拟合结果。

拟合函数种类中的特定函数拟合函数是数学中的一个重要概念，指的是用一个已知的函数去逼近一组离散数据点，以求得一个与这组数据点最接近的函数。

在实际应用中，拟合函数被广泛应用于数据分析、曲线拟合、模型建立等领域。

本文将详细介绍拟合函数种类中的特定函数，包括多项式拟合、指数拟合、对数拟合、幂函数拟合和三角函数拟合。

我们将依次介绍每种拟合函数的定义、用途和工作方式。

1. 多项式拟合定义：多项式拟合是指用一个多项式去逼近一组离散数据点。

多项式是由常数项和各次幂的单项式相加而成，形如：f(x)=a n x n+a n−1x n−1+...+a2x2+a1x+a0。

用途：多项式拟合广泛应用于曲线拟合和数据分析领域。

通过寻找最佳的多项式系数，可以将离散数据点之间的关系转化为连续曲线，从而更好地描述和预测数据。

工作方式：多项式拟合的工作方式通常是通过最小二乘法来确定多项式的系数。

最小二乘法是一种寻找使得拟合曲线与实际数据点之间误差平方和最小的方法。

通过最小化误差平方和，可以得到最佳的多项式系数，从而实现对数据的拟合。

2. 指数拟合定义：指数拟合是指用一个指数函数去逼近一组离散数据点。

指数函数形如：f(x)=ae bx，其中a和b为参数。

用途：指数拟合常用于描述具有指数增长或衰减趋势的数据。

例如，在生物学、物理学、经济学等领域，很多现象都符合指数规律，因此可以使用指数拟合来分析和预测这些现象。

工作方式：指数拟合通常使用非线性最小二乘法进行求解。

非线性最小二乘法是将实际数据点代入到目标函数中，并通过调整参数a和b来使得目标函数与实际数据点之间的误差平方和最小化。

通过迭代计算，可以得到最佳的参数值，从而实现对数据的拟合。

3. 对数拟合定义：对数拟合是指用一个对数函数去逼近一组离散数据点。

对数函数形如：f(x)=alog(bx)，其中a和b为参数。

用途：对数拟合常用于描述具有对数增长或衰减趋势的数据。

在许多领域中，例如生物学、经济学和物理学等，很多现象都符合对数规律，因此可以使用对数拟合来分析和预测这些现象。

验证性因素分析中评价模型与数据拟合程度时常用的拟合指标
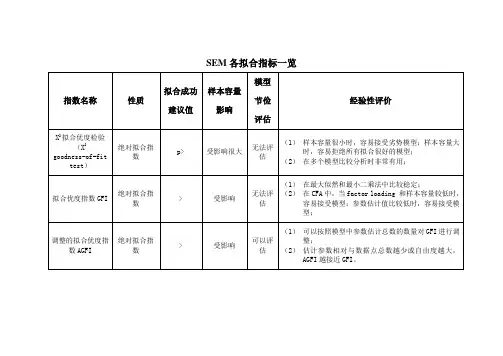
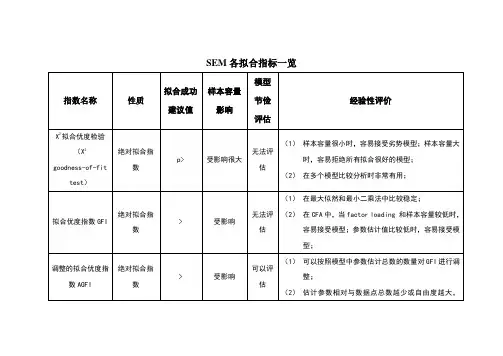
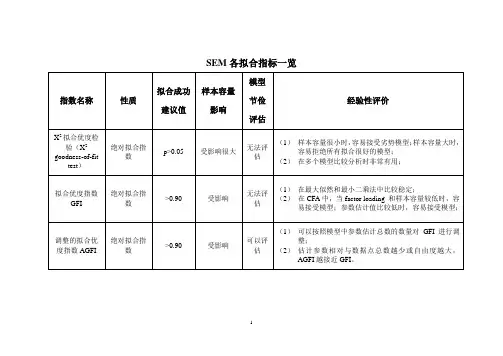
(1)χ²(chi-square)检验。

这一指标容易受样本容量的影响，样本量大时，χ²容易达到显著水平，几乎拒绝所有拟合较好的模型。

一般用χ²/df作为替代性检验指数。

χ²/df＜3表示模型整体拟合度较好，χ²/df＜5表示模型整体可以接受，χ²/df＞10表示整体模型非常差。

（2）RMSEA。

若RMSEA取值小于等于0.05，表示数据与定义模型拟合较好；RMSEA取值小于等于0.08时，表示模型与数据的拟合程度可以接受。

(3)其他拟合指数。

常用的有
“拟合良好性指标” (goodness of fit index，简称GFI)、
“调整拟合良好性指标”(adjusted goodness of fit index，简称AGFI)、
“常规拟合指标”(normal of fit index，简称NFI)、
“非常规拟合指标”(non-normal of fit index，简称NNFI)、
“比较拟合指标”(comparative fit index，简称CFI)、
“标准化残差均方根” (standardized root mean square residual，简称SRMR)、
“省俭性指标” (parsimony normed fit index，简称PNFI)。

amos指标意义解释AMOS指标是结构方程模型（Structural Equation Model, SEM）中常用的一个统计指标，用于评估模型的拟合程度和指导模型修正。

AMOS是Analysis of Moment Structures的缩写，是一种基于最大似然估计的结构方程模型分析软件。

在SEM中，结构方程模型用于描述和检验变量之间的关系，并通过测量模型和结构模型来评估数据与理论模型的拟合度。

AMOS指标主要包括以下几个方面的统计量：1. 模型拟合度指标：AMOS提供多种指标来评估模型拟合度，包括χ2（卡方）值、χ2/自由度比值、比较拟合指数（CFI）、增量拟合指数（IFI）、标准化均方残差（SRMR）等。

这些指标可以帮助研究者判断模型的整体拟合情况。

2. 参数估计指标：AMOS提供了各个变量之间的路径系数估计值，用于表示变量之间的直接和间接关系。

这些路径系数可以帮助研究者理解变量之间的因果关系，并提供了模型修正的依据。

3. 因子载荷指标：AMOS提供了因子载荷（factor loading）的估计值，用于表示测量模型中各个指标（测量项）与对应因子（潜变量）之间的关系。

这些因子载荷可以帮助研究者评估测量模型的信度和效度。

4. 共变量指标：AMOS可以提供共变量矩阵，用于表示变量之间的协方差或相关关系。

这些共变量指标可以帮助研究者理解变量之间的关联性，并提供了模型修正的依据。

5. 模型修正指标：基于AMOS的模型拟合结果，研究者可以进行模型修正，例如删除或添加路径、修改因子载荷、修正共变量关系等，以提高模型的拟合度和解释力。

AMOS指标提供了评估结构方程模型拟合度和指导模型修正的依据，帮助研究者理解变量之间的关系，并提供了数据与理论模型之间的比较和修正的依据。

中介效应是指一个变量在两个其他变量之间的作用机制。

在社会科学研究中，特别是心理学和社会学领域，中介效应是一个重要的研究课题。

研究人员经常使用统计模型来检验中介效应的存在和大小。

AMOS模型是一种常用的结构方程建模软件，它可以用于估计中介效应的大小。

而中介效应大小的指标之一是模型拟合指数，它可以帮助研究人员判断他们的模型对观察数据的拟合程度。

了解AMOS模型拟合指数的正常值对于正确解释中介效应的大小至关重要。

1. AMOS模型拟合指数AMOS模型拟合指数是用来评价结构方程模型（SEM）对观察数据的拟合程度的指标。

常见的AMOS模型拟合指数包括：- 拟合优度指数（Goodness of Fit Index, GFI）- 比较拟合指数（Comparative Fit Index, CFI）- 均方根误差逼近度指数（Root Mean Square Error of Approximation, RMSEA）- 标准化均方根残差（Standardized Root Mean Square Residual, SRMR）2. AMOS模型拟合指数的正常值根据研究者的经验和已有的文献，一般认为，GFI和CFI的值应该大于0.90，RMSEA的值应该小于0.08，SRMR的值应该小于0.05。

当这些值达到或接近这些标准时，可以认为模型对观察数据的拟合是较好的。

3. 如何解释AMOS模型拟合指数当进行结构方程建模时，研究人员首先需要对模型的理论基础有清晰的认识。

需要根据实际数据进行模型的拟合和估计，并对拟合指数进行解释。

如果拟合指数达到或超过正常值，那么这个模型就有较好的拟合度；反之，则需要考虑修改模型。

4. 其他影响AMOS模型拟合指数的因素除了模型本身的设定和数据质量外，AMOS模型拟合指数还可能受到其他因素的影响。

比如样本量的大小、模型的复杂程度、变量之间的相关关系等都可能对拟合指数产生影响，因此在解释拟合指数时需要综合考虑这些因素。

曲线拟合拟合优度
曲线拟合是通过一个数学函数来近似描述一组离散数据点的过程。

拟合优度（Goodness of Fit）是用来评估拟合函数与实际数据的适应程度的指标。

一般来说，拟合优度越高，拟合函数与实际数据的吻合度越好。

常用的拟合优度指标包括：
1. 相关系数（Coefficient of Determination）：常用符号为 R²，表示拟合函数的变异程度与实际数据的变异程度之比。

取值范围为 0 到 1，值越接近 1 表示拟合优度越高。

2. 均方误差（Mean Square Error）：用于衡量拟合函数预测值与实际值之间的差距。

均方误差越小，拟合优度越高。

3. 标准残差（Standardized Residuals）：计算每个数据点的残差（预测值与实际值之差）与拟合函数的标准差之比。

标准残差越接近 0，拟合优度越高。

需要注意的是，拟合优度不是唯一的评估指标，不同的拟合方法和数据集可能会选择不同的指标。

因此，在比较不同拟合模型或方法的优劣时，应综合考虑多个指标。

拟合值和预测值
拟合值和预测值是统计学中常见的两个概念，它们是对数据进行
处理和分析的重要指标，能够帮助我们对数据进行更加深入的了解。

下面将对拟合值和预测值进行详细解释和举例说明。

一、拟合值
拟合值是指在一组数据中，根据一定的统计方法得到的最有可能
的数值。

当我们有一组数据时，我们通常想要知道这些数据的总体规律。

如果我们用某种方法来获取一个总体规律，那么我们就可以根据
这个规律来预测新数据的值。

这就是拟合值的作用。

常见的拟合方法
有最小二乘法和最大似然估计法。

例如，我们有一组数据{1,2,3,4,5}，我们用最小二乘法来拟合
这组数据，得到的线性拟合函数为y=0.8x+0.6。

那么当x=6时，我们
可以预测y的值为y=5.4。

二、预测值
预测值是指根据已知数据的规律，对未知数据进行估计得到的值。

当我们有一部分数据，但是又想要预测一部分未知数据时，我们可以
使用预测值来估计。

预测值可以根据拟合值、标准差等统计指标来计算。

例如，我们有一组数据{x1,x2,x3,…,xn}，y1,y2,y3,…,yn分别为对应的结果。

我们用最小二乘法得到拟合函数y=a+bx。

那么当x=xk 时，由于y=a+bx具有较好的拟合效果，我们可以用y=a+b*xk来预测y 的值。

综上所述，拟合值和预测值都是数据分析中常用的工具，对于探
索数据背后的规律以及预测未知数据都有重要的作用。

同时，我们需
要注意在使用拟合值和预测值时要避免过度拟合和过分依赖拟合结果。

比较拟合指数比较拟合指数是一种用来衡量统计模型多个版本的准确性和预测能力的指标。

它通常用于判断哪个模型的预测结果更准确、更稳定，并且能够对数据做出更好的解释。

比较拟合指数可以对多个模型的表现进行评估，因此可以帮助我们选出最佳的模型。

通常情况下，最佳模型应该是能够解释数据的大部分变异性（即具有高的拟合度）并保持在未来的预测中达到最准确结果的模型。

常见的比较拟合指数包括 R-squared （R平方值）、均方差是（Mean Square Error）、均方根误差（Root Mean Square Error）、平均绝对误差（Mean Absolute Error）等。

1. R-squared（R平方值）R-squared是最常见的比较拟合指数之一。

R-Squared的范围从0到1，表示模型预测结果中解释的数据变异性的百分比。

值越接近1，模型对数据的解释能力越强，预测结果越准确。

通常情况下，一个模型的R-squared数值必须在0.7以上才能被视为有用和有效的模型。

2. 均方误差（Mean Square Error）均方误差是用来衡量模型预测结果和实际观测值之间的差异的指标。

它的计算方法是将每个观测值与模型预测值之间的差异平方，然后将这些差异取平均值。

均方误差值越小，模型的预测结果越准确。

合适的比较拟合指数取决于数据类型、模型类型以及数据分析目的。

因此，不应仅仅关注一个比较拟合指数。

通常，我们要搜寻多个指标同时进行评估，找到一个相对比较全面的指标。

在选择最佳模型时，我们应该考虑：1. 预测准确性：这个模型对未来数据做的预测有多准确？2. 异常值和误差：这个模型与数据之间的差异有多大？这里需要注意异常值的处理，是否减去或忽略。

3. 解释性：这个模型能够解释该数据的大部分变异性。

这个主要是考虑到数据之间的相关性4. 其他因素：模型的时间和资源成本，可拓展性，可重复性等。

最后要明确的是，比较拟合指数并不是唯一选择模型的标准，它们可以是选取模型中的一个因素，同时需要结合其他因素，如模型的可解释性、适用于的数据类型、其他因素等来进行综合比较。

结构方程模型拟合度指标的选择及其意义解释1. 前言结构方程模型（SEM）是一种灵活、全面的分析方法，常用于探讨复杂变量之间的关系。

评价SEM模型的拟合度可以帮助研究者更好地理解模型的合理性。

在本文中，我们将介绍SEM中常用的拟合度指标和它们的意义。

2. 最小拟合度、最大似然估计和χ²检验SEM中最初的拟合度指标是“最小拟合度”（Minimum Fit Function），也称作”最小方差”或”最小二乘残差”。

最小拟合度是指模型计算值与观测值之间的差异，即样本协方差矩阵与模型预测的协方差矩阵之间的差异，差异越小，模型拟合度越好。

最小拟合度可能存在多个最优解，因此需要另外的指标来辅助选择最优解。

最大似然估计是一种常用的拟合度指标。

它测量的是模型中参数的估计值，这些参数的选择使得样本观测值出现的可能性最大。

最大似然估计在假设数据的分布以及其他研究问题的前提下，同时考虑模型中的测量误差和模型假设，因此能够提供更准确的拟合度指标。

χ²检验（Chi-Square Goodness-of-Fit Test）是一种统计检验方法，用于评估观测值与模型预测之间的差异是否显著。

在χ²检验中，计算出的χ²值越小，两者之间的差异越小，模型拟合度越好。

但是，χ²检验的信度可能受到样本大小的影响，因此需要其他的指标来支持拟合度的评价。

3. 相对拟合度指标为了解决χ²检验的缺陷，相对拟合度指标（Relative Fit Indices）被提出。

这些指标是一类比较拟合度指标，用于比较两种或多种模型的优劣，并将每个模型的拟合度指标与一个基准值相比较。

因此，相对拟合度指标可以消除样本大小的影响。

比较常用的相对拟合度指标包括“指定模型拟合度指数”（Comparative Fit Index，CFI）和“调整后的拟合指数”（Adjusted Goodness-of-Fit Index，AGFI）。

Amos软件操作1.模型设定结构方程模型分析过程可以分为模型构建、模型运算、模型修正以及模型解释四个步骤。

下面以一个研究实例作为说明，使用Amos软件进行计算，阐述在实际应用中结构方程模型的构建、运算、修正与模型解释过程。

2.模型构建的思路根据构建的理论模型，通过设计问卷对留学生学习汉语的学习动机、学习策略和焦虑调查得到实际数据，然后利用对缺失值进行处理后的数据进行分析，并对文中提出的模型进行拟合、修正和解释。

3.潜变量和可测变量的设定模型中共包含2个因素(潜变量)：学习动机、学习策略，7个可测变量：融入型动机、工具型动机、焦虑、记忆策略、认知策略、情感策略和社交策略。

4.关于调查数据的收集本次问卷调研的对象为不同国家的留学生5.缺失值的处理采用表列删除法，即在一条记录中，只要存在一项缺失，则删除该记录。

数据的的信度和效度检验1）．数据的信度检验信度（reliability）指测量结果（数据）一致性或稳定性的程度。

一致性主要反映的是测验内部题目之间的关系，考察测验的各个题目是否测量了相同的内容或特质。

稳定性是指用一种测量工具（譬如同一份问卷）对同一群受试者进行不同时间上的重复测量结果间的可靠系数。

如果问卷设计合理，重复测量的结果间应该高度相关。

由于本案例并没有进行多次重复测量，所以主要采用反映内部一致性的指标来测量数据的信度。

Cronbach在1951年提出了一种新的方法（Cronbach's Alpha系数），这种方法将测量工具中任一条目结果同其他所有条目作比较，对量表进行内部一致性估计。

2）．数据的效度检验效度（validity）指测量工具能够正确测量出所要测量的特质的程度，分为内容效度（content validity）、效标效度（criterion validity）和结构效度（construct validity）三个主要类型。

内容效度也称表面效度或逻辑效度，是指测量目标与测量内容之间的适合性与相符性。