图形的拼组与巧求周长

图示法在解决实际问题中的应用
辅助理解题意
在解决组合图形周长问题时，图示法可以帮助我们更好地理解题意， 明确所求目标。
直观展示思路
通过图示法，我们可以直观地展示解题思路，使得解题过程更加清 晰明了。
提高解题效率
图示法可以帮助我们快速找到解题的关键点，从而提高解题效率。同 时，图示法也有助于我们检查解题过程和结果的正确性。
平移法
平移法原理
通过平移组合图形中的一部分或 全部，使得原本分散或难以计算 的边聚集在一起，便于计算周长。
平移法应用
适用于包含重复形状或具有对称 性的组合图形。
平移法步骤
首先确定需要平移的部分，然后 按照一定方向和距离进行平移， 使得相关边聚集在一起，最后计
算周长。
旋转法
旋转法原理
通过旋转组合图形中的一部分或全部，改变图形的方向和位置， 使得原本难以计算的边变得易于计算。
06
总结与展望
图示法解决组合图形周长问题的意义和价值
直观性
图示法通过直观的图形展 示，帮助学生更好地理解 组合图形的构成和周长计 算过程，降低学习难度。
形象性
图示法将抽象的数学问题 转化为形象的图形问题， 有助于学生形成空间观念 和形象思维。
创新性
图示法鼓励学生从不同角 度思考问题，寻找多种解 题方法，培养学生的创新 意识和实践能力。
01
02
03
直观性
图示法通过图形展示，使 问题更加直观，易于理解。
形象性
图示法能够将抽象的数学 问题转化为形象的图形问 题，降低解题难度。
灵活性
图示法可以根据问题的具 体情况灵活调整图形的形 状和大小，使解题过程更 加灵活多变。
图示法的基本原理和步骤

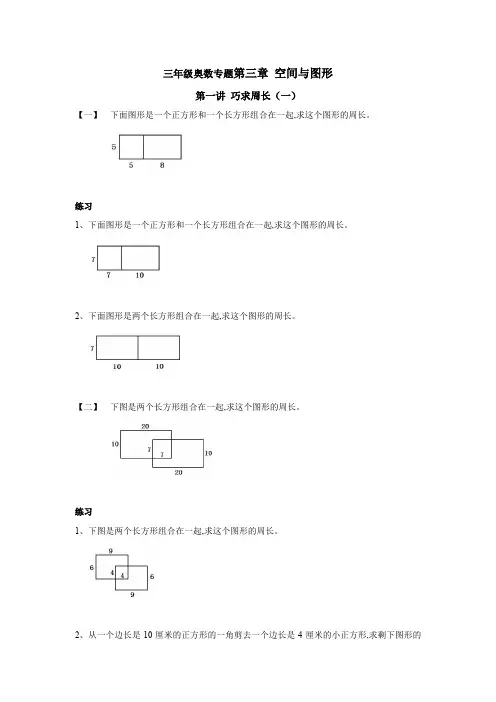
三年级奥数专题第三章空间与图形第一讲巧求周长（一）【一】下面图形是一个正方形和一个长方形组合在一起,求这个图形的周长。

练习1、下面图形是一个正方形和一个长方形组合在一起,求这个图形的周长。

2、下面图形是两个长方形组合在一起,求这个图形的周长。

【二】下图是两个长方形组合在一起,求这个图形的周长。

练习1、下图是两个长方形组合在一起,求这个图形的周长。

2、从一个边长是10厘米的正方形的一角剪去一个边长是4厘米的小正方形,求剩下图形的周长。

【三】下图是一个楼梯的侧面图,求此图形的周长。

练习1、下图是一个楼梯的侧面图,你能算出它的周长吗？2、如下图所示,丹丹和小玲同时从学校到图书城,丹丹沿A路线行走,小玲沿B路线行走,如果两人速度一样,谁先到图书城？为什么？【四】下图是由6个边长1厘米的正方形拼成的。

这个图形的周长是多少厘米？练习1、下图是由5个边长为3厘米的正方形组成的图形,求这个图形的周长。

2、下图是由6个边长为2厘米的正方形组成,求此图形的周长。

【五】两个大小相同的正方形拼成一个长方形后,周长比原来两个正方形周长的和减少了4米。

原来一个正方形的周长是多少米？练习1、把两个大小相同的正方形拼成一个长方形后,周长比原来两个正方形周长的和减少了8厘米,原来一个正方形的周长是多少厘米？2、把一个正方形剪成两个大小相同的长方形后,两个长方形周长的和比原来正方形周长增加16分米,原来正方形的周长是多少分米？【六】一个正方形的边长是4厘米,将9个这样的正方形如下图一样拼成一个大正方形,问拼成的这个大正方形的周长是多少厘米？练习1、把16个边长是2厘米的小正方形拼成一个大正方形,这个拼成的大正方形周长是多少厘米？2、把8个边长为5分米的小正方形如下图拼成一个长方形,这个长方形的周长为多少厘米？【七】将一张边长为18厘米的正方形纸,剪成4个完全一样的小正方形纸片,问这4个小正方形周长的和比原来的正方形周长增加了多少厘米？练习1、将一张边长为10厘米的正方形纸,剪成2个完全一样的小长方形,那么这2个小长方形周长之和比原来的正方形的周长增加了多少厘米？2、把一个边长为28厘米的正方形,如下图剪成6个完全一样的长方形,这六个长方形周长的和与原来的正方形相比,增加了多少厘米？课外作业1、下面图形是三个相同的正方形组合在一起,求这个图形的周长。

组合图形的周长计算重点：图形周长公式的运用难点：周长在组合图形中的运用与转换温故知新：我们已经学会长方形、正方形的周长与面积的计算，利用公式很容易算出它们的面积与周长.但在遇到一些较复杂的有关长方形和正方形的周长和面积计算时，一些同学就会感到棘手。

这两讲我们将教给大家一些平移、转化、分解、合并等技巧，使大家在解题中能顺利地找到突破口，化难为易,化繁为简.1．周长是图形四周的长度.2。

周长的单位是米、分米、厘米。

３．周长的计算公式是（长+宽）×2知识讲解例1。

有一块长8分米,宽４分米的长方形纸板与两块边长4分米的正方形拼成一个正方形.拼成的正方形的周长是多少分米?例２。

两个大小数点相同的正方形拼成一个长方形后,周长比原来的两个正方形周长的和减少６厘米。

原来一个正方形的周长是多少厘米？例３.求图３和图４的周长。

(单位：米）图３图４题海拾贝例1.图7是一座厂房的平面图,求这座厂房平面图的周长。

例2。

图9是个多边形,图中每个角都是直角，它的周长是多少？例3.一个正方形被分成3个大小、形状完全不一样的长方形（如图），每个小长方形的周长都是24厘米，求这个正方形的周长。

例４。

如图所示是由四个一样大的长方形和一个周长是4分米的小正方形拼成的一个边长是11分米的大正方形。

每个长方形的长和宽各是多少？周长是多少?例5。

一根铁丝长１２厘米,能围成几种长和宽都是整厘米数的长方形,每咱长方形的长和宽各是几厘米?围成的正方形的边长是几厘米？课堂练习1．把一个长10厘米，宽5厘米的长方形,分成两个大小一样的正方形,每个正方形的周长是多少？2.用一个长8厘米，宽４厘米的长方形与7个边长4厘米的正方形,拼成一个大正方形。

拼成的大正方形的周长是多少?３．求图12、图13的周长。

4.图１4是一座楼房的平面图,这座楼房平面图的周长是多少米？1米５。

把一个正方形分成甲、乙两个部分(如图1５），比较甲、乙两个部分周长的长短,并求出乙的周长。

组合图形的周长计算重点：图形周长公式的运用难点：周长在组合图形中的运用与转换温故知新：我们已经学会长方形、正方形的周长与面积的计算，利用公式很容易算出它们的面积与周长。

但在遇到一些较复杂的有关长方形和正方形的周长和面积计算时，一些同学就会感到棘手。

这两讲我们将教给大家一些平移、转化、分解、合并等技巧，使大家在解题中能顺利地找到突破口，化难为易，化繁为简。

1.周长是图形四周的长度。

2.周长的单位是米、分米、厘米。

3.周长的计算公式是(长+宽)×2知识讲解例1．有一块长8分米，宽4分米的长方形纸板与两块边长4分米的正方形拼成一个正方形。

拼成的正方形的周长是多少分米？例2.两个大小数点相同的正方形拼成一个长方形后，周长比原来的两个正方形周长的和减少6厘米。

原来一个正方形的周长是多少厘米？例3.求图3和图4的周长。

（单位：米）图3 图4题海拾贝例1.图7是一座厂房的平面图，求这座厂房平面图的周长。

例2.图9是个多边形，图中每个角都是直角，它的周长是多少？例3.一个正方形被分成3个大小、形状完全不一样的长方形（如图），每个小长方形的周长都是24厘米，求这个正方形的周长。

例4.如图所示是由四个一样大的长方形和一个周长是4分米的小正方形拼成的一个边长是11分米的大正方形。

每个长方形的长和宽各是多少？周长是多少？例5.一根铁丝长12厘米，能围成几种长和宽都是整厘米数的长方形，每咱长方形的长和宽各是几厘米？围成的正方形的边长是几厘米？课堂练习1.把一个长10厘米，宽5厘米的长方形，分成两个大小一样的正方形，每个正方形的周长是多少？2.用一个长8厘米，宽4厘米的长方形与7个边长4厘米的正方形，拼成一个大正方形。

拼成的大正方形的周长是多少？3.求图12、图13的周长。

4.图14是一座楼房的平面图，这座楼房平面图的周长是多少米？1米5.把一个正方形分成甲、乙两个部分（如图15），比较甲、乙两个部分周长的长短，并求出乙的周长。

巧求周长的几种方法《巧求周长的几种方法》小朋友们，今天我们一起来学习巧求周长的有趣方法！比如说，有一个长方形的操场，长是 8 米，宽是 6 米。

那它的周长怎么算呢？我们可以这样想，长方形有两条长和两条宽，所以周长就是 2 乘以长加上 2 乘以宽，也就是2×8 + 2×6 = 28 米。

再看一个例子，有一个正方形的手帕，边长是 5 分米。

正方形的四条边都一样长，所以周长就是 4 乘以边长，即4×5 = 20 分米。

还有一种方法叫平移法。

比如有一个不规则的图形，我们可以把它的边平移一下，变成一个规则的图形，再求周长。

就像一个缺了角的长方形，我们把缺的角平移补起来，就好算了。

小朋友们，学会这些方法，求周长就不难啦！《巧求周长的几种方法》大家好呀！今天来给大家讲讲巧求周长的办法。

先来说说相加法。

假如有一个三角形，三条边分别是 3 厘米、4 厘米、5 厘米，那它的周长就是把三条边加起来，3 + 4 + 5 = 12 厘米，是不是很简单？再说说公式法。

像圆形的周长，咱们就有专门的公式，C = 2πr 或者 C = πd，这里的 r 是半径，d 是直径，π 呢，一般约等于3.14。

比如说一个圆的半径是 2 厘米，那周长就是2×3.14×2 = 12.56 厘米。

还有一种叫分解法。

比如一个复杂的图形，咱们可以把它分成几个简单的图形，分别求出周长再相加。

怎么样，这些方法不错吧？《巧求周长的几种方法》朋友们，咱们一起研究研究巧求周长的法子。

举个例子，有个不规则的多边形，看起来很复杂，但是我们仔细观察，会发现有些边是相等的。

像这样，我们把相等的边找出来，计算就轻松多啦。

还有的时候，我们可以利用对称的特点。

比如说一个轴对称的图形，我们只需要算出一半的周长，再乘以 2 就行。

另外，别忘了标数法。

就像一个方格图里的图形，我们在每条边上标上数字，再相加，周长就出来了。

学会这些小窍门，求周长就不再头疼啦！《巧求周长的几种方法》嗨，各位！今天聊聊怎么巧妙地求出周长。

自主检测
• 1、把4个边长为3厘米的正三角形拼成一个 大正三角形，问这个大正三角形的周长是 多少厘米？（三角形3条边一样长的三角形叫做正三角形）
3厘米
• 2、一个正方形的边长是8厘米，把它剪成 两个同样大小的长方形，问每个长方形的 周长是多少厘米？（自己独立画图解决）
宝宝学拼图，把3个边长为4厘米的正方形拼成一个 大长方形，问这个长方形的周长是多少厘米？
1厘米
这个新的图形周 长怎么算啊？
1厘米
？3 厘米
• 方法一
用长方形周长公式解答。 把这三个正方形组成的图形看作一个长方形。 （3+1）×2=8（厘米）
• 方法二
用原来三个长方形的周长减去2条边长 1×4×3- 4=8（厘米）
一个正方形的边长是6厘米，把这个正方形分成三个 同样大小的长方形，问每个长方形的周长是多少厘
米？
边长6厘米
？
你能自己试试 看吗！
思路回眸
• 从以上的例题可以看出，将几个图形拼成 一个图形，或将一个图形分解成几个图形化的规律，然后才能有效 的解决问题。

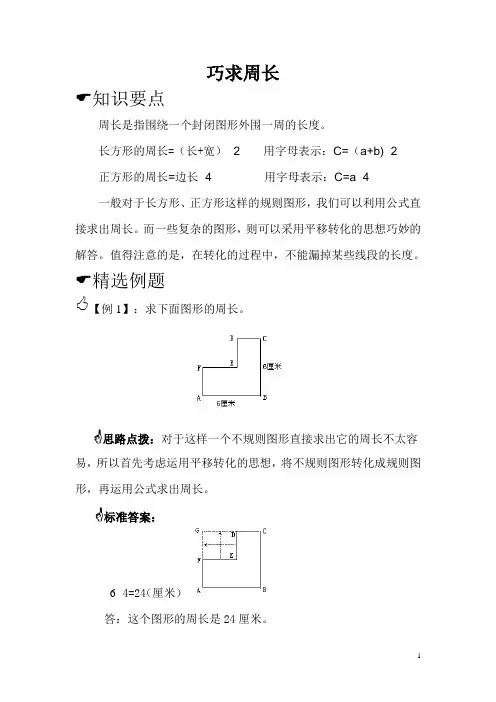
巧求周长☜知识要点周长是指围绕一个封闭图形外围一周的长度。

长方形的周长=（长+宽）×2 用字母表示：C=（a+b)×2正方形的周长=边长×4 用字母表示：C=a×4一般对于长方形、正方形这样的规则图形，我们可以利用公式直接求出周长。

而一些复杂的图形，则可以采用平移转化的思想巧妙的解答。

值得注意的是，在转化的过程中，不能漏掉某些线段的长度。

☜精选例题【例1】：求下面图形的周长。

☝思路点拨：对于这样一个不规则图形直接求出它的周长不太容易，所以首先考虑运用平移转化的思想，将不规则图形转化成规则图形，再运用公式求出周长。

☝标准答案：6×4=24（厘米）答：这个图形的周长是24厘米。

✌活学巧用1、求下图的周长。

（1）（2）（3）【例2】：求下图的周长。

4厘米☝思路点拨：这是一个不规则图形，首先确定周长的范围；再转化成一个正方形。

转化之后，我们会发现，不规则图形的周长等于转化后正方形的周长。

正方形的边长为4×3=12（厘米）☝标准答案：4×3×4=12×4=48（厘米）答：这个图形的周长是48厘米。

✌活学巧用1、下面图形是由5个边长为3分米的正方形组成，求它的周长。

2、有两个相同的长方形，长是7厘米，宽是3厘米，如果把它们按如图所示叠放在一起，这个图形的周长是多少厘米？3、有两个完全一样的长方形，长是8厘米，宽是2厘米，如果把它们按如图所示叠放在一起，这个图形的周长是多少厘米？【例3】：求下图的周长。

☝思路点拨：将上图转化成长方形，这时原图的周长转化成了一个长方形的周长加上两条3米长的线段的和，求出这两部分的和就求出了原来这个图形的周长。

☝标准答案：（12+5）×2+3×2= 34+6= 40（米）答：这个图形的周长是40米。

✌活学巧用1、求下面图形的周长。

（1）（2）（3）【例4】：用3个边长为4厘米的正方形组成一个长方形，求所组成的长方形的周长。

三年级奥数巧算周长
引言
本文将介绍一些三年级学生可以使用的巧算周长的方法。

通过掌握这些方法，学生可以快速而准确地计算图形的周长，从而提高数学能力和思维逻辑。

直线边长的简单计算
对于直线边长相等的图形（如正方形、长方形），可以使用简单的计算方法来确定周长。

直接将边长乘以边数即可得到周长。

例如，一个正方形的边长为5厘米，由于正方形的四条边长度相等，所以周长为5乘以4，即20厘米。

不规则图形的计算
对于不规则图形，我们可以采用分块的方法来计算周长。

首先将图形划分为多个矩形或正方形的组合，逐个计算每个矩形或正方形的周长，然后将这些周长相加即可得到整个图形的周长。

圆的周长计算
圆的周长计算相对复杂一些。

我们可以利用圆周率（约等于
3.14）和圆的直径（或半径）来计算周长。

周长等于直径（或半径）乘以2再乘以圆周率。

例如，一个圆的直径为10厘米，则周长等
于10乘以2乘以3.14，即约为62.8厘米。

总结
通过掌握直线边长的简单计算方法、不规则图形的分块计算方
法以及圆的周长计算方法，三年级学生可以更轻松地计算图形的周长。

这些方法不仅能提高数学能力，还能锻炼思维逻辑和解决问题
的能力。

请注意：本文所介绍的计算方法仅适用于简单的图形，对于复
杂的图形或涉及到其他数学概念的图形计算，请咨询数学老师或参
考相关教材。

农场规划师(拼接图形求周长)知识图谱农场规划师知识精讲一．规则拼接图形求周长1．拼接过程中拼一次减少两个长或两个宽；2．通过大图形寻找内部图形长、宽倍数关系；3．环形问题考虑外周长和内周长．二．一刀两“段”求周长每剪一刀，周长总和的增加量等于被剪开线段长的两倍．三点剖析本讲主要培养学生的多维感知能力，其次培养学生的实践应用能力．本讲内容是在基本图形周长计算的基础上，进一步学习规则拼接图形求周长．课堂引入例题1、 艾小莎和唐小果最近玩了一个游戏——农场规划师．她们说这不仅是游戏，而且还能学数学呢！ 还给大家展示了关卡三：给你一块土地，你需要种上小麦、大豆和玉米．艾小莎把这块土地分成了如下相同的三块，并且做出了明显的分界线，然后在土地上种上了这三种植物．种完之后，艾小莎打算离开这片庄园回家了．这时，系统提示：其他人或动物可能会来破坏农作物，是否需要在周围围上栅栏呢？你能帮艾小莎算一下需要多长的栅栏呢？例题2、 唐小果规划时，把整块土地规划成如下三小块，你知道她的栅栏需要多长吗？小麦大豆玉米注：每块地长20米，宽15米这个肯定需要，我们是不是要先量一量这一周的长度呢？不需要啦，你刚刚种的时候不是有每块土地的长度吗？用这个就可以了．注：每块地长30米，宽15米拼接图形的周长例题1、下图是一个正方形被分成3个大小、形状完全一样的长方形，每个小长方形的周长都是24厘米．求这个正方形的周长．我是不是应该先求出正方形的边长呢？例题2、如图，三个形状大小完全一样的小长方形组成一个大长方形，每个小长方形的周长都是36厘米，大长方形的长和宽各是多少厘米？小长方形组成了大长方形，那它们的长和宽一定有关系吧？例题3、如图所示，5个同样大小的小长方形拼成了一个大长方形．已知小长方形的长是12厘米，求大长方形的周长．这个跟之前的相比较，还是有点复杂哦~例题4、如图，在一个长方形中有一段阴影部分．如果阴影部分恰好是正方形，那么图中大长方形的周长是多少厘米？6厘米9厘米例题5、如图，用一个边长是6厘米的正方形和4个一样大的小长方形，一起拼成一个边长是30厘米的大正方形，________厘米．例题6、如图，由一些相同的小长方形和一个小正方形拼成的大正方形．已知图中大正方形的周长为400，小正方的周长为240，求每个小长方形的周长是多少？例题7、用12个边长为1的小正方形拼一个大长方形，这个长方形的周长最短是多少？12个小正方形能组成一个什么样的大长方形呢？随练1、下图中的正方形被分成了4个相同的长方形，每个长方形的周长都是40厘米．求这个正方形的周长．随练2、如图，五个相同的小正方形拼成一个大长方形，已知大长方形的周长为48厘米，求小长方形的周长．随练3、图中阴影部分是正方形，那么最大长方形的周长是多少厘米？一刀两“段”求周长例题1、如图，一个正方形纸片，被竖着剪了1刀后，分成了2个小长方形纸片，这2个小长方形纸片的周长总和为72厘米，那么原来正方形纸片的边长为________厘米．剪之前和之后比较，好像多了两条边呀……例题2、如图，一个边长5厘米的正方形纸片，被竖着剪了4刀，分成了5个小长方形纸片，那么这5个小长方形纸片的周长总和为________厘米．例题3、如图，一个正方形纸片，被横着剪2刀、竖着剪1刀后，分成了6个小长方形纸片，这6个小长方形纸片的周长总和为200厘米，那么原来正方形纸片的边长为________厘米．一刀两段，三刀就是六段了呀！随练1、如图，一个边长8厘米的正方形纸片，被竖着剪了2刀，分成了3个小长方形纸片，那么这3个小长方形纸片的周长总和为__________厘米．随练2、如图，一个正方形纸片，被横着剪1刀、竖着剪1刀后，分成了4个小长方形纸片，这4个小长方形纸__________厘米．易错纠改例题1、一个长5厘米，宽3厘米的长方形，沿对角线对折后，得到如下图所示的几何图形，阴影部分的周长是________厘米．为此唐小虎与姐姐唐小果有了如下的讨论：求阴影部分的周长？阴影部分是两个三角形，需要知道它们的每条边长才能求周长呀！但是题目里没给……但是你想想这个阴影部分是怎么形成的呢？好吧，那我想想……同学们，大家来帮帮小虎吧！拓展1、如图，用5个完全相同的长方形拼成了一个周长是55厘米的大长方形，那么小长方形的宽是__________厘米．2、如图，一个边长8厘米的正方形纸片，被横着剪了3刀，分成了4个小长方形纸片，那么这4个小长方形纸片的周长总和为__________厘米．3、如图，八个同样大小的小长方形拼成一个大长方形，已知大长方形的周长为112厘米，求小长方形的周长．4、如图所示，在长方形ABCD中，120AB 厘米，截去一个正方形EBCF后，求剩下的长方形AEFD的周长．5、如图，用一个边长是3厘米的正方形和4个一样大的小长方形，一起拼成一个边长是17厘米的大正方形，那么小长方形的长是__________厘米．6、将12个长4厘米，宽3厘米的长方形纸板拼接成一个大的长方形（包含正方形），拼接时，要使得没有重叠部分并且不中空，那么，拼成的长方形的周长最短是__________厘米，最长是__________厘米．7、如图，一个长10厘米，宽6厘米的长方形纸片，被横着剪了2刀，竖着剪了1刀，分成了6个小长方形纸片，__________厘米．8、一块边长为30厘米的正方形蛋糕，横着切2刀，竖着切2刀，分成了9个小长方形，那么这9块小长方形蛋糕的周长总和为________厘米．9、分析并口述题目的做题思路及方法．4个一样的宽为2厘米的长方形拼成一个大长方形．大长方形的周长是多少厘米？。

图形的拼组与巧求周长知识回顾小红有一张长8米，宽5米的长方形彩纸，要在彩纸上取一块最大的正方形纸，这个正方形纸的周长是多少米？剩下部分的周长是多少米？（画图）一、图形的拼组①正方形拼成长方形或正方形【例1】4个边长为4厘米的小正方形拼成大的长方形或正方形，你能算出它们的周长吗？（画图并计算）【例2】用16张边长是1分米的正方形拼成长方形或正方形，怎样拼，才能使拼成的图形周长最短？【变式训练1-1】将9个边长是2厘米的正方形，拼成一个长方形或者正方形，有几种拼法？每种拼法的周长是多少？【变式训练2-1】将一个边长是6厘米的大正方形切成边长是1厘米的小正方形，可以切成多少个？这些小正方形的周长之和比原来大正方形的周长增加或减少了多少？【变式训练2-2】将12个边长是2分米的小正方形拼成一个长方形，有几种拼法？怎么拼周长最短？②长方形拼成长方形或正方形【例3】将两个长5厘米宽3厘米的长方形拼成一个大长方形，拼成的长方形的周长是多少厘米？【例4】用3个长是2厘米，宽是1厘米的长方形拼成一个新的长方形，能拼成几种不同的长方形？每个长方形的周长是多少？【变式训练3-1】有两个同样的长方形，长是4厘米，宽是3厘米，把它们拼成一个大长方形，这个大长方形的周长至少是多少厘米？【变式训练4-1】如果3个长是4厘米，宽是2厘米的长方形拼成一个新的长方形，能拼成几种不同的长方形？每个长方形的周长是多少？巧求周长【例5】有一个大长方形的周长是24厘米，小正方形的周长是12厘米，求这两个正方形拼成的新图形的周长是多少厘米？【变式训练5-1】把边长分别是5厘米、4厘米、3厘米和2厘米的4个正方形按从大到小的顺序排成一行(如图),排成的图形周长是多少厘米?【变式训练5-2】用15个边长2厘米的小正方形摆成如下图的形状,求图形周长是多少厘米?下图中甲、乙两部分的周长相等吗？甲乙【家庭作业】一、填空1、一个长方形宽是20米，长是宽的2倍，长是（）米，周长是（）米。

中考数学复习考点知识专题讲解利用组合与分解求不规则图形的面积或周长一、组合对于一些求不规则图形的面积或周长的数学题，我们往往不能直接求出问题的解．但如果把某些图形组合在一起，看成一个整体，这样就可以转化成规则的图形，从而使问题变得更简单．例1 如图l，在Rt△ABC中，∠C＝90°，CB＝CA＝4，分别以A，B，C为圆心，12AC为半径画弧，三条弧与边AB所围成的阴影部分的面积是_______．分析先求出△ABC的面积S＝12CA×CB＝12×4×4＝8．将3个半径相同的扇形组合成一个半圆，则这个半圆的面积S1＝12πR2＝12π×22＝2π，因此，阴影部分的面积等于△ABC的面积减半圆的面积，即S－S1＝8－2π．(A)4π (B)3π (C)2π (D)π例2如图2，正方形MNEF的四个顶点在直径为4的大圆上，小圆与正方形各边都相切，AB与CD是大圆的直径，AB⊥CD，CD⊥MN，则图中阴影部分的面积是( )(A)4 (B)3 (C)2 (D)π分析根据对称性，4个阴影部分组合在一起构成14个大圆，其面积S＝14πR2＝14π×42＝4π．例3 如图3，已知正方形ABCD的对角线长为22，将正方形ABCD沿直线EF折叠，则图中阴影部分的周长为___________．分析易求出正方形的边长是2．将折叠的部分还原，实际上是这些小三角形的边都与正方形ABCD的四边重合，则这些阴影三角形的边组合在一起实际上是正方形的四边，因此阴影部分的周长为8．例4 如图4，⊙A和⊙B都与x轴和y轴相切，圆心A和圆心B的图象上，则图中阴影部分的面积和等于_______（结都在反比例函数y＝1x果保留π）的图象分析由题意，设⊙A圆心的坐标为(a，a)．在函数y＝1x上，易求得a＝l，两个圆的半径相等，即r＝a＝1．图中2个阴影部分的可以组合成一个圆，其面积为S＝πr2＝π．例5为增加绿化面积，某小区将原来正方形地砖更换为如图5所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为a，则阴影部分的面积为( )(A)2a2(B)3a2(C)4a2(D)5a2分析将4个直角阴影三角形组合成一个边是a的正方形，因此阴影部分可以看成2个边是a的正方形的面积和，即2a2．例6 如图6，依次以三角形、四边形、…、n边形的各顶点为圆心画半径为l的圆，且圆与圆之间两两不相交．把三角形与各圆重叠部分面积之和记为S3，四边形与各圆重叠部分面积之和记为S4，…，n边形与各圆重叠部分面积之和记为S n，则S90的值为_______．分析将90边形的重叠部分面积之和组合成一个扇形，其内角和是(90－2) ×180°．因此，S90＝()290218044360rππ-⨯=．例7边长为2的两种正方形卡片如图①所示，卡片中的扇形半径均为2．图②是交替摆放A ，B 两种卡片得到的图案．若摆放这个图案共用两种卡片21张，则这个图案中阴影部分图形的面积和为_______（结果保留π）．分析A ，B 两种卡片可各1张以组合成1个正方形，21张这两种类型卡片可以组合成10个正方形和1个A 种图形，则这个图案中阴影部分图形的面积和为：10×22＋22－4 ×22＝84－π． 二、分解分解的思想是一种重要的解题思想，就是把一（或几）个整体（包括式子和图形）分解若干个部分，然后分别对每个部分进行研究，总结其变化规律．利用分解思想解题的实质在于”化整为零，各个击破”． 1、把分式分解成分子和分母例7一组按规律排列的式子a2，43a ，65a ，87a ，…则第n 个数据是_______．（用含n 的式子表示）分析 我们把这些变化的式子分解成分子和分母来考查．先研究分子a 2，a 4，a 2，a 8，…底数a 不变，而指数2，4，6，8，…是一列偶数，第n 个数据的指数应该是2n ，故第n 个数的分子应该是a 2n ；再考查分母1，3，，7，…，是一列奇数，则第n 个数的分母应该是2n －1，则第n 个数据是221n a n ． 2、把单项式分解成系数和字母例8 观察一列单项式x ，3x 2，5x 3，7x ，9x 2，11x 3，…，则第2013个单项式是_______．分析 把这些单项式分解为系数和字母来考查，先研究系数l ，3，5，7，9，11，…，是一列奇数，第n 个奇数是2n －1，故2013个单项式的系数应该是2013×2－1＝4025；再考查字母x ，x 2，x 2，x ，x 2，x 2，…其底数x 不变，而指数1，2，3，l ，2，3，…呈周期性变化，变化周期是3，因此，可以总结出规律第n 个单项式的指数是：当n ＝3k ＋1（k ＝0，1，2，3，…）时，x 的指数是1；当n ＝3k ＋2（k ＝0，1，2，3，…）时，x 的指数是2；n＝3k(k＝1，2，3，…)时，x的指数是3．而2013＝671×3，则2013个单项式x的指数是3，故第2013个单项式是4025x3．3、把（不）等式两边的式子分解例9观察下列各式的计算过程：52＝0 ×l ×100＋25，152＝l×2×100＋25，252＝2×3×100＋25，352＝3 ×4×100＋25，……请猜测，第n个算式（n为正整数）应表示为______．分析先考查等号左边的数字：指数2不变，而底数分别是5，15，25，35，…分别可以写成5×l，5×3，5×5，5×7，…在这些乘积中，第一个数字5固定，而第二个数字分别是l，3，5，7，…，是一列奇数，则第n个奇数可以表示为2n，－1，则第n个等式等号的左边可以表示为[5（2n－1）]2．再考查等号右边的数字：第一个数字分别是0，1，2，3，…每个数字分别比相应等式的序号小1，第n个等式对应数应该表示为n－1；第二个数字分别是1，2，3，4，…每个数字分别与相应等式的序号相同，则第n个等式对应的数应该表示为n；第三、四个数字100，25固定，则数字间的”×与＋”不变，所以n个等式等号右边的式子可表示为100n(n －1)＋25．综上，第n个算式（n为正整数）应表示为[5(2n－1)]2＝100n(n －1)＋25．4、把图形分解例11 如图7，一段抛物线：y＝－x(x－3)（0≤x≤3），记为C1，它与x轴交于点O，A1；将C1绕点A1旋转1800得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x 轴于点A3；…如此进行下去，直至得C n．若P(37，m)在第n段抛物线C n上，则m＝_______，n＝_______．分析把以上图形分解成两部分，即x轴的上面的部分和x轴的下面的部分．先考查x轴的上面的部分C3，C5，C7，…，C2k－1：即当n＝3，5，7，…，2k－1时，C3，C5，C7，…，C n相当于把C1向右平移6，12，18，…，6（k－l）个单位，则第n段抛物线C2k－1的解析式为：y＝－[x－6(k－l)][x－6(k－l)－3]＝－（x－6k＋6）（x－6k＋3）（其中，6（k－1）≤x≤6（k－l）＋3）．①再考查x轴的下面的部分C2，C4，C6，…，C2k：即当n＝4，6，8，…，2k时，则C4，C6，…，C2k相当于把C2向右平移6，12，18，…，6（k－1)个单位，则第n段抛物线C2n的解析式为y＝[x－6(k－1)－3][x－6(k－1)－6]＝（x－6k＋6）（x－6k＋3）(其中，6(k－1)＋3≤x≤6（k－l）＋6）．②由于6×（7－1）≤37≤6×(7－1)＋3，则k ＝7，而n ＝7×2－1＝13，把k ＝7，x ＝37代入①，得m ＝2，故m ＝2，n ＝13．例5如图，小方格都是边长为l 的正方形，则以格点为圆心，半径为1和2的两种弧围成的“叶状”阴影图案的面积为______．分析 连结AC 从图中看出由直线段AB 和曲段线AB 为成弓形（阴影部分）的面积与直线段BC 和曲段线BC 为成弓形（空白部分）的面积相等．因此这两片“叶”实际上是可以补成两个弓形，即半径为2的14圆中去掉一个直角边为2的等腰直角三角形．故其面积是：21122222442ππ⎛⎫⨯⨯-⨯⨯=- ⎪⎝⎭．。

我会做！ 6米
4米
3分米
长方形的周长=（长+宽）×2 =（6+4） ×2 =20（米）
正方形的周长＝边长×4
＝3ⅹ4 ＝12（分米）
人教版数学三年级上册第七单元第5课时 拼组图形规律的探究及周长的计算
一行16个，摆了1行。16ⅹ1＝16 摆成一个长方形。
每行8个，摆2行。摆成一个长 方形。
8×2＝16
• 计算长方形的周长：（16＋1）×2＝34 （分米）
第二种摆法： 长方形的长：8×1＝8（分米）
长方形的宽：2×1＝2（分米）
长方形的周长：（8＋2）×2＝ 20（分米）
第三种摆法：摆成的图形是正方形。 它的边长是：4ⅹ1＝4（分米）
正方形的周长：4×4＝16（分米）
通过探究你有哪些发现？
每行的个数和行数最接近或相等时， 摆出的图形周长最短。
3、12×3＝36 （12＋3）×2＝30（分米）
9ⅹ4＝36 （9＋4）×2＝26（分米）
5、6×6＝36
6×4＝24(分米)
通过这节课的学习，你有哪些收获？
总结:1、每行个数×行数＝小正方形的总数。
2、计算摆成的图形的长和宽。（每个小 的边长×每行的个数＝长，每个小正方 的边长×行数＝宽）
3、计算周长。（长＋宽）×2＝周长。
如果用36张正方形纸拼呢？ 1、36×1＝36 （36＋1）×2＝74（分米）
2、18×2＝36 （18＋2）×2＝40（分米）
每行4个，摆4行。摆成一个 正方形。
4ⅹ4＝16
探究活动：每行摆的个数、行数与小正方形 的总数的关系。
每行摆的个数 16 8 4
行数 1 2 4
小正方形的总数 16×1＝16 8ⅹ2＝16 4×4＝16

人教版三年级数学上册第七单元第4课时《拼组图形规律的探究及周长的计算教学设计》教学内容：人教版三年级数学上册第七单元拼组图形规律的探究及周长的计算。

教学目标：1、通过动手操作，找出用若干个同样的正方形拼组长方形或正方形的方法。

2、探索并思考拼组图形周长较短的原因:在于图形越接近正方形，隐藏在里面的边越多。

3、能正确熟练地计算拼组图形的周长。

能运用所学知识解决实际问题。

感受数学与生活的密切联系。

提高学生的动手操作能力。

教学重点：理解拼组图形的周长，探索拼组图形方法及周长的计算。

教学难点：拼组图形周长的计算方法。

教法学法：演示法、操作探究法、交流合作自主探究法。

教具学具准备：多媒体课件，正方形圆片教学过程：一、复习旧知计算长方形、正方形的周长。

1、一个长方形长6m,宽4m,它的周长是多少m？2、一个边长是3dm的正方形，它的周长是多少dm?学生独立完成，集体订正。

（设计意图：充分尊重学生，根据他们的认知水平巩固周长的计算公式）二、导入新课出示课本第86页主题图。

例5用16张边长是1分米的正方形纸拼长方形和正方形，怎样拼，才能使拼成的图形周长最短？三、探究新知1、探究拼组图形的方法。

（1）小组合作，利用学具摆一摆。

（2）组长回报，展示成果。

（3）教师整合归纳。

利用ppt动画把学生的结果演示出来。

2、探究：每行摆的个数，行数与正方形的总数的关系。

（利用表格进行对比。

）3、探究拼组图形周长的计算方法。

每个正方形的边长×每行的个数＝拼组图形的长，每个正方形的边长×行数＝拼组图形的宽。

通过探究你有什么发现？每行的个数和行数越接近，摆出的图形周长最短。

例5.（1）16×1＝16（1行16个，摆了1行，拼成一个长方形）（2）8×2＝16 （每行8个，摆了2行，拼成一个长方形）（3）4×4＝16（每行4个，摆了4行，拼成一个正方形）4、计算。

（1）16×1＝16（长方形的长）1×1＝1（长方形的宽）（16＋1）×2＝34（分米）（2）8×1＝82×1＝2（8＋2）×2＝20（分米）（3）4×1＝44×4＝16（分米）四、知识运用。

备注：在数学的学习中，分类讨论是一个非常重要的解题思路。
16=4×4，即这个大正方形是由4×4的小正方形构成。 所以大正方形的周长是：4×2×4×2=64厘米
小结：这类题目，画个草图会一目了然 动动手： p.91随堂1
例2：一个铁环如下图所示，有一个甲壳虫沿着铁环爬行，1分钟走1米，15分 钟之后，它已经绕着铁环爬行了3圈，求铁环的周长。
【分析】1分钟走1米，15分钟就是15米，正好3圈铁环长，则一圈铁环正好5 米。甲壳虫沿铁环爬行一圈就是铁环的周长。
分析这类题目，应该学会按题目意思画图，并可演示。
动动手： p.92随堂2
例3：有5张长2厘米，宽1厘米的长方形硬纸片，用它们拼成一个大的长方形。 这个大长方形的周长最少是多少厘米？ 【分析】图形题的关键是按题目要求画出示意图。
5张给定的长方形纸片可以按以上图示方式排列组成大长方形。当两张纸 片并在一起时，新图形的周长，是两小图形的周长减去重叠部分。所以，要使
再画一个破坏这个规则的不规则图形，进行变换试试。
动动手：p.93随堂5
例6：下图中，甲、乙两个图形的面积哪个大？周长哪个长？
【分析】甲、乙两个图形，共同的是曲线部
甲
分，而不是共同部分，分别是长方形的长和
乙
宽。所以周长相同。
沿对角线画一条直线，很容易可以看出
甲、乙两个图形的面积的大小。
动动手： p.94随堂6
大长方形的周长最少，则重叠部分应该尽量多，或选择长边重叠。显然， 大长方形周长应该是：5×（2+1）×2-4×2×2=14厘米。 5个纸片拼成大长方形，有4个重合处。每个重合处有两条边。
动动手：p.92随堂3
例4：求下图的周长。（单位：分米）
50 50

第四讲 巧求周长一、知识要点： 一个图形的周长是指围成它的所有线段的长度和，我们已经学会了求长方形、正方形这些标准图形的周长。

对于一些不规则的比较复杂的几何图形，要求它们的周长，我们可以运用平移的方法，把它转化为标准的长方形或正方形，然后再利用周长公式进行计算。

将一个大长方形或正方形分割成若干个长方形和正方形，那么图形周长就会增加几个长或宽；反之，将若干个小长方形或正方形组合成一个大长方形或正方形，图形周长就会减少几个长或宽。

二、自我探究：【例1】下面图形是一个正方形和一个长方形组合在一起，求这个图形的周长。

【例2】下图是由6个边长2厘米的正方形拼成的，这个图形的周长是几厘米？【例3】两个大小相同的正方形拼成一个长方形后，周长比原来两个正方形周长的和减少了6厘米。

原来一个正方形的周长是多少厘米？5 511【例4】用24个边长是1厘米的正方形拼成一个长方形，这个长方形的周长是多少厘米？【例5】下图是一个楼梯的侧面图，求此图形的周长。

三、自我挑战：第一关：1.下面图形是两个长方形组合在一起，求这个图形的周长。

710102.把一个正方形剪成两个大小相同的长方形后，两个长方形的周长和比原来正方形的周长增加28分米。

原来正方形的周长是多少？3.下图是由6个边长为2厘米的正方形组成的，求此图形的周长。

71010720204. 一个周长为20厘米的正方形，从中间剪开成为两个大小相等的长方形。

这两个长方形周长共多少厘米？第二关：1. 把边长是48厘米的正方形剪成三个同样大小的长方形，算一算，每个长方形的周长是多少厘米？2. 一个长方形的周长是正方形的4倍，正方形的边长与长方形的宽为6厘米。

长方形的长是多少厘米？3. 下面图形是两个长方形组合在一起，求这个图形的周长。

第三关：1. 小华家给长方形的院子装上了篱笆墙，由于门宽2米，所以篱笆墙共长16米，而这个长方形的宽是长的一半。

长和宽各是多少米？2.下图由四个长方形重叠而成，后一个长方形的顶点正好是前一个长方形的中心，求这个图形的周长？。