等腰三角形的证明习题及答案

等腰三角形练习题(含答案)等腰三角形第1课时：等腰三角形的性质1.已知等腰三角形的一个底角为50°，则其顶角为80°。

2.如图，△ABC中，AB=AC，BC=6cm，AD平分∠BAC，则BD=3cm。

3.如图，△ABC中，AB=AC，D为BC中点，∠BAD=35°，则∠C的度数为45°。

4.已知等腰三角形的一个内角为50°，则这个等腰三角形的顶角为80°。

5.如图，在△ABC中，D是BC边上一点，且AB=AD=DC，∠BAD=40°，求∠C的度数为100°。

6.如图，△ABC中，AB=AC，D是BC的中点，E，F分别是AB，AC上的点，且AE=AF。

证明：DE=DF。

第2课时：等腰三角形的判定1.在△ABC中，∠A=40°，∠B=70°，则△ABC为钝角三角形。

2.已知△ABC中，∠B=50°，∠A=80°，AB=5cm，则AC=5cm。

3.如图，在△ABC中，AD⊥BC于点D，且BD=DC，则△ABC为等腰三角形。

4.如图，已知△ABC中，∠A=36°，AB=AC，BD为∠ABC的平分线，则图中共有2个等腰三角形。

5.如图，D是△XXX的BC边上的中点，DE⊥AC，DF⊥AB，垂足分别是E，F，且DE=DF。

证明：AB=AC。

6.如图，AB∥CD，直线l交AB于点E，交CD于点F，FG平分∠EFD交直线AB于点G。

证明：△EFG是等腰三角形。

等边三角形第1课时：等边三角形的性质与判定1.如图，a∥b，等边△ABC的顶点B，C在直线b上，则∠1的度数为60°。

2.在△ABC中，∠A=60°，现有下面三个条件：①AB=AC；②∠B=∠C；③∠A=∠B。

能判定△ABC为等边三角形的有条件①、②、③。

3.如图，在等边△ABC中，BD⊥AC于D，若AB=4，则AD=2.4.如图，△ABC是等边三角形，∠CBD=90°，BD=BC，连接AD交BC于点E，求∠BAD的度数为75°。

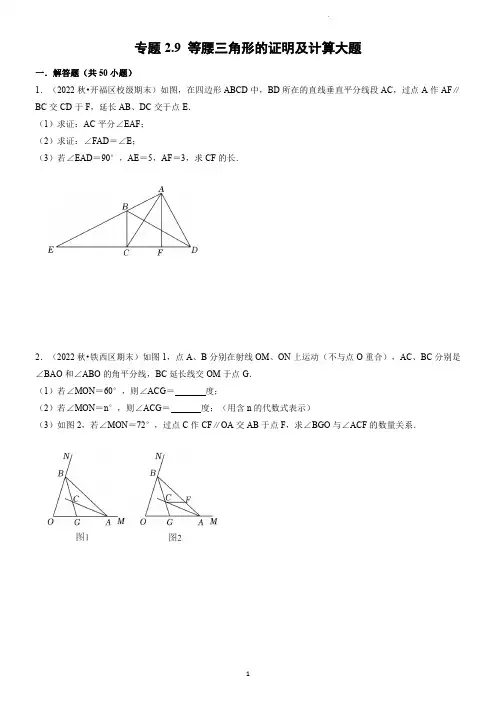
专题2.9等腰三角形的证明及计算大题一．解答题（共50小题）1．（2022秋•开福区校级期末）如图，在四边形ABCD中，BD所在的直线垂直平分线段AC，过点A作AF∥BC交CD于F，延长AB、DC交于点E．（1）求证：AC平分∠EAF；（2）求证：∠FAD＝∠E；（3）若∠EAD＝90°，AE＝5，AF＝3，求CF的长．2．（2022秋•铁西区期末）如图1，点A、B分别在射线OM、ON上运动（不与点O重合），AC、BC分别是∠BAO和∠ABO的角平分线，延长线交OM于点G．（1）若∠MON＝60°，则∠ACG＝度；（2）若∠MON＝n°，则∠ACG＝度；（用含n的代数式表示）（3）如图2，若∠MON＝72°，过点C作CF∥OA交AB于点F，求∠BGO与∠ACF的数量关系．3．（2022秋•单县期末）如图，已知点A、C分别在∠GBE的边BG、BE上，且AB＝AC，AD∥BE，∠GBE 的平分线与AD交于点D，连接CD．求证：①AB＝AD；②CD平分∠ACE．4．（2022秋•巴彦县期末）如图，在△ABC中，点D是边BC上一点，点E在边AC上，且BD＝CE，∠BAD ＝∠CDE，∠ADE＝∠C．（1）如图1，求证：△ADE是等腰三角形；（2）如图2，若DE平分∠ADC，在不添加辅助线的情况下，请直接写出图中所有与∠CDE相等的角（∠CDE 除外）．5．（2022秋•石家庄期末）如图，在△ABC中，AB＝AC，点D为AC上一点，且满足AD＝BD＝BC．点E是AB的中点，连接ED并延长，交BC的延长线于点F，连接AF．（1）求∠BAC和∠ACB的度数；（2）求证：△ACF是等腰三角形．6．（2022秋•思明区校级期末）如图，在△ABC中，∠ABC＝3∠C，AD平分∠BAC，BE⊥AD于E，求证：BE=12（AC﹣AB）．（提示：延长BE交AC于点F）．7．（2022秋•赛罕区校级期中）如图，在△ABC中，BO平分∠ABC，CO平分∠ACB，过点O作BC的平行线分别交AB、AC于点M、N．（1）求证：MO＝MB；（2）若AB＝7，AC＝6，求△AMN的周长．8．（2022秋•建阳区期中）如图所示，已知点A，C分别在∠GBE的边BG，BE上，且AB＝AC，AD∥BE，∠GBE的平分线BD与AD交于点D，连接CD．（1）求证：AC＝AD；（2）猜想：∠BAC与∠BDC之间有何数量关系，并对你的猜想加以证明．9．（2022秋•微山县期中）已知：如图，在四边形ABCD中，AB∥DC，AC平分∠BAD，AC⊥BC于点C．（1）若∠B＝75°，求∠D的度数；（2）求证：AB＝2CD．10．（2022秋•高港区期中）如图，△ABC中，AD是高，CE是中线，点G是CE的中点，DG⊥CE，点G为垂足．（1）求证：DC＝BE；（2）若∠AEC＝75°，求∠BCE的度数．11．（2022秋•播州区期末）已知△ABC中，∠ACB的平分线CD交AB于点D，DE∥BC．（1）如图1，如果点E是边AC的中点，AC＝8，求DE的长；（2）如图2，若DE平分∠ADC，∠ABC＝30°，在BC边上取点F使BF＝DF，若BC＝9，求DF的长．12．（2022春•汉阳区校级期中）如图，已知在△ABC中，CF平分∠ACB，且AF⊥CF于点F，BE平分△ABC 的一个外角，且AE⊥BE于点E．（1）求证：EF∥BC．（2）若BC＝5，AC＝4，EF＝4，求AB的长．13．（2022春•桓台县期末）如图，在△ABC中，AB＝AC，∠ABC的平分线BE交AC于点D，AF⊥AB交BE于点F．（1）如图1，若∠BAC＝40AFE的度数．（2）如图2，若BD⊥AC，垂足为D，BF＝8，求DF的长．14．（2022秋•新兴县期中）在△ABC中，BD是∠ABC的平分线，AD⊥BD，垂足是D．（1）求证：∠2＝∠1+∠C；（2）若ED∥BC，∠ABD＝28°，求∠ADE的度数．15．（2022秋•浦城县期中）在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，∠BAC的平分线AF交CD于点E，交BC于F，CM⊥AF于M，CM的延长线交AB于点N．（1）求证：EM＝FM；（2）求证：AC＝AN．16．（2022春•凤翔县期末）如图，在△ABC中，BC＝8cm，BP、CP分别是∠ABC和∠ACB的平分线，且PD ∥AB，PE∥AC．（1）求△PDE的周长；（2）若∠A＝50°，求∠BPC的度数．17．（2022春•宣汉县期末）如图，在等腰△ABC中，AB＝AC，AD是BC边上的高，点E、F分别是边AB、AC上的点，且EF∥BC．（1）试说明△AEF是等腰三角形；（2）试比较DE与DF的大小关系，并说明理由．18．（2022春•未央区校级期末）如图，在△ABC中，AB＝AC＝2，∠B＝∠C＝40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE＝40°，DE交线段AC于E．（1）当∠BDA＝115°时，∠EDC＝°，∠DEC＝°；点D从B向C运动时，∠BDA逐渐变（填“大”或“小”）；（2）当DC等于多少时，△ABD≌△DCE，请说明理由；（3）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数．若不可以，请说明理由．19．（2022秋•雨花区校级月考）已知△ABC中，∠ACB的平分线CD交AB于点D，DE平分∠ADC，DE∥BC．（1）如图1，如果点E是边AC的中点，AC＝10，求DE的长；（2）在（1）的条件下，求证：△ADC是等腰三角形．（3）如图2，若∠ABC＝30°，在BC边上取点F使BF＝DF，若BC＝18，求DF的长．20．（2022秋•庄浪县期中）如图，在Rt△ABC中，∠C＝90°，∠A＝60°，AB＝10cm，若点M从点B出发以2cm/s的速度向点A运动，点N从点A出发以1cm/s的速度向点C运动，设M、N分别从点B、A同时出发，运动的时间为ts．（1）用含t的式子表示线段AM、AN的长；（2）当t为何值时，△AMN是以MN为底边的等腰三角形？（3）当t为何值时，MN∥BC？并求出此时CN的长．21．（2022秋•兰陵县期中）如图，在△ABC中，AD为∠BAC的平分线，BP⊥AD，垂足为P．已知AB＝5，BP＝2，AC＝9．试说明∠ABC＝3∠ACB．22．（2022春•浦东新区期末）已知△ABC中，∠A＝70°，BP是∠ABC的平分线，CP是∠ACD的平分线．（1）如图1，求∠P的度数；（2）过点P作EF∥BC与边AB、AC分别交于点E、点F（如图2），判断线段BE、EF、CF之间的数量关系，并说明理由．23．（2022秋•天心区校级期中）如图，△ABC中，AC＝BC，∠ACB＝120°，点D在AB边上运动（D不与A、B重合），连接CD．作∠CDE＝30°，DE交AC于点E．（1）当DE∥BC时，△ACD的形状按角分类是；（2）在点D的运动过程中，△ECD的形状可以是等腰三角形吗？若可以，请求出∠AED的度数；若不可以，请说明理由．24．（2022秋•香坊区校级月考）已知BD是△ABC的角平分线，DE∥BC，交AB于点E．（1）如图1，求证：BE＝DE．（2）如图2，在过点D作DF∥AB，连接EF，过点E作EG⊥BC，若EG＝3，BF＝5，在不添加任何辅助线的情况下，请直接写出面积等于152的所有三角形．25．（2022春•莱州市期末）已知，如图，在△ABC中，过点A作AD平分∠BAC，交BC于点F，过点C作CD⊥AD，垂足为D，在AC上取一点E，使DE＝CE，求证：DE∥AB．26．（2022春•莲池区期中）如图①，△ABC中，∠ABC、∠ACB的平分线交于O点，过O点作BC平行线交AB、AC于E、F．试说明：EO＝BE探究一：请写出图①中线段EF与BE、CF间的关系，并说明理由．探究二：如图②，△ABC若∠ABC的平分线与△ABC的外角平分线交于O，过点O作BC的平行线交AB于E，交AC于F．这时EF与BE、CF的关系又如何？请直接写出关系式，不需要说明理由．27．（2022ABC中，∠C＝90°，AB＝5cm，BC＝3cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．（1）出发2秒后，求△ABP的周长．（2）问t为何值时，△BCP为等腰三角形？（3）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？28．（2022秋•莆田期末）如图1，在△ABC中，∠BAC＝75°，∠ACB＝35°，∠ABC的平分线BD交边AC 于点D．（1）求证：△BCD为等腰三角形；（2）若∠BAC的平分线AE交边BC于点E，如图2，求证：BD+AD＝AB+BE；（3）若∠BAC外角的平分线AE交CB延长线于点E，请你探究（2）中的结论是否仍然成立？直接写出正确的结论．29．（2022秋•黄埔区期末）如图，在△ABC中，AD平分∠BAC交BC于D，DE∥AC交AB于E，过E作EF ⊥AD，垂足为H，并交BC延长线于F．（1）求证：AE＝ED；（2）请猜想∠B与∠CAF的大小关系，并证明你的结论．30．（2022秋•涞水县期末）如图，在△ABC中，AB＝AC，∠BAC＝100°，点D在BC边上，△ABD、△AFD 关于AD所在的直线对称，∠FAC的角平分线交BC边于点G，连接FG．（1）求∠DFG的度数．（2）设∠BAD＝θ，当θ为何值时，△DFG为等腰三角形？31．（2022秋•富源县校级期中）如图所示，在△ABC中，D、E分别是AB，AC上的一点，BE与CD交于点O，给出下列四个条件：①∠DBO＝∠ECO；②∠BDO＝∠CEO；③BD＝CE；④OB＝OC．（1）上述四个条件中，哪两个可以判定△ABC是等腰三角形．（2）选择第（1）题中的一种情形为条件，试说明△ABC是等腰三角形；（3）在上述条件中，若∠A＝60°，BE平分∠B，CD平分∠C，则∠BOC的度数？32．如图1，DB为△ABC的角平分线，CE为∠ACB的外角平分线，过点A作AF⊥BD，交射线BD于点F，作AG⊥CE于G，连接EG．（1）求证：FG∥BC；（2）如图2，射线BD与CE相交于点M，若∠M＝45°，AB＝FG＝6，求AD的长．33．（2022秋•平定县期中）如图，已知△ABC和△CDE均为等边三角形，且点B、C、D在同一条直线上，连接AD、BE，交CE和AC分别于G、H点，连接GH．（1）请说出AD＝BE的理由；（2）试说出△BCH≌△ACG的理由；（3）试猜想：△CGH是什么特殊的三角形，并加以说明．34．（2022秋•海淀区校级期中）已知点C为线段AB上一点，分别以AC、BC为边在线段AB同侧作△ACD 和△BCE，且CA＝CD，CB＝CE，∠ACD＝∠BCE，直线AE与BD交于点F，（1）如图①，若∠ACD＝60°，则∠AFB＝；如图②，若∠ACD＝90°，则∠AFB＝；如图③，若∠ACD＝120°，则∠AFB＝；（2）如图④，若∠ACD＝α，则∠AFB＝（用含α的式子表示）；（3）将图④中的△ACD绕点C顺时针旋转任意角度（交点F至少在BD、AE中的一条线段上），变成如图⑤所示的情形，若∠ACD＝α，则∠AFB与α的有何数量关系？并给予证明．35．（2022•承德县模拟）已知：在等边△ABC中，点D、E、F分别为边AB、BC、AC的中点，点G为直线BC上一动点，当点G在CB延长线上时，有结论“在直线EF上存在一点H，使得△DGH是等边三角形”成立（如图①），且当点G与点B、E、C重合时，该结论也一定成立．问题：当点G在直线BC的其它位置时，该结论是否仍然成立？请你在下面的备用图②③④中，画出相应图形并证明相关结论．36．（2022•徐州）如图1，△ABC为等边三角形，面积为S．D1、E1、F1分别是△ABC三边上的点，且AD1＝BE1＝CF1=12AB，连接D1E1、E1F1、F1D1，可得△D1E1F1是等边三角形，此时△AD1F1的面积S1=14S，△D1E1F1的面积S1=14S．（1）当D2、E2、F2分别是等边△ABC三边上的点，且AD2＝BE2＝CF2=13AB时如图2，①求证：△D2E2F2是等边三角形；②若用S表示△AD2F2的面积S2，则S2＝；若用S表示△D2E2F2的面积S2′，则S2′＝．（2）按照上述思路探索下去，并填空：当D n、E n、F n分别是等边△ABC三边上的点，AD n＝BE n＝CF n=1n+1AB时，（n为正整数）△D n E n F n是三角形；若用S表示△AD n F n的面积S n，则S n＝；若用S表示△D n E n F n的面积S n′，则S′n＝．37．（2022春•和平县期末）如图，在等边△ABC中，点D，E分别在边BC、AC上，若CD＝3，过点D作DE ∥AB，过点E作EF⊥DE，交BC的延长线于点F．（1）求证：△CDE为等边三角形；（2）求EF的长．38．（2022秋•韶关期末）已知：如图，△ABC、△CDE都是等边三角形，AD、BE相交于点O，点M、N分别是线段AD、BE的中点．（1）求证：AD＝BE；（2）求∠DOE的度数；（3）求证：△MNC是等边三角形．39．（2022秋•莱芜区期末）如图：在△ABC中，AB＝BC＝AC，AE＝CD，AD与BE相交于点P，BQ⊥AD 于Q．求证：①△ADC≌△BEA；②BP＝2PQ．40．（2022秋•乌海期末）如图．在等边△ABC中，∠ABC与∠ACB的平分线相交于点O，且OD∥AB，OE ∥AC．（1）试判定△ODE的形状，并说明你的理由；（2）线段BD、DE、EC三者有什么关系？写出你的判断过程．41．（2022秋•桐城市期末）如图，已知D是△ABC的边BC上的一点，CD＝AB，∠BDA＝∠BAD，AE是△ABD的中线．（1）若∠B＝60°，求∠C的值；（2）求证：AD是∠EAC的平分线．42．（2022•阳城县模拟）数学课上，李老师出示了如下的题目：“在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED＝EC，如图，试确定线段AE与DB 的大小关系，并说明理由”．小敏与同桌小聪讨论后，进行了如下解答：（1）特殊情况，探索结论当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：AE DB（填“＞”，“＜”或“＝”）．（2）特例启发，解答题目解：题目中，AE与DB的大小关系是：AE DB（填“＞”，“＜”或“＝”）．理由如下：如图2，过点E作EF∥BC，交AC于点F．（请你完成以下解答过程）（3）拓展结论，设计新题在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED＝EC．若△ABC的边长为1，AE＝2，求CD的长（请你直接写出结果）．43．（2022秋•松山区校级月考）如图，点P在等边△ABC内，点D在△ABC外，且∠ABP＝∠ACD，BP＝CD，问：△APD是什么形状三角形，试说明理由．44．（2022春•江岸区校级期中）（1）如图1，△ADE为等边三角形，AD∥EB，且EB＝DC，求证：△ABC 为等边三角形．（2）相信你一定能从（1）中得到启示并在图2中作一个等边△ABC，使三角形的三个定点A、B、C分别在直线l1、l2、l3上，（l1∥l2∥l3且这三条平行线两两之间的距离不相等）．请你画出图形，并写出简要作法．（3）①如图3，当所作△ABC的三个定点A、B、C分别在直线l2、l3、l1上时，如图所示，请结合图形填空：a：先作等边△ADE，延长DE交l3于B点，在l1上截取EC＝，连AC、BC，则△ABC即为所求．b：证明△ABC为等边三角形时，可先证明≌从而为证明等边三角形创造条件．②若使等边△ABC的三个定点A、B、C分别在直线l3、l1、l2上时，请在图4中用类似的方法作出图形，并将构造的全等三角形用阴影标出．（只需画出图形，不要求写作法及证明过程）45．（2022秋•盘龙区校级月考）如图，在△ABC中，AB＝AC，D是三角形外一点，且∠ABD＝60°，BD+DC ＝AB．求证：∠ACD＝60°．46．（2022秋•雨城区校级期中）如图，点O是等边△ABC内一点，∠AOB＝110°，∠BOC＝α，将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．（1）△COD是什么三角形？说明理由；（2）若AO＝n2+1，AD＝n2﹣1，OD＝2n（n为大于1的整数），求α的度数；（3）当α为多少度时，△AOD是等腰三角形？47．（2022•饶平县校级模拟）已知：在△AOB和△COD中，OA＝OB，OC＝OD．（1）如图①，若∠AOB＝∠COD＝60°，求证：①AC＝BD②∠APB＝60°．（2）如图②，若∠AOB＝∠COD＝α，则AC与BD间的等量关系式为，∠APB的大小为（直接写出结果，不证明）48．（2022秋•濠江区校级期中）如图△ABC为等边三角形，直线a∥AB，D为直线BC上任一动点，将一60°角的顶点置于点D处，它的一边始终经过点A，另一边与直线a交于点E．（1）若D恰好在BC的中点上（如图1）求证：△ADE是等边三角形；（2）若D为直线BC上任一点（如图2），其他条件不变，上述（1）的结论是否成立？若成立，请给予证明；若不成立，请说明理由．49．（2022•浙江模拟）如图，等边△ABC的边长为10，点P是边AB的中点，Q为BC延长线上一点，CQ：BC＝1：2，过P作PE⊥AC于E，连PQ交AC边于D，求DE的长？50．（2022秋•东海县校级期中）为了使同学们更好地解答本题，我们提供了思路点拨，你可以依照这个思路填空，并完成本题解答的全过程，当然你也可以不填空，只需按照解答的一般要求，进行解答即可．如图，已知AB＝AD，∠BAD＝60°，∠BCD＝120°，延长BC，使CE＝CD，连接DE，求证：BC+DC＝AC．思路点拨：（1）由已知条件AB＝AD，∠BAD＝60°，可知：△ABD是三角形；（2）同理由已知条件∠BCD＝120°得到∠DCE＝，且CE＝CD，可知；（3）要证BC+DC＝AC，可将问题转化为两条线段相等，即＝；（4）要证（3）中所填写的两条线段相等，可以先证明…．请你完成证明过程：。

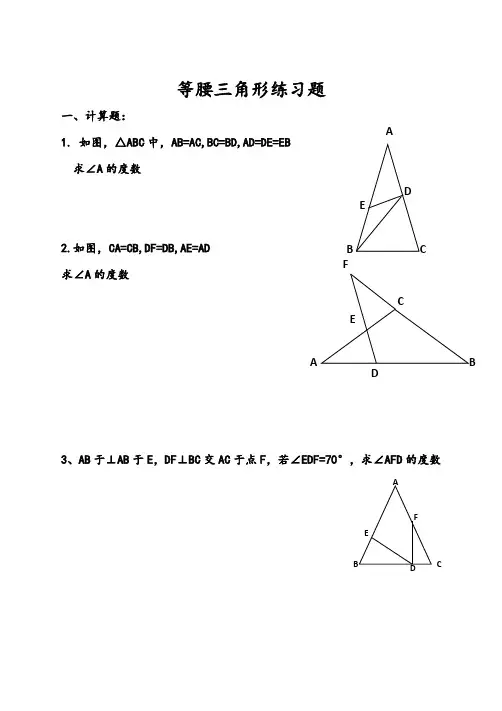
等腰三角形练习题一、计算题：1. 如图，△ABC 中，AB=AC,BC=BD,AD=DE=EB 求∠A 的度数2.如图，CA=CB,DF=DB,AE=AD 求∠A 的度数3、AB 于⊥AB 于E ，DF ⊥BC 交AC 于点F ，若∠EDF=70°，求∠AFD 的度数CFDA4. 如图，△ABC 中，AB=AC,BC=BD=ED=EA 求∠A 的度数5. 如图，△ABC 中，AB=AC ，D 在BC 上, ∠BAD=30°,在AC 上取点E ，使AE=AD, 求∠EDC 的度数6. 如图，△ABC 中，∠C=90°，D 为AB 上一点，作DE ⊥BC 于E ，若BE=AC,BD=21,DE+BC=1,求∠ABC 的度数BBDC7. 如图，△ABC 中，AD 平分∠BAC ，若AC=AB+BD 求∠B ：∠C 的值二、证明题：8. 如图，△DEF 中，∠EDF=2∠E ，FA ⊥DE 于点A ，问：DF 、AD 、AE 间有什么样的大小关系9. 如图，△ABC 中，∠B=60°，角平分线AD 、CE 交于点O求证：AE+CD=ACABCDAD FEABCDE12. 如图,△ABC 中,AB=AC,D 为△ABC 外一点，且∠ABD=∠ACD =60° 求证：CD=AB-BD13.已知：如图，AB=AC=BE ，CD 为△ABC 中AB 边上的中线求证：CD=21CE14. 如图，△ABC 中，∠1=∠2，∠EDC=∠BAC 求证：BD=EDECA BDE1 2 ABCD15. 如图，△ABC 中，AB=AC,BE=CF,EF 交BC 于点G 求证：EG=FG16. 如图，△ABC 中，∠ABC=2∠C ，AD 是BC 边上的高，B 到点E ，使BE=BD求证：AF=FC17. 如图，△ABC 中，AB=AC,AD 和BE 两条高，交于点H ，且AE=BE 求证：AH=2BDABDFECBD18. 如图，△ABC 中，AB=AC, ∠BAC=90°,BD=AB, ∠ABD=30° 求证：AD=DC19. 如图，等边△ABC 中，分别延长BA 至点E ，延长BC 至点D ，使AE=BD 求证：EC=ED20. 如图，四边形ABCD 中，∠BAD+∠BCD=180°，AD 、BC 的延长线交于点F ，DC 、AB 的延长线交于点E ，∠E 、∠F 的平分线交于点H 求证：EH ⊥FHBCDHADCEF一、计算题：1. 如图，△ABC 中，AB=AC,BC=BD,AD=DE=EB 求∠A 的度数设∠ABD 为x,则∠A 为2x 由8x=180° 得∠A=2x=45°2.如图，CA=CB,DF=DB,AE=AD 求∠A 的度数 设∠A 为x, 由5x=180° 得∠A=36°3. 如图，△ABC 中，AB=AC ，D 在BC 上，DE ⊥AB 于E ，DF ⊥BC 交AC 于点F ，若∠EDF=70°， 求∠AFD 的度数 ∠AFD=160°CFDAB4. 如图，△ABC中，AB=AC,BC=BD=ED=EA求∠A的度数设∠A为x∠A=71805. 如图，△ABC中，AB=AC，D在BC上, ∠BAD=30°,在AC上取点E，使AE=AD, 求∠EDC的度数设∠ADE为x∠EDC=∠AED－∠C=15°BB2xx－15°6. 如图，△ABC 中，∠C=90°，D 为AB 上一点，作DE ⊥BC 于E ，若BE=AC,BD=21,DE+BC=1,求∠ABC 的度数 延长DE 到点F,使EF=BC 可证得:△ABC ≌△BFE 所以∠1=∠F 由∠2+∠F=90°, 得∠1+∠F=90°在Rt △DBF 中, BD=21,DF=1所以∠F =∠1=30°7. 如图，△ABC 中，AD 平分∠BAC ，若AC=AB+BD 求∠B ：∠C 的值在AC 上取一点E,使AE=AB 可证△ABD ≌△ADE 所以∠B=∠AEDFABCDE由AC=AB+BD,得DE=EC,所以∠AED=2∠C 故∠B ：∠C=2:1 二、证明题：8. 如图，△ABC 中，∠ABC,∠CAB 的平分线交于点P ，过点P 作DE ∥AB ，分别交BC 、AC 于点D 、E 求证：DE=BD+AE 证明△PBD 和△PEA 是等腰三角形9. 如图，△DEF 中，∠EDF=2∠E ，FA ⊥DE 于点A ，问：DF 、AD 、AE 间有什么样的大小关系 DF+AD=AE在AE 上取点B,使AB=AD10. 如图，△ABC 中，∠B=60°，角平分线AD 、CE 交于点O 求证：AE+CD=AC 在AC 上取点F,使AF=AE 易证明△AOE ≌△AOF, 得∠AOE=∠AOF由∠B=60°，角平分线AD 、CE,CBAD EPAD FEBOABC DEF得∠AOC=120°所以∠AOE=∠AOF=∠COF=∠COD=60° 故△COD ≌△COF,得CF=CD 所以AE+CD=AC11. 如图，△ABC 中，AB=AC, ∠A=100°，BD 平分∠ABC, 求证：BC=BD+AD延长BD 到点E,使BE=BC,连结CE 在BC 上取点F,使BF=BA 易证△ABD ≌△FBD,得AD=DF 再证△CDE ≌△CDF,得DE=DF 故BE=BC=BD+AD也可:在BC 上取点E,使BF=BD,连结DF 在BF 上取点E,使BF=BA,连结DE先证DE=DC,再由△ABD ≌△EBD,得AD=DE,最后证明DE=DF 即可 12. 如图,△ABC 中,AB=AC,D 为△ABC 外一点，且∠ABD=∠ACD =60° 求证：CD=AB-BD在AB 上取点E ，使BE=BD ， 在AC 上取点F ，使CF=CD得△BDE 与△CDF 均为等边三角形， 只需证△ADF ≌△AEDACFACEFABC DEF13.已知：如图，AB=AC=BE ，CD 为△ABC 中AB 边上的中线求证：CD=21CE延长CD 到点E,使DE=CD.连结AE 证明△ACE ≌△BCE14. 如图，△ABC 中，∠1=∠2，∠EDC=∠BAC 求证：BD=ED在CE 上取点F,使AB=AF 易证△ABD ≌△ADF, 得BD=DF,∠B=∠AFD由∠B+∠BAC+∠C=∠DEC+∠EDC+∠C=180° 所以∠B=∠DEC 所以∠DEC=∠AFD 所以DE=DF,故BD=ED15. 如图，△ABC 中，AB=AC,BE=CF,EF 交BC 于点G 求证：EG=FGECA BDE1 2FF16. 如图，△ABC 中，∠ABC=2∠C ，AD 是BC 边上的高，B 到点E ，使BE=BD 求证：AF=FC17. 如图，△ABC 中，AB=AC,AD 和BE 两条高，交于点H ，且AE=BE 求证：AH=2BD由△AHE ≌△BCE,得BC=AH18. 如图，△ABC 中，AB=AC, ∠BAC=90°,BD=AB,∠ABD=30° 求证：AD=DC作AF ⊥BD 于F,DE ⊥AC 于E 可证得∠DAF=DAE=15°, 所以△ADE ≌△ADF 得AF=AE,由AB=2AF=2AE=AC, 所以AE=EC,因此DE 是AC 的中垂线,所以AD=DCABDFE CBD19. 如图，等边△ABC 中，分别延长BA 至点E ，延长BC 至点D ，使AE=BD 求证：EC=ED延长BD 到点F,使DF=BC, 可得等边△BEF,只需证明△BCE ≌△FDE 即可20. 如图，四边形ABCD 中，∠BAD+∠BCD=180°，AD 、BC 的延长线交于点F ，DC 、AB 的延长线交于点E ，∠E 、∠F 的平分线交于点H 求证：EH ⊥FH 延长EH 交AF 于点G 由∠BAD+∠BCD=180°, ∠DCF+∠BCD=180° 得∠BAD=∠DCF, 由外角定理,得∠1=∠2, 故△FGM 是等腰三角形 由三线合一,得EH ⊥BCDFABDCEFHG 12 M。

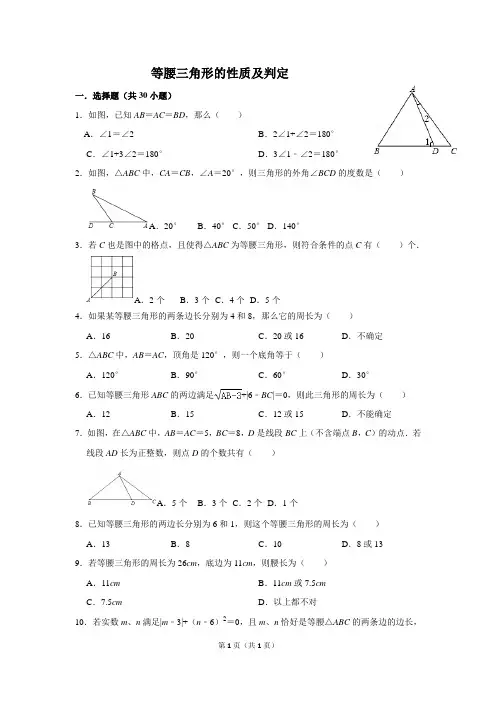
等腰三角形的性质及判定一．选择题（共30小题）1．如图，已知AB＝AC＝BD，那么（）A．∠1＝∠2B．2∠1+∠2＝180°C．∠1+3∠2＝180°D．3∠1﹣∠2＝180°2．如图，△ABC中，CA＝CB，∠A＝20°，则三角形的外角∠BCD的度数是（）A．20°B．40°C．50°D．140°3．若C也是图中的格点，且使得△ABC为等腰三角形，则符合条件的点C有（）个．A．2个B．3个C．4个D．5个4．如果某等腰三角形的两条边长分别为4和8，那么它的周长为（）A．16B．20C．20或16D．不确定5．△ABC中，AB＝AC，顶角是120°，则一个底角等于（）A．120°B．90°C．60°D．30°6．已知等腰三角形ABC的两边满足+|6﹣BC|＝0，则此三角形的周长为（）A．12B．15C．12或15D．不能确定7．如图，在△ABC中，AB＝AC＝5，BC＝8，D是线段BC上（不含端点B，C）的动点．若线段AD长为正整数，则点D的个数共有（）A．5个B．3个C．2个D．1个8．已知等腰三角形的两边长分别为6和1，则这个等腰三角形的周长为（）A．13B．8C．10D．8或139．若等腰三角形的周长为26cm，底边为11cm，则腰长为（）A．11cm B．11cm或7.5cmC．7.5cm D．以上都不对10．若实数m、n满足|m﹣3|+（n﹣6）2＝0，且m、n恰好是等腰△ABC的两条边的边长，则△ABC的周长是（）A．12B．15C．12或15D．911．已知△ABC中，∠ACB＝90°，AC＝8，BC＝6．在射线BC上取一点D，使得△ABD 为等腰三角形，这样的等腰三角形有几个？（）A．2个B．3个C．4个D．5个12．若等腰三角形的一边长等于6，另一边长等于4，则它的周长等于（）A．15或17B．16C．14D．14或1613．若等腰三角形的顶角为70°，则它的一个底角度数为（）A．70°或55°B．55°C．70°D．65°14．如图，在3×3的正方形网格中，点A、B在格点上，要找一个格点C，使△ABC是等腰三角形（AB是其中一腰），则图中符合条件的格点有（）A．2个B．3个C．4个D．5个15．等腰三角形的一个角是30°，则这个等腰三角形的底角为（）A．75°B．30°C．75°或30°D．不能确定16．如图，在△ABC中，AB＝AC，∠A＝36°，BD平分∠ABC交AC于E，CD平分∠ACB 交BE于D，图中等腰三角形的个数是（）A．3个B．4个C．5个D．6个17．如图，直线l1，l2相交于点A，点B是直线外一点，在直线l1，l2上找一点C，使△ABC 为一个等腰三角形，满足条件的点C有（）A．2个B．4个C．6个D．8个18．如图，已知OA＝OB＝OC，BC∥AO，若∠A＝36°，则∠B等于（）A．54°B．60°C．72°D．76°19．如图，△ABC中，∠B＝∠C，BD＝CD，则下列判断不一定正确的是（）A．AB＝AC B．AD⊥BCC．∠BAD＝∠CAD D．△ABC是等边三角形20．等腰三角形的边长为2和3，那么它的周长为（）A．8B．7C．8或7D．以上都不对21．等腰三角形的顶角是40°，则它的底角是（）A．55°B．70°C．40°或70°D．55°或70°22．如图所示，在三角形ABC中，AB＝AC，∠BAC＝108°，在BC上分别取点D，E使∠BAD＝∠B，∠CAE＝∠C，则图中的等腰三角形有（）A．3个B．4个C．5个D．6个23．三角形三个内角的比是∠A：∠B：∠C＝1：1：2，则△ABC是（）A．等腰三角形B．等腰直角三角形C．等边三角形D．不能确定24．小方画了一个有两边长为3和5的等腰三角形，则这个等腰三角形的周长为（）A．11B．13C．8D．11或1325．如图钢架中，∠A＝a，焊上等长的钢条P1P2，P2P3，P3P4，P4P5…来加固钢架．若P1A ＝P1P2，且恰好用了4根钢条，则α的取值范围是（）A．15°≤a＜18°B．15°＜a≤18°C．18°≤a＜22.5°D．18°＜a≤22.5°26．已知等腰△ABC中，∠A＝120°，则底角的大小为（）A．60°B．30°或120°C．120°D．30°27．如图，在△ABC中，AB＝AC＝13，该三角形的面积为65，点D是边BC上任意一点，则点D分别到边AB，AC的距离之和等于（）A．5B．6.5C．9D．1028．如图，直线L1∥L2，点A、B在L1上，点C在L2上，若AB＝AC、∠ABC＝70°，则∠1的大小为（）A．20°B．40°C．35°D．70°29．若等腰△ABC中有一个内角为40°，则这个等腰三角形的一个底角的度数为（）A．40°B．100°C．40°或100°D．40°或70°30．等腰三角形的周长为18，其中一条边的长为8，则另两条边的长是（）A．5、5B．2、8C．5、5或2、8D．以上结果都不对二．填空题（共15小题）31．等腰三角形的一个内角为30°，那么其它两个角的度数为______．32．已知AD是△ABC的高，若AB＝AC，BC＝4，则CD＝______，33．如图，在平面直角坐标系中，点A，B分别在y轴和x轴上，∠ABO＝60°，在y轴上找一点P，使△P AB是等腰三角形，则符合条件的P点共有______个．34．如图，直线a、b相交于点O，∠1＝50°，点A在直线a上，直线b上存在点B，使以点O、A、B为顶点的三角形是等腰三角形，这样的B点有______．35．若等腰三角形的两边的长分别为3和10，则它的周长为______．36．如果等腰三角形的两边长分别是6、8，那么它的周长是______．37．如图，Rt△ABC中，AC⊥BC，AE＝AO，BF＝BO，则∠EOF的度数是______．38．等腰△ABC的边长分别为6和8，则△ABC的周长为______．39．已知等腰三角形中顶角的度数是底角的3倍，那么底角的度数是______．40．已知等腰三角形的周长为20，底长为x，则x的取值范围是______．41．用一条长为20cm的细绳围成一个等腰三角形，已知一边长是另一边长的2倍，则腰长为______cm．42．如图，△ABC中，AB＝AC，D、E是BC边上两点，AD＝AE，BE＝6，DE＝4，则EC ＝______．43．如图，△ABC中，AB＝AC，∠C═30°，DA⊥BA于点A，BC＝16cm，则AD＝______．44．如图，AB＝AC＝CD，∠BAC＝56°，则∠B＝______，∠D＝______．45．如图，已知每个小方格的边长为1，A，B两点都在小方格的顶点上，请在图中找一个顶点C，使△ABC为等腰三角形，则这样的顶点C有______个．三．解答题（共5小题）46．如图，在△ABC中，∠C＝∠ABC＝2∠A，BD是AC边上的高，求∠DBC的度数．47．在△ABC中，AD平分∠BAC，E是BC上一点，BE＝CD，EF∥AD交AB于F点，交CA的延长线于P，CH∥AB交AD的延长线于点H，①求证：△APF是等腰三角形；②猜想AB与PC的大小有什么关系？证明你的猜想．48．如图，在△ABC中，AB＝AC，点D在BC上，且BD＝BA，点E在BC的延长线上，且CE＝CA．（1）若∠BAC＝90°（图1），求∠DAE的度数；（2）若∠BAC＝120°（图2），求∠DAE的度数；（3）当∠BAC＞90°时，探求∠DAE与∠BAC之间的数量关系，直接写出结果．49．已知等腰三角形的周长为24cm，其中两边之差为6cm，求这个等腰三角形的腰长．50．如图，在△ABC中，AB＝AC，CE平分∠ACB，EC＝EA．（1）求∠A的度数；（2）若BD⊥AC，垂足为D，BD交EC于点F，求∠1的度数．等腰三角形的性质及判定参考答案与试题解析一．选择题（共30小题）1．解：∵AB＝AC＝BD，∴∠B＝∠C，∠BAD＝∠1，∵∠1＝∠C+∠2，∴∠BAD＝∠1＝∠C+∠2，∵∠B+∠1+∠BAD＝180°，∴∠C+2∠1＝180°，∵∠C＝∠1﹣∠2，∴∠1﹣∠2+2∠1＝180°，即3∠1﹣∠2＝180°．故选：D．2．解：∵CA＝CB，∠A＝20°，∴∠B＝∠A＝20°，∴∠BCD＝∠A+∠B＝40°，故选：B．3．解：如图：分情况讨论．①AB为等腰△ABC底边时，符合条件的C点有2个；②AB为等腰△ABC其中的一条腰时，符合条件的C点有2个．故选：C．4．解：若4为腰，8为底边，此时4+4＝8，不能构成三角形，故4不能为腰；若4为底边，8为腰，此时三角形的三边分别为4，8，8，周长为4+8+8＝20，综上三角形的周长为20．故选：B．5．解：∵△ABC中，AB＝AC，顶角是120°，∴∠B＝∠C，∠A＝120°∵∠A+∠B+∠C＝180°，∴∠B＝∠C＝＝30°，故选：D．6．解：∵+|6﹣BC|＝0，∴AB﹣3＝0，6﹣BC＝0，解得AB＝3，BC＝6，（1）若AB是腰长，BC为底，则三角形的三边长为：3、3、6，不能能组成三角形，（2）若AB是底边长，BC为腰，则三角形的三边长为：3、6、6，能组成角形，周长为3+6+6＝15．故此三角形的周长为15．故选：B．7．解：过A作AE⊥BC，∵AB＝AC，∴EC＝BE＝BC＝4，∴AE＝＝3，∵D是线段BC上的动点（不含端点B、C）．∴3≤AD＜5，∴AD＝3或4，∵线段AD长为正整数，∴AD的可以有三条，长为4，3，4，∴点D的个数共有3个，故选：B．8．解：当等腰三角形的腰为1时，三边为1，1，6，1+1＝2＜6，三边关系不成立，当等腰三角形的腰为6时，三边为1，6，6，三边关系成立，周长为1+6+6＝13．故选：A．9．解：∵11cm是底边，∴腰长＝（26﹣11）＝7.5cm，故选：C．10．解：|m﹣3|+（n﹣6）2＝0，∴m﹣3＝0，n﹣6＝0，解得m＝3，n＝6，当m＝3作腰时，三边为3，3，6，不符合三边关系定理；当n＝6作腰时，三边为3，6，6，符合三边关系定理，周长为：3+6+6＝15．故选：B．11．解：在Rt△ABC中，AB＝＝10，①如图1，当AB＝AD＝10时，CD＝CB＝6时，CD＝CB＝6，得△ABD的等腰三角形．②如图2，当AB＝BD＝10时，△ABD是等腰三角形；③如图3，当AB为底时，AD＝BD时，△ABD是等腰三角形．故选：B．12．解：当4为底边时，腰长为6，则这个等腰三角形的周长＝4+6+6＝16；当6为底边时，腰长为4，则这个等腰三角形的周长＝4+4+6＝14；故选：D．13．解：∵等腰三角形的顶角为70°，∴它的一个底角度数为（180°﹣70°）＝55°，故选：B．14．解：如图所示：由勾股定理得：AB＝＝，①若AB＝BC，则符合要求的有：C1，C2，C3共4个点；②若AB＝AC，则符合要求的有：C4，C5共2个点；若AC＝BC，则不存在这样格点．∴这样的C点有5个．故选：D．15．解：①当这个角为顶角时，底角＝（180°﹣30°）÷2＝75°；②当这个角是底角时，底角＝30°；故选：C．16．解：∵AB＝AC，∠A＝36°，∴△ABC是等腰三角形．∴∠C＝∠ABC＝72°．∵BD平分∠ABC交AC于E，∴∠ABE＝∠EBC＝36°，∵∠A＝∠ABE＝36°，∴△ABE是等腰三角形．∵∠BEC＝∠A+∠ABE＝72°＝∠C，∴△BEC是等腰三角形．∵∠DBC＝∠DCB＝36°，∴△BCD是等腰三角形，∵∠EDC＝∠DBC+∠DCB＝72°＝∠DEC，∴△CDE是等腰三角形，∴共有5个等腰三角形．故选：C．17．解：以A为圆心，AB长为半径画弧，交l1、l2于4个点；以B为圆心，AB长为半径画弧交l1、l2于2个点，再作AB的垂直平分线交l1、l2于2个点，共有8个点，故选：D．18．解：∵OA＝OC，∴∠ACO＝∠A＝36°，∵BC∥AO，∴∠BCA＝∠A＝36°，∴∠BCO＝72°，∵OB＝OC，∴∠B＝72°．故选：C．19．解：∵∠B＝∠C，∴AB＝AC，∴选项A不符合题意；∵∠B＝∠C，∴AB＝AC，BD＝CD，∴AD⊥BC，∠BAD＝∠CAD，∴选项B、选项C不符合题意；当△ABC中有一个角为60°时，△ABC是等边三角形，∴选项D符合题意；故选：D．20．解：分两种情况讨论：当这个三角形的底边是2时，三角形的三边分别是2、3、3，能够组成三角形，则三角形的周长是8；当这个三角形的底边是3时，三角形的三边分别是2、2、3，能够组成三角形，则三角形的周长是7．故等腰三角形的周长为8或7．故选：C．21．解：因为等腰三角形的两个底角相等，又因为顶角是40°，所以其底角为＝70°．故选：B．22．解：∵AB＝AC，∠BAC＝108°，∴∠B＝∠C＝36°，△ABC是等腰三角形，∵∠BAD＝∠B＝36°，∴△ABD是等腰三角形，∵∠CAE＝∠C＝36°，∴△AEC是等腰三角形，∴∠ADC＝∠DAC＝72°，∴△ADC是等腰三角形，同理，△ABE是等腰三角形，∴∠ADE＝∠AED＝72°，∴△ADE是等腰三角形，故选：D．23．解：∵∠A+∠B+∠C＝180°，∠A：∠B：∠C＝1：1：2，∴∠A＝∠B＝45°，∠C＝90°．则该三角形的等腰直角三角形．故选：B．24．解：由题意知，应分两种情况：（1）当腰长为3时，能构成三角形，周长＝2×3+5＝11；（2）当腰长为5时，能构成三角形，周长＝2×5+3＝13．故选：D．25．解：∵AP1＝P1P2，P1P2＝P2P3，P3P4＝P2P3，P3P4＝P4P5，∴∠A＝∠P1P2A，∠P2P1P3＝∠P2P3P1，∠P3P2P4＝∠P3P4P2，∠P4P3P5＝∠P4P5P3，∴∠P3P5P4＝4∠A＝4α°，∵要使得这样的钢条只能焊上4根，∴∠P5P4B＝5α°，由题意，∴18°≤α＜22.5°．故选：C．26．解：∵在等腰△ABC中，∵∠A＝120°，∴∠A为等腰三角形的顶角，∴∠B＝∠C，∵∠A＝120°，∴∠B＝∠C＝30°；故选：D．27．解：连接AD，∵在△ABC中，AB＝AC＝13，该三角形的面积为65，∴三角形ABC的面积＝△ABD的面积+△ACD的面积＝AB•DN+AC•DM＝AB•（DN+DM）＝×13×（DN+DM）＝65，解得：DN+DM＝10．故选：D．28．解：∵AB＝AC，∴∠ACB＝∠ABC＝70°，∵直线l1∥l2，∴∠1+∠ACB+∠ABC＝180°，∴∠1＝180°﹣∠ABC﹣∠ACB＝180°﹣70°﹣70°＝40°．故选：B．29．解：当40°的角为等腰三角形的顶角时，底角的度数＝＝70°；当40°的角为等腰三角形的底角时，其底角为40°，故它的底角的度数是70°或40°．故选：D．30．解：当腰长为8时，底长为：18﹣8×2＝2；2+8＞8，能构成三角形；当底长为8时，腰长为：（18﹣8）÷2＝5；5+5＞8，能构成三角形．故另两条边的长是5、5或2、8．故选：C．二．填空题（共15小题）31．解：①30°是顶角，则底角＝（180°﹣30°）＝75°；②30°是底角，则顶角＝180°﹣30°×2＝120°．∴另两个角的度数分别是75°、75°或30°、120°．故答案为75°、75°或30°、120°．32．解：∵AD是△ABC的高，AB＝AC，∴CD＝BD＝BC＝4＝2，故答案为：2．33．解：①当AB＝AP时，在y轴上有2点满足条件的点P．②当AB＝BP时，在y轴上有1点满足条件的点P．③当AP＝BP时，在y轴上有一点满足条件的点P．综上所述：符合条件的点P共有4个．故答案为：434．解：要使△OAB为等腰三角形分三种情况讨论：①当OB＝AB时，作线段OA的垂直平分线，与直线b的交点为B，此时有1个；②当OA＝AB时，以点A为圆心，OA为半径作圆，与直线b的交点，此时有1个；③当OA＝OB时，以点O为圆心，OA为半径作圆，与直线b的交点，此时有2个，1+1+2＝4，故答案为：435．解：（1）若3为腰长，10为底边长，由于3+3＜10，则三角形不存在；（2）若10为腰长，则符合三角形的两边之和大于第三边．所以这个三角形的周长为10+10+3＝23．故答案为：23．36．解：当6是腰长时，周长＝6+6+8＝20；当8是腰长时，周长＝6+8+8＝22．故周长是20或22．故答案为：20或22．37．解：∵Rt△ABC中，AC⊥BC，∴∠A+∠B＝90°，∵AE＝AO，BF＝BO，∴∠AOE＝∠AEO＝，∠BOF＝∠BFO＝，∴∠EOF＝180°﹣∠AOE﹣∠BOF＝180°﹣（+）＝（∠A+∠B）＝45°，故答案为45°．38．解：当6为底时，三角形的三边为6，8、8可以构成三角形，周长为6+8+8＝22；当8为底时，三角形的三边为8，6、6可以构成三角形，周长为8+6+6＝20．则△ABC的周长为22或20．故答案为：22或20．39．解：设底角为x°，则顶角为3x°，根据题意得：x+x+3x＝180解得：x＝36；故答案为：36°．40．解：根据三角形的三边关系，x＜（20﹣x），解得x＜10，∴x的取值范围是0＜x＜10．故答案为：0＜x＜10．41．解：设较短的边长为xcm，则较长的边长为2xcm，①若较短的边为底边，较长的边为腰，则x+2x+2x＝20，解得x＝4，此时三角形三边长分别为4cm，8cm，8cm，能组成三角形；②若较短的边为腰，较长的边为底边，则x+x+2x＝20，解得x＝5，此时三角形三边长分别为5cm，5cm，10cm，∵5+5＝10，∴不满足三角形任意两边之和大于第三边，故不能围成三角形；综上所述，等腰三角形的腰长8cm，故答案为8．42．证明：∵BE＝6，DE＝4，∴BD＝BE﹣DE＝2，过A作AP⊥BC于P，∵AB＝AC，AP⊥BC，∴BP＝CP，同理有DP＝EP，∴CE＝BD＝2，故答案为：2．43．解：∵AB＝AC，∴∠B＝∠C＝30°，∴∠BAC＝180°﹣2×30°＝120°，∵DA⊥BA，∴∠BAD＝90°，∴∠CAD＝120°﹣90°＝30°，∴∠CAD＝∠C，∴AD＝CD，在Rt△ABD中，∵∠B＝30°，∠BAD＝90°，∴BD＝2AD，∴BC＝BD+CD＝2AD+AD＝3AD，∵BC＝16cm，∴AD＝cm，故答案为：cm．44．解：∵AB＝AC，∠BAC＝56°∴∠B＝∠ACB＝＝62°，∵AC＝CD，∴∠CAD＝∠D，∵∠ACB＝∠CAD+∠D，∴∠D＝∠ACB＝31°，故答案为：62°，31°．45．解：当AB为底时，作AB的垂直平分线，可找出格点C的个数有5个，当AB为腰时，分别以A、B点为顶点，以AB为半径作弧，可找出格点C的个数有3个；∴这样的顶点C有8个．故答案为：8．三．解答题（共5小题）46．解：∵∠C＝∠ABC＝2∠A，∴∠C+∠ABC+∠A＝5∠A＝180°，∴∠A＝36°．则∠C＝∠ABC＝2∠A＝72°．又BD是AC边上的高，则∠DBC＝90°﹣∠C＝18°．47．①证明：∵EF∥AD，∴∠1＝∠4，∠2＝∠P，∵AD平分∠BAC，∴∠1＝∠2，∴∠4＝∠P，∴AF＝AP，即△APF是等腰三角形；②AB＝PC．理由如下：证明：∵CH∥AB，∴∠5＝∠B，∠H＝∠1，∵EF∥AD，∴∠1＝∠3，∴∠H＝∠3，在△BEF和△CDH中，∵，∴△BEF≌△CDH（AAS），∴BF＝CH，∵AD平分∠BAC，∴∠1＝∠2，∴∠2＝∠H，∴AC＝CH，∴AC＝BF，∵AB＝AF+BF，PC＝AP+AC，∴AB＝PC．48．解：（1）如图1，∵AB＝AC，∠BAC＝90°，∴∠B＝∠ACB＝45°，∵BD＝BA，∴∠BAD＝∠BDA＝（180°﹣∠B）＝67.5°，∵CE＝CA∴∠CAE＝∠E＝∠ACB＝22.5°，∴∠BAE＝180°﹣∠B﹣∠E＝112.5°，∴∠DAE＝∠BAE﹣∠BAD＝45°，（2）如图2，∵AB＝AC，∠BAC＝90°，∴∠B＝∠ACB＝30°，∵BA＝BD，∴∠BAD＝∠BDA＝75°，∴∠DAC＝45°，∵CA＝CE，∴∠E＝∠CAE＝15°，∴∠DAE＝∠DAC+∠CAE＝60°；（3）∠DAE＝∠BAC，理由：设∠CAE＝x，∠BAD＝y，则∠B＝180°﹣2y，∠E＝∠CAE＝x，∴∠BAE＝180°﹣∠B﹣∠E＝2y﹣x，∴∠DAE＝∠BAE﹣∠BAD＝2y﹣x﹣y＝y﹣x，∠BAC＝∠BAE﹣∠CAE＝2y﹣x﹣x＝2y﹣2x ∴∠DAE＝∠BAC．49．解：设三角形的腰为x，底为y，根据题意得或，解得或，又知6+6＜12，不能构成三角形，即等腰三角形的腰长为：10cm．50．解：（1）∵EA＝EC，∴设∠A＝∠2＝x，∵EC平分∠ACB，∴∠ACB＝2x，∵AB＝AC，∴∠ABC＝∠ACB＝2x，在△ABC中，∴x+2x+2x＝180°，∴x＝36°，∴∠A＝36°；（2）∵∠A＝∠2，∴∠2＝36°，∵BD⊥AC，∴∠DFC＝90°﹣36°＝54°，∴∠1＝∠DFC＝54°．第1页（共1页）。

等腰三角形证明1.如图，已知：点D,E在△ABC的边BC上，AB=AC,AD=AE,求证：BD=CE2. 如图：△ABC中,AB=AC,PB=PC．求证：AD⊥BC3. 已知：如图,BE和CF是△ABC的高线,BE=CF,H是CF、BE的交点．求证：HB=HC4. 如图,在△ABC中,AB=AC,E为CA延长线上一点,ED⊥BC于D交AB于F. 求证:△AEF为等腰三角形.5. 如图,△ABC中,D在BC延长线上,且AC=CD,CE是△ACD的中线,CF平分∠ACB,交AB于F,求证:(1)CE⊥CF;(2)CF∥AD.6.如图：Rt△ABC中,∠C=90°,∠A=22.5°,DC=BC, DE⊥AB．求证：AE=BE．7.已知:如图，△BDE是等边三角形，A在BE延长线上，C在BD的延长线上，且AD=AC。

求证：DE+DC=AE。

等腰三角形练习题答案1. 证：作AM⊥BC于M∵AD=AE,∴DM=EM∵AB=AC,∴BM=CM∴BM－DM=CM－EM∴BD=CE2. 证明：在△ABP和△ACP中∵AB=AC,BP=PC,AP=AP∴△ABP≌△ACP (SSS)∴∠BAP=∠CAP∴AD⊥BC(等腰三角形顶角平分线又是底边的垂线)3. 证明：∵△ABC是等边三角形∴AB=AC,∠BAC=60°在△ABD和△ACE中∵AB=AC,∠1=∠2,BD=CE∴△ABD≌△ACE (SAS)∴AD=AE,∠BAD=∠CAE=60°∴在△ADE中∵AD=AE,∠DAE=60°∴△ADE为等边三角形．4. 证明：连结AC和AD在△ABC和△AED中AB=AE BC=ED ∠B=∠E∴△ABC≌△AED (SAS)∴∠ACB=∠ADE,AC=AD∴△ACD是等腰三角形∴∠ACD=∠ADC;∠BCA=∠CDE∴∠C=∠D5. 证明：∵BE、CF是△ABC的高线．∴∠1=∠2=90°∴△BCF和△CBE都是Rt△．在Rt△BCF和Rt△CBE中∵CF=BE,BC=CB∴Rt△BCF≌Rt△CBE∴∠3=∠4在△HBC中∵∠3=∠4∴HB=HC(同一三角形中,等角对等边)6. 证明:∵AE=AD,∠1=∠2,∠A公共角∴△AEF≌△ADC (AAS)∴AB=AC,EB=DC∴∠ABC=∠ACB∴∠3=∠4,BF=CF∴DF=EF7. 证明:∵AB=AC∴∠B=∠C∵ED⊥BC∴∠B+∠BFD=∠B+∠EFA=90°∠C+∠E=90°。

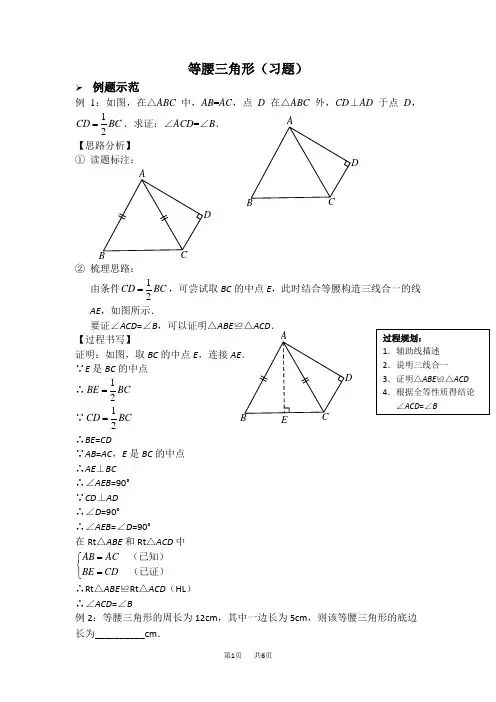
等腰三角形（习题）例题示范例1：如图，在△ABC 中，AB =AC ，点D 在△ABC 外，CD ⊥AD 于点D ，12CD BC =．求证：∠ACD =∠B ． 【思路分析】① 读题标注：② 梳理思路： 由条件12CD BC =，可尝试取BC 的中点E ，此时结合等腰构造三线合一的线AE ，如图所示．要证∠ACD =∠B ，可以证明△ABE ≌△ACD ．【过程书写】证明：如图，取BC 的中点E ，连接AE ．∵E 是BC 的中点 ∴12BE BC = ∵12CD BC = ∴BE =CD∵AB =AC ，E 是BC 的中点∴AE ⊥BC∴∠AEB =90°∵CD ⊥AD∴∠D =90°∴∠AEB =∠D =90°在Rt △ABE 和Rt △ACD 中AB AC BE CD =⎧⎨=⎩（已知）（已证）∴Rt △ABE ≌Rt △ACD （HL ）∴∠ACD =∠B例2：等腰三角形的周长为12cm ，其中一边长为5cm ，则该等腰三角形的底边长为__________cm ．AC D【思路分析】等腰三角形一边长为5cm，这一边可能是底，也可能是腰，故需分类讨论：①如果5cm为底，则根据周长为12cm，可知腰长为3.5cm．此时两边之和大于第三边，这个三角形存在．②如果5cm为腰，则根据周长为12cm，可知底边长为2cm．此时两边之和大于第三边，这个三角形存在．综上，该等腰三角形的底边长为5cm或2cm．巩固练习1.已知：如图，在△ABC中，AB=AC，∠A=80°，求∠C的度数．2.如图，在△ABC中，AB=AC，BE∥AC，∠BDE=100°，∠BAD=70°，则∠E=______．第2题图第3题图3.已知：如图，在△ABC中，AB=AC，D为AB边上一点，若CD=AD=BC，则∠A=_________．4.如图，在△ABC中，∠ABC的平分线和∠ACB的平分线相交于点E，过点E作MN∥BC，交AB于点M，交AC于点N．若BM+CN=9，则线段MN的长为（）A．6 B．7 C．8 D．95.已知：如图，在△ABC中，AB=AC，AD是BC边上的中线，点P在AD上．求证：PB=PC．6.已知：如图，B，D，E，C在同一直线上，AB=AC，AD=AE．求证：BD=CE．7.已知等腰三角形的两边长分别为4和8，则该等腰三角形的周长为_________________．8.若等腰三角形的一个角比另一个角大30°，则该等腰三角形的顶角的度数为_____________．9.已知：如图，线段AB的端点A在直线l上，AB与l的夹角是30°，请在直线l上另找一点C，使△ABC是等腰三角形．这样的点能找几个？请找出所有符合条件的点．思考小结1.要证明边相等或角相等，可以考虑两种思路：①如果边或者角在两个三角形里面，则证明两个三角形__________；②如果边或角在一个三角形里面，证明三角形是_______三角形．2.将两个含30°角的三角板如图放置，则△ABD是_________三角形（“等腰”或“等边”），故AB_____BD，BC=____BD，所以BC=____AB，从而得到对于含有30°角的直角三角形，30°角所对的直角边是斜边的_______．【参考答案】巩固练习1.50°2.50°3.36°4. D5.证明略提示：利用等腰三角形三线合一的性质，得AD垂直平分BC，从而得到PB=PC 6.证明略提示：根据等边对等角可得∠B=∠C，∠ADE=∠AED，进而可得∠BAD=∠CAE，从而证明△ABD≌△ACE，根据全等三角形对应边相等，可得BD=CE7.208.80°或40°9.这样的点能找4个，作图略 思考小结1.①全等②等腰2.等边，=，12，12，一半。

等腰三角形的判定家庭作业 1.（5分）CD 是等腰直角三角形ABC 斜边上的高，写出图中的等腰三角形 .2.（5分）已知等腰三角形ABC 中，AB=AC ，D 为BC 边上一点，连接AD ，若△ACD 和△ABD 都是等腰三角形，则 ∠C 的度数是 .3.（5分）如图，在△ABC 中，AB=AC ， BF 与CF 是角平分线且交于点F ，DE ∥BC，若BD+CE=9，则线段DE 的长为 （ ）A ．6个B ．7个C ．8个D ．9个4.（5分）如图，△ABC 中AB=AC ，∠A=36°，BD 平分∠ABC 交AC 于D ，则图中的等腰三角形有（ ）A ．1个B ．2个C ．3个D ．4个 5.（5分）如图，O 是∠ABC ，∠ACB 的平分线的交点， OD ∥AB ，交BC 于D ，OE ∥AC 交BC 于E ， 若BC=10cm ，则△DOE 的周长为( ) A .8cm B .9cmC .10cmD .11cm6.（10分）已知，OD 平分∠AOB ，ED ∥OB ，求证：EO=ED.7.（12分）如图,在ΔABC 中,BD 平分∠ABC ，CD 平分∠ACB 的外角，且EF ∥BC. 请你猜想：线段EF 、BE 和CF 的关系如何？并证明.8.（12分）如图，在△ABC 中BC=AC ，CD ⊥AB ，DE ∥BC ，试说明△ADE 和△CED 都是等腰三角形.9.（16分）(1)如图，∠BAC=90°，AD ⊥BC ，垂足为D ，BE 平分∠ABC ，交AC 于E ，交AD 于F.试判断△AEF 的形状，并说明理由；(2)如图，已知∠BAC=90°，AD ⊥BC ，垂足为D ，AE=AF.试说明BE 平分∠ABC.10.（12分）已知，如图，CE 是△ABC 的角平分线，过点E 画BC 的平行线，交AC于点D ，交外角∠ACG 的平分线于点F.试证明DE=DF.11.（13分）已知，如图，AD 平分∠BAC ，∠B ＝2∠C ，求证：AC ＝AB+BD ．尖子班补充作业1.已知：如图，OA 平分∠BAC ，∠1=∠2（第3题） A B CD EF B 第1题 A B C D第4题A B C O D E 第5题 A BO D E 第6题 AB C M E F D第7题ECA B C D EF第9题A B C D E F G 第10题A B CD 第11题求证：△ABC 是等腰三角形.2.已知：如图，在△ABC 中，∠ACB ＝90°，高CD 和角平分线AE 交于点F ，FG ∥AB 交BC 于点G ， 求证：CG ＝BGCADBE F G 第2题答案（供参考）家庭作业1.△ABC、△ACD和△BCD2.45°或36°3.D4.C5.C6.略7.关系是：EF=BE－CF，证明提示：证明BE=ED，FC=FD8.略9.⑴△AEF是等腰三角形，提示：∠AFE=∠ABE+∠BAD，∠AEF=∠EBC+∠C可证∠BAD=∠C而∠ABE=∠EBC，所以∠AFE=∠AEF⑵略10.提示：证明DE=DC，DC=DF11.提示：在AC上截取AE=AB，连接DE，证明△ABD≌△AED，则BD=DE，再证ED=EC尖子班补充作业1.提示：过O点作OG⊥AB，OH⊥AC，G、H是垂足，证明△OGB≌△OHC，则∠ABO=∠ACO，因此，可证∠ABC=∠ACB2.提示：过E点作EH⊥AC，H是垂足，证明△CFG≌△EHB，注意利用家庭作业的第9题⑴的结论.。

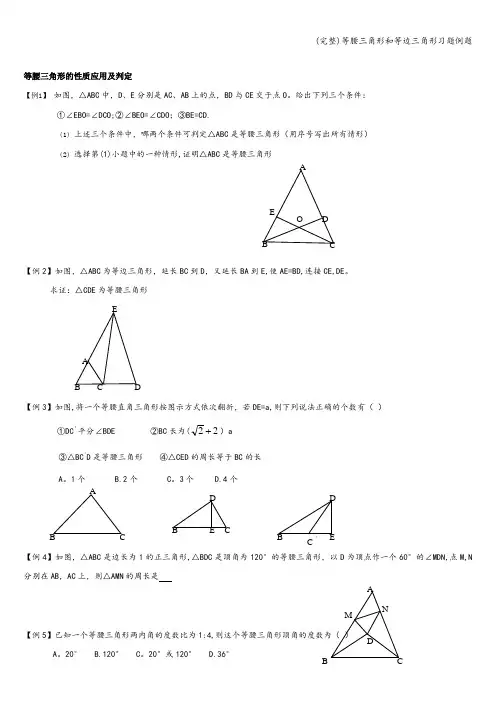
等腰三角形的性质应用及判定【例1】 如图，△ABC 中，D 、E 分别是AC 、AB 上的点，BD 与CE 交于点O 。

给出下列三个条件：①∠EBO=∠DCO;②∠BEO=∠CDO ；③BE=CD.(1) 上述三个条件中，哪两个条件可判定△ABC 是等腰三角形（用序号写出所有情形） (2) 选择第(1)小题中的一种情形,证明△ABC 是等腰三角形【例2】如图，△ABC 为等边三角形，延长BC 到D ，又延长BA 到E,使AE=BD,连接CE,DE 。

求证：△CDE 为等腰三角形【例3】如图,将一个等腰直角三角形按图示方式依次翻折，若DE=a,则下列说法正确的个数有（ ） ①DC '平分∠BDE②BC 长为(22 ）a③△BC 'D 是等腰三角形 ④△CED 的周长等于BC 的长 A 。

1个 B.2个 C 。

3个 D.4个【例4】如图，△ABC 是边长为1的正三角形,△BDC 是顶角为120°的等腰三角形，以D 为顶点作一个60°的∠MDN,点M,N分别在AB ，AC 上，则△AMN 的周长是【例5】已知一个等腰三角形两内角的度数比为1:4,则这个等腰三角形顶角的度数为（ ） A 。

20° B.120° C 。

20°或120° D.36°AEBCO D EA BCDD BE CDBC '. E ACB A MNDBC【例6】等腰三角形两边长分别为4和9，则第三边长为【例7】如图，点O 事等边△ABC 内一点,∠AOB=110°，∠BOC=α，将△BOC 绕点C 按顺时针方向旋转60°得△ADC ，连接OD ，则△COD 是等边三角形；（1）当α为多少度时，△AOD 是等腰三角形？(2）求证：△COD 是等边三角形（3）当α=150°时，试判断△AOD 的形状,并说明理由等边三角形的性质应用及判定【例8】如图，在等边△ABC 中，点D ，E 分别在边BC ，AB 上，BD=AE,AD 与CE 交于点F.求证：(1）AD=CE;(2）求∠DFC 的度数。

等腰三角形证明练习题一．选择题（共20小题）1．如图，在△ABC中，∠C=90°，AB的垂直平分线交AB与D，交BC于E，连接AE，若CE=5，AC=12，则BE的长是（）A ．13 B．10 C．12 D．52．如图，在△ABC中，AB=AC，∠A=36°，BD、CE分别是∠ABC、∠BCD的角平分线，则图中的等腰三角形有（）A ．5个B．4个C．3个D．2个3．如图，在△ABC中，AD是它的角平分线，AB=8cm，AC=6cm，则S△ABD：S△ACD=（）A ．4：3 B．3：4 C．16：9 D．9：164．如图，在△ABC中，AB=AC，∠A=40°，AB的垂直平分线交AB于点D，交AC于点E，连接BE，则∠CBE的度数为（）A ．70°B．80°C．40°D．30°5．如图，在△ABC中，AB=AC，且D为BC上一点，CD=AD，AB=BD，则∠B的度数为（）A ．30°B．36°C．40°D．45°6．如图，点O在直线AB上，射线OC平分∠AOD，若∠AOC=35°，则∠BOD等于（）A ．145°B．110°C．70°D．35°7．如图，在△ABC中，∠ACB=90°，BA的垂直平分线交BC边于D，若AB=10，AC=5，则图中等于60°的角的个数是（）A ．2 B．3 C．4 D．58．如图，已知BD是△ABC的中线，AB=5，BC=3，△ABD和△BCD的周长的差是（）A ．2 B．3 C．6 D．不能确定9．在Rt△ABC中，如图所示，∠C=90°，∠CAB=60°，AD平分∠CAB，点D到AB的距离DE=3.8cm，则BC等于（）A 3.8cmB 7.6cmC 11.4cmD 11.2cm10．△ABC中，点O是△ABC内一点，且点O到△ABC三边的距离相等；∠A=40°，则∠BOC=（）A 110°B 120°C 130°D 140°11．如图，已知点P在∠AOB的平分线OC上，PF⊥OA，PE⊥OB，若PE=6，则PF的长为（）A 2B 4C 6D 812．如图，△ABC中，DE是AB的垂直平分线，交BC于点D，交AB于点E，已知AE=1cm，△ACD的周长为12cm，则△ABC的周长是（）A 13cmB 14cmC 15cmD 16cm13．如图，∠BAC=130°，若MP和QN分别垂直平分AB和AC，则∠PAQ等于（）A ．50°B．75°C．80°D．105°14．如图，要用“HL”判定Rt△ABC和Rt△A′B′C′全等的条件是（）A．AC=A′C′，BC=B′C′B．∠A=∠A′，AB=A′B′C．AC=A′C′，AB=A′B′D．∠B=∠B′，BC=B′C′15．如图，MN是线段AB的垂直平分线，C在MN外，且与A点在MN的同一侧，BC交MN于P点，则（）A ．BC＞PC+AP B．BC＜PC+AP C．BC=PC+AP D．BC≥PC+AP16．如图，已知在△ABC中，AB=AC，D为BC上一点，BF=CD，CE=BD，那么∠EDF 等于（）A ．90°﹣∠A B．90°﹣∠AC．180°﹣∠A D．45°﹣∠A17．如图，在△ABC中，AB=AC，AD平分∠BAC，那么下列结论不一定成立的是（）A．△ABD≌△ACD B．AD是△ABC的高线C．AD是△ABC的角平分线D．△ABC是等边三角形18．如图，点P是△ABC内的一点，若PB=PC，则（）A．点P在∠ABC的平分线上B．点P在∠ACB的平分线上C．点P在边AB的垂直平分线上D．点P在边BC的垂直平分线上19．如图，在∠ECF的两边上有点B，A，D，BC=BD=DA，且∠ADF=75°，则∠ECF的度数为（）A ．15°B．20°C．25°D．30°20．如图，P为∠AOB的平分线OC上任意一点，PM⊥OA于M，PN⊥OB于N，连接MN交OP于点D．则①PM=PN，②MO=NO，③OP⊥MN，④MD=ND．其中正确的有（）A ．1个B．2个C．3个D．4个二．解答题（共10小题）21．如图，已知ON是∠AOB的平分线，OM、OC是∠AOB外的射线．（1）如果∠AOC=α，∠BOC=β，请用含有α，β的式子表示∠NOC．（2）如果∠BOC=90°，OM平分∠AOC，那么∠MON的度数是多少？22．（2014秋•阿坝州期末）如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F．（1）求证：OE是CD的垂直平分线．（2）若∠AOB=60°，请你探究OE，EF之间有什么数量关系？并证明你的结论．23．如图，在△ABC中，∠ABC=2∠C，BD平分∠ABC，DE⊥AB（E在AB之间），DF⊥BC，已知BD=5，DE=3，CF=4，试求△DFC的周长．24．如图，点D是△ABC中BC边上的一点，且AB=AC=CD，AD=BD，求∠BAC的度数．25．如图，在△ABC中，AB=AC，∠A=α．（1）直接写出∠ABC的大小（用含α的式子表示）；（2）以点B为圆心、BC长为半径画弧，分别交AC、AB于D、E两点，并连接BD、DE．若=30°，求∠BDE的度数．26．如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DE⊥AB于点E，DF⊥AC 于点F．求证：（1）∠B=∠C．（2）△ABC是等腰三角形．27．如图，AB=AC，∠C=67°，AB的垂直平分线EF交AC于点D，求∠DBC的度数．28．如图，△ABC中，AB=AD=AE，DE=EC，∠DAB=30°，求∠C的度数．29．阅读理解：“在一个三角形中，如果角相等，那么它们所对的边也相等．”简称“等角对等边”，如图，在△ABC中，已知∠ABC和∠ACB的平分线上交于点F，过点F作BC的平行线分别交AB、AC于点D、E，请你用“等角对等边”的知识说明DE=BD+CE．30．如图，AD是△ABC的平分线，DE，DF分别垂直AB、AC于E、F，连接EF，求证：△AEF是等腰三角形．31.如图:△ABC和△ADE是等边三角形．证明：BD=CE．AEDB C32..如图：△ABC 和△ADE 是等边三角形，AD 是BC 边上的中线。

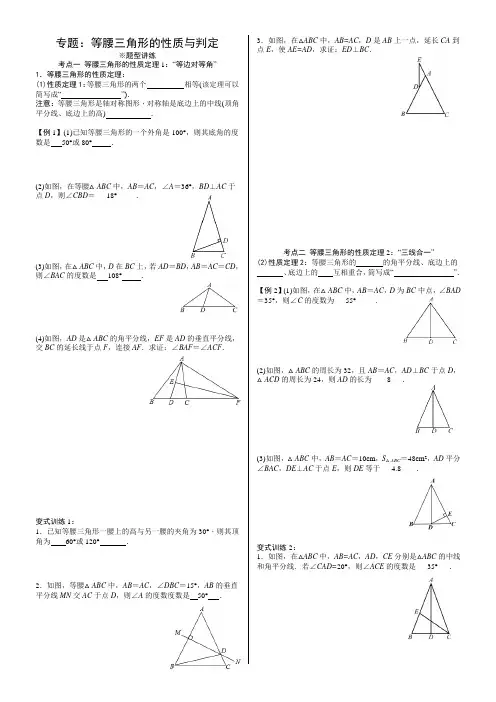
专题：等腰三角形的性质与判定※题型讲练考点一等腰三角形的性质定理1：“等边对等角”1．等腰三角形的性质定理：(1)性质定理1：等腰三角形的两个相等(该定理可以简写成“”)．注意：等腰三角形是轴对称图形，对称轴是底边上的中线(顶角平分线、底边上的高) ．【例1】(1)已知等腰三角形的一个外角是100°，则其底角的度数是50°或80°．(2)如图，在等腰△ABC中，AB＝AC，∠A＝36°，BD⊥AC于点D，则∠CBD＝___18°_____．(3)如图，在△ABC中，D在BC上，若AD＝BD，AB＝AC＝CD，则∠BAC的度数是108°．(4)如图，AD是△ABC的角平分线，EF是AD的垂直平分线，交BC的延长线于点F，连接AF．求证：∠BAF＝∠ACF．变式训练1：1．已知等腰三角形一腰上的高与另一腰的夹角为30°，则其顶角为60°或120°．2．如图，等腰△ABC中，AB＝AC，∠DBC＝15°，AB的垂直平分线MN交AC于点D，则∠A的度数度数是50°．3．如图，在△ABC中，AB=AC，D是AB上一点，延长CA到点E，使AE=AD，求证：ED⊥BC．考点二等腰三角形的性质定理2：“三线合一”(2)性质定理2：等腰三角形的的角平分线、底边上的、底边上的互相重合，简写成“”．【例2】(1)如图，在△ABC中，AB＝AC，D为BC中点，∠BAD ＝35°，则∠C的度数为___55°_____．(2)如图，△ABC的周长为32，且AB＝AC，AD⊥BC于点D，△ACD的周长为24，则AD的长为____8___．(3)如图，△ABC中，AB＝AC＝10cm，S△ABC＝48cm2，AD平分∠BAC，DE⊥AC于点E，则DE等于___4.8____．变式训练2：1．如图，在△ABC中，AB=AC，AD，CE分别是△ABC的中线和角平分线．若∠CAD=20°，则∠ACE的度数是___35°___．2．如图，△ABC中，AB＝AC，点D是BC边的中点，作∠EAB ＝∠BAD，AE边交CB的延长线于点E，延长AD到点F，使AF＝AE，连接CF．试证明：BE＝CF．考点三等腰三角形的判定定理：“等角对等边”1．等腰三角形的判定定理：如果一个三角形有相等，那么这两个角所对的边也相等(简写成“”)．【例2】(1)如图，∠B＝∠C＝36°，∠ADE＝∠AED＝72°，则图中的等腰三角形的个数为( D )A．3个B．4个C．5个D．6个(2)如图，在△ABC中，∠ACB＝90°，CD是AB边上的高，AE是∠BAC的角平分线，AE与CD交于点F，求证：△CEF是等腰三角形．(3)如图，AD是△ABC的角平分线，BE⊥AD交AD的延长线于点E，EF∥AC交AB于点F．求证：AF＝FB．变式训练3：1．如图，在△ABC中，BP平分∠CBA，AP平分∠CAB，且DE∥AB，若CB＝12，AC＝18，则△CDE的周长是____30____．2．如图，△ABC中，∠B＝2∠C，AD是∠BAC的平分线．求证：AC＝AB＋BD．考点四等腰三角形的综合问题【例4】如图，在△ABC中，AB＝AC，点D、E、F分别在AB 、BC 、AC边上，且BE＝CF，BD＝CE．(1)求证：△DEF是等腰三角形；(2)当∠A＝50°时，求∠DEF的度数．※课后练习1．等腰三角形是轴对称图形，它的对称轴是( D )A．过顶点的直线B．腰上的高所在的直线C．顶角的角平分线D．底边的垂直平分线2．如图，在△ABC中，AB＝AC，∠A＝30°，以B为圆心，BC 的长为半径画弧，交AC于点D，连接BD，则∠ABD＝(B) A．30°B．45°C．60°D．90°3．如图所示，已知AB＝AC＝BD，那么∠1和∠2之间的关系是(D)A．∠1＝2∠2 B．2∠1－∠2＝180°C．∠1＋3∠2＝180°D．3∠1－∠2＝180°4．已知等腰三角形中有一个内角为70°，则该等腰三角形的顶角度数为70°或40°．5．如图，已知OC平分∠AOB，CD∥OB，若OD＝4 cm，则CD等于____4 cm ___．6．如图，在△ABC中，∠B=∠C，点E在CA延长线上，EP⊥BC于点P，交AB于点F．若AF=3，BF=5，则CE的长度为11．7．在平面直角坐标系中，O为坐标原点，已知点A(2，4)，在坐标轴上确定一点P，使△AOP为等腰三角形，则所有符合条件的点P有8 个．8．如图，在△ABC中，AB＝AC，D，E分别在AC，AB边上，且BC＝BD，AD＝DE＝EB．则∠A的度数为45°．9．如图所示，在△ABC中，∠BAC＝90°，AD⊥BC于D，BE 交AD于F，交AC于E．(1)若BE平分∠ABC，试判断△AEF的形状，并说明理由；(2)若AE＝AF，请证明BE平分∠ABC．10．如图，AD是∠BAC的平分线，AB=AC+DC．求证：∠C=2∠B．证明：在AB上截取AE=AC，连接DE．∵AB=AC+DC，AE=AC，∴BE=DC．∵AD是∠BAC的平分线，∴∠EAD=∠CAD，∴△AED≌△ACD( SAS )．∴DE=DC=BE，∠AED=∠C，∴∠B=∠EDB．∵∠AED=∠B+∠EDB，∴∠AED=2∠B，∴∠C=2∠B．11．如图，在△ABC中，AB=AC，D是BC上任意一点，过点D 分别向AB，AC引垂线，垂足分别为E，F．(1)当点D在BC的什么位置时，DE=DF?请给出证明．(2)过点C作AB边上的高CG，请问DE，DF，CG的长度之间存在怎样的数量关系?并加以证明．解：(1)当D为BC的中点时，DE=DF．∵D为BC的中点，∴BD=CD．∵AB=AC，∴∠B=∠C．∵DE⊥AB，DF⊥AC，∴∠DEB=∠DFC=90°，∴△BED≌△CFD( AAS )，∴DE=DF．(2)CG=DE+DF．连接AD，∵S△ABC=S△ADB+S△ADC，AB×CG=AB×DE+AC×DF，又∵AB=AC，∴CG=DE+DF．12．在△ABC中，∠C＝90°，AC＝BC＝2，将一块三角板的直角顶点放在斜边AB的中点P处，将此三角板绕点P旋转，三角板的两直角边分别交射线AC，CB于点D，E，图1，图2，图3是旋转得到的三种图形．(1)以图2为例证明：PD=PE；(2)△PBE能否构成等腰三角形？若能，求出∠PEB的度数；若不能，请说明理由．。

解等腰三角形的性质的练习题1. 设等腰三角形ABC中，AB=AC，以点D为底边BC的中点，连接AD。

证明：△ABD≌△ACD。

解析：首先，根据等腰三角形的定义，AB=AC。

其次，由于D为BC的中点，所以BD=DC。

再根据SSS（边边边）对应的性质，我们可以得出△ABD≌△ACD。

也就是说，两个三角形的三边分别对应相等，从而可以得出两个三角形全等。

2. 设等腰三角形ABC中，AB=AC，以AB为底边，且与AC相交于点D的高为AH。

证明：∠HAB=∠HAC。

解析：首先，我们知道等腰三角形ABC的两边AB和AC相等，所以可以得出∠A=∠B=∠C。

又因为AD为高，所以∠HAD=90°，而角HAB是等腰三角形ABC的顶角，所以角HAB也等于∠C。

综上所述，可以得出∠HAB=∠HAC。

3. 设等腰三角形ABC中，AB=AC，以AB为底边，且与AC相交于点D的中线DE。

证明：DE=BC/2。

解析：首先，我们知道等腰三角形ABC的两边AB和AC相等，所以可以得出DE=BC/2。

这是因为DE是底边BC的中线，所以根据中线分割定理，DE等于底边BC的一半，即DE=BC/2。

4. 设等腰三角形ABC中，AB=AC，以角A的平分线AM为旋转轴，将△ABC旋转180°得到△ADE。

证明：△ADE≌△ABC。

解析：首先，我们需要说明如何将△ABC旋转180°得到△ADE。

根据题意，我们以角A的平分线AM为旋转轴，将△ABC旋转180°。

旋转后，点A和点D重合，点B和点E重合，点C不动。

根据旋转的定义，可以得出△ADE≌△ABC。

5. 设等腰三角形ABC中，AB=AC，以角A的平分线AM为旋转轴，将△ABC旋转180°得到△ADE。

证明：BD=DC，BE=EC。

解析：如前一题所述，旋转后，点A和点D重合，点B和点E重合，点C不动。

由等腰三角形的定义可知，BD=DC，BE=EC。

专题04 等腰三角形的证明知识对接考点一、怎样解与等腰三角形有关的问题解与等腰三角形的边有关的问题时，常利用三角形的三边关系:确定能否构成三角形.当已知等腰三角形的边不能确定是腰还是底时,要分类讨论,还要考虑三角形的存在性，即两腰之和大于底边.解与等腰三角形的角有关的问题时，常利用三角形的内角和定理,遇到顶角、底角未知或仅知道两角之差但不确定大小关系时，还要注意分类讨论. 考点二、等腰三角形中的分类讨论在解决与等腰三角形的边、角有关的问题时,如果不知道已知的边是腰还是底边或不知道已知的角是顶角还是底角,就需要分类讨论.1.已知等腰三角形的两边长分别为a,b(a≠b),求周长C 时,分两种情况: (1)若腰长为a 且2a>b,则周长C=2a+b; (2)若腰长为b 且2b>a,则周长C=2b+a.2.已知等腰三角形的一个角为α,求顶角或底角的度数时,有三种情况: (1)若α为钝角,则α为顶角,底角的度数为(180°-α).(2)若α为直角,则α为顶角,且该三角形为等腰直角三角形,底角为45°.(3)若α为锐角,则应分两种情况讨论:①当α为顶角时,底角的度数为(180°-α);②当α为底角时,顶角的度数为180°-2α.特别注意:无论哪种情况,都要注意三角形的三边必须满足“任意两边之和大于第三边”,三个角必须满足“三角形的内角和等于180°”.专项训练一、单选题1．（2021·河北九年级一模）求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形．已知：如图，CAE ∠是ABC 的外角，12∠=∠，AD ∥BC ．求证AB AC =．以下是排乱的证明过程：∥又12∠=∠， ∥∥B C ∠=∠， ∥∥AD ∥BC ，∥∥1B ∠=∠，2C ∠=∠， ∥∥AB AC =．证明步骤正确的顺序是（ ） A ．∥→∥→∥→∥→∥ B ．∥→∥→∥→∥→∥ C ．∥→∥→∥→∥→∥ D ．∥→∥→∥→∥→∥【答案】B 【分析】根据平行线的性质得出1,2B C ∠=∠∠=∠，再利用12∠=∠等量代换，得出B C ∠=∠，即可判定ABC 是等腰三角形，即可证明． 【详解】 具体步骤为： ∥∥AD ∥BC ，∥∥1B ∠=∠，2C ∠=∠， ∥又12∠=∠， ∥∥B C ∠=∠， ∥∥AB AC =． 故选：B ． 【点睛】本题考查平行线的性质，等量代换，等腰三角形的判定与性质，解题关键是熟练掌握平行线的性质与等腰三角形的判定与性质．2．（2021·江西）如图，在∥ABC 中，∥A ＝36°，AB ＝AC ，BD 是∥ABC 的角平分线．若在边AB 上截取BE ＝BC ，连接DE ，则图中等腰三角形共有( )A ．2个B ．3个C ．4个D ．5个【答案】D 【详解】试题分析：在∥ABC 中，∥A=36°，AB=AC ，求得∥ABC=∥C=72°，且∥ABC 是等腰三角形；因为CD 是∥ABC 的角平分线，所以∥ACD=∥DCB=36°，所以∥ACD 是等腰三角形；在∥BDC中，由三角形的内角和求出∥BDC=72°，所以∥BDC 是等腰三角形；所以BD=BC=BE ，所以∥BDE 是等腰三角形；所以∥BDE=72°，∥ADE=36°，所以∥ADE 是等腰三角形．共5个． 故选D考点：角平分线，三角形的内角和、外角和，平角3．（2021·河北）已知：如图，ABC 中，B C ∠=∠，求证：AB AC =，在证明该结论时，只添加一条辅助线：∥作BAC ∠的平分线AD 交BC 于点D ，∥过点A 作AD BC ⊥于点D ，∥取BC 中点D ，连接AD ，∥作BC 的垂直平分线AD ，其中作法正确的个数是（ ）A ．1B ．2C ．3D ．4【答案】B 【分析】根据辅助线构造的条件和三角形全等的判定方法结合在一起判断求解． 【详解】∥作BAC ∠的平分线AD 交BC 于点D ，则B CBAD CAD AD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∥∥ABD ∥∥ACD ， ∥AB =AC ， ∥∥作法正确；∥过点A 作AD BC ⊥于点D ，则B C BDA CDA AD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∥∥ABD ∥∥ACD ， ∥AB =AC ， ∥∥作法正确；∥取BC 中点D ，连接AD ， 无法证明∥ABD ∥∥ACD ， ∥∥作法不正确；∥作BC 的垂直平分线无法证明点A 在其上，∥∥作法不正确；故选B．【点睛】本题考查了等腰三角形的性质证明，三角形全等的判定，熟练掌握三角形全等的判定定理是解题的关键．4．（2021·云南文山·）若等腰三角形一腰上的高等于腰长的一半，则这个等腰三角形的底角为（）A．30B．60︒C．30或60︒D．15︒或75︒【答案】D【分析】首先根据题意作图，然后分别从等腰三角形一腰上的高在内部与在外部去分析，根据直角三角形中，如果直角边是斜边的一半，则此直角边所对的角是30°角，再由等边对等角的知识，即可求得这个三角形的底角．【详解】解：如图∥：∥CD∥AB，∥∥ADC=90°，∥CD=12AC，∥∥A=30°，∥AB=AC，∥∥B=∥ACB=18030752︒︒︒-=；如图∥：∥CD∥AB，∥∥ADC=90°，AC，∥CD=12∥∥CAD=30°，∥AB=AC，∥∥B=∥ACB∥∥DAC=∥B+∥ACB=2∥B=30°，∥∥B=∥ACB=15°．∥这个三角形的底角为：75°或15°．故选：D．【点睛】此题考查了直角三角形的性质与等腰三角形的性质．解题的关键是注意数形结合思想与分类讨论思想的应用，小心别漏解．5．（2021·广东九年级二模）已知a、b、4分别是等腰三角形三边的长，且a、b是关于x 的一元二次方程2620-++=的两个根，则k的值等于（）x x kA．6B．7C．-7或6D．6或7【答案】D【分析】当a＝4或b＝4时，即x＝4，代入方程即可得到结论，当a＝b时，即∥＝（−6）2−4×（k ＋2）＝0，解方程即可得到结论．【详解】解：∥a、b、4分别是等腰三角形三边的长，∥当a＝4或b＝4时，即：42−6×4＋k＋2＝0，解得：k＝6，此时，2680-+=的两个根为：x1=2，x2=4，符合题意；x x当a＝b时，即∥＝（−6）2−4×（k＋2）＝0，解得：k＝7，此时，2690-+=的两个根为：x1=x2=3，符合题意；x x综上所述，k的值等于6或7，故选：D．【点睛】本题考查了根的判别式，一元二次方程的解，等腰三角形的性质，熟练掌握一元二次方程的判别式和等腰三角形的性质，进行分类讨论，是解题的关键．6．（2021·甘肃兰州·九年级）如图，等腰三角形ABC中，AB＝AC，∥A＝46°，CD∥AB于点D，则∥DCB＝（）A ．46°B ．67°C ．44°D ．23°【答案】D 【分析】根据等腰三角形的性质即可求解． 【详解】解：∥等腰三角形ABC 中，AB =AC ， ∥∥ABC =∥ACB ∥∥A =46°，∥∥ABC =12×（180°-46°）=12×134°=67°， ∥CD ∥AB 于D ，∥∥DCB =90°-∥ABC =90°-67°=23°， 故选：D ． 【点睛】本题考查了等腰三角形的性质，本题的解题关键是求出∥ABC 的度数即可得出答案． 7．（2021·苏州高新区第二中学九年级二模）定义：等腰三角形的一个底角与其顶角的度数的比值()1k k >称为这个等腰三角形的“优美比”．若在等腰三角形ABC 中，36,A ∠=︒则它的优美比k 为（ ）A ．32B ．2C ．52D ．3【答案】B 【分析】由已知可以写出∥B 和∥C ，再根据三角形内角和定理可以得解． 【详解】解：由已知可得：∥B=∥C=k∥A=（36k ）°， 由三角形内角和定理可得：2×36k+36=180， ∥k=2， 故选B ． 【点睛】本题考查等腰三角形的应用，熟练掌握等腰三角形的性质、三角形内角和定理及方程思想的应用是解题关键 ．8．（2021·四川成都·九年级一模）在螳螂的示意图中，AB∥DE ，∥ABC 是等腰三角形，∥ABC ＝124°，∥CDE ＝72°，则∥ACD ＝（ ）A ．16°B ．28°C ．44°D ．45°【答案】C 【分析】延长ED ，交AC 于F ，根据等腰三角形的性质得出28A ACB ，根据平行线的性质得出28CFD A，【详解】解：延长ED ，交AC 于F ，ABC ∆是等腰三角形，124ABC ∠=︒，28AACB， //AB DE ，28CFD A，72CDE CFD ACD，722844ACD，故选：C ．【点睛】本题考查了等腰三角形的性质，平行线的性质，三角形外角的性质，熟练掌握性质定理是解题的关键．9．（2021·全国九年级专题练习）如图，AD 是等腰三角形ABC 的顶角平分线，5BD =，则CD 等于（ ）A ．10B ．5C ．4D ．3【答案】B 【分析】根据等腰三角形三线合一的性质即可判断CD 的长． 【详解】∥AD 是等腰三角形ABC 的顶角平分线 ∥CD=BD=5． 故选：B ． 【点睛】本题考查等腰三角形的三线合一，关键在于熟练掌握基础知识．10．（2021·河北九年级专题练习）已知m 、n 、4分别是等腰三角形(非等边三角形)三边的长，且m 、n 是关于x 的一元二次方程2x ﹣6x +k+2=0的两个根，则k 的值等于( ) A ．7 B ．7或6 C ．6或﹣7 D ．6【答案】B 【分析】当m =4或n =4时，即x =4，代入方程即可得到结论，当m =n 时，即∥=(﹣6)2﹣4×(k +2)=0，解方程即可得到结论． 【详解】当m=4或n=4时，即x=4， ∥方程为42﹣6×4+k+2=0， 解得：k=6；当m=n 时，2x ﹣6x +k+2=0 ∥1a =，6b =-，2c k =+，∥()()22464120b ac k =-=--⨯⨯+=⊿， 解得：7k =，综上所述，k 的值等于6或7， 故选：B ． 【点睛】本题主要考查了一元二次方程的根、根的判别式以及等腰三角形的性质，由等腰三角形的性质得出方程有一个实数根为2或方程有两个相等的实数根是解题的关键． 二、填空题11．（2021·江苏九年级）若一条长为32cm 的细线能围成一边长等于8cm 的等腰三角形，则该等腰三角形的腰长为___cm ． 【答案】12 【分析】根据题意，分腰长为8cm 和底边为8cm 两种情况并结合三角形的构成条件分类讨论即可． 【详解】解：若腰长为8cm ，则此三角形的另一边长为32-8-8=16（cm ）， 而8+8=16，无法构成三角形， ∥此情形舍去；若底边为8cm ，则腰长为（32-8）÷2=12（cm ）， 此时12+12＞8，12+8＞8，可以构成三角形． 故答案为：12． 【点睛】本题考查了三角形的构成条件、等腰三角形的性质、分类讨论的数学思想，根据题意结合三角形构成条件进行分类讨论是解题的关键．12．（2021·江苏九年级二模）顶角是36︒的等腰三角形叫做黄金三角形．如图，AC AD BE 、、是正五边形ABCDE 的3条对角线，图中黄金三角形的个数是_________．【答案】6 【分析】根据正五边形的内角和和黄金三角形的定义进行判断即可． 【详解】解：设BE 与AC 、AD 交于M 、N ，ABCDE 是正五边形，内角和为5218540(0)-⨯︒=︒，每一个内角为5405108︒÷=︒，∥∥ABC＝∥BAE＝∥AED＝∥BCD＝∥CDE＝108°，∥AB＝BC＝AE＝ED，∥∥BAC＝∥BCA＝36°，∥EAD＝∥ADE＝36°，∥∥CAD＝36°，∥ACD＝∥ADC＝72°，∥AC＝AD，∥∥ACD是黄金三角形，同理可求：∥BAN＝∥ANB＝∥AME＝∥EAM＝72°，∥CBM＝∥BMC＝∥DNE＝∥DEN＝72°，∥∥AMN、∥DEN、∥EAM、∥CMB，∥ABN也是黄金三角形．则图中黄金三角形的个数有6个．故答案为：6．13．（2021·浙江九年级期末）ABC中，∥A=36°，∥B是锐角．当∥B=72°时，我们可以如图作线段BD将ABC分成两个小等腰三角形如果存在一条线段将ABC分成两个小三角形，这两个小三角形都是等腰三角形，则∥B的角度还可以取到的有____________．【答案】54°，36°，18°，12°【分析】直线从A、B、C出发分三种情况讨论，利用等边对对角、三角形的外角性质、三角形的内角和建立方程求解，再结合题干看是否存在即可得出答案．【详解】∠=解：这条直线从A、B、C出发皆可，设B x()I假设从A出发，如下图：∥当BD=AD，AD=DC时，B BAD DAC C∴∠=∠∠=∠∴︒-︒-=︒-1803636x x此时x的值不存在；∥当BD=AD，AC=DC时∠=∠，ADC DACB BAD∠=∠ADC B BAD BAC BAD∠=∠+∠=∠-∠∴=︒-236x xx=︒；解得：12∥当BD=AD，AD=AC时∠=∠∠=∠，ADC CB BADC x x∠=︒--︒=︒-ADC B BAD x∠=∠+∠=，180361442x x∴=︒-2144解得：48x=︒︒>︒，此种情况不存在；此时4836∥当AB=AD，AD=DC时，∠=∠∠=∠，ADC CB ADBC x∠=︒-，18036∠=--︒BAD x1802()∴︒-=︒---︒x x180********x=︒（不符合题意）解得：96()II假设从B出发，如下图：∥当AD =BD ，BD =BC 时36272BDC A ABD ∠=∠+∠=︒⨯=︒72,72C B ∴∠=︒∠=︒,此情况成立；∥AD =BD ，BD =DC 时7236BDC DBC x ∠=︒∠=-︒， 3618036x x ∴-︒=︒-︒-解得：90x =︒，此时不成立；()III 假设从C 出发，如下图：∥BD =DC ，AC =DC 时362ADC A B DCB x ∠=∠=︒=∠+∠=解得：18x =︒，此时成立； ∥BD =DC ，AD =DC180362108ADC ∠=︒-︒⨯=︒,2108ADC B DCB x ∠=∠+∠==︒解得：54x =︒，此时成立； ∥BD =BC ，AD =DC 1802xBDC BCD ︒-∠=∠=，36A ACD ∠=∠=︒，BDC A ACD ∠=∠+∠ 18036362x︒-∴=︒+︒x=︒；解得：36综上所述，∥B的角度还可以取到的有54︒、36︒、12︒、18︒．故答案为：54°，36°，18°，12°．【点睛】本题考查了等腰三角形的性质、三角形内角和、三角形外角的性质，解题的关键是分情况讨论，注意不要漏掉．14．（2021·黑龙江牡丹江·中考真题）过等腰三角形顶角顶点的一条直线，将该等腰三角形分成的两个三角形均为等腰三角形，则原等腰三角形的底角度数为____．【答案】45°或36°【分析】根据等腰三角形的性质和三角形内角和定理即可得出答案．【详解】解：∥如图1，当过顶角的顶点的直线把它分成了两个等腰三角形，则AC=BC，AD=CD=BD，设∥A=x°，则∥ACD=∥A=x°，∥B=∥A=x°，∥∥BCD=∥B=x°，∥∥A+∥ACB+∥B=180°，∥x+x+x+x=180，解得x=45，∥原等腰三角形的底角是45°；∥如图2，∥ABC 中，AB =AC ，BD =AD ，AC =CD ， ∥AB =AC ，BD =AD ，AC =CD ， ∥∥B =∥C =∥BAD ，∥CDA =∥CAD ， ∥∥CDA =2∥B ， ∥∥CAB =3∥B ， ∥∥BAC +∥B +∥C =180°， ∥5∥B =180°， ∥∥B =36°，∥原等腰三角形的底角为36°； 故答案为45°或36° 【点睛】本题考查了等腰三角形的性质及其判定．作此题的时候，首先大致画出符合条件的图形，然后根据等腰三角形的性质、三角形的内角和定理及其推论找到角之间的关系，列方程求解． 15．（2021·江苏盐城·中考真题）如图，在矩形ABCD 中，3AB =，4=AD ，E 、F 分别是边BC 、CD 上一点，EF AE ⊥，将ECF △沿EF 翻折得EC F '△，连接AC '，当BE =________时，AEC '是以AE 为腰的等腰三角形．【答案】78或43【分析】对AEC '是以AE 为腰的等腰三角形分类讨论，当=AE EC '时，设BE x =，可得到4EC x =-，再根据折叠可得到=4EC EC x '=-，然后在Rt∥ABE 中利用勾股定理列方程计算即可；当=AE AC '时，过A 作AH 垂直于EC '于点H ，然后根据折叠可得到=C EF FEC '∠∠，在结合EF AE ⊥，利用互余性质可得到BEA AEH =∠∠，然后证得∥ABE ∥∥AHE ，进而得到BE HE =，然后再利用等腰三角形三线合一性质得到EH C H '=，然后在根据数量关系得到14=33BE BC =．【详解】解：当=AE EC '时，设BE x =，则4EC x =-， ∥ECF △沿EF 翻折得EC F '△，∥=4EC EC x '=-，在Rt∥ABE 中由勾股定理可得：222AE BE AB =+即222(4)3x x -=+， 解得：7=8x ； 当=AE AC '时，如图所示，过A 作AH 垂直于EC '于点H ，∥AH ∥EC '，=AE AC '， ∥EH C H '=， ∥EF AE ⊥，∥=90C EF AEC ''+︒∠∠，90BEA FEC +=︒∠∠ ∥ECF △沿EF 翻折得EC F '△， ∥=C EF FEC '∠∠， ∥BEA AEH =∠∠，在∥ABE 和∥AHE 中B AHE AEB AEH AE AE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∥∥ABE ∥∥AHE （AAS ）， ∥BE HE =， ∥=BE HE HC '=， ∥12BE EC '=∥EC EC '=， ∥12BE EC =， ∥14=33BE BC =，综上所述，7483BE =或，故答案为：7483或【点睛】本题主要考查等腰三角形性质，勾股定理和折叠性质，解题的关键是分类讨论等腰三角形的腰，然后结合勾股定理计算即可． 三、解答题16．（2021·江苏徐州·中考真题）如图，将一张长方形纸片ABCD 沿E 折叠，使,C A 两点重合．点D 落在点G 处．已知=4AB ，8BC =． （1）求证：AEF ∆是等腰三角形； （2）求线段FD 的长．【答案】（1）见解析；（2）3 【分析】（1）根据矩形的性质可得//AD BC ,则FEC AFE ∠=∠,因为折叠，FEC AEF ∠=∠，即可得证；（2）设FD x =用含x 的代数式表示AF ，由折叠，AG DC =，再用勾股定理求解即可 【详解】（1）四边形ABCD 是矩形∴//AD BC∴FEC AFE ∠=∠因为折叠，则FEC AEF ∠=∠AEF AFE ∴∠=∠∴AEF ∆是等腰三角形（2）四边形ABCD 是矩形8,4AD BC CD AB ∴====,90D ∠=︒设FD x =，则8AF AD x x =-=-因为折叠，则FG x =，4AG CD ==,90G D ∠=∠=︒ 在Rt AGF △中222FG AF AG =-即222(8)4x x =-- 解得：3x =∴3FD =【点睛】本题考查了矩形的性质，等腰三角形的判定定理，图像的折叠，勾股定理，熟悉以上知识点是解题的关键．17．（2021·湖南郴州市·）如图1，在等腰直角三角形ABC 中，90BAC ∠=︒．点E ，F 分别为AB ，AC 的中点，H 为线段EF 上一动点（不与点E ，F 重合），将线段AH 绕点A 逆时针方向旋转90︒得到AG ，连接GC ，HB ．（1）证明：AHB AGC ≌；（2）如图2，连接GF ，HC ，AF 交AF 于点Q ． ∥证明：在点H 的运动过程中，总有90HFG ∠=︒；∥若4AB AC ==，当EH 的长度为多少时，AQG 为等腰三角形？【答案】（1）见详解；（2）∥见详解；∥当EH 的长度为2AQG 为等腰三角形 【分析】（1）由旋转的性质得AH =AG ，∥HAG =90°，从而得∥BAH =∥CAG ，进而即可得到结论； （2）∥由AHB AGC ≌，得AH =AG ，再证明AEH AFG ≌，进而即可得到结论；∥AQG 为等腰三角形，分3种情况：（a ）当∥QAG =∥QGA =45°时，（b ）当∥GAQ =∥GQA =67.5°时，（c ）当∥AQG =∥AGQ =45°时，分别画出图形求解，即可． 【详解】解：（1）∥线段AH 绕点A 逆时针方向旋转90︒得到AG ， ∥AH =AG ，∥HAG =90°，∥在等腰直角三角形ABC 中，90BAC ∠=︒，AB =AC ， ∥∥BAH =90°-∥CAH =∥CAG ， ∥AHB AGC ≌；（2）∥∥在等腰直角三角形ABC 中，AB =AC ，点E ，F 分别为AB ，AC 的中点， ∥AE =AF ，AEF 是等腰直角三角形， ∥AH =AG ，∥BAH =∥CAG ， ∥AEH AFG ≌， ∥∥AEH =∥AFG =45°，∥∥HFG =∥AFG +∥AFE =45°+45°=90°，即：90HFG ∠=︒； ∥∥4AB AC ==，点E ，F 分别为AB ，AC 的中点， ∥AE =AF =2，∥∥AGH =45°，AQG 为等腰三角形，分3种情况：（a ）当∥QAG =∥QGA =45°时，如图，则∥HAF =90°-45°=45°， ∥AH 平分∥EAF ， ∥点H 是EF 的中点，∥EH 12=（b ）当∥GAQ =∥GQA =（180°-45°）÷2=67.5°时，如图，则∥EAH =∥GAQ =67.5°， ∥∥EHA =180°-45°-67.5°=67.5°， ∥∥EHA =∥EAH ， ∥EH =EA =2；（c ）当∥AQG =∥AGQ =45°时，点H 与点F 重合，不符合题意，舍去，综上所述：当EH 的长度为2时，AQG 为等腰三角形．【点睛】本题主要考查等腰直角三角形的性质，旋转的性质，全等三角形的判定和性质，勾股定理，熟练掌握全等三角形的判定定理，根据题意画出图形，进行分类讨论，是解题的关键．18．（2021·江苏九年级二模）如图（1），已知矩形ABCD 中，6cm AB BC ==，，点E 为对角线AC 上的动点．连接BE ，过E 作EB 的垂线交CD 于点F ．（1）探索BE 与EF 的数量关系，并说明理由．（2）如图（2），过F 作AC 垂线交AC 于点G ，交EB 于点H ，连接CH ．若点E 从A 出发沿AC 方向以/s 的速度向终点C 运动，设E 的运动时间为s t ． ∥是否存在t ，使得H 与B 重合？若存在，求出t 的值；若不存在，说明理由； ∥t 为何值时，CFH △是等腰三角形； ∥当CG GH =时，求CGH 的面积．【答案】（1）BE =；（2）∥t=1，∥t =； 【分析】(1)连接BF ，易证B. C. F. E 四点共圆，,AD EFtan ACD tan EBF CD BE∠==∠=即可求证出BE = ；(2)∥存在，当H 、B 重合时，如图所示，结合(1)知可得BG =3，CG =，同理可知CF =2，FG =1,EG CG ==CE =，由此可得t=1，∥先得出60CFH ∠=︒ ，再由△FHC 为等腰三角形，推出△FHC 为等边三角形进而得出45CEB ∠=︒ ，△ABE =15°，△EBC =75°，根据△BCH =30°得出CH=CB=CF ，根据题意列等式64t -=求出t =，∥过点E 作MN 垂直AB ，设AE =，求证出 ~FEM EBN ∆∆ ，根据相似的性质结合4DF t =，64CF t =- ，32FG t =- 得出EG =-=，再结合EGH FGE ∽得出()232t -=进而表示出CG ，代入面积公式()21CG 2CGH S ∆==即可； 【详解】解：(1)连接BF ，如图：已知矩形ABCD 中，BE EF ⊥ ， ∥∥BEF =∥BCF =90°，∥点B ， C ，F ， E 四点共圆，∥∥EBF =∥ACD （同圆中同弧所对圆周角相等），∥,AD EFtan ACD tan EBF CD BE∠==∠=∥BE =(2) ∥存在，当H 、B 重合时，如图所示：由(1)知，∥EBF =30°， ∥∥ACD =∥EBF =30°， 则∥ACB =60°，∥FH AC ⊥ 即∥BGC =90°，BC =∥BG =3，CG =，同理可得CF=2，FG=1，EG CG ==∥CE =， ∥AE AC CE =- ，又∥已知矩形ABCD 中，6cm AB BC ==，，∥AC =，∥AE =∥点E 从A 出发沿AC 方向以/s 的速度向终点C 运动， ∥t=1； ∥∥∥CFH 为等腰三角形， 又∥∥ACD =30°， ∥60CFH ∠=︒ ， ∥∥CFH 为等边三角形， ∥FG =GH ，又由（1）知90BEF ∠=︒， ∥FG =GH =EG ， ∥45CEB ∠=︒ ， ∥∥ABE =15°， ∥∥EBC =75°， ∥∥BCH =30°，∥∥CHB 为等腰三角形， ∥CH =CB =CF ，∥3CE CG EG =+=，∥3AE CE == ，即3= ，解得：t =， ∥由题意知：过点E 作MN 垂直AB ，设AE =，则由（1）得EN =，3t AN =，∥∥FME =∥ENB ，∥FEM +∥BEN=∥BEN +∥EBN=90°， ∥∥FEM =∥EBN ， ∥FEM EBN ∆~∆ ， ∥ME MFBN EN= ，，∥MF =t ，∥4DF DM MF AN MF t =+=+=，则64CF t =- ， ∥32FG t =- ，∥CG = ，EG AC AE CG =--=-=，在t R EFH ∆中，EG FH ⊥ ，,EGH FGE ∴∽ ,EG GH FG EG∴= ∥2EG GH FG =⨯ ，∥()()232t =⨯-，∥()232t -∥CG GH =，∥()()221122CGH S CG ∆===； 【点睛】此题属于四边形综合试题，考查动点问题，涉及到圆周角，三角形相似，特殊角的直角三角形各边的关系及等边三角形的证明，有一定难度．19．（2021·苏州市胥江实验中学校九年级）如图，在ABC 中，以AB 为直径的O 交BC 边于点D ，交AC 边于点E ．过点D 作O 的切线，交AC 于点F ，交AB 的延长线于点G ，且DF AC ⊥，连接DE ．（1）求证：ABC 是等腰三角形； （2）求证：2DE EF AC =⋅；（3）若6BG =，2CF =，求O 的半径． 【答案】（1）见解析；（2）见解析；（3）3 【分析】（1）DF 是△O 的切线，得到∥ODF =90°，再求出∥C +∥FDC =90° ，∥C =∥BDO ，由OB =OD ，得∥BDO =∥ABC ．∥C =∥ABC ，即可求解．（2）因为AB 是直径，得到90ADB ∠=︒,知道AB AC =,BAD CAD ∠=∠,BD DE =,推出，ABD DEF ∽，得到AC DEDE EF=即可求解； （3）求出∥ODG∥∥AFG ，得出比例式，即可求出圆的半径． 【详解】（1）证明： ∥DF 是△O 的切线， ∥OD ∥DF ． ∥∥ODF =90°．又∥∥BDO +∥ODF +∥FDC =180°， ∥∥BDO +∥FDC =90°． ∥DF ∥AC ， ∥∥DFC =90°， ∥∥C +∥FDC =90°． ∥∥C =∥BDO ． ∥OB =OD ， ∥∥BDO =∥ABC ． ∥∥C =∥ABC ． ∥AB =AC ．∥∥ABC 是等腰三角形； （2）连接AD ，∥AB 是直径 90ADB ∴∠=︒, AB AC =,BAD CAD ∴∠=∠,BD DE ∴=,在ABD △和DEF 中90ADB DFE ABD DEF∠=∠=︒⎧⎨∠=∠⎩ ABD DEF ∴∽,AB BDDE EF∴= ,AB AC BD DE ==AC DEDE EF∴= 2DE EF AC ∴=⋅ （3）解：∥AB =AC ， ∥∥ABC =∥C ， ∥OB =OD ， ∥∥ABC =∥ODB ， ∥∥ODB =∥C ， ∥OD ∥AC ， ∥∥GOD ∥∥GAF ， ,OD GOAF GA∴= ∥设△O 的半径是r ，则AB =AC =2r ， ∥AF =2r -2， 6,2262r rr r+∴=-+ ∥r =3，经检验：3r =是原方程的根，且符合题意， 即△O 的半径是3．【点睛】本题考查了切线的性质，圆内接四边形，相似三角形的性质和判定，圆周角定理，等腰三角形的性质等知识点，能综合运用知识点进行推理是解此题的关键． 20．（2021·广东中山·）如图，已知等腰ABC ∆的顶角36A ∠=︒．（1）根据要求用尺规作图：作ABC ∠的平分线交AC 于点D ；（不写作法，只保留作图痕迹．）（2）在（1）的条件下，证明：BDC ∆是等腰三角形． 【答案】（1）见解析；（2）见解析 【分析】（1）以点B 为圆心，适当长为半径画弧，交AB 、BC 于点M 、N ，然后以点M 、N 为圆心，大于MN 长的一半为半径画弧，交于点O ，连接BO ，交AC 于点D ，则问题可求解； （2）由题意易得72ABC C ∠=∠=︒，然后可得72C CDB ∠=∠=︒，则问题可求证． 【详解】.解：（1）如图所示：BD 即为所求；（2）∥36A ∠=︒，∥()18036272ABC C ∠=∠=︒-︒÷=︒， ∥BD 平分ABC ∠，∥72236ABD DBC ∠=∠=︒÷=︒， ∥1803672872CDB ∠=︒-︒-=︒， ∥72C CDB ∠=∠=︒， ∥BD BC =，∥BDC都是等腰三角形．【点睛】本题主要考查角平分线的尺规作图及等腰三角形的性质与判定，熟练掌握角平分线的尺规作图及等腰三角形的性质与判定是解题的关键．21．（2021·浙江）如图，矩形ABCD中，点E为BC边上一点，把ABE△沿着AE折叠得到AEF，点F落在AD边的上方，线段EF与AD边交于点G．（1）求证：AGE是等腰三角形（2）试写出线段FG，GD，EC三者之间的数量关系式（用同一个等式表示），并证明．【答案】（1）证明见解析；（2）GD=GF+EC，证明见解析．【分析】（1）根据矩形性质、折叠性质及等角对等边可以得到证明；（2）根据折叠性质及（1）可得AG+GD=FG+GA+EC，从而得到GD=GF+EC．【详解】解：(1)证明:在矩形ABCD中，有:AD∥BC且AD=BC.∥∥DAE=∥BEA.∥∥ABE沿着AE折叠得到∥AEF.∥∥AEB= ∥AEG.∥∥GAE=∥GEA.∥GA=GE.∥∥AGE是等腰三角形.(2)GD=GF+EC.证明:根据折叠的性质:BE=EF.∥GE=GA、AG+GD=BE+EC.∥AG+GD=EF+EC.∥EF=FG+GE=FG+GA.∥AG+GD=FG+GA+EC.∥GD=GF+EC.【点睛】本题考查矩形的折叠问题，熟练掌握矩形的性质、折叠的性质、等腰三角形的判定与性质是解题关键．22．（2021·安徽）如图，AB为半圆O的直径，点C为半圆上不与A，B重合的一动点，AC ＝CD，连接AC，CD，AD，BC，延长BC交AD于F，交半圆O的切线AE于E．（1）求证：∥AEF是等腰三角形；（2）填空：∥若AE BE＝5，则BF的长为；∥当∥E的度数为时，四边形OACD为菱形．【答案】（1）见详解；（2）∥3；∥60°【分析】（1）由AB为半圆O的直径，AE是切线，可得∥EAC=∥ABC，结合圆周角定理的推论可得∥EAC=∥CAD，从而得ACE≌ACF，，进而即可得到结论；（2）∥由等腰三角形的性质得EF=2CE，再利用勾股定理求出AB的值，然后利用面积法求出AC的值，进而即可求解；∥利用菱形的性质和圆的性质，可得ACO是等边三角形，结合圆周角定理，即可求得答案．【详解】（1）证明：∥AB为半圆O的直径，AE是切线，∥∥ACB=90°，∥EAB=90°，∥∥EAC+∥CAB=∥CAB+∥ABC=90°，∥∥EAC=∥ABC，∥AC＝CD，∥∥ABC =∥CAD，∥∥EAC=∥CAD，又∥∥ACE=∥ACF=90°，AC=AC，∥ACE≌ACF，∥AE=AF，∥∥AEF是等腰三角形；（2）∥∥∥AEF是等腰三角形，AE=AF，AC∥BE，∥点C是EF的中点，即:EF=2CE，∥AE ∥AB ，∥AB∥1122AEBSAE AB BE AC =⋅=⋅，∥2AE AB AC BE ⋅===，∥1CE =， ∥EF =2CE =2， ∥BF =BE -EF =5-2=3， 故答案是：3； ∥连接OC ，∥四边形OACD 为菱形， ∥OA =OD =CD =AC =OC ， ∥ACO 是等边三角形， ∥∥AOC =60°， ∥∥ABE =30°， ∥∥E =90°-30°=60°． 故答案是：60°．【点睛】本题主要考查圆周角定理，切线的性质，菱形的性质，等腰三角形的判定和性质，熟练掌握圆周角定理及其推论，是解题的关键．23．（2021·广东）如图，已知等腰三角形ABC 的顶角∥A ＝108°．（1）在BC 上作一点D ，使AD ＝CD （要求：尺规作图，保留作图痕迹，不必写作法和证明）．（2）求证：∥ABD 是等腰三角形．【答案】（1）见解析；（2）见解析【分析】（1）根据线段垂直平分线的尺规作图直接进行求解即可；（2）由题意易得∥B＝∥C＝36°，然后根据三角形内角和与外角的性质及等腰三角形的判定可进行求解．【详解】解：（1）如图，点D即为所求；（2）连接AD，∥AB＝AC，∥A＝108°，∥∥B＝∥C＝36°，由（1）得：AD＝CD，∥∥DAC＝∥C＝36°，∥∥ADB＝∥DAC+∥C＝72°，∥BAD＝∥BAC﹣∥DAC＝108°﹣36°＝72°，∥∥BAD＝∥BDA，∥AB＝BD，∥∥ABD是等腰三角形．【点睛】本题主要考查线段垂直平分线及等腰三角形的判定与性质，熟练掌握各个知识点是解题的关键．。

专题13.3 等腰三角形知识点1：等腰三角形1.等腰三角形的定义：有两条边相等的三角形叫做等腰三角形．相等的两边叫做腰，另一边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫底角．2.等腰三角形的性质：（1）等腰三角形的两个底角相等（简写成“等边对等角”）．（2）等腰三角形的顶角平分线，底边上的中线、 底边上的高互相重合（通常称作“三线合一”）．3.等腰三角形的判定定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）．知识点2：等边三角形1.定义：三条边相等的三角形叫做等边三角形．2.等边三角形的性质和判定：（1）等边三角形的三个内角都相等，并且每一个角都等于60°。

（2）三个角都相等的三角形是等边三角形。

（3）有一个角是60°的等腰三角形是等边三角形。

知识点3：直角三角形的一个定理在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．【例题1】如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求：△ABC各角的度数．【例题2】证明：在直角三角形中，如果一个锐角等于30°， 那么它所对的直角边等于斜边的一半． 已知：如图，在Rt △ABC 中，∠C=90°，∠BAC=30°．求证：BC=AB ．【例题7】已知等边三角形的边长为3，点P 为等边三角形内任意一点，则点P 到三边的距离之和为（ ）A ．B ．C ．D ．不能确定【例题3】如图，已知AC ⊥BC ，BD ⊥AD ，AC 与BD 交于点O ，AC=BD.求证：(1)BC=AD ；(2)△OAB 是等腰三角形.一、选择题1.已知等边三角形的边长为3，点P 为等边三角形内任意一点，则点P 到三边的距离之和为（ ）12C AA．B．C．D．不能确定2.如图所示，点D是△ABC的边AC上一点（不含端点），AD=BD，则下列结论正确的是（）A．AC＞BC B．AC=BC C．∠A＞∠ABC D．∠A=∠ABC3．如图，∠AOB=120°，OP平分∠AOB，且OP=2．若点M，N分别在OA，OB上，且△PMN 为等边三角形，则满足上述条件的△PMN有（）A．1个B．2个C．3个D．3个以上4.如图所示，底边BC为2，顶角A为120°的等腰△ABC中，DE垂直平分AB于D，则△ACE的周长为（）A．2+2B．2+C．4 D．3二、解答题5.已知：在△ABC中，AB=AC，D为AC的中点，DE⊥AB，DF⊥BC，垂足分别为点E，F，且DE=DF．求证：△ABC是等边三角形．6.如图，在△ABC中，过C作∠BAC的平分线AD的垂线，垂足为D，DE∥AB交AC于E．求证：AE=CE．7.求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形．已知：∠CAE 是△ABC 的外角，∠1=∠2，AD ∥BC （如图）．求证：AB=AC ．8.已知：如图，AD ∥BC ，BD 平分∠ABC ．求证：AB=AD ．9.证明：等腰三角形两底角的平分线相等．已知：如图，在△ABC 中，AB=AC ，BD 、CE 是△ABC 的平分线．求证：BD=CE ．10.证明：等腰三角形两腰上的高相等．已知：如图，在△ABC 中，AB=AC ，BE 、CF 分别是△ABC 的高．E DCAB11.证明：等腰三角形两腰上的中线相等．已知：如图，在△ABC 中，AB=AC ，BD 、CE 分别是两腰上的中线．求证：BD=CE ．12.已知：如图，在△ABC 中，AB=AC=2a ，∠ABC=∠ACB=15°，CD 是腰AB 上的高．求：CD 的长．13．已知：如图，△ABC 中，∠ACB=90°，CD 是高，∠A=30°．求证：BD=AB ．14.已知直角三角形的一个锐角等于另一个锐角的2倍，这个角的平分线把对边分成两条线段．求证：其中一条是另一条的2倍．已知：在Rt △ABC 中，∠A=90°，∠ABC=2∠C ，BD 是∠ABC 的平分线．1415.已知：如图，在Rt △ABC 中，∠C=90°，BC=AB ．求证：∠BAC=30°．16.已知，如图，点C 为线段AB 上一点，△ACM 、△CBN 是等边三角形．求证：AN=BM ．17．一个直角三角形房梁如图所示，其中BC ⊥AC ，∠BAC=30°，AB=10cm ， CB 1⊥AB ，B 1C ⊥AC 1，垂足分别是B 1、C 1，那么BC 的长是多少？18.如图，△ABC 中，AB=AC ，∠A=36°，AC 的垂直平分线交AB 于E ，D 为垂足，连接EC ．（1）求∠ECD 的度数；（2）若CE=5，求BC 长．12专题13.3 等腰三角形知识点1：等腰三角形1.等腰三角形的定义：有两条边相等的三角形叫做等腰三角形．相等的两边叫做腰，另一边叫做底边，两腰所夹的角叫做顶角，底边与腰的夹角叫底角．2.等腰三角形的性质：（1）等腰三角形的两个底角相等（简写成“等边对等角”）．（2）等腰三角形的顶角平分线，底边上的中线、 底边上的高互相重合（通常称作“三线合一”）．3.等腰三角形的判定定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）．知识点2：等边三角形1.定义：三条边相等的三角形叫做等边三角形．2.等边三角形的性质和判定：（1）等边三角形的三个内角都相等，并且每一个角都等于60°。

等腰三角形【分类解析】例1. 如图，已知在等边三角形ABC 中，D 是AC 的中点，E 为BC 延长线上一点，且CE ＝CD ，DM ⊥BC ，垂足为M 。

求证：M 是BE 的中点。

AD1 BM C E分析：欲证M 是BE 的中点，已知DM ⊥BC ，所以想到连结BD ，证BD ＝ED 。

因为△ABC 是等边三角形，∠DBE ＝21∠ABC ，而由CE ＝CD ，又可证∠E ＝21∠ACB ，所以∠1＝∠E ，从而问题得证。

证明：因为三角形ABC 是等边三角形，D 是AC 的中点 所以∠1＝21∠ABC 又因为CE ＝CD ，所以∠CDE ＝∠E 所以∠ACB ＝2∠E 即∠1＝∠E所以BD ＝BE ，又DM ⊥BC ，垂足为M所以M 是BE 的中点 （等腰三角形三线合一定理）例2. 如图，已知：ABC ∆中，AC AB =，D 是BC 上一点，且CA DC DB AD ==，，求BAC ∠的度数。

ABCD分析：题中所要求的BAC ∠在ABC ∆中，但仅靠AC AB =是无法求出来的。

因此需要考虑DB AD =和CA DC =在题目中的作用。

此时图形中三个等腰三角形，构成了内外角的关系。

因此可利用等腰三角形的性质和三角形的内外角关系定理来求。

解：因为AC AB =，所以C B ∠=∠ 因为DB AD =，所以C DAB B ∠=∠=∠；因为CD CA =，所以CDA CAD ∠=∠（等边对等角） 而 DAB B ADC ∠+∠=∠ 所以B DAC B ADC ∠=∠∠=∠22， 所以B 3BAC ∠=∠又因为180=∠+∠+∠BAC C B即180B 3C B =∠+∠+∠ 所以36B =∠ 即求得108BAC =∠说明1. 等腰三角形的性质是沟通本题中角之间关系的重要桥梁。

把边的关系转化成角的关系是此等腰三角形性质的本质所在。

本条性质在解题中发挥着重要的作用，这一点在后边的解题中将进一步体现。

练习一一、选择题1．等腰三角形的周长为26㎝，一边长为6㎝，那么腰长为（）Ａ．6㎝Ｂ．10㎝Ｃ．6㎝或10㎝Ｄ．14㎝2．已知△ABC，AB =AC，∠B=65°，∠C度数是( )A．50° B．65° C．70° D． 75°3．等腰三角形是轴对称图形，它的对称轴是（）A．过顶点的直线B．底边的垂线C．顶角的平分线所在的直线D．腰上的高所在的直线/二、填空题4．等腰三角形的两个_______相等（简写成“____________”）．5．已知△ABC，AB =AC，∠A=80°，∠B度数是_________．6．等腰三角形的两个内角的比是1：2，则这个等腰三角形的顶角的度数是_______________．7．等腰三角形的腰长是6，则底边长5，周长为__________．三、解答题8．如图AB=AD，AD∥BC，求证：BD平分∠ABC．（写出每步证明的重要依据）[9．如图，在△ABC中，AB=AC，D、E分别在AC、AB边上，且BC=BD，AD=DE=EB，求∠A的度数.一、选择题1．B2．B3．C二、填空题4．底角，等边对等角~5．50°6．36°或90°7．16或17三、解答题8．如图AB=AD，AD∥BC，求证：BD平分∠ABC．证明：∵AB=AD（已知）∴∠ABD=∠ADB（等边对等角）∵AD∥BC（已知）∴∠ADB=∠CBD（两直线平行，内错角相等）∴∠ABD=∠CBD（等量代换）|∴BD平分∠ABC．（角平分线定义）9．45练习2一、选择题1．△ABC是等边三角形，D、E、F为各@边中点，则图中共．有正三角形( )A．2个 B．3个C．4个 D．5个2．△ABC中，∠A：∠B：∠C=1：2：3，则BC：AB等于 ( )A． 2：1 B．1：2 C．1：3 D．2 ：3二、填空题3．等边三角形的周长为6㎝，则它的边长为 ________．4．等边三角形的两条高线相交所成钝角的度数是__________．5．在△ABC中，∠A=∠B=∠C，则△ABC是_____三角形．6．△ABC中，∠AC B=90°∠B=60°，BC=3㎝，则AB=_______．—三、解答题7．△ABC是等边三角形，点D在边BC上，DE∥AC，△BDE是等边三角形吗试说明理由．8．已知：如图，P，Q是△ABC边上BC上的两点，且BP=PQ=QC=AP=AQ，求∠BAC的度数．《9．已知：△ABC中，∠ACB=90°，AD=BD，∠A=30°，求证：△BDC是等边三角形．一、选择题[AQ CPB1．D 2．B二、填空题 3．2㎝ 4．120° 5．等边 6．6㎝ 三、解答题7．△ABC 是等边三角形．理由是 ∵△ABC 是等边三角形；∴∠A =∠B =∠C=60° ∵DE ∥AC ，∴∠BED =∠A=60°，∠BDE =∠C =60° ∴∠B =∠BED =∠BDE ∴△ABC 是等边三角形 8．∠BAC=120°9．证明：∵△ABC 中，∠ACB=90°，∠A=30°（已知）∴∠A +∠B=90°（直角三角形两锐角互余）》∴∠B= 90°－∠A= 90°－30°=60°∵△ABC 中，∠ACB=90°，∠A=30°（已知） ∴BC=（在直角三角形中，一个锐角等于30，那么它所对的直角边等于斜边的一半）∴△BDC 是等边三角形（有一个角是60°角的等腰三角形是等边三角形）。

三角形的证明（等腰三角形一）（北师版）一、单选题(共8道，每道12分)1.如图，在等腰三角形ABC中，AB=AC=8，，D为底边BC上一动点（不与点B，C重合），DE⊥AB，DF⊥AC，垂足分别为E，F，则DE+DF的长为( )A.2B.3C.4D.5答案：C解题思路：试题难度：三颗星知识点：等面积法2.如图，在△ABC中，AB=AC，AD⊥BC，垂足为D，E是AC的中点，则=( )A.1：2B.1：3C.1：4D.2：3答案：B解题思路：试题难度：三颗星知识点：等腰三角形3.如图，△ABD，△ACE都是等边三角形，BE和CD交于点O，连接BC，则∠BOC的度数为( )A.120°B.125°C.135°D.150°答案：A解题思路：试题难度：三颗星知识点：三角形全等的性质与判定4.如图，点C在线段AB上，在AB的同侧作等边三角形ACM和等边三角形BCN，连接AN，BM．若∠MBN=38°，则∠ANB等于( )A.82°B.92°C.90°D.98°答案：A解题思路：试题难度：三颗星知识点：等边三角形的性质5.如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，∠A=∠ABE，若AC=5，BC=3，则BD的长为( )A.2.5B.1.5C.2D.1答案：D解题思路：试题难度：三颗星知识点：三线合一6.如图，在△ABC中，BC=9cm，BP，CP分别是∠ABC和∠ACB的平分线，且PD∥AB，PE∥AC，则△PDE的周长是( )A.6cmB.9cmC.10cmD.12cm答案：B解题思路：试题难度：三颗星知识点：角平分线加平行会出现等腰三角形7.如图，已知AE平分∠BAC，BE⊥AE于E，ED∥AC，∠ABE=54°，则∠BED的度数为( )A.108°B.120°C.126°D.144°答案：C解题思路：试题难度：三颗星知识点：由“三线合一”想到构造等腰三角形8.如图，在3×3的网格中，每个网格线的交点称为格点．已知图中A，B两个格点，请在图中再寻找另一个格点C，使△ABC成为等腰三角形，则满足条件的点C有( )A.4个B.6个C.8个D.10个答案：C解题思路：试题难度：三颗星知识点：等腰三角形的存在性。

北师大数学八年级下册第一章三角形的证明第1节等腰三角形练习一、选择题1．等腰三角形的一个角是80°，则它顶角的度数是（ ）A ．80°B ．80°或20°C ．80°或50°D ．20° 答案：B解析：解答：当80°的角是底角时，等腰三角形两底角相等，根据三角形内角和定理得到顶角为20°；另一种情况是80°是顶角.分析：等腰三角形等边对等角，结合三角形内角和为180°，从而得出两种结果.2．已知等腰三角形的两边长分别是3和5，则该三角形的周长是（ ）A ．8B ．9C ．10或12D ．11或13答案：D解析：解答：当3是腰时，两腰和为6加上底边5，周长为11；当5是腰时，两腰和为10加上底边3，周长为13.分析：等腰三角形两腰相等，结合三角形中两小边和大于第三边.3．在等腰△ABC 中，AB =AC ，中线BD 将这个三角形的周长分为15和12两个部分，则这个等腰三角形的底边长为（ ）A ．7B ．11C ．7或11D ．7或10答案：C解析：解答：设AB =AC =x BC =y则有12,2152x x x y +=+=⎧⎨⎩或者12,2152x x x y +=+=⎧⎨⎩ 所以x =8， y =11或者x =10，y =7.即三角形AB =AC =8，BC =11.或AB =AC =10，BC =7.故选C.分析：等腰三角形两腰相等，会解二元一次方程.4．等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为（ ）A ．60°B ．120°C ．60°或150°D ．60°或120°答案：D解析：解答：分两种情况：一种是这个高在三角形内,即此三角形是锐角三角形顶角=180°-90°-30°=60°，另一种是这个高落在一腰延长线上,即此三角形为钝角三角形顶角的补角=180°-90°-30°=60°，顶角=180°-60°=120°.分析：此题要注意分两种情况，要考虑锐角三角形和钝角三角形.5.在等腰△ABC中，AB=AC，BD⊥AC，∠ABC=72°，则∠ABD=（）A．36°B．54°C．18 °D．64°答案：B解析：解答：∵AB=AC，∠ABC=72°，∴∠ABC=∠ACB=72°，∴∠A=36°.∵BD⊥AC，∴∠ABD=90°-36°=54°.分析：根据等腰三角形的性质由已知可求得∠A的度数，再根据垂直的定义和三角形内角和定理不难求得∠ABD的度数.6. 在△ABC中，D是BC上的点，AB=AD=DC，∠B=70°，则∠C的度数为（）A．35°B．40°C．45°D．50°答案：A解析：解答：∵AB=AD, ∴∠ADB=∠B=70°.∵AD=DC，∴12C DAC ADB∠=∠=∠=35°.分析：等腰三角形两底角相等，再根据三角形的外角等于和它不相邻的两个内角和.7. 在△ABC中，∠B=∠C，AB=5，则AC的长为（）A．2 B．3 C．4 D．5答案：D解析：解答：∵∠B=∠C，∴AB=AC=5．分析：等腰三角形的性质可得AB=AC，继而得出AC的长．8. 在矩形ABCD中，AB＜BC，AC，BD相交于点O，则等腰三角形的个数是（）A．8 B．6 C．4 D．2答案：C解析：解答：∵四边形ABCD是矩形，∴AO=BO=CO=DO，∴△ABO，△BCO，△DCO，△ADO都是等腰三角形.分析：根据矩形的对角线相等且互相平分可得AO=BO=CO=DO，进而得到等腰三角形.9. 在等腰△ABC中，AB=AC，其周长为20 cm，则AB边的取值范围是（）A．1 cm＜AB＜4 cm B．5 cm＜AB＜10 cm C．4 cm＜AB＜8 cm D．4 cm＜AB＜10cm 答案：B解析：解答：∵在等腰△ABC中，AB=AC，其周长为20cm，∴设AB=AC=x cm，则BC=（20-2x）cm，∴2x＞20−2x，即20−2x＞0.解得5 cm＜x＜10 cm．分析：设AB=AC=x，则BC=20-2x，根据三角形的三边关系即可得出结论.10. 在△ABC中，∠ACB=90°，BE平分∠ABC，ED⊥AB于D．如果∠A=30°，AE=6cm，那么CE等于（）A. 4 cm B．2 cm C. 3 cm D.1 cm答案：C解析：解答：∵ED⊥AB，∠A=30°，∴AE=2ED，∵AE=6cm，∴ED=3cm.∵∠ACB=90°，BE平分∠ABC，∴ED=CE，∴CE=3cm.分析：根据在直角三角形中，30度所对的直角边等于斜边的一半得出AE=2ED，求出ED，再根据角平分线到两边的距离相等得出ED=CE，即可得出CE的值11.在平面直角坐标系xOy中，A（0，2），B（0，6），动点C在直线y=x上．若以A、B、C三点为顶点的三角形是等腰三角形，则点C的个数是( )A．2 B．3 C．4 D．5答案B解析：解答：AB的垂直平分线与直线y=x相交于点C1，∵A（0，2），B（0，6），∴AB=6-2=4，点A为圆心，以AB的长为半径画弧，与直线y=x的交点为C2，C3∴点B到直线y=x的距离为6×32=33，∵33＞4，∴以点B为圆心，以AB的长为半径画弧，与直线y=x没有交点，所以，点C的个数是1+2=3．分析：根据线段垂直平分线上的点到线段两端点的距离相等可得AB的垂直平分线与直线y=x 的交点为点C再求出AB的长，以点A为圆心，以AB的长为半径画弧，与直线y=x的交点为点C，求出点B到直线y=x的距离可知以点B为圆心，以AB的长为半径画弧，与直线没有交点12. 在△ABC中，AB=20 cm，AC=12 cm，点P从点B出发以每秒3 cm的速度向点A运动，点Q从点A同时出发以每秒2 cm的速度向点C运动，其中一个动点到达端点时，另一个动点也随之停止运动，当△APQ是以PQ为底的等腰三角形时，运动的时间是（）A．2.5秒B．3秒C．3.5秒D．4秒答案：D解析：解答：设运动的时间为x cm/s，在△ABC中，AB=20cm，AC=12cm点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动当△APQ是等腰三角形时，AP=AQ，AP=20-3x，AQ=2x即20-3x=2x，解得x=4．分析：设运动的时间为x，则AP=20-3x，当APQ是等腰三角形时，AP=AQ，则20-3x=2x，解得x即可.13. 等腰但不等边的三角形的角平分线、高线、中线的总条数是（）A．3 B．5 C．7 D．9答案：C解析：解答：等腰但不等边的三角形底边上的角平分线、中线、高线三线重合成一条；腰上的三条线不重合，因而共有7条线.分析：画出图形，根据等腰三角形的性质进行分析即可得到答案14. 已知△ABC中，三边a，b，c满足|b-c|+（a-b）2=0，则∠A等于（）A. 60°B．45°C．90°D．不能确定答案：A解析：解答：△ABC中，三边a，b，c满足|b-c|+（a-b）2=0∴b-c=0，a-b=0，∴a=b=c，∴三角形是等边三角形，∴∠A=60°.分析：根据非负数的性质列式求解得到a=b=c，然后选择答案即可.15.等腰三角形周长为36cm，两边长之比为4：1，则底边长为（）A．16cm B．4cm C．20cm D．16cm或4cm答案：B解析：解答：因为两边长之比为4：1，所以设较短一边为x，则另一边为4x；(1)假设x为底边，4x为腰；则8x+x=36，x=4，即底边为4；(2)假设x为腰，4x为底边，则2x+4x=36，x=6，4x=24；∵6+6＜24，∴该假设不成立．所以等腰三角形的底边为4cm．分析：题中只给出了两边之比，没有明确说明哪个是底哪个是腰，所以应该分两种情况进行分析，再结合三角形三边的关系将不合题意的解舍去.二、填空题16. 等腰三角形的一个外角为110°，则底角的度数可能是_______.答案：70°或55°解析：解答：当110°是等腰三角形底角的外角时，底角为70°；当110°是等腰三角形顶角的外角时，因为等腰三角形两底角相等，所以一个底角的度数等于外角110°的一半，即55°分析：外角与它相邻的内角互补，外角等于和它不相邻的两个内角和.17. 等腰三角形的对称轴是____________.答案：底边上的高(顶角平分线或底边的中线)所在的直线解析：解答：根据等腰三角形的性质，等腰三角形的对称轴是底边上的高（顶角平分线或底边的中线）所在的直线．分析：本题根据等腰三角形是轴对称图形，其对称轴是底边上的高所在的直线，因为等腰三角形底边上的高，顶角平分线，底边上的中线三线合一，所以等腰三角形的对称轴是底边上的高（顶角平分线或底边的中线）所在的直线．18.△ABC中，AB=AC，∠A=36°，BD平分∠ABC，则∠1 =_______度，此三角形有_______个等腰三角形．答案：72°/3解析：解答：∵AB=AC，∠A=36°，∴△ABC是等腰三角形，∠C=∠ABC=（180°−36°）12⨯=72°.∵BD为∠ABC的平分线，∴∠ABD=∠A=∠DBC=36°，∴AD=BD，△ADB是等腰三角形，∴∠1=180°-36°-72°=72°=∠C，∴BC=BD，△CDB是等腰三角形.图中共有3个等腰三角形．分析：由已知条件，根据三角形内角和等于180、角的平分线的性质求得各个角的度数，然后利用等腰三角形的判定进行找寻，注意做到由易到难，不重不漏.19. 在△ABC中，与∠A相邻的外角是100°，要使△ABC是等腰三角形，则∠B的度是_________.答案：80°或50°或20°解析：解答：∵∠A的相邻外角是100°，∴∠A=80°．分两种情况：（1）当∠A为底角时，另一底角∠B=∠A=80°；（2）当∠A为顶角时，则底角∠B=∠C=(180°−80°)12⨯=50°（3）当∠B是顶角时，∠B=180°-2∠A=20°．综上所述，∠B的度数是80°或50°或20°.分析：已知给出了∠A的相邻外角是100°，没有明确是顶角还是底角，所以要进行分类讨论，分类后还有用内角和定理去验证每种情况是不是都成立.20. 在△ABC中，若∠A=80°，∠B=50°，AC=5，则AB=_______.答案：5解析：解答：∵∠A=80°，∠B=50°，∴∠C=180°-80°-50°=50°.∴AB=AC=5.分析：由已知条件先求出∠C的度数是50°，根据等角对等边的性质求解即可.三、解答题.21.在△ABC中，AB=AC，AD是BC边上的高，∠C=63°，BC=4，求∠BAD的度数及DC的长.答案：27°/2 解答：∵AB =AC ，∠C =63°，∴∠B =∠C =63°，∴∠BAC =180°-63°-63°=54°. 又∵AD 是BC 边上的高，∴AD 是∠BAC 的平分线，AD 是BC 边上的中线，∴∠BAD =12∠BAC =27°，DC =12BC =2. 解析：分析：根据等腰三角形的两个底角相等求出顶角∠BAC 的度数，再由等腰三角形的三线合一性质即可求出∠BAD =12∠BAC =27°，DC =12BC =2. 22.在△ABC 中，AB =AC ，BD ⊥AC 于D ，CE ⊥AB 于E ，BD 、CE 相交于F .求证：AF 平分∠BAC答案：证明：∵AB =AC ，∴∠ABC =∠ACB .又∵BD ⊥AC ，CE ⊥AB ，∴∠BEC =∠CDB =90°. 在△BCE 和△CBD 中，∠ABC =∠ACB ，∠BEC =∠CDB ，BC =BC.∴△BCE ≌△CBD （AAS ）.∴BE =CD.∵AB =AC ，BE =CD ，∴AB -BE =AC -CD ，∴AE =AD.∴在△AEF 和△ADF 中，AE =AD , AF =AF.△AEF ≌△ADF （HL ）.∴∠EAF =∠DAF ，AF 平分∠BAC.解析：分析：要通过两次三角形全等，再结合等腰三角形的性质得出结论.23.如图，已知点B 、C 、D 在同一条直线上，△ABC 和△CDE 都是等边三角形.BE 交AC 于F ，AD 交CE 于H ，求证：（1）△BCE ≌△ACD ； 答案：证明：∵△ABC 和△CDE 都是等边三角形，∴∠BCA =∠DCE =60°，BC =AC =AB ，EC =CD =ED ，∴∠BCE =∠ACD .在△BCE 和△ACD 中，,,,BC AC BCE ACD CE CD =⎧∠=∠=⎪⎨⎪⎩∴△BCE ≌△ACD （S A S ）；（2）CF =CH ； 答案：∵△BCE ≌△ACD ，∴∠CBF =∠CAH ．∵∠ACB =∠DCE =60°，在△BCF 和△ACH 中，∴∠ACH =60°，∴∠BCF =∠ACH ，,,,CBF CAH BC AC BCF ACH ∠=∠=∠=∠⎧⎪⎨⎪⎩∴△BCF ≌△ACH （A S A ），∴CF =CH ；（3）△FCH 是等边三角形；答案：∵CF =CH ，∠ACH =60°，∴△CFH 是等边三角形．（4）FH ∥BD.答案：证明：∵△CHF 为等边三角形∴∠FHC =60°，∵∠HCD =60°，∴FH ∥BD解析：分析：由等边三角形的三边相等，三角都是60°，再根据平角的关系，就能证明△BCE ≌△ACD ；由△BCE ≌△ACD 得出对应角相等，结合等边三角形的边角特点证明△BCF ≌△ACH ，能得出CF =CH ；两边等，加上一个角60°推出△CFH 是等边三角形；根据内错角相等，两直线平行推出FH ∥BD .24. 如图，已知AB =AC =AD ，且AD ∥BC ，求证：∠C =2∠D答案：证明：∵AB=AC=AD，∴∠C=∠ABC，∠D=∠ABD.∴∠ABC=∠CBD+∠D.∵AD∥BC，∴∠CBD=∠D，∴∠ABC=∠D+∠D=2∠D，又∵∠C=∠ABC，∴∠C=2∠D.解析：分析：首先根据AB=AC=AD，∵AD∥BC，∴∠D=∠DBC可得∠C=∠ABC，∠D=∠ABD，∠ABC=∠CBD+∠D；然后根据AD∥BC，可得∠CBD=∠D，据此判断出∠ABC=2∠D，再根据∠C=∠ABC，即可判断出∠C=2∠D25.如图，在△ABC中，∠B与∠C的平分线交于点O，过O点作DE∥BC，分别交AB、AC于D、E，若AB=5，AC=4，求△ADE的周长.答案：解答：∵在△ABC中，∠B与∠C的平分线交于点O，∴∠DBO=∠CBO，∠ECO=∠BCO，∵DE∥BC，∴∠DOB=∠CBO，∠EOC=∠BCO，∴∠DBO=∠DOB，∠ECO=∠EOC，∴OD=BD，OE=CE，∵AB=5，AC=4，∴△ADE的周长为：AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+AC=5+4=9.解析：分析：由在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，易证得△DOB与△EOC是等腰三角形，即DO=DB，EO=EC，继而可得△ADE的周长等于AB+AC，即可求得答案．。