不完全市场下投资组合选择的鞅方法

不完备市场上基于虚拟证券的鞅测度
朱捷;王生喜;王杰
【期刊名称】《哈尔滨商业大学学报:自然科学版》
【年(卷),期】2022(38)5
【摘要】基于多维扩散过程所驱动的不完备市场,引入虚拟证券,研究了不同准则下的最优鞅测度问题.首次提出了均方误差次优准则及相对均方差次优准则,并在上述两个准则下,得到了鞅测度的显式表达,验证了上述鞅测度在二阶矩意义上与极小鞅测度、相对熵极小鞅测度以及方差最优鞅测度无差异.
【总页数】7页(P604-609)
【作者】朱捷;王生喜;王杰
【作者单位】广东科技学院;厦门大学嘉庚学院
【正文语种】中文
【中图分类】O211.63
【相关文献】
1.跳扩散半鞅的最小鞅测度与最小熵鞅测度
2.最小对称熵鞅测度和不完备市场中的定价问题
3.右连续信息域下连续半鞅的方差最优鞅测度
4.证券市场上虚假陈述行不的法律责任
5.虚拟资本与我国公司在证券市场上的融资
因版权原因，仅展示原文概要，查看原文内容请购买。

Lévy市场下保险公司的最优投资策略作者：孙海霞来源：《财会学习》 2017年第18期文 / 孙海霞摘要：本文假设投资者是损失厌恶的，保险公司的盈余和风险资产价格过程都是列维过程。

保险公司的目标是当最终财富超过他的期望水平时，期望效用最大。

本文主要通过鞅方法，把动态问题转化为静态问题，求出最优投资策略和最终财富的确切表达式。

关键词：鞅方法；最优投资；损失厌恶一、引言随着保险公司可以在资本市场进行投资，越来越多的投资者关注保险公司的投资组合问题，在现实生活中保险公司投资决策者并不是完全理性的，最著名的就是累积前景理论 (CPT) 来弥补 EUM 的缺陷，在 Guo(2014) 之前没有人把 CPT 引入保险公司的投资决策中，Guo(2014) 即引入进来，并指出保险公司的盈余是服从列维过程，然而在保险公司在资本市场进行投资的时候，价格过程由于受到很多因素的影响，不是一个连续的过程，而是存在一个跳的的过程，至今还没有文章在CPT 原理中加入保险公司的风险资产价格服从列维过程。

本文假设者是损失厌恶的，满足 S- 型效用函数，为了使模型更具有现实性，我们假定保险公司投资于一种无风险资产和 n 种风险资产，风险资产的价格过程服从列维过程，并且假定保险公司的盈余过程也是服从列维过程的。

再运用鞅方法，得出最优投资策略和最优财富过程。

二、模型假设保险公司在时间 [0，T] 内在资本市场投资 n+1 种资产，一种无风险资产和 n 种风险资产，其中无风险资产的价格满足根据效用最大化准则，保险公司的最优投资问题可以表示成如下形式：三、最优模型的求解用鞅方法去解决这一问题，定义折现因子为：结果表明，最终财富是一个不连续的过程，在好的状态下的时候不会超过最终财富时，投资者将获得超过参考点的财富。

在不好的状态下的时候，会超过最终财富时，投资者的最终财富为零。

这是由于对于损失厌恶投资而言，面对损失时是风险喜好的，投资者为了获得更大的收益，可以接受更大的损失。

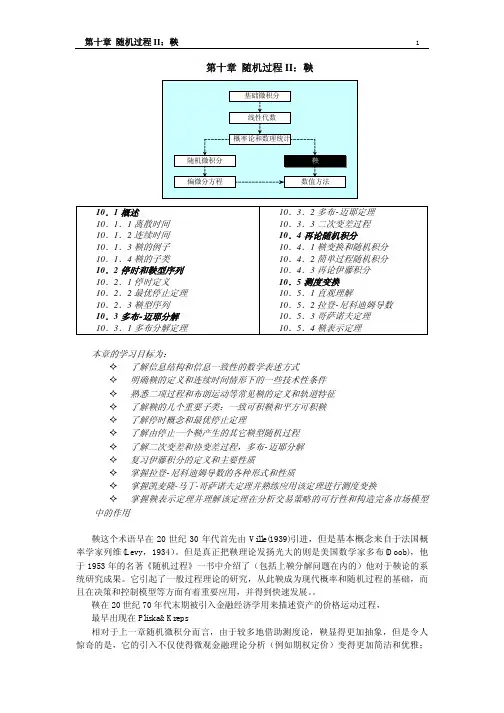
剀利公式：在反等价鞅策略下，每次下赌注的百分之多少，才可以实现最快的盈利？答案：K = W - (1-W)/RK：每次下注所占总资金的比例， W：你的策略的胜率， R下注的赔率投硬币游戏：W=0.5 R=2 那么 K = 0.5-(1-0.5)/2 = 0.25也就是说，投硬币游戏中，只要你每次投入你的总资金的四分之一，永远遵守这个几率的玩下去，那么，你将以最快的速度成为亿万富翁。

这个公式是引用自Ed Seykota 的风险管理文章。

外汇市场和期货市场呢？我们引用剀利公式的基础方程：K = (W*R-1)/(R-1)K,W, R的定义同上。

于是，我们发现，盈利有一个基本的前提，那就是你的胜率乘以你的赔率，结果必须大于1，否则无论如何都不可能盈利。

投硬币游戏中W*R=1，正好期望值是持平的。

但是由于我们“永远亏不光”，而且我们总有“停手”的那一天，所以，我们可以选择我们赚到一亿美元时候停手，所以，成为亿万富翁仍然是可能的。

根据剀利公式的基础方程，来考虑外汇市场和期货市场。

假设我每一单的胜率是W=0.5，每一单的止赢和止损的比例是2:1,也就是说，赔率R=3。

这样，根据剀利基础方程，K=(0.5*3-1)/(3-1) = 25%，也就是说，每一单的仓位设置，需要达到总资金的25%时候是最优解。

如果胜率是0.4,那么K=10%如果止赢和止损比是3:1,那么赔率R=4, 胜率W=0.4 那么K = (0.4*4-1)/(4-1) = 20%胜率W=0.3的话K = (0.3*4-1)/(4-1) = 6.7%看到这里，我想你应该明白了为什么无数的汇市和期市的老手告诉我们：“每次投入资金的10%-20%，止赢和止损的比例设置成2:1和3:1，这样即使你的胜率是40%甚至30%，你都可以稳定盈利!"这就是最最普遍的资金管理技巧的数学基础－－剀利公式！看到这里，你可能为说，要是这么简单的话，为什么股市汇市期市里面有90%的人赔钱呢？注意到，剀利公式只有战略上的指导意义，而并不具有操作意义。

股票市场中不完全信息两阶段博弈分析股票市场中不完全信息两阶段博弈分析摘要：股票市场作为一个充满不完全信息的环境，对于投资者而言存在很大的不确定性。

本文将利用博弈论的分析方法，通过两阶段的博弈模型来探讨股票市场中的投资决策问题。

在第一阶段，投资者基于已有的信息作出决策，并表达出预期的市场走势。

在第二阶段，根据市场的实际表现，投资者再次作出决策并调整策略。

通过分析两阶段博弈模型，可以更好地理解股票市场中的投资行为，为投资者提供决策依据。

关键词：股票市场、不完全信息、两阶段博弈、投资决策引言股票市场作为一种充满不完全信息的环境，投资者面临着巨大的不确定性。

在进行投资决策时，投资者往往需要基于市场现有的信息进行判断，但这些信息并不完全反映市场的真实情况。

因此，投资者需要运用各种方法和手段来分析市场走势，并根据自身的判断作出相应的投资决策。

博弈论作为一种经济学分析工具，能够帮助我们更好地理解和解决不完全信息下的决策问题。

博弈论研究的是在一定的策略和规则下个体之间的互动行为。

在股票市场中，投资者之间的交易和决策也可以看作是一种博弈行为。

本文将运用博弈论的分析方法，通过两阶段的博弈模型来探讨股票市场中的投资决策问题。

一、股票市场中的不完全信息不完全信息是指在进行决策时，个体无法获得或掌握全部有关决策环境的信息。

在股票市场中，投资者面临着大量的信息，包括市场行情、公司财务状况、宏观经济政策等。

然而，这些信息往往不够全面和准确，投资者需要在有限的信息基础上做出决策。

投资者在进行投资决策时，往往会借助各种方法和工具来分析市场走势。

例如，投资者可以通过技术分析来研究历史走势，以预测未来的市场表现；或者通过基本面分析来评估公司的财务状况和经营业绩。

这些方法和工具可以帮助投资者更好地理解市场，但并不能保证投资决策的准确性。

二、两阶段博弈模型在股票市场中，投资者的决策是一个连续过程。

为了更好地分析投资者的行为，我们可以将投资过程划分为两个阶段的博弈模型。

鞅方法在股票市场中的应用作者：李年平杨莉周俊来源：《经济研究导刊》2009年第18期摘要:从股票市场出发,通过对指数O—U模型期权定价进行再分析,在此基础上引入概率测度p*,从而在指数鞅成立条件下利用买卖平价关系得到定价公式,并应用于上证综合指数与深证成分指数收益率分析,得到股票市场的一般性结论。

关键词:鞅方法;股票市场;等价鞅测度;上证综合指数;深证成分指数中图分类号:F830.91文献标志码:A文章编号:1673-291X(2009)18-0074-02一、引言自1953年Doob首次系统地提出鞅论以来,作为有效的理论工具已广泛应用到各个领域,如马氏过程、点过程、估计理论、随机过程等。

在这些应用中,等价鞅测度成为了分析金融产品定价,消费金融投机套利机会,降低金融产品投资风险的主要工具。

在中国股票市场中,等价鞅测度是定价期权的关键,鞅假设是检验中国股票市场弱势有效性[1]的基础,面对金融危机中的股票市场,如何利用鞅方法对股票市场进行期权定价的有效分析呢?文献[2]给出了零时刻的定价公式,而本文从鞅方法基本内容出发,通过对股票市场中指数O—U模型期权定价进行再分析,得到对股票市场中的期权定价加入有效性假设研究的基础上的股票市场结论。

二、预备知识1.鞅的定义。

为了便于后面的说明,现在引入鞅的定义。

由于研究股票市场需要,故定义贴现股票价格过程的鞅测度。

在等价鞅测度下,下面命题对研究股票收益率十分必要。

命题[4]:在等价鞅测度下,每一种风险资产的期望收益率都等于无风险资产收益率。

三、主要结论为了研究股票市场期权定价加入有效性假设的一般性结论,先定义弱势有效市场假设。

定义4[1]:弱势有效市场的市场效率最低,是指当前股票价格能够充分的反映股票本身历史价格所包含的信息,在这种市场上,股票价格过去的变动趋势对于判断价格的未来走势没有任何关系,股票价格是相对独立的。

弱势在文献[2]中,对指数O—U模型给出了零时刻的价格定价公式,在这基础上,我们引入p*等价鞅测度,而在期权定价的鞅方法中最重要是找到等价鞅测度[5],使得贴现的股票价格过程是鞅。