当前位置：文档之家 › 工程力学梁横截面上的切应力及梁的切应力强度条件

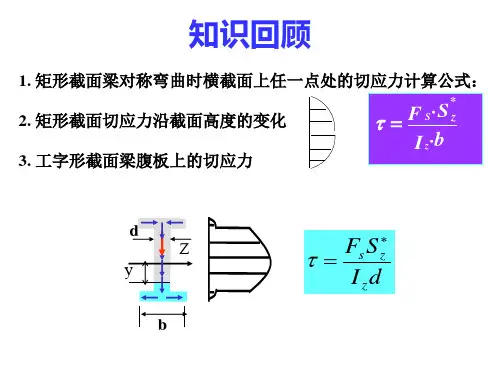
工程力学梁横截面上的切应力及梁的切应力强度条件

  • 格式：ppt
  • 大小：521.50 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

材料力学 弯曲应力与强度条件

材料力学 弯曲应力与强度条件
F
150 50
A
l 2
B
l 2
96 .4 C 50
200
z
M max
FL 16kNm 4
y
max max
200 50 96.4 153.6mm 96.4mm

max
My max IZ My max IZ
24.09MPa 15.12MPa
max
例题
长为2.5m的工字钢外伸梁，如图示，其外伸部分为0.5m，梁上 承受均布荷载，q=30kN/m，试选择工字钢型号。已知工字钢抗弯 强度［σ］=215MPa。
q 30 kN m
A
0.5m
解：1、求支反力，画梁的弯矩图，确 定危险截面 FA 46.9KN , FB 28.1KN
E
y
X
A

0:
y
A
N dA E
A

dA
E

A
ydA 0
S Z ydA yc A 0(中性轴通过截面形心）
M
A
Z
0:
M Z ydA M
A
M yE dA
y
E


y 2 dA 令： y 2 dA I Z A



C截面
c
B
B截面
∴铸铁梁工作安全。如果T截面倒
例题
A
y 铸铁制作的悬臂梁，尺寸及受力如图示，图中F＝20kN。梁 的截面为T字形，形心坐标yc=96.4mm。已知材料的拉伸许用应 150 力和压缩许用应力分别为[σ]+＝40MPa， [σ]－＝100MPa。试 校核梁的强度是否安全。 F 50 96 .4

第九章 梁的应力

第九章 梁的应力

38
第二节 梁的切应力、切应力强度条件
◆例题
例 7 ： FS = 15 b = 120 mm，d 20 mm， yC
= 45 mm。试求 ：tmax ；腹板与翼
缘交接处切应力 ta
解：
Sz ,max
d (d
b 2
yC )2
9.03 105
b(h02 h2 ) 2d (h2 4 y2 )
第九章
37
第二节 梁的切应力、切应力强度条件 ◆ 梁的正应力与梁的剪应力比较
s max

Fl bh2

6Fl bh2
6
t max

3F 2 bh
s max t max

6Fl bh2
2bh 3F

4
l h

第九章
当 l >> h 时，smax >> tmax
E
ymax

2. 应力计算
第九章
D d 0.701m
22
ymax
d
2
1.0 103 m
s max

E
ymax


285 MPa
10
第一节 梁的正应力、正应力强度条件
静力学方面
ysdA M
A
联立求解得：
E y2dA M
A
1

M EI z
结 论:
中性层曲率：
22
ymax
d
2
1.0 103 m
s max

E
ymax


285 MPa
3. 弯矩计算
1 M

《工程力学》——梁的强度与刚度

《工程力学》——梁的强度与刚度
（１）、 公式： （２）、 认为最大弯曲切应力近似等于腹板的平均切应力。
《工程力学》——沙市大学建筑工程系
四、 弯曲切应力的强度计算：
１、 强度条件： τmax≤[τ] [τ]---梁所用材料的许用切应力
（危险截面）。 (２)、 利用弯曲正应力强度条件求解。
《工程力学》——沙市大学建筑工程系
二、例题：
例1：简支矩形截面木梁如图所示，L=5m,承 受均布载荷q=3.6kN/m，木材顺 纹许用应力 ［σ］＝10MPa，梁截面的高宽比h/b=2，试 选择梁的截面尺寸。
《工程力学》——沙市大学建筑工程系
有的变短。其中有一层既不伸长也不缩短， 这一层称为中性层。
中性轴：中性层与横截面的交线称为中性轴。
《工程力学》——沙市大学建筑工程系
《工程力学》——沙市大学建筑工程系
２、纯弯曲时梁的正应力的分布规律： 以中性轴为分界线分为拉区和压区，正弯
矩上压下拉，负弯矩下压上拉，正应力成线 性规律分布，最大的正应力发生在上下边沿 点。
１、 对于塑性材料，一般截面对中性轴上下 对称，最大拉、压应力相等，而塑性材料的 抗拉、压强度又相等。
《工程力学》——沙市大学建筑工程系
塑性材料的弯曲正应力强度条件为：
（1）、强度校核 （2）、截面设计 （3）、确定许可荷载
《工程力学》——沙市大学建筑工程系
２、 弯曲正应力强度计算的步骤为： (１)、 画梁的弯矩图，找出最大弯矩
2、求截面对形心轴z轴的惯性矩
《工程力学》——沙市大学建筑工程系
第二十五讲 弯曲正应力强度计算（一）
目的要求：掌握塑性材料弯曲正应力强度 计算。
教学重点：弯曲正应力强度条件的应用。 教学难点：弯曲正应力强度条件的理解。

材料力学土木类第四章 弯曲应力.ppt

材料力学土木类第四章 弯曲应力.ppt
2、这些切应力沿 y方向的分量
ty沿宽度相等。
最大切应力tmax 在中性轴z处
t max

FS
S
* z
Izd

FS

1 2

πd 2 4

2d
3π

πd 4 d
64
4FS 4FS 3 π d 2 3A 4
2d /3p
d
tmax
O
k
k'
O' y
薄壁环形截面梁弯曲切 应力的分布特征：
(1) <<r0→沿壁厚切应 tmax
r0
tmax
力的大小不变；
O
(2) 内、外壁上无切应力 t
→切应力的方向与圆周
y
相切；
(3) y轴是对称轴→切应 力分布与 y轴对称；与 y
最大切应力tmax 仍发生
在中性轴z上。
轴相交的各点处切应力
为零。
薄壁环形截面梁最大切应力的计算
45
45
Wz

Iz ymax

75103 9.5 274.6
28.8MPa [t ]
满足强度条件
例4-20 图示外伸梁，由工字钢制成。已知材料的许 用正应力[σ ]=160MPa,许用剪应力 [τ ]=90MPa。试 选择工字钢的型号。
50kN
80kN
A 150 500
B 500 47.5kN
50kN 7.5kN.m
料均为Q235钢，其[s ]=170MPa，[t ]=100MPa。试校
核该梁的强度。
50kN 50kN 50kN
F1 F2
100 9.5
10 320 10

《工程力学(工程静力学与材料力学)(第3版)》习题解答：第8章 剪应力分析

《工程力学(工程静力学与材料力学)(第3版)》习题解答：第8章 剪应力分析
1．绘出梁的剪力图和弯矩图；
2．确定梁内横截面上的最大拉应力和最大压应力；
3．确定梁内横截面上的最大切应力；
4．画出横截面上的切应力流。
知识点：弯曲切应力公式的应用、切应力流
难度：难
解答：
1．图（a）：
kN
， kN
剪力与弯矩图如图（b）、（c）；
2．形心C位置
MPa
MPa
3． m3
MPa
4．切应力流如图（e）。
（A）下移且绕点O转动；
（B）下移且绕点C转动；
（C）下移且绕z轴转动；
（D）下移且绕 轴转动。
知识点：弯曲中心、薄壁截面梁产生平面弯曲的加载条件
难度：一般
解答：
正确答案是D。
8－19试判断下列图示的切应力流方向哪一个是正确的。
知识点：横向弯曲时梁横截面上的切应力流、弯曲切应力分析方法
难度：难
解答：
（A）细长梁、横截面保持平面；
（B）弯曲正应力公式成立，切应力沿截面宽度均匀分布；
（C）切应力沿截面宽度均匀分布，横截面保持平面；
（D）弹性范围加载，横截面保持平面。
知识点：弯曲时梁横截面上切应力分析
难度：易
解答：
正确答案是B。
公式 推导时应用了局部截面的正应力合成的轴力，该正应力 则要求弯曲正应力公式成立；另外推导时在 时，应用了 沿截面宽度均匀分布假设。
难度：难
解答：
正确答案是D。
8－21简支梁受力与截面尺寸如图所示。试求N－N截面上a、b两点的铅垂方向的切应力以及腹板与翼缘交界处点c的水平切应力。
知识点：弯曲切应力公式的应用、切应力流
难度：难
解答：
FQ = 120kN，形心C位置。

工程力学(基础力学、材料力学)14(30)第九章6节

工程力学(基础力学、材料力学)14(30)第九章6节


158.4 106 170
158.4kNm
930 103 ( m m3 )
查表选36c型号 I z 17310 cm 4 ; d 14 mm ; I z
3、切应力校核 max
4、结论：选36c型号
F
s max z
S Fs max 112.5 10 27( MPa) I z d 29.9 1014 Izd S z
q B l/2 17 KN 12 KN 12KN.m
F C l/2 D
检查此梁是否安全。
解：（1）作内力图
Fs图
13KN
max
M max Wz
M图
max
Fs max S zmax I zb
39KN.m
（2）计算几何性质
查表得
W z 309cm 3 0.309 103 m 3 Iz S z , max 18.9cm 0.189m
max [ ]
对于等直梁
F
S ,max
S
b
* z max
I
[ ]
z
b 为中性轴处的宽度。
对于横力弯曲下的等直梁 ，其横截面上一般既有弯矩
又有剪力。 梁上最大正应力发生在弯矩最大的横截面上距中性轴最远 的各点处 。 而梁上最大的切应力发生在剪力 最大的横截面上中性轴上 的各点处 。
梁除满足正应力强度条件外，还需满足切应力强度条件。
z
b 120(m m) F max 1.5 h 180(m m) bh b=140mm；h=210mm
lx Fs ( x) F x 0; Fs max F l x Fs1 ( x) F x l ; Fs1max F l

材料力学《第五章》弯曲应力

材料力学《第五章》弯曲应力
上海交通大学
1
2
c
O1
d
O2
a
1 1 2
b
2
M
d
O2
c
O1
a
1
b
2
O z y
由变形的连续形可知：
从伸长到缩短的过程中，必存在一 层纵向纤维既不伸长也不缩短，保 持原来的长度。 中性层：由既不伸长也不缩短的纵 M 向纤维组成。 中性轴：中性层与梁横截面的交线。 中性轴垂直于梁横截面的纵向对称轴。 a
1
1
2
c
O1
d
O2
a
1 1 2
b
2
M
d
O2
c
O1
b
2
3. 在伸长区，梁宽度减小， 在缩短区，梁宽度增加。 与轴向拉、压时变形相似。
上海交通大学
O z y
二、假设 1. 梁弯曲平面假设 梁弯曲变形后，横截面仍保持为平 面，并仍与已变弯后的梁轴线垂直， 只是绕该截面内某轴转过一个微小 M 角度。 2. 单向受力假设 设想梁由许多层纵向纤维组成，弯 曲时各纵向纤维处于单向受拉或单 向受压状态。 由实验现象和假设可推知： 弯曲变形时： 靠近梁顶面的纵向纤维受压、缩短； 靠近梁底面的纵向纤维受拉、伸长。
O1Biblioteka 1dqr2
O2
M
a
1
y
b
2
中性层下方，y 为正值， s 也为正值，表示为拉应力； 中性层上方，y 为负值， s 也为负值，表示为压应力。 y =0 (中性轴上)，s = 0 ； y |max (上、下表层)， s max 。
由(b)式可得s 的分布规律，但因r 的数值未知，中性轴的位置未确定， y 无从算起，所以仍不能计算正应力，用静力学关系解决。

梁的切应力及强度条件

梁的切应力及强度条件

2.2mm的钢板加强加强段的横截面尺寸如图所示.已知许用弯曲
正应力[]=152MPa，许用切应力 []=95MPa.试校核此梁的强度. 解：加强后的梁是阶梯状
10
变截面梁. 所以要校核
2.2m
上的弯曲正应力； （2）F靠近支座时支座截面上的切应力； （3）F移至未加强的梁段在截面变化处的正应力.
F A C 5m FSmax B
FS max FRA F 30kN
查型钢表中，20a号工字钢，有
Iz S
* z max
17.2cm
d=7mm
据此校核梁的切应力强度
F S max S max Izd
* z max
+
24.9MPa [ ]
以上两方面的强度条件都满足，所以此梁是安全的.
5m 37.5 kN· m
M max 37.5kN m
所以梁的最大正应力为
（a）正应力强度校核 由型钢表查得20a工字钢的 W z 237cm
σ max
M max 158MPa [σ ] Wz
+
3
(Stresses in Beams)
（b）切应力强度校核 在计算最大切应力时，应取荷载F在紧靠任一支座例如支 座A处所示，因为此时该支座的支反力最大，而梁的最大切应 力也就最大.
两截面上距中性轴 y1 处的正应力为1 和2.
FN1 σ1dA
A1
y
x
My1 M dA y1dA FN1 A1 I I z A1 z M 1dA Sz Iz M dM FN 2 σ 2dA Sz A1 Iz
A1
dFS’
A
B1
m’

《材料力学》讲义4-4梁横截面上正应力梁正应力条件

《材料力学》讲义4-4梁横截面上正应力梁正应力条件
q 3.5 2 7kN / m
4m
L 1
F 7 6 3 31.5kN
L2
4
2m
25 10m
31.5 31.5 31.5 31.5
WZ

M max

189103 215
879cm3
查表:
189kNm
I 36a
例题 4.31
承受相同弯矩Mz的三根直梁，其截面组成方式如图所示。图（a） 的截面为一整体；图（b）的截面由两矩形截面并列而成（未粘接）；图 （c）的截面有两矩形截面上下叠合而成（未粘接）。三根梁中的最大正 应力分别为σmax（a）、 σmax（b）、 σmax（c）。关于三者之间的关系 有四种答案，试判断哪一种是正确的。
平面假设：
变形前杆件的横截面变形后仍
为平面。
中性层
中性轴：
中性层与横截面的交线称 为中性轴。
mn
o1
o2
m
n
中性轴
F
mn
mn
M
M
中性轴
z
m
n
y
o

o
dA
mn
dx
z
y
d

dx
y
F
yd d y
d

E y E

FN
dA
A
E

ydA
许用应力[σ] ＝160MPa ，试计算：1.F加在辅助梁的什么位置，才 能保证两台吊车都不超载？2.辅助梁应该选择多大型号的工字钢？
200kN吊车
150kN吊车 1.确定F加在辅助梁的位置
A FA
C 辅助梁
x F

工程力学 第9章 杆件横截面上的切应力分析

工程力学 第9章 杆件横截面上的切应力分析

第 9 章 弹性杆件横截面上的切应力分析
对于实心截面杆件以及某些薄壁截面杆件，当其横截面上仅有 扭矩（Mx）或剪力（FQy 或 FQz）时，与这些内力分量相对应的分布 内力，其作用面与横截面重合。这时分布内力在一点处的集度，即为 切应力。 分析与扭矩和剪力对应的切应力方法不完全相同。对于扭矩存 在的情形，依然借助于平衡、变形协调与物性关系，其过程与正应力 分析相似。对于剪力存在的情形，在一定的前提下，则仅借助于平衡 方程。 本章重点介绍圆截面杆在扭矩作用下其横截面切应力以及薄壁 杆件的弯曲切应力分析。
§ 9-1 圆轴扭转时横截面上的切应力
９－１－１ 圆轴扭转变形特征 －反对称性论证圆轴扭转时横截面保持平面 ９－１－２ 变形协调方程 ９－１－３ 物性关系－剪切胡克定律 ９－１－４ 静力学方程 ９－１－５ 圆轴扭转时横截面上的切应力表达式
§ 9-2 非圆截面杆扭转时的切应力
图 9－8 例 9－2 图
解： 1．各轴所承受的扭矩 各轴所传递的功率分别为 P1 ＝14 kw ， P 2 ＝ P3 ＝P 1 ／2＝7 kw 转速分别为 n1 ＝ 120 r／min
n 3＝n1 ×
据此，算得各轴承受的扭矩：
z1 36 ＝120 × r/min ＝360r/min z3 12
14 M x1 = M e1 = 9549 × N ⋅ m = 1114 N ⋅ m 120 7 M x2 = M e2 = 9549 × N ⋅ m = 557 N ⋅ m 120 7 M x2 = M e2 = 9549 × N ⋅ m = 185 .7 N ⋅ m 360
2．计算最大切应力 E 、H、C 轴横截面上的最大切应力分别为

工程力学-弯曲应力解析

工程力学-弯曲应力解析

6 弯曲应力1、平面弯曲梁横截面上的正应力计算。

正应力公式是在梁纯弯曲情况下导出的，并被 推广到横力弯曲的场合。

横截面上正应力公式为j zM y I σ=横截面上最大正应力公式为 max zM W σ=2、横力弯曲梁横截面上的切应力计算，计算公式为*2z QS I bτ= 该公式是从矩形截面梁导出的，原则上也适用于槽形、圆形、工字形、圆环形截面梁横截面切应力的计算。

3、非对称截面梁的平面弯曲问题，开口薄壁杆的弯曲中心。

4、梁的正应力强度条件和切应力强度条件为[]max σσ≤[]max ττ≤根据上述条件，可以对梁进行强度校核、截面设计和容许荷载的计算，与此相关的还要考虑梁的合理截面问题。

5、梁的极限弯矩6.1图6-6所示简支梁用其56a号工字钢制成，试求此梁的最大切应力和同一截面腹板部分在与翼板交界处的切应力。

图 6.1[解]作剪力图如图(c).由图可知，梁的最大剪力出现在AC段，其值为max7575000Q kN N==利用型钢表查得，56a号工字钢*247.7310z zS I m-=⨯,最大切应力在中性轴上。

由此得以下求该横截面上腹板与翼板交界处C的切应力。

此时*zS是翼板面积对中性轴的面积矩，由横截面尺寸可计算得*3435602116621()9395009.401022zS mm m-=⨯⨯-==⨯由型钢表查得465866zI cm=,腹板与翼板交界处的切应力为*max max maxmax23*max7500012600000126.47.731012.510zazzzQ S QMPII d dSτ--=====⨯⨯⨯⨯aMP6.12解题范例483750009.40108.6658661012.510fc a MP τ---⨯⨯==⨯⨯⨯6.2长为L 的矩形截面悬臂梁，在自由端作用一集中力F ，已知b ＝120mm ，h ＝180mm 、L ＝2m ，F ＝1.6kN ，试求B 截面上a 、b 、c 各点的正应力。

材料力学第5版(孙训方编,高等教育出版社)第四章

材料力学第5版(孙训方编,高等教育出版社)第四章

FB
Fa l
AC段梁
FS(x)
M x
FSx FA
Fb l
0 x a
M x
FA x
Fb x l
0
x
a
第30页 / 共207页
材料力学 F
F
FS(x)
x
M x
如截面法，保留右侧梁， 计算更简便。
第四章 弯曲应力
Fb
Fa
FA l , FB l
CB段梁
FS x
Fb l
F
F
l
l
b
Fa a x l
非对称弯曲——梁不具有纵对称面(例如Z形截面梁)，因 而挠曲线无与它对称的纵向平面；或梁虽有纵对称面但外力并 不作用在纵对称面内，从而挠曲线不与梁的纵对称面一致。
第6页 / 共207页
材料力学
第四章 弯曲应力
对称弯曲时和特定条件下的非对称弯曲时，梁的挠曲线 与外力所在平面相重合，这种弯曲称为平面弯曲(对称弯曲 以及特殊条件下的非对称弯曲）。
l
F l a x
l
第15页 / 共207页
材料力学
第四章 弯曲应力
梁的横截面上位于横截面 内的内力FS是与横截面左右两 侧的两段梁在与梁轴相垂直方 向的错动(剪切)相对应，故称 为剪力（参见课本P8）；梁的 横截面上作用在纵向平面内的 内力偶矩是与梁的弯曲相对应， 故称为弯矩。
第16页 / 共207页
体(图b)的平衡条件可知：
FS
FA
Fl
l
a,
M
FA x
Fl a
l
x
第13页 / 共207页
材料力学
第四章 弯曲应力
它们的指向和转向如图b中

材料力学 正应力及其强度条件

材料力学 正应力及其强度条件

中性层
中性轴
对 称 z o 轴 中 性 y 轴
中性层
F
F
m
n
2．纯弯曲正应力公式的推导 （一）几何关系： o
中性层
d q
m
n
中性轴
m
n o
z m o 1
m
n
z
r
o
o 2
n
中性轴
y
dx
n m dx
y
变形前:
y
l = dx = r × dq
变形后:
100
例题 4.22 &
图示T形截面简支梁在中点承受集中力F＝32kN，梁的长度L＝2m。T形 截面的形心坐标yc＝96.4mm，横截面对于z轴的惯性矩Iz＝1.02×108mm4。求 弯矩最大截面上的最大拉应力和最大压应力。 y
F
150 50
A l 2 l 2
B
96 . 4 C 50
F
实验现象：
F
ü1、变形前互相平行的纵向直
m
n
线、变形后变成弧线，且凹边纤 维缩短、凸边纤维伸长。
ü2、变形前垂直于纵向线的横向
m
n
线,变形后仍为直线，且仍与弯曲 了的纵向线正交，但两条横向线 间相对转动了一个角度。
§由现象1
j靠近凹入的一侧，纤维缩短，靠近凸出的 一侧，纤维伸长； k由于纤维从凹入一侧的伸长或缩短到突出 一侧的缩短或伸长是连续变化，故中间一定 有一层，其纤维长度不变，这层纤维称为中 性层。中性层与横截面的交线称为中性轴； l弯曲变形时，梁的横截面绕中性轴旋转。
28 . 1
kNm
13. 16

工程力学 第九章 梁的强度刚度计算

工程力学 第九章 梁的强度刚度计算

由结果知，梁的强度不满足要求。
返回 下一张 上一张
y2
z
例9-6 试为图示钢轨枕木选择矩形截面。已知矩形截面尺寸的比 例为b:h=3:4,枕木的弯曲许用正应力[]=15.6MPa,许用剪应力 P P 0 0 .2 m 1 .6 m []=1.7MPa,钢轨传给枕木的压力P=49KN。 .2 m
a
M D ya Iz
返回 下一张 上一张
10.7
第二节 梁横截面上的剪应力
一、矩形截面梁：
矩形截面剪应力计算公式： τ沿截面高度按抛物线规律变化：
2Iz 4
3
QS
* z
I zb
bh
4
τ m ax
2 3
y
h 2
, 0 ; y 0 , max
6 Qh 4 bh
校核梁的正应力强度。
解：(1) 内力及抗弯截面模量计算: MC=3.0KN.m; MD=-4.8KN.m
W1 W2
P1
A
a C a
P2
D
a B
y1

z

763 5 .2
146 . 7 cm
3
y1

z

763 8 .8
86 . 7 cm
3
4 .8 k N m
y2
(2)C截面的正应力强度校核:
4 Q 3 A1
max 2
Q A2
返回 下一张 上一张
例9-3 矩形截面简支梁如图,已知：l=2m，h=15cm，b=10cm， h1=3cm，q=3kN/m。试求A支座截面上K点的剪应力及该截面的最 b q 大剪应力。 解：1.求剪力：QA=3kN

第七章梁的应力和强度计算

第七章梁的应力和强度计算

M
qL2/8
x
+
2 2 q L3 6 0 3 0 M 40 N 5 max 8 8
29
q=3.6kN/m
求最大应力并校核强度
M M 6 4050 max 6 max s 2 max 2 W b h 0 . 1 2 0 . 1 8 z
qL 2
Q
6 .2 5 MP 7 MP a [ s a ]
+
–
qL 2
x
F .5 5400 Smax 1 tmax 1 .5 A 0 .1 2 0 .1 8 0.375MP 0.9MP a [ t] a
应力之比
M
qL2/8 +
x
s 2 A L max M max 1. 6 7 t Q h 30 max W z 3
• • • •
梁的应力种类 正应力计算 应力强度条件及应用 切应力计算
31
s 30 MP , s a 60 MP t c T型截面铸铁梁，截面尺寸如图示。
试校核梁的强度。
综合题
分析： 非对称截面，要寻找中性轴位置 作弯矩图，寻找需要校核的截面 要同时满足
s s ,s
t , m0 30 1 2
例7.2.1 受均布载荷作用的简支
梁如图所示，试求： （1）1—1截面上1、2两点的 正应力； （2）此截面上的最大正应力；
（3）全梁的最大正应力；
（4）已知E=200GPa，求1—1 截面的曲率半径。
qL 8
2
120 y +
z
M M1 Mmax
x
解：画M图求截面弯矩
b
d
3 bh 2 Iz bh 12 矩形 W z h y 6 max 2

梁横截面的切应力和切应力强度条件.

梁横截面的切应力和切应力强度条件.

A
FS qL/ 2
L3m
M
qL²/ 8
Fsmax 5400 (N )
B
z M max 4050 (N.m)
x
-qL/ 2 x
求最大应力并校核强度
max
M max Wz
6M max bh2
6 4050 0.12 0.182
6.25MPa [ ] 7MPa
(1) 沿截面高度按二次抛物线规律变化； (2) 同一横截面上的最大切应力max在中性轴处 ( y=0 )；
(3)上下边缘处（y=±h/2)，切应力为零。
二、非矩形截面梁——圆截面梁
d
Fs
max
切应力的分布特征：
边缘各点切应力的方向与圆周相切；切应 力分布与 y 轴对称；与 y 轴相交各点处的 切应力其方向与 y 轴一致。
向与圆周相切；
max
(3) y 轴是对称轴 → 切应力分布与 y 轴
对称；与 y 轴相交的各点处切应力
为零。
r0 O
y
max
最大切应力max 仍发生在中性轴z上。
max
r0
max
O
y
A 2πr0
O
2r0 /p
C
y
薄壁环形截面梁最大切应力的计算
Ip
2
A
d
A
2πr0
r02
2πr03
Ip Iz I y 2Iz
梁的跨度较短，M 较小，而 Fs 较大时，要校核切应力强度; 铆接或焊接的组合截面，其腹板的厚度与高度比小于型钢的
相应比值时，要校核切应力强度; 各向异性材料（如木材）的抗剪能力较差，要校核切应力强度。
q 3.6kN / m
A

梁的切应力及强度条件

梁的切应力及强度条件

在 20a号工字钢梁的中段用两块横截面为120mm10mm而长度
2.2mm的钢板加强加强段的横截面尺寸如图所示.已知许用弯曲
正应力[]=152MPa，许用切应力 []=95MPa.试校核此梁的强
度解.：加强后的梁是阶梯状
变截面梁. 所以要校核
（1）F位于跨中时跨中截面
2.2m
z
上的弯曲正应力；
（2）F靠近支座时支座截面上的切应力；
h/2 y
y1bdA1
b (h2 24
y2)
FS Sz
FS
h2 (
y2)
Izb 2Iz 4
z
y1 y
O A1 B1
dy 1 m1
可见，切应力沿截面高度按抛物线规律变化.
y
y=±h/2（即在横截面上距中性轴最远处）0
y=0（即在中性轴上各点处），切应力达到最大值
max
FS h2 8I z
FS h2 8 bh3 12
假设求应力的点到中性轴的距离为y.
y
FS
S
z
Izd
d — 腹板的厚度
z
O
y
S
* z
—
距中性轴为y的横线以外部分的横截
面面积A对中性轴的静矩.
max
FS BH 2 Izb 8
(B
b)
h2 8
（a）腹板上的切应力沿腹板高度按二
次抛物线规律变化；
A*
y
max
τmax
（b）最大切应力也在中性轴上.这也是
τmax超过[]很多，应重新选择更大的截面.现已25b工字钢进
行试算
查表得
Iz
S
* z max
18.9cm,

切应力公式推导

切应力公式推导

将MC、Iz、y代入正应力计算公式，则有
σ K M Iz Cy 0 . 5 3 8 1 1 3 3 4 0 0 ( 0 .0) 6 3 .0 1 96 P 0 a 3 .0M 9 P
K点的正应力为正值，表明其应为拉应力。
§6－2 梁的正应力强度条件及其应用
一、梁的正应力强度条件
对梁的某一横截面来讲，最大正应力发生在距中性轴最
由型钢规格表查得56b号工字钢的Wz为
W z24 417 0 6m 3
此时最大正应力
例题6－4 图
(b) M图
281kN.m
281kN.m
375kN.m
σma x M W m z a x 2 34 7 1 1 4 5 3 6 0 0 7 15 13 60 P a 1M 53Pa
例题6－4 图
例题61图截面对中性轴的惯性矩105831218y代入正应力计算公式则有mpa09pa10091058362梁的正应力强度条件及其应用一梁的正应力强度条件对梁的某一横截面来讲最大正应力发生在距中性轴最远的位置此时maxmax而对整个等截面梁来讲最大正应力应发生在弯矩最大的横截面上距中性轴最远的位置即maxmaxmaxmaxmaxmaxmax对圆形截面32的数值可以在型钢表中查得
I z ( 0 . 1 1 0 . 0 1 3 2 0 . 1 3 0 . 0 1 0 . 0 3 2 ) 2 ( 0 . 0 1 0 3 . 0 3 3 2 0 . 8 0 0 . 0 3 0 . 0 8 2 ) 3 0 . 5 1 2 7 5 m 4 0 3
（4）强度校核 因材料的抗拉与抗压强度不同，而且截面关于中性轴不
根据式（6−6）可以求解与梁强度有关的三种问题。
（1）强度校核
σmax
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

三、T字型截面梁的切应力
T字型截面可以看成是由两个矩形组成，下面的 狭长矩形与工字形截面的腹板相似，该部分上的切 应力仍用下式计算：
τ

FS
S
* z
I zb1
最大切应力仍然发生在截面的中性轴上。
四、圆形及环形截面梁的切应力 圆形及薄壁环形截面其最大竖向切应力也都发生在
中性轴上，并沿中性轴均匀分布，计算公式分别为
M+dM
FS dx
σ
现假设用一水平截面将微段梁截 开，并保留下部脱离体，由于脱离 体侧面上存在竖向切应力τ ，根据 切应力互等定理可知，在脱离体的
顶面上一定存在切应力τ '，且 τ '=τ ,如图所示。
dx τ
z y τ' τ
y dx
以FN1、FN2分别代表作用在脱离体左侧面、右侧 面上法向内力的总和，dFS代表水平截面上切应力的 总和，如图所示。
翼缘上的水平切应力可认为沿翼缘厚度是均匀 分布的，其计算公式仍与矩形截面的切应力的形式 相同，即
τ

FS
S
* z
Izδ
式中FS为横截面上的剪力；Sz*为欲求应力点到翼 缘边缘间的面积对中性轴的静矩；Iz横截面对中性轴的 惯性矩；δ为翼缘的厚度。
水平切应力的大小沿水平方向的分布如图所示。实 践和理论推导已经证明，在整个工字型截面上切应力 的方向可用图c表示。从图中表示切应力方向的许多小 箭头来看，它们好象是两股沿截面流动的水流，从上 （或下）翼缘的两端开始，共同朝向中间流动，到腹 板处汇合成一股，沿着腹板向下（或上）到下（或上） 翼缘处再分为两股向两侧流动。对所有的薄壁杆，其 横截面上切应力的方向，都有这个特点。这种现象称 为切应力流。掌握了切应力流的特性，则不难由剪力 的方向确定薄壁杆横截面上切应力的方向。
τ

FS
S
* z
I zb1
式中：FS为横截面上的剪力；Sz*为欲求应力点到 截面边缘间的面积对中性轴的静矩；Iz为横截面对中 性轴的惯性矩；b1为腹板的厚度。
切应力沿腹板高度的分布规律如图所示，仍是按
抛物线规律分布，最大切应力τ max仍发生在截面的 中性轴上。
2.翼缘上的切应力
翼缘上的切应力的情况比较复杂，既有平行于y 轴的切应力分量（竖向分量），也有与翼缘长边平 行的切应力分量（水平分量）。当翼缘的厚度很小 时，竖向切应力很小，一般不予考虑。
l=3m，h=160mm，b=100mm，y=40mm，F=3kN，求m −m
截面上K点的切应力。
解：先求出m −m截面上的剪力为3kN。
截面对中性轴的惯性矩 A
A*
F F m l/6 mB
K
y y* zh
l/3 l/3 l/3
b
Iz

bh3 12

0.1 0.16 3 12
0.341 10 4 m4

0
Iz
Iz
经整理得
τ

FS
S
* z
I zb
τ

FS
S
* z
I zb
式（10−8）即为矩形截面梁横截面任一点的切应
力计算公式。式中：FS为横截面上的剪力；S z*为面
积A1对中性轴的静矩；Iz横截面对中性轴的惯性矩；
b为截面的宽度。
b
对于矩形截面梁，由图可知 h
z y
τmax
S
* z
b(h 2
由 Fx 0
FN1
dFS FN2
dx
得
FN2 FN1 dFS 0 （a）
其中
FN1
σdA
A1
My1 dA M
I A1
z
Iz
A1
y1dA

MS*z Iz
（b） b
式中的A1是横截面上距中性轴为y的横
线以外部分的面积，如图所示。
h
z y
S
* z

A1 y1dA
是A1对中性轴的静矩。
y A1
FN1

MSz* Iz
同样有
FN 2

(M

dM
)S
* z
Iz
（c）
由于微段的长度很小，脱离体水平截面上的切应
力可认为是均匀分布的，所以有
dFS τ'bdx （d）
FN1
dFS FN2
dx
将FN1、FN2、dFS代入式（a），得
(M

dM
)S
* z

MS*z
τ' bdx

y) y
1 (h 22

y)

b (h2 24

y2)
y A1
(a)
(b)
将其代入上式，可得
τ
FS
h2 (
y2)
2Iz 4
τ FS ( h2 y 2 ) 2Iz 4
此式表明矩形截面梁横截面上切应力沿梁高
按二次抛物线形规律分布。在截面上、下边缘
（ y h）处，τ=0，而在中性轴上（y=0）的切
的最大切应力不能超过材料的许用切应力，即
τmax

F S* S,max z,max Izb

τ
此式即为切应力的强度条件。
在进行梁的强度计算时，必须同时满足正应力强 度条件和切应力强度条件。一般情况下，梁的强度计 算由正应力强度条件控制。因此，按正应力强度条件 设计的截面常可使切应力远小于许用切应力。所以一 般情况下，总是根据梁横截面上的最大正应力来设计 截面，然后再按切应力强度条件进行校核。但在少数 情况下，梁的切应力强度条件也可能起到控制作用。 例如梁的跨度较短，或在支座附近作用有较大的荷载， 因而使梁中出现的弯矩较小而剪力很大时；在铆接或 焊接的组合截面钢梁中，其横截面的腹板厚度与高度 之比小于一般型钢截面的相应比值时。
圆形截面
τmax

4 3

FS A
FS为横截面上的剪力，A为圆形截面的面积。
薄壁环形截面
τmax

2

FS A
FS为横截面上的剪力，A为薄壁环型截面的面积。
五、梁的切应力强度条件
对于等截面梁来说，最大切应力应发生在剪力
最大的横截面的中性轴上。即
τ max

F S* S,max z,max Izb
为了保证梁的安全工作，梁在荷载作用下产生
§10-3 梁横截面上的切应力及梁的切应力强度条件 一、矩形截面梁的切应力
1.两条假设 （1）横截面上各点处的切应力均与侧边平行。 （2）横截面上距中性轴等距离各点的切应力相等。 2.切应力公式的推导
从图所示的梁中取出长为dx的微段。
微段梁上的受力情况如图所示。 微段梁上的应力情况如图所示。
FS
M
2
应力有最大值，如图所示。即
b
τmax

FSh2 8I z

3FS 2bh

3FS 2A
τmax

3FS 2A
h
z y
y A1 (a)
τmax (b)
式中的A=bh是横截面的面积。由此可见，矩形截面
梁横截面上的最大切应力是截面上平均切应力的1.5倍。
例题10−5 一矩形截面的简支梁如图所示。已知：
面积A*对中性轴的静矩 S*z A* y* 0.1 0.04 0.06 0.24103m3
则K点的切应力
τ

FS S z Izb

3103 0.24103 0.341104 0.1

0.21Pa
0.21MPa
二、工字形截面梁的切应力
1.腹板上的切应力