必修数学一四、五、二综合练习高一数学下学期期末模拟试卷

2021年高一下学期期末模拟数学试题2 Word 版含答案 一、填空题：（本大题共14小题，每小题5分，共70分。

）1．不等式的解为 ▲ ．2．某人射击1次，命中7~10环的概率如下表所示：则该人射击一次，至少命中9环的概率为 ▲ ．3．某人5次上班途中所花的时间（单位：分钟）分别为，8，10，11，9.已知这组数据的平均数为10，则其方差为 ▲ ．4．若变量满足约束条件则的最大值为 ▲ ．5．设表示两条直线，表示两个平面，现给出下列命题：① 若，则； ② 若，则；③ 若，则； ④ 若，则．其中正确的命题是___ _____．（写出所有正确命题的序号）6．根据如图所示的伪代码，可知输出的结果是 ▲ ．7．已知等差数列满足：，.则数列的前项和为= ▲ ．8．已知是圆的一条直径，在上任取一点，过作弦与垂直，则弦的长度大于半径的概率是 ▲ ．9．已知两点、分别在直线的同侧，则的取值范围是 ．10．在中，，,，则 ▲ ．11．已知函数，仿照等差数列求和公式的推导方法，化简：1111()()()()(1)(3)(5)(7)(9)9753f f f f f f f f f ++++++++= ▲ ． 12．若，，．则下列不等式：①； ②； ③； ④.其中成立的是 ▲ ．(写出所有正确命题的序号).13、黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：命中环数 10环 9环 8环 7环概率 0．12 0．18 0．280．32则第个图案中有白色地面砖块.14．已知数列满足（为常数，），若，则▲ ．二、解答题：本大题共6小题，共计90分，请在答题卡指定区域内作答，解答时应写出文字说明、证明或演算步骤.15．（本题满分14分）中，角、、的对边分别为、、，且，，成等差数列.（1）求角的大小；（2）若，，求的面积.16. (本小题满分14分)设关于的一元二次方程,⑴将一颗质地均匀的骰子先后抛掷两次,第一次向上的点数记为,第二次向上的点数记为,求使得方程有实根的概率;⑵若、是从中任取的两个数,求方程无解的概率.17、(本题满分15分) 已知函数，且的解集为.（1）求的解析式；（2）当时，求的最大值.18．（本题满分15分）已知数列满足：，数列满足.（1）若是等差数列，且求的值及的通项公式；（2）若是等比数列，求的前项和；（3）若是公比为的等比数列，问是否存在正实数，使得数列为等比数列？若存在，求出的值；若不存在，请说明理由.19．（本题满分16分）xx年上海世博会某国要建一座八边形的展馆区，它的主体造型的平面图是由两个相同的矩形和构成的面积为200的十字型地域．．．．．，计划在正方形上建一座“观景花坛”，造价为4200元，在四个相同的矩形上(图中阴影部分)铺花岗岩地坪，造价为210元,再在四个空角（如等）上铺草坪，造价为80元.设长为,长为.(1)试找出与满足的等量关系式；(2)设总造价为元,试建立与的函数关系；(3)若总造价不超过138000元，求长的取值范围.20．（本题满分16分）设正项等差数列的前n项和为，其中．是数列中满足的任意项．（1）求证：；（2）若也成等差数列，且，求数列的通项公式；（3）求证：．新沂市高流中学 xx～xx高一下学期期末模拟试题2参考答案一、填空题：1．； 2．0.3； 3．2； 4．3；5．； 6．13； 7．； 8．；9．；（或填） 10．； 11．8； 12．①③④； 13．126； 14．.二、解答题：15．（1），，成等差数列……..２分由正弦定理得2sin cos sin cos sin cos sin()sin-=+=+=……..５分A ABC C B B C A（另解：由射影定理得，，），，……..７分（2）由余弦定理得，……..９分，由条件得……..11分……..14分、16．（1）40名驾车者中醉酒驾车的频率为，人数为人，所以酒后驾车的人数为38人；........4分（2）250.25350.15450.2550.15650.1750.1850.0548 S=⨯+⨯+⨯+⨯+⨯+⨯+⨯=.. (9)分（3）……..14分17．（1），，……..1分、、三点共线，，即……..2分，当且仅当，即时取等号．当时，，……..5分此时，又，，……..6分直线的方程为，即：．……..8分（2）由条件得，所以，……..9分而，① ……..11分又， ② ……..13分由①②得或（舍去），． ……..15分18．（1）因为是等差数列，， ……..2分，解之得或者（舍去） ……..4分． ……..5分（2）若是等比数列，其中公比，， ……..6分， ……..7分，当时，； ……..8分当时， ……..10分（3）因为是公比为的等比数列，所以， ……..11分若为等比数列，则， ……..12分，即， ……..13分，无解．不存在正实数，使得数列为等比数列．……..15分另解：因为是公比为的等比数列，，， ……..12分若为等比数列，则，， ……..13分，无解，不存在正实数，使得数列为等比数列．……..15分19．(1) ……..4分(2)由（1）得 ……..6分 222240000042002104802400038000S x xy y x x =+⋅+⋅=++，；……..10分 （3）由，得， ……..12分，，即， ……..15分所以长的取值范围是． ……..16分20．（1）设等差数列的公差为，因为 ，所以， ……..1分又，， ……..3分所以，即； …..4分（2）由已知取，即 ……..6分把代入解得，． ……..9分 又时，，当时，都成等差数列；； ……..10分（3）由条件得都大于0，11(1)(1)22m n m m d n n d S S ma na --⎡⎤⎡⎤∴⋅=+⋅+⎢⎥⎢⎥⎣⎦⎣⎦11222221(1)(1)(1)22()[][]222k m d n d a a m n k d k a S --++++-≤⋅=⋅+=……..14分，即． ……..16分31019 792B 礫23428 5B84 宄'n36377 8E19 踙35399 8A47 詇30850 7882 碂30403 76C3 盃H26469 6765 来22982 59C6 姆29148 71DC 燜9 20665 50B9 傹。

2021年高一下学期期末模拟数学试题 Word 版含答案一、填空题(本大题共14小题，每小题5分，共70分)1．已知集合{}{}045,0122≥+-=≥+-=x x x B x x x A ，则_____． 2．已知，则的最大值是 ． 3．的值为 ．4．已知正项等比数列的公比q 满足，则的值为 ． 5．表面积为的球的内接正方体的体积为 ．6．已知，则的值为 ．7．在等差数列中，若，则的值为 ．8．设α，β为两个不重合的平面，l ，m ，n 为两两不重合的直线，给出下列四个命题： ①若α∥β，l ⊂α，则l ∥β；②若m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β； ③若l ∥α，l ⊥β，则α⊥β；④若m 、n 是异面直线，m ∥α，n ∥α，且l ⊥m ，l ⊥n ，则l ⊥α. 其中真命题的序号是 ． 9．已知，则 ．10．在中，三个内角A ，B ，C 所对的边分别是a ，b ，c ，已知，的面积等于，则 ． 11．已知等比数列的公比为q ，其前项和为S n ，若S 3，S 9，S 6成等差数列，则q 3＝ ． 12．在△ABC 中，角A 、B 、C 对应的边分别为a 、b 、c ，若，那么 c = ．13．数列的通项，其前项和为S n ，则S 30＝ ．14．已知函数满足对任意，都有成立，则实数a 的取值范围是__________.二、解答题(本大题共6小题，共90分)15．(本小题14分) 已知函数．(1)求的值；(2)当时，求的最大值和最小值．A 116．(本小题14分)如图，在正方体ABCD－A1B1C1D1中，E、F为棱AD、AB的中点．（1）求证：EF∥平面CB1D1；（2）求证：平面CAA1C1⊥平面CB1D1．17．(本小题14分)设数列的前n项和为S n，已知.（1）若数列为公差为11的等差数列，求a1；（2）若数列为以为首项的等比数列，求数列的前m项和.18．(本小题16分)运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)（单位：千米/小时）．假设汽油的价格是每升2元，而汽车每小时耗油升，司机的工资是每小时14元． （1）求这次行车总费用y 关于x 的表达式；（2）当x 为何值时，这次行车的总费用最低，并求出最低费用的值．19．(本小题16分)在△ABC 中，已知． （1）求∠C 的大小；（2）设角A ，B ，C 的对边依次为a ，b ，c ，若c ＝2，且△ABC 是锐角三角形，求 a 2＋b 2的取值范围．20．(本小题16分)设数列为等比数列，数列满足*-∈++⋅⋅⋅+-+=N n a a a n na b n n n ,2)1(121，已知，其中．⑴求数列的首项和公比； ⑵当m =1时，求；⑶设为的前n 项和，若对于任意的正整数n ，都有，求实数m 的取值范围．【参考答案】一、填空题(本大题共14小题，每小题5分，共70分)1． 2． 9 3．4．5． 8 6． 7． 8 8．①③④ 9． -1 10． 4 11． 12． 13． 15 14．二、解答题(本大题共6小题，共90分)15．解：(1)x x xx xx x x x x f 2cos 22cos 2cos 2)22sin(212cos )4cos()4sin(12cos 2)2cos 1()(222==+=++--+=πππ ……………………………5分所以………………………………7分 (2) ………………………………10分因为，所以………………………………………12分 所以当时，有最大值；当时，有最小值1. ………………… 14分 16．解：（1）证明:连结BD .在正方体ABCD －A 1B 1C 1D 1中，对角线BD //B 1D 1.又 E 、F 为棱AD 、AB 的中点，所以EF //BD .………… 3分 所以EF //B 1D 1. 又B 1D 1平面CB 1D 1，EF 平面CB 1D 1， 所以EF ∥平面CB 1D 1.………………………………7分（2） 在正方体ABCD －A 1B 1C 1D 1中，AA 1⊥平面A 1B 1C 1D 1，而B 1D 1平面A 1B 1C 1D 1， 所以AA 1⊥B 1D 1. ……………………………… 9分又在正方形A 1B 1C 1D 1中，A 1C 1⊥B 1D 1，……………………………… 11分所以B 1D 1⊥平面CAA 1C 1. ……………………………… 13分 又 B 1D 1平面CB 1D 1，平面CAA 1C 1⊥平面CB 1D 1． ……………………………… 14分 17．解：（1）依题意，得 ……………………………… 4分 解得：……………………………… 7分（2） 依题意，得，解得：q =2……………………………… 10分 从而， ……………………………… 12分所以……………………………… 14分18．解：（1）设行车所用时间为(h) , ………2分则]100,50[,13014)3602(21302∈⨯++⨯⨯=x xx x y ………5分 所以，这次行车总费用y 关于x 的表达式是………8分 （2）10263601302181302360130218130=⨯⋅⨯≥⨯+⨯=x x x x y ………12分 当且仅当，即时，上述不等式中等号成立 ………15分所以，当时，这次行车的总费用最低，最低费用为元………16分19．解：（1）依题意：，即，……………… 3分 又，∴，∴ ………………………… 6分（2）由三角形是锐角三角形可得…………………… 8分 由正弦定理得)32sin(34sin 34,sin 34sin sin A B b A A C c a -===⨯=π………… 11分 所以]2)234cos(122cos 1[316)]32(sin [sin 3162222A A A A b a --+-=-+=+ππ]2sin 232cos 212[cos 38316)]234cos(2[cos 38316A A A A A ---=-+-=π )62sin(38316)2sin 232cos 21(38316π-+=--=A A A …………… 14分 因为，所以，所以，从而 ……… 16分20．解：⑴由已知，所以 …………………………2分 ，所以，解得，所以数列的公比……4分⑵当m=1时，…………………………5分因为，………………………①， 所以，……………………②，②－①得，…………………………7分即])21(1[31)21(1])21(1[2123n n n n n b ----=-----+-=-， 所以 ……………10分 ⑶，…………………………12分 因为，所以由得，注意到，当n 为奇数时，；当为偶数时，，所以的最大值为，最小值为．…………………………14分 因为对于任意的正整数n 都有， 所以，解得，即实数m 的取值范围是[2，3]．…………………………16分"28061 6D9D 涝27614 6BDE 毞38946 9822 頢P )28954 711A 焚38777 9779 靹T!w-[。

师大附中2021-2021学年高一下学期期末模拟数学试卷一、选择题中,角的对边分别为,向量假设,且,那么角的大小为( )A. B. C. D.【答案】C【解析】试题分析：依题意，得∴.由利用正弦定理得,即∴,.考点：向量根本概念及正弦定理的应用2.2.,给出以下四个不等式:①; ②; ③; ④.其中一定成立的不等式为( )A. ①②③B. ①②④C. ①③④D. ②③④【答案】A【解析】当时函数单调递增，因为，所以有，①成立；因为函数在定义域R上单调递增，而，所以，从而有，②成立；因为，所以，那么，所以，即。

因为，所以，从而有，③成立；，当时，，那么，即，所以④不一定成立。

综上可得，选A,…的第四项等于( )A. -24B. 0C. 12D. 24【答案】A【解析】由x，3x+3，6x+6成等比数列得选A.考点：该题主要考察等比数列的概念和通项公式，考察计算才能.的定义域为〔〕A. B.C. D.【答案】D【解析】试题分析：要使函数解析式有意义需满足：解得且，即选D.考点：1.对数函数；2.一元二次不等式.的首项为，公差为，其前项和为，假设直线与圆的两个交点关于直线对称，那么〔〕A. B. C. D.【答案】C【解析】试题分析：由直线与圆的两个交点关于直线对称，可得直线与直线直线是互相垂直的关系，且直线过圆心，从而有、，进而有，应选择C.考点：直线与圆、等差数列求和.是等差数列，，的前项和为，那么使得到达最大的是〔〕A. 18B. 19C. 20D. 21【答案】C【解析】分析：利用等差数列的通项公式得到关于和d的方程，联立方程解出和d进而求得，即可得到到达最大值时n的值。

详解：〔〕=所以,而所以,可得故有,当n=20时，有最大值为400.应选C。

点睛：此题主要考察了等差数列的通项公式和前n项和公式以及等差数列的性质，利用等差数列的通项公式得到关于和d的方程，联立方程解出和d进而求得，即可得到到达最大值时n的值。

2023-2024学年高一数学下学期期末模拟卷一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的． 1．（22-23高一下·天津和平·期末）一组数据7,6,8,4,4,9,5的第30百分位数为（ ） A ．7 B ．6 C ．5 D ．4【答案】C【解析】将数据从小到大排列为4,4,5,6,7,8,9，共7个数据，由730×%=2.1，故第30百分位数是第三个数据为5.故选：C2．（23-24高一下·广东·期末）复数312i 1iz +=−（i 为虚数单位）在复平面内对应的点位于（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限【答案】D【解析】()()()()312i 1i 12i 12i 3i 31i 1i 1i1i 1i 222z−++−−=====−−−−+ ， ∴复数z 在复平面内对应的点的坐标是31,22−，位于第四象限．故选：D3．（河南省郑州市第十一中学2023-2024学年高一下学期4月月考数学试题）如图，△A B C ′′′是水平放置ABC 的直观图，其中1B C C A ′′′′==，A B ′′//x ′轴，A C ′′//y ′轴，则BC =（ ）A B ．2 C D ．4【答案】C【解析】在△A B C ′′′，1B C C A ′′′′==，45B A C ∠′′′=°， 由余弦定理可得：2222cos 45B C A C A B A C A B ′′′′′′′′′′=+−××°，即2A B ′′A B ′′0=，而A B ′′0>，解得A B ′′=由斜二测画法可知：△ABC 中，AB AC ⊥，AB =A B ′′=2AC =C A ′′2=，故BC 故选：C.4．（22-23高一下·安徽宣城·期末）某单位有职工500人，青年职工300人，中年职工150人，老年职工50人，为了解该单位职工的健康情况，用分层抽样从中抽取样本，若抽出的中年职工为15人，则抽出的老年职工的人数为（ ） A ．5 B ．15C ．30D ．50【答案】A【解析】设抽出的样本总人数为n 人，则由题意可得15015500n =，解得50n =， 所以抽出的老年职工的人数为50505500×=人，故选：A 5．（22-23高一下·湖南岳阳·期末）设,R x y ∈，向量()2,6a =− ，()1,b x = ，且//a b ，则a b +=（ ）A B ．C ．10D ．【答案】D【解析】由向量()2,6a =− ，()1,b x =， 因为//a b，可得261x =−×，解得3x =−，所以(3,9)a b =+− ，所以a + .故选：D. 6．（22-23高一下·山东枣庄·期末）将一枚质地均匀的骰子连续抛掷2次，至少出现一次6点的概率为（ ） A ．1318B ．2536C ．1136D ．518【答案】C【解析】一枚质地均匀的骰子连续抛掷2次，可能出现的情况为：()()()()()()()()()()()()1,1,1,2,1,3,1,4,1,5,1,6,2,1,2,2,2,3,2,4,2,5,2,6， ()()()()()()()()()()()()3,1,3,2,3,3,3,4,3,5,3,6,4,1,4,2,4,3,4,4,4,5,4,6，()()()()()()()()()()()()4,1,4,2,4,3,4,4,4,5,4,6,6,1,6,2,6,3,6,4,6,5,6,6，共36种，其中至少出现一次6点的情况有：()()()()()()()()()()()1,6,2,6,3,6,4,6,5,6,6,6,6,1,6,2,6,3,6,4,6,5，共11种，故至少出现一次6点的概率为：1136.故选：C. 7．（22-23高一下·江苏南京·期末）在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，π6B ∠=，边BC，则cos A =（ ）A B ．12C ．D ．12−【答案】D【解析】作AD BC ⊥，垂足为D ，在Rt ABD 中，π6B ∠=，AD =，所以，tan 302AD a BD ==°，sin 30AD AB ==°，π3BAD ∠=，由2aBD =可知，D 为BC 的中点，AD 为BC 的垂直平分线， 所以ABC 为等腰三角形，2π3BAC ∠=，所以2π1cos cos 32A ==−.故选：D 8．（22-23高一下·黑龙江·期末）已知等腰直角ABC 的斜边2AB =，M ，N 分别为AC （M 与C 不重合），AB 上的动点，将AMN 沿MN 折起，使点A 到达点A ′的位置，且平面A MN ′⊥平面BCMN ．若点A ′，B ，C ，M ，N 均在球O 的球面上，则球O 表面积的最小值为（ ）．A ．8π3B ．3π2C D ．4π3【答案】A【解析】显然M 不与A 重合，由点,,,,A B C M N ′均在球O 的球面上，得,,,B C M N 共圆，则πC MNB ∠+∠=，又ABC 为等腰直角三角形，AB 为斜边，即有MN AB ⊥，如图，将AMN 翻折后，MN A N ⊥′，MN BN ⊥，又平面A MN ′⊥平面BCMN ，平面A MN ′ 平面BCMN =MN ，A N ′⊂平面A NM ′，BN ⊂平面BCMN ，于是A N ′⊥平面BCMN ，BN ⊥平面A MN ′，显然,A M BM ′的中点,D E 分别为A NM ′△，四边形BCMN 外接圆圆心， 则DO ⊥平面A NM ′，EO ⊥平面BCMN ，因此//,//DO BN EO A N ′， 取NM 的中点F ，连接,DF EF ，则有////,////EF BN DO DF A N EO ′，四边形EFDO 为平行四边形，设A N x ′=且01x <<，1222xDOEF BN −===，A M ′=， 从而球O 的半径R ，有22222332()()2443321A M R DO x x x ′+−−+===+， 当23x =时，2min ()23R =，所以球O 表面积的最小值为28π4π3R =.故选：A二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9．（22-23高一下·陕西·期末）制造业PMI指数反映制造业的整体增长或衰退，制造业PMI指数的临界点为50%．我国2021年10月至2022年10月制造业PMI指数如图所示，则（）A．2022年10月中国制造业PMI指数为49.2%，比上月下降0.9个百分点，低于临界点B．2021年10月至2022年10月中国制造业PMI指数的极差为2.9%C．2021年10月至2022年10月中国制造业PMI指数的众数为50.2%D．2021年11月至2022年2月中国制造业PMI指数的标准差小于2022年7月至2022年10月中国制造业PMI指数的标准差【答案】ABD【解析】对于A，由图可知：2022年10月中国制造业PMI指数为49.2%，2022年9月中国制造业PMI指数为50.1%，∴2022年10月中国制造业PMI指数比上月下降0.9个百分点，且低于临界点，A正确；−=，B正对于B，2021年10月至2022年10月中国制造业PMI指数的极差为50.3%47.4% 2.9%确；对于C，由图中数据知：众数为50.1%，C错误；对于D，由图中数据波动幅度知：2021年11月至2022年2月中国制造业PMI指数比2022年7月至2022年10月更稳定，∴年11月至2022年2月中国制造业PMI指数的标准差更小，D正确.故选：ABD.202210．（22-23高一下·湖南岳阳·期末）将一枚质地均匀且标有数字1，2，3，4，5，6的骰子随机掷两次，记录每次正面朝上的数字，甲表示事件“第一次掷出的数字是1”，乙表示事件“第二次掷出的数字是2”，丙表示事件“两次掷出的数字之和是8”，丁表示事件“两次掷出的数字之和是7”.则（）A．事件甲与事件丙是互斥事件B．事件甲与事件丁是相互独立事件C．事件乙包含于事件丙D．事件丙与事件丁是对立事件【答案】AB【解析】由题意，事件甲：第一次掷出的数字是1有：(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)，事件乙：第二次掷出的数字是2有：(1,2),(2,2),(3,2),(4,2),(5,2),(6,2)，事件丙：两点数之和为8的所有可能为：(2,6),(3,5),(4,4),(5,3),(6,2)， 事件丁：两点数之和为7的所有可能为：(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)，其中11561(),(),(),()6636366P P P P =====甲乙丙丁， 对于A 中，事件甲与事件丙不能同时发生，所以事件甲与事件丙是互斥事件，所以A 正确； 对于B 中，由1111(),()()366636P P P ==×=甲丁甲丁，所以()()()P P P =甲丁甲丁， 所以事件甲与事件丁是相互独立事件，所以B 正确； 对于C 中，事件乙不包含于事件丙，所以C 错误；对于D 中，根据对立事件的定义，可得事件丙与事件丁不对立，所以D 错误.故选：AB.11．（22-23高一下·辽宁·期末）如图，正方体1111ABCD A B C D −的棱长为1，线段11B D 上有两个动点E 、F ，且12EF =，则下列结论中正确的是（ ）A ．AC BE ⊥B ．//EF 平面ABCDC ．三棱锥A BEF −的体积为定值D ．直线AC 与平面AEF 的成角为π3【答案】ABC【解析】A 选项，根据正方体的性质可知1,AC BD AC BB ⊥⊥，由于1BD BB B ∩=，1,BD BB ⊂平面11BDD B ， 所以AC ⊥平面11BDD B ，由于BE ⊂平面11BDD B ， 所以AC BE ⊥，所以A 选项正确. B 选项，根据正方体的性质可知//EF BD ， 由于EF ⊄平面ABCD ，BD ⊂平面ABCD ， 所以//EF 平面ABCD ，所以B 选项正确.C 选项，对于三棱锥A BEF −，三角形BEF 的面积为定值，A 到平面BEF 的距离为定值，所以三棱锥A BEF −的体积为定值，所以C 选项正确.D 选项，根据正方体的性质可知，1111//,=A AC A C A C C ，设1A 到平面11AB D 的距离为h ，111111A AB D A A B D V V −−=，即2111=111332h××××××，解得h设直线AC 与平面AEF 的成角为θ，则11sin =12h A C θ≠，所以θ不是π3，D 选项错误.故选：ABC三、填空题：本题共3小题，每小题5分，共15分．12．（23-24高二下·湖南长沙·期中）设一组样本数据1210,,,x x x 的平均值是1，且2221210,,,x x x 的平均值是3，则数据1210,,,x x x 的方差是 . 【答案】2【解析】由题意得2221210121010,30x x x x x x +++=+++= ， 所以数据1210,,,x x x 的方差()()()2221210211110x x x s−+−++−=()()2221210121021030201021010xx x x x x +++−++++−+== .13．（23-24高一下·重庆渝中·期中）一个母线长为2的圆锥的侧面积是底面积的2倍，则该圆锥的侧面积为 ． 【答案】2π【解析】设圆锥的底面半径为r ，母线长为l ，则2l =，且22rl r ππ=，所以1r =，侧面积为2π．14．（22-23高一下·四川凉山·期末）在ABC 中，G 为ABC 的重心，ABC S = ，1cos 2BAC ∠=，则GB GC ⋅的最大值为 .【答案】6−【解析】延长AG 交BC 于点D ，因为G 是ABC 的重心，则D 为BC 的中点，21()33AG AD AB AC ==+ ，2133GB AB AG AB AC =−=− ，()21213333GC GB BC AB AC AC AB AC AB =+=−+−=− ，由1cos 2BAC ∠=，()0,BAC π∠∈，，解得36AB AC ⋅= ，则()222121152233339GB GC AB AC AC AB AB AC AB AC ⋅=−⋅−=⋅−−11(54)5cos 4993AB AC AB AC AB AC AB AC π ≤⋅−⋅=⋅⋅−⋅166AB AC =−⋅=−， 当且仅当||6ABAC == 等号成立，此时ABC 为等边三角形.四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．（13分）（23-24高一上·江西南昌·期末）某新鲜蛋糕供应商推出了一款新品小蛋糕，每斤小蛋糕的成本为8元，售价为20元，未售出的小蛋糕，另外渠道半卖半送，每斤损失4元，根据历史资料，得到该小蛋糕的每日需求量的频率分布直方图，如图所示．（1）求出a 的值，并根据频率分布直方图估计该小蛋糕的每日平均需求量的平均数；（2）若蛋糕供应商每天准备100斤这种小蛋糕，根据频率分布直方图，估计这种蛋糕每日利润不少于1000元的概率．【答案】（1）0.02a =，88；（2）0.55 【解析】（1）由题意可得(0.00520.010.1520.025)101a ×++++×=，解得0.02a =， 该小蛋糕的每日平均需求量的平均数为550.05650.1750.15x =×+×+×850.2950.251050.21150.0588+×+×+×+×=．（2）设每日销售这种小蛋糕x 斤，所获利润为y 元，则12(100)416400y x x x =−−×=−，当1000y =时，87.5x =， 这种蛋糕每日利润不少于1000元，即每日需求量不少于87.5斤， 所以概率为(9087.5)0.020.250.20.050.55P =−×+++=， 所以估计这种蛋糕每日利润不少于1000元的概率为0.55．16．（15分）（23-24高一下·广东·期末）已知ABC 的三个内角,,A B C 所对的边分别为,,a b c，满足cos sin c B B a b =+．（1）求C ；（2）若ABC 为锐角三角形，且4a b +=，求ABC 的周长的取值范围．【答案】（1）π3C=；（2）6,4【解析】（1）已知cos sinc B B a b=+，由正弦定理得：sin cos sin sin sinC B C B A B+=+，()sin cos sin sin sinC B C B B C B=++sin cos cos sin sinB C B C B=++，sin sin cos sinC B B C B=+，又sin0B≠cos1C C−=1π1cos sin262C C C−=−=，又因为0πC<<，所以ππ5π666C−<−<，且π1sin62C−=，所以ππ66C−=，即π3C=．（2）法一：由正弦定理得：sin sin sina b cA B C==，即sin sin sina b cA B C+=+，且π3C=，)())sin sin sin sin120a b A B A A+=+=+°−3sin2A A1π2cos2sin426a b c A A c A+=+=+=，即2πsin6cA=+．而由ABC为锐角三角形，2π3A B+=，2ππ32B A−<，得ππ62A<<，所以ππ2π,633A+∈，即πsin6A+∈．所以c∈，且4a b+=，所以ABC的周长的取值范围为6,4．法二：由4a b+=，不妨设a b>，由ABC为锐角三角形，只需π2A<，由余弦定理得：222cos02b c aAbc+−=>，即()()()()22222204424b c a c a b a b a b a b a+−>⇒>−=+−=−=−．又()()222231634c a b ab a b ab a a=+−=+−=−−．（*）所以()()1634424a a a−−>−，得：2320320a a−+>，823a<<．由（*）式得：()22161634312164,3c a a a a=−−=−+∈，所以c ∈ ，且4a b +=，所以ABC 的周长的取值范围为6,4 ．17．（15分）（23-24高一上·安徽·期末）与国家安全有关的问题越来越受到社会的关注和重视.为了普及国家安全教育，某校组织了一次国家安全知识竞赛，已知甲、乙、丙三位同学答对某道题目的概率分别为35，25，p，且三人答题互不影响. （1）求甲、乙两位同学恰有一个人答对的概率； （2）若甲、乙、丙三个人中至少有一个人答对的概率为2225，求p 的值. 【答案】（1）1325；（2）12 【解析】（1）设A =“甲答对”，B =“乙答对”，则()35P A =，()25P B =，()25P A =，()35P B =， “甲，乙两位同学恰有一个人答对”的事件为AB AB ，且AB 与AB 互斥由三人答题互不影响，知A ，B 互相独立，则A 与B ，A 与B ，A 与B 均相互独立， 则()()()()()()()332213555525P AB AB P AB P AB P A P B P A P B ∪=+=+=×+×=， 所以甲，乙两位同学恰有一个人答对的概率为1325. （2）设C =“丙答对”，则(),()1P C p P C p ==−，设D “甲，乙，丙三个人中至少有一个人答对”，由（1）知，()()()()()()232211115525P D P D P A P B P C p =−=−=−××−=，解得12p =，所以p 的值为12.18．（17分）（23-24高一下·广东广州·阶段练习）如图，已知等腰梯形ABCD 中，//AD BC ，122AB AD BC ===，E 是BC 的中点，AE BD M ∩=，将BAE 沿着AE 翻折成1B AE ，使1B M ⊥平面AECD .（1）求证：CD ⊥平面1B DM ； （2）求1B E 与平面1B MD 所成的角；（3）在线段1B C 上是否存在点P ，使得//MP 平面1B AD ，若存在，求出11B PB C的值；若不存在，说明理由. 【答案】（1）证明见解析；（2）30°；（3）存在，此时P 点是线段1B C 的中点且1112B P BC = 【解析】（1）如图，在梯形ABCD 中，连接DE ，因为 E 是BC 的中点，所以122ABAD BE BC ====，又因为AD BE ，且AD BE =， 故四边形ABED 是菱形，从而AE BD ⊥，所以BAE 沿着AE 翻折成1B AE △后，1B M ⊥平面AECD ，因为DM ⊂平面AECD ， 则有1,AE B M AE DM ⊥⊥，又11,,B M DM M B M DM ∩=⊂平面1B DM ， 所以⊥AE 平面1B DM ，由题意，易知,AD CE AD CE =∥,所以四边形AECD 是平行四边形，故AE CD ∥， 所以CD ⊥平面1B DM .（2）因为⊥AE 平面1B MD ，所以线段1B E 在平面1B MD 内的射影为线段1B M ，所以1B E 与平面1B MD 所成的角为1EB M ∠， 由已知条件，可知ABAE CD ==，122AB AD BE BC ====， 所以1B AE △是正三角形，所以1B M 平分1AB E ∠，所以130EB M °∠=， 所以1B E 与平面1B MD 所成的角为30°.（3）假设线段1B C 上存在点P ，使得//MP 平面1B AD ，过点P 作PQ CD ∥交1B D 于Q ，连接,MP AQ ，如图所示：所以AM CD PQ ∥∥，所以,,,A M P Q 四点共面，又因为//MP 平面1B AD ，所以MP AQ ∥，所以四边形AMPQ 为平行四边形， 所以12PQ AM CD ==，所以P 是1B C 的中点， 故在线段1B C 上存在点P ，使得//MP 平面1B AD ，且1112B P B C =.19．（17分）（23-24高一下·安徽合肥·期中）现定义“n 维形态复数n z ”：cos isin n z n n θθ=+，其中i 为虚数单位，*n ∈N ，0θ≠.（1）当π4θ=时，证明：“2维形态复数”与“1维形态复数”之间存在平方关系； （2）若“2维形态复数”与“3维形态复数”相等，求πsin 4θ +的值； （3）若正整数m ，()1,2n m n >>，满足1m z z =，2n m z z =，证明：存在有理数q ，使得12m q n q =⋅+−.【答案】（1）证明见解析；；（2；（3）证明见解析. 【解析】（1）当π4θ=时, ππcos isin 44n z n n =+,则)1ππcos isin 1i 44z =++,2ππcos isin 2i 2z +=.因为)()2221211i 12i i i 2z z =+=++== ， 故“2维形态复数”与“1维形态复数”之间存在平方关系. （2）因为“2维形态复数”与“3维形态复数”相等,所以cos 2isin 2cos3isin 3θθθθ+=+,因此cos 2cos3sin 2sin 3θθθθ= =，解cos 2cos3θθ=， 得()322πk k θθ=+∈Z 或()322πk k θθ+=∈Z ,解sin 2sin 3θθ=， 得()322πk k θθ=+∈Z 或()322ππk k θθ+=+∈Z,由于两个方程同时成立,故只能有()322πk k θθ=+∈Z ,即()2πk k θ∈Z .所以πππsin sin 2πsin 444k θ +=+== （3）由1m z z =，得cos isin cos isin m m θθθθ+=+, 由（2）同理可得()112πm k k θθ=+∈Z ，即()()1112πm k k θ−=∈Z . 因为1m >,所以()112π1k k m θ∈−Z . 因为221n m z z z ==,由（1）知221z z =,所以2n z z =.由（2）同理可得()2222πn k k θθ=+∈Z ,即()()2222πn k k θ−=∈Z . 因为2n >,所以()222π2k k n θ∈−Z ，所以()12122π2π,12k k k k m n =∈−−Z , 又因为0θ≠,所以120k k ≠,所以()11221,2k m k k n k −=∈−Z , 即()()111122222211,k k k m n n k k k k k =−+=⋅+−∈Z ， 所以存在有理数12k q k =,使得12m q n q =⋅+−.。

绝密★考试结束前2022-2023学年高一下学期期末数学模拟试卷（试卷满分150分，考试用时120分钟）姓名___________ 班级_________ 考号_______________________注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效. 3．考试结束后，将本试卷和答题卡一并交回.一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求.1．（2022春·福建福州·高一福建省福州格致中学校考期末）设R m ∈，复数()()222321i z mm m m =−−++−，若z 为纯虚数，则m =（ ）A ．3或1−B ．3C ．12或1− D ．12 【答案】B 【解析】因为复数()()222321i z mm m m =−−++−为纯虚数，所以22230210m m m m −−= +−≠，解得3m =.故选：B2．（2022春·河北沧州·高一统考期末）已知a ，b ，c 分别为ABC 的内角A ，B ，C 所对的边，sin sin cos B C A =，则C =（ ）A ．6πB ．4π C ．3πD ．2π【答案】D【解析】∵sin sin cos B C A =，∴cos b c A =由余弦定理知22222222b c a b c a b c bc b+−+−=⋅=， 整理得222+=a b c ，故2C π=.故选：D3．（2022春·湖南衡阳·高一统考期末）一组数据按从小到大的顺序排列为56，59，60，62，a ，若这组数据的极差为7，则这组数据的方差为（ ） A ．6 B ．30 C ．25 D ．5 【答案】A【解析】由题意得56763a =+=，所以这组数据的平均数为5659606263605++++=，方差为16104965++++=，故选：A ．4．（2022春·山东菏泽·高一统考期末）紫砂壶是中国特有的手工制造陶土工艺品，其制作始于明朝正德年间.紫砂壶的壶型众多，经典的有西施壶､掇球壶､石瓢壶､潘壶等.其中石瓢壶的壶体可以近似看成一个圆台，如图给出了一个石瓢壶的相关数据（单位：cm ），那么该壶的最大盛水量为（ ）A ．3152cm πB ．368cm π C．3cm D ．3204cm π 【答案】A【解析】由题意得上底面半径为4，面积21=4=16S ππ×，下底面半径为6，面积22=6=36S ππ×，圆台高h 为6，则圆台的体积((1211=+1636615233V S S h πππ+×=3cm .故选：A 5．（2023春·江苏镇江·高一扬中市第二高级中学校考期末）已知非零向量a ，b满足)b = ，π,3a b = ，若()a b a −⊥ ，则向量a 在向量b 方向上的投影向量为（ ）A ．14bB ．12b CD ．b【答案】A【解析】因为()a b a −⊥ ，所以()20a b a a a b −⋅−⋅，∴2102a a b −=，又)b =2，∴1a = 或0a = （舍去），所以21a b a ⋅ ，所以a在b 方向上的投影向量为14a b b b b b⋅⋅=⋅ .故选：A. 6．（2023秋·贵州黔西·高一统考期末）若函数π()cos 3f x x =+，π()cos 26g x x=+，则函数()f x 的图象经过怎样的变换可以得到函数()g x 的图象（ ） A ．将横坐标缩短到原来的12倍，再向左平移5π12个单位，纵坐标保持不变 B ．将横坐标缩短到原来的12倍，再向右平移π12个单位，纵坐标保持不变C ．先向右平移5π12个单位，再将横坐标缩短到原来的12倍，纵坐标保持不变D．先向右平移π12个单位，再将横坐标缩短到原来的2倍，纵坐标保持不变【答案】B【解析】对A ，()f x 的图象横坐标缩短到原来的12倍,得到πcos(2)3yx +，再向左平移5π12个单位，纵坐标保持不变得到 5ππ7πcos 2(co 2πs 21s 2663co y x x x =++=+=−+ ，故A 不正确； 对B ，()f x 的图象横坐标缩短到原来的12倍,得到πcos(2)3yx +，再向右平移π12个单位，纵坐标保持不变得到 πππcos 2(cos 2()1236y x x g x=−+=+=，故B 正确； 对C ，()f x 的图象先向右平移5π12个单位得到5πππcos cos 12312y x x=−+=−， 再将横坐标缩短到原来的12倍，纵坐标保持不变得到πcos 212yx−，故C 不正确；对D ，()f x 的图象先向右平移π12个单位得到πππcos cos 1234y x x =−+=+， 再将横坐标缩短到原来的2倍，纵坐标保持不变得到1πcos 24y x+ ，故D 错误.故选：B7．（2022春·湖北武汉·高一校联考期末）如图，某系统由A ，B ，C ，D 四个零件组成，若每个零件是否正常工作互不影响，且零件A ，B ，C ，D 正常工作的概率都为()01p p <<，则该系统正常工作的概率为（ ）A ．()211p p p −− B ．()211p p p −− C ．()()2111p p p −−− D ．()211p p p −−【答案】C【解析】记零件或系统X 能正常工作的概率为()P X ，该系统正常工作的概率为:()()()()()()()11P AB P C P D P A B P C P D =−=−∪()()()()()()()2111111P AB P C P D p p p =−−−=−−− ,故选：C.8．（2022春·广东广州·高一校联考期末）如图（1）所示，已知球的体积为36π，底座由边长为12的正三角形铜片ABC 沿各边中点的连线垂直向上折叠成直二面角所得，如图（2）所示．则在图（1）所示的几何体中，下列结论中正确的是（ ）A ．CD 与BE 是异面直线B ．异面直线AB 与CD 所成角的大小为45°C ．由A 、B 、C 三点确定的平面截球所得的截面面积为3π D．球面上的点到底座底面DEF 的最大距离为3【答案】C【解析】取,DF EF 中点N ，M ，连接,,,,,AB BC AC BM MN CN ，如图，因BEF △为正三角形，则BM EF ⊥，而平面BEF ⊥平面DFE ，平面BEF 平面DFE EF =，BM ⊂平面BEF ，于是得BM ⊥平面DFE ，同理CN ⊥平面DFE ，即//BM CN ，BM CN == 因此，四边形BCNM 是平行四边形，有////BC NM DE ， 则直线CD 与BE 在同一平面内，A 不正确； 由选项A ，同理可得//AB DF ，则异面直线AB 与CD 所成角等于直线DF 与CD 所成角60 ，B 不正确；由选项A 知，132BCMN DE ===，同理可得3AB AC ==，正ABC 外接圆半径r = 由A 、B 、C 三点确定的平面截球所得的截面圆是ABC 的外接圆， 此截面面积为3π，C 正确； 体积为36π的球半径R ，由34π36π3R =得3R =，由选项C 知，球心到平面ABC 的距离d =由选项A ，同理可得点A 到平面DFE 的距离为即平面ABC 与平面DFE 的距离为所以球面上的点到底座底面DEF 的最大距离为3R d BM ++=+D 不正确. 故选：C二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9．（2023春·四川成都·高一成都实外校考期末）已知复数ππsin i cos 66z +，则（ ）A ．zB ．z 在复平面内对应的点在第四象限C ．z z z +=D ．z 是关于x 的方程210x x −+=的一个根【答案】BCD【解析】依题意，复数12z =，复数z A 错误；12z =在复平面内对应的点1(,2在第四象限，B 正确；||1z =，11((122z z ++，则z z z +=，C 正确；2211111((1(02222z z −+=−+=−−=，即z 是关于x 的方程210x x −+=的一个根，D 正确.故选：BCD10．（2023秋·河南郑州·高一统考期末）已知()cos αβ+4cos 25α=−，其中α，β为锐角，则以下命题正确的是（ ）A ．3sin 25α= B ．()cos αβ−C ．cos cos αβ=．1tan tan 3αβ=【答案】AC【解析】因为 ()4cos 5αβα+=− ( ,αβ 为锐角),故 3sin25α=, 故 A 正确;因为 ()sin αβ+,所以 ()()cos cos 2αβααβ −=−+()cos2cos ααβ++ ()sin2sin ααβ+4355=−×+= 故 B 错误;由 ()cos cos cos αβαβ−=sin sin αβ+()cos cos cos sin sin αβαβαβ+=−,故 cos cos αβ=()()11cos cos 22αβαβ ++−== 故 C 正确;且 ()1sinsin [cos 2αβαβ=− ()1cos ]2αβ −+=, 所以 tan tan 3αβ=, 故 D 错误.故选: AC.11．（2022春·山东聊城·高一统考期末）已知a ，b ，c 分别是ABC 三个内角A ，B ，C 的对边，则下列命题中正确的是（ ） A ．若sin sin A B >，则A B >B ．若ABC 是边长为1的正三角形，则AB BC ⋅C ．若6B π=，b =，2c =，则ABC 有一解D ．若O 是ABC 所在平面内的一点，且2OB OC OB OC OA −=+− ，则ABC 是直角三角形【答案】AD 【解析】A ：由sin sin a bA B=，又sin sin A B >，即a b >，故A B >，正确； B ：由已知1||||cos1202AB BC AB BC ⋅=°=− ，错误；C ：由sin sin c b CB==，则sin C =506C π<<，故4C π=或34π，错误；D ：由OB OC CB −=、OB OA AB −= 、OC OA AC −= ，故CB AB AC =+ ， 所以在ABC 中CB 边上的中线长等于CB 的一半， 即ABC 是A 为直角的直角三角形，正确.故选：AD12．（2022春·甘肃天水·高一天水市第一中学校考期末）如图，在棱长为1的正方体1111ABCD A B C D −中，点P 是线段1AD 上的动点，下列命题正确的是（ ）A ．异面直线1PC 与1BC 所成角的大小为定值 B ．二面角1P BCD −−的大小为定值C ．若Q 是对角线1AC 上一点，则PQ QC +长度的最小值为43D ．若R 是线段BD 上一动点，则直线PR 与直线1AC 不可能平行 【答案】ABC【解析】如图1，由AB ⊥平面11BCC B ，1B C ⊂平面11BCC B ，得1AB B C ⊥，又11B C BC ⊥，1AB BC B = ，1,AB BC ⊂平面11ABC D ，所以1B C ⊥平面11ABC D ，1PC ⊂平面11ABC D ，所以11B C PC ⊥，即异面直线1PC 与1B C 所成角是90°为定值，A 正确；如图1，二面角1P BC D −−即为二面角1A BC D −−，为定值，B 正确；图1把11AC D △和1AC C △沿1AC 摊平，得平面四边形12ACC D ，如图2．作2CP AD ⊥于P ，1CP AC Q = ，此时PQ QC CP +=最小， 四边形12ACC D中，2AC AD ==1AC =1121C C C D ==， 由对称性知21CD AC ⊥，11AC CCCGAC ⋅==22CD CG ==AG ===，2243CD AG CP AD ⋅=， 所以PQ QC +的最小值是43，C 正确；图2取AD 中点E ，连接1A E 交1AD 于P ，连接CE 交BD 于R ，连接RP ，如图3，则111EPAEAEERPA A D BC RC ===，所以1//PR A C ，D 错．故选：ABC ．图3三、填空题：本题共4小题，每小题5分，共20分13．（2022秋·广东深圳·高一深圳中学校考期末）一组数据12,x x ，…，n x 的平均数是30，则数据121x +，221x +，…，21n x +的平均数是________． 【答案】61【解析】∵样本数据12,,,n x x x 的平均数是30，∴130ni i x n ==∑，∴数据1121,21,,21n x x x +++ 的平均数()111221161n ni i i i x x x n n ===+=+=∑∑ 故答案为：6114．（2023春·江苏无锡·高一辅仁高中校考期末）圆锥侧面展开图扇形的圆心角为60°，底面圆的半径为6，则圆锥的侧面积为______． 【答案】216π【解析】设圆锥的底面周长为c ，母线长为l ，则2π612πc ×，因为圆锥侧面展开图扇形的圆心角为60°，所以π12π3c ll==，解得36l =， 则圆锥的侧面积为113612π216π22lc =××=，故答案为：216π.15．（2022春·湖北襄阳·高一统考期末）已知三棱台111ABC A B C 的上下底面均为正三角形，1AB =，112A B =，侧棱长111AA BB CC ==，若11AA BB ⊥，则此棱台的高为___．【解析】由已知可得该三棱台为正三棱台，还原成棱锥如图所示，由于下底边是上底边的两倍， ∴大棱锥的高为棱台的高的两倍， 取BC 的中点D ,B 1C 1的中点D 1,连接PDD 1,AD ,A 1D 1,O ,O 1是上下底面的中心，连接POO 1. 由正棱台性质可得BC ⊥DD 1，BC ⊥PO , ∴BC ⊥平面PD 1A 1,∴BC ⊥P A 1，又∵11AA BB ⊥，故AA 1⊥平面PB 1C 1,∴A 1P ⊥PD 1.1AB =，112A B =，22122,339PO AO DO AD AD AD =×=×=ADAB =1PO AD OO ==,16．（2022春·江苏常州·高一常州高级中学校考期末）如图，在ABC 中，已知2,5,60,,AB AC BAC BC AC ==∠= 边上的两条中线,AM BN 相交于点P ，则MPN ∠的余弦值为__________.【解析】由题可得，11(),22AM AB AC BN AC AB =+=−， cos 605AB AC AB AC ⋅=⋅=，所以()221111122244AM BN AB ACAC AB AB AC AB AC ⋅=+⋅−=−+−⋅25125344=−+−×=，12AM AB =+ ，12BN AC =−所以cos cos ,AM BNMPN AM BN AM BN⋅∠===⋅故答案为:.四．解答题：本小题共6小题，共70分。

2020年下期期末测试模拟卷高一数学（人教A 版2019）（测试范围：必修第一册）（本卷满分150分，考试时间120分钟） 测试范围：必修第一册（人教A 版2019）一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的.1．已知集合}101{-=，，M ，}|{M b a b a x x N ∈⋅==、，，则集合M 与集合N 的关系是( )。

A 、N M =B 、N M ⊄C 、M ≠⊂ND 、∅=N M 【答案】A【解析】∵}101{-=，，M ，}101{-=，，N ，故有N M =，故选A 。

2．若命题p ：)(B A x ∈，则p ⌝为( )。

A 、A x ∈且B x ∉ B 、A x ∉或B x ∉C 、A x ∉且B x ∉D 、)(B A x ∉ 【答案】B【解析】∵)(B A x ∈，∴A x ∈且B x ∈，∴p ⌝：A x ∉或B x ∉，故选B 。

3．已知0>x ，0>y ，且182=+yx ，则xy 的最小值为( )。

A 、2 B 、8 C 、16 D 、64 【答案】D 【解析】∵xyy x y x 8822821=⋅≥+=，∴8≥xy ，即xy 最小值为64，故选D 。

4．若关于x 的不等式012<++c bx x a(1>ab )的解集为空集，则1)2()1(21-++-=ab c b a ab T 的最小值为( )。

A 、2B 、2C 、22D 、4 【答案】D【解析】01>a，042≤-a c b ，得42ab c ≥，∴)1(2211)2()1(2122-++≥-++-=ab b a ab ab c b a ab T ， 令m ab =-1，则0>m ，∴42222)1()1(212≥++=++++≥mm m m m T ，故选D 。

5．若函数)2lg()(2a x ax x f +-=的值域为R ，则实数a 的取值范围为( )。

2022年高一数学下学期期末模拟试卷及答案（共七套）（理科）2022年高一数学下学期期末模拟试卷及答案（一）（理科）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={1，2，3，4}，B={y|y=3x﹣2，x∈A}，则A∩B=（）A．{1}B．{4}C．{1，3}D．{1，4}2．设变量x，y满足约束条件，则目标函数z=2x+5y的最小值为（）A．﹣4 B．6 C．10 D．173．在△ABC中，如果sinA=sinC，B=30°，角B所对的边长b=2，则△ABC的面积为．4．已知点A（1，3），B（4，﹣1），则与向量同方向的单位向量为（）A．B．C．D．5．已知等差数列{a n}中，前n项和为S n，若a2+a8=10，则S9=（）A．36 B．40 C．42 D．456．a，b为正实数，若函数f（x）=ax3+bx+ab﹣1是奇函数，则f（2）的最小值是（）A．2 B．4 C．8 D．167．若圆（x﹣3）2+（y+5）2=r2上的点到直线4x﹣3y﹣2=0的最近距离等于1，则半径r的值为（）A．4 B．5 C．6 D．98．函数y=log a（x+2）﹣1（a＞0，a≠1）的图象恒过定点A，若点A 在直线mx+ny+1=0上，其中m＞0，n＞0，则+的最小值为（）A．3+2 B．3+2C．7 D．119．若cos（﹣α）=，则sin2α=（）A． B．C．﹣D．﹣10．如图是一几何体的三视图，正视图是一等腰直角三角形，且斜边BD长为2；侧视图为一直角三角形；俯视图为一直角梯形，且AB=BC=1，则此几何体的体积是（）A．B．C． D．111．已知等差数列前n项和为S n．且S13＜0，S12＞0，则此数列中绝对值最小的项为（）A．第5项B．第6项C．第7项D．第8项12．已知△ABC是边长为1的等边三角形，点D、E分别是边AB、BC 的中点，连接DE并延长到点F，使得DE=2EF，则•的值为（）A．﹣B．C．D．二、填空题：本大题共4小题，每小题5分，共20分．把答案直接答在答题纸上．13．已知关于x的不等式的解集是．则a=．14．在锐角△ABC中，AB=3，AC=4，S△ABC=3，则BC=．15．实数x，y满足x2+y2+xy=1，则x+y的最小值为．16．已知数列{a n}中，a1=1，a n=2a n﹣1+2n（n≥2），则a n=．三、解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤．17．已知函数f（x）=4tanxsin（﹣x）cos（x﹣）﹣．（1）求f（x）的定义域与最小正周期；（2）讨论f（x）在区间[﹣，]上的单调性．18．已知数列{a n}是首项为正数的等差数列，a1•a2=3，a2•a3=5．（1）求数列{a n}的通项公式；（2）设b n=（a n+1）•2，求数列{b n}的前n项和T n．19．如图，在直三棱柱ABC﹣A1B1C1中，∠ACB=90°．BC=CC1=a，AC=2a．（1）求证：AB1⊥BC1；（2）求二面角B﹣AB1﹣C的正弦值．20．已知圆C的方程：x2+y2﹣2x﹣4y+m=0，其中m＜5．（1）若圆C与直线l：x+2y﹣4=0相交于M，N两点，且|MN|=，求m的值；（2）在（1）条件下，是否存在直线l：x﹣2y+c=0，使得圆上有四点到直线l的距离为，若存在，求出c的范围，若不存在，说明理由．21．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知A=，b2﹣a2=c2．（1）求tanC的值；（2）若△ABC的面积为3，求b的值．22．已知函数f（x）=log4（4x+1）+2kx（k∈R）是偶函数．（1）求k的值；（2）若方程f（x）=m有解，求m的取值范围．参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={1，2，3，4}，B={y|y=3x﹣2，x∈A}，则A∩B=（）A．{1}B．{4}C．{1，3}D．{1，4}【考点】1E：交集及其运算．【分析】把A中元素代入y=3x﹣2中计算求出y的值，确定出B，找出A与B的交集即可．【解答】解：把x=1，2，3，4分别代入y=3x﹣2得：y=1，4，7，10，即B={1，4，7，10}，∵A={1，2，3，4}，∴A∩B={1，4}，故选：D．2．设变量x，y满足约束条件，则目标函数z=2x+5y的最小值为（）A．﹣4 B．6 C．10 D．17【考点】7C：简单线性规划．【分析】作出不等式组表示的平面区域，作出直线l0：2x+5y=0，平移直线l0，可得经过点（3，0）时，z=2x+5y取得最小值6．【解答】解：作出不等式组表示的可行域，如右图中三角形的区域，作出直线l0：2x+5y=0，图中的虚线，平移直线l0，可得经过点（3，0）时，z=2x+5y取得最小值6．故选：B．3．在△ABC中，如果sinA=sinC，B=30°，角B所对的边长b=2，则△ABC的面积为2+．【考点】HP：正弦定理．【分析】由sinA=sinC，利用正弦定理可得a=c，结合B=30°，可求C=A=75°，由正弦定理，可得a，c的值，进而利用三角形面积公式即可计算得解．【解答】解：∵在△ABC中，由sinA=sinC，可得a=c，∴△ABC是等腰三角形，又∵B=30°，∴可得：C=A=75°，∴由正弦定理，可得a====c，∴△ABC的面积S△ABC=ac•sinB=×（）×（）×=2+．故答案为：2+．4．已知点A（1，3），B（4，﹣1），则与向量同方向的单位向量为（）A．B．C．D．【考点】96：平行向量与共线向量；95：单位向量．【分析】由条件求得=（3，﹣4），||=5，再根据与向量同方向的单位向量为求得结果．【解答】解：∵已知点A（1，3），B（4，﹣1），∴=（4，﹣1）﹣（1，3）=（3，﹣4），||==5，则与向量同方向的单位向量为=，故选A．5．已知等差数列{a n}中，前n项和为S n，若a2+a8=10，则S9=（）A．36 B．40 C．42 D．45【考点】85：等差数列的前n项和．【分析】由等差数列的性质可得：a1+a9=a2+a8=10，再利用求和公式即可得出．【解答】解：由等差数列的性质可得：a1+a9=a2+a8=10，则S9===45．故选：D．6．a，b为正实数，若函数f（x）=ax3+bx+ab﹣1是奇函数，则f（2）的最小值是（）A．2 B．4 C．8 D．16【考点】3L：函数奇偶性的性质．【分析】由奇函数的性质和定义来建立等式，化简后根据条件用a表示b，代入解析式后求出f（2），再根据基本不等式求出最小值．【解答】解：因为f（x）=ax3+bx+ab﹣1是奇函数，所以，即，由a，b为正实数，所以b=＞0，所以f（x）=ax3+x，则f（2）=8a+≥2 =8（当且仅当8a=，即a=时取等号），故选：C．7．若圆（x﹣3）2+（y+5）2=r2上的点到直线4x﹣3y﹣2=0的最近距离等于1，则半径r的值为（）A．4 B．5 C．6 D．9【考点】J8：直线与圆相交的性质．【分析】由题意可得，圆心（3，﹣5）到直线的距离等于r+1，利用点到直线的距离公式求得r的值．【解答】解：由题意可得，圆心（3，﹣5）到直线的距离等于r+1，即|=r+1，求得r=4，故选：A．8．函数y=log a（x+2）﹣1（a＞0，a≠1）的图象恒过定点A，若点A 在直线mx+ny+1=0上，其中m＞0，n＞0，则+的最小值为（）A．3+2 B．3+2C．7 D．11【考点】4H：对数的运算性质．【分析】函数y=log a（x+2）﹣1（a＞0，a≠1）的图象恒过定点A（﹣1，﹣1），可得m+n=1．于是+=（m+n）=3++，再利用基本不等式的性质即可得出．【解答】解：函数y=log a（x+2）﹣1（a＞0，a≠1）的图象恒过定点A（﹣1，﹣1），∵点A在直线mx+ny+1=0上，其中m＞0，n＞0，∴﹣m﹣n+1=0，即m+n=1．则+=（m+n）=3++≥3+2=3+2，当且仅当n=m=2﹣时取等号．故选：A．9．若cos（﹣α）=，则sin2α=（）A． B．C．﹣D．﹣【考点】GF：三角函数的恒等变换及化简求值．【分析】法1°：利用诱导公式化sin2α=cos（﹣2α），再利用二倍角的余弦可得答案．法°：利用余弦二倍角公式将左边展开，可以得sinα+cosα的值，再平方，即得sin2α的值【解答】解：法1°：∵cos（﹣α）=，∴sin2α=cos（﹣2α）=cos2（﹣α）=2cos2（﹣α）﹣1=2×﹣1=﹣，法2°：∵cos（﹣α）=（sinα+cosα）=，∴（1+sin2α）=，∴sin2α=2×﹣1=﹣，故选：D．10．如图是一几何体的三视图，正视图是一等腰直角三角形，且斜边BD长为2；侧视图为一直角三角形；俯视图为一直角梯形，且AB=BC=1，则此几何体的体积是（）A．B．C． D．1【考点】L!：由三视图求面积、体积．【分析】由三视图知几何体为四棱锥与三棱锥的组合体，画出其直观图，判断几何体的高，计算底面面积，代入体积公式计算．【解答】解：由三视图知几何体为四棱锥与三棱锥的组合体，其直观图如图：根据三视图中正视图是一等腰直角三角形，且斜边BD长为2，∴棱锥的高为1，底面直角梯形的底边长分别为1、2，高为1，∴底面面积为=，∴几何体的体积V=××1=．故选A．11．已知等差数列前n项和为S n．且S13＜0，S12＞0，则此数列中绝对值最小的项为（）A．第5项B．第6项C．第7项D．第8项【考点】85：等差数列的前n项和；8B：数列的应用．【分析】由等差数列的性质可得a6+a7＞0，a7＜0，进而得出|a6|﹣|a7|=a6+a7＞0，可得答案．【解答】解：∵S13===13a7＜0，S12===6（a6+a7）＞0∴a6+a7＞0，a7＜0，∴|a6|﹣|a7|=a6+a7＞0，∴|a6|＞|a7|∴数列{a n}中绝对值最小的项是a7故选C．12．已知△ABC是边长为1的等边三角形，点D、E分别是边AB、BC 的中点，连接DE并延长到点F，使得DE=2EF，则•的值为（）A．﹣B．C．D．【考点】9R：平面向量数量积的运算．【分析】由题意画出图形，把、都用表示，然后代入数量积公式得答案．【解答】解：如图，∵D、E分别是边AB、BC的中点，且DE=2EF，∴•========．故选：C．二、填空题：本大题共4小题，每小题5分，共20分．把答案直接答在答题纸上．13．已知关于x的不等式的解集是．则a=2．【考点】7E：其他不等式的解法．【分析】把a=0代入不等式中得到解集不是原题的解集，故a不为0，所以把不等式转化为a（x+1）（x﹣）大于0，根据已知解集的特点即可求出a的值．【解答】解：由不等式判断可得a≠0，所以原不等式等价于，由解集特点可得a＞0且，则a=2．故答案为：214．在锐角△ABC中，AB=3，AC=4，S△ABC=3，则BC=．【考点】HP：正弦定理．【分析】由已知利用三角形面积公式可求sinA，利用同角三角函数基本关系式可求cosA，进而利用余弦定理即可计算得解BC的值．【解答】解：∵AB=3，AC=4，S△ABC=3=AB•AC•sinA=sinA，∴解得：sinA=，∵A为锐角，∴cosA=，∴由余弦定理可得：BC===．故答案为：．15．实数x，y满足x2+y2+xy=1，则x+y的最小值为﹣．【考点】7F：基本不等式．【分析】由x2+y2+xy=1，可得（x+y）2=1+xy≤1+，即可得出．【解答】解：由x2+y2+xy=1，可得（x+y）2=1+xy≤1+，解得：x+y≥﹣，当且仅当x=y=﹣时取等号．故答案为：﹣．16．已知数列{a n}中，a1=1，a n=2a n﹣1+2n（n≥2），则a n=（2n﹣1）•2n﹣1．【考点】8H：数列递推式．【分析】a n=2a n﹣1+2n（n≥2），可得﹣=1，利用等差数列的通项公式即可得出．【解答】解：∵a n=2a n﹣1+2n（n≥2），∴﹣=1，可得数列是等差数列，公差为1，首项为．∴==，解得a n=（2n﹣1）•2n﹣1．n=1时也成立．∴a n=（2n﹣1）•2n﹣1．故答案为：（2n﹣1）•2n﹣1．三、解答题：本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤．17．已知函数f（x）=4tanxsin（﹣x）cos（x﹣）﹣．（1）求f（x）的定义域与最小正周期；（2）讨论f（x）在区间[﹣，]上的单调性．【考点】GL：三角函数中的恒等变换应用；H2：正弦函数的图象．【分析】（1）利用三角函数的诱导公式以及两角和差的余弦公式，结合三角函数的辅助角公式进行化简求解即可．（2）利用三角函数的单调性进行求解即可．【解答】解：（1）∵f（x）=4tanxsin（﹣x）cos（x﹣）﹣．∴x≠kπ+，即函数的定义域为{x|x≠kπ+，k∈Z}，则f（x）=4tanxcosx•（cosx+sinx）﹣=4sinx（cosx+sinx）﹣=2sinxcosx+2sin2x﹣=sin2x+（1﹣cos2x）﹣=sin2x﹣cos2x=2sin（2x﹣），则函数的周期T=；（2）由2kπ﹣≤2x﹣≤2kπ+，k∈Z，得kπ﹣≤x≤kπ+，k∈Z，即函数的增区间为[kπ﹣，kπ+]，k∈Z，当k=0时，增区间为[﹣，]，k∈Z，∵x∈[﹣，]，∴此时x∈[﹣，]，由2kπ+≤2x﹣≤2kπ+，k∈Z，得kπ+≤x≤kπ+，k∈Z，即函数的减区间为[kπ+，kπ+]，k∈Z，当k=﹣1时，减区间为[﹣，﹣]，k∈Z，∵x∈[﹣，]，∴此时x∈[﹣，﹣]，即在区间[﹣，]上，函数的减区间为∈[﹣，﹣]，增区间为[﹣，]．18．已知数列{a n}是首项为正数的等差数列，a1•a2=3，a2•a3=5．（1）求数列{a n}的通项公式；（2）设b n=（a n+1）•2，求数列{b n}的前n项和T n．【考点】8E：数列的求和；8H：数列递推式．【分析】（1）设数列{a n}的公差为d，由a1•a2=3，a2•a3=5，解得a1=1，d=2，即可得a n=2n﹣1．（2）由（1）知b n=（a n+1）•2=2n•22n﹣4=n•4n，利用错位相减法求和即可．【解答】解：（1）设数列{a n}的公差为d，因为a1•a2=3，a2•a3=5．解得a1=1，d=2，所以a n=2n﹣1．（2）由（1）知b n=（a n+1）•2=2n•22n﹣4=n•4n，T n=1•41+2•42+3•43+…+n•4n．4T n=1•42+2•43+…+（n﹣1）•4n+n•4n+1，两式相减，得﹣3T n=41+42+43+…+4n﹣n•4n+1=﹣n•4n+1=，所以T n=．19．如图，在直三棱柱ABC﹣A1B1C1中，∠ACB=90°．BC=CC1=a，AC=2a．（1）求证：AB1⊥BC1；（2）求二面角B﹣AB1﹣C的正弦值．【考点】MT：二面角的平面角及求法．【分析】（1）由已知可得AC⊥平面B1BCC1，则AC⊥BC1，再由BC=CC1，得BC1⊥B1C，由线面垂直的判定可得BC1⊥平面AB1C，从而得到AB1⊥BC1；（2）设BC1∩B1C=O，作OP⊥AB1于点P，连结BP．由（1）知BO⊥AB1，进一步得到AB1⊥平面BOP，说明∠OPB是二面角B﹣AB1﹣C 的平面角．然后求解直角三角形得答案．【解答】（1）证明：∵ABC﹣A1B1C1是直三棱柱，∴CC1⊥平面ABC，则AC⊥CC1．又∵AC⊥BC，BC∩CC1=C，∴AC⊥平面B1BCC1，则AC⊥BC1，∵BC=CC1，∴四边形B1BCC1是正方形，∴BC1⊥B1C，又AC∩B1C=C，∴BC1⊥平面AB1C，则AB1⊥BC1；（2）解：设BC1∩B1C=O，作OP⊥AB1于点P，连结BP．由（1）知BO⊥AB1，而BO∩OP=O，∴AB1⊥平面BOP，则BP⊥AB1，∴∠OPB是二面角B﹣AB1﹣C的平面角．∵△OPB1～△ACB1，∴，∵BC=CC1=a，AC=2a，∴OP=，∴=．在Rt△POB中，sin∠OPB=，∴二面角B﹣AB1﹣C的正弦值为．20．已知圆C的方程：x2+y2﹣2x﹣4y+m=0，其中m＜5．（1）若圆C与直线l：x+2y﹣4=0相交于M，N两点，且|MN|=，求m的值；（2）在（1）条件下，是否存在直线l：x﹣2y+c=0，使得圆上有四点到直线l的距离为，若存在，求出c的范围，若不存在，说明理由．【考点】JE：直线和圆的方程的应用．【分析】（1）圆的方程化为（x﹣1）2+（y﹣2）2=5﹣m，圆心C（1，2）到直线l：x+2y﹣4=0的距离为，由此解得m=4．（2）假设存在直线l：x﹣2y+c=0，使得圆上有四点到直线l的距离为，由于圆心C（1，2），半径r=1，由此利用圆心C（1，2）到直线l：x﹣2y+c=0的距离，能求出c的范围．【解答】解：（1）圆的方程化为（x﹣1）2+（y﹣2）2=5﹣m，圆心C（1，2），半径，则圆心C（1，2）到直线l：x+2y﹣4=0的距离为：…由于，则，有，∴，解得m=4．…（2）假设存在直线l：x﹣2y+c=0，使得圆上有四点到直线l的距离为，…由于圆心C（1，2），半径r=1，则圆心C（1，2）到直线l：x﹣2y+c=0的距离为：，…解得．…21．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知A=，b2﹣a2=c2．（1）求tanC的值；（2）若△ABC的面积为3，求b的值．【考点】HR：余弦定理．【分析】（1）由余弦定理可得：，已知b2﹣a2=c2．可得，a=．利用余弦定理可得cosC．可得sinC=，即可得出tanC=．（2）由=×=3，可得c，即可得出b．【解答】解：（1）∵A=，∴由余弦定理可得：，∴b2﹣a2=bc﹣c2，又b2﹣a2=c2．∴bc﹣c2=c2．∴b=c．可得，∴a2=b2﹣=，即a=．∴cosC===．∵C∈（0，π），∴sinC==．∴tanC==2．（2）∵=×=3，解得c=2．∴=3．22．已知函数f（x）=log4（4x+1）+2kx（k∈R）是偶函数．（1）求k的值；（2）若方程f（x）=m有解，求m的取值范围．【考点】3H：函数的最值及其几何意义；4H：对数的运算性质．【分析】（1）利用函数是偶函数，利用定义推出方程求解即可．（2）通过方程有解，求出函数的最值，即可推出m的范围．【解答】（本小题满分12分）解：（1）由函数f（x）是偶函数可知，f（﹣x）=f（x），∴log4（4x+1）+2kx=log4（4﹣x+1）﹣2kx，即log4=﹣4kx，∴log44x=﹣4kx，∴x=﹣4kx，即（1+4k）x=0，对一切x∈R恒成立，∴k=﹣．…（2）由m=f（x）=log4（4x+1）﹣x=log4=log4（2x+），∵2x＞0，∴2x+≥2，∴m≥log42=．故要使方程f（x）=m有解，m的取值范围为[，+∞）．…2022年高一数学下学期期末模拟试卷及答案（二）（理科）一、选择题：（本大题共12小题，每题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请把答案填写在答题纸上）1．若＜＜0，则下列结论正确的是（）A．a2＞b2 B．ab＞b2C．a﹣b＜0 D．|a|+|b|=|a+b|2．已知角θ的始边与x轴的正半轴重合，终边在直线y=2x上，则cos2θ=（）A．B．C．D．3．有下列说法：①若向量、满足||＞||，且与方向相同，则＞；②|+|≤||+||；③共线向量一定在同一直线上；④由于零向量的方向不确定，故其不能与任何向量平行；其中正确说法的个数是（）A．0 B．1 C．2 D．34．在△ABC中，，则△ABC一定是（）A．等腰三角形B．直角三角形C．等腰直角三角形 D．等腰三角形或直角三角形5．已知点A（﹣1，1），B（1，2），C（﹣2，﹣1），D（3，4），则向量在方向上的投影为（）A．B．C．D．6．要得到函数y=2cosx•sin（x+）﹣的图象，只需将y=sinx的图象（）A．先向左平移个单位长度，再将所有点的横坐标缩短为原来的倍（纵坐标不变）B．先向左平移个单位长度，再将所有点的横坐标缩短为原来的2倍（纵坐标不变）C．先将所有点的横坐标缩短为原来的2倍（纵坐标不变），再向左平移个单位长度D．先将所有点的横坐标缩短为原来的倍（纵坐标不变），再向左平移个单位长度7．在△ABC中，内角A，B，C所对的边分别是a，b，c．已知8b=5c，C=2B，则cosC=（）A． B．C．D．8．已知S n是等差数列{a n}的前n项和，且S6＞S7＞S5，有下列五个说法：①S6为S n的最大值，②S11＞0，③S12＜0，④S13＜0，⑤S8﹣S5＞0，其中说法正确的个数是（）A．1 B．2 C．3 D．49．已知a、b为正实数，且a+2b=3ab，若a+b﹣c≥0对于满足条件的a，b恒成立，则c的取值范围为（）A．（﹣∞，]B．C．（﹣∞，6]D．（﹣∞，]10．数列{a n}满足：a1=1，且对任意的m，n∈N+都有a m+n=a m+a n+m•n，则=（）A．B．C．D．11．在△ABC中，A=60°，b=1，其面积为，则等于（）A．3B．C．D．12．若数列{a n}满足=0，n∈N*，p为非零常数，则称数列{a n}为“梦想数列”．已知正项数列为“梦想数列”，且b1b2b3…b99=399，则b8+b92的最小值是（）A．3 B．6 C．9 D．12二．填空题：（本大题共4小题，每小题5分，共20分）13．已知△ABC得三边长成公比为的等比数列，则其最大角的余弦值为______．14．x，y满足约束条件，若z=y﹣ax取得最大值的最优解不唯一，则实数a的值为______．15．已知函数f（x）=x2+ax+b（a，b∈R）的值域为[0，+∞），若关于x的不等式f（x）＜c的解集为（m，m+4），则实数c的值为______．16．已知数列{a n}的首项为2，数列{b n}为等比数列且b n=，若b11•b12=2，则a23=______．三．解答题：（本题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．已知tan（π+α）=2，求下列各式的值：（1）；（2）．18．在△ABC中，角A，B，C所对的边长分别为a，b，c，B=45°，b=3．（Ⅰ）若cosC+cosA=1，求A和c的值；（Ⅱ）若=（2sin，﹣1），=（cos，2sin2），f（A）=•，求f（A）的取值范围．19．已知数列{a n}中，a1=1，a2=2，且a n+1=4a n﹣3a n﹣1（n∈N*，n≥2）（Ⅰ）令b n=a n+1﹣a n，求证：数列{b n}为等比数列；（Ⅱ）求数列{a n}及数列{n•（a n﹣）}的前n项和S n．20．已知f（x）=ax2﹣（ab+b）x+1．（1）当b=1时，求不等式f（x）＜0的解集；（2）若a，b均为正实数且f（﹣2）=9，求2a+b的最小值．21．已知△ABC的三内角A，B，C所对的边分别是a，b，c，△ABC 的面积S=且sinA=．（1）求sinB；（2）若边c=5，求△ABC的面积S．22．已知各项均为正数的数列{a n}满足log2a n﹣log2a n﹣1=1n∈N*，n≥2，且a4=16．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）设数列{b n}满足b n=，是否存在正整数m，n（1＜m ＜n），使得b1，b m，b n成等比数列？若存在，求出所有的m，n的值；若不存在，请说明理由．（Ⅲ）令c n=，记数列{c n}的前n项和为S n，其中n∈N*，证明：≤S n＜2．参考答案与试题解析一、选择题：（本大题共12小题，每题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请把答案填写在答题纸上）1．若＜＜0，则下列结论正确的是（）A．a2＞b2 B．ab＞b2C．a﹣b＜0 D．|a|+|b|=|a+b|【考点】不等式的基本性质．【分析】根据不等式的性质得到b＜a＜0，然后分别进行判断即可．【解答】解：由＜＜0，得b＜a＜0，则a2＜b2，故A错误，ab＜b2，故B错误，a﹣b＞0，故C错误，|a|+|b|=|a+b|=﹣a﹣b，故D正确故选：D．2．已知角θ的始边与x轴的正半轴重合，终边在直线y=2x上，则cos2θ=（）A．B．C．D．【考点】二倍角的余弦；任意角的三角函数的定义．【分析】根据直线的斜率等于倾斜角的正切值，由已知直线的斜率得到tanθ的值，然后根据同角三角函数间的基本关系求出cosθ的平方，然后根据二倍角的余弦函数公式把所求的式子化简后，把cosθ的平方代入即可求出值．【解答】解：根据题意得：tanθ=2，∴cos2θ==，则cos2θ=2cos2θ﹣1=﹣1=﹣．故选B3．有下列说法：①若向量、满足||＞||，且与方向相同，则＞；②|+|≤||+||；③共线向量一定在同一直线上；④由于零向量的方向不确定，故其不能与任何向量平行；其中正确说法的个数是（）A．0 B．1 C．2 D．3【考点】向量的物理背景与概念．【分析】根据平面向量的有关定义进行分析判断．【解答】解：：（1）∵向量不能比较大小，故①错误；（2）|∵+|2=||2+||2+2=||2+||2+2||||cosθ，（||+||）2=||2+||2+2||||，∴|+|≤||+||，故②正确；（3）共线向量只需方法相同或相反即可，不一定在同一直线上，故③错误；（4）零向量与任一向量都是共线的，即零向量与任一向量平行，故④错误．故选：B．4．在△ABC中，，则△ABC一定是（）A．等腰三角形B．直角三角形C．等腰直角三角形 D．等腰三角形或直角三角形【考点】三角形的形状判断．【分析】利用正弦定理==2R与二倍角的正弦即可判断三角形的形状．【解答】解：∵在△ABC中=，∴=，又由正弦定理==2R得：=，∴=，∴sin2A=sin2B，∴2A=2B或2A=π﹣2B，∴A=B或A+B=．故△ABC是等腰三角形或直角三角形．故选D．5．已知点A（﹣1，1），B（1，2），C（﹣2，﹣1），D（3，4），则向量在方向上的投影为（）A．B．C．D．【考点】平面向量数量积的含义与物理意义．【分析】先求出向量、，根据投影定义即可求得答案．【解答】解：，，则向量方向上的投影为：•cos＜＞=•===，故选A．6．要得到函数y=2cosx•sin（x+）﹣的图象，只需将y=sinx的图象（）A．先向左平移个单位长度，再将所有点的横坐标缩短为原来的倍（纵坐标不变）B．先向左平移个单位长度，再将所有点的横坐标缩短为原来的2倍（纵坐标不变）C．先将所有点的横坐标缩短为原来的2倍（纵坐标不变），再向左平移个单位长度D．先将所有点的横坐标缩短为原来的倍（纵坐标不变），再向左平移个单位长度【考点】函数y=Asin（ωx+φ）的图象变换．【分析】由条件利用函数y=Asin（ωx+φ）的图象变换规律，得出结论．【解答】解：∵函数y=2cosx•sin（x+）﹣=2cosx（sinx•+cosx•）﹣=sin2x+﹣=sin（2+），∴把y=sinx的图象先向左平移个单位长度可得y=sin（x+）的图象，再将所有点的横坐标缩短为原来的倍（纵坐标不变），可得y=sin （2x+）的图象，故选：A．7．在△ABC中，内角A，B，C所对的边分别是a，b，c．已知8b=5c，C=2B，则cosC=（）A． B．C．D．【考点】正弦定理的应用；三角函数中的恒等变换应用．【分析】直接利用正弦定理以及二倍角公式，求出sinB，cosB，然后利用平方关系式求出cosC的值即可．【解答】解：因为在△ABC中，内角A，B，C所对的边分别是a，b，c．已知8b=5c，C=2B，所以8sinB=5sinC=5sin2B=10sinBcosB，所以cosB=，B为三角形内角，所以B∈（0，）．C．所以sinB==．所以sinC=sin2B=2×=，cosC==．故选：A．8．已知S n是等差数列{a n}的前n项和，且S6＞S7＞S5，有下列五个说法：①S6为S n的最大值，②S11＞0，③S12＜0，④S13＜0，⑤S8﹣S5＞0，其中说法正确的个数是（）A．1 B．2 C．3 D．4【考点】命题的真假判断与应用；等差数列的前n项和．【分析】S6＞S7＞S5，利用前n项和公式可得：a7＜0，a6+a7＞0，可得a6＞0＞a7，|a6|＞|a7|．d＜0．S6最大．S11==11a6＞0．即可判断出正确命题的个数．【解答】解：∵S6＞S7＞S5，∴6a1+d＞7a1+d＞5a1+d，化为：a7＜0，a6+a7＞0，∴a6＞0＞a7，|a6|＞|a7|．∴d＜0．S6最大．①S6为S n的最大值，正确；S11==11a6＞0．②S11＞0，正确；③S12=6（a6+a7）＞0，所以S12＜0不正确；④S13=13a12＜0，S13＜0正确；⑤S8﹣S5=a6+a7+a8=3a7＜0，所以S8﹣S5＞0，不正确；综上可得：①②④正确．故选：C．9．已知a、b为正实数，且a+2b=3ab，若a+b﹣c≥0对于满足条件的a，b恒成立，则c的取值范围为（）A．（﹣∞，]B．C．（﹣∞，6]D．（﹣∞，]【考点】基本不等式．【分析】利用基本不等式可求出a+b的最小值（a+b）min，要使a+b ﹣c≥0对于满足条件的a，b恒成立，只要值（a+b）min﹣c≥0即可．【解答】解：a，b都是正实数，且a+2b=3ab，则+=3，满足①，则a+b=（a+b）••（+）=（3++）≥（3+2×）=1+当且仅当=时，即a=b②时，等号成立．联立①②解得a=，b=，故a+b的最小值为1+，要使a+b﹣c≥0恒成立，只要1+﹣c≥0，即c≤1+，故c的取值范围为（﹣∞，1+]．故选A．10．数列{a n}满足：a1=1，且对任意的m，n∈N+都有a m+n=a m+a n+m•n，则=（）A．B．C．D．【考点】数列递推式；数列的求和．【分析】由数列{a n}满足：a1=1，且对任意的m，n∈N+都有a m+n=a m+a n+m•n，可得a n+1=a n+a1+n，即a n+1﹣a n=1+n，利用“累加求和”、“裂项求和”方法即可得出．【解答】解：由数列{a n}满足：a1=1，且对任意的m，n∈N+都有a m+n=a m+a n+m•n，则a n+1=a n+a1+n，∴a n+1﹣a n=1+n，∴a n=（a n﹣a n﹣1）+（a n﹣1﹣a n﹣2）+…+（a2﹣a1）+a1=n+（n﹣1）+…+2+1=．∴==2．则=2++…+=2=．故选：D．11．在△ABC中，A=60°，b=1，其面积为，则等于（）A．3B．C．D．【考点】正弦定理．【分析】由A的度数求出sinA和cosA的值，根据三角形的面积公式表示出三角形ABC的面积，把b，sinA及已知的面积代入求出c的值，再由cosA，b，c的值，利用余弦定理求出a的值，由a及sinA 的值，根据正弦定理求出三角形ABC外接圆的直径2R，根据等比合比性质即可求出所求式子的值．【解答】解：∵A=60°，b=1，其面积为，∴S=bcsinA=c=，即c=4，∴由余弦定理得：a2=b2+c2﹣2bccosA=1+16﹣4=13，∴a=，由正弦定理得：===2R==，则=2R=．故选B12．若数列{a n}满足=0，n∈N*，p为非零常数，则称数列{a n}为“梦想数列”．已知正项数列为“梦想数列”，且b1b2b3…b99=399，则b8+b92的最小值是（）A．3 B．6 C．9 D．12【考点】数列的应用．【分析】由新定义得到数列{b n}为等比数列，然后由等比数列的性质得到b50=3，再利用基本不等式b8+b92≥2，即可求得b8+b92的最小值．【解答】解：依题意可得b n+1=qb n，则数列{b n}为等比数列，b1b2b3…b99=399，则b50=3，b8+b92≥2=2b50=6，b8+b92的最小值6，故答案选：B．二．填空题：（本大题共4小题，每小题5分，共20分）13．已知△ABC得三边长成公比为的等比数列，则其最大角的余弦值为．【考点】余弦定理；等比数列的性质．【分析】根据三角形三边长成公比为的等比数列，根据等比数列的性质设出三角形的三边为a，a，2a，根据2a为最大边，利用大边对大角可得出2a所对的角最大，设为θ，利用余弦定理表示出cosθ，将设出的三边长代入，即可求出cosθ的值．【解答】解：根据题意设三角形的三边长分别为a，a，2a，∵2a＞a＞a，∴2a所对的角为最大角，设为θ，则根据余弦定理得：cosθ==﹣．故答案为：﹣14．x，y满足约束条件，若z=y﹣ax取得最大值的最优解不唯一，则实数a的值为2或﹣1．【考点】简单线性规划．【分析】由题意作出其平面区域，将z=y﹣ax化为y=ax+z，z相当于直线y=ax+z的纵截距，由几何意义可得．【解答】解：由题意作出其平面区域，将z=y﹣ax化为y=ax+z，z相当于直线y=ax+z的纵截距，由题意可得，y=ax+z与y=2x+2或与y=2﹣x平行，故a=2或﹣1；故答案为：2或﹣1．15．已知函数f（x）=x2+ax+b（a，b∈R）的值域为[0，+∞），若关于x的不等式f（x）＜c的解集为（m，m+4），则实数c的值为4．【考点】二次函数的性质．【分析】根据题意可知b=，把不等式解的问题转化为方程根的问题，利用韦达定理求解即可．【解答】解：f（x）=x2+ax+b（a，b∈R）的值域为[0，+∞），∴=0，∴b=，∵f（x）＜c的解集为（m，m+4），∴f（x）﹣c=0的根为m，m+4，即x2+ax+﹣c=0的根为m，m+4，∵（m+4﹣m）2=（﹣a）2﹣4（﹣c），∴4c=16，c=4．故答案为4．16．已知数列{a n}的首项为2，数列{b n}为等比数列且b n=，若b11•b12=2，则a23=4096．【考点】数列递推式．【分析】由于数列{b n}为等比数列且b n=，可得b1b2…•b22=•…•=，化简代入即可得出．【解答】解：∵数列{b n}为等比数列且b n=，∴b1b2…b22=•…•===211，∴a23=212=4096．故答案为：4096．三．解答题：（本题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤）17．已知tan（π+α）=2，求下列各式的值：（1）；（2）．【考点】三角函数的化简求值．【分析】（1）利用诱导公式以及同角三角函数基本关系式化简表达式为正切函数的形式，代入求解即可．（2）利用同角三角函数基本关系式化简表达式为正切函数的形式，代入求解即可．【解答】解：（1）由已知得tanα=2．∴．（2）=18．在△ABC中，角A，B，C所对的边长分别为a，b，c，B=45°，b=3．（Ⅰ）若cosC+cosA=1，求A和c的值；（Ⅱ）若=（2sin，﹣1），=（cos，2sin2），f（A）=•，求f（A）的取值范围．【考点】三角函数中的恒等变换应用；平面向量数量积的运算；余弦定理．【分析】（Ⅰ）由题意和内角和定理求出C，由两角差的余弦公式、两角和的正弦公式化简已知的等式，由A的范围和特殊角的三角函数值求出A，判断出△ABC的形状，由勾股定理求出c；（Ⅱ）利用二倍角公式及变形，两角和的正弦公式化简f（A），由A 的范围和正弦函数的图象与性质，求出f（A）的取值范围．【解答】解：（Ⅰ）∵B=45°，∴C=180°﹣A﹣B=135°﹣A，∴==，又∵A+450∈，∴A+450=900，得A=45°．∴△ABC为等腰直角三角形，．…（Ⅱ）∵=（2sin，﹣1），=（cos，2sin2），∴=sinA﹣（1﹣cosA）=由得，，∴，则，即f（A）的取值范围是…19．已知数列{a n}中，a1=1，a2=2，且a n+1=4a n﹣3a n﹣1（n∈N*，n≥2）（Ⅰ）令b n=a n+1﹣a n，求证：数列{b n}为等比数列；（Ⅱ）求数列{a n}及数列{n•（a n﹣）}的前n项和S n．【考点】数列的求和；等比数列的通项公式．【分析】（Ⅰ）对任意的n∈N*，n≥2，由a n+1=4a n﹣3a n﹣1，变形a n+1﹣a n=3a n﹣3a n﹣1=3（a n﹣a n﹣1），令b n=a n+1﹣a n，显然b n=a n+1﹣a n≠0，则，即可证明．（II）由（Ⅰ）可知．当n≥2时，，利用“累加求和”方法、“错位相减法”即可得出．【解答】（Ⅰ）证明：对任意的n∈N*，n≥2，∵a n+1=4a n﹣3a n﹣1，∴a n+1﹣a n=3a n﹣3a n﹣1=3（a n﹣a n﹣1），令b n=a n+1﹣a n，显然b n=a n+1﹣a n≠0，则，∴数列{b n}是首项为b1=a2﹣a1=1，公比q为3的等比数列．（Ⅱ）解：由（Ⅰ）可知．∴当n=1时，a1=1，当n≥2时，a2﹣a1=b1=1，，，…，累加得，∵，则，∴，，∴=，∴．20．已知f（x）=ax2﹣（ab+b）x+1．（1）当b=1时，求不等式f（x）＜0的解集；（2）若a，b均为正实数且f（﹣2）=9，求2a+b的最小值．【考点】利用导数求闭区间上函数的最值．【分析】（1）代入b值，不等式可因式分解为（ax﹣1）（x﹣1）＜0，对参数a分类讨论，得出解集；（2）由条件可知2a+b+ab=4，由不等式性质，可得，利用换元法解不等式即可．【解答】解：（1）当b=1时，f（x）=ax2﹣（a+1）x+1=（ax﹣1）（x ﹣1），所以（ax﹣1）（x﹣1）＜0．①当a=0时，此不等式解集为{x|x＞1}②当a＜0时，此不等式解集为当a＞0时，若即0＜a＜1时，此不等式解集为；若即a=1时，此不等式解集为∅；若即a＞1时，此不等式解集为．…（2）f（﹣2）=4a+2ab+2b+1=9得：2a+b+ab=4，∵，∴，解得：（（舍去））当且仅当2a=b，即时上式取等号．所以2a+b的最小值为．…21．已知△ABC的三内角A，B，C所对的边分别是a，b，c，△ABC 的面积S=且sinA=．（1）求sinB；（2）若边c=5，求△ABC的面积S．【考点】余弦定理；正弦定理．【分析】（1）利用余弦定理、三角形面积计算公式可得C，再利用同角三角函数基本关系式、三角形内角和定理、和差公式即可得出．（2）利用正弦定理、三角形面积计算公式即可得出．【解答】解：（1）由余弦定理有c2=a2+b2﹣2abcosC，∴a2+b2﹣c2=2abcosC，则，又，∴cosC=sinC，tanC=1，在△ABC中，∵，在△ABC中或，但A+B+C=π，∴，∴，sinB==×=．（2）由正弦定理有，又c=5，∴，得b=7，∴S=bcsinA==．22．已知各项均为正数的数列{a n}满足log2a n﹣log2a n﹣1=1n∈N*，n≥2，且a4=16．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）设数列{b n}满足b n=，是否存在正整数m，n（1＜m ＜n），使得b1，b m，b n成等比数列？若存在，求出所有的m，n的值；若不存在，请说明理由．（Ⅲ）令c n=，记数列{c n}的前n项和为S n，其中n∈N*，证明：≤S n＜2．【考点】数列的求和；数列递推式．【分析】（I）利用等差数列的通项公式及其对数的运算性质即可得出．（II）b n==，由b1，b m，b n成等比数列，可得=，即=，由﹣2m2+4m+1＞0，解出即可得出．（Ⅲ），利用“裂项求和”方法与数列的单调性即可得出．【解答】解：（Ⅰ）∵对任意的n∈N*，n≥2，，即：，∴数列{}是首相为，公差为1的等差数列．∴，∴．（Ⅱ）b n==，若b1，b m，b n成等比数列，则=，即=．可得=，∴﹣2m2+4m+1＞0，解得：＜m＜1+．又m∈N*，且m＞1，∴m=2，此时n=12．故当且仅当m=2，n=12．使得b1，b m，b n成等比数列．（Ⅲ）证明：，∴S n=c1+c2+c3+…+c n=∴，即结论成立．2022年高一数学下学期期末模拟试卷及答案（三）（理科）一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．）1．若tanα＜0，cosα＜0，则α的终边所有的象限为（）A．第一象限B．第二象限C．第三象限D．第四象限2．计算sin45°cos15°+cos45°sin15°=（）A．B． C．D．3．若点（sin，cos）在角α的终边上，则sinα的值为（）A．B． C．D．4．若tanα=3，则的值等于（）A．2 B．3 C．4 D．65．在数列{a n}中，若为定值，且a4=2，则a2a6等于（）A．32 B．4 C．8 D．166．在等差数列{a n}中，已知a1+a5+a9=3，则数列{a n}的前9项和S9=（）A．9 B．15 C．18 D．247．已知a，b，c为△ABC的三个角A，B，C所对的边，若3bcosC=c（1﹣3cosB），则=（）A．2：3 B．4：3 C．3：1 D．3：28．等比数列{a n}的前n项和为S n，已知a2a5=2a3，且a4与2a7的等差中项为，则S5=（）A．29 B．31 C．33 D．369．若在△ABC中，2cosBsinA=sinC，则△ABC的形状一定是（）A．等腰直角三角形B．直角三角形C．等腰三角形D．等边三角形10．数列{a n}满足a n+a n+1=（n∈N*），a2=2，S n是数列{a n}的前n项和，则S21为（）A．5 B．C．D．11．在等比数列{a n}中，a1=2，前n项和为S n，若数列{a n+1}也是等比数列，则S n等于（）A．2n+1﹣2 B．3n C．2n D．3n﹣112．已知实数a＞0，b＞0，若是4a与2b的等比中项，则下列不对的说法是（）A．B．0＜b＜1 C． D．二、填空题（本大题包括4小题，每小题5分，共20分，把正确答案填在答题卡中的横线上）13．sin15°cos165°=．14．已知实数1＜a＜2，3＜b＜4，则的取值范围是．。

2020年高一数学第二学期期末模拟试卷及答案（共五套）2020年高一数学第二学期期末模拟试卷及答案（一）一、选择题：1．重庆市2013年各月的平均气温（℃）数据的茎叶图如，则这组数据的中位数是（）A．19 B．20 C．21.5 D．232．等差数列{a n}中，a1+a5=10，a4=7，则数列{a n}的公差为（）A．1 B．2 C．3 D．43．在区间[﹣2，3]上随机选取一个数X，则X≤1的概率为（）A．B．C．D．4．执行如图所示的程序框图，输出的k值为（）A．3 B．4 C．5 D．65．已知x，y满足约束条件，则z=﹣2x+y的最大值是（）A．﹣1 B．﹣2 C．﹣5 D．16．在梯形ABCD中，∠ABC=，AD∥BC，BC=2AD=2AB=2，将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为（）A．B．C．D．2π7．某三棱锥的三视图如图所示，则该三棱锥的表面积是（）A．2+B．4+C．2+2 D．58．对于集合{a1，a2，…，a n}和常数a0，定义w=为集合{a1，a2，…，a n}相对a0的“正弦方差”，则集合{，， }相对a0的“正弦方差”为（）A．B．C．D．与a0有关的一个值二、填空题：9．某电子商务公司对1000名网络购物者2015年度的消费情况进行统计，发现消费金额（单位：万元）都在区间[0.3，0.9]内，其频率分布直方图如图所示．在这些购物者中，消费金额在区间[0.5，0.9]内的购物者的人数为______．10．在△ABC中，a=4，b=5，c=6，则=______．11．等比数列{a n}的前n项和为S n，公比不为1．若a1=1，且对任意的n∈N+都有a n+2+a n+1﹣2a n=0，则S5=______．12．已知1＜a＜2，2＜a+b＜4，则5a﹣b的取值范围是______．13．如图，在正三棱柱A1B1C1﹣ABC中，AB=2，A1A=2，D，F 分别是棱AB，AA1的中点，E为棱AC上的动点，则△DEF周长的最小值为______．14．已知函数f（x）=．（1）若f（x）＞k的解集为{x|x＜﹣3或x＞﹣2}，则k的值等于______；（2）对任意x＞0，f（x）≤t恒成立，则t的取值范围是______．三、解答题：本大题共5小题，共50分.15．海关对同时从A，B，C三个不同地区进口的某种商品进行抽样检测，从各地区进口此商品的数量（单位：件）如表所示．工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测．地区 A B C数量50 1510（Ⅰ）求这6件样品来自A，B，C各地区商品的数量；（Ⅱ）若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．16．如图，在长方体ABCD﹣A1B1C1D1中，AB=16，AA1=8，BC=10，点E，F 分别在A1B1C1D1上，A1E=D1F=4，过点E，F的平面α与此长方体的面相交，交线围成一个正方形EFGH．（I）在图中画出这个正方形EFGH（不必说明画法和理由），并说明G，H在棱上的具体位置；（II）求平面α把该长方体分成的两部分体积的比值．17．已知函数f（x）=sinxcosx﹣cos2x+，△ABC三个内角A，B，C的对边分别为a，b，c且f（A）=1．（I）求角A的大小；（Ⅱ）若a=7，b=5，求c的值．18．某超市随机选取1000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买．甲乙丙丁10√×√√21×√×√720√√√×30√×√×85 √××××√××98（1）估计顾客同时购买乙和丙的概率；（2）估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；（3）如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？19．已知数列{a n}和{b n}满足a1a2a3…a n=（n∈N*）．若{a n}为等比数列，且a1=2，b3=6+b2．（Ⅰ）求a n和b n；（Ⅱ）设c n=（n∈N*）．记数列{c n}的前n项和为S n．（i）求S n；（ii）求正整数k，使得对任意n∈N*均有S k≥S n．参考答案与试题解析一、选择题：1．重庆市2013年各月的平均气温（℃）数据的茎叶图如，则这组数据的中位数是（）A．19 B．20 C．21.5 D．23【考点】茎叶图．【分析】根据中位数的定义进行求解即可．【解答】解：样本数据有12个，位于中间的两个数为20，20，则中位数为，故选：B2．等差数列{a n}中，a1+a5=10，a4=7，则数列{a n}的公差为（）A．1 B．2 C．3 D．4【考点】等差数列的通项公式．【分析】设数列{a n}的公差为d，则由题意可得2a1+4d=10，a1+3d=7，由此解得d的值．【解答】解：设数列{a n}的公差为d，则由a1+a5=10，a4=7，可得2a1+4d=10，a1+3d=7，解得d=2，故选B．3．在区间[﹣2，3]上随机选取一个数X，则X≤1的概率为（）A．B．C．D．【考点】几何概型．【分析】利用几何槪型的概率公式，求出对应的区间长度，即可得到结论．【解答】解：在区间[﹣2，3]上随机选取一个数X，则﹣2≤X≤3，则X≤1的概率P=，故选：B．4．执行如图所示的程序框图，输出的k值为（）A．3 B．4 C．5 D．6【考点】程序框图．【分析】根据程序运行条件，分别进行判断，即可得到结论．【解答】解：第一次运行，n=5，不是偶数，则n=3×5+1=16，k=1，第二次运行，n=16，是偶数，则n==8，k=2，第三次运行，n=8，是偶数，则n==4，k=3，第四次运行，n=4，是偶数，则n==2，k=4，第五次运行，n=2，是偶数，则n==1，k=5，此时满足条件n=1，输出k=5．故选：C．5．已知x，y满足约束条件，则z=﹣2x+y的最大值是（）A．﹣1 B．﹣2 C．﹣5 D．1【考点】简单线性规划．【分析】首先画出平面区域，z=﹣2x+y的最大值就是y=2x+z在y轴的截距的最大值．【解答】解：由已知不等式组表示的平面区域如图阴影部分，当直线y=2x+z经过A时使得z最大，由得到A（1，1），所以z的最大值为﹣2×1+1=﹣1；故选：A．6．在梯形ABCD中，∠ABC=，AD∥BC，BC=2AD=2AB=2，将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为（）A．B．C．D．2π【考点】棱柱、棱锥、棱台的体积．【分析】画出几何体的直观图，利用已知条件，求解几何体的体积即可．【解答】解：由题意可知几何体的直观图如图：旋转体是底面半径为1，高为2的圆柱，挖去一个相同底面高为1的倒圆锥，几何体的体积为：=．故选：C．7．某三棱锥的三视图如图所示，则该三棱锥的表面积是（）A．2+B．4+C．2+2 D．5【考点】由三视图求面积、体积．【分析】根据三视图可判断直观图为：OA⊥面ABC，AC=AB，E为BC中点，EA=2，EA=EB=1，OA=1，：BC⊥面AEO，AC=，OE=判断几何体的各个面的特点，计算边长，求解面积．【解答】解：根据三视图可判断直观图为：OA⊥面ABC，AC=AB，E为BC中点，EA=2，EC=EB=1，OA=1，∴可得AE⊥BC，BC⊥OA，运用直线平面的垂直得出：BC⊥面AEO，AC=，OE=∴S△ABC=2×2=2，S△OAC=S△OAB=×1=．S△BCO=2×=．故该三棱锥的表面积是2，故选：C．8．对于集合{a1，a2，…，a n}和常数a0，定义w=为集合{a1，a2，…，a n}相对a0的“正弦方差”，则集合{，， }相对a0的“正弦方差”为（）A．B．C．D．与a0有关的一个值【考点】进行简单的合情推理．【分析】先根据题意表示出正弦方差μ，进而利用二倍角公式把正弦的平方转化成余弦的二倍角，进而利用两角和公式进一步化简整理，求得结果即可．【解答】解：因为集合{，， }相对a0的“正弦方差”，所以W===故选：C．二、填空题：9．某电子商务公司对1000名网络购物者2015年度的消费情况进行统计，发现消费金额（单位：万元）都在区间[0.3，0.9]内，其频率分布直方图如图所示．在这些购物者中，消费金额在区间[0.5，0.9]内的购物者的人数为600．【考点】频率分布直方图．【分析】频率分布直方图中每一个矩形的面积表示频率，先算出频率，在根据频率和为1，算出a的值，再求出消费金额在区间[0.5，0.9]内的购物者的频率，再求频数．【解答】解：由题意，根据直方图的性质得（1.5+2.5+a+2.0+0.8+0.2）×0.1=1，解得a=3由直方图得（3+2.0+0.8+0.2）×0.1×1000=600．故答案为：600．10．在△ABC中，a=4，b=5，c=6，则=1．【考点】余弦定理；二倍角的正弦；正弦定理．【分析】利用余弦定理求出cosC，cosA，即可得出结论．【解答】解：∵△ABC中，a=4，b=5，c=6，∴cosC==，cosA==∴sinC=，sinA=，∴==1．故答案为：1．11．等比数列{a n}的前n项和为S n，公比不为1．若a1=1，且对任意的n∈N+都有a n+2+a n+1﹣2a n=0，则S5=11．【考点】等比数列的性质；数列的求和．【分析】由题意可得a n q2+a n q=2a n ，即q2+q=2，解得q=﹣2，或q=1（舍去），由此求得S5=的值．【解答】解：∵等比数列{a n}的前n项和为S n，a1=1，且对任意的n ∈N+都有a n+2+a n+1﹣2a n=0，∴a n q2+a n q=2a n ，即q2+q=2，解得q=﹣2，或q=1（舍去）．∴S5==11，故答案为11．12．已知1＜a＜2，2＜a+b＜4，则5a﹣b的取值范围是（2，10）．【考点】简单线性规划．【分析】由线性约束条件画出可行域，然后求出目标函数的范围．【解答】解：画出1＜a＜2，2＜a+b＜4的可行域，如图：目标函数z=5a﹣b在直线2=a+b与直线a=2的交点B（2，0）处，z 值的上界取：10，在直线4=a+b与直线a=1的交点A（1，3）处，目标函数z值的下界取：2，5a﹣b的取值范围是（2，10）．故答案为：（2，10）．13．如图，在正三棱柱A1B1C1﹣ABC中，AB=2，A1A=2，D，F 分别是棱AB，AA1的中点，E为棱AC上的动点，则△DEF周长的最小值为+2．【考点】平面的基本性质及推论．【分析】由正三棱柱A1B1C1﹣ABC的性质可得：AA1⊥AB，AA1⊥AC．在Rt△ADF中，利用勾股定理可得DF=2．因此只要求出DE+EF 的最小值即可得出．把底面ABC展开与侧面ACC1A1在同一个平面，如图所示，只有当三点D，E，F在同一条直线时，DE+EF取得最小值．利用余弦定理即可得出．【解答】解：由正三棱柱A1B1C1﹣ABC，可得AA1⊥底面ABC，∴AA1⊥AB，AA1⊥AC．在Rt△ADF中，DF==2．把底面ABC展开与侧面ACC1A1在同一个平面，如图所示，只有当三点D，E，F在同一条直线时，DE+EF取得最小值．在△ADE中，∠DAE=60°+90°=150°，由余弦定理可得：DE==．∴△DEF周长的最小值=+2．故答案为： +2．14．已知函数f（x）=．（1）若f（x）＞k的解集为{x|x＜﹣3或x＞﹣2}，则k的值等于﹣；（2）对任意x＞0，f（x）≤t恒成立，则t的取值范围是[，+∞）．【考点】其他不等式的解法；函数恒成立问题．【分析】（1）根据不等式和方程之间的关系，转化为方程进行求解即可．（2）任意x＞0，f（x）≤t恒成立，等等价于t≥=恒成立，根据基本不等式即可求出．【解答】解：（1）：f（x）＞k⇔kx2﹣2x+6k＜0．由已知{x|x＜﹣3，或x＞﹣2}是其解集，得kx2﹣2x+6k=0的两根是﹣3，﹣2．由根与系数的关系可知（﹣2）+（﹣3）=，解得k=﹣，（2）任意x＞0，f（x）≤t恒成立，等价于t≥=恒成立，∵x+≥2=2，当且仅当x=时取等号，∴t≥，故答案为：（1）：﹣，（2）：[，+∞）三、解答题：本大题共5小题，共50分.15．海关对同时从A，B，C三个不同地区进口的某种商品进行抽样检测，从各地区进口此商品的数量（单位：件）如表所示．工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测．地区 A B C数量50 1510（Ⅰ）求这6件样品来自A，B，C各地区商品的数量；（Ⅱ）若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．【考点】古典概型及其概率计算公式．【分析】（Ⅰ）先计算出抽样比，进而可求出这6件样品来自A，B，C各地区商品的数量；（Ⅱ）先计算在这6件样品中随机抽取2件的基本事件总数，及这2件商品来自相同地区的事件个数，代入古典概型概率计算公式，可得答案．【解答】解：（Ⅰ）A，B，C三个地区商品的总数量为50+150+100=300，故抽样比k==，故A地区抽取的商品的数量为：×50=1；B地区抽取的商品的数量为：×150=3；C地区抽取的商品的数量为：×100=2；（Ⅱ）在这6件样品中随机抽取2件共有：=15个不同的基本事件；且这些事件是等可能发生的，记“这2件商品来自相同地区”为事件A，则这2件商品可能都来自B 地区或C地区，则A中包含=4种不同的基本事件，故P（A）=，即这2件商品来自相同地区的概率为．16．如图，在长方体ABCD﹣A1B1C1D1中，AB=16，AA1=8，BC=10，点E，F 分别在A1B1C1D1上，A1E=D1F=4，过点E，F的平面α与此长方体的面相交，交线围成一个正方形EFGH．（I）在图中画出这个正方形EFGH（不必说明画法和理由），并说明G，H在棱上的具体位置；（II）求平面α把该长方体分成的两部分体积的比值．【考点】棱柱、棱锥、棱台的体积．【分析】（I）过E作EM⊥AB于M，由勾股定理可得MH=6，从而确定出G，H的位置；（II）两部分均为底面为梯形的直棱柱，代入棱柱的体积公式求出两部分的体积即可得出体积比．【解答】解：（I）作出图形如图所示：过E作EM⊥AB于M，∵四边形EFGH为正方形，∴EH=EF=BC=10，∵EM=AA1=8，∴MH==6，∴AH=AM+MH=10，∴DG=10，即H在棱AB上，G在棱CD上，且AH=DG=10．（II）设平面α把该长方体分成的两部分体积分别为V1，V2，则V1=S•AD=×（4+10）×8×10=560，V2=V长方体﹣V1=16×8×10﹣560=720．∴==．17．已知函数f（x）=sinxcosx﹣cos2x+，△ABC三个内角A，B，C的对边分别为a，b，c且f（A）=1．（I）求角A的大小；（Ⅱ）若a=7，b=5，求c的值．【考点】二倍角的余弦；二倍角的正弦；余弦定理．【分析】（I）由f（x）=sinxcosx﹣cos2x+利用二倍角公式及辅助角公式对已知化简，然后结合f（A）=1，及A∈（0，π）可求A；（Ⅱ）由余弦定理a2=b2+c2﹣2bccosA可求c【解答】解：（I）因为f（x）=sinxcosx﹣cos2x+==sin（2x﹣）…又f（A）=sin（2A﹣）=1，A∈（0，π），…所以，∴…（Ⅱ）由余弦定理a2=b2+c2﹣2bccosA得到，所以c2﹣5c﹣24=0 …解得c=﹣3（舍）或c=8 …所以c=818．某超市随机选取1000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买．甲乙丙丁10√×√√21×√×√720√√√×30√×√×85 √××××√××98（1）估计顾客同时购买乙和丙的概率；（2）估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；（3）如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？【考点】相互独立事件的概率乘法公式．【分析】（1）从统计表可得，在这1000名顾客中，同时购买乙和丙的有200人，从而求得顾客同时购买乙和丙的概率．（2）根据在甲、乙、丙、丁中同时购买3种商品的有300人，求得顾客顾客在甲、乙、丙、丁中同时购买3种商品的概率．（3）在这1000名顾客中，求出同时购买甲和乙的概率、同时购买甲和丙的概率、同时购买甲和丁的概率，从而得出结论．【解答】解：（1）从统计表可得，在这1000名顾客中，同时购买乙和丙的有200人，故顾客同时购买乙和丙的概率为=0.2．（2）在这1000名顾客中，在甲、乙、丙、丁中同时购买3种商品的有100+200=300（人），故顾客顾客在甲、乙、丙、丁中同时购买3种商品的概率为=0.3．（3）在这1000名顾客中，同时购买甲和乙的概率为=0.2，同时购买甲和丙的概率为=0.6，同时购买甲和丁的概率为=0.1，故同时购买甲和丙的概率最大．19．已知数列{a n}和{b n}满足a1a2a3…a n=（n∈N*）．若{a n}为等比数列，且a1=2，b3=6+b2．（Ⅰ）求a n和b n；（Ⅱ）设c n=（n∈N*）．记数列{c n}的前n项和为S n．（i）求S n；（ii）求正整数k，使得对任意n∈N*均有S k≥S n．【考点】数列与不等式的综合；数列的求和．【分析】（Ⅰ）先利用前n项积与前（n﹣1）项积的关系，得到等比数列{a n}的第三项的值，结合首项的值，求出通项a n，然后现利用条件求出通项b n；（Ⅱ）（i）利用数列特征进行分组求和，一组用等比数列求和公式，另一组用裂项法求和，得出本小题结论；（ii）本小题可以采用猜想的方法，得到结论，再加以证明．【解答】解：（Ⅰ）∵a1a2a3…a n=（n∈N*）①，当n≥2，n∈N*时，②，由①②知：，令n=3，则有．∵b3=6+b2，∴a3=8．∵{a n}为等比数列，且a1=2，∴{a n}的公比为q，则=4，由题意知a n＞0，∴q＞0，∴q=2．∴（n∈N*）．又由a1a2a3…a n=（n∈N*）得：，，∴b n=n（n+1）（n∈N*）．（Ⅱ）（i）∵c n===．∴S n=c1+c2+c3+…+c n====；（ii）因为c1=0，c2＞0，c3＞0，c4＞0；当n≥5时，，而=＞0，得，所以，当n≥5时，c n＜0，综上，对任意n∈N*恒有S4≥S n，故k=4．2020年高一数学第二学期期末模拟试卷及答案（二）一、选择题：本大题共8个小题，每小题4分，共32分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．命题“∃x0＞0，2≤0”的否定是（）A．∀x＞0，2x＞0 B．∀x≤0，2x＞0 C．∀x＞0，2x＜0 D．∀x≤0，2x＜02．设l，m是两条不同的直线，α是一个平面，则下列命题正确的是（）A．若l⊥m，m⊂α，则l⊥αB．若l⊥α，l∥m，则m⊥αC．若l∥α，m⊂α，则l∥m D．若l∥α，m∥α，则l∥m3．在△ABC中，三个内角A，B，C的对边分别是a．b．c，已知B=30°，c=150，b=50，那么这个三角形是（）A．等边三角形B．等腰三角形C．直角三角形D．等腰三角或直角三角形4．如图所示的程序框图，若输出的S=31，则判断框内填入的条件是（）A．i＞4？B．i＞5？C．i≤4？D．i≤5？5．设{a n}（n∈N*）是等差数列，S n是其前n项的和，且S5＜S6，S6=S7＞S8，则下列结论错误的是（）A．d＜0 B．a7=0C．S9＞S5D．S6与S7均为S n的最大值6．如图所示，E是正方形ABCD所在平面外一点，E在面ABCD上的正投影F恰在AC上，FG∥BC，AB=AE=2，∠EAB=60°，有以下四个命题：（1）CD⊥面GEF；（2）AG=1；（3）以AC，AE作为邻边的平行四边形面积是8；（4）∠EAD=60°．其中正确命题的个数为（）A．1 B．2 C．3 D．47．下列命题中，正确的命题个数为（）①△ABC的三边分别为a，b，c，则该三角形是等边三角形的充要条件为a2+b2+c2=ab+ac+bc；②数列{a n}的前n项和为S n，则S n=An2+Bn是数列{a n}为等差数列的充要条件；③在数列{a n}中，a1=1，S n是其前n项和，满足S n+1=S n+2，则{a n}是等比数列；④已知a1，b1，c1，a2，b2，c2都是不等于零的实数，关于x的不等式a1x2+b1x+c1＞0和a2x2+b2x+c2＞0的解集分别为P，Q，则==是P=Q的充分必要条件．A．1 B．2 C．3 D．48．如图，设P为正四面体A﹣BCD表面（含棱）上与顶点不重合的一点，由点P到四个顶点的距离组成的集合记为M，如果集合M中有且只有2个元素，那么符合条件的点P有（）A．4个B．6个C．10个D．14个二、填空题（共6小题，每题4分，满分24分，将答案填在答题纸上）9．已知数列{a n}的前n项和为S n，a n≠0（n∈N*），a n a n+1=S n，则a3﹣a1=______．10．执行如图所示的程序框图，输出的a值为______．11．已知一个三棱锥的三视图如图所示，主视图和左视图都是腰长为1的等腰直角三角形，那么，这个三棱锥的表面积为______．12．a＞0，b＞0，a+b=1，则+的最小值为______．13．如图，四面体ABCD的一条棱长为x，其余棱长均为1，记四面体ABCD的体积为F（x），则函数F（x）的单调增区间是______；最大值为______．14．在数列{a n}中，若a n2﹣a n﹣12=p（n≥2，n∈N×，p为常数），则称{a n}为“等方差数列”，下列是对“等方差数列”的判断；①若{a n}是等方差数列，则{a n2}是等差数列；②{（﹣1）n}是等方差数列；③若{a n}是等方差数列，则{a kn}（k∈N*，k为常数）也是等方差数列；④若{a n}既是等方差数列，又是等差数列，则该数列为常数列．其中正确命题序号为______．（将所有正确的命题序号填在横线上）三、解答题（本大题共4小题，共44分.解答应写出文字说明、证明过程或演算步骤.）15．已知p：＞1，q：∃x∈R，ax2+ax﹣1≥0，r：（a﹣m）（a﹣m﹣1）＞0．（1）若p∧q为真，求实数a的取值范围；（2）若￢p是￢r的必要不充分条件，求m的取值范围．16．如图△ABC中，已知点D在BC边上，满足•=0．sin∠BAC=，AB=3，BD=．（Ⅰ）求AD的长；（Ⅱ）求cosC．17．如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，且∠ABC=120°，点E是棱PC的中点，平面ABE与棱PD交于点F．（1）求证：AB∥EF；（2）若PA=PD=AD=2，且平面PAD⊥平面ABCD，求①二面角E﹣AF﹣D的二面角的余弦值；②在线段PC上是否存在一点H，使得直线BH与平面AEF所成角等于60°，若存在，确定H的位置，若不存在，说明理由．18．已知等差数列{a n}的公差d≠0，若a2=5且a1，a3，a6成等比数列．（1）求数列{a n}的通项公式；（2）若数列{b n}满足b1=0且对任意的n≥2，均有|b n﹣b n﹣1|=2①写出b3所有可能的取值；②若b k=2116，求k的最小值．参考答案与试题解析一、选择题：本大题共8个小题，每小题4分，共32分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．命题“∃x0＞0，2≤0”的否定是（）A．∀x＞0，2x＞0 B．∀x≤0，2x＞0 C．∀x＞0，2x＜0 D．∀x≤0，2x＜0【考点】命题的否定．【分析】利用特称命题的否定是全称命题，写出结果即可．【解答】解：因为特称命题的否定是全称命题，所以，命题“∃x0＞0，2≤0”的否定是：∀x＞0，2x＞0．故选：A．2．设l，m是两条不同的直线，α是一个平面，则下列命题正确的是（）A．若l⊥m，m⊂α，则l⊥αB．若l⊥α，l∥m，则m⊥αC．若l∥α，m⊂α，则l∥m D．若l∥α，m∥α，则l∥m【考点】直线与平面平行的判定．【分析】根据题意，依次分析选项：A，根据线面垂直的判定定理判断．C：根据线面平行的判定定理判断．D：由线线的位置关系判断．B：由线面垂直的性质定理判断；综合可得答案．【解答】解：A，根据线面垂直的判定定理，要垂直平面内两条相交直线才行，不正确；C：l∥α，m⊂α，则l∥m或两线异面，故不正确．D：平行于同一平面的两直线可能平行，异面，相交，不正确．B：由线面垂直的性质可知：平行线中的一条垂直于这个平面则另一条也垂直这个平面．故正确．故选B3．在△ABC中，三个内角A，B，C的对边分别是a．b．c，已知B=30°，c=150，b=50，那么这个三角形是（）A．等边三角形B．等腰三角形C．直角三角形D．等腰三角或直角三角形【考点】三角形的形状判断．【分析】由正弦定理求出sinC=，C=60°或120°．再根据三角形的内角和公式求出A的值，由此即可这个三角形的形状．【解答】解：∵△ABC中，已知B=30°，b=50，c=150，由正弦定理可得，∴sinC=，可得：C=60°或120°．当C=60°，∵B=30°，∴A=90°，△ABC是直角三角形．当C=120°，∵B=30°，∴A=30°，△ABC是等腰三角形．故△ABC是直角三角形或等腰三角形，故选：D．4．如图所示的程序框图，若输出的S=31，则判断框内填入的条件是（）A．i＞4？B．i＞5？C．i≤4？D．i≤5？【考点】程序框图．【分析】根据框图的流程知，算法的功能是计算S=1+2+22+...+2n的值，由输出的S是31，得退出循环体的n值为5，由此得判断框的条件．【解答】解：根据框图的流程得：算法的功能是计算S=1+2+22+ (2)的值，∵输出的S是31，∴S==2n+1﹣1=31，解得n=4；退出循环体的n值为5，∴判断框的条件为n≥5或n＞4．故选：A．5．设{a n}（n∈N*）是等差数列，S n是其前n项的和，且S5＜S6，S6=S7＞S8，则下列结论错误的是（）A．d＜0 B．a7=0C．S9＞S5D．S6与S7均为S n的最大值【考点】等差数列的前n项和．【分析】利用结论：n≥2时，a n=s n﹣s n﹣1，易推出a6＞0，a7=0，a8＜0，然后逐一分析各选项，排除错误答案．【解答】解：由S5＜S6得a1+a2+a3+…+a5＜a1+a2++a5+a6，即a6＞0，又∵S6=S7，∴a1+a2+…+a6=a1+a2+…+a6+a7，∴a7=0，故B正确；同理由S7＞S8，得a8＜0，∵d=a7﹣a6＜0，故A正确；而C选项S9＞S5，即a6+a7+a8+a9＞0，可得2（a7+a8）＞0，由结论a7=0，a8＜0，显然C选项是错误的．∵S5＜S6，S6=S7＞S8，∴S6与S7均为S n的最大值，故D正确；故选C．6．如图所示，E是正方形ABCD所在平面外一点，E在面ABCD上的正投影F恰在AC上，FG∥BC，AB=AE=2，∠EAB=60°，有以下四个命题：（1）CD⊥面GEF；（2）AG=1；（3）以AC，AE作为邻边的平行四边形面积是8；（4）∠EAD=60°．其中正确命题的个数为（）A．1 B．2 C．3 D．4【考点】平面与平面垂直的判定．【分析】连结EG，通过证明AB⊥平面EFG得出CD⊥平面EFG，在直角三角形AEG中求出AG，EF，求出三角形ACE的面积，根据AG判断出F的位置，利用全都三角形判断∠EAD．【解答】解：连结EG，（1）∵EF⊥平面ABCD，AB⊂平面ABCD，∴EF⊥AB，∵FG∥BC，BC⊥AB，∴AB⊥FG，又EF⊂平面EFG，FG⊂平面EFG，EF∩FG=F，∴AB⊥平面EFG，∵AB∥CD，∴CD⊥平面EFG．故（1）正确．（2）∵AB⊥平面EFG，∴AB⊥EG，∵∠EAB=60°，AE=2，∴AG=AE=1，故（2）正确．（3））∵AG=1=，∴F为AC的中点．∵AE=2，AC==2，AF==，∴EF==．∴S△ACE===2，∴以AC，AE作为邻边的平行四边形面积为2S△ACE=4，故（3）错误；（4）过F作FM⊥AD于M，则AM=1，由（1）的证明可知AD⊥平面EFM，故而AD⊥EM，∴Rt△EAG≌Rt△EAM，∴∠EAM=∠EAG=60°，故（4）正确．故选：C7．下列命题中，正确的命题个数为（）①△ABC的三边分别为a，b，c，则该三角形是等边三角形的充要条件为a2+b2+c2=ab+ac+bc；②数列{a n}的前n项和为S n，则S n=An2+Bn是数列{a n}为等差数列的充要条件；③在数列{a n}中，a1=1，S n是其前n项和，满足S n+1=S n+2，则{a n}是等比数列；④已知a1，b1，c1，a2，b2，c2都是不等于零的实数，关于x的不等式a1x2+b1x+c1＞0和a2x2+b2x+c2＞0的解集分别为P，Q，则==是P=Q的充分必要条件．A．1 B．2 C．3 D．4【考点】命题的真假判断与应用．【分析】①根据等边三角形的性质结合充分条件和必要条件的定义进行判断，②根据等差数列的定义和性质进行判断，③根据数列项和前n项和的关系，结合等比数列的定义进行判断．④举反例进行判断即可．【解答】解：①若a=b=c，则a2+b2+c2=ab+ac+bc成立，反之若a2+b2+c2=ab+ac+bc，则2（a2+b2+c2）=2（ab+ac+bc），整理得（a﹣b）2+（a﹣c）2+（b﹣c）2=0，当且仅当a=b=c时成立故充分性成立，故①正确；②当n=1时，a1=A+B；当n≥2时，a n=S n﹣S n﹣1=2An+B﹣A，显然当n=1时也满足上式，∴a n﹣a n﹣1=2A，∴{a n}是等差数列．反之，若数列{a n}为等差数列，∴S n=na1+d=n2+（a1﹣）n，令A=，B=a1﹣，则S n=An2+Bn，A，B∈R．综上，“S n=An2+Bn，是“数列{a n}为等差数列”的充要条件．故②正确，③在数列{a n}中，a1=1，S n是其前n项和，满足S n+1=S n+2，则当n≥2时，S n=S n﹣1+2，两式作差得S n+1﹣S n=S n+2﹣S n﹣1﹣2，即a n+1=a n，即=，（n≥2），当n=1时，S2=S1+2，即a1+a2=a1+2，即a2=﹣a1+2=2﹣=，则=≠，即{a n}不是等比数列；故③错误，④举反例，不等式x2+x+1＞0与x2+x+2＞0的解集都是R，但是≠，则==是P=Q的充分必要条件错误，故④错误．故正确的是①②，故选：B．8．如图，设P为正四面体A﹣BCD表面（含棱）上与顶点不重合的一点，由点P到四个顶点的距离组成的集合记为M，如果集合M中有且只有2个元素，那么符合条件的点P有（）A．4个B．6个C．10个D．14个【考点】计数原理的应用．【分析】根据分类计数加法原理可得，由题意符合条件的点只有两类，一在棱的中点，二在面得中心，问题得以解决．【解答】解：符合条件的点P有两类：（1）6条棱的中点；（2）4个面的中心．共10个点．故集合M中有且只有2个元素，那么符合条件的点P有4+6=10．故选：C二、填空题（共6小题，每题4分，满分24分，将答案填在答题纸上）9．已知数列{a n}的前n项和为S n，a n≠0（n∈N*），a n a n+1=S n，则a3﹣a1=1．【考点】数列递推式．【分析】由题意可得a n+1=，从而可得a2==1，a3===1+a1；从而解得．【解答】解：∵a n a n+1=S n，∴a n+1=；∴a2==1；a3===1+a1；∴a3﹣a1=1+a1﹣a1=1，故答案为：1．10．执行如图所示的程序框图，输出的a值为﹣．【考点】程序框图．【分析】根据框图的流程依次计算程序运行的结果，发现a值的周期为4，再根据条件确定跳出循环的i值，从而可得输出的a值．【解答】解：由程序框图知：第一次循环a==﹣2，i=2；第二次循环a==﹣，i=3；第三次循环a==，i=4；第四次循环a==3，i=5；第五次循环a==﹣2，i=6；…∴a值的周期为4，又跳出循环的i值为11，∴输出的a=﹣．故答案为：﹣．11．已知一个三棱锥的三视图如图所示，主视图和左视图都是腰长为1的等腰直角三角形，那么，这个三棱锥的表面积为．【考点】由三视图求面积、体积．【分析】如图所示，该三棱锥为P﹣ABC，满足PD⊥底面BAC，D 为点P在底面ABC的射影，四边形ABCD是边长为1的正方形，PD=1，即可得出．【解答】解：如图所示，该三棱锥为P﹣ABC，满足PD⊥底面BAC，D为点P在底面ABC的射影，四边形ABCD是边长为1的正方形，PD=1，这个三棱锥的表面积S=+++=．故答案为：．12．a＞0，b＞0，a+b=1，则+的最小值为5+2．【考点】基本不等式．【分析】根据基本不等式即可求出最小值．【解答】解：∵a＞0，b＞0，a+b=1，∴+=（a+b）（+）=2+3++≥5+2=5+2，当且仅当a=，b=时取等号，∴则+的最小值为5+2，故答案为：5+2，13．如图，四面体ABCD的一条棱长为x，其余棱长均为1，记四面体ABCD的体积为F（x），则函数F（x）的单调增区间是，；最大值为．【考点】棱柱、棱锥、棱台的体积．【分析】如图所示，设BC=x，AB=AC=AD=CD=BD=1．取AD的中点O，连接OB，OC，则OB⊥AD，OC⊥AD，OB=OC=．又OB∩OC=O，则AD⊥平面OBC．取BC的中点E，连接OE，则OE ⊥BC，可得OE，可得F（x）==（0＜x＜）．利用导数研究其单调性即可得出．【解答】解：如图所示，设BC=x，AB=AC=AD=CD=BD=1．取AD的中点O，连接OB，OC，则OB⊥AD，OC⊥AD，OB=OC=．又OB∩OC=O，则AD⊥平面OBC，取BC的中点E，连接OE，则OE⊥BC，OE==．∴S△OBC==．∴F（x）==×1=（0＜x＜）．F′（x）=，令F′（x）≥0，解得，此时函数F（x）单调递增；令F′（x）＜0，解得，此时函数F（x）单调递减法．因此当x=时，F（x）取得最大值，==．故答案分别为：，．14．在数列{a n}中，若a n2﹣a n﹣12=p（n≥2，n∈N×，p为常数），则称{a n}为“等方差数列”，下列是对“等方差数列”的判断；①若{a n}是等方差数列，则{a n2}是等差数列；②{（﹣1）n}是等方差数列；③若{a n}是等方差数列，则{a kn}（k∈N*，k为常数）也是等方差数列；④若{a n}既是等方差数列，又是等差数列，则该数列为常数列．其中正确命题序号为①②③④．（将所有正确的命题序号填在横线上）【考点】等差数列的性质．【分析】根据等差数列的性质及题中的等方差数列的新定义，即可判断出正确的答案．【解答】解：①因为{a n}是等方差数列，所以a n2﹣a n﹣12=p（n≥2，n ∈N×，p为常数）成立，得到{a n2}为首项是a12，公差为p的等差数列；②因为a n2﹣a n﹣12=（﹣1）2n﹣（﹣1）2n﹣1=1﹣（﹣1）=2，所以数列{（﹣1）n}是等方差数列；③数列{a n}中的项列举出来是：a1，a2，…，a k，a k+1，a k+2，…，a2k，…，a3k，…数列{a kn}中的项列举出来是：a k，a2k，a3k，…因为a k+12﹣a k2=a k+22﹣a k+12=a k+32﹣a k+22=…=a2k2﹣a k2=p所以（a k+12﹣a k2）+（a k+22﹣a k+12）+（a k+32﹣a k+22）+…+（a2k2﹣a2k﹣12）=a2k2﹣a k2=kp，类似地有a kn2﹣a kn﹣12=a kn﹣12﹣a kn﹣22=…=a kn+32﹣a kn+22=a kn+22﹣a kn+12=a kn+12﹣a kn2=p同上连加可得a kn+12﹣a kn2=kp，所以，数列{a kn}是等方差数列；④{a n}既是等方差数列，又是等差数列，所以a n2﹣a n﹣12=p，且a n﹣a n﹣1=d（d≠0），所以a n+a n﹣1=，联立解得a n=+，所以{a n}为常数列，当d=0时，显然{a n}为常数列，所以该数列为常数列．综上，正确答案的序号为：①②③④故答案为：①②③④三、解答题（本大题共4小题，共44分.解答应写出文字说明、证明过程或演算步骤.）15．已知p：＞1，q：∃x∈R，ax2+ax﹣1≥0，r：（a﹣m）（a﹣m﹣1）＞0．（1）若p∧q为真，求实数a的取值范围；（2）若￢p是￢r的必要不充分条件，求m的取值范围．【考点】必要条件、充分条件与充要条件的判断；复合命题的真假．【分析】分别求出p，q，r为真时的a的范围，（1）p∧q为真，则p，q均为真，得到关于a的不等式组，解出即可；（2）问题转化为r是p的必要不充分条件，得到关于m的不等式，解出即可．【解答】解：（1）p为真时：由＞1解得﹣2＜a＜1，q为真时，当a＞0，一定存在ax2+ax﹣1≥0，当a＜0，△=a2+4a≥0，解得a≤﹣4，故q为真时，实数a的取值范围为a＞0或a≤﹣4，∵p∧q为真，则p，q均为真，∴a的取值范围为（0，1）；（2）关于r：（a﹣m）（a﹣m﹣1）＞0，解得：a＞m+1或a＜m，若￢p是￢r的必要不充分条件，即r是p的必要不充分条件，即p⇒r，∴m+1≤﹣2或m＞1，即m≤﹣3或m＞1，。

新高一数学下期末一模试卷(及答案)一、选择题1．已知向量a v ，b v 满足4a =v，b v 在a v 上的投影（正射影的数量）为-2，则2a b -v v 的最小值为（ ） A ．43B ．10C ．10D ．82．设集合{}1,2,4A =，{}240B x x x m =-+=．若{}1A B ⋂=，则B =( ) A ．{}1,3-B ．{}1,0C ．{}1,3D ．{}1,53．在ABC V 中，角A ，B ，C 所对的边为a ，b ，c ，且B 为锐角，若sin 5sin 2A cB b=，7sin B =，57ABC S =△，则b =（ ） A ．23B ．27C ．15D ．144．已知集合 ，则A ．B ．C ．D ．5．《九章算术》中，将底面是直角三角形的直三棱柱称为“堑堵”．某“堑堵”的三视图如图所示，则它的表面积为（ ）A ．2B ．422+C ．442+D ．642+6．已知()f x 是定义域为(,)-∞+∞的奇函数，满足(1)(1)f x =f +x -，若(1)2f =，则(1)(2)f +f (3)(2020)f f +++=L （ ）A ．50B ．2C ．0D ．50-7．若||1OA =u u u v ，||3OB u u u v 0OA OB ⋅=u u u v u u u v，点C 在AB 上，且30AOC ︒∠=，设OC mOA nOBu u u v u u u v u u u v =+(,)m n R ∈，则mn的值为（ ） A ．13B ．3C ．33D 38．有5支彩笔（除颜色外无差别），颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔，则取出的2支彩笔中含有红色彩笔的概率为A ．45B ．35C ．25D ．159．函数223()2xx xf x e +=的大致图像是（ ）A ．B ．C ．D ．10．已知1sin 34πα⎛⎫-= ⎪⎝⎭，则cos 23πα⎛⎫+= ⎪⎝⎭（ ） A ．58-B ．58C ．78-D ．7811．定义在R 上的奇函数()f x 满足()()2f x f x +=-，且当[]0,1x ∈时，()2cos x f x x =-，则下列结论正确的是（ ）A ．()20202019201832f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭B ．()20202019201832f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭C ．()20192020201823f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭D ．()20192020201823f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭12．已知0.6log 0.5a =，ln0.5b =，0.50.6c =，则（ ） A ．a c b >>B ．a b c >>C ．c a b >>D ．c b a >>二、填空题13．已知三棱锥S ABC -的所有顶点都在球O 的球面上，SC 是球O 的直径.若平面SCA ⊥平面SCB ，SA AC =，SB BC =，三棱锥S ABC -的体积为9，则球O 的表面积为______．14．已知函数32()21f x x x ax =+-+在区间上恰有一个极值点，则实数a 的取值范围是____________15．若三点1(2,3),(3,2),(,)2A B C m --共线，则m 的值为 ． 16．已知点()M a b ，在直线3415x y +＝22a b +_______． 17．在ABC ∆中，120B =o ，1BC =，且ABC ∆的面积为32，则AC =__________．18．设,x y 满足约束条件210,{0,0,0,x y x y x y --≤-≥≥≥若目标函数()0,0z ax by a b =+>>的最大值为1,则14a b+的最小值为_________． 19．某三棱锥的三视图如下图所示，正视图、侧视图均为直角三角形，则该三棱锥的四个面中，面积最大的面的面积是 ．20．在直三棱柱111ABC A B C -中，90ACB ∠=o ，12AA =，1AC BC ==，则异面直线1A B 与1AC 所成角的余弦值是_____________．三、解答题21．在中角所对的边分别是，，，．求的值； 求的面积．22．已知矩形ABCD 的两条对角线相交于点20M （，），AB 边所在直线的方程为360x y --=，点11T -（，）在AD 边所在直线上. （1）求AD 边所在直线的方程； （2）求矩形ABCD 外接圆的方程.23．从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分布表和频率分布直方图：（1）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的概率； （2）求频率分布直方图中的a ，b 的值；24．如图，在正方体1111ABCD A B C D -中，S 是11B D 的中点，E ，F ，G 分别是BC ，DC ，SC 的中点.求证：（1）直线//EG 平面11BDD B ； （2）平面//EFG 平面11BDD B .25．已知ABC ∆中，内角,,A B C 所对边分别为,,a b c ，若()20a c cosB bcosC --=. (1)求角B 的大小；(2)若2b =，求a c +的取值范围. 26．已知数列{a n }满足a 1＝1，1114n na a +=-，其中n ∈N *． （1）设221n n b a =-，求证：数列{b n }是等差数列，并求出{a n }的通项公式．（2）设41nn a c n =+，数列{c n c n +2}的前n 项和为T n ，是否存在正整数m ，使得11n m m T c c +<对于n ∈N *，恒成立？若存在，求出m 的最小值；若不存在，请说明．【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【解析】 【分析】b r 在a r上的投影（正射影的数量）为2-可知||cos ,2b a b <>=-r r r ，可求出||2b ≥r ，求22a b -r r 的最小值即可得出结果.【详解】因为b r 在a r上的投影（正射影的数量）为2-， 所以||cos ,2b a b <>=-r r r，即2||cos ,b a b =-<>r r r ，而1cos ,0a b -≤<><r r ， 所以||2b ≥r，因为2222222(2)44||4||||cos ,4||a b a b a a b b a a b a b b -=-=-⋅+=-<>+r r r r r r r r r r r r r r22=1644(2)4||484||b b -⨯⨯-+=+r r所以22484464a b -≥+⨯=r r ，即28a b -≥r r ，故选D.【点睛】本题主要考查了向量在向量上的正射影，向量的数量积，属于难题.2．C解析：C 【解析】∵ 集合{}124A ，，=，{}2|40B x x x m =-+=，{}1A B ⋂= ∴1x =是方程240x x m -+=的解，即140m -+= ∴3m =∴{}{}{}22|40|43013B x x x m x x x =-+==-+==，，故选C3．D解析：D 【解析】 【分析】 利用正弦定理化简sin 5sin 2A cB b=，再利用三角形面积公式，即可得到,a c，由sin 4B =，求得cos B ，最后利用余弦定理即可得到答案． 【详解】 由于sin 5sin 2A c B b=，有正弦定理可得： 52a c b b =，即52a c =由于在ABC V中，sin B =，ABC S =△1sin 2ABC S ac B ==V联立52157sin 247sin 4a c ac B B ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩，解得：5a =，2c = 由于B 为锐角，且7sin B =，所以23cos 1sin 4B B =-=所以在ABC V 中，由余弦定理可得：2222cos 14b a c ac B =+-=，故14b =（负数舍去） 故答案选D 【点睛】本题考查正弦定理，余弦定理，以及面积公式在三角形求边长中的应用，属于中档题．4．D解析：D 【解析】 试题分析：由得，所以，因为，所以，故选D.【考点】 一元二次不等式的解法，集合的运算【名师点睛】对于集合的交、并、补运算问题，应先把集合化简再计算，常常借助数轴或韦恩图处理.5．D解析：D 【解析】 【分析】根据题意和三视图知几何体是一个放倒的直三棱柱，由三视图求出几何元素的长度，由面积公式求出几何体的表面积． 【详解】根据题意和三视图知几何体是一个放倒的直三棱柱，底面是一个直角三角形，两条直角边2,斜边是2，且侧棱与底面垂直，侧棱长是2， ∴几何体的表面积12222222264 2.2S =⨯+⨯⨯=+ 故选D ． 【点睛】本题考查三视图求几何体的表面积，由三视图正确复原几何体是解题的关键，考查空间想象能力．6．C解析：C【解析】 【分析】利用()f x 是定义域为(,)-∞+∞的奇函数可得：()()f x f x -=-且()00f =，结合(1)(1)f x =f +x -可得：函数()f x 的周期为4；再利用赋值法可求得：()20f =，()32f =-，()40f =，问题得解.【详解】因为()f x 是定义域为(,)-∞+∞的奇函数， 所以()()f x f x -=-且()00f = 又(1)(1)f x =f +x -所以()()()()()21111f x f x f x f x f x ⎡⎤⎡⎤+=++=-+=-=-⎣⎦⎣⎦ 所以()()()()()4222f x f x f x f x f x ⎡⎤⎡⎤+=++=-+=--=⎣⎦⎣⎦ 所以函数()f x 的周期为4，在(1)(1)f x =f +x -中，令1x =，可得：()()200f f ==在(1)(1)f x =f +x -中，令2x =，可得：()()()3112f f f =-=-=- 在(1)(1)f x =f +x -中，令3x =，可得：()()()4220f f f =-=-= 所以(1)(2)f +f ()()()()2020(3)(2020)12344f f f f f f ⎡⎤+++=⨯+++⎣⎦L 50500=⨯=故选C 【点睛】本题主要考查了奇函数的性质及函数的周期性应用，还考查了赋值法及计算能力、分析能力，属于中档题．7．B解析：B 【解析】 【分析】利用向量的数量积运算即可算出． 【详解】解：30AOC ︒∠=Qcos ,OC OA ∴<>=u u u r u u u r2OC OA OC OA⋅∴=u u u r u u u r u u u r u u u r()2mOA nOB OA mOA nOBOA+⋅∴=+u u u r u u u r u u u r u u u r u u u r u u u r=1OA =Q，OB =，0OA OB ⋅=u u u r u u u r= 229m n ∴=又C Q 在AB 上0m ∴>，0n > 3m n∴= 故选：B 【点睛】本题主要考查了向量的基本运算的应用，向量的基本定理的应用及向量共线定理等知识的综合应用．8．C解析：C 【解析】选取两支彩笔的方法有25C 种，含有红色彩笔的选法为14C 种，由古典概型公式，满足题意的概率值为142542105C p C ===. 本题选择C 选项. 考点：古典概型名师点睛：对于古典概型问题主要把握基本事件的种数和符合要求的事件种数，基本事件的种数要注意区别是排列问题还是组合问题，看抽取时是有、无顺序，本题从这5支彩笔中任取2支不同颜色的彩笔，是组合问题，当然简单问题建议采取列举法更直观一些.9．B解析：B 【解析】由()f x 的解析式知仅有两个零点32x =-与0x =，而A 中有三个零点，所以排除A ，又()2232xx x f x e-++'=，由()0f x '=知函数有两个极值点，排除C ，D ，故选B ． 10．C【解析】 由题意可得：1sin sin cos 32664ππππααα⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦， 则217cos 2cos 22cos 121366168πππααα⎛⎫⎛⎫⎛⎫+=+=+-=⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 本题选择C 选项.11．C解析：C 【解析】 【分析】根据f （x ）是奇函数，以及f （x+2）=f （-x ）即可得出f （x+4）=f （x ），即得出f （x ）的周期为4，从而可得出f （2018）=f （0），2019122f f ⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭，20207312f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭然后可根据f （x ）在[0，1]上的解析式可判断f （x ）在[0，1]上单调递增，从而可得出结果. 【详解】∵f（x ）是奇函数；∴f（x+2）=f （-x ）=-f （x ）；∴f（x+4）=-f （x+2）=f （x ）； ∴f（x ）的周期为4；∴f（2018）=f （2+4×504）=f （2）=f （0），2019122f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,20207 312f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭∵x∈[0，1]时，f （x ）=2x -cosx 单调递增；∴f(0)＜12f ⎛⎫⎪⎝⎭ ＜712f ⎛⎫ ⎪⎝⎭ ∴()20192020201823f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭,故选C. 【点睛】本题考查奇函数，周期函数的定义，指数函数和余弦函数的单调性，以及增函数的定义，属于中档题.12．A解析：A 【解析】由0.50.6log 0.51,ln 0.50,00.61><<<，所以1,0,01a b c ><<<，所以a c b >>，故选A .二、填空题13．36π【解析】三棱锥S−ABC 的所有顶点都在球O 的球面上SC 是球O 的直径若平面SCA ⊥平面SCBSA=ACSB=BC 三棱锥S−ABC 的体积为9可知三角形SBC 与三角形SAC 都是等腰直角三角形设球的半解析：36π三棱锥S−ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径， 若平面SCA ⊥平面SCB ，SA=AC ，SB=BC ，三棱锥S−ABC 的体积为9， 可知三角形SBC 与三角形SAC 都是等腰直角三角形，设球的半径为r ， 可得112932r r r ⨯⨯⨯⨯= ，解得r=3. 球O 的表面积为：2436r ππ= .点睛：与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.14．【解析】【分析】【详解】由题意则解得-1＜a ＜7经检验当a=-1时的两个根分别为所以符合题目要求时在区间无实根所以 解析：17a -≤<【解析】 【分析】 【详解】由题意，2()34f x x x a '=+-，则(1)(1)0f f ''-<，解得-1＜a ＜7，经检验当a=-1时，2()3410f x x x '=++=的两个根分别为121,13x x =-=-，所以符合题目要求，7a =时，2()3410f x x x '=++=,在区间无实根，所以17a -≤<．15．【解析】试题分析：依题意有即解得考点：三点共线 解析：12【解析】试题分析：依题意有AB AC k k =，即531522m --=+，解得12m =. 考点：三点共线．16．3【解析】【分析】由题意可知表示点到点的距离再由点到直线距离公式即可得出结果【详解】可以理解为点到点的距离又∵点在直线上∴的最小值等于点到直线的距离且【点睛】本题主要考查点到直线的距离公式的应用属于解析：3 【解析】 【分析】22a b +()0,0到点(),a b 的距离，再由点到直线距离公式即可得出结果. 【详解】()0,0到点(),a b的距离，又∵点(),M a b在直线:3425l x y+=()0,0到直线34150x y+-=的距离，且3d==.【点睛】本题主要考查点到直线的距离公式的应用，属于基础题型.17．【解析】【分析】根据三角形面积公式得到再由余弦定理得到AC长【详解】在中且的面积为由正弦定理的面积公式得到：再由余弦定理得到故得到故答案为：【点睛】本题主要考查余弦定理的应用以及三角形面积公式;在解【解析】【分析】根据三角形面积公式得到11 2.222S AB AB=⨯⨯⨯=⇒=再由余弦定理得到AC长.【详解】在ABC∆中，120B=o，1BC=，且ABC∆的面积为2，由正弦定理的面积公式得到：11 2.2S AB AB=⨯⨯=⇒=再由余弦定理得到22202cos1207AC AB BC AB BC=+-⨯⨯⨯=故得到AC=.【点睛】本题主要考查余弦定理的应用以及三角形面积公式;在解与三角形有关的问题时，正弦定理、余弦定理是两个主要依据. 解三角形时，有时可用正弦定理，有时也可用余弦定理，应注意用哪一个定理更方便、简捷一般来说 ,当条件中同时出现ab及2b、2a时，往往用余弦定理，而题设中如果边和正弦、余弦函数交叉出现时，往往运用正弦定理将边化为正弦函数再结合和、差、倍角的正余弦公式进行解答.18．【解析】【分析】【详解】试题分析：试题分析：由得平移直线由图象可知当过时目标函数的最大值为即则当且仅当即时取等号故的最小值为考点：1利用可行域求线性目标函数的最值；2利用基本不等式求最值【方法点晴】解析：9【解析】【分析】【详解】试题分析：试题分析： 由()0,0z ax by a b =+>>得a z y x b b =-+，平移直线,a z y x b b =-+由图象可知，当a z y x b b=-+过()1,1A 时目标函数的最大值为1，即1z a b =+=，则1414()a b a b a b ⎛⎫+=++ ⎪⎝⎭ 441452549b a b a a b a b =+++≥+⋅=+=，当且仅当4b a a b =，即122b a ==时，取等号，故14a b+的最小值为9．考点：1、利用可行域求线性目标函数的最值；2、利用基本不等式求最值．【方法点晴】本题主要考查可行域、含参数目标函数最优解和均值不等式求最值，属于难题．含参变量的线性规划问题是近年来高考命题的热点，由于参数的引入，提高了思维的技巧、增加了解题的难度， 此类问题的存在增加了探索问题的动态性和开放性，此类问题一般从目标函数的结论入手，对目标函数变化过程进行详细分析，对变化过程中的相关量的准确定位，是求最优解的关键．19．【解析】试题分析：该三棱锥底面是边长为2的正三角形面积为有两个侧面是底边为2高为2的直角三角形面积为2另一个侧面是底边为2腰为的等腰三角形面积为所以面积最大的面的面积是考点：三视图7【解析】试题分析：该三棱锥底面是边长为23，有两个侧面是底边为2，高为2的直角三角形，面积为2，另一个侧面是底边为2，腰为2277．考点：三视图．20．【解析】【分析】先找出线面角运用余弦定理进行求解【详解】连接交于点取中点连接则连接为异面直线与所成角在中同理可得异面直线与所成角的余弦值是故答案为【点睛】本题主要考查了异面直线所成的角考查了空间想象 30【解析】【分析】先找出线面角，运用余弦定理进行求解【详解】连接1AB 交1A B 于点D ，取11B C 中点E ，连接DE ，则1DE AC P ，连接1A E 1A DE ∴∠为异面直线1A B 与1AC 所成角在111Rt AC B n 中，111AC =，1111122C E C B == 15A E ∴=, 同理可得16A D =,5DE = 222165530cos 10652A DE ⎛⎫⎛⎫⎛⎫+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∠==⨯⨯, ∴异面直线1A B 与1AC 所成角的余弦值是30 故答案为30 【点睛】本题主要考查了异面直线所成的角，考查了空间想象能力，运算能力和推理论证能力，属于基础题． 三、解答题21．（1）；（2）【解析】【分析】)利用同角三角函数基本关系式可求，由正弦定理可得的值；由，可得为锐角，由可得，利用两角和的正弦函数公式可求的值，利用三角形面积公式即可得解．【详解】 ，，．， 由正弦定理可得：，C 为锐角， 由可得：， ，【点睛】本题主要考查了同角三角函数基本关系式，正弦定理的应用，两角和的正弦函数公式，三角形面积公式在解三角形中的综合应用，属于中档题．正弦定理是解三角形的有力工具，其常见用法有以下三种：（1）知道两边和一边的对角，求另一边的对角（一定要注意讨论钝角与锐角）；（2）知道两角与一个角的对边，求另一个角的对边；（3）证明化简过程中边角互化；（4）求三角形外接圆半径.22．（1）3x ＋y ＋2＝0；（2）(x －2)2＋y 2＝8.【解析】【分析】(1) 直线AB 斜率确定，由垂直关系可求得直线AD 斜率，又T 在AD 上，利用点斜式求直线AD 方程；（2）由AD 和AB 的直线方程求得A 点坐标，以M 为圆心，以AM 为半径的圆的方程即为所求.【详解】(1)∵AB 所在直线的方程为x －3y －6＝0，且AD 与AB 垂直，∴直线AD 的斜率为－3． 又∵点T (－1,1)在直线AD 上，∴AD 边所在直线的方程为y －1＝－3(x ＋1)，即3x ＋y ＋2＝0．(2)由360320x y x y --=⎧⎨++=⎩,得02x y =⎧⎨=-⎩, ∴点A 的坐标为(0，－2)，∵矩形ABCD 两条对角线的交点为M (2,0)，∴M 为矩形ABCD 外接圆的圆心，又|AM |()()22200222-++= ∴矩形ABCD 外接圆的方程为(x －2)2＋y 2＝8．【点睛】本题考查两直线的交点，直线的点斜式方程和圆的方程,考查计算能力，属于基础题. 23．（1）0.9（2）0.085,0.125a b ==【解析】试题分析：（Ⅰ）先频数分布表求出课外阅读时间不少于12小时的人数，再由对立事件的频率公式求出一名学生该周课外阅读时间少于12小时的频率；（Ⅱ）结合频数分布表、直方图确定课外阅读时间落在[4，6）、[8，10）的人数为17，求出对应的频率，分别由频率/组距求出a 、b 的值试题解析：（1）根据频数分布表，100名学生中课外阅读时间不少于12小时的学生共有6+2+2=10名，所以样本中的学生课外阅读时间少于12小时的频率是1010.9100-=． 从该校随机选取一名学生，估计这名学生该周课外阅读时间少于12小时的概率为0.9 （2）课外阅读时间落在组[4,6)的有17人，频率为0.17，所以0.170.0852a ===频率组距， 课外阅读时间落在组[8,10)的有25人，频率为0.25， 所以0.250.1252b ===频率组距 考点：频率分布直方图 24．（1）证明见解析（2）证明见解析【解析】【分析】（1）结合几何体，因为,E G 分别是,BC SC 的中点，所以//EG SB .，再利用线面平行的判定定理证明.（2）由,F G 分别是,DC SC 的中点，得//FG SD .由线面平行的判定定理//FG 平面11BDD B .，再由（1）知，再利用面面平行的判定定理证明.【详解】证明：（1）如图，连接SB ，,E G Q 分别是,BC SC 的中点，//EG SB ∴.又SB ⊂Q 平面11,BDD B EG ⊄平面11BDD B ，所以直线//EG 平面11BDD B .（2）连接,,SD F G Q 分别是,DC SC 的中点，//FG SD ∴.又∵SD ⊂平面11,BDD B FG ⊄平面11,BDD B//FG ∴平面11BDD B .又EG ⊂平面,EFG FG ⊂平面,EFG EG FG G ⋂=，∴平面//EFG 平面11BDD B .【点睛】本题主要考查了线面平行，面面平行的判断定定理，还考查了转化化归的能力，属于中档题.25．（1）3B π=；（2）(]2,4.【解析】【分析】（1）利用正弦定理化简()20a c cosB bcosC --=得：() 2sinA sinC cosB sinBcosC -=，再由正弦两角和差公式和化为：()2sinAcosB sinBcosC cosBsinC sin B C =+=+，再由()sin B C sinA +=得出cos B 的值即可；（2）由sin 3b B =得出a A =，c C =，得到a c A C +=+，进而得到sin 6a c A π+=+⎛⎫ ⎪⎝⎭，再根据角的范围得到sin 6A π⎛⎫ ⎪⎝⎭+的范围即可. 【详解】(1)Q 由()20a c cosB bcosC --=，可得：() 2sinA sinC cosB sinBcosC -=，2sinAcosB sinBcosC cosBsinC ∴=+，可得：()2sinAcosB sin B C sinA =+=，(0,)A π∈Q ，0sinA >，∴可得12cosB =， 又由(0,)B π∈得：3B π=，(2)sin b B =Qa A =，c C =， Q 23A C π+=，]sin sin()a c A C A A B ∴+==++1sin sin()sin sin 32A A A A A π⎤⎤=++=+⎥⎥⎣⎦⎣⎦14cos 4sin()26A A A π⎤=+=+⎥⎣⎦， 203A π<<Q ，5666A πππ<+<， 可得：1sin ,162A π⎛⎫⎛⎤+∈ ⎪ ⎥⎝⎭⎝⎦， ∴a c +的取值范围(]2,4.【点睛】本题主要考查解三角形，侧重考查正弦定理的应用，考查辅助角公式的运用，考查逻辑思维能力和运算能力，属于中档题.26．（1）12n n a n +=；（2）3 【解析】试题分析：(1)结合递推关系可证得b n +1-b n =2，且b 1＝2，即数列{b n }是首项为2，公差为2的等差数列，据此可得数列{}n a 的通项公式为12n n a n +=． (2)结合通项公式裂项有21122n n c c n n ，+⎛⎫=- ⎪+⎝⎭求和有111213212n T n n ⎛⎫=+--< ⎪++⎝⎭．据此结合单调性讨论可得正整数m 的最小值为3． 试题解析：（1）证明：b n +1-b n 1222121n n a a +=--- 222112114n n a a =--⎛⎫-- ⎪⎝⎭ 4222121n n n a a a =-=--． 又由a 1＝1，得b 1＝2，所以数列{b n }是首项为2，公差为2的等差数列，所以b n ＝2+(n -1)×2＝2n ，由221n n b a =-，得12n n a n+=． （2）解：2n c n =，()2411222n n c c n n n n +⎛⎫==- ⎪++⎝⎭所以111213212n T n n ⎛⎫=+--< ⎪++⎝⎭． 依题意，要使11n m m T c c +<对于n ∈N *恒成立，只需()134m m +≥，解得m ≥3或m ≤-4．又m ＞0，所以m ≥3，所以正整数m 的最小值为3．。

新高一数学下期末模拟试题附答案一、选择题1．△ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知5a =，2c =，2cos 3A =，则b= A ．2B ．3C ．2D ．32．如图，在ABC ∆中，已知5AB =，6AC =，12BD DC =，4AD AC ⋅=，则AB BC ⋅=A ．-45B ．13C ．-13D ．-373．某空间几何体的三视图如图所示，则该几何体的体积为（ ）A ．73B ．8π3- C ．83D ．7π3- 4．已知D ，E 是ABC 边BC 的三等分点，点P 在线段DE 上，若AP xAB yAC =+，则xy 的取值范围是( ) A ．14,99⎡⎤⎢⎥⎣⎦B ．11,94⎡⎤⎢⎥⎣⎦C ．21,92⎡⎤⎢⎥⎣⎦D ．21,94⎡⎤⎢⎥⎣⎦5．在ABC 中，角A ，B ，C 所对的边为a ，b ，c ，且B 为锐角，若sin 5sin 2A cB b=，7sin B =，57ABC S =△b =（ ） A ．3B ．7C 15D 146．设l ，m 是两条不同的直线，α是一个平面，则下列命题正确的是 （ ） A ．若l m ⊥，m α⊂，则l α⊥ B ．若l α⊥，//l m ，则m α⊥ C ．若//l α，m α⊂，则//l mD ．若//l α，//m α，则//l m7．已知()f x 是定义域为(,)-∞+∞的奇函数，满足(1)(1)f x =f +x -，若(1)2f =，则(1)(2)f +f (3)(2020)f f +++=（ ）A ．50B ．2C ．0D ．50-8．已知{}n a 的前n 项和241n S n n =-+，则1210a a a +++=（ ）A ．68B ．67C ．61D ．609．在ABC 中，已知,2,60a x b B ===，如果ABC 有两组解，则x 的取值范围是( )A ．4323⎛⎫ ⎪ ⎪⎝⎭，B ．4323⎡⎤⎢⎥⎣⎦，C ．4323⎡⎫⎪⎢⎪⎣⎭， D ．432,3⎛⎤⎥ ⎝⎦10．已知0,0a b >>，并且111,,2a b成等差数列，则4a b +的最小值为（ ） A ．2B ．4C ．5D ．911．已知圆()()22:341C x y -+-=和两点(),0A m -，()(),00B m m >，若圆C 上存在点P ，使得90APB ∠=︒，则m 的最大值为（ ） A ．7B ．6C ．5D ．412．如图，在△ABC 中, 13AN NC =,P 是BN 上的一点,若29AP m AB AC −−→−−→−−→=+,则实数m 的值为( )A ．B ．C ．19D ．二、填空题13．设a ＞0，b ＞033a 与3b 的等比中项，则11a b+的最小值是__． 14．一个空间几何体的三视图及部分数据如图所示，则这个几何体的体积是___________15．抛物线214y x =-上的动点M 到两定点(0,1)(1,3)--、的距离之和的最小值为__________．16．设向量(12)(23)a b ==，，，，若向量a b λ+与向量(47)c =--，共线，则λ= 17．函数()12x f x =-的定义域是__________．18．在200m 高的山顶上，测得山下一塔顶与塔底的俯角分别是30°,60°，则塔高 为19．已知点()M a b ，在直线3415x y +＝上，则22a b +的最小值为_______． 20．设，则________三、解答题21．已知函数31()log 1a m xf x x -=-（0a >，且1a ≠）的图象关于坐标原点对称．（1）求实数m 的值；（2）比较()2f 与()3f 的大小，并请说明理由．22．在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球，现从甲、乙两个盒子中各取出1个球，每个球被取出的可能性相等． （Ⅰ）求取出的两个球上标号为相同数字的概率； （Ⅱ）求取出的两个球上标号之积能被3整除的概率．23．ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知2cos (cos cos )C a B b A c +=. （1）求角C ；（2）若7c =33ABC S ∆=ABC ∆的周长. 24．已知数列{}n a 的前n 项和n S ，且23n s n n =+；（1）求它的通项n a .（2）若12n n n b a -=，求数列{}n b 的前n 项和n T .25．以原点为圆心，半径为r 的圆O 222:()0O x y r r +=>与直线380x --=相切. （1）直线l 过点(6)-且l 截圆O 所得弦长为43l l 的方程；（2）设圆O 与x 轴的正半轴的交点为M ，过点M 作两条斜率分别为12,k k 12,k k 的直线交圆O 于,A B 两点，且123k k ⋅=-，证明：直线AB 恒过一个定点，并求出该定点坐标.26．某校高一()1班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损，可见部分如图．(1)求分数在[)50,60的频数及全班人数；(2)求分数在[)80,90之间的频数，并计算频率分布直方图中[)80,90间矩形的高； (3)若要从分数在[)80,100之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中，至少有一份分数在[)90,100之间的概率．【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【解析】 【分析】 【详解】由余弦定理得，解得（舍去），故选D.【考点】余弦定理【名师点睛】本题属于基础题,考查内容单一,根据余弦定理整理出关于b的一元二次方程,再通过解方程求b.运算失误是基础题失分的主要原因,请考生切记！2．D解析：D【解析】【分析】先用AB和AC表示出2AAB BC AB C AB⋅=⋅-，再根据，12BD DC=用用AB和AC表示出AD，再根据4AD AC⋅=求出AAB C⋅的值，最后将AAB C⋅的值代入2AAB BC AB C AB⋅=⋅-，，从而得出答案．【详解】()2A=AAB BC AB C AB AB C AB⋅=⋅-⋅-，∵12BD DC=，∴111B C?C B222AD A A AD AD A AD A -=-=-+（），整理可得：12AB33AD AC+＝，221A A4 33AD AC AB C C∴⋅⋅+=＝∴A=-12AB C⋅，∴2=A=122537AB BC AB C AB⋅⋅---=-．，故选：D．【点睛】本题考查了平面向量数量积的运算，注意运用平面向量的基本定理，以及向量的数量积的性质，考查了运算能力，属于中档题．3．B解析：B【解析】【分析】由三视图可知，该几何体是由一个四棱锥挖掉半个圆锥所得，故利用棱锥的体积减去半个圆锥的体积，就可求得几何体的体积. 【详解】由三视图可知，该几何体是由一个四棱锥挖掉半个圆锥所得，故其体积为21118222123233ππ-⋅⋅⋅-⋅⋅⋅⋅=.故选B. 【点睛】本小题主要考查由三视图判断几何体的结构，考查不规则几何体体积的求解方法，属于基础题.4．D解析：D 【解析】 【分析】利用已知条件推出x +y ＝1，然后利用x ，y 的范围，利用基本不等式求解xy 的最值． 【详解】解：D ，E 是ABC 边BC 的三等分点，点P 在线段DE 上，若AP xAB yAC =+，可得x y 1+=，x ，12y ,33⎡⎤∈⎢⎥⎣⎦，则2x y 1xy ()24+≤=，当且仅当1x y 2==时取等号，并且()2xy x 1x x x =-=-，函数的开口向下， 对称轴为：1x 2=，当1x 3=或2x 3=时，取最小值，xy 的最小值为：29．则xy 的取值范围是：21,.94⎡⎤⎢⎥⎣⎦故选D ． 【点睛】本题考查函数的最值的求法，基本不等式的应用，考查转化思想以及计算能力．5．D解析：D 【解析】 【分析】 利用正弦定理化简sin 5sin 2A cB b=，再利用三角形面积公式，即可得到,a c ，由sin B =，求得cos B ，最后利用余弦定理即可得到答案． 【详解】由于sin 5sin 2A c B b=，有正弦定理可得： 52a c b b =，即52a c =由于在ABC中，sin 4B =，4ABC S =△1sin 24ABCS ac B ==，联立521sin 2sin a c ac B B ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩，解得：5a =，2c = 由于B为锐角，且sin 4B =，所以3cos 4B ==所以在ABC 中，由余弦定理可得：2222cos 14b a c ac B =+-=，故b =（负数舍去） 故答案选D 【点睛】本题考查正弦定理，余弦定理，以及面积公式在三角形求边长中的应用，属于中档题．6．B解析：B 【解析】 【分析】利用,l α可能平行判断A ，利用线面平行的性质判断B ，利用//l m 或l 与m 异面判断C ，l 与m 可能平行、相交、异面，判断D .【详解】l m ⊥，m α⊂，则,l α可能平行，A 错；l α⊥，//l m ，由线面平行的性质可得m α⊥，B 正确； //l α，m α⊂，则//l m ， l 与m 异面；C 错，//l α，//m α，l 与m 可能平行、相交、异面，D 错，.故选B. 【点睛】本题主要考查线面平行的判定与性质、线面面垂直的性质，属于中档题.空间直线、平面平行或垂直等位置关系命题的真假判断，除了利用定理、公理、推理判断外，还常采用画图（尤其是画长方体）、现实实物判断法（如墙角、桌面等）、排除筛选法等；另外，若原命题不太容易判断真假，可以考虑它的逆否命题，判断它的逆否命题真假，原命题与逆否命题等价.7．C解析：C 【解析】 【分析】利用()f x 是定义域为(,)-∞+∞的奇函数可得：()()f x f x -=-且()00f =，结合(1)(1)f x =f +x -可得：函数()f x 的周期为4；再利用赋值法可求得：()20f =，()32f =-，()40f =，问题得解.【详解】因为()f x 是定义域为(,)-∞+∞的奇函数， 所以()()f x f x -=-且()00f = 又(1)(1)f x =f +x -所以()()()()()21111f x f x f x f x f x ⎡⎤⎡⎤+=++=-+=-=-⎣⎦⎣⎦ 所以()()()()()4222f x f x f x f x f x ⎡⎤⎡⎤+=++=-+=--=⎣⎦⎣⎦ 所以函数()f x 的周期为4，在(1)(1)f x =f +x -中，令1x =，可得：()()200f f ==在(1)(1)f x =f +x -中，令2x =，可得：()()()3112f f f =-=-=- 在(1)(1)f x =f +x -中，令3x =，可得：()()()4220f f f =-=-= 所以(1)(2)f +f ()()()()2020(3)(2020)12344f f f f f f ⎡⎤+++=⨯+++⎣⎦ 50500=⨯=故选C 【点睛】本题主要考查了奇函数的性质及函数的周期性应用，还考查了赋值法及计算能力、分析能力，属于中档题．8．B解析：B 【解析】 【分析】首先运用11,1,2n nn S n a S S n -=⎧=⎨-≥⎩求出通项n a ，判断n a 的正负情况，再运用1022S S -即可得到答案． 【详解】当1n =时，112S a ==-；当2n ≥时，()()()22141141125n n n a S S n n n n n -⎡⎤=-=-+----+=-⎣⎦， 故2,125,2n n a n n -=⎧=⎨-≥⎩；所以，当2n ≤时，0n a <，当2n >时，0n a >.因此，()()()12101234101022612367a a a a a a a a S S +++=-+++++=-=-⨯-=.故选：B ． 【点睛】本题考查了由数列的前n 项和公式求数列的通项公式，属于中档题，解题时特别注意两点，第一，要分类讨论，分1n =和2n ≥两种情形，第二要掌握()12n n n a S S n -=-≥这一数列中的重要关系，否则无法解决此类问题，最后还要注意对结果的处理，分段形式还是一个结果的形式.9．A解析：A 【解析】 【分析】已知,,a b B ，若ABC 有两组解，则sin a B b a <<，可解得x 的取值范围. 【详解】由已知可得sin a B b a <<，则sin602x x ︒<<，解得2x <<故选A. 【点睛】本题考查已知两边及其中一边的对角，用正弦定理解三角形时解的个数的判断. 若ABC 中，已知,,a b B 且B 为锐角，若0sin b a B <<，则无解；若sin b a B =或b a ≥，则有一解；若sin a B b a <<，则有两解. 10．D 解析：D 【解析】 ∵111,,2a b成等差数列， ()111141445529a b a a b a b a b a b b a b ⎛⎫∴+=∴+=++=+++⋅= ⎪⎝⎭，， 当且仅当a =2b 即33,2a b ==时“=“成立， 本题选择D 选项.点睛：在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误．11．B解析：B 【解析】由题意知，点P 在以原点（0，0）为圆心，以m 为半径的圆上，又因为点P 在已知圆上，所以只要两圆有交点即可，所以15m -=，故选B.考点：本小题主要考查两圆的位置关系，考查数形结合思想，考查分析问题与解决问题的能力.12．C解析：C 【解析】 【分析】先根据共线关系用基底AB AC→→，表示AP→，再根据平面向量基本定理得方程组解得实数m的值. 【详解】如下图，∵,,B P N 三点共线，∴，∴，即,∴①,又∵13AN NC =，∴，∴28=99AP m AB AC m AB AC →→→→→=++②，对比①，②，由平面向量基本定理可得：．【点睛】本题考查向量表示以及平面向量基本定理，考查基本分析求解能力.二、填空题13．【解析】由已知是与的等比中项则则当且仅当时等号成立故答案为2【点睛】本题考查基本不等式的性质等比数列的性质其中熟练应用乘1法是解题的关键 解析：【解析】由已知0,0a b >>33a 与b 的等比中项，则233,1a b ab =⋅∴=则111111122ab a b ab a b a b a b ⎛⎫⎛⎫+=+⨯=+⨯=+≥= ⎪ ⎪⎝⎭⎝⎭，当且仅当1a b ==时等号成立 故答案为2【点睛】本题考查基本不等式的性质、等比数列的性质，其中熟练应用“乘1法”是解题的关键．14．【解析】【分析】先还原几何体再根据柱体体积公式求解【详解】空间几何体为一个棱柱如图底面为边长为的直角三角形高为的棱柱所以体积为【点睛】本题考查三视图以及柱体体积公式考查基本分析求解能力属基础题 解析：32【解析】 【分析】先还原几何体，再根据柱体体积公式求解 【详解】空间几何体为一个棱柱，如图，底面为边长为1,3的直角三角形，高为3的棱柱，所以体积为1313322⨯⨯⨯=【点睛】本题考查三视图以及柱体体积公式，考查基本分析求解能力，属基础题15．4【解析】【分析】【详解】由题意得交点设作与准线垂直垂足为作与准线垂直垂足为则解析：4 【解析】 【分析】 【详解】由题意得交点(0,1)F - ，设(1,3)A - ，作AN 与准线垂直，垂足为N ，作MH 与准线垂直，垂足为H ，则314MA MF MA MH AN +=+≥=+=16．2【解析】【分析】由题意首先求得向量然后结合向量平行的充分必要条件可得的值【详解】=由向量共线的充分必要条件有：故答案为2【点睛】本题主要考查平面向量的坐标运算向量平行的充分必要条件等知识意在考查学【解析】 【分析】由题意首先求得向量a b λ+，然后结合向量平行的充分必要条件可得λ的值. 【详解】a b λ+=(,2(2,3)(2,23λλλλ+=++））， 由向量共线的充分必要条件有：()()(2)7(23)42λλλ+⋅-=+⋅-⇒=. 故答案为2． 【点睛】本题主要考查平面向量的坐标运算，向量平行的充分必要条件等知识，意在考查学生的转化能力和计算求解能力.17．【解析】由得所以所以原函数定义域为故答案为 解析：(],0-∞【解析】由120x -≥，得21x ≤，所以0x ≤，所以原函数定义域为(],0-∞，故答案为(],0-∞.18．【解析】【分析】【详解】试题分析：根据题意设塔高为x 则可知a 表示的为塔与山之间的距离可以解得塔高为考点：解三角形的运用点评：主要是考查了解三角形中的余弦定理和正弦定理的运用属于中档题 解析：【解析】 【分析】 【详解】试题分析：根据题意，设塔高为x ，则可知00tan 60=,t 2an 30=00200a ax-，a 表示的为塔与山之间的距离，可以解得塔高为．考点：解三角形的运用点评：主要是考查了解三角形中的余弦定理和正弦定理的运用，属于中档题．19．3【解析】【分析】由题意可知表示点到点的距离再由点到直线距离公式即可得出结果【详解】可以理解为点到点的距离又∵点在直线上∴的最小值等于点到直线的距离且【点睛】本题主要考查点到直线的距离公式的应用属于解析：3 【解析】 【分析】22a b +()0,0到点(),a b 的距离，再由点到直线距离公式即可得出结果.22a b +可以理解为点()0,0到点(),a b 的距离，又∵点(),M a b 在直线:3425l x y +=上，∴22a b +的最小值等于点()0,0到直线34150x y +-=的距离，且22304015334d ⨯+⨯-==+.【点睛】本题主要考查点到直线的距离公式的应用，属于基础题型.20．-1【解析】【分析】由分段函数的解析式先求出f(-2)的值并判定符号从而可得f(f(-2))的值【详解】∵fx=1-xx≥0x2x<0-2<0∴f-2=-22=4>0所以f(f(-2))=f4=1-解析：-1 【解析】 【分析】由分段函数的解析式先求出的值并判定符号，从而可得的值.【详解】， ，所以，故答案为-1. 【点睛】本题主要考查分段函数的解析式，属于简单题. 求分段函数的函数值，要先确定要求值的自变量属于哪一段区间，然后代入该段的解析式求值，当出现的形式时，应从内到外依次求值．三、解答题21．（1）1m =-；（2）当1a >时， ()()23f f >；当01a <<时， ()()23f f <，理由见解析 【解析】 【分析】（1）将图象关于坐标原点对称转化为函数为奇函数，从而有()()f x f x -=-在函数的定义域内恒成立，进而求得m 的值，再进行检验； （2）根所在（1）中求得的m 值，得到1()log 1ax f x x +=-，再求得()()2,3f f 的值，对 a 分两种情况讨论，从而得到()()2,3f f 的大小关系.【详解】 解：（1）31()log 1am x f x x -=-，31()()log 1a m x f x x -⋅-∴-=--．又函数()f x 的图象关于坐标原点对称，()f x ∴为奇函数，()()f x f x ∴-=-在函数的定义域内恒成立，331()1log log 11a am x m xx x -⋅--∴=----， 331()1111m x m xx x -⋅--∴⋅=---，()6210m x ∴-=在函数的定义域内恒成立，1m ∴=-或1m =．当1m =时，函数的真数为1-，不成立，1m ∴=-．（2）据（1）求解知，1()log 1ax f x x +=-， (2)log 3a f ∴=，(3)log 2a f =．当1a >时，函数()log a g x x =在(0,)+∞上单调递增，23<，log 2log 3(3)(2)a a f f ∴<⇒<；当01a <<时，函数()log a g x x =在(0,)+∞上单调递减，23<，log 2log 3(3)(2)a a f f ∴>⇒>．【点睛】本题考查利用函数的奇偶性求解析式中参数值、对数函数的单调性比较大小，考查数形结合思想、分类讨论思想的运用，在比较大小时，注意对a 分1a >和01a <<两种情况讨论. 22．(1) ． (2)．【解析】 【分析】 【详解】设从甲、乙两个盒子中各取1个球，其数字分别为x ，y ． 用（x ，y ）表示抽取结果，则所有可能的结果有16种，即（1，1），（1，2），（1，3），（1，4），（2，1），（2，2），（2，3），（2，4），（3，1），（3，2），（3，3），（3，4），（4，1），（4，2），（4，3），（4，4）．（1）设“取出的两个球上的标号相同”为事件A ， 则A ＝{（1，1），（2，2），（3，3），（4，4）}． 事件A 由4个基本事件组成，故所求概率P （A ）＝＝．（2）设“取出的两个球上标号的数字之积能被3整除”为事件B ，则B ＝{（1，3），（3，1），（2，3），（3，2），（3，3），（3，4），（4，3）}事件B 由7个基本事件组成，故所求概率P （A ）＝．考点：古典概型的概率计算 23．（1）3C π=（2）57【解析】 【分析】 【详解】试题分析：（1）根据正弦定理把2cos (cos cos )C a B b A c +=化成2cos (sin cos sin cos )sin C A B B A C +=，利用和角公式可得1cos ,2C =从而求得角C ；（2）根据三角形的面积和角C 的值求得6ab =，由余弦定理求得边a 得到ABC ∆的周长. 试题解析：（1）由已知可得2cos (sin cos sin cos )sin C A B B A C +=12cos sin()sin cos 23C A B C C C π∴+=⇒=⇒= （2）1313sin 36222ABC S ab C ab ab ∆=⇒=⇒= 又2222cos a b ab C c +-=2213a b ∴+=，2()255a b a b ∴+=⇒+=ABC ∆∴的周长为57考点：正余弦定理解三角形.24．（1）22n a n =+（2）12n n T n +=•【解析】 【分析】（1）由2S 3n n n =+，利用n a 与n S 的关系式，即可求得数列的通项公式；（2）由（1）可得2(1)nn b n =+，利用乘公比错位相减法，即可求得数列{}n b 的前n 项和.【详解】（1）由2S 3n n n =+，当1n =时，11S 4a ==；当1n >时，2213(1)3(1)n n n a S S n n n n -=-=+----22n =+，当1n =也成立， 所以则通项22n a n =+；（2）由（1）可得2(1)nn b n =+，-123223242(1)2n n T n =•+•+•+++•，231222322(1)2n n n T n n +=•+•++•++•，两式相减得2314(222)(1)2n n n T n +-=++++-+21112(12)4(1)2212n n n n n -++-=+-+=--所以数列{}n b 的前n 项和为12n n T n +=•.【点睛】本题主要考查了数列n a 和n S 的关系、以及“错位相减法”求和的应用，此类题目是数列问题中的常见题型，解答中确定通项公式是基础，准确计算求和是关键，易错点是在“错位”之后求和时，弄错等比数列的项数，着重考查了的逻辑思维能力及基本计算能力等. 25．（1）2x =-或20x +-=100x +-=；（2）(2,0). 【解析】分析：（1）先由直线和圆相切得到圆的方程，再由垂径定理列式，分直线斜率存在与不存在两种情况得到结果；（3）联立直线和圆，由韦达定理得到交点的坐标，由这两个点写出直线方程，进而得到直线过定点. 详解：(1)∵圆222:(0)O x y r r +=>与直线0x y -+=80x --=相切， ∴圆心O到直线的距离为4d ==，∴圆O 的方程为：2216x y +=若直线l 的斜率不存在，直线l 为2x =- 1x =， 此时直线l截圆所得弦长为若直线l 的斜率存在，设直线l为()2y k x =+()1y k x =-，由题意知，圆心到直线的距离为1d == 2d =，解得：12k =-， 此时直线l为100x +-=，则所求的直线l 为2x =-或20x +-=-100x += （2）由题意知，()4,0M ()2,0A -，设直线()1:4MA y k x =-， 与圆方程联立得：()12224y k x x y ⎧=+⎨+=⎩ ()122416y k x x y ⎧=-⎨+=⎩， 消去y 得：()()222211114440k x k x k +++-= ()22221111816160k x k x k +-+-=，∴()21211611M A k x x k-=+∴()2121411Ak xk-=+，12181Ak yk -=+用13k -换掉1k 得到B 点坐标 ∴21213649B k x k -=+，121249B k y k =+ 12141B k y k =+∴直线AB 的方程为21112221118444131k k k y x k k k ⎛⎫-+=- ⎪+-+⎝⎭整理得：()121423k y x k =-- 则直线AB 恒过定点为()2,0.点睛：本题主要考查直线与圆锥曲线位置关系，所使用方法为韦达定理法：因直线的方程是一次的，圆锥曲线的方程是二次的，故直线与圆锥曲线的问题常转化为方程组关系问题，最终转化为一元二次方程问题，故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一，尤其是弦中点问题，弦长问题，可用韦达定理直接解决，但应注意不要忽视判别式的作用．26．（1）2，25；（2）0.012；（3）0.7. 【解析】 【分析】(1)先由频率分布直方图求出[)50,60的频率，结合茎叶图中得分在[)50,60的人数即可求得本次考试的总人数；(2)根据茎叶图的数据，利用(1)中的总人数减去[)50,80外的人数，即可得到[)50,80内的人数，从而可计算频率分布直方图中[)80,90间矩形的高；(3)用列举法列举出所有的基本事件，找出符合题意得基本事件个数，利用古典概型概率计算公式即可求出结果． 【详解】(1)分数在[)50,60的频率为0.008100.08⨯=，由茎叶图知：分数在[)50,60之间的频数为2，∴全班人数为2250.08=． (2)分数在[)80,90之间的频数为25223-=；频率分布直方图中[)80,90间的矩形的高为3100.01225÷=． (3)将[)80,90之间的3个分数编号为1a ，2a ，3a ，[)90,100之间的2个分数编号为1b ，2b ，在[)80,100之间的试卷中任取两份的基本事件为：()12a ,a ，()13a ,a ，()11a ,b ，()12a ,b ，()23a ,a ，()21a ,b ，()22a ,b ，()31a ,b ，()32a ,b ，()12b ,b 共10个，其中，至少有一个在[)90,100之间的基本事件有7个，故至少有一份分数在[)90,100之间的概率是70.710=． 【点睛】本题考查了茎叶图和频率分布直方图的性质，以及古典概型概率计算公式的应用，此题是基础题．对于古典概型，要求事件总数是可数的，满足条件的事件个数可数，使得满足条件的事件个数除以总的事件个数即可.。

【必考题】高一数学下期末模拟试题及答案一、选择题2 32 ，cos A 1． △ABC 的内角 A 、B 、 C 的对边分别为 a 、 b 、 c.已知 a 5 ， c ，则b= A ． B ． C ． 2D ． 32 32． 已知 a n n 项和是 S n B ． dS 9S 17S 18 S 8S 10 ，则（ 是公差为 d 的等差数列，前 ，若 ）S 17S 18 0A ． d 0 ， 0 ， 0 C ． d0 ， D ． d 0 ， v -2 ，则 a v2b 的最v v a ， b 满足 ）v va v 4 ，b 在 a 上的投影（正射影的数量）为 3． 已知向量 小值为（ A ． 4 B ． 10C ．D ． 8 ）3104． 设 m ， n 为两条不同的直线， ，为两个不同的平面，则（/ /m， m / / m / / ， n / / m// n m/ / A ．若 ，则 B ．若 ，则 C ．若 m // n ， n，则 mD ．若 m/ / ，，则 uu u v uu u v u u u vPC ) 的5． 已知 ABC 是边长为 4 的等边三角形， P 为平面 ABC 内一点，则 PA ?(PB 最小值是（） 63 A ．B ．C ． 4D ． 26． 已知函数 （x ）定义域是 [-2 ， 3] ，则 y=f （ 2x-1 ）的定义域是（）y=f 5 21 20,B ．1,4, 2 5,5A ． C ．D ．， m 是两条不同的直线， 是一个平面，则下列命题正确的是（ ）m7．设 l ， l // m ，则 m m l l // mll / / a 2 ，则 ，则 B ．若 D ．若 ll / / m ， A ．若 C ．若 l // m， m/ / ，则 ， 2a na 1C ． La 10n 项和 S nn4n 1 ，则 8． 已知 的前 （ ）A ． 68673 ， 61D ． 60AOC B ． u u u v 1， | OB |u u u v u u u v u u u vOA OB 9． 若 | OA | 0 ，点 C 在 AB 上，且 30 ，设u u u v OC u u u v mOA u u u v nOB ( m ,n mnR) ，则 的值为（ ）1 33 33A ．B ．C ．D ． 310． 某三棱锥的三视图如图所示，则该三棱锥的体积为（）A ． 20 11． 如图，已知三棱柱B ． 10 ABCC ． 30 A 1 B 1C 1 的各条棱长都相等，且D ． 60底面 ABC ， CC 1M 是侧棱 AB 1 和 CC 1 的中点，则异面直线 BM 所成的角为 ()A ．B ．C ．D ．32ABC 中，根据下列条件解三角形，其中有一解的是（ 12． 在 A ． aB ． bC ． aD ． b）30oB45ooA 120oC607 ， b 3 ， 5 2 B ， 6 ， c 10 ， b 15 ， 6 ， 3 ， c 6 二、填空题≤m 的概率为 13． 在区间 [﹣2， 4] 上随机地取一个数 x ，若 x 满足 |x| ，则 m=．14． 在ABC 中，若 BAB 2BC 的最大值为 ．， 3 ，则 AC3oo15．sin10 1 3 tan 7016． 如图，在正方体 ABCD A 1B 1C 1 D 1 中， E 、 分别是 DD 1 、 F DC 上靠近点 D 的三等分点，则异面直线与 A 1C 1 所成角的大小是 EF.17．已知圆的方程为x2 +y2﹣6x﹣8y＝0，设该圆过点（3，5）的最长弦和最短弦分别为AC 和BD，则四边形ABCD 的面积为1tan1 1 tan 2 1tan3 L1tan 44 1tan 4518．= ．19．如图，棱长均为 2 的正四棱锥的体积为．x2 m20．已知函数 f ( x). mx 1，若对于任意的x m, m 1 f ( x) 0 ，则实数都有的取值范围为三、解答题21．已知数列{ a n} 是一个等差数列，且a2＝1，a5＝－5.求{ a n} 的通项a n；(1)(2) 求{ a n} 前n 项和S n 的最大值．4sin x cos 022．将函数g x x 的图象向左平移个单位长度后得到62f x 的图象．（1）若 f x f为偶函数，求的值；7,（2）若 f x 在上是单调函数，求的取值范围．623．某班50 名学生在一次百米测试中，成绩全部介于13 秒与18 秒之间，将测试结果按如13,14 ，第二组14,15 ，第五组17,18 .下图是按上述分下方式分成五组：第一组，组方法得到的频率分布直方图.按上述分组方法得到的频率分布直方图.（1）若成绩大于或等于 人数；14 秒且小于 16 秒认为良好，求该班在这次百米测试中成绩良好的 m,n 13,14 17,18 .求事（2）设 m,n 表示该班某两位同学的百米测试成绩，且已知 件“mn 1 ”发生的概率 .n 项和为 S n ，且 a n 是 S n 与 a n b n 24． 已知数列 b 1 2 ，的前 2 的等差中项．数列 中， yx 2 上．点 P b n , b n在直线 1（1）求 a 1 和 a 2 的值； a n b n （2）求数列 ， 的通项公式；c n n 项和 （3）设 c na nb n ，求数列 T n ．的前 1 4a na 1＝ 1，a n 1n ∈N * ． { a n } 满足 25． 已知数列 ，其中 1 22 a n 4 a nb n（1）设 ，求证：数列 { b n } 是等差数列，并求出 { a n } 的通项公式．1 1 T n（2）设 c n，数列 { c n c n +2} 的前 n 项和为 T n ，是否存在正整数 m ，使得 c m c m n 11对于 n ∈ N * ，恒成立？若存在，求出 m 的最小值；若不存在，请说明．26． 如图，平行四边形ABCD 中， E ， 分别是 BC ， DC 的中点， G 为 与 的F BF DE u u u v v v u u u v、 CG u u u v AB v v u u u v DE u u u v BF 交点，若 b ，试以 a ， b为基底表示 、 ． a , AD 【参考答案】 *** 试卷处理标记，请不要删除一、选择题1．D解析：D【解析】【分析】【详解】由余弦定理得，解得（舍去），故选 D.【考点】余弦定理【名师点睛】本题属于基础题,考查内容单一,根据余弦定理整理出关于 b 的一元二次方程,再通过解方程求b.运算失误是基础题失分的主要原因2．D解析：D【解析】【分析】,请考生切记！a n利用等差数列的通项公式求和公式可判断出数列的单调性，并结合等差数列的求和公式可得出结论.【详解】Q S9S8S10 ，a9S18 0 ，a9a10a100 ，a10 0 ，d0 .9 a90 .S17 故选：17a9D.0 ，【点睛】本题考查利用等差数列的前n 项和判断数列的单调性以及不等式，考查推理能力与计算能.力，属于中等题3．D解析：D【解析】【分析】r| b | cos r ra, br| b |rb 在r a ra 上的投影（正射影的数量）为r 22 可知 2 ，可求出 2 ，求的最小值即可得出结果.2b【详解】r r 因为 b 在 a 上的投影（正射影的数量）为2 ，r | b | cos r r a, b 所以 r 2 ， 2 r r a,br r即 | b |，而 0 ，1 cos a, b cos r | b | ra 所以 2 ， r 2 2br ( a r 2b) r r a r 4a r b r 4b r r rr r a, br 2 2 2 2 2因为 | a | 4 | a ||b | cos 4 | b |r 2 2=16 4 4 r 2 2b ( 2) 4 | b | 48 4 | b |r r 2b ra a 8 ，故选 D.所以 48 4 4 64 ，即 【点睛】本题主要考查了向量在向量上的正射影，向量的数量积，属于难题4．C解析： C 【解析】【分析】 根据空间线面关系、面面关系及其平行、垂直的性质定理进行判断． 【详解】.，则 m 与 n 平行、相交、异面都可以，位置关系不确定；对于 A 选项，若 m// I， n// l ， mmm//l 对于 B 选项，若，且 ， ，根据直线与平面平行的判定定理m// m// 知， ， ，但与 n 不平行；a 、b 使得 n a ，；对于 n C 选项，若 m// n ， ，在平面内可找到两条相交直线 b ，于是可得出 m a ， m ，在平面b ，根据直线与平面垂直的判定定理可得m对于 D 选项，若 内可找到一条直线 a 与两平面的交线垂直，根据平面与am 才与平面平面垂直的性质定理得知 ，只有当 m//a 时， 垂直．故选 C ．【点睛】 本题考查空间线面关系以及面面关系有关命题的判断，判断时要根据空间线面、面面平行 与垂直的判定与性质定理来进行，考查逻辑推理能力，属于中等题．5．AA 解析： 【解析】【分析】 建立平面直角坐标系，表示出点的坐标，利用向量坐标运算和平面向量的数量积的运算，求得最小值，即可求解 【详解】 . 由题意，以BC 中点为坐标原点，建立如图所示的坐标系，则 A(0, 2 P( x, y) 3), B( 2,0), C(2,0) ，u u u r PA u u u r PC) u u u r y), PB u u u ry), PC 设 ，则 u u u r ( x, 2 3 ( 2 x, (2 x, y) ，2 2 y u u u r 2( 2 y) 2 x 所以 PA ?( P B x ( 2 x) (2 3 y) 4 3 y 222[ x( y 3)3] ，uu u r u u u r u u u rPC ) 取得最小值为 2 ( 3)6 ，所以当 x 0, y3 时， PA ?(PB 故选 A.【点睛】本题主要考查了平面向量数量积的应用问题，根据条件建立坐标系，利用坐标法是解答的 关键，着重考查了推理与运算能力，属于基础题6．C解析： C 【解析】.∵函数 y=f(x) 定义域是 [-2,3] ， ∴由 -2 ? 2x-1 ? 3， 1 2解得 -? x ? 2，12即函数的定义域为 , 2 ， 本题选择 7．B解析： B 【解析】 【分析】C 选项 .l , 与 m 异面判断l // m或利用 可能平行判断A ，利用线面平行的性质判断B ，利用 l 与 m 可能平行、相交、异面，判断C ， lD .【详解】l , m ，m l ll / /l / / ，则 可能平行，A错；m ， l // m ，由线面平行的性质可得， B 正确；m与 m 异面；C 错， l // m ， l ，则 ， m 可能平行、相交、异面， ， m/ / ， l 与 错， .故选 B.D 【点睛】.空间直线、平面平本题主要考查线面平行的判定与性质、线面面垂直的性质，属于中档题行或垂直等位置关系命题的真假判断，除了利用定理、公理、推理判断外，还常采用画图 （尤其是画长方体）、现实实物判断法（如墙角、桌面等）、排除筛选法等；另外，若原 命题不太容易判断真假，可以考虑它的逆否命题，判断它的逆否命题真假，原命题与逆否 命题等价 .8．B解析： B 【解析】 【分析】S 1, n 1首先运用 a n a n ，判断 a n 的正负情况，再运用 S 102S 2 即可求出通项 S n S n 1 , n 2得到答案． 【详解】 当 n 1 时， S 1 a 1 2 ； 22n2 时， a n S nS n n4n 1 n 14 n 1 1 2n5 ，当 12, n 1a n故 ；2n n 5,n 2 时， 20 ，当 所以，当 a na n0 .n 2 时， 因此，a 1a 2 La 10a 1 a 2a 3 a 4 La 10S 10 2S 2 61 23 67 .B ． 故选： 【点睛】本题考查了由数列的前 n 项和公式求数列的通项公式，属于中档题，解题时特别注意两 a n S n S n n 2 点，第一，要分类讨论，分n 1 和 n 2 两种情形，第二要掌握 这1 一数列中的重要关系，否则无法解决此类问题，最后还要注意对结果的处理，分段形式还 是一个结果的形式 9．B解析： B 【解析】【分析】 利用向量的数量积运算即可算出． 【详解】 .解： Q AOC30u u u r u u u r OC, OA3 2cosu u u r uu u r OC u u u r OC OA u u u r OA3 2u u u r nOB u u u r mOA u u u r mOA u u u r OA 3 2u u u r nOB u u u r u u u r nOB u u u r OAu u u r 2 m OA uu u r u u u r OA 3 2u u u r 2 OA uu u r 2 u u u r 22 m u u u r Q OA 2mnOA OB n OB OAu uu r u u u r OBu u u r OA 1 ， 3 ， OB 0 m m 2323n 22 2m9n又Q C 在AB 上m m n故选： 0 ，n 0 3B 【点睛】本题主要考查了向量的基本运算的应用，向量的基本定理的应用及向量共线定理等知识的 综合应用．10．B解析： B 【解析】【分析】 根据三视图还原几何体，根据棱锥体积公式可求得结果 【详解】由三视图可得几何体直观图如下图所示：.1 215 2h 4；底面面积： S 5 3可知三棱锥高：1 3 1 3 152三棱锥体积：VSh 4 10本题正确选项： 【点睛】 本题考查棱锥体积的求解，关键是能够通过三视图还原几何体，从而准确求解出三棱锥的 B高和底面面积 11．A.解析： A 【解析】 【分析】 由题意设棱长为a ，补正三棱柱 ABC-A 2B 2C 2，构造直角三角形 A 2BM ，解直角三角形求出BM ，利用勾股定理求出 【详解】A 2M ，从而求解． 设棱长为 a ，补正三棱柱 ABC-A 2B 2C 2（如图）．平移 AB 1 至 A 2B ，连接 A 2M ，∠ MBA 2 即为 AB 1 与 BM 所成的角， a 2( ) 2 5a ，22a在△A 2BM 中， 2a ， BM A B 23a ( ) 213 222222 A 2M ， a ， A 2 BBMMBA 2, ．A 2 Ma2故选 A ．【点睛】 本题主要考查了异面直线及其所成的角和勾股定理的应用，计算比较复杂，要仔细的做．12．D解析： D 【解析】【分析】 根据三角形解的个数的判断条件得出各选项中对应的 项. 【详解】ABC 解的个数，于此可得出正确选1 27 2asin B 7ABC 无解；对于 A 选项， asin B b ，此时， ，2 2对于 B 选项， csin B b c ，此时， ABC 有两5 ， c sin B5 2120o ，则 对于 C 选项， A 为最大角，由于 a b ，此时， ABC 无解； .故选 D.A Q 60o，且 对于 D 选项， Q Cc b ，此时， ABC 有且只有一解【点睛】本题考查三角形解的个数的判断，解题时要熟悉三角形个数的判断条件，考查推理能力， 属于中等题 .二、填空题13．3【解析】【分析】【详解】如图区间长度是 6区间﹣ 24上随机地取一个数x若 x 满足 |x| 3解析： 3 【解析】 【分析】 【详解】≤的m 概率为若 m 对于 3概率大于若 m 小于 3概率小于所以 m=3故答案为 如图区间长度是 6，区间 [﹣ 2， 4] 上随机地取一个数 x ，若 x 满足 |x| ≤m 的概率为 ，若 m 对 于 3 概率大于 ，若 m 小于 3，概率小于 ，所以 m=3 ． 故答案为 3．14．【解析】【分析】【详解】设最大值为考点：解三角形与三角函数化简点 评：借助于正弦定理三角形内角和将边长用一内角表示转化为三角函数求最值 只需将三角函数化简为的形式 解析： 2 【解析】 【分析】 【详解】7ABBC sin3 3 2 2 32 3A Q 2AB 2sin,设2 3 sinAB 2 B C2sin 4sin 2 7 sinBC 2sin，最大值为 2 7考点：解三角形与三角函数化简点评：借助于正弦定理，三角形内角和将边长用一内角表示，转化为三角函数求最值，只 a2b 2需将三角函数化简为asin bcossin的形式15．【解析】【分析】将写成切化弦后利用两角和差余弦公式可将原式化为利 用二倍角公式可变为由可化简求得结果【详解】本题正确结果：【点睛】本题 考查利用三角恒等变换公式进行化简求值的问题涉及到两角和差余弦公式二解析： 1【解析】 【分析】o osin10 cos10 3 写成 tan60o ，切化弦后，利用两角和差余弦公式可将原式化为 将 ，利o ocos 60 cos 70o1 2 sin 20sin 20ocos70o可化简求得结果 用二倍角公式可变为 ，由 .oocos 60 cos 70【详解】o o o ocos 60 cos 70si n 60 sin 70ooo o oosin10 13tan70sin10 1 tan 60 tan70sin10oocos60 cos70oo cos 7060o o osin10 cos101 2 sin 201 2cos60osin101ooooooocos60 cos70cos60 cos70 cos60 cos70本题正确结果： 【点睛】1本题考查利用三角恒等变换公式进行化简求值的问题，涉及到两角和差余弦公式、二倍角 .公式的应用 16．【解析】【分析】连接可得出证明出四边形为平行四边形可得可得出异面 直线与所成角为或其补角分析的形状即可得出的大小即可得出答案【详解】连 接在正方体中所以四边形为平行四边形所以异面直线与所成的角为易知为等 解析： 60o【解析】 【分析】连接 EF // C D 1 ，证明出四边形 A 1B // C D 1 ，可得 CD 1 ，可得出 A 1 BCD 1 为平行四边形，可得 出异面直线 EF 与 A 1C 1 所成角为BA 1C 1 或其补角，分析 A 1BC 1 的形状，即可得出BA 1C 1 的大小，即可得出答案 【详解】.DE DD 1DF DC1 3BC 1 ，Q 连接 CD 1 、 A 1B 、 ， EF //CD 1 ，A 1D 1 // A D AD //BC A 1D 1 //B C 在正方体 ABCDA 1B 1C 1D 1 中， ， ， ， 所以，四边形 A 1 B// C D 1 ， BA 1C 1 . A 1 BCD 1 为平行四边形， 所以，异面直线 EF 与 A 1C 1 所成的角为 oA 1 BC 1 为等边三角形，BA 1C 160 易知 .60o . 故答案为： 【点睛】本题考查异面直线所成角的计算，一般利用平移直线法，选择合适的三角形求解，考查计 算能力，属于中等题 .17．20【解析】【分析】根据题意可知过（ 35）的最长弦为直径最短弦为过 （ 35）且垂直于该直径的弦分别求出两个量然后利用对角线垂直的四边形的面 x ﹣积等于对角线乘积的一半求出即可【详解】解：圆的标准方程为（解析： 20 【解析】【分析】 根据题意可知，过（6 3， 5）的最长弦为直径，最短弦为过（3， 5）且垂直于该直径的弦，分别求出两个量，然后利用对角线垂直的四边形的面积等于对角线乘积的一半求出即可． 【详解】解：圆的标准方程为（ x ﹣ 3） 2+（y ﹣ 4）2＝ 52， 由题意得最长的弦 |AC|＝ 2×5＝ 10， 根据勾股定理得最短的弦 |BD |＝ 225211 2，且 AC ⊥ BD ， 4 6 四边形 ABCD 的面积 S ＝ | 1210× 4 ．AC|?|BD|6 20 6 故答案为 20 ． 6 【点评】考查学生灵活运用垂径定理解决数学问题的能力，掌握对角线垂直的四边形的面积计算方 法为对角线乘积的一半．18．【解析】【分析】根据式子中角度的规律可知变形有由此可以求解【详 解】根据式子中角度的规律可知变形有所以故答案为：【点睛】本题主要考查 两角和的正切公式的应用以及归纳推理的应用属于中档题 解析： 【解析】 【分析】23245o45o,045o根据式子中角度的规律，可知，tan tantano1 ，变形有 1 tan 1 tan2 ，由此可以求解．tan 451 tan 【详解】ooo根据式子中角度的规律，可知45 045 ,045 ，tan tantano1 ，变形有 tan 1 tan 12 ．所以tan 451 tan 1 tan1 1 tan 442 ， 1 tan 2 1 tan 432 ，L otan 45tan 44 ， 1 tan 221 tan 232 ， 1 2 ，231 tan1 1 tan2 1 tan3 L 1 1 tan 452 ．故答案为： 【点睛】232 ．本题主要考查两角和的正切公式的应用以及归纳推理的应用，属于中档题．19．【解析】在正四棱锥中顶点 S 在底面上的投影为中心 O 即底面ABCD 在底面正方形 ABCD 中边长为 2 所以 OA=在直角三角形 SOA 中所以故答案为 4 2解析： 3【解析】在正四棱锥中，顶点 S 在底面上的投影为中心 O ，即 SO 底面 ABC D，在底面正方形 SOA 中，在直角三角形 ABCD 中，边长为 2，所以 OA=2 22 22SOSA OA2221 Vsh 313 4 2 3所以 2 224 2故答案为 320．【解析】【分析】【详解】因为函数的图象开口向上的抛物线所以要使对 于任意的都有成立解得所以实数的取值范围为【考点】二次函数的性质 2 2,0 解析：【解析】 【分析】 【详解】 2因为函数f ( x) xmx 1 的图象开口向上的抛物线，所以要使对于任意的x m, m 1 f ( x) 0 成立，都有 m 2 m 2 f ( m) f ( m 1 20 m(m 2 2，解得m 0 ，1)m 11) 1 02,0 2所以实数 m 的取值范围为 ． 【考点】 二次函数的性质．三、解答题21． （ 1） a n ＝－ 2n ＋ 5.（2） 4 【解析】（Ⅰ）设 {a n }的公差为 d ，由已知条件，，解出 a 1＝ 3， d ＝－ 2．所以 a n ＝ a 1＋(n －1)d ＝－ 2n ＋ 5．（Ⅱ） S n ＝ na 1＋ d ＝－ n 2＋4n ＝－ (n － 2)2＋ 4，所以 n ＝ 2 时， S n 取到最大值 4． , 22． （ 1） 0；（ 2） ．6 2【解析】 【分析】 g x f x f x（1）首先化简 解析式，然后求得左移个单位后函数的解析式，根据 f的奇偶性求得的值，进而求得的值. 2sin 2 x21 ，求得 f x（2）根据（ 1）中求得的 2x2 的取值范围，66762 f x 根据 的取值范围，求得, 上是单调函数，以及 的取值范围，根据 在2正弦型函数的单调性列不等式，解不等式求得【详解】 的取值范围 .3 2 12 （1） Q g x4sin x cos x sin x3 sin 2 x 1 cos 2 x2sin 2x1 ，6f x2sin 2 x2 1 ，6 又 fx 2为偶函数，则（ k Z k ），Q 0 ，．2662ff0 ．6, 7 6 Q x 2 x222 ,22（2）， ，6 6 23, 7 6 6 22 ,， ， Q 0，622 2 2762Q f x , 上是单调函数． 且 0在．6 2 2, 6 2【点睛】． 本小题主要考查三角恒等变换，考查根据三角函数的奇偶性求参数，考查三角函数图像变 换，考查三角函数单调区间有关问题的求解，考查运算求解能力，属于中档题 .3 523． （1） 29 人；（ 2） ． 【解析】 【分析】（1）根据频率分布直方图，良好即第二三两组，计算出第二三两组的频率即可算出人数； 13,14 ，17,18 两组的人数， m n 1 即两位同学来（2）结合频率分布直方图，计算出自不同的两组，利用古典概型求解概率即可 【详解】.[14,16) 50 0.20 50 0.38 29 （人）， （1）由直方图知，成绩在 所以该班成绩良好的人数为（2）由直方图知，成绩在 内的人数为： 29 人；[13,14) 50 0.06 3 人；的人数为 [17,18] 50 0.04 2 人；. 成绩在 的人数为 事件“m n 1”发生即这两位同学来自不同的两组，此题相当于从这五人中任取 2 人，求这两人来自不同组的概率1 1C 2 C 3 C56 10 35P其概率为 .2 3 5P( m n 1)【点睛】此题考查用样本的频率分布估计总体分布；利用频率直方图求相关数据；古典概型及其概 率的计算． nn 224． （ 1） a 1 2 ， a 24 （ 2）a n 2 ，b n2n （ 3） T nn 1 24【解析】 【分析】2 a n 2 ，分别令 （1）根据题意得到 S n2 ，得到 a 1 ， a 2 ；（ 2）当 n 1 ， n n 2a nx S n S n 时， 1 时，得到 a n 的通项，根据点 P b n , b n 在直线，再验证 n 1 1 y 2 上，得 b n ，得到 2 ，得到 b n 为等差数列，从而得到其通项；（b n b n 3）根据1 n 项和 c na n c n 的通项，然后利用错位相减法，得到前T n .【详解】 2a n 2S n S 1 解：（ 1）由 当 n 1 时，得 2a 1 2a 2S n2 ，即 2a 1 a 1 a 1 2 ，解得 a 12 ；当 n2 时，得 S 2 2 ，即 2a 2 a 2 2 ，解得 a 24 .2 a n 2 （2）由 ①得 2a nS n 2 n S n 2 ）②；（ 11 2a n 2a n S n 将两式相减得 1 ，1 即 2a n 2a n a n ，1 a n 2a n n2 所以 ，1 因为 a 1 a n a n2 0 ，所以 a n 0 ，12 n 2 所以，1a n 所以数列是首项为 2，公比为 2 的等比数列，n 1n 1n所以 a nb n a 1 22 22 .y x 2 上，数列 b 1 2 ，点 P b n , b n 在直线 中， 1 得 b n b n2 ，1b n 2 所以数列 是首项为 2，公差为 2 的等差数列， 2 12n .所以 b n n n 1（3） c n 所以 T na nb n2n 2 ，234nn 11 2 2423 252n 1 2n 2232n 1 2n 22T 1 2 3 n 1 n n上式减下式得234n 1n 2T n 22 1 22 2 2n 22n2 4 n 1 1 n 2n 2n 2n 22n 2n 2所以 T n 1 24 .【点睛】本题考查由 a n 档题 . 和 S n 的关系求数列通项，等差数列基本量计算，错位相减法求和，属于中 n 1 ；（ 2） 325． （ 1） a n 2n【解析】 试题分析：(1) 结合递推关系可证得 b n+1-b n 2，且 b 1＝ 2，即数列 { b n } 是首项为 2，公差为 2 的等差数 n 1 a n 列，据此可得数列的通项公式为 a n．2n 1n 1，求和有c n c n2 (2) 结合通项公式裂项有 2n 21 2 1 1n 2T n2 13 ．据此结合单调性讨论可得正整数m 的最小值为 3．n 1 试题解析：2 2 2 22a n 2a n 11 4a n（1）证明： b n+1-b n2 112a n 1 11 4a n 2a n 22a n 2 ．1 1又由 a 1＝ 1，得 b 1＝ 2，所以数列 { b n } 是首项为 2，公差为 2 的等差数列，所以 b n ＝ 2+( n- 22a n n 1 ．b n，得 a 1) ×2＝2n ，由 n12n4 n 1n 12 nc c 2（2）解： 所以 c n， n n 2n 2n 2 1 2 11 T n2 13 ．n 1 n 1 2m m 41T nn ∈N * 恒成立，只需 对于 m ≥3或 m ≤-4．又 依题意，要使 3 ，解得 c m c m 1m ＞ 0，所以 u u u v26． CGm ≥3，所以正整数 vm 的最小值为 3．1 3v ( a b ) 【解析】分析：直接利用共线向量的性质、向量加法与减法的三角形法则求解即可.u u u v DE u u u v DC u u u v CE uu u v 1 u u u v vb ，1 2v a 详解：由题意，如图 AB CB 2 u u u v BF u u u v BC u u u v CF u u u v AD 1 u u u v ABv1 2v ， a b 2，则 G 是 VBCD AC 交 于点 O ，则 O是连接 的重心，连接 的中点，BD BD BD ∴点 G 在 AC 上，u u u v 2 u u u vCO2 u u u v OC 1 u u u vAC v b 2 3 1 3v ∴ ， CG a 33 2 故答案为u u u v DE v u uu v v b 1 2 1 31 2v v ； a b ； BFa u u u v CGv b v a ∴ ． 点睛：向量的运算有两种方法，一是几何运算往往结合平面几何知识和三角函数知识解 答，运算法则是：（１）平行四边形法则（平行四边形的对角线分别是两向量的和与 差）；（２）三角形法则（两箭头间向量是差，箭头与箭尾间向量是和）；二是坐标运 算：建立坐标系转化为解析几何问题解答（求最值与范围问题，往往利用坐标运算比较简 单）．。

新高一数学下期末一模试题(带答案)一、选择题1．若，则（ ）A ．B ．C ．D ．2．已知ABC V 为等边三角形，2AB =，设P ，Q 满足AP AB λ=uu u r uu u r ，()()1AQ AC λλ=-∈R u u u r u u u r ，若32BQ CP ⋅=-uu u r uu r ，则λ=（ ）A ．12B ．122± C ．1102± D ．3222± 3．在ABC V 中，角A ，B ，C 所对的边为a ，b ，c ，且B 为锐角，若sin 5sin 2A cB b=，7sin B =，57ABC S =△，则b =（ ） A ．23B ．27C ．15D ．144．已知数列{}n a 的前n 项和22n S n n =+，那么它的通项公式是（ ）A ．21n a n =-B ．21n a n =+C ．41n a n =-D ．41n a n =+5．《九章算术》中，将底面是直角三角形的直三棱柱称为“堑堵”．某“堑堵”的三视图如图所示，则它的表面积为（ ）A ．2B ．422+C ．442+D ．642+6．《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有女子善织，日益功，疾，初日织五尺，今一月织九匹三丈（1匹=40尺，一丈=10尺），问日益几何？”其意思为：“有一女子擅长织布，每天比前一天更加用功，织布的速度也越来越快，从第二天起，每天比前一天多织相同量的布，第一天织5尺，一月织了九匹三丈，问每天增加多少尺布？”若一个月按30天算，则每天增加量为A ．12尺 B ．815尺 C ．1629尺 D ．1631尺 7．已知01a b <<<，则下列不等式不成立．．．的是 A ．11()()22ab>B ．ln ln a b >C ．11a b> D ．11ln ln a b >8．已知两个正数a ，b 满足321a b +=，则32a b+的最小值是( )A ．23B ．24C ．25D ．269．设函数()sin()cos()f x x x ωϕωϕ=+-+0,||2πωϕ⎛⎫><⎪⎝⎭的最小正周期为π，且f x f x -=（）（），则（ ）A ．()f x 在0,2π⎛⎫⎪⎝⎭上单调递增 B ．()f x 在,22ππ⎛⎫- ⎪⎝⎭上单调递减C ．()f x 在0,2π⎛⎫⎪⎝⎭上单调递减D ．()f x 在,22ππ⎛⎫- ⎪⎝⎭上单调递增10．1()xf x e x=-的零点所在的区间是（ ） A ．1(0,)2B ．1(,1)2C ．3(1,)2D ．3(,2)211．与直线40x y --=和圆22220x y x y ++-=都相切的半径最小的圆的方程是 A ．()()22112x y +++= B ．()()22114x y -++= C ．()()22112x y -++=D ．()()22114x y +++=12．在正三棱柱111ABC A B C -21，则1BC 与侧面1ACC A 所成角的大小为（ ）A ．30oB ．45oC ．60oD ．90o二、填空题13．已知数列{}n a 前n 项和为n S ，若22nn n S a =-，则n S =__________．14．已知函数()3sin(2)cos(2)(||)2f x x x πϕϕϕ=---<的图象关于y 轴对称,则()f x 在区[6π-,5]12π上的最大值为__. 15．已知a 0>，b 0>，且111a b +=，则b3a 2b a++的最小值等于______． 16．已知抛物线()220y px p =>的准线与圆()22316x y -+=相切，则p 的值为__________．17．函数sin 232y x x =的图象可由函数sin 232y x x =+的图象至少向右平移_______个长度单位得到。

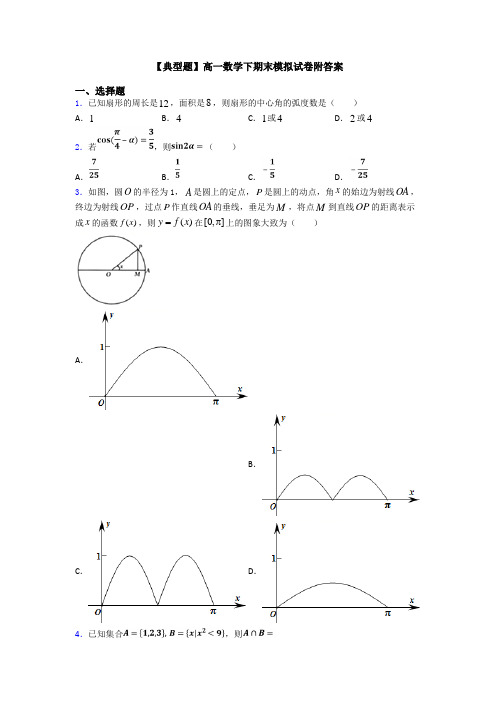
【典型题】高一数学下期末模拟试卷附答案一、选择题1．已知扇形的周长是12，面积是8，则扇形的中心角的弧度数是（ ） A ．1 B ．4 C ．1或4D ．2或42．若，则（ ）A ．B ．C ．D ．3．如图，圆O 的半径为1，A 是圆上的定点，P 是圆上的动点，角x 的始边为射线OA ，终边为射线OP ，过点P 作直线OA 的垂线，垂足为M ，将点M 到直线OP 的距离表示成x 的函数()f x ，则()y f x =在[0,]π上的图象大致为（ ）A ．B ．C ．D ．4．已知集合 ，则A ．B ．C ．D ．5．已知数列{}n a 的前n 项和22n S n n =+，那么它的通项公式是（ ）A ．21n a n =-B ．21n a n =+C ．41n a n =-D ．41n a n =+6．《九章算术》中，将底面是直角三角形的直三棱柱称为“堑堵”．某“堑堵”的三视图如图所示，则它的表面积为（ ）A ．2B ．422+ C ．442+ D ．642+ 7．若,l m 是两条不同的直线，m 垂直于平面α，则“l m ⊥”是“//l α”的（ ） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件8．已知0,0a b >>，并且111,,2a b 成等差数列，则4a b +的最小值为（ ） A ．2B ．4C ．5D ．99．如图，已知三棱柱111ABC A B C -的各条棱长都相等，且1CC ⊥底面ABC ，M 是侧棱1CC 的中点，则异面直线1AB 和BM 所成的角为( )A ．2πB ．C ．D ．3π 10．（2018年天津卷文）设变量x ，y 满足约束条件5,24,1,0,x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩ 则目标函数35z x y =+的最大值为 A ．6B ．19C ．21D ．4511．在空间四边形ABCD 的边AB ，BC ，CD ，DA 上分别取E ，F ，G ，H 四点，如EF 与HG 交于点M ，那么 ( ) A ．M 一定在直线AC 上 B ．M 一定在直线BD 上C ．M 可能在直线AC 上，也可能在直线BD 上 D ．M 既不在直线AC 上，也不在直线BD 上12．若函数()(),1231,1x a x f x a x x ⎧>⎪=⎨-+≤⎪⎩是R 上的减函数，则实数a 的取值范围是( )A ．2,13⎛⎫⎪⎝⎭B ．3,14⎡⎫⎪⎢⎣⎭C ．23,34⎛⎤⎥⎝⎦D ．2,3⎛⎫+∞⎪⎝⎭二、填空题13．已知两个正数,x y 满足4x y +=,则使不等式14m x y+≥恒成立的实数m 的范围是__________14．如图是抛物线形拱桥，当水面在l 时，拱顶离水面2米，水面宽4米，水位下降1米后，水面宽 米.15．函数()12x f x -的定义域是__________．16．已知f （x ）是定义在R 上的偶函数，且在区间（−∞，0）上单调递增.若实数a 满足f（2|a-1|）＞f （2-），则a 的取值范围是______.17．若圆x 2＋y 2＝4和圆x 2＋y 2＋4x －4y ＋4＝0关于直线l 对称，则直线l 的方程为____________．18．若()1,x ∈+∞，则131y x x =+-的最小值是_____． 19．在△ABC 中，85a b ==，，面积为12，则cos 2C =______．20．函数()sin f x x ω=（0>ω）的图像与其对称轴在y 轴右侧的交点从左到右依次记为1A ，2A ，3A ，⋅⋅⋅，n A ，⋅⋅⋅，在点列{}n A 中存在三个不同的点k A 、l A 、p A ，使得△k l p A A A 是等腰直角三角形，将满足上述条件的ω值从小到大组成的数记为n ω，则6ω=________. 三、解答题21．某高校在2012年的自主招生考试成绩中随机抽取100名中学生的笔试成绩，按成绩分组，得到的频率分布表如表所示．组号 分组 频数 频率第1组 [)160,165 5 0.050第2组 [)165,170 ① 0.350第3组 [)170,175 30 ②第4组 [)175,180 20 0.200 第5组[)180,185100.100（1）请先求出频率分布表中,①②位置的相应数据，再完成频率分布直方图； （2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试； （3）在（2）的前提下，学校决定在6名学生中随机抽取2名学生接受A 考官进行面试，求：第4组至少有一名学生被考官A 面试的概率．22．已知函数()()22f x sin x cos x 23sin x cos x x R =--∈（I ）求2f 3π⎛⎫⎪⎝⎭的值 （II ）求()f x 的最小正周期及单调递增区间. 23．投资商到一开发区投资72万元建起一座蔬菜加工厂，经营中，第一年支出12万元，以后每年支出增加4万元，从第一年起每年蔬菜销售收入50万元，设表示前n 年的纯利润总和（前年总收入-前年的总支出 -投资额72万元）（Ⅰ）该厂从第几年开始盈利？（Ⅱ）该厂第几年平均纯利润达到最大？并求出年平均纯利润的最大值. 24．已知x ，y ，()0,z ∈+∞，3x y z ++=．（1）求111x y z++的最小值 （2）证明：2223x y z ≤++．25．已知函数2()4f x x ax =-++，()|1||1|g x x x =++-． （1）当1a =时，求不等式()()f x g x ≥的解集；（2）若不等式()()f x g x ≥的解集包含[–1，1]，求a 的取值范围．26．在ABC △中，内角,,A B C 所对的边分别为,,a b c .已知sin 4sin a A b B =，2225()ac a b c =--.（I ）求cos A 的值； （II ）求sin(2)B A -的值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【解析】设扇形的半径为r ，弧长为 l ，则121282l r S lr +===，， ∴解得28r l ==， 或44r l ==，41lrα==或， 故选C ．2．D解析：D 【解析】试题分析：，且，故选D.【考点】三角恒等变换【名师点睛】对于三角函数的给值求值问题，关键是把待求角用已知角表示： （1）已知角为两个时，待求角一般表示为已知角的和或差．（2）已知角为一个时，待求角一般与已知角成“倍的关系”或“互余、互补”关系．3．B解析：B【解析】 【分析】计算函数()y f x =的表达式，对比图像得到答案. 【详解】 根据题意知：cos cos OM OP x x ==M 到直线OP 的距离为：sin cos sin OM x x x = 1()cos sin sin 22f x x x x ==对应图像为B 故答案选B 【点睛】本题考查了三角函数的应用，意在考查学生的应用能力.4．D解析：D 【解析】 试题分析：由得，所以，因为，所以，故选D.【考点】 一元二次不等式的解法，集合的运算【名师点睛】对于集合的交、并、补运算问题，应先把集合化简再计算，常常借助数轴或韦恩图处理.5．C解析：C 【解析】分类讨论：当1n =时，11213a S ==+=，当2n ≥时，221(2)2(1)141n n n a S S n n n n n -⎡⎤=-=+--+-=-⎣⎦， 且当1n =时：1414113n a -=⨯-== 据此可得，数列的通项公式为：41n a n =-. 本题选择C 选项.6．D解析：D 【解析】 【分析】根据题意和三视图知几何体是一个放倒的直三棱柱，由三视图求出几何元素的长度，由面积公式求出几何体的表面积． 【详解】根据题意和三视图知几何体是一个放倒的直三棱柱，底面是一个直角三角形，两条直角边,斜边是2，且侧棱与底面垂直，侧棱长是2，∴几何体的表面积12222262S =⨯+⨯⨯=+ 故选D ． 【点睛】本题考查三视图求几何体的表面积，由三视图正确复原几何体是解题的关键，考查空间想象能力．7．B解析：B 【解析】若l m ⊥，因为m 垂直于平面α，则//l α或l α⊂；若//l α，又m 垂直于平面α，则l m ⊥，所以“l m ⊥”是“//l α的必要不充分条件，故选B ． 考点：空间直线和平面、直线和直线的位置关系． 8．D解析：D 【解析】 ∵111,,2a b成等差数列， ()111141445529a b a a b a b a b a b b a b ⎛⎫∴+=∴+=++=+++⋅= ⎪⎝⎭，， 当且仅当a =2b 即33,2a b ==时“=“成立， 本题选择D 选项.点睛：在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误．9．A解析：A 【解析】 【分析】由题意设棱长为a ，补正三棱柱ABC-A 2B 2C 2，构造直角三角形A 2BM ，解直角三角形求出BM ，利用勾股定理求出A 2M ，从而求解． 【详解】设棱长为a ，补正三棱柱ABC-A 2B 2C 2（如图）．平移AB 1至A 2B ，连接A 2M ，∠MBA 2即为AB 1与BM 所成的角， 在△A 2BM 中，22252()22a A B a BM a a ==+=，，222313()22a A M a a =+=，222222,2A B BM A M MBA π∴+=∴∠=， ． 故选A ． 【点睛】本题主要考查了异面直线及其所成的角和勾股定理的应用，计算比较复杂，要仔细的做．10．C解析：C 【解析】分析：首先画出可行域，然后结合目标目标函数的几何意义确定函数取得最大值的点，最后求解最大值即可.详解：绘制不等式组表示的平面区域如图所示，结合目标函数的几何意义可知目标函数在点A 处取得最大值，联立直线方程：51x y x y +=⎧⎨-+=⎩，可得点A 的坐标为：()2,3A ，据此可知目标函数的最大值为：max 35325321z x y =+=⨯+⨯=.本题选择C 选项.点睛：求线性目标函数z ＝ax ＋by (ab ≠0)的最值，当b ＞0时，直线过可行域且在y 轴上截距最大时，z 值最大，在y 轴截距最小时，z 值最小；当b ＜0时，直线过可行域且在y 轴上截距最大时，z 值最小，在y 轴上截距最小时，z 值最大.11．A解析：A 【解析】如图，因为EF∩HG=M，所以M∈EF，M∈HG，又EF ⊂平面ABC ，HG ⊂平面ADC ， 故M∈平面ABC ，M∈平面ADC ， 所以M∈平面ABC∩平面ADC=AC. 选A. 点睛：证明点在线上常用方法先找出两个平面，然后确定点是这两个平面的公共点，再确定直线是这两个平面的交线．12．C解析：C 【解析】 【分析】由题意结合分段函数的解析式分类讨论即可求得实数a 的取值范围. 【详解】当1x >时，x a 为减函数，则01a <<，当1x ≤时，一次函数()231a x -+为减函数，则230a -<，解得：23a >， 且在1x =处，有：()12311a a -⨯+≥，解得：34a ≤， 综上可得，实数a 的取值范围是23,34⎛⎤ ⎥⎝⎦. 本题选择C 选项. 【点睛】对于分段函数的单调性，有两种基本的判断方法：一保证各段上同增(减)时，要注意上、下段间端点值间的大小关系；二是画出这个分段函数的图象，结合函数图象、性质进行直观的判断．二、填空题13．【解析】【分析】由题意将代入进行恒等变形和拆项后再利用基本不等式求出它的最小值根据不等式恒成立求出m 的范围【详解】由题意知两个正数xy满足则当时取等号；的最小值是不等式恒成立故答案为【点睛】本题考查 解析：94m ≤【解析】 【分析】由题意将4x y +=代入14x y+进行恒等变形和拆项后，再利用基本不等式求出它的最小值，根据不等式恒成立求出m 的范围． 【详解】由题意知两个正数x ，y 满足4x y +=， 则14559144444x y x y y x x y x y x y +++=+=++≥+=，当4y x x y=时取等号； 14x y ∴+的最小值是94， 不等式14m x y +≥恒成立，94m ∴≤．故答案为94m ≤． 【点睛】本题考查了利用基本不等式求最值和恒成立问题，利用条件进行整体代换和合理拆项再用基本不等式求最值，注意一正二定三相等的验证．14．2米【解析】【分析】【详解】如图建立直角坐标系设抛物线方程为将A （2-2）代入得m=-2∴代入B 得故水面宽为米故答案为米考点：抛物线的应用解析：26米 【解析】 【分析】 【详解】如图建立直角坐标系，设抛物线方程为2x my =， 将A （2，-2）代入2x my =， 得m=-2，∴22x y =-，代入B ()0,3x -得06x =故水面宽为266考点：抛物线的应用15．【解析】由得所以所以原函数定义域为故答案为 解析：(],0-∞【解析】由120x -≥，得21x ≤，所以0x ≤，所以原函数定义域为(],0-∞，故答案为(],0-∞.16．【解析】【分析】【详解】由题意在上单调递减又是偶函数则不等式可化为则解得解析：13(,)22【解析】 【分析】 【详解】由题意()f x 在(0,)+∞上单调递减，又()f x 是偶函数，则不等式1(2)(a f f ->可化为1(2)a f f ->，则12a -<112a -<，解得1322a <<． 17．x －y ＋2＝0【解析】【分析】设直线l 方程为y ＝kx+b 由题意可得圆心C1和C2关于直线l 对称利用得k 由C1和C2的中点在直线l 上可得b 从而得到直线方程【详解】由题意可得圆C1圆心为（00）圆C2的解析：x －y ＋2＝0 【解析】 【分析】设直线l 方程为y ＝kx +b ，由题意可得圆心C 1和C 2关于直线l 对称，利用121C C l k k ⨯=-得k,由C 1和C 2的中点在直线l 上可得b ，从而得到直线方程． 【详解】由题意可得圆C 1圆心为（0，0），圆C 2的圆心为（﹣2，2）， ∵圆C 1：x 2+y 2＝4和圆C 2：x 2+y 2+4x ﹣4y +4＝0关于直线l 对称， ∴点（0，0）与（﹣2，2）关于直线l 对称，设直线l 方程为y ＝kx +b ， ∴2020k ---＝﹣1且022+＝k •022-+b ， 解得k ＝1，b ＝2，故直线方程为x ﹣y ＝﹣2， 故答案为：x －y ＋2＝0． 【点睛】本题考查圆与圆关于直线的对称问题，可转为圆心与圆心关于直线对称，属基础题．18．【解析】【分析】由已知可知然后利用基本不等式即可求解【详解】解：（当且仅当取等号）故答案为【点睛】本题主要考查了利用基本不等式求最值解题的关键是配凑积为定值属于基础试题解析：3+【解析】 【分析】由已知可知()11y 3x 3x 13x 1x 1=+=-++--，然后利用基本不等式即可求解． 【详解】 解：x 1>，()11y 3x 3x 13x 1x 1∴=+=-++--33≥=，（当且仅当13x =+取等号）故答案为3． 【点睛】本题主要考查了利用基本不等式求最值，解题的关键是配凑积为定值，属于基础试题．19．【解析】【分析】利用面积公式即可求出sinC 使用二倍角公式求出cos2C 【详解】由题意在中面积为12则解得∴故答案为【点睛】本题考查了三角形的面积公式二倍角公式在解三角形中的应用其中解答中应用三角形 解析：725【解析】 【分析】利用面积公式即可求出sinC ．使用二倍角公式求出cos2C ． 【详解】由题意，在ABC ∆中，8a =，5b =，面积为12， 则120122S absinC sinC ===，解得35sinC =． ∴297212122525cos C sin C =-=-⨯=． 故答案为725． 【点睛】本题考查了三角形的面积公式，二倍角公式在解三角形中的应用，其中解答中应用三角形的面积公式和余弦的倍角公式，合理余运算是解答的关键，着重考查了运算与求解能力，属于基础题．20．【解析】【分析】由可求得的横坐标进而得到的坐标；由正弦函数周期特点可知只需分析以为顶点的三角形为等腰直角三角形即可由垂直关系可得平面向量数量积为零进而求得的通项公式代入即可得到结果【详解】由得：……解析：112π【解析】 【分析】 由2x k πωπ=+可求得n A 的横坐标，进而得到n A 的坐标；由正弦函数周期特点可知只需分析以1A ，2n A ，41n A -为顶点的三角形为等腰直角三角形即可，由垂直关系可得平面向量数量积为零，进而求得n ω的通项公式，代入6n =即可得到结果. 【详解】由2x k πωπ=+，k Z ∈得：()212k x πω+=，k Z ∈1,12A πω⎛⎫∴ ⎪⎝⎭，23,12A πω⎛⎫- ⎪⎝⎭，35,12A πω⎛⎫ ⎪⎝⎭，47,12A πω⎛⎫- ⎪⎝⎭，…… 若123A A A ∆为等腰直角三角形，则212232,2,240A A A A πππωωω⎛⎫⎛⎫⋅=-⋅=-= ⎪ ⎪⎝⎭⎝⎭解得：2πω=，即12πω=同理若147A A A ∆为等腰直角三角形，则14470A A A A ⋅= 232πω∴= 同理若1611A A A ∆为等腰直角三角形，则166110A A A A ⋅= 352πω∴= 以此类推，可得：()212n n πω-= 6112πω∴=故答案为：112π【点睛】本题考查正弦型函数图象与性质的综合应用问题，关键是能够根据正弦函数周期性的特点确定所分析成等腰直角三角形的三个顶点的位置，进而由垂直关系得到平面向量数量积为零，构造方程求得结果.三、解答题21．（1）①35人，②0.300，直方图见解析；（2）3人、2人、1人；（3）35. 【解析】 【分析】（1）由频率分布直方图能求出第2组的频数，第3组的频率，从而完成频率分布直方图． （2）根据第3,4,5组的频数计算频率，利用各层的比例，能求出第3,4,5组分别抽取进入第二轮面试的人数．（3）设第3组的3位同学为123,,A A A ，第4组的2位同学为12,B B ，第5组的1位同学为1C ，利用列举法能出所有基本事件及满足条件的基本事件的个数，利用古典概型求得概率． 【详解】（1）①由题可知，第2组的频数为0.3510035⨯=人， ②第3组的频率为300.300100=， 频率分布直方图如图所示，（2）因为第3,4,5组共有60名学生，所以利用分层抽样在60名学生中抽取6名学生进入第二轮面试，每组抽取的人数分别为： 第3组： 306360⨯=人， 第4组：人，第5组：106160⨯=人， 所以第3,4,5组分别抽取3人、2人、1人进入第二轮面试．（3）设第3组的3位同学为123,,A A A ，第4组的2位同学为12,B B ，第5组的1位同学为1C ，则从这六位同学中抽取两位同学有15种选法，分别为：12,A A （），13,A A （），11,A B （），12,A B （），11,A C （），23,A A （），21,A B （），22,A B （），21,A C （），31,A B （），32,A B （），31,A C （），12,B B （），11,B C （），21,B C （），其中第4组的2位同学12,B B 中至少有一位同学入选的有9种，分别为：11122122A B A B A B A B （，），（，），（，），（，），31321211A B A B B B B C （，），（，），（，），（，），21B C （，），∴第4组至少有一名学生被A 考官面试的概率为93155=． 【点睛】本题考查频率分直方图、分层抽样的应用，考查概率的求法，考查数据处理能力、运算求解能力，是基础题．22．（I ）2；（II ）()f x 的最小正周期是π，2+k +k k 63Z ππππ⎡⎤∈⎢⎥⎣⎦，. 【解析】 【分析】（Ⅰ）直接利用三角函数关系式的恒等变换，把函数的关系式变形成正弦型函数，进一步求出函数的值．（Ⅱ）直接利用函数的关系式，求出函数的周期和单调区间． 【详解】（Ⅰ）f （x ）＝sin 2x ﹣cos 2x 23-sin x cos x ， ＝﹣cos2x 3-sin2x ， ＝﹣226sin x π⎛⎫+ ⎪⎝⎭， 则f （23π）＝﹣2sin （436ππ+）＝2， （Ⅱ）因为()2sin(2)6f x x π=-+． 所以()f x 的最小正周期是π． 由正弦函数的性质得3222,262k x k k Z πππππ+≤+≤+∈， 解得2,63k x k k Z ππππ+≤≤+∈， 所以，()f x 的单调递增区间是2[,]63k k k ππ+π+π∈Z ，． 【点睛】本题主要考查了三角函数的化简，以及函数的性质，是高考中的常考知识点，属于基础题，强调基础的重要性；三角函数解答题中，涉及到周期，单调性，单调区间以及最值等考点时，都属于考查三角函数的性质，首先应把它化为三角函数的基本形式即，然后利用三角函数的性质求解．23．（I ）从第三年开始盈利；（II ）第6年，投资商年平均纯利润达到最大，年平均纯利润最大值16万元 【解析】 【分析】 【详解】(Ⅰ)依题意前年总收入- 前年的总支出- 投资额72万元,可得由得,解得由于,所以从第3年开始盈利.(Ⅱ)年平均利润当且仅当,即时等号成立即第6年, 投资商平均年平均纯利润最大,最大值为16万元 24．（1）3（2）见解析 【解析】 【分析】（1）根据基本不等式即可求出，（2）利用x 2+y 2+z 213=（x 2+y 2+z 2+x 2+y 2+y 2+z 2+x 2+z 2），再根据基本不等式即可证明 【详解】（1）因为330x y z xyz ++≥>，31110x y zxyz++≥>， 所以()1119x y z x y z ⎛⎫++++≥⎪⎝⎭,即1113x y z ++≥，当且仅当1x y z ===时等号成立，此时111x y z++取得最小值3． （2）()()()2222222222223x y z x y y z z x x y z ++++++++++=()22223x y z xy yz zx +++++≥()233x y z ++==．当且仅当1x y z ===时等号成立，【点睛】本题考查了基本不等式求最值和不等式的证明，属于中档题． 25．（1）117{|1}2x x -+-≤≤；（2）[1,1]-． 【解析】 【详解】试题分析：（1）分1x <-，11x -≤≤，1x >三种情况解不等式()()f x g x ≥；（2）()()f x g x ≥的解集包含[1,1]-，等价于当[1,1]x ∈-时()2f x ≥，所以(1)2f -≥且(1)2f ≥，从而可得11a -≤≤．试题解析：（1）当1a =时，不等式()()f x g x ≥等价于21140x x x x -+++--≤.①当1x <-时，①式化为2340x x --≤，无解；当11x -≤≤时，①式化为220x x --≤，从而11x -≤≤； 当1x >时，①式化为240x x +-≤，从而1x <≤. 所以()()f x g x ≥的解集为1{|1}2x x --≤≤. （2）当[]1,1x ∈-时，()2g x =.所以()()f x g x ≥的解集包含[]1,1-，等价于当[]1,1x ∈-时()2f x ≥.又()f x 在[]1,1-的最小值必为()1f -与()1f 之一，所以()12f -≥且()12f ≥，得11a -≤≤.所以a 的取值范围为[]1,1-.点睛:形如||||x a x b c -+-≥(或c ≤)型的不等式主要有两种解法：(1)分段讨论法：利用绝对值号内式子对应方程的根，将数轴分为(,]a -∞，(,]a b ，(,)b +∞ (此处设a b <)三个部分，将每部分去掉绝对值号并分别列出对应的不等式求解，然后取各个不等式解集的并集．(2)图像法：作出函数1||||y x a x b =-+-和2y c =的图像，结合图像求解． 26．（Ⅰ）（Ⅱ） 【解析】试题分析：利用正弦定理“角转边”得出边的关系2a b =，再根据余弦定理求出cos A ， 进而得到sin A ，由2a b =转化为sin 2sin A B =，求出sin B ，进而求出cos B ，从而求出2B 的三角函数值，利用两角差的正弦公式求出结果. 试题解析：（Ⅰ）解：由sin 4sin a A b B =，及sin sin a bA B=，得2a b =.由)222ac a b c=--，及余弦定理，得2225cos 25acbc aA bcac +-===-.（Ⅱ）解：由（Ⅰ），可得sin 5A =，代入sin 4sin a A b B =，得sin sin 45a A Bb ==. 由（Ⅰ）知，A为钝角，所以cos B ==.于是4sin22sin cos 5B B B ==，23cos212sin 5B B =-=，故()43sin 2sin2cos cos2sin 55B A B A B A ⎛-=-=⨯-= ⎝⎭ 考点：正弦定理、余弦定理、解三角形【名师点睛】利用正弦定理进行“边转角”寻求角的关系，利用“角转边”寻求边的关系，利用余弦定理借助三边关系求角，利用两角和差公式及二倍角公式求三角函数值. 利用正、余弦定理解三角形问题是高考高频考点，经常利用三角形内角和定理，三角形面积公式，结合正、余弦定理解题.。