黄浦新王牌 秋季周末同步提高补习班 方Y老师 高三数学
- 格式:doc
- 大小:573.00 KB
- 文档页数:11

第一单元整数与整除复习卷(1)一、判断(1)所有正整数一定有因数1和他本身。
………………………………………………()(2)一个数的倍数一定是它因数的倍数。
………………………………………………()(3)素数都是素因数。
……………………………………………………………………()(4)偶数的因数一定是偶数。
……………………………………………………………()(5)若两数的最小公倍数是它们的乘积,则他们两个互素。
…………………………()(6)除了2是素数外,其它能被2整除的数都是偶数;………………………………()二、填空1.最小的自然数、最小的素数、最小的奇数合数这三个数的和为_________________;2.下列数对①1.5和3;②9和7;③26和104;④30和10;⑤0.7和0.7;⑥a和3a中,第一个数能整除第二个数的有__________________;第一个数能除尽第二个数的有___________________;3.如果两个素数的和为91,他们的差_____________(填“是”或“不是”)素数;4.24的因数有___________个,素因数有___________个;5.在1、39、47、51、63、71、105、147、252中,素数有__________________________,合数有_______________________;6.快速写出最大公因数或最小公倍数:(1)(2,2015)=________;(2)(43,86)=________;(3)(24,25)=________;[2,2015]=________;[43,86]=________;[24,25]=________;(4)(30,45)=________;(5)(17,68)=________;(6)(51,30)=________;[30,45]=________;[17,68]=________;[51,30]=________;7.60和90的公因数为___________________________;8.一个数的最大因数与最小倍数之和是85的因数,则这个数为___________________;9.两个数互素,且他们的积是24,则他们的和是___________________;10.四个连续奇数的和为32,则他们中最小的奇数是_________________;11.百位为9,能被3整除的最小偶数是_________________;12.一个同时能被2、3、5整除的三位数,百位比十位数字大7,这个数是________________;13.一个合数的因数含有10以内所有的奇数,这个合数最小是_______________;14.若分解素因数后,a=3×5×11,b=2×5×m,且他们的最小公倍数为330,则它们的最大公因数是____________;三、解答15.求下列各组数的最大公因数和最小公倍数。



第一讲 集合的概念及表示方Y 老师内容概要一、集合的有关概念 1、集合的概念我们常常把一些对象放在一起考察,如: (1)2010年南非世界杯参赛队员的全体; (2)港澳台来上海为世博服务的志愿者的全体; (3)建平中学2014届高三毕业生的全体; (4)所有的锐角三角形。
我们把一些确定对象组成的整体叫做集合,简称集。
集合中的各个对象叫集合的元素。
我们常用大写字母A 、B 、C 、 等表示集合,小写字母a 、b 、c 、 等表示元素。
如果a 是集合A 的元素,记为A a ∈,否则记为A a ∉。
2、集合中集合元素的特性(1)确定性:集合的元素是确定的,我们可以判定任何一个对象是不是这个集合的元素,A a ∈与A a ∉二者必居其一。
(2)无顺序性:集合元素的摆放不管顺序。
如{}21,和{}12,表示同一集合。
(3)无重复性:集合中的元素不重复出现,其中的任何两个元素都不相同。
3、集合的分类我们把含有有限个元素的集合叫有限集,含有无限个元素的集合叫无限集。
不含任何元素的集合叫空集,空集用φ表示。
二、集合的表示方法(1)列举法:将集合的元素一一列举出来,放在大括号内。
如{}3,2;(2)描述法:形如(){}x f x |表示集合,其中x 是集合元素的一般形式,()x f 是x 满足的性质。
如{}2|>x x ;(3)图示法:在有些场合我们常用图像表示集合。
(4)符号法:如空集用φ表示。
常用数集的字母表示:实数集—R ,有理数集—Q ,整数集—Z ,自然数集—N ,正整数集*N ,+R 、-R 分别表示正实数集和负实数集等等。
题型示例例1.用适当方法表示下列集合(1)方程0652=+-x x 的解的集合;(2)第一象限内点的集合;(3)被3除余数为1的自然数的集合;(4)二次函数28x y -=的图像上,满足N x ∈且N y ∈的点的集合; (5)满足Z x∈-36且Z x ∈的实数x 的集合。

上海最好的秋季补习班黄浦新王牌姜HZ 老师数学归纳法数学归纳法是证明与自然数N 有关的命题的一种特殊方法,它主要用来研究与正整数有关的数学问题.这种方法由下面两步组成:证明当n =1时表达成立,证明如果当n =k 时成立,那么当n =k +1时同样成立(归纳假设、递推步骤).在完成了上面两个步骤后,可以推断这个命题对于n 从1开始的所有正整数都成立.一、数学归纳法的一般步骤以及添项问题【例1】用数学归纳法证明“2n >2n 2﹣2n +1对于n ≥n 0的正整数n 均成立”时,第一步证明中的起始值n 0应取( )A .1B .3C .6D .10【例2】设f (x )是定义在整数集上的函数,且f (x )满足:“当f (k )≥k 2成立时,总可以推出f (k +1)≥(k +1)2成立”.那么下列命题总成立的是( )A .若f (3)≥9成立,则当k ≥1时均有f (k )≥k 2成立B .若f (5)≥25成立,则当k ≤5时均有f (k )≥k 2成立C .若f (7)<49成立,则当k ≥8时均有f (k )<k 2成立D .若f (4)=25成立,则当k ≥4时均有f (k )≥k 2成立【例3】用数学归纳法证明不等式“)2(241321...2n 11n 1 n n +++++”时的过程中,由n =k 到n =k +1时,不等式的左边( )A .增加了一项)12(k 1+ B .增加了两项12k 1)12(k 1+++ C .增加了两项12k 1)12(k 1+++,又减少了一项1k 1+ 数学归纳法 知识梳理 例题解析D .增加了一项)12(k 1+,又减少了一项1k 1+ 【巩固训练】1.用数学归纳法证明真命题:“凸n 边形的内角和公式形式是)m (m *∈N n 、π时,(1)第一步n 的值应取____;(2)第一步m 的值应取___.2.已知n 为正偶数,用数学归纳法证明)21...4121(211...41-3121-1nn n n +++++=-+++时,若已假设n =k (k ≥2为偶数)时命题为真,则还需要用归纳假设再证( ) A .n =k +1时等式成立B .n =k +2时等式成立C .n =2k +2时等式成立D .n =2(k +2)时等式成立3. 数学归纳法证明:111111111......234212122n n n n n-+-++-=+++-++(*n N ∈)时,当n 从k 到1k +时等式左边增加的项为 ;等式右边增加的项为 .二、数学归纳法的应用【例4】用数学归纳法证明:x 2n -1﹣y 2n -1能被x ﹣y 整除.(n ∈N *)【例5】设i 为虚数单位,n 为正整数.试用数学归纳法证明(cos x +i sin x )n =cos nx +i sinn x .【例6】平面内有n 条直线,其中无任何两条平行,也无任何三条共点,求证:这n 条直线把平面分割成)(2n 212++n 块.【例7】是否存在常数a ,b ,c 使得等式)(12)1(n )1( (322)12222c bn an n n n +++=+∙++∙+∙对于一切正整数n 都成立?并证明你的结论.【巩固训练】1.已知f (n )=(2n +7)•3n +9,存在自然数m ,使得对任意n ∈N *,都能使m 整除f (n ),则最大的m 的值为( )A .30B .26C .36D .62.已知函数()0f x ≥,对任意实数,x y 满足()()()()()2f x y f x f y f x f y +=++,求证:()()2f nx n f x =(n N *∈).3.用数学归纳法证明:当x >﹣1,n ∈N +时,(1+x )n ≥1+nx .三、归纳-猜测-论证【例8】观察以下等式:211=,22343++=,2345675++++=,……,将上述等式推广到一般情形:对n N *∈,有等式: .【例9】是否存在自然数m ,使得()(27)39n f n n =+⋅+ 对于任意*n N ∈都能被m 整除,若存在,求出m ;若不存在,请说明理由.【例10】数列{a n } 的前n 项和S n =2n ﹣a n ,先计算数列的前4项,后猜想a n 并用数学归纳法证明之.【例11】已知数列{x n }满足;,11,21x 11*+∈+==N n x x nn ;(1)猜想数列{x 2n }的单调性,并证明你的结论; (Ⅱ)证明:11)52(61x -+≤-n n n x .【巩固训练】1.对任意的正整数n ,猜测:2n -1与(n +1)2的大小.写出你的结论.并用数学归纳法加以证明.2.2005200620062005与,哪个大.3.当n为正整数时,定义函数N(n)表示n的最大奇因数.如N(3)=3,N(10)=5,….记S(n)=N(1)+N(2)+N (3)+…+N(2n).则(1)S(4)=;(2)S(n)=.反思总结数学归纳法是高考中比较重要的方法,不会单独出题,只有在于数列和证明之类题型中才可能会用。
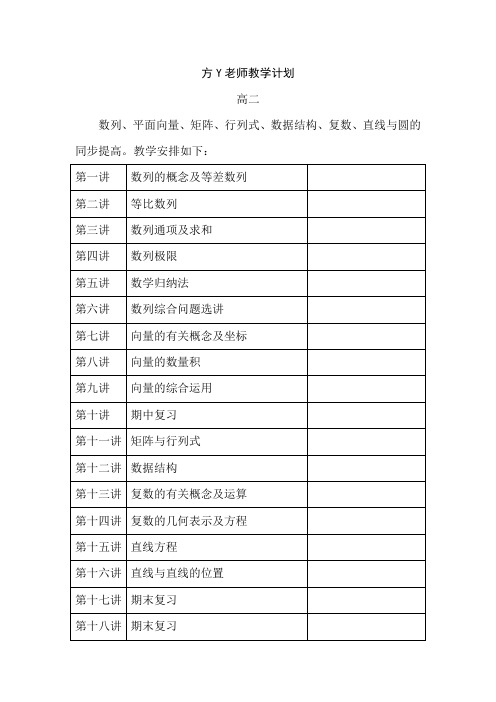
方Y老师教学计划高二数列、平面向量、矩阵、行列式、数据结构、复数、直线与圆的同步提高。
教学安排如下:第一讲数列的概念及等差数列第二讲等比数列第三讲数列通项及求和第四讲数列极限第五讲数学归纳法第六讲数列综合问题选讲第七讲向量的有关概念及坐标第八讲向量的数量积第九讲向量的综合运用第十讲期中复习第十一讲矩阵与行列式第十二讲数据结构第十三讲复数的有关概念及运算第十四讲复数的几何表示及方程第十五讲直线方程第十六讲直线与直线的位置第十七讲期末复习第十八讲期末复习数列的有关概念、等差数列及其性质知识梳理一、数列的有关概念1、数列的概念:按_________________________叫数列。
数列可以看作以正整数集(或它的子集)为定义域的函数)(n f a n =,当自变量按照从小到大的顺序依次取值时,所对应的一列函数值.一般地,若对任意*∈N n ,都有1+<n n a a ,则称{}n a 为单调递增数列;若对任意*∈N n ,都有1+>n n a a ,则称{}n a 为单调递减数列;若对任意*∈N n ,都有n T n a a =+(*∈N T ,T为常数),则称{}n a 为周期为T 的周期数列,特别地,周期为1的数列称为常数列。
2、通项公式的概念:如果数列{}n a 的第n 项n a 与n 之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.按照数列的函数性概念,数列的通项公式是定义在正整数集(或它的子集)上的函数的表达式,若用()n a n ,来表示,数列的图像是一列离散的点;数列不一定有通项公式,如果有通项公式,其表现形式也不一定唯一;数列可以用递推关系表示.3、数列前n 项和的概念:我们把n n a a a S +++= 21叫数列{}n a 的前n 项的和。
前n项的和与n a 之间的关系:⎩⎨⎧∈≥-==*-),2()1(11N n n S S n S a n n n .二、等差数列1、等差数列的概念:________________________________________________________, 即对一切*∈N n 都有d a a n n =-+1.2、等差数列的通项公式:d n a a n )1(1-+=. 变式:())(n m d m n a a m n ≤-+=;mn a a d mn --=.(1)等差中项的的概念:若b A a ,,成等差数列,则A 叫a 与b 的等差中项,2ba A +=.b a A +=2是b A a ,,成等差数列的_________条件.(2)等差数列的前n 项和公式:(1)___________=n S ;(2)._____________=n S(3)等差数列的性质(1)当公差0≠d 时,其通项公式()d a dn d n a a n -+=-+=111是项数n 的一次函数。
高三数学 春季班资料 第一讲专题一 函数综合应用一.深刻理解函数的概念与性质函数的定义、函数的三要素(定义域、值域、对应法则)、反函数的定义及与原函数的关系、函数的四大性质(单调性、奇偶性、周期性、最值)时函数有关概念的重要内容,只有对这些概念做到准确、深刻理解,才能正确、灵活地加以运用.例1、解答下列各题: (1)已知函数f (x )=⎩⎨⎧<<--≥)02( )(log )0( 22x x x x .则()________11=--x f .(2)(2004年上海高考题)若函数f(x)=a 2+-b x 在[0,+∞)上为增函数,则实数a 、b 的取值范围是 .(3)(2010年上海高考题题17).若0x 是方程131()2x x =的解,则0x 属于区间 ( ) (A)(23,1) (B)(12,23) (C)(13,12) (D)(0,13)(4)(江苏2012年高考题10)设()f x 是定义在R 上且周期为2的函数,在区间[11]-,上, 0111()201x x axf x bx x <+-⎧⎪=+⎨⎪+⎩≤≤≤,,,,其中a b ∈R ,.若1322f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,则3a b +的值为 .(5)(虹口18)数列{}n a 满足()()()⎩⎨⎧>≤--=-77336n a n n a a n n ,且{}n a 是递增数列,则实数a 的取值范围是( ). A 、⎪⎭⎫ ⎝⎛3,49 B 、⎪⎭⎫⎢⎣⎡3,49 C 、()3,1 D 、()3,2(6)(长宁2013年二模试题)函数()()1sin 122+++=x x x x f 的最大值和最小值分别为m M ,,则._____=+m M① 当且仅当0a =时,()f x 是偶函数;② 函数()f x 一定存在零点;③ 函数在区间(,]a -∞上单调递减;④ 当01a <<时,函数()f x 的最小值为2a a -.那么所有真命题的序号是 .(8)(09年山东高考题)定义在R 上的函数()f x 满足2log (1),0()(1)(2),0x x f x f x f x x -≤⎧=⎨--->⎩,则(2009)f 的值为【答】( )(A )-1 (B) 0 (C) 1 (D) 2(9)(2013年上海高考题)对区间I 上有定义的函数()x g ,记()(){}I x x g y y I g ∈==,|,已知定义域为[]3,0的函数()x f y =有反函数()x f y 1-=,且[)()[)2,11,01=-f ,(]()[)1,04,21=-f ,若()0=-x x f 有解0x ,则._______0=x例2.函数()()()⎥⎦⎤⎢⎣⎡+-+-=2111log 22x a x a x f . (1)若()x f 的定义域为R ,求a 的范围;(2)若值域为[)+∞-,2,求a 的值.例3.(2007年上海高考题)本题满分14分) 已知函数0()(2≠+=x x a x x f ,常数)a ∈R . (1)当2=a 时,解不等式12)1()(->--x x f x f ;(2)讨论函数)(x f 的奇偶性,并说明理由.例4.已知函数()()()01,lg >>>∈-=+b a R k kb a x f x x 的定义域为()+∞,0,是否存在这样的b a ,,使得()x f 在()+∞,1上取正值,且()4lg 3=f ?若存在求出b a ,的值,若不存在,请说明理由.二.数形结合解决数学问题是函数的显著特征之一借助于图像研究函数性质是研究函数的一种常用方法. 函数的几何特征与函数的数量特征紧密结合,有效地揭示了各类函数的定义域、值域、单调性、奇偶性、周期性等基本属性. 在解决数学问题时,利用图像的直观有助于理解题意,探寻解题思路,检验解题结果. 因此,既要从多角度观察图像,又要熟练掌握图像的平移变换、对称变换、翻折变换。
一、张Y老师个人简介
1)我的学历:国家“985”工程重点大学数学专业研究生毕业;
2)我的职场现状:上海市一线重点高中数学教师,9年高中数学教学经验,对上海高
考数学及自主招生数学考试的重难点了如指掌;
3)我的授课理念:深入浅出、重点突出、化难为易、衔接自如、顺理成章;
4)我的授课风格:思路清晰、板书严谨、幽默风趣、抑扬顿挫、激情澎湃;
5)我的职业习惯:乐于利用课余时间为学生进行一对一的答疑解难,善于从学生角度
解开学生对问题的疑惑;
6)我的教学业绩:所教学生多人已考入国内一流大学。
二、张Y老师暑期班新高三课程计划。
浦东高中补习浦东新王牌高考培训
2017年寒春数学教学计划龚Y老师
寒假:
高一:函数为主。
重点是对数函数、反函数、函数的周期性、函数的图像变换等。
内容讲全后,会讲一些难度较大的函数的综合题。
寒假中三角讲不讲取决于函数部分的进度(较大的可能是不讲)。
高二:上课的重点内容是排列组合、二项式定理、概率统计。
高三:继续第一轮复习,内容大致为解析几何、立体几何、排列组合、二项式等。
春季:
高一:三角,数列
高二:解析几何,立体几何,复数
高三:第一轮剩余知识点复习,第二轮专题复习,第三轮冲刺复习(难点突破、知识点整理、高考真题剖析、易错题型总结等)。
方Y老师教学计划高三上学期:配合学校第一轮复习,突出重点内容、重点方法;寒假班:高考疑难解析;春季班:专题讲解,第一阶段讲知识综合运用专题,第二阶段讲解题方法专题。
上学期教学安排如下:第一讲集合与命题第二讲不等式第三讲函数的概念与性质第四讲幂函数与指数函数第五讲对数函数与二次函数第六讲函数综合问题选讲第七讲三角函数(一)第八讲三角函数(二)第九讲三角函数(三)第十讲数列(一)第十一讲数列(二)第十二讲向量第十三讲解析几何—直线第十四讲解析几何—二次曲线第十五讲解析几何—直线与二次曲线第十六讲排列组合第十七讲概率统计第十八讲 综合问题选讲第一讲 集合与命题一、知识梳理1.集合(1)集合元素具有___________性、_________性和_____________性。
(2)集合的表示方法有________________________________________.(3)集合与元素之间的关系有_____________________;集合与集合之间的关系有_________________________________________________.(4)集合运算:_______________=B A ;_______________=B A ; ________________=A C U 。
2.命题(1)四种命题:若原命题是“若α,则β”,则逆命题是_____________________;否命题是_______________________;逆否命题是_________________________.其中等价的命题是______________________________________________.(2)充要条件:如果βα⇒,那么α叫β的________条件,β叫α的________条件;α是β的充要条件是指_______________________.(3)子集与推出关系:设{}{}βα具有性质,具有性质b b B a a A ||==,且B A ⊆,则α是β的________________条件,β是α的____________________条件.二、双基回眸1、下列五个关系式:{}φ=0;φ=0;φ∉0;{}φ⊇0;{}φ≠0. 其中正确的个数是_______. 2、已知集合M =⎭⎬⎫⎩⎨⎧=+149|22y x x ,N =⎭⎬⎫⎩⎨⎧=+123|y x y ,则=N M . 3、已知全集U =A B 中有m 个元素,()()B C A C U U 中有n 个元素.若B A 非空,则B A 的元素个数为 .4、已知+∈∈R y R x ,,集合}1,2,{},1,,1{2+--=---++=y y y B x x x x A .若B A =,则22y x +的值是5、集合{}R x y R y A x∈=∈=,2|,{}1,0,1-=B ,则下列结论正确的是________.①{}1,0=B A ; ②()+∞=,0B A ; ③()()0,∞-=B A C U ; ④(){}0,1-=B A C U . 6、下列4个命题:①命题“若Q 则P ”与命题“若P 则Q ”互为逆否命题;②“22bm am <”是“b a <”的必要不充分条件; ③“矩形的两条对角线相等”的否命题为假;④命题“φ{1,2}或4∉{1,2,4}”为真命题.其中真命题的序号是_____________.三、题型示例【方法指导】例1、(04年上海高考题,14分) 已知集合A ={x |(x -2)·(x -3a -1)<0},函数y =lg2a -xx -(a 2+1)的定义域为集合B .(1)若a =2,求集合B ;(2)若A =B ,求实数a 的值. 例2、已知函数()()112>+-+=a x x a x f x . ①证明:()x f 在()+∞-,1上是增函数; ②证明方程()0=x f 没有负数根.【疑难解析】例3、(1)已知集合A ={}2|3100x x x --≤,B ={}|121x m x m +≤≤-,且B A ⊆,则实数m 的取值范围是 .(2)设集合{}(){}222|40,,|2110,A x x x x R B x x a x a x R =+=∈=+++-=∈. 若A B B =,求实数a 的取值范围.【能力提升】以集合语言为背景的综合题例4、已知{}n a 是等差数列,d 为公差且不为0,1a 和d 均为实数,它的前n 项和记作n S ,设集合⎭⎬⎫⎩⎨⎧∈⎪⎭⎫ ⎝⎛=*N n n S a A n n |,,()⎭⎬⎫⎩⎨⎧∈=-=R y x y x y x B ,,14|,22.试问: 下列结论是否正确,如果正确,请给予证明;如果不正确,请举例说明:① 若以集合A 中的元素作为点的坐标,则这些点都在同一条直线上; ② A ∩B 至多有一个元素; ③ 当01≠a 时,一定有A ∩B ≠∅.例5、(湖北高考题)设集合{}6,5,4,3,2,1=M ,k S S S ,,,21 都是含两个元素的M 的子集,且满足:对任意的{}{}{}()k j i j i b a S b a S j j j i i i ,,2,1,,,,, ∈≠==,都有⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≠⎭⎬⎫⎩⎨⎧j j j j i i i i a b b a a b b a ,min ,min其中{}y x ,min 表示y x ,中的较小者),求k 的最大值.拓展练习一.填空题1、(04年上海高考)已知集合{})3(lo g 52+=a A ,,{}b a B ,=. 若{}2=B A ,则._________=B A 2、(2010重庆理数)设U={}0,1,2,3,A={}20x U x mx ∈+=,若{}2,1=A C U ,则实数=m ________.3、命题“若B A =,则B A ⊆”及其逆命题,否命题,逆否命题这四个命题中,真命题的的个数是_____________.4、(上海高考题).若全集U=R ,)(),(x g x f 均为二次函数,{}0)(|A <=x f x ,{}0)(|<=x g x B ,则不等式组⎩⎨⎧≥<0)(0)(x g x f 的解集用A 、B 表示为______________. 5、(湖北高考题)已知{|(1,0)(0,1),},{|(1,1)(1,1),}P a a m m R Q b b n n R ==+∈==+-∈是两个向量集合,则=Q P .6、 (上海市长宁区2008学年高三年级第一次质量调研)已知命题:(3)(1)0,p x x -+>命题22:210(0)q x x m m -+->>,若命题p 是命题q 的充分不必要条件,则实数m 的范围是____________.7、已知命题:p 存在R x ∈,022≤++a ax x .若命题p 是假命题,则实数a 的取值范围是 . 8、(09年北京高考)设A是整数集的一个非空子集,对于k A 1k A,1-k A,,那么且如果,∉+∉∈k 是A 的一个“孤立元”,给定S={}87654321,,,,,,,,则由S 的三个元素构成的所有集合中,不含“孤立元”的集合共有__________个.9、(10年上海高考)从集合{}d c b a U ,,,=的子集中选出四个不同的子集,需同时满足以下两个条件(1)U 、φ都要选出;(2)对选出的任意两个子集,必有A B B A ⊆⊆或,那么共有_________种不同的选法.二.选择题1、(上海高考)若集合{}{}R x x y y T R x y y S x ∈-==∈==,1|,,3|2,则T S 是( ) (A )S (B )T (C )φ (D )有限集2、设集合{}*∈+==N n n x x A ,1|2,{}Z m m m x x B ∈+-==,54|2,则A 与B 的关系为( )(A )A B ⊆ (B )B A = (C )B A ⊆ (D )以上都不对3、(2010年湖北)记实数n x x x ,,,21 中的最大数为{}n x x x ,,,max 21 ,最小数为{}n x x x ,,,min 21 ,已知ABC ∆三边的长为)(,,c b a c b a ≤≤,定义它的倾斜度为⎭⎬⎫⎩⎨⎧⋅⎭⎬⎫⎩⎨⎧=a c c b b a a c c b b a l ,,min ,,max ,则“1=l ”是“ABC ∆为等边三角形”的( )(A )充分不必要条件 (B )必要非充分条件 (C )充要条件 (D )既非充分又非必要条件4、(湖北高考题)有限集合S 中的元素的个数记为)(S card ,设集合A 、B 都为有限集合,给出下列命题:①φ=B A 的充要条件是)()()(card B card A card B A += ;②B A ⊆的必要条件是)()(B card A card ≤;③A 真包含于B 的充分条件是)()(B card A card ≤;④B A =的充要条件是)()(B card A card =.则以上命题正确的命题的个数是( ) (A )1 (B )2 (C )3 (D )4三. 解答题1、已知命题p :方程a 2x 2+ax -2=0在[-1,1]上有解;命题q :只有一个实数x 满足不等式x 2+2ax +2a ≤0.若命题“p 或q ”是假命题,求a 的取值范围.2、已知关于x 的不等式2(4)(4)0kx k x --->,其中k R ∈. (1)当k 变化时,试求不等式的解集A ; (2)对于不等式的解集A ,若满足AZ B =(其中Z 为整数集). 试探究集合B 能否为有限集?若能,求出使得集合B 中元素个数最少的k 的所有取值,并用列举法表示集合B ;若不能,请说明理由.3、已知集合(){}R x x f x x A ∈==,|,集合()(){}R x x f f x x B ∈==,|. (1)判断集合A 与B 之间的关系,并证明你的判断;(2)当()x f 是R 上的递增函数时,是否有B A =?证明你的判断.4、设n *∈N 为正整数,规定:()()()() x f f f x f n =(n 个f ),已知()()()()⎩⎨⎧≤<-≤≤-=2111012x x x x x f . (1)解不等式()x x f ≤;(2)设集合{}2,1,0=A ,对任意x ∈A ,证明:()x x f =3; (3)探求⎪⎭⎫ ⎝⎛982012f ;(4)若集合()[]{}2,0,|12∈==x x x f x B ,证明:B 中至少包含8个元素.参考答案一.填空题1.{}5,2,1;2.3-;3.2个;4.B C A R ;5、(){}1,1;6.()2,0;9、()1,0∈a ;9、;10、4个; 11.6个;12、36.二.选择题1、A ;2.C ;3.B 三、解答题1、()()1,00,1 -∈a .2、(1)()()⎪⎭⎫ ⎝⎛+=<⎪⎭⎫ ⎝⎛+∞+∞-=>∞-==4,40;,44,0;4,0k k A k k k A k A k 时时时 ; (2){}3,2,1,0,1,2,3---=B .3、(1)若φ=A ,则B A ⊆;若φ≠A ,设A x ∈0,则()00x f x =,所以()()()000x x f x f f ==,所以B x ∈0,B A ⊆∴.(2)结论:B A =,下证A B ⊆.若φ=B ,则A B ⊆成立;若φ≠B ,设任意的B x ∈0,则有()()00x x f f =,下证()00x x f =.用反证法:假设()00x x f >,由于()x f 是R 上的增函数,故()()()000x x f x f f >>,与已知矛盾!同理,()00x x f <也将导致矛盾!故()00x x f =,即A x ∈0,从而A B ⊆,结合(1)知B A =4、 (1)f (x )≤x 的解集为⎥⎦⎤⎢⎣⎡2,32.(2)∵f (0)=2,f (1)=0,f (2)=1,∴当x =0时,f 3(0)=f (f (f (0)))=f (f (2))=f (1)=0; 当x =1时,f 3(1)=f (f (f (1)))=f (f (0))=f (2)=1; 当x =2时,f 3(2)=f (f (f (2)))=f (f (1))=f (0)=2. 即对任意x ∈A ,恒有f 3(x )=x .(3)929812981=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛f ,91492989822=⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛f f f f ,95914983=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛f f ,9895984=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛f f , ,一般地⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+98984r r k f f ,所以98989842012=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛f f (4)3232=⎪⎭⎫ ⎝⎛f ,3232=⎪⎭⎫ ⎝⎛∴n f ,323212=⎪⎭⎫ ⎝⎛∴f ,∴23∈B .由(2)知,对x =0或1或2,恒有f 3(x )=x ,∴f 12(x )=f 4×3(x )=x ,则0,1,2∈B .由(3)知,对x =89,29,149,59,恒有f 12(x )=f 4×3(x )=x ,∴89,29,149,59∈B . 综上所述,23,0,1,2,89,29,149,59∈B .∴B 中至少含有8个元素.。