(浙江专用)2019届高考数学总复习 第2篇 第1讲 函数及其相关概念限时训练 理

知识点一函数的概念1．函数的定义、定义域、值域2．两个函数相等的条件（1）定义域相同．（2)对应关系完全一致．知识点二函数的表示及分段函数1．函数的表示方法函数的三种表示法:解析法、图象法、列表法．2．分段函数如果函数y＝f（x)，x∈A，根据自变量x在A中不同的取值范围，有着不同的对应关系，那么称这样的函数为分段函数．分段函数是一个函数，分段函数的定义域是各段定义域的并集,值域是各段值域的并集．知识点三函数的单调性与最大（小）值1．函数的单调性(1）增函数、减函数：设函数f（x）的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量的值x1，x2，当x1<x2时，都有f（x1)<f（x2)，那么就说函数f（x)在区间D上是增函数；当x1〈x2时，都有f（x1）〉f（x2)，那么就说函数f（x）在区间D上是减函数．(2）函数的单调性:若函数f(x）在区间D上是增（减)函数，则称函数f（x)在这一区间上具有(严格的)单调性，区间D叫做f(x）的单调区间．（3)单调性的常见结论:若函数f（x)，g（x)均为增(减）函数，则f(x)＋g(x）仍为增（减)函数;若函数f(x）为增（减）函数，则－f(x)为减（增)函数；若函数f（x)为增(减）函数，且f(x）〉0，则错误!为减(增)函数．2．函数的最大值、最小值最值类别最大值最小值条件设函数y＝f(x）的定义域为I,如果存在实数M满足(1)对于任意的x∈I，都有f(x)≤M；（2)存在x0∈I，使得f(x0）＝M（1)对于任意的x∈I，都有f(x)≥M；（2）存在x0∈I，使得f（x0）＝M结论M是函数y＝f（x)的最大值M是函数y＝f（x）的最小值性质:定义在闭区间上的单调函数，必有最大(小）值．知识点四函数的奇偶性1．函数奇偶性的概念偶函数奇函数条件对于函数f(x)的定义域内任意一个x，都有f(－x)＝f(x）f（－x）＝－f（x)结论函数f（x)是偶函数函数f（x)是奇函数2。

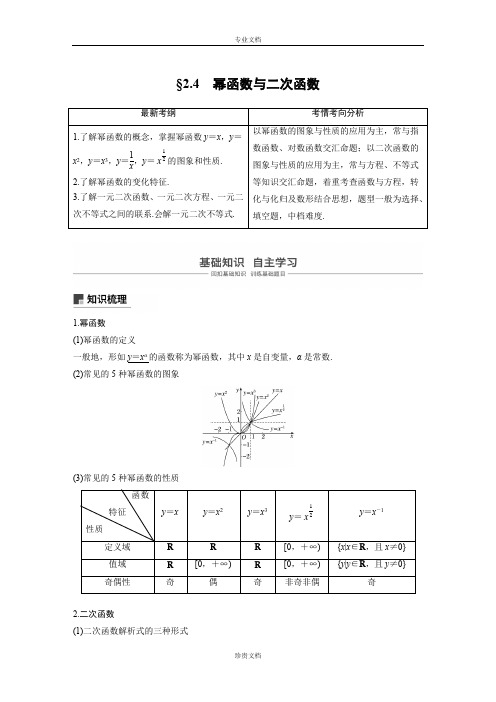
§2.4 幂函数与二次函数1.幂函数 (1)幂函数的定义一般地，形如y ＝x α的函数称为幂函数，其中x 是自变量，α是常数. (2)常见的5种幂函数的图象(3)常见的5种幂函数的性质2.二次函数(1)二次函数解析式的三种形式一般式：f (x )＝ax 2＋bx ＋c (a ≠0).顶点式：f (x )＝a (x －m )2＋n (a ≠0)，顶点坐标为(m ，n ). 零点式：f (x )＝a (x －x 1)(x －x 2)(a ≠0)，x 1，x 2为f (x )的零点. (2)二次函数的图象和性质知识拓展1.幂函数的图象和性质(1)幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限，至于是否出现在第二、三象限内，要看函数的奇偶性.(2)幂函数的图象过定点(1,1)，如果幂函数的图象与坐标轴相交，则交点一定是原点. (3)当α＞0时，y ＝x α在[0，＋∞)上为增函数； 当α＜0时，y ＝x α在(0，＋∞)上为减函数.2.若f (x )＝ax 2＋bx ＋c (a ≠0)，则当⎩⎪⎨⎪⎧ a >0，Δ<0时恒有f (x )>0，当⎩⎪⎨⎪⎧a <0，Δ<0时，恒有f (x )<0.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)二次函数y ＝ax 2＋bx ＋c ，x ∈[a ，b ]的最值一定是4ac －b 24a.( × )(2)二次函数y ＝ax 2＋bx ＋c ，x ∈R 不可能是偶函数.( × )(3)在y ＝ax 2＋bx ＋c (a ≠0)中，a 决定了图象的开口方向和在同一直角坐标系中的开口大小.( √ )(4)函数y ＝122x 是幂函数.( × )(5)如果幂函数的图象与坐标轴相交，则交点一定是原点.( √ ) (6)当n <0时，幂函数y ＝x n 是定义域上的减函数.( × ) 题组二 教材改编2.[P79T1]已知幂函数f (x )＝k ·x α的图象过点⎝⎛⎭⎫12，22，则k ＋α等于( )A.12B.1C.32 D.2 答案 C解析 由幂函数的定义，知⎩⎪⎨⎪⎧k ＝1，22＝k ·⎝⎛⎭⎫12α. ∴k ＝1，α＝12.∴k ＋α＝32.3.[P44A 组T9]已知函数f (x )＝x 2＋4ax 在区间(－∞，6)内单调递减，则a 的取值范围是( ) A.a ≥3 B.a ≤3 C.a ＜－3 D.a ≤－3答案 D解析 函数f (x )＝x 2＋4ax 的图象是开口向上的抛物线，其对称轴是x ＝－2a ，由函数在区间(－∞，6)内单调递减可知，区间(－∞，6)应在直线x ＝－2a 的左侧， ∴－2a ≥6，解得a ≤－3，故选D. 题组三 易错自纠 4.幂函数21023()a a f x x-+＝(a ∈Z )为偶函数，且f (x )在区间(0，＋∞)上是减函数，则a 等于( )A.3B.4C.5D.6 答案 C解析 因为a 2－10a ＋23＝(a －5)2－2， f (x )＝2(5)2a x--(a ∈Z )为偶函数，且在区间(0，＋∞)上是减函数， 所以(a －5)2－2<0，从而a ＝4,5,6，又(a －5)2－2为偶数，所以只能是a ＝5，故选C.5.已知函数y ＝ax 2＋bx ＋c ，如果a >b >c 且a ＋b ＋c ＝0，则它的图象可能是( )答案 D解析 由a ＋b ＋c ＝0和a >b >c 知，a >0，c <0， 由c <0，排除A ，B ，又a >0，排除C.6.已知函数y ＝x 2－2x ＋3在闭区间[0，m ]上有最大值3，最小值2，则m 的取值范围为________. 答案 [1,2]解析 如图，由图象可知m 的取值范围是[1,2].题型一 幂函数的图象和性质1.已知幂函数f (x )的图象经过点⎝⎛⎭⎫2，22，则f (4)等于( ) A.16 B.116 C.2 D.12答案 D2.若四个幂函数y ＝x a ，y ＝x b ，y ＝x c ，y ＝x d 在同一坐标系中的图象如图所示，则a ，b ，c ，d 的大小关系是( )A.d ＞c ＞b ＞aB.a ＞b ＞c ＞dC.d ＞c ＞a ＞bD.a ＞b ＞d ＞c答案 B解析 由幂函数的图象可知，在(0,1)上幂函数的指数越大，函数图象越接近x 轴，由题图知a ＞b ＞c ＞d ，故选B.3.若a <0，则0.5a ,5a ,5－a的大小关系是( )A.5－a <5a <0.5aB.5a <0.5a <5－aC.0.5a <5－a <5aD.5a <5－a <0.5a答案 B解析 5－a ＝⎝⎛⎭⎫15a ，因为a <0时，函数y ＝x a 在(0，＋∞)上单调递减，且15<0.5<5，所以5a <0.5a <5－a. 思维升华 (1)幂函数的形式是y ＝x α(α∈R )，其中只有一个参数α，因此只需一个条件即可确定其解析式.(2)在区间(0,1)上，幂函数中指数越大，函数图象越靠近x 轴(简记为“指大图低”)，在区间(1，＋∞)上，幂函数中指数越大，函数图象越远离x 轴.(3)在比较幂值的大小时，必须结合幂值的特点，选择适当的函数，借助其单调性进行比较，准确掌握各个幂函数的图象和性质是解题的关键. 题型二 求二次函数的解析式典例 (1)已知二次函数f (x )＝x 2－bx ＋c 满足f (0)＝3，对任意x ∈R ，都有f (1＋x )＝f (1－x )成立，则f (x )的解析式为________________. 答案 f (x )＝x 2－2x ＋3 解析 由f (0)＝3，得c ＝3， 又f (1＋x )＝f (1－x )，∴函数f (x )的图象关于直线x ＝1对称， ∴b2＝1，∴b ＝2， ∴f (x )＝x 2－2x ＋3.(2)已知二次函数f (x )与x 轴的两个交点坐标为(0,0)和(－2,0)且有最小值－1，则f (x )＝________. 答案 x 2＋2x解析 设函数的解析式为f (x )＝ax (x ＋2)， 所以f (x )＝ax 2＋2ax ，由4a ×0－4a 24a＝－1，得a ＝1，所以f (x )＝x 2＋2x . 思维升华 求二次函数解析式的方法跟踪训练 (1)已知二次函数f (x )＝ax 2＋bx ＋1(a ，b ∈R ，a ≠0)，x ∈R ，若函数f (x )的最小值为f (－1)＝0，则f (x )＝________. 答案 x 2＋2x ＋1解析 设函数f (x )的解析式为f (x )＝a (x ＋1)2＝ax 2＋2ax ＋a ， 由已知f (x )＝ax 2＋bx ＋1，∴a ＝1， 故f (x )＝x 2＋2x ＋1.(2)若函数f (x )＝(x ＋a )(bx ＋2a )(a ，b ∈R )是偶函数，且它的值域为(－∞，4]，则该函数的解析式f (x )＝________. 答案 －2x 2＋4解析 由f (x )是偶函数知f (x )图象关于y 轴对称，∴－a ＝－⎝⎛⎭⎫－2ab ，即b ＝－2，∴f (x )＝－2x 2＋2a 2，又f (x )的值域为(－∞，4]，∴2a 2＝4，故f (x )＝－2x 2＋4.题型三 二次函数的图象和性质命题点1 二次函数的图象典例 对数函数y ＝log a x (a ＞0且a ≠1)与二次函数y ＝(a －1)x 2－x 在同一坐标系内的图象可能是( )答案 A解析 当0＜a ＜1时，y ＝log a x 为减函数，y ＝(a －1)x 2－x 开口向下，其对称轴为x ＝12(a －1)＜0，排除C ，D ；当a ＞1时，y ＝log a x 为增函数，y ＝(a －1)x 2－x 开口向上，其对称轴为x ＝12(a －1)＞0，排除B.故选A.命题点2 二次函数的单调性典例 函数f (x )＝ax 2＋(a －3)x ＋1在区间[－1，＋∞)上是递减的，则实数a 的取值范围是( ) A.[－3,0)B.(－∞，－3]C.[－2,0]D.[－3,0]答案 D解析 当a ＝0时，f (x )＝－3x ＋1在[－1，＋∞)上递减，满足题意.当a ≠0时，f (x )的对称轴为x ＝3－a 2a，由f (x )在[－1，＋∞)上递减知⎩⎪⎨⎪⎧a <0，3－a 2a ≤－1，解得－3≤a ＜0.综上，a 的取值范围为[－3,0]. 引申探究若函数f (x )＝ax 2＋(a －3)x ＋1的单调减区间是[－1，＋∞)，则a ＝________. 答案 －3解析 由题意知f (x )必为二次函数且a <0， 又3－a2a＝－1，∴a ＝－3. 命题点3 二次函数的最值典例 已知函数f (x )＝ax 2＋2ax ＋1在区间[－1,2]上有最大值4，求实数a 的值. 解 f (x )＝a (x ＋1)2＋1－a .(1)当a ＝0时，函数f (x )在区间[－1,2]上的值为常数1，不符合题意，舍去；(2)当a ＞0时，函数f (x )在区间[－1,2]上是增函数，最大值为f (2)＝8a ＋1＝4，解得a ＝38；(3)当a ＜0时，函数f (x )在区间[－1,2]上是减函数，最大值为f (－1)＝1－a ＝4，解得a ＝－3. 综上可知，a 的值为38或－3.引申探究本题改为：求函数f (x )＝x 2＋2ax ＋1在区间[－1,2]上的最大值. 解 ∵f (x )＝(x ＋a )2＋1－a 2，∴f (x )的图象是开口向上的抛物线，对称轴为x ＝－a . (1)当－a ＜12即a ＞－12时，f (x )max ＝f (2)＝4a ＋5，(2)当－a ≥12即a ≤－12时，f (x )max ＝f (－1)＝2－2a ，综上，f (x )max＝⎩⎨⎧4a ＋5，a ＞－12，2－2a ，a ≤－12.命题点4 二次函数中的恒成立问题典例 (1)已知函数f (x )＝x 2－x ＋1，在区间[－1,1]上，不等式f (x )>2x ＋m 恒成立，则实数m 的取值范围是________________. 答案 (－∞，－1)解析 f (x )>2x ＋m 等价于x 2－x ＋1>2x ＋m ， 即x 2－3x ＋1－m >0，令g (x )＝x 2－3x ＋1－m ， 要使g (x )＝x 2－3x ＋1－m >0在[－1,1]上恒成立，只需使函数g (x )＝x 2－3x ＋1－m 在[－1,1]上的最小值大于0即可. ∵g (x )＝x 2－3x ＋1－m 在[－1,1]上单调递减， ∴g (x )min ＝g (1)＝－m －1.由－m －1>0，得m <－1. 因此实数m 的取值范围是(－∞，－1).(2)已知a 是实数，函数f (x )＝2ax 2＋2x －3在x ∈[－1,1]上恒小于零，则实数a 的取值范围为________. 答案 ⎝⎛⎭⎫－∞，12 解析 2ax 2＋2x －3<0在[－1,1]上恒成立. 当x ＝0时，－3<0，成立； 当x ≠0时，a <32⎝⎛⎭⎫1x －132－16， 因为1x ∈(－∞，－1]∪[1，＋∞)，当x ＝1时，右边取最小值12，所以a <12.综上，实数a 的取值范围是 ⎝⎛⎭⎫－∞，12. 思维升华 解决二次函数图象与性质问题时要注意(1)抛物线的开口，对称轴位置，定义区间三者相互制约，常见的题型中这三者有两定一不定，要注意分类讨论.(2)要注意数形结合思想的应用，尤其是给定区间上的二次函数最值问题，先“定性”(作草图)，再“定量”(看图求解)，事半功倍. (3)由不等式恒成立求参数取值范围的思路及关键①一般有两个解题思路：一是分离参数；二是不分离参数； ②两种思路都是将问题归结为求函数的最值或值域.跟踪训练 (1)设abc ＞0，二次函数f (x )＝ax 2＋bx ＋c 的图象可能是( )答案 D解析 由A ，C ，D 知，f (0)＝c ＜0，从而由abc ＞0，所以ab ＜0，所以对称轴x ＝－b2a ＞0，知A ，C 错误，D 满足要求；由B 知f (0)＝c ＞0， 所以ab ＞0，所以x ＝－b2a＜0，B 错误.(2)(2018·浙江名校协作体联考)y ＝2ax 2＋4x ＋a －1的值域为[0，＋∞)，则a 的取值范围是( ) A.(2，＋∞) B.(－∞，－1)∪(2，＋∞) C.[－1,2] D.[0,2]答案 D解析 由已知，t ＝2ax 2＋4x ＋a －1取遍[0，＋∞)上的所有实数，当a ＝0时，t ＝4x －1能取遍[0，＋∞)上的所有实数，只需定义域满足⎣⎡⎭⎫14，＋∞. 当a ≠0时，只需⎩⎪⎨⎪⎧2a >0，Δ＝16－8a (a －1)≥0，解得0＜a ≤2.综上，0≤a ≤2.(3)设函数f (x )＝ax 2－2x ＋2，对于满足1<x <4的一切x 值都有f (x )>0，则实数a 的取值范围为________. 答案 ⎝⎛⎭⎫12，＋∞解析 由题意得a ＞2x －2x 2对1＜x ＜4恒成立，又2x －2x 2＝－2⎝⎛⎭⎫1x －122＋12，14＜1x ＜1， ∴⎝⎛⎭⎫2x －2x 2max ＝12， ∴a ＞12.数形结合思想和分类讨论思想在二次函数中的应用典例 (14分)设函数f (x )＝x 2－2x ＋2，x ∈[t ，t ＋1]，t ∈R ，求函数f (x )的最小值.思想方法指导 研究二次函数的性质，可以结合图象进行；对于含参数的二次函数问题，要明确参数对图象的影响，进行分类讨论. 规范解答解 f (x )＝x 2－2x ＋2＝(x －1)2＋1，x ∈[t ，t ＋1]，t ∈R ，函数图象的对称轴为x ＝1. [2分] 当t ＋1＜1，即t ＜0时，函数图象如图(1)所示，函数f (x )在区间[t ，t ＋1]上为减函数， 所以最小值为f (t ＋1)＝t 2＋1；[6分]当t ≤1≤t ＋1，即0≤t ≤1时，函数图象如图(2)所示，在对称轴x ＝1处取得最小值，最小值为f (1)＝1；[9分]当t ＞1时，函数图象如图(3)所示，函数f (x )在区间[t ，t ＋1]上为增函数， 所以最小值为f (t )＝t 2－2t ＋2.[12分] 综上可知，f (x )min ＝⎩⎪⎨⎪⎧t 2＋1，t ＜0，1，0≤t ≤1，t 2－2t ＋2，t ＞1.[14分]1.若函数f (x )＝(m －1)x 2＋2mx ＋3为偶函数，则f (x )在区间(－5，－3)上( ) A.先减后增 B.先增后减 C.单调递减 D.单调递增答案 D2.若幂函数f (x )＝(m 2－4m ＋4)·268m m x -+在(0，＋∞)上为增函数，则m 的值为( )A.1或3B.1C.3D.2答案 B解析 由题意得m 2－4m ＋4＝1，m 2－6m ＋8＞0， 解得m ＝1.3.已知a ，b ，c ∈R ，函数f (x )＝ax 2＋bx ＋c ，若f (1)＝f (3)＞f (4)，则( ) A.a >0,4a ＋b ＝0 B.a ＜0,4a ＋b ＝0C.a ＞0,2a ＋b ＝0D.a ＜0,2a ＋b ＝0答案 B解析 由f (1)＝f (3)，得二次函数f (x )的对称轴为x ＝－b 2a＝2， 4a ＋b ＝0，又f (3)＞f (4)，故函数在(2，＋∞)上单调递减，故a ＜0.4.已知二次函数f (x )满足f (2＋x )＝f (2－x )，且f (x )在[0,2]上是增函数，若f (a )≥f (0)，则实数a 的取值范围是( )A.[0，＋∞)B.(－∞，0]C.[0,4]D.(－∞，0]∪[4，＋∞)答案 C解析 由题意可知函数f (x )的图象开口向下，对称轴为x ＝2(如图)，若f (a )≥f (0)，从图象观察可知0≤a ≤4.5.已知二次函数f (x )＝2ax 2－ax ＋1(a <0)，若x 1<x 2，x 1＋x 2＝0，则f (x 1)与f (x 2)的大小关系为( )A.f (x 1)＝f (x 2)B.f (x 1)>f (x 2)C.f (x 1)<f (x 2)D.与a 值有关答案 C解析 该二次函数图象的开口向下，对称轴为直线x ＝14， 又依题意，得x 1<0，x 2>0，又x 1＋x 2＝0，∴当x 1，x 2在对称轴的两侧时，14－x 1>x 2－14，故f (x 1)<f (x 2). 当x 1，x 2都在对称轴的左侧时，由单调性知f (x 1)<f (x 2).综上，f (x 1)<f (x 2).6.若关于x 的不等式x 2－4x －2－a ＞0在区间(1,4)内有解，则实数a 的取值范围是( )A.(－∞，－2)B.(－2，＋∞)C.(－6，＋∞)D.(－∞，－6)答案 A解析 不等式x 2－4x －2－a ＞0在区间(1,4)内有解等价于a ＜(x 2－4x －2)max ，令f (x )＝x 2－4x －2，x ∈(1,4)，所以f (x )＜f (4)＝－2，所以a ＜－2.7.已知P ＝322-，Q ＝⎝⎛⎭⎫253，R ＝⎝⎛⎭⎫123，则P ，Q ，R 的大小关系是________. 答案 P ＞R ＞Q解析 P ＝322-＝⎝⎛⎭⎫223，根据函数y ＝x 3是R 上的增函数，且22＞12＞25，得⎝⎛⎭⎫223＞⎝⎛⎭⎫123＞⎝⎛⎭⎫253， 即P ＞R ＞Q .8.(2018届台州路桥中学检测)已知幂函数y ＝f (x )的图象过点(2，2)，则f (9)＝________. 答案 3解析 设f (x )＝x α，因为它过点(2，2)，所以2＝2α，所以α＝12，所以f (x )＝12x ， 所以f (9)＝129＝3.9.对于任意实数x ，函数f (x )＝(5－a )x 2－6x ＋a ＋5恒为正值，则a 的取值范围是__________. 答案 (－4,4)解析 由题意可得⎩⎪⎨⎪⎧5－a >0，Δ＝36－4(5－a )(a ＋5)<0， 解得－4<a <4.10.(2008·浙江)已知t 为常数，函数y ＝|x 2－2x －t |在区间[0,3]上的最大值为2，则t ＝________. 答案 1解析 可分三种情况讨论，①⎩⎪⎨⎪⎧ 4＋4t ≤0，|9－6－t |＝2或②⎩⎪⎨⎪⎧ 4＋4t >0，t ≥1，|1－2－t |＝2或③⎩⎪⎨⎪⎧ 4＋4t >0，t <1，|9－6－t |＝2，解①得∅，解②得t ＝1，解③得∅，综上，t ＝1.11.已知y ＝f (x )是偶函数，当x >0时，f (x )＝(x －1)2，若当x ∈⎣⎡⎦⎤－2，－12时，n ≤f (x )≤m 恒成立，则m －n 的最小值为________.答案 1解析 ∵f (x )为偶函数，∴当x <0时，－x ＞0，f (x )＝f (－x )＝(－x －1)2＝(x ＋1)2，当x ∈⎣⎡⎦⎤－2，－12时，f (x )max ＝1，f (x )min ＝0， ∴0≤f (x )≤1，∴m ≥1，n ≤0，∴(m －n )min ＝1.12.已知函数f (x )＝x 2＋(2a －1)x －3.(1)当a ＝2，x ∈[－2,3]时，求函数f (x )的值域；(2)若函数f (x )在[－1,3]上的最大值为1，求实数a 的值.解 (1)当a ＝2时，f (x )＝x 2＋3x －3，x ∈[－2,3]，对称轴x ＝－32∈[－2,3]， ∴f (x )min ＝f ⎝⎛⎭⎫－32＝94－92－3＝－214， f (x )max ＝f (3)＝15，∴函数f (x )的值域为⎣⎡⎦⎤－214，15. (2)对称轴为x ＝－2a －12. ①当－2a －12≤1，即a ≥－12时， f (x )max ＝f (3)＝6a ＋3，∴6a ＋3＝1，即a ＝－13满足题意； ②当－2a －12＞1，即a ＜－12时， f (x )max ＝f (－1)＝－2a －1，∴－2a －1＝1，即a ＝－1满足题意.综上可知，a ＝－13或－1.13.(2017·浙江“超级全能生”联考)已知在(－∞，1]上递减的函数f (x )＝x 2－2tx ＋1，且对任意的x 1，x 2∈[0，t ＋1]，总有|f (x 1)－f (x 2)|≤2，则实数t 的取值范围为( )A.[－2，2]B.[1，2]C.[2,3]D.[1,2]答案 B 解析 由于函数f (x )＝x 2－2tx ＋1的图象的对称轴为x ＝t ，函数f (x )＝x 2－2tx ＋1在区间(－∞，1]上递减，∴t ≥1.∴当x ∈[0，t ＋1]时，f (x )max ＝f (0)＝1，f (x )min ＝f (t )＝t 2－2t 2＋1＝－t 2＋1，要使对任意的x 1，x 2∈[0，t ＋1]，都有|f (x 1)－f (x 2)|≤2，只需1－(－t 2＋1)≤2，解得－2≤t ≤ 2.又t ≥1，∴1≤t ≤ 2.故选B.14.当x ∈(1,2)时，不等式x 2＋mx ＋4<0恒成立，则m 的取值范围是________.答案 (－∞，－5]解析 方法一 ∵不等式x 2＋mx ＋4<0对x ∈(1,2)恒成立，∴mx <－x 2－4对x ∈(1,2)恒成立，即m <－⎝⎛⎭⎫x ＋4x 对x ∈(1,2)恒成立， 令y ＝x ＋4x ，则函数y ＝x ＋4x在x ∈(1,2)上是减函数.∴4<y <5，∴－5<－⎝⎛⎭⎫x ＋4x <－4，∴m ≤－5. 方法二 设f (x )＝x 2＋mx ＋4，当x ∈(1,2)时，由f (x )<0恒成立，得⎩⎪⎨⎪⎧ f (1)≤0，f (2)≤0， 解得⎩⎪⎨⎪⎧m ≤－5，m ≤－4，即m ≤－5.15.若函数f (x )＝x 2－a |x －1|在[0，＋∞)上单调递增，则实数a 的取值范围是________. 答案 [0,2]解析 f (x )＝⎩⎪⎨⎪⎧x 2－ax ＋a ，x ∈[1，＋∞)，x 2＋ax －a ，x ∈(－∞，1)， 当x ∈[1，＋∞)时，f (x )＝x 2－ax ＋a ＝⎝⎛⎭⎫x －a 22＋a －a 24， 当x ∈(－∞，1)时，f (x )＝x 2＋ax －a ＝⎝⎛⎭⎫x ＋a 22－a －a 24. ①当a 2>1，即a >2时，f (x )在⎣⎡⎭⎫1，a 2上单调递减，在⎝⎛⎭⎫a 2，＋∞上单调递增，不合题意；②当0≤a 2≤1，即0≤a ≤2时，符合题意； ③当a 2<0，即a <0时，不符合题意. 综上，a 的取值范围是[0,2].16.设函数f (x )＝x 2＋px ＋q (p ，q ∈R ).(1)若p ＝2，当x ∈[－4，－2]时，f (x )≥0恒成立，求q 的取值范围；(2)若不等式|f (x )|>2在区间[1,5]上无解，试求所有的实数对(p ，q ). 解 (1)当p ＝2时，f (x )＝x 2＋2x ＋q ≥0恒成立，只需f (x )min ≥0.因为f (x )＝x 2＋2x ＋q 在[－4，－2]上单调递减，所以f (x )min ＝f (－2)＝q ≥0.即q 的取值范围为[0，＋∞).(2)要使|f (x )|>2在区间[1,5]上无解，必须满足⎩⎪⎨⎪⎧ －2≤f (1)≤2，－2≤f (5)≤2， 所以⎩⎪⎨⎪⎧－2≤p ＋q ＋1≤2，－2≤5p ＋q ＋25≤2， 所以－3≤p ＋q ≤1，即－1≤－p －q ≤3，又－27≤5p ＋q ≤－23，两式相加可以得到－7≤p ≤－5.因为f (x )的对称轴为x ＝－p 2， 所以－p 2∈⎣⎡⎦⎤52，72，则f (x )的对称轴在区间[1,5]内，要使|f (x )|>2在区间[1,5]上无解， 还要满足f ⎝⎛⎭⎫－p 2≥－2， 即4q －p 24≥－2，可以得到q ≥p 24－2. 解不等式组⎩⎪⎨⎪⎧ －3≤p ＋q ≤1，－27≤5p ＋q ≤－23，q ≥p 24－2，可得p ＝－6，代入不等式组，得q ＝7.所以满足题意的实数对(p ，q )只有一对(－6,7).。

浙江省2019届高考数学总复习专题02 函数优质考卷分项解析一、选择题1. 设函数f(x) = (x^2 3x + 2)/(x 1)，则f(x)的定义域为（）A. x ≠ 1B. x ∈ RC. x > 1D. x < 12. 下列函数中，既是奇函数又是减函数的是（）A. y = x^3B. y = x^3C. y = x^2D. y = x^23. 已知函数f(x) = |x 2|，则f(3)的值等于（）A. 1B. 1C. 2D. 24. 设函数f(x) = (1/2)^x，则f(x)的反函数为（）A. y = 2^xB. y = (1/2)^xC. y = log2(x)D. y = log(1/2)(x)5. 若函数f(x) = 2x + 3在区间[1, 1]上的值域为[1, 5]，则函数g(x) = f(x) 2的值域为（）A. [3, 1]B. [1, 3]C. [1, 3]D. [1, 1]二、填空题6. 已知函数f(x) = x^2 2x，则f(x)的零点为______。

7. 设函数f(x) = (1/2)^x，若f(a) = 4，则a的值为______。

8. 若函数f(x) = |x 1| + |x + 1|的最小值为2，则x的取值范围为______。

9. 已知函数f(x) = x^3 3x，则f(x)的极小值点为______。

10. 设函数f(x) = e^x，若f(a) = 1，则a的值为______。

三、解答题11. 设函数f(x) = (x 1)/(x + 2)，求f(x)的定义域、值域和单调性。

12. 已知函数f(x) = ax^2 + bx + c（a ≠ 0），讨论f(x)的图像与x轴交点的个数。

13. 设函数f(x) = x^3 3x，求f(x)的极值。

14. 已知函数f(x) = (1/2)^x，求f(x)的反函数，并讨论其单调性。

15. 设函数f(x) = |x 1|，求f(x)在区间[0, 2]上的最大值和最小值。

第1讲函数的图象与性质[考情考向分析] 1.高考对函数的三要素，函数的表示方法等内容的考查以基础知识为主，难度中等偏下.2.对图象的考查主要有两个方面：一是识图，二是用图，即利用函数的图象，采用数形结合的思想解决问题.3.对函数性质的考查，主要是将单调性、奇偶性、周期性等综合在一起考查，既有具体函数也有抽象函数．常以选择题、填空题的形式出现，且常与新定义问题相结合，难度较大．热点一函数的性质及应用1．单调性：单调性是函数在其定义域上的局部性质．利用定义证明函数的单调性时，规范步骤为取值、作差、判断符号、下结论．复合函数的单调性遵循“同增异减”的原则．2．奇偶性(1)奇函数在关于原点对称的区间上的单调性相同，偶函数在关于原点对称的区间上的单调性相反．(2)在公共定义域内：①两个奇函数的和函数是奇函数，两个奇函数的积函数是偶函数；②两个偶函数的和函数、积函数都是偶函数；③一个奇函数、一个偶函数的积函数是奇函数．(3)若f(x)是奇函数且在x＝0处有定义，则f(0)＝0.(4)若f(x)是偶函数，则f(x)＝f(－x)＝f(|x|)．(5)图象的对称性质：一个函数是奇函数的充要条件是它的图象关于原点对称；一个函数是偶函数的充要条件是它的图象关于y轴对称．3．周期性定义：周期性是函数在定义域上的整体性质．若函数在其定义域上满足f(a＋x)＝f(x)(a≠0)，则其一个周期T＝|a|.常见结论：(1)若f(x＋a)＝－f(x)，则函数f(x)的最小正周期为2|a|，a≠0.(2)若f (x ＋a )＝1f (x )，则函数f (x )的最小正周期为2|a |，a ≠0. (3)若f (a ＋x )＝f (b －x )，则函数f (x )的图象关于直线x ＝a ＋b2对称．例1 (1)设函数f (x )＝cos ⎝ ⎛⎭⎪⎫π2－πx ＋(x ＋e )2x ＋e的最大值为M ，最小值为N ，则(M ＋N －1)2 018的值为( ) A ．1 B ．2 C ．22 018D ．32 018答案 A解析 由已知x ∈R ，f (x )＝cos ⎝ ⎛⎭⎪⎫π2－πx ＋(x ＋e )2x 2＋e 2＝sin πx ＋x 2＋e 2＋2e x x 2＋e 2＝sin πx ＋2e x x 2＋e 2＋1，令g (x )＝sin πx ＋2e xx 2＋e 2，易知g (x )为奇函数，由于奇函数在对称区间上的最大值与最小值的和为0，M ＋N ＝f (x )max ＋f (x )min ＝g (x )max ＋1＋g (x )min ＋1＝2，(M ＋N －1)2 018＝1，故选A.(2)已知定义在R 上的函数f (x )满足：函数y ＝f (x －1)的图象关于点(1,0)对称，且x ≥0时恒有f (x ＋2)＝f (x )，当x ∈[0,1]时，f (x )＝e x－1，则f (－2 017)＋f (2 018)＝________. 答案 1－e解析 因为函数y ＝f (x －1)的图象关于点(1,0)对称，所以y ＝f (x )的图象关于原点对称， 又定义域为R ，所以函数y ＝f (x )是奇函数， 因为当x ≥0时恒有f (x ＋2)＝f (x )，所以f (－2 017)＋f (2 018)＝－f (2 017)＋f (0) ＝－f (1)＋f (0)＝－(e 1－1)＋(e 0－1)＝1－e.思维升华 (1)可以根据函数的奇偶性和周期性，将所求函数值转化为给出解析式的范围内的函数值．(2)利用函数的单调性解不等式的关键是化成f (x 1)<f (x 2)的形式． 跟踪演练1 (1)(2018·浙江省“五校联考”)已知函数f (x )＝⎩⎪⎨⎪⎧|(x －a )2－1|＋a ，x ≥0，|x －a |＋2a －1，x <0的最小值为2a －1，则实数a 的取值范围是( )A ．a ＝1B ．0<a ≤1C．a<0或a＝1 D．a<0或a≥1答案 C解析在平面直角坐标系内画出函数f(x)的图象(图略)，由图易得当a≥0时，函数f(x)在[0，＋∞)上的最小值为a，在(－∞，0)上单调递减，当x→0(x<0)时，f(x)→3a－1，要使函数f(x)的最小值为2a－1，则有a＝2a－1≤3a－1，解得a＝1；当－1≤a<0时，函数f(x)在[0，＋∞)上的最小值为a，在(－∞，0)上的最小值为2a－1，要使函数f(x)的最小值为2a－1，则有2a－1≤a，解得a≤1，所以－1≤a<0；当a<－1时，函数f(x)在[0，＋∞)上的最小值为a2＋a－1，在(－∞，0)上的最小值为2a－1，要使函数f(x)的最小值为2a－1，则有2a－1≤a2＋a－1，解得a≤0或a≥1，所以a<－1.综上所述，实数a的取值范围为a<0或a＝1，故选C.(2)(2018·全国Ⅱ)已知f(x)是定义域为(－∞，＋∞)的奇函数，满足f(1－x)＝f(1＋x)．若f(1)＝2，则f(1)＋f(2)＋f(3)＋…＋f(50)等于( )A．－50 B．0 C．2 D．50答案 C解析∵f(x)是奇函数，∴f(－x)＝－f(x)，∴f(1－x)＝－f(x－1)．∵f(1－x)＝f(1＋x)，∴－f(x－1)＝f(x＋1)，∴f(x＋2)＝－f(x)，∴f(x＋4)＝－f(x＋2)＝－[－f(x)]＝f(x)，∴函数f(x)是周期为4的周期函数．由f(x)为奇函数且定义域为R得f(0)＝0，又∵f(1－x)＝f(1＋x)，∴f(x)的图象关于直线x＝1对称，∴f(2)＝f(0)＝0，∴f(－2)＝0.又f(1)＝2，∴f(－1)＝－2，∴f(1)＋f(2)＋f(3)＋f(4)＝f(1)＋f(2)＋f(－1)＋f(0)＝2＋0－2＋0＝0，∴f(1)＋f(2)＋f(3)＋f(4)＋…＋f(49)＋f(50)＝0×12＋f(49)＋f(50)＝f(1)＋f(2)＝2＋0＝2.故选C.热点二函数图象及应用1．作函数图象有两种基本方法：一是描点法；二是图象变换法，其中图象变换有平移变换、伸缩变换、对称变换．2．利用函数图象可以判断函数的单调性、奇偶性，作图时要准确画出图象的特点． 例2 (1)(2018·全国Ⅱ)函数f (x )＝e x－e－xx2的图象大致为( )答案 B解析 ∵y ＝e x －e －x 是奇函数，y ＝x 2是偶函数， ∴f (x )＝e x－e －xx是奇函数，图象关于原点对称，排除A. 当x ＝1时，f (1)＝e －e －11＝e －1e >0，排除D.又e>2，∴1e <12，∴e－1e >32，排除C.故选B.(2)函数f (x )＝e x＋a e －x与g (x )＝x 2＋ax 在同一坐标系内的图象不可能是( )答案 C解析 因为g (x )＝x 2＋ax 的图象过原点，所以图象中过原点的抛物线是函数g (x )的图象，在选项C 中，上面的图象是函数f (x )的图象，下面的是函数g (x )的图象，所以－a2>0，所以a <0，因为f ′(x )＝e x －a e －x ，所以f ′(x )>0在R 上恒成立，所以函数f (x )在定义域内单调递增，不是选项C 中的图象，故选C.思维升华 (1)根据函数的解析式判断函数的图象，要从定义域、值域、单调性、奇偶性等方面入手，结合给出的函数图象进行全面分析，有时也可结合特殊的函数值进行辅助推断，这是判断函数图象问题的基本方法．(2)判断复杂函数的图象，常借助导数这一工具，先对原函数进行求导，再利用导数判断函数的单调性、极值或最值，从而对选项进行筛选．要注意函数求导之后，导函数发生了变化，故导函数和原函数定义域会有所不同，我们必须在原函数的定义域内研究函数的极值和最值． 跟踪演练2 (1)函数f (x )＝sin ⎝ ⎛⎭⎪⎫lnx －1x ＋1的图象大致为( )答案 B解析 由于x ≠0，故排除A. f (－x )＝sin ⎝ ⎛⎭⎪⎫ln －x －1－x ＋1＝－f (x )， 又函数f (x )的定义域为(－∞，－1)∪(1，＋∞)， 所以函数为奇函数，图象关于原点对称，排除C.f (2)＝sin ⎝ ⎛⎭⎪⎫ln 13＝－sin(ln 3)<0，排除D ，故选B.(2)函数f (x )＝|x |＋a x(a ∈R )的图象不可能是( )答案 C解析 对于A ，当a ＝0时，f (x )＝|x |，且x ≠0，故可能；对于B ，当x >0且a >0时，f (x )＝x ＋a x≥2a ，当且仅当x ＝a 时等号成立，当x <0且a >0时，f (x )＝－x ＋ax在(－∞，0)上为减函数，故可能；对于D ，当x <0且a <0时，f (x )＝－x ＋a x≥2－x ·a x＝2－a ，当且仅当x ＝－－a 时等号成立，当x >0且a <0时，f (x )＝x ＋a x在(0，＋∞)上为增函数，故可能，且C 不可能．故选C. 热点三 基本初等函数的图象和性质1．指数函数y ＝a x(a >0，a ≠1)与对数函数y ＝log a x (a >0，a ≠1)的图象和性质，分0<a <1，a >1两种情况，着重关注两函数图象中的公共性质．2．幂函数y ＝x α的图象和性质，主要掌握α＝1,2,3，12，－1五种情况．例3 (1)(2017·全国Ⅰ)设x ，y ，z 为正数，且2x＝3y＝5z，则( ) A ．2x <3y <5z B ．5z <2x <3y C ．3y <5z <2x D ．3y <2x <5z答案 D解析 令t ＝2x＝3y＝5z， ∵x ，y ，z 为正数，∴t >1.则x ＝log 2t ＝lg t lg 2，同理，y ＝lg t lg 3，z ＝lg tlg 5.∴2x －3y ＝2lg t lg 2－3lg t lg 3＝lg t (2lg 3－3lg 2)lg 2×lg 3＝lg t (lg 9－lg 8)lg 2×lg 3>0，∴2x >3y .又∵2x －5z ＝2lg t lg 2－5lg t lg 5＝lg t (2lg 5－5lg 2)lg 2×lg 5＝lg t (lg 25－lg 32)lg 2×lg 5<0，∴2x <5z ，∴3y <2x <5z .故选D.(2)已知函数f (x )＝⎩⎪⎨⎪⎧a x，x <0，(a －3)x ＋4a ，x ≥0满足对任意x 1≠x 2，都有f (x 1)－f (x 2)x 1－x 2<0成立，则a的取值范围是( )A.⎝ ⎛⎦⎥⎤0，14 B ．(1,2]C ．(1,3) D.⎝ ⎛⎭⎪⎫12，1 答案 A 解析 由f (x 1)－f (x 2)x 1－x 2<0，得f (x )是减函数，即⎩⎪⎨⎪⎧0<a <1，a －3<0，4a ≤1，得a ∈⎝ ⎛⎦⎥⎤0，14，故选A.思维升华 (1)指数函数、对数函数、幂函数是高考的必考内容之一，重点考查图象、性质及其应用，同时考查分类讨论、等价转化等数学思想方法及运算能力． (2)比较代数式大小问题，往往利用函数图象或者函数的单调性． 跟踪演练3 (1)(2018·浙江省台州中学模拟)设a ＝131log ,2b ＝132log ,3c ＝log 343，则a ，b ，c 的大小关系是( )A ．a <b <cB ．c <b <aC ．b <a <cD ．b <c <a答案 B 解析 131log 2＝log 32，132log 3＝log 332，因为y ＝log 3x 在(0，＋∞)上单调递增，所以log 32>log 332>log 343，即131log 2>132log 3>log 343，则a >b >c ，故选B.(2)对任意实数a ，b 定义运算“Δ”：a Δb ＝⎩⎪⎨⎪⎧a ，a －b ≤2，b ，a －b >2，设f (x )＝3x ＋1Δ(1－x )，若函数f (x )与函数g (x )＝x 2－6x 在区间(m ，m ＋1)上均为减函数，则实数m 的取值范围是( ) A ．[－1,2] B ．(0,3] C ．[0,2] D ．[1,3]答案 C解析 由题意得f (x )＝⎩⎪⎨⎪⎧－x ＋1，x >0，3x ＋1，x ≤0，∴函数f (x )在(0，＋∞)上单调递减，函数g (x )＝(x －3)2－9在(－∞，3]上单调递减，若函数f (x )与g (x )在区间(m ，m ＋1)上均为减函数，则⎩⎪⎨⎪⎧m ≥0，m ＋1≤3，得0≤m ≤2，故选C.真题体验1．(2018·全国Ⅲ改编)函数y ＝－x 4＋x 2＋2的图象大致为________．(填序号)答案 ④解析 方法一 f ′(x )＝－4x 3＋2x ，则f ′(x )>0的解集为⎝ ⎛⎭⎪⎫－∞，－22∪⎝ ⎛⎭⎪⎫0，22，此时f (x )单调递增；f ′(x )<0的解集为⎝ ⎛⎭⎪⎫－22，0∪⎝ ⎛⎭⎪⎫22，＋∞，此时f (x )单调递减． 方法二 当x ＝1时，y ＝2，所以排除①②.当x ＝0时，y ＝2，而当x ＝12时，y ＝－116＋14＋2＝2316>2， 所以排除③.2．(2017·天津改编)已知奇函数f (x )在R 上是增函数，g (x )＝xf (x )．若a ＝g (－log 25.1)，b ＝g (20.8)，c ＝g (3)，则a ，b ，c 的大小关系为________．答案 b <a <c解析 依题意a ＝g (－log 25.1) ＝(－log 25.1)·f (－log 25.1) ＝log 25.1f (log 25.1)＝g (log 25.1)． 因为f (x )在R 上是增函数，可设0<x 1<x 2， 则0<f (x 1)<f (x 2)．从而x 1f (x 1)<x 2f (x 2)，即g (x 1)<g (x 2)． 所以g (x )在(0，＋∞)上亦为增函数． 又log 25.1>0,20.8>0,3>0， 且log 25.1<log 28＝3,20.8<21<3， 而20.8<21＝log 24<log 25.1， 所以3>log 25.1>20.8>0，所以c >a >b .3．(2017·山东改编)设f (x )＝⎩⎨⎧x ，0<x <1，2(x －1)，x ≥1，若f (a )＝f (a ＋1)，则 f ⎝ ⎛⎭⎪⎫1a ＝________. 答案 6解析 若0<a <1，由f (a )＝f (a ＋1)， 得a ＝2(a ＋1－1)， ∴a ＝14，∴f⎝ ⎛⎭⎪⎫1a ＝f (4)＝2×(4－1)＝6. 若a ≥1，由f (a )＝f (a ＋1)， 得2(a －1)＝2(a ＋1－1)，无解．综上，f ⎝ ⎛⎭⎪⎫1a ＝6. 4．(2017·全国Ⅱ)已知函数f (x )是定义在R 上的奇函数，当x ∈(－∞，0)时，f (x )＝2x 3＋x 2，则f (2)＝________. 答案 12解析 方法一 令x >0，则－x <0. ∴f (－x )＝－2x 3＋x 2.∵函数f (x )是定义在R 上的奇函数， ∴f (－x )＝－f (x )．∴f (x )＝2x 3－x 2(x >0)． ∴f (2)＝2×23－22＝12. 方法二 f (2)＝－f (－2) ＝－[2×(－2)3＋(－2)2]＝12. 押题预测1．在同一直角坐标系中，函数f (x )＝x a(x ≥0)，g (x )＝log a x 的图象可能是( )押题依据 指数、对数、幂函数的图象识别问题是高考命题的热点，旨在考查其基本性质的灵活运用，题目难度一般不大，位于试卷比较靠前的位置． 答案 D解析 方法一 分a >1,0<a <1两种情形讨论．当a >1时，y ＝x a与y ＝log a x 均为增函数，但y ＝x a递增较快，排除C ；当0<a <1时，y ＝x a为增函数，y ＝log a x 为减函数，排除A.由于y ＝x a递增较慢，故选D. 方法二 幂函数f (x )＝x a的图象不过(0,1)点，排除A ；B 项中由对数函数g (x )＝log a x 的图象知0<a <1，而此时幂函数f (x )＝x a的图象应是增长越来越慢的变化趋势，故B 错，D 正确；C 项中由对数函数g (x )＝log a x 的图象知a >1，而此时幂函数g (x )＝x a的图象应是增长越来越快的变化趋势，故C 错．2．设函数y ＝f (x )(x ∈R )为偶函数，且∀x ∈R ，满足f ⎝ ⎛⎭⎪⎫x －32＝f ⎝ ⎛⎭⎪⎫x ＋12，当x ∈[2,3]时，f (x )＝x ，则当x ∈[－2,0]时，f (x )等于( ) A ．|x ＋4| B ．|2－x | C ．2＋|x ＋1|D ．3－|x ＋1|押题依据 利用函数的周期性、奇偶性求函数值是高考的传统题型，考查学生思维的灵活性． 答案 D解析 由f ⎝ ⎛⎭⎪⎫x －32＝f⎝ ⎛⎭⎪⎫x ＋12， 可得f (x ＋2)＝f (x )，则当x ∈[－2，－1]时，x ＋4∈[2,3]，f (x )＝f (x ＋4)＝x ＋4＝x ＋1＋3；当x ∈[－1,0]时，－x ∈[0,1]，2－x ∈[2,3]，f (x )＝f (－x )＝f (2－x )＝2－x ＝3－x －1，故选D.3．已知函数f (x )＝1ln (x ＋1)－x，则y ＝f (x )的图象大致为( )押题依据 图象的识别和变换是高考的热点，此类问题既考查了基础知识，又考查了学生的灵活变换能力． 答案 B解析 方法一 由题意得⎩⎪⎨⎪⎧x ＋1>0，x ≠0，∴f (x )的定义域为{x |x >－1且x ≠0}． 令g (x )＝ln(x ＋1)－x ，则g ′(x )＝1x ＋1－1＝－xx ＋1， 当－1<x <0时，g ′(x )>0；当x >0时，g ′(x )<0.∴f (x )在区间(－1,0)上为减函数，在区间(0，＋∞)上为增函数，对照各选项，只有B 符合．方法二 取特殊值，用排除法求解，f (2)＝1ln 3－2<0，排除A.f ⎝ ⎛⎭⎪⎫－12＝1ln 12＋12＝1ln e 2<0， 排除C ，D ，故选B.4．已知函数h (x )(x ≠0)为偶函数，且当x >0时，h (x )＝⎩⎪⎨⎪⎧－x 24，0<x ≤4，4－2x ，x >4，若h (t )>h (2)，则实数t 的取值范围为________．押题依据 分段函数是高考的必考内容，利用函数的单调性求解参数的范围，是一类重要题型，是高考考查的热点．本题恰当地应用了函数的单调性，同时考查了函数的奇偶性的性质． 答案 (－2,0)∪(0,2)解析 因为当x >0时，h (x )＝⎩⎪⎨⎪⎧－x 24，0<x ≤4，4－2x ，x >4.所以函数h (x )在(0，＋∞)上单调递减，因为函数h (x )(x ≠0)为偶函数，且h (t )>h (2)， 所以h (|t |)>h (2)，所以0<|t |<2，所以⎩⎪⎨⎪⎧t ≠0，|t |<2，即⎩⎪⎨⎪⎧t ≠0，－2<t <2，解得－2<t <0或0<t <2.综上，所求实数t 的取值范围为(－2,0)∪(0,2)．A 组 专题通关1．(2018·浙江省重点中学联考)已知函数f (x )＝x 2－4x ＋1的定义域为[1，t ]，在该定义域内函数的最大值与最小值之和为－5，则实数t 的取值范围是( ) A ．(1,3] B ．[2,3] C ．(1,2]D ．(2,3)解析 若t ≤2，则函数的最大值为f (1)＝－2，函数的最小值为f (t )＝t 2－4t ＋1，由题意得t 2－4t －1＝－5，解得t ＝2；若t >2，因为定义域为[1，t ]，所以函数的最小值为f (2)＝－3，函数的最大值为max[f (1)，f (t )]＝max{－2，t 2－4t ＋1}＝－2.结合函数图象(图略)，得t 2－4t ＋1≤－2，解得1≤t ≤3，所以2<t ≤3.综上所述，2≤t ≤3，故选B.2．已知函数f (x )＝a －2x a ＋2x是奇函数，则f (a )的值等于( )A ．－13B ．3C ．－13或3D.13或3 答案 C解析 函数f (x )为奇函数，则f (－x )＝－f (x )，即a －2－x a ＋2－x ＝－a －2x a ＋2x 在定义域内恒成立， 整理可得a ·2x －1a ·2x ＋1＝－a ＋2x a ＋2x，即a 2＝1恒成立，∴a ＝±1， 当a ＝1时，函数f (x )的解析式为 f (x )＝1－2x 1＋2x ，f ()a ＝f ()1＝1－211＋21＝－13，当a ＝－1时，函数f (x )的解析式为f (x )＝－1－2x －1＋2x ，f ()a ＝f ()－1＝－1－2－1－1＋2－1＝3.综上可得f ()a 的值为－13或3.3．(2018·浙江省名校协作体联考)已知函数f (x )＝ax 3＋x 2＋x ＋b ，下列图象一定不能表示f (x )的图象的是( )解析 由题意得f ′(x )＝3ax 2＋2x ＋1，对于选项D ，可知a <0，Δ＝4－12a ≤0，此时a 无解，所以D 不正确，故选D.4．已知函数f (x )＝1－2x1＋2x ，实数a ，b 满足不等式f (2a ＋b )＋f (4－3b )>0，则下列不等式恒成立的是( ) A ．b －a <2 B ．a ＋2b >2 C ．b －a >2 D ．a ＋2b <2答案 C解析 由题意得f (－x )＝1－2－x 1＋2－x ＝2x －12x＋1＝－1－2x2x ＋1＝－f (x )，故函数f (x )为奇函数． 又f (x )＝－2x－11＋2x ＝－(2x＋1)－21＋2x ＝－1＋21＋2x ，故函数f (x )在R 上单调递减． ∵f (2a ＋b )＋f (4－3b )>0， ∴f (2a ＋b )>－f (4－3b )＝f (3b －4)， ∴2a ＋b <3b －4，∴b －a >2.故选C.5．已知f (x )是定义在(－∞，＋∞)上的偶函数，且在(－∞，0]上单调递增，若a ＝15log 3,f ⎛⎫ ⎪⎝⎭b ＝f (log 35)，c ＝f (0.20.5)，则a ，b ，c 的大小关系为( )A ．a <b <cB ．c <a <bC ．b <a <cD ．c <b <a答案 C解析 ∵f (x )是定义在(－∞，＋∞)上的偶函数，∴a ＝15log 3f ⎛⎫⎪⎝⎭＝f ()－log 53＝f ()log 53，∵12＝log 55<log 53<1,1＝log 33<log 35， 0<0.20.5＝55<12， ∴0.20.5<log 53<log 35，∵f (x )在(－∞，0]上是增函数，f (x )是定义在R 上的偶函数，∴f (x )在[0，＋∞)上为减函数， 则f ()0.20.5>f ()log 53>f ()log 35，即b <a <c ，故选C.6．若函数f (x )＝⎩⎪⎨⎪⎧2x＋1，x ≥1，－x 2＋ax ＋1，x <1在R 上是增函数，则a 的取值范围为( )A ．[2,3]B ．[2，＋∞)C ．[1,3]D ．[1，＋∞)答案 A解析 由题意得⎩⎪⎨⎪⎧a 2≥1，－1＋a ＋1≤2＋1，∴a ∈[2,3]，故选A.7．已知函数f (x )＝ln(ax 2＋bx ＋c )的部分图象如图所示，则a －b ＋c 等于()A ．－1B ．1C ．－5D ．5答案 D解析 由题图知，直线x ＝2，x ＝4是函数f (x )的渐近线，即有x 1＝2，x 2＝4是方程ax 2＋bx ＋c ＝0的两根，x 3＝1，x 4＝5是方程ax 2＋bx ＋c ＝1的两根，∴由根与系数的关系，得2＋4＝1＋5＝－b a ，2×4＝c a ，1×5＝c －1a， ∴⎩⎪⎨⎪⎧a ＝13，b ＝－2，c ＝83，∴a －b ＋c ＝5，故选D.8．已知log 2x ＝log 3y ＝log 5z <0，则2x ，3y ，5z的大小排序为( )A.2x <3y <5zB.3y <2x <5zC.5z <2x <3yD.5z <3y <2x答案 A解析 x ，y ，z 为正实数，且log 2x ＝log 3y ＝log 5z <0， 令log 2x ＝log 3y ＝log 5z ＝k (k <0)， ∴x2＝2k －1，y3＝3k －1，z5＝5k －1，可得2x ＝21－k ，3y ＝31－k ，5z＝51－k，又1－k >0， ∴函数f (x )＝x1－k在(0，＋∞)上单调递增，∴2x <3y <5z.故选A.9．(2018·浙江省温州六校协作体联考)设函数f (x )＝⎩⎪⎨⎪⎧3x－2，x >0，－3－x＋2，x <0，则下列结论错误的是( )A ．函数f (x )的值域为RB ．函数f (x )为奇函数C ．函数f (|x |)为偶函数D ．函数f (x )是单调函数 答案 D解析 在平面直角坐标系内画出函数f (x )的图象(图略)，由图易得函数f (x )的值域为R ，A 正确；函数f (x )的定义域为(－∞，0)∪(0，＋∞)，且当x >0时，f (－x )＝－3－(－x )＋2＝－3x＋2＝－f (x )，同理当x <0时，也有f (－x )＝－f (x )，所以函数f (x )为奇函数，B 正确；f (|－x |)＝f (|x |)，所以函数f (|x |)为偶函数，C 正确；函数f (x )是分段函数，在各个区域内具有单调性，在整个定义域内函数f (x )不是单调函数，D 错误，综上所述，故选D. 10．已知定义在R 上的函数f (x )满足：①函数f (x )的图象的对称中心为(1,0)，且对称轴为x ＝－1；②当x ∈[－1,1]时，f (x )＝⎩⎨⎧1－x ，x ∈(0，1]，1－x 2，x ∈[－1，0]，则f ⎝ ⎛⎭⎪⎫72＝________. 答案 －32解析 由题意作出f (x )的部分图象如图所示，则f ⎝ ⎛⎭⎪⎫72＝－ 1－⎝ ⎛⎭⎪⎫－122＝－32.11．(2018·全国Ⅲ)已知函数f (x )＝ln(1＋x 2－x )＋1，f (a )＝4，则f (－a )＝________. 答案 －2解析 ∵f (x )＋f (－x )＝ln(1＋x 2－x )＋1＋ln(1＋x 2＋x )＋1＝ln(1＋x 2－x 2)＋2＝2， ∴f (a )＋f (－a )＝2，∴f (－a )＝－2.12．已知函数f (x )是奇函数，当x <0时，f (x )＝－x 2＋x .若不等式f (x )－x ≤2log a x (a >0且a ≠1)对∀x ∈⎝ ⎛⎦⎥⎤0，22恒成立，则实数a 的取值范围是________． 答案 ⎣⎢⎡⎭⎪⎫14，1 解析 由已知得当x >0时，f (x )＝x 2＋x ， 故x 2≤2log a x 对∀x ∈⎝ ⎛⎦⎥⎤0，22恒成立， 即当x ∈⎝ ⎛⎦⎥⎤0，22时， 函数y ＝x 2的图象不在y ＝2log a x 图象的上方， 由图(图略)知，0<a <1且2log a 22≥12， 解得14≤a <1.B 组 能力提高13．(2018·浙江省金丽衢十二校联考)如果存在正实数a ，使得f (x ＋a )为奇函数，f (x －a )为偶函数，我们称函数f (x )为“Θ函数”．给出下列四个函数： ①f (x )＝sin x ； ②f (x )＝cos x ； ③f (x )＝sin x －cos x ；④f (x )＝sin 2⎝⎛⎭⎪⎫x ＋π8.其中“Θ函数”的个数为( ) A ．1 B ．2 C ．3D ．4答案 B解析 对于函数f (x )＝sin x ，f (x ＋k 1π)(k 1∈Z )为奇函数，f ⎝⎛⎭⎪⎫x ＋π2＋k 2π(k 2∈Z )为偶函数，所以不存在正实数a ，使得f (x ＋a )为奇函数，f (x －a )为偶函数，所以f (x )＝sin x不是“Θ函数”；对于函数f (x )＝cos x ，f (x ＋k 3π)(k 3∈Z )为偶函数，f ⎝⎛⎭⎪⎫x ＋π2＋k 4π(k 4∈Z )为奇函数，所以不存在正实数a ，使得f (x ＋a )为奇函数，f (x －a )为偶函数，所以f (x )＝cos x 不是“Θ函数”；对于函数f (x )＝sin x －cos x ＝2sin ⎝⎛⎭⎪⎫x －π4，则存在a ＝π4使得f (x ＋a )为奇函数，f (x －a )为偶函数，所以f (x )＝sin x －cos x 是“Θ函数”；对于函数f (x )＝sin 2⎝ ⎛⎭⎪⎫x ＋π8＝sin ⎝⎛⎭⎪⎫2x ＋π4，则存在a ＝3π8使得f (x ＋a )为奇函数，f (x －a )为偶函数，所以f (x )＝sin 2⎝⎛⎭⎪⎫x ＋π8是“Θ函数”．综上所述，“Θ函数”的个数为2，故选B.14．(2018·浙江省杭州二中月考)设f (x )＝ex1＋e x ，[x ]表示不超过x 的最大整数，则函数g (x )＝⎣⎢⎡⎦⎥⎤f (x )－12＋⎣⎢⎡⎦⎥⎤f (－x )－12的值域是( ) A ．{－1,0,1} B ．{－1,0} C ．{－2，－1,0} D ．{0,1}答案 B解析 设h (x )＝f (x )－12，则g (x )＝[h (x )]＋[h (－x )]，又因为h (－x )＝f (－x )－12＝e－x1＋e －x－12＝11＋e x －12＝－e x1＋e x ＋12＝－h (x )，所以函数h (x )＝f (x )－12为奇函数，易知h (x )在R 上单调递增，且h (x )∈⎝ ⎛⎭⎪⎫－12，12.当x <0时，g (x )＝－1＋0＝－1；当x ＝0时，g (x )＝0＋0＝0；当x >0时，g (x )＝0－1＝－1.综上所述，函数g (x )＝⎣⎢⎡⎦⎥⎤f (x )－12＋⎣⎢⎡⎦⎥⎤f (－x )－12的值域为{－1,0}，故选B.15．已知定义在R 上的奇函数f (x )和偶函数g (x )满足12f (x )－g (x )＝x －1x 2＋1，若g (x ＋5)＋g ⎝⎛⎭⎪⎫1x －1<g (x )＋g ⎝ ⎛⎭⎪⎫1x ，则x 的取值范围是____________________．答案 {x |x >－2且x ≠0且x ≠1} 解析 因为12f (x )－g (x )＝x －1x 2＋1，所以12 f (－x )－g (－x )＝－x －1x 2＋1，即－12 f (x )－g (x )＝－x －1x 2＋1，因此g (x )＝1x 2＋1. 因为g (x )＋g ⎝ ⎛⎭⎪⎫1x ＝1x 2＋1＋11x2＋1＝1，所以由g (x ＋5)＋g ⎝⎛⎭⎪⎫1x －1<g (x )＋g ⎝ ⎛⎭⎪⎫1x ，得1(x ＋5)2＋1＋(x －1)21＋(x －1)2<1， 即1(x ＋5)2＋1<11＋(x －1)2，解得x >－2，结合分母不为零得x 的取值范围是 {x |x >－2且x ≠0且x ≠1}．16．(2018·天津)已知a ∈R ，函数f (x )＝⎩⎪⎨⎪⎧x 2＋2x ＋a －2，x ≤0，－x 2＋2x －2a ，x >0.若对任意x ∈[－3，＋∞)，f (x )≤|x |恒成立，则a 的取值范围是________．答案 ⎣⎢⎡⎦⎥⎤18，2解析 如图所示，若对任意x ∈[－3，＋∞)，要使函数y ＝f (x )的图象恒在y ＝|x |图象的下方，则必有⎩⎪⎨⎪⎧f (－3)≤3， ①f (0)≤0， ②且在(0，＋∞)内直线y ＝x 与y ＝－x 2＋2x －2a 相切或相离，所以x ＝－x 2＋2x －2a 有两个相等实根或无实根，即对于方程x 2－x ＋2a ＝0， Δ＝(－1)2－4×2a ≤0，解得a ≥18.由①②得9－6＋a －2≤3且a －2≤0，所以a ≤2.综上，18≤a ≤2.。