当前位置：文档之家 › 第六章 误差椭圆(cehui2010)

第六章 误差椭圆(cehui2010)

  • 格式：ppt
  • 大小：2.53 MB
  • 文档页数：75

下载文档原格式

  / 75

合集下载

误差椭圆

误差椭圆
2 2 E(∆P2 ) = E(∆x2 ) + E(∆y2 ) = σ x +σ y
2 E[∆x ] = E[( x− x)2 ] = E[( x − E(x)) 2 ] = σ x 2 2 E[∆y ] = E[( y− y)2 ] = E[( y − E( y)) 2 ] = σ y 2 ~
~
σ = σ +σ
p
ϕ
p′′
p′′′
∆ϕ
y
由广义误差传播律: 由广义误差传播律
Qϕϕ = Qxx cos2 ϕ + Qyy sin2 ϕ + Qxy sin 2ϕ
2 2 2 σϕ = σ 0 Qϕϕ = σ 0 (Qxx cos2 ϕ + Qyy sin2 ϕ + Qxy sin(2ϕ)
三、位差的极大值 E和极小值 F
上
E = σ QEE =
2 2 0
σ02
2
(Qxx + Qyy + K),
∆ψ = cosψ∆E + sinψ∆F Q = QEE cos2 ψ + QFF sin2 ψ + QEF sin 2 ψ ψψ
QEF = 0
Qψψ = QEE cos2 ψ + QFF sin 2 ψ
2 2 2 σψ = σ 0 Qψψ = σ 0 (QEE cos2 ψ + QFF sin 2 ψ ),
∧
Q∧ Q∧ Q∧ Q∧ Q∧ Q∧
∧
X1 X i
∧
X1Y i
∧
L Q∧ L Q∧ L
∧
X1 X u
∧
Y1 Y1
Y1 X i
Y1 Y i
Y1 X u

Padding 投影误差椭圆

Padding 投影误差椭圆

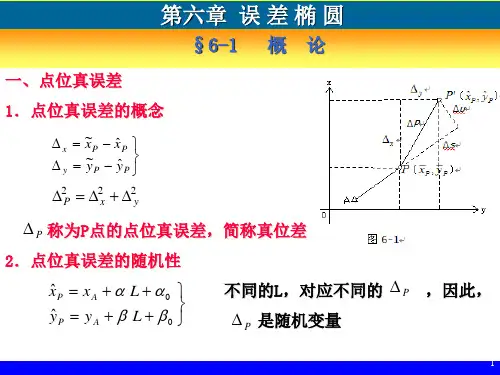
Padding投影误差椭圆误差椭圆，英文名称是error ellipse，是指待定点位置各方向上误差分布规律的椭圆。

点位误差曲线一种典型的曲线，作图也不方便，因此降低了他的实用价值。

但是它的形状与以E、F为长短半轴的椭圆很相似，此椭圆称为点位误差椭圆，即误差椭圆。

φE、E、F称为误差椭圆的参数。

通过原点P的线段PA与误差椭圆的交点，为PA的纵向误差，与该线段垂直的线段PB，与误差椭圆的交点为PA的纵向误差。

应用在测量工作中，特别是在精度要求较高的工程测量中，往往利用点位误差椭圆对布网方案进行精度分析。

其中s定义椭圆的规模，可以是任意的数（例如，s=1）。

现在的问题是如何选择s，使得所得到的椭圆规模代表我们所选择的置信水平（例如，95％的置信水平对应于s=5.991）。

我们的2D数据从零协方差的高斯分布中采样得到。

这意味着x值和y值也是高斯分布。

因此，等式（2）的左手侧实际上代表独立正态分布数据样本的平方和。

根据所谓的卡方（Chi-Square）分布，高斯数据点平方的总和是已知的。

卡方分布用“自由度”的形式定义，它表示未知量的数目来。

在我们的例子中，有两个未知数，因此自由度是二。

因此，我们可以很容易地获取上述和的概率，通过计算卡方似然，s等于一个特定的值。

事实上，由于我们感兴趣的是置信区间，我们正在寻找s小于或等于某个特定值的概率，这个特定值可以用累积卡方分布得到。

由于统计人员都是懒惰的（这个翻译我也是醉了【好吧，其实就是我翻译的】原文为“As statisticians are lazy people”期待大家可以给出更好的翻译），我们通常无法尝试计算这个概率，而只是看一个概率表。

测量平差学习情境6 误差椭圆

测量平差学习情境6 误差椭圆
学习情境6 误差椭圆
教学内容 主要介绍点位真误差和点位误差、任意方向上 的位差、待定点的误差曲线与误差椭圆以及点与点
能正确陈述点位真误差和点位误差及其计算方 法；能正确陈述任意方向上的位差及其位差的极值； 能正确陈述误差曲线和误差椭圆；能基本正确陈述 相对误差椭圆。
1
技能目标 能正确计算点在任意方向上的位差，能正确计 算位差的极值方向和极值；能正确绘制误差曲线和 误差椭圆，能根据误差椭圆求点在任意方向上的位 差，能计算点与点之间的相对误差椭圆参数并绘制 相对误差椭圆。
13
2. 点位任意方向上的位差σψ：从椭圆的中心作 方向线，然后再作该方向线的垂线（要与椭圆上一 点相切），则垂足到椭圆中心的长度便是点位在该 方向上的位差（见图6-8），图中线段OD的长度就 等于该方向上的位差，即σψ=OD
图6-8
14
子情境3 相对误差椭圆 一、两点之间相对位置的精度 1.相对位置的表示 两点相对位置可用其两点的坐标差来表示,即 用矩阵表达为
11
②确定点位中误差。 ③待定点P至任意已知三角点（视其无误差）的边 长中误差。 ④待定点P至任意已知三角点（视其无误差）的方 位角中误差。
12
误差曲线不是一种典型曲线，作图也不方便， 因此降低了它的实用价值。但其形状与以E、F为 长、短半轴的椭圆很相似。在以xe、ye为坐标轴 的坐标系中，该椭圆的方程为 1.误差椭圆的绘制 误差椭圆是一种规则图形,作图比较容易。因 此，实际应用中常以E、F为长、短半轴来绘制标 准的椭圆来代替相应的误差曲线，用来计算待定点 在各方向上的位差，故称该椭圆为误差椭圆。
3
子情境1 点位真误差及点位误差 一、点位真误差 在测量工作中，通过野外所进行的一系列的观 测，然后对观测数据进行平差处理便可得到点的平 面坐标平差值(x^，y^）。 但是，观测值总是带有观测误差的，而由观测 值所计算的平差值虽然较观测值更合理、可靠，但 是，它是不可能消除误差的，即待定点坐标的平差 值(x^,y^），不是待定点坐标的真值(x，y)，这两 者之间是有差异的。

第六章误差椭圆.

第六章误差椭圆.

Q y1 y2 Qx2 y2 Q y2 y2
Q y1 xk Qx2 xk Q y2 xk
Q y1 yk Qx2 yk Q y2 yk
Qxk y1
Qxk x2
Qxk y2
Qxk xk
Q
xk
yk
Q yk y1 Q yk x2 Q yk y2 Q yk xk Q yk yk
按平差值函数协因数的计算方法求解。
例如，四等平面控制网，测角中误差为 2.5，可取 0 2.5 ）
4．点位误差的实用计算公式
ˆ
2 x
ˆ
2 y
ˆ ˆ
02Q
2 0
Q
xx yy
ˆ
2 P
ˆ
02(Qxx
Qyy )
ˆ P ˆ 0 Qxx Qyy
2020/6/17 6
第六章 误 差 椭 圆
§6-2 点位误差
二、任意方向 上的位差
2020/6/17 1
第六章 误 差 椭 圆
§6-1 概 论
二、点位方差 1．点位方差定义
点位中误差
点位方差
xˆ P yˆ P
xA yA
L 0 L 0
E( xˆ P ) E( yˆ P )
xA yA
0 0
E(L) xA E(L) yA
0 0
L~ L~
x~P ~yP
2020/6/17 4
第六章 误 差 椭 圆
§6-2 点位误差
一、点位误差 1．点位误差的计算
2 x
2 y
2 0
2 0
1
px 1
py
02Qxx
02Q
y
y
Q
x1
x1
2（．1）间接平的差计法算计问算题 Qxx ,Qyy

测量平差---误差椭圆

测量平差---误差椭圆
2
( )
2 1
tan 2ϕ0 =
2Qxy ˆˆ Qx −Qy ˆ ˆ
=
2×0.36 = 0.81818 3.81−2.93
13 /40
2 ϕ0 =39°17′或219°17′, ° 或 ° ϕ0=19°39′或109°39′ ° 或 °
主页
误差椭圆
ˆˆ 因为 Qxy > 0 故 ，
黑龙江工程学院
1 2 3 4 5 6 7 8 9
tan 2ϕ0 =
2Qxy Qx −Qy
2 2 σϕ =σ0 (Qx cos2 ϕ0 +Qy sin 2 ϕ0 +Qxy sin 2ϕ0 )
2 =σ0 (Qx cos2 ϕ0 +Qy sin 2 ϕ0 +Qxy ⋅
极值方向的判别方法: 极值方向的判别方法 Qxy ＞0，极大值在第Ⅰ、Ⅲ象限 ，极小值方向在第Ⅱ、 极小值方向在第Ⅱ ，极大值在第Ⅰ 8 /40 Qxy，极大值在第Ⅱ 象限， 象限； ＜0，极大值在第Ⅱ、Ⅳ象限，极小值方向在 Ⅳ象限； 象限。 第Ⅰ、Ⅲ象限。
______
= cosϕ∆x + sin ϕ∆y
∆x ∆x = [cosϕ sin ϕ] ∆y
由协方差传播律得: 由协方差传播律得 或
2 2 2 σϕ =σx cos2 ϕ +σy sin 2 ϕ +σxy sin 2ϕ 2 2 σϕ =σ0 Q ϕ
7 /40
2 =σ0 Qx cos2 ϕ +Qy sin 2 ϕ +Qxy sin 2ϕ
主页
2 2 2 2 2 σP =σx +σ y =σs +σu ―点位方差计算式
误差椭圆
黑龙江工程学院

误差椭圆

误差椭圆
③ 张正禄, 李晓东. 局部相对误差椭圆—测量控制网的一种相邻精度[J].
测绘通报. 1989,(4):9-13.
④ 许才军, 刘大杰. 广义相对误差椭球（圆）[J]. 武汉测绘科技大学学报. 1990,15(2):19-27.
谢谢
误差椭圆
ERROR ELLIPSE
0 引言
① 水平面内沿中线方向的长度偏差 ② 水平面内垂直于中线的左右偏差 ③ 垂直面内垂直于腰线的上下偏差
目录（INDEX）
点位误差
误差曲线
误差椭圆
相对误差椭圆
1 点位误差
点位误差的表示 坐标真误差： 点位真误差： 由平差结果的无偏性可知：
根据方差的定义：
两边取期望：
4 相对误差椭圆
设两点间的坐标差：
写成矩阵形式：
按权逆阵传播定律：
4 相对误差椭圆
4 相对误差椭圆
导线测量网相对误差椭圆
Байду номын сангаас
小结
• 点位误差
坐标轴方向 径向方向 任意方向 存在极值
• 误差曲线
反映点位误差在 各个方向的位差 形象、直观 不规则、麻烦
• 误差椭圆
误差曲线的近似 规则化形状 能够直接量取任 意方向的位差
1 点位误差
点位误差的表示
用中误差表示：
1 点位误差
点位误差的方向与极值
展开得
1 点位误差
点位误差的方向与极值
（1）大小取决于权倒数和旋转角的大小
（3）上式有极值存在
1 点位误差
点位误差的方向与极值
2 误差曲线
0
330 2.5 2 30
0 2.00
30 2.34
60 2.23

误差椭圆的三个参数

误差椭圆的三个参数

误差椭圆，也被称为置信椭圆或测量误差椭圆，是在统计学和测量学中广泛使用的一个概念。

主要用于表示二维数据点的分布、测量误差的范围或不确定性。

它由三个主要参数定义：中心、主轴和次轴。

中心：这是误差椭圆的几何中心，代表了所有测量数据的平均位置或最可能的位置。

在理想的情况下，如果我们有无限精确的测量设备，所有的测量数据都会落在这个点上。

然而，在现实世界中，由于各种因素的影响，如设备误差、环境噪声等，测量数据通常会在这个点附近分布。

主轴：主轴是误差椭圆的长轴，代表了数据点分布的主要方向。

它的长度通常被定义为包含一定比例（例如，68%，95%或99%）测量数据的椭圆的半径。

这个比例的选择取决于我们对误差的容忍度或我们对数据的信心水平。

主轴的方向也是非常重要的，因为它可以告诉我们哪些因素对测量结果的影响最大。

次轴：次轴是误差椭圆的短轴，与主轴垂直。

次轴的长度代表了数据点在垂直于主轴的方向上的分布范围。

与主轴一样，次轴的长度也被定义为包含一定比例测量数据的椭圆的半径。

如果次轴的长度小于主轴的长度，这意味着测量数据在主轴方向上的变化比在次轴方向上的变化更大，也就是说，某些因素对测量结果的影响较小。

这三个参数共同定义了误差椭圆，为我们提供了一个直观的方式来理解和表示二维测量数据的不确定性或误差范围。

通过分析和比较不同误差椭圆的这三个参数，我们可以更好地理解我们的测量系统的性能，找出可能的改进方向，以及更准确地解释我们的测量结果。

误差椭圆.

误差椭圆.

仿式(3.5-3)可得

2 P
(x23 .5-4)y2
这说明，尽管点位真误差△P
在不同坐标系的两个坐标轴上的投
影长度不等，但点位方差 总P2 是等 于两个相互垂直的方向上的坐标方
差之和，即它与坐标系的选择无关。
图3.5-2
如果再将点P的真位差△P投影于AP方向和垂直于AP的
方向上，则得 s和 （见u 图3.5-1）， 、s 为点u 的纵向误差和 横向误差，此时有
(2)计算P2点的误差椭圆的元素
由
tan 20
2Qxˆ2 yˆ2 Qxˆ2 - Qyˆ2
2 0.2106 -1.1353 0.4912 - 0.8624
得
= E624.33
14
14
误差椭圆
K2
(Qxˆ2
- Qyˆ2
)2

4Q 2 xˆ2 yˆ2
0.561
E2
1 2

给出后，可根据这个图得到坐标平差值在任一方向的位差大
小。如图3.5-6为控制网中P点的点位误差曲线，A、B、C为已
知点。由图3.5-6可知，
，
，

xP

Pa
，
yP Pb
E Pc E
F Pd F
由图还可得到坐标平差值函数的中
误差。例如要想得到平差后方位角
垂直P的A 于中P误A方差向上，的可P位A 先差从Pg图，中这量是出 PA
2
2
误差椭圆
知识准备
1.点位真误差 在测量中，为了确定待定点的平面直角坐标，通常需进
行一系列观测。由于观测值总是带有观测误差，因而根据观
测 而值不，是通 待过 定平点差 坐计 标算 的所 真获 值得~x，的是~y。待定点坐标的平差值 xˆ ， yˆ，

eep 椭圆概率误差

eep 椭圆概率误差

eep 椭圆概率误差摘要：1.椭圆概率误差的概念解释2.椭圆概率误差的计算方法3.椭圆概率误差的应用场景4.降低椭圆概率误差的方法5.总结正文：在统计学和机器学习中，椭圆概率误差（Ellipsoid Probability Error，简称eep）是一个重要的概念，它用来衡量模型预测结果的不确定性。

椭圆概率误差主要应用于贝叶斯学习中，帮助我们更好地理解模型预测的不确定性。

椭圆概率误差是基于椭圆几何的概念而来。

在二维空间中，椭圆表示的是一个固定长轴和短轴的椭圆形状。

在贝叶斯学习中，椭圆概率误差描述的是真实值在一个椭圆区域内分布的概率。

这个椭圆的形状和大小由模型参数和不确定性程度决定。

计算椭圆概率误差的方法主要包括以下几个步骤：1.估计模型参数：通过最大似然估计或贝叶斯估计等方法，得到模型参数的估计值。

2.计算不确定性：根据模型参数的估计值，计算预测结果的不确定性。

不确定性越大，椭圆的概率误差越大。

3.计算椭圆边界：根据不确定性，计算椭圆的边界。

边界上的点表示模型预测结果的不确定性最大，而边界内的点表示不确定性较小。

4.计算概率误差：根据椭圆边界，计算真实值落在椭圆内的概率。

椭圆概率误差在许多应用场景中具有重要意义，例如：1.导航系统：在导航系统中，椭圆概率误差可以帮助我们确定目标位置的不确定性，从而提高导航准确性。

2.金融风险管理：在金融领域，椭圆概率误差可以用于衡量投资组合的风险和收益，辅助投资者做出更明智的决策。

3.医疗诊断：在医学领域，椭圆概率误差可以帮助医生评估诊断结果的不确定性，降低误诊率。

为了降低椭圆概率误差，我们可以采取以下方法：1.增加数据量：更多的高质量数据可以提高模型的准确性，从而降低椭圆概率误差。

2.优化模型结构：选择更适合问题的模型结构，如深度学习模型，可以降低模型的预测不确定性。

3.改进参数估计方法：使用更先进的参数估计方法，如贝叶斯优化，可以提高参数估计的准确性，进而降低椭圆概率误差。

误差第六章读书报告2

误差第六章读书报告2

《两种模型误差的可区分性及其可靠性理论》读书报告李春福（120091217）湖北·武汉·洪山区鲁磨路388号，中国地质大学信息工程学院1200926，430074摘要：本文通过对误差的一般性认识，进而了解和学习了两种模型误差的可区分性及其可靠性理论。

通过学习，我基本掌握了其研究的指导思想和处理问题的方法，最后以独特的方式，来总结两种模型误差的可区分性及其可靠性理论的认识和学习心得。

关键词：误差模型误差可区分性可靠性一、引言到目前为止，我们应对误差的方法大体可归纳为：1、粗差，设定限差M，大于M就舍去，小于M就认为没有粗差，这样就存在两类误差，不是误差、而被舍去和是粗差而接受为无差值。

2、偶然误差采用平差模型进行平均分配误差，以使观测值在限差内。

3、系统误差一般设置参数，作为一个未知数进行平差，在《误差理论与可靠性理论》第三章得到详细论述。

二、补偿误差与粗差的同时性（提出问题）我们在学习本书的过程中，一个重要的术语是模型误差，它与系统误差构成了人们正确研究误差理论的难点和热点。

因为现实中，我们总是习惯用模型和定量描述的方法去研究客观世界及其规律，由于人们知识等的限制，在选择模型时就会出现选择模型误差，这种误差与系统误差一般都会同时出现在所研究的过程中，传统的做法总是把他们分开处理，譬如说，在补偿系统误差时乃假设粗差已不存在，而在粗差检测时又假设系统误差已经改正。

事实上，这种假设的前提几乎是不可能出现的，在摄影测量加密时，这两类不同的误差是经常是同时存在且相互影响的。

所以对于系统误差的补偿、粗差的检测和定位已经变形分析，人们总是希望所要研究的模型误差与其他模型误差能很好的想区分，就目前来说，单个被选假设下的可靠性理论发展已经很成熟，所以作者在本书第六章专门强调从单个备选假设下的可靠性理论发展到两个备选假设下的可靠性理论——可区分行理论是十分必要的。

对于单个备选假设下的可区分性问题，一般是依托扩展的高斯--马尔科夫模型研究。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

sin
2 )
d
d
(Qxx cos2
Qyy sin 2
Qxy sin 2) 0
0
tan
20
2Qxy (Qxx Qyy )
确定极大值方向 和极小值方向 的方法如下：
当 Qxy 0 时， E 在第一、第三象限； F在第二、
第四象限；
当 Qxy 0 时，E 在第二、第四象限； F 在第一、
11 Px Py
(6-2-2)
从式(6-2-2)中可以看出，若想求得点位中误差 P,
要解决两个问题，一个是方差因子
2 0
（或中误
差 0 ）;另一个就是P点的坐标未知数x和y的协因
数 和 Qxx
Qyy
。下面就针对这两个问题的解决方法简
要说明：
2．Qxx , Qyy 的计算问题
按条件平差和间接平差两种平差方法介绍。
E2
ˆ
2 0
(Qxx
cos2
E
Qyy
sin
2 E
Qxy
sin
2E )
(6-2-17)
F2
ˆ
2 0
(Qxx
cos2 F
Qyy
sin
2 F
Qxy
sin
2F )
（6-2-18）
简便公式 另外，还可以对上式进行变换，导
出计算和的简便公式。 由三角公式变换
Q
1 2
(Q Q ) ±
xx
yy
(Q xx
E 1.24dm F 0.95dm
方法二 用公式（6-2-22）、（6-2-23）进行计算得
Qxx Qyy 1.236 1.192 0.044 , Qxx Qyy 1.236 1.192 2.428
H (Qxx Qyy )2 4Q2 xy 0.6295
E2
1 2
2 0
(Qxx
Qxk x1
Qxk y1
Qxk x2
Qxk y2
Qxk xk
Qxk
yk
Q
yk
x1
Qyk y1
Qyk x2
Qyk y2
Qyk xk
Qyk
yk
(6-2-3)
其中主对角线元素 Qxixi , Qyi yi 就是待定点坐标 xi 和 yi
的协因数（或称权倒数），Qxi 和 yi Qyixi 则是它们的相关 协因数（或称相关权倒数），在相应协因数（权倒数）
（1）间接平差法计算 当控制网中有k个待定点，并以这k个待定点
的坐标作为未知数（未知数个数为 t 2k ），
即 Xˆ x1 y1 x2 y2 xk yk T ，按间接平差法进
行平差时，法方程系数阵的逆阵就是未知数的协 因数阵 QXˆXˆ ，即
QXˆXˆ
N 1 bb
(BT PB)1
Qx1
ˆ
0
1,
试用两种方法求
解：1. 极值方向的计算与确定
tan
20
2Qxy (Qxx Qyy )
2 (0.314) 0.044
14.27273
所以
20 9400 ; 27400 0 4700 ; 13700
因为Qxy 0，所以极大值E在第二、四象限，极小 值F在第一、三象限，所以有
E 13700 或 31700 F 4700 或 22700
而 x 和 y 或 s 和 u 等等，也只能代表待
定点在x和y轴方向上以及在AP边的纵向、横向上 的位差。但在有些情况下，往往需要研究点位在某 些特殊方向上的位差大小，例如，在线路工程中和 各种地下工程中，贯通工程是经常性的重要的工作 之一，如图6-3示，
§6-2 点位误差
一、点位误差的计算
705926.8
3
341512.6 6
723217.0 9
442001.3
2个图形条件，以B点为 极的1个极条件
v1 v3 v4 v5 v7 0.1 0 v3 v6 v7 v9 1.7 0
0.04v1 1.31v2 0.22v4 1.45v5 0.20v6 2.02v7 0.56v8 1.02v9 2.2 0
则
f
T x
f
T y
0.32 1.59 0
0 0
0 1.26 1.26 0.05 0.25 0.25 0.25
0.51 0 0.26 2.531 0 1.29
（4）计算协因数 将上述数据代入得
Qxx
f Q T x LˆLˆfΒιβλιοθήκη xfT x
fx
f
T x
AT
N
1 aa
Af
x
3.6081.736 1.872
cos( BA
Lˆ4
Lˆ5 )
yD yB yBD SBD sin BD
S AB
sin Lˆ1 sin Lˆ7
sin(Lˆ6 Lˆ7 ) sin Lˆ9
sin( BA
Lˆ4
Lˆ5 )
由此得权函数式为
dxD 0.32v1 1.26v4 1.26v5 0.05v6 0.51v7 0.26v9 dyD 1.59v1 0.25v4 0.25v5 0.25v6 2.531v7 1.29v9
设待定点P的最或然坐标为 xˆP 和 yˆ P ，计算xˆP和 yˆ P
使用的已知点坐标为 x0 和 y0（认为没有误差），
则应有以下函数式
xˆ P yˆ P
x0 y0
x(Lˆ) y(Lˆ)
(6-2-5)
对(6-2-5)求微分，得其权函数式为
dx p dy p
f T x dLˆ f T y dLˆ
4．点位误差实用计算公式
以上两种情况得到的都是 0的估值，习惯上用
ˆ0 (或m0 )表示，所以实用上只能得到待定点纵、横
坐标的方差估值以及相应的点位方差的估值，即
ˆ
2 x
ˆ
2 y
ˆ ˆ
Q 2
0 xx
Q 2
0 yy
和
ˆ
2 P
ˆ
2 0
(Qxx
Qyy )
(6-2-8) (6-2-9)
则点位中误差为 ˆ P ˆ 0 Qxx Qyy（有时也用M 表示，即 M ˆ P ）。
试计算D点坐标的协因数 Qxx、Qyy、Qxy 。
解：（1）条件方程系数阵
1
0 11 1
0
1
0
0
A 0
0 10 0
1
1 0 1
0.04 1.31 0 0.22 1.45 0.20 2.02 0.56 1.02
（2）法方程系数阵和逆阵为
N aa
5.0 2.0 3.29
5.0 4.0 3.24
9.333..422349
N 1 aa
0.279 0.083 0.069
0.083 0.373 0.100
000...110606609
（3）列权函数式 由B点推算D的坐标可用下式
xD xB xBD SBD cos BD
S AB
sin Lˆ1 sin Lˆ7
sin(Lˆ6 Lˆ7 ) sin Lˆ9
x
B
2
1.5 a
1
0.5
-2.5 -2 -1.5 -1 -0.5 0
b 0.5 1 1.5 2 2.5
y
A
-0.5 PC
-1
-1.5
-2
C
第六章 误差椭圆
1 点位方差
2 P
2 xP
2 yP
则P点的点位中误差
P
2
2
xP
yP
2．点位方差与坐标系统的无关性
2 P
2 xP
2 yP
2 P
2 S
2 u
连线的两侧，而 Qxix j、Qxiy j 、Qyix j 、Qyi （ y j i j ）则是i点j
和点的纵横坐标
x
和
i
y
i与
x
j
和
y
j之间的互协因数，它
们位于主对角线元素连线的两侧，并成对称关系。
当平差问题中只有一个待定点时，即k=1,t=2时
QXˆXˆ
(BT PB)1
Qxx Qyx
Qxy
2. 极大值E、F极小值的计算
方法一 将E 和 F分别代入式（6-2-17）、（6-2-
18）得
E 2 1 (1.236 cos2 137 00 1.192 sin 2 137 00 0.314 sin(2 137 00)) 1.529
F 2 1 (1.236 cos2 4700 1.192 sin 2 4700 0.314 sin(2 4700)) 0.899
Qyy
H)
1.528
F2
1 2
2 0
(Qxx
Qyy
H)
0.899
E 1.24dm F 0.95dm
复 习 Review
点位误差（位差）
2 P
2 x
2 y
QP
Qxx Qyx
Qxy
Qyy
任意方向位差
x 0 Qxx y 0 Qyy
2
2 0
Qxx cos2 Qyy sin2 Qxy sin 2
f xT f yT
P 1 AT P 1 AT
N
1 aa
AP
1
N
1 aa
AP
1
f f
x y
Qxy
f xT QLˆLˆ
fy
f xT P 1 f y
f
x
T
P
1
AT
N
1 aa
AP
1
f
y
(6-2-7)
式中，P 1是观测值的权逆阵，N aa 是条件平差的法