焦耳定律公式,焦耳定律公式单位

焦耳定律与电功率焦耳定律和电功率是两个密切相关的概念，它们在电学领域中起着重要的作用。

焦耳定律是指电流通过电阻时所产生的热量与电阻、电流以及时间的关系，而电功率则是描述电流流过电路中所产生的功率大小。

本文将对焦耳定律和电功率进行详细论述，并分析它们的应用。

一、焦耳定律焦耳定律由英国物理学家詹姆斯·普雷斯科特·焦耳在19世纪提出，它阐述了电流通过电阻导线时所产生的热量与电阻、电流以及时间的关系，其数学表达式可以表示为：Q = I^2 * R * t式中，Q表示热量，单位为焦耳(J)；I表示电流强度，单位为安培(A)；R表示电阻，单位为欧姆(Ω)；t表示时间，单位为秒(s)。

焦耳定律告诉我们，当电流通过电阻时，电阻本身会吸收电能并将其转化为热能。

根据焦耳定律，如果电流强度增大或电阻增大，产生的热量也会相应增大；而如果时间增长，所产生的热量也会增加。

二、电功率电功率是描述电路中电流流过的功率大小的物理量。

它表示单位时间内功率的转变量，可以用以下公式计算：P = I * V式中，P表示电功率，单位为瓦特(W)；I表示电流强度，单位为安培(A)；V表示电压，单位为伏特(V)。

电功率告诉我们，电路中的电流通过电阻时会产生功率，并且功率与电流的大小以及电压的大小有关。

当电流增大或电压增大时，电功率也会相应增大。

三、焦耳定律与电功率的关系焦耳定律与电功率之间存在着密切的关系。

根据焦耳定律的公式Q = I^2 * R * t，我们可以将电流I表示为I = V / R，其中V表示电压。

将这个表达式代入焦耳定律的公式中，可以得到：Q = (V^2 / R) * R * t化简可得：Q = V^2 * t根据功率的定义P = I * V，可以将电流I表示为I = P / V。

将这个表达式代入焦耳定律的公式中，可以得到：Q = (P / V) * R * t化简可得：Q = P * t由此可见，当电流通过电阻时，所产生的热量与电功率乘以时间是等效的。

关于电的公式
与电相关的公式有很多，以下是一些常见的公式：
欧姆定律：I=U/R，其中I是电流，U是电压，R是电阻。

电阻的计算：R=ρL/S，其中ρ是电阻率，L是导体的长度，S是导体横截面积。

焦耳定律：Q=I²Rt，其中Q是热量，I是电流，R是电阻，t是时间。

电功的计算：W=UIt=Pt=U²t/R=I²Rt，其中W是电功，U是电压，P 是功率，t是时间。

电功率的计算：P=UI=U²/R=I²R，其中P是电功率，U是电压，I是电流，R是电阻。

串联电路：I=I1=I2=…=In（电流处处相等），U=U1+U2+…+Un（总电压等于各部分电路两端电压之和），R=R1+R2+…+Rn（总电阻等于各分电阻之和）。

并联电路：I=I1+I2+…+In（干路上的电流等于各支路电流之和），U1=U2=…=Un（各支路两端电压相等）。

1千卡(KCAL)=4.184千焦耳(KJ)
1千焦耳(KJ)=0.239千卡(KCAL)
焦耳--瓦特：
1焦耳(J)=1瓦特×秒(W·s)
1度(1kw·h)=3.6×10^6焦耳(J)
焦耳--牛顿：
1焦耳(J)=1牛顿×米(N·m)
热量（Joule）的公制单位，简称“焦”，是为了纪念英国著名物理学家詹姆斯·普雷斯科特·焦耳而创立的。

焦耳定律是定量说明传导电流将电能转换为热能的定律。

内容是：电流通过导体产生的热量跟电流的二次方成正比，跟导体的电阻成正比，跟通电的时间成正比。

焦耳定律数学表达式：Q=I²Rt（适用于所有电路）；对于纯电阻电路可推导出：Q=W=Pt；Q=UIt；Q=(U²/R)t
从焦耳定律公式可知，电流通过导体产生的热量跟电流强度的平方成正比、跟导体的电阻成正比、跟通电时间成正比。

若电流做的功全部用来产生热量。

即W=UIt。

根据欧姆定律，有W=I²Rt。

需要说明的是W=(U^2/R)t是从欧姆定律推导出来的，只能在电流所做功将电能全部转化为热能的条件下才成立(纯电阻电路）。

例如对电炉、电烙铁这类用电器，这两公式和焦耳定律才是等效的。

焦耳定律公式单位全文共四篇示例，供读者参考第一篇示例：焦耳定律是研究能量转化和利用的重要定律之一，广泛应用于物理学和工程学领域。

在焦耳定律中，能量的转化和传递过程遵循特定的规律，可以通过数学公式进行描述和计算。

本文将重点介绍焦耳定律公式及其相关单位，希望能帮助读者更好地理解和应用这一重要定律。

焦耳定律公式是描述能量转化和传递过程的数学表达式，通常表示为Q = mcΔT，其中Q表示热量的数量，m表示物体的质量，c表示物体的比热容，ΔT表示温度的变化量。

这个公式告诉我们，在物体受热或失热的过程中，热量的变化取决于物体的质量、比热容和温度的变化量。

在焦耳定律中，能量的单位是焦耳（J），物体的质量的单位是千克（kg），比热容的单位是焦耳/千克·摄氏度（J/kg·℃），温度的单位是摄氏度（℃）。

根据焦耳定律公式，焦耳表示的是能量的数量，是热量的单位。

如果需要转换其他单位，可以通过换算关系进行计算。

在实际应用中，焦耳定律常常用于计算物体受热或失热的过程中所吸收或释放的热量。

当一个物体受热升温时，根据焦耳定律公式可以计算出物体所吸收的热量；当一个物体失热降温时，可以计算出物体所释放的热量。

这种计算在物理学、化学及工程学实践中具有重要的应用价值。

除了热量的传递过程外，焦耳定律也可以应用于其他能量转化过程中。

当物体做功时，同样可以利用焦耳定律公式进行能量计算；或者当物体发生化学反应时，也可以通过焦耳定律进行能量平衡分析。

焦耳定律公式及其相关单位是描述和计算能量转化和传递过程中不可或缺的工具。

第二篇示例：焦耳定律是一个重要的物理定律，描述了能量转换的原理。

根据焦耳定律，一个物体在接受热能的将会发生温度的变化，这个变化的幅度取决于物体的热容和接受的热量。

焦耳定律公式的单位是关键的，通过正确的单位转换，我们可以更好地理解能量转换的过程。

焦耳定律公式如下：Q = mcΔTQ表示物体接受的热量（单位焦耳），m表示物体的质量（单位千克），c表示物体的比热容（单位焦耳/（千克·摄氏度）），ΔT表示物体温度的变化（单位摄氏度）。

焦耳定律公式和电功计算公式
马克斯·弗里德曼·福克纳（Maxwell Faraday）电学定律的发明，为电学的发展提供了
一个理论基础，这就是福克纳焦耳定律。

福克纳焦耳定律在构成电流电路时提供了一种描
述电流的有效方法，它也可以用来计算电压的变化，计算电功和功率等。

福克纳焦耳定律推导出来的公式是：
▼
∆Φ=E·∆t
其中，Φ是磁感应方量，即穿过磁感应循环的电压；E是电势差；∆t是通过磁感应循环
的时间。

电功计算公式：
▼
W=V·I·t
其中，W表示电功，单位是瓦特；V表示电压，单位是伏特；I是电流，单位是安培；t是
时间，单位是秒。

因此，福克纳焦耳定律和电功计算公式是计算电功的有效工具，可以准确地描述和计算电
路中的电子及电压的变化，确保电路的稳定性并实现效率最大化。

电动机、发电机和其他
电气电子设备的许多故障，也可以通过福克纳焦耳定律和电功计算公式来查找解决方案。

此外，这些公式在研究发电厂物理机理、汽车电子节能和各种电动系统驱动机构中也发挥
重要作用。

总体而言，福克纳焦耳定律和电功计算公式已经成为现代高科技电子设备的重要参考标准，它的重要性不言而喻。

因此，充分了解和熟悉这些公式，对于从业人员来说是非常重要的。

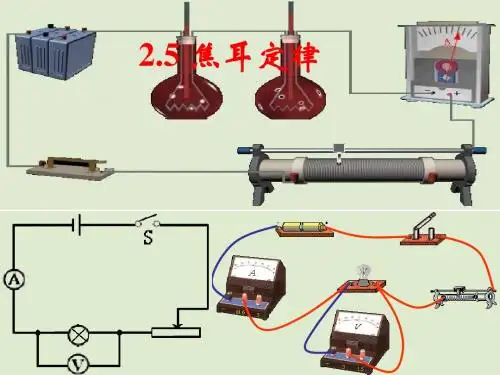
焦耳定律及应用焦耳定律是一个工程学和物理学中的定律，它表明了电流通过电阻发热的物理学原理。

该定律由英国物理学家詹姆斯·普雷斯科特·焦耳于1841年提出。

焦耳定律的公式为Q=I2×R×t，其中Q表示所产生的热量，I表示电流的强度，R表示电阻的大小，t表示电流流经电阻的时间。

这个公式非常重要，因为它提供了计算电阻热损耗的方法。

焦耳定律的应用非常广泛，从家庭到工业生产都有大量的应用。

例如，极其常见的烤面包器就是使用焦耳定律制作的。

烤面包器中的电线和其他电阻材料，都具有高阻抗，所以当电流通过它们时，就会产生大量的热量，这样就能将面包加热至所需的温度。

同样地，吹风机、热水器、橡胶机等电器设备也都是利用焦耳定律产生高温的。

焦耳定律还有许多其他应用，例如热成像。

热成像是一个非常有用的技术，使用红外线摄像机来检测物体的表面温度。

利用焦耳定律，可以计算出物体表面上每个点的温度。

这种技术可以用于医学成像，也可以用于公路管理和建筑结构工程，避免出现过高或过低的温度，从而避免可能的破坏。

另一个应用焦耳定律的领域是电池。

在电池中，当化学能在电解液中转化为电能时，会产生电流。

电池需要经过一定的电阻才能把这个电流传送给设备。

如果电池透过的电阻过多，那么产生的电流就会过小，设备将无法使用。

如果电池透过的电阻过少，那么电池将会产生过多的电流，从而使电池的寿命缩短。

最后，焦耳定律还可以应用于电路。

在电路中，电源必须提供足够的能量来让电流流经电路元件，但必须防止电阻过大，产生过量的热量。

因此，焦耳定律告诉我们如何在设计电路时平衡电能和电流的流量，从而确保电路可以可靠地工作。

总之，焦耳定律是一个很有用的物理原理，可以应用于各种领域。

无论我们是想要生产新产品，还是希望简化和熟练使用技术，我们都可以从焦耳定律中受益。

能量单位焦耳的定义
焦耳（简称焦，符号为J），是能量和做功的国际单位。

在经典力学里，1焦耳能量相等于1牛顿力的作用点在力的方向上移动1米距离所做的功。

为纪念英国物理学家詹姆斯·普雷斯科特·焦耳而命名为焦耳。

1焦=1牛·米，也等于1瓦的功率在1秒内所做的功，1焦=1瓦·秒。

焦耳定律是指电能和热能的转化关系，它是英国物理学家焦耳在1841年发现的。

焦耳定律的具体内容是：电流通过导体所产生的热量与电流的平方成正比，与导体的电阻成正比，与通电时间成正比。

焦耳定律的数学公式是Q=I²Rt，其中Q表示热量，单位是焦耳；I表示电流，单位是安培；R表示电阻，单位是欧姆；t表示时间，单位是秒。

这个公式适用于所有电流热效应的计算。

焦耳在用电阻丝给水加热的时候发现，设置不同的参数，电阻丝产生的热量就不一样，水的温度也就不同。

他决定对其展开定量研究。

通过大量的实验，焦耳最终发现了焦耳定律。

焦耳定律为电路照明设计、电热设备设计和计算电力设备的发热提供了依据。

在纯电阻电路中，以焦耳定律的公式为依据，还能推导出其他的计算电路热量的公式。

但是需要注意的是，焦耳定
律的公式适用于所有电路，而推导出来的公式只适用于纯电阻电路。

国际单位制用焦[耳](J)表示功或能的单位。

1焦耳等于在1牛力作用下，在该力的方向上运动1米所做的功；在电学中等于1W・s，即1A的电流流过1Ω的电阻在1秒内释放的能量。

焦耳定律原始公式
焦耳定律是关于电能转化为热能的物理定律，它描述了通过
电流通过电阻时所产生的热量的大小。

焦耳定律的原始公式可
以表示为：
\[Q=I^2Rt\]
其中，Q表示通过电流I在电阻R上流过时间t所产生的热量。

根据焦耳定律，当电流通过一个电阻时，电流在电阻中产生
的能量将被转化为热能。

该公式表明，电流的大小（I的平方）和电阻的大小（R）是影响产生的热量（Q）的因素，时间（t）是电流通过电阻的时间。

这个公式可以从几个方面解释。

首先，电功率（P）定义为单位时间内的能量转化，可以表示为：
\[P=\frac{W}{t}\]
其中，W表示能量，t表示时间。

根据电功率和电流的关系，我们知道：
\[P=IV\]
这里，I表示电流，V表示电压。

然后，根据欧姆定律，电流可以通过电压和电阻表示：
\[I=\frac{V}{R}\]
将这个表达式代入电功率公式中，得到：
\[P=\frac{V^2}{R}\]
最后，将电功率乘以时间，可得到能量转化的大小：
\[W=Pt=\frac{V^2}{R}\cdott=\frac{V^2t}{R}\]
我们知道，能量可以用热量来表示，因此将W表示为Q，即可得到焦耳定律的原始公式：
\[Q=I^2Rt\]
这个公式告诉我们，通过电流I在电阻R上流过时间t所产生的热量Q与电流的平方成正比，与电阻和时间成正比。

可以看出，增大电流、电阻或时间都会增加产生的热量。