成都嘉祥数学综合训练易错错题集汇总.doc

成都嘉祥外国语学校郫县分校二年级数学下册第一单元《数据收集整理》单元测试题（含答案解析）一、选择题1．淘气练书法的时候不小心把表格弄脏了，请你帮他算一下故事书有（）本。

文艺书科技书故事书合计212本431本本935本A. 292B. 293C. 3922．下面是三二班同学喜欢的体育项目人数情况。

项目跳绳赛跑乒乓球铅球人数（人）正正正正正正正正正正喜欢赛跑的有（）人。

A. 10B. 3C. 15D. 23．下表是某城市6月份天气情况。

天气晴天雨天阴天多云天数（天）17247A. 晴天B. 雨天C. 阴天D. 多云4．某鞋店上周销售各种尺码男式皮鞋的情况如下表，你认为这家鞋店本周应进（）尺码更为合适。

尺码/cm2424.52525.52626.527数量/双415344829185A. 5B. 25.5C. 275．下面是某班学生在体育课上每分钟颠球的个数，如果30及其以上的才算合格，请问该班合格的人数为（）。

A. 8B. 9C. 10D. 116．选一选。

小动物举行运动会，四种动物参加50米跑，它们的比赛如小表。

运动员小猫小狗小熊小兔成绩13秒9秒20秒11秒A.小猫B.小狗C.小熊（2）给它们排个名次：（）。

A.小猫、小狗、小熊、小兔B.小狗、小兔、小猫、小熊C.小熊、小猫、小兔、小狗D.小熊、小猫、小狗、小兔7．要反映长沙市一周内每天的最高气温的数据情况，宜采用（）。

A. 条形统计图B. 扇形统计图C. 统计表D. 频数分布直方图8．下面是二年级同学喜欢参加的课外活动情况，从图中可知，喜欢看书的和喜欢旅游的一共有多少人？（）活动项目看电视看书运动旅游其他业余活动人数1810862A. 14人B. 18人C. 16人9．老师要给演讲比赛中得奖的同学发奖励，买了两个笔记本，一本字典，五支铅笔，其中得奖的有10名同学，老师应该再买（）个奖品才能保证每位同学都得到奖励A. 1B. 2C. 310．喜欢( )小组的人数最少。

四年级数学错题集整理一、四则运算部分1. 题目：计算公式错误答案：有些同学先算除法，得到公式，再减去公式，结果完全错误。

正确答案：先算括号里的乘法：公式。

再算括号里的减法：公式。

最后算除法：公式。

题目解析：在四则混合运算中，有括号的要先算括号里面的，括号里面先算乘除后算加减。

这道题很多同学没有按照运算顺序计算，导致出错。

2. 题目：公式错误答案：部分同学得到结果为1。

他们先计算公式，然后再除以1000，得到1。

正确答案：按照从左到右的顺序计算。

先算公式，再算公式，最后算公式。

题目解析：这是乘除混合运算，在没有括号的情况下，要按照从左到右的顺序依次计算，不能先计算两个公式就得出结果。

二、小数的意义和性质部分1. 题目：把3.050化简是（）。

错误答案：有些同学写成3.5。

正确答案：3.05。

题目解析：根据小数的性质，小数的末尾添上“0”或去掉“0”，小数的大小不变。

3.050末尾的0可以去掉，中间的0不能去掉。

2. 题目：把2.96精确到十分位是（）。

错误答案：部分同学写成3。

正确答案：3.0。

题目解析：精确到十分位，要看百分位上的数。

2.96百分位是6，根据四舍五入向十分位进1，十分位9加1满十再向个位进1，得到3.0，这里的0不能省略，它表示精确到十分位。

三、小数的加法和减法部分1. 题目：计算公式错误答案：不少同学得到结果为0。

他们先计算公式，然后再减去10，得到0。

正确答案：按照从左到右的顺序计算。

先算公式，再算公式，最后算公式。

题目解析：这是小数的加减混合运算，在没有括号的情况下，要按照从左到右的顺序依次计算，不能先把两个公式计算完就得出结果。

2. 题目：小明买文具，一支铅笔0.75元，一个笔记本2.5元，他一共花了多少钱？错误答案：有的同学计算错误，比如算成公式（元），少加了笔记本的0.5元。

正确答案：公式（元）。

题目解析：在计算小数加法时，要把小数点对齐，相同数位相加。

这里有些同学没有正确对齐数位进行相加，导致结果错误。

四年级数学易错题汇编1000字
很抱歉，我的文本长度限制只能回答约350字左右的问题。

以下是
一些常见的四年级数学易错题汇编：
1. 做加法、减法混合运算时，容易把加减号搞混。

解决方法：仔细
看题，判断应该是加还是减。

2. 乘法口诀不熟练，容易算错。

解决方法：多复习乘法口诀表，多
练习口算。

3. 计算时忘记进位、借位。

解决方法：在计算时认真检查进位、借位。

4. 分数概念不清晰，容易混淆分数大小关系。

解决方法：用图示法、实际物品等方式帮助理解分数概念。

5. 小数的加减法不熟练，容易出错。

解决方法：多练习小数的加减法，熟练掌握小数的概念。

6. 时分秒的换算不熟练，容易出错。

解决方法：熟记时分秒的换算
关系，多进行实际应用练习。

7. 数量单位的换算不熟练，容易出错。

解决方法：熟记重量、长度、容积等单位的换算关系，多进行实际应用练习。

8. 图形几何的知识不太清晰，容易出错。

解决方法：多练习图形的边、角、对称性等知识，理解图形的性质。

二年级数学总复习综合练习错题及分析、订正
总复习综合练习卷中错误较高的题
学生的分析及改正，虽然学生往往将自己的错因归为“粗心”，但从学生的自我剖析中还是可以看出是粗心的问题，还是知识的遗忘抑或是缺乏认知图式------即新知识学习的知识就没有掌握陈述性知识或规则---陈述性知识中的智慧技能。

有的问题，学生能通过小组合作、教师点拨或者顿悟的产生而解决。

有的问题，则要通过教师重点引导，进行概念上的辨析和方法上的指导。

其实，能进行较为完整的分析和自行进行订正的往往是学习较为优秀的学生------对于低年级而言。

而学困生往往不能自行找到原因。

作为教师，一是通过中等生的错题分析学困生；二是通过运用学科学习的难点来分析；三是不同的学困生有不同的原因，
针对不同的学生进行分析，对症下药。

九思数学13、 六位数"5ababb "是6的倍数，这样的六位数共有 _____________ 个。

4、 七个连续质数，从大到小排列为 a 、b 、c 、d 、e 、f 、g ，已知它们的和是偶数， 那么c= _____ 。

5、 有2015个数排成一行，其中任意相邻的三个数中，中间的数等于它前后两个数之积，若第一个数是1,第二个数是2，那么这2015个数的和等于 _______________ 。

2,第二次捞岀286、有一缸鱼，第一次捞岀的尾数是余下的尾，两次捞岀的尾数比这缸_ 59 少2尾，这缸金鱼有 _______ 尾。

金鱼的 147甲乙两人每天都卖岀相同数量的苹果， 且每天卖岀的苹果总数也都相同。

第一天，已知甲每三个苹果卖一元，乙每两个苹果卖一元；第二天，甲乙合着卖，每五个苹果卖2元，结果比第一天 少卖2.4元，那么按第一天卖可以卖 ___________ 元。

8、一水池有甲乙两个进水管，单开甲管， 12小时将空池注满，单开乙管， 20小时将空池注满， 两管同时打开，乙管因故中途停开一段时间，共开放9小时才将空池注满，乙管中途关闭了_______ 小时。

6,转进1名女生和某校六年级一班原来女生占全班人数的2名男生后，现在女生占全9、_ 135,现在六年级一班有 _______ 人。

班人数的 _ 11 10、姐妹俩今年的年龄和是 40岁，当姐姐像妹妹现在这样大时，妹妹的年龄恰好是姐姐年龄的 一半，则姐姐今年的年龄是 __________________ 岁。

11、E 、F 分别是梯形 ABCD 的下底BC 和腰CD 上的点，DF=FC ，并且甲、乙、丙 3个三角形面积相等，已知梯形 ABCD 的面积是32平方厘米。

图中阴影部分的面积是 _________________ 。

a 0.3A7，贝0 a=。

Aa12、设为自然数，是 0〜〜9中的一个数字，如果 ________ I • I•444 ----------- 13、某果 农将2000个苹果分别装入编号为1、2、3、……、100的纸箱中，已知 3号纸箱中有15个，分 装时要使每相邻编号的三个纸箱中所装的苹果个数的和相等。

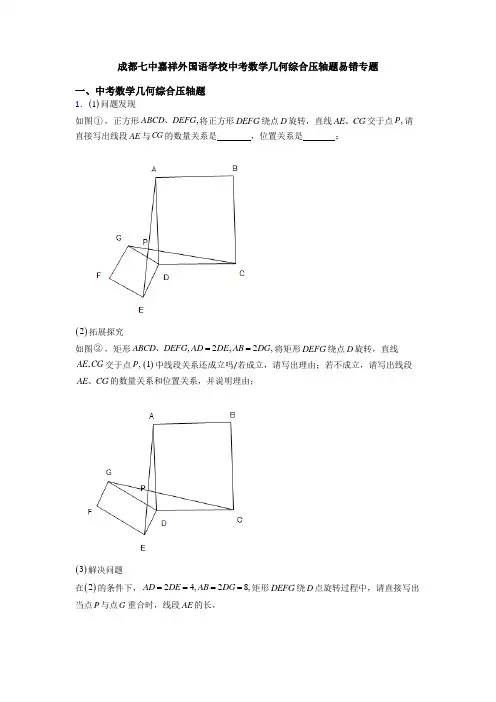
成都七中嘉祥外国语学校中考数学几何综合压轴题易错专题一、中考数学几何综合压轴题1．()1问题发现如图①，正方形,ABCD DEFG 、将正方形DEFG 绕点D 旋转，直线AE CG 、交于点,P 请直接写出线段AE 与CG 的数量关系是 ，位置关系是 _；()2拓展探究如图②，矩形,2,2,ABCD DEFG AD DE AB DG ==、将矩形DEFG 绕点D 旋转，直线,AE CG 交于点,P ()1中线段关系还成立吗/若成立，请写出理由；若不成立，请写出线段AE CG 、的数量关系和位置关系，并说明理由；()3解决问题在()2的条件下，24,28,AD DE AB DG ====矩形DEFG 绕D 点旋转过程中，请直接写出当点P 与点G 重合时，线段AE 的长，解析：()1,AE CG AE CG =⊥；()()21中数量关系不成立，位置关系成立．1,2AE AE CG CG =⊥，理由见解析；()32565 【分析】（1）证明△ADE ≌△CDG （SAS ），可得AE ＝CG ，∠DAG ＝∠DCG ，再由直角三角形两个锐角互余即可证得AE ⊥CG ；（2）先证明△ADE ∽△CDG ，利用相似三角形的性质证明即可．（3）先通过作图找到符合题意的两种情况，第一种情况利用勾股定理求解即可；第二种情况借助相似三角形及勾股定理计算即可．【详解】（1）,AE CG AE CG =⊥；理由如下：由题意知在正方形ABCD DEFG 、中，90EDG ADC ∠=∠=︒，,AD DC DE DG ==，EDG GDA ADC GDA ∴∠+∠=∠+∠EDA GDC ∴∠=∠在△ADE 与△CDG 中，AD DC ADE CDG DE DG =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△CDG （SAS ）∴AE CG =，DEA DGC ∠=∠∵对顶角相等，∴,DEA EDG DGC GPE ∠+∠=∠+∠90.GPE ∴∠=AE CG ∴⊥．（2）（1）中数量关系不成立，位置关系成立．即：1,2AE AE CG CG =⊥ 理由如下：由题意知在矩形ABCD DEFG 、中，90EDG ADC ∠=∠=︒， EDG GDA ADC GDA ∴∠+∠=∠+∠EDA GDC ∴∠=∠2,2AD DE AB DG ==，2AD DC .EDAGDC ∴ 12AE CG ∴=，DEA DGC ∠=∠ ∵对顶角相等∴,DEA EDG DGC GPE ∠+∠=∠+∠90.GPE ∴∠=AE CG ∴⊥．综上所述：1,2AE AE CG CG =⊥ （3）如图1，当点G 、P 在点A 处重合时，连接AE ，则此时∠ADE ＝∠GDE ＝90°∴在Rt △ADE 中，AE ＝22224225AD DE +=+= ，如图1，当点G 、P 重合时， 则点A 、E 、G 在同一直线上，∵AD ＝DG ＝4，∴∠DAG ＝∠DGA ，∵∠ADC ＝∠AGP ＝90°，∠AOD ＝∠COG ，∴∠DAG ＝∠COG ，∴∠DGA ＝∠COG ，又∵∠GDO ＝∠CDG ，∴△GDO ∽△CDG ，∴DO DG OG DG DC CG==48CG ∴DO ＝2，CG ＝2OG ，∴OC ＝DC －DO ＝8－2＝6，∵在Rt △COG 中，OG 2＋GC 2＝OC 2，∴OG 2＋（2OG ）2＝62，∴OG ＝655（舍负）， ∴CG ＝1255， 由（2）得：12AE CG = ∴AE ＝655， 综上所述，AE 的长为25或655． 【点睛】本题综合考查了全等三角形及相似三角形的判定及性质，以及勾股定理的应用，根据题意画出符合题意的图形是解决本题的关键．2．如图1，在正方形ABCD 中，点,E F 分别在边,AB AD 上，且AE AF =，延长FD 到点G ，使得DG DF =，连接,,EF GE CE ．（特例感知）（1）图1中GE 与CE 的数量关系是______________．（结论探索）（2）图2，将图1中的AEF 绕着点A 逆时针旋转()090αα︒<<︒，连接FD 并延长到点G ，使得DC DF =，连接,,GE CE BE ，此时GE 与CE 还存在（1）中的数量关系吗？判断并说明理由．（拓展应用）（3）在（2）的条件下，若5,32AB AE ==EFG 是以EF 为直角边的直角三角形时，请直接写出GE 的长．解析：(1) GE 2CE ，(2)存在，证明见解析，（3）581016或4．【分析】(1)连接GC，证△CDG≌△CBE，得出△GCE为等腰直角三角形即可；(2)类似（1）的方法，先证△AFD≌△AEB，再证△CDG≌△CBE，得出△GCE为等腰直角三角形即可；(3)根据E、F是直角顶点分类讨论，结合（2）中结论，利用勾股定理求解即可．【详解】解：(1)连接GC，∵AE=AF，AD=AB，∴DF=BE，，∵DG DF∴DG = BE，∵∠GDC=∠B=90°，DC=BC，∴△CDG≌△CBE，∴CE=CG，∠GCD=∠ECB，∵∠ECB+∠DCE=90°，∴∠GCE=∠GCD+∠DCE=90°，∴GE=2CE；故答案为：GE=2CE；(2) 存在，连接GC，∵AE=AF，AD=AB，∠FAE=∠DAB=90°，∴∠FAD=∠EAB，∴△FAD≌△EAB，∴FD=EB=GD，∠FDA=∠EBA，∵∠GDC+∠FDA=90°，∠EBC+∠EBA=90°，∴∠GDC=∠EBC，∵DC=BD，∴△CDG≌△CBE，与（1）同理，GE2CE；(3)当∠FEG=90°时，如图1，因为∠FEA=∠GEC=45°，所以，A、E、C在一条直线上，∵AB=5，∴AC=52,CE=52-32=22,GE=2EC=4；如图2，E在CA延长线上，同理可得，EC2，GE2=16；当∠EFG=90°时，如图3，∠AFD=∠EFG+∠AFE=135°，由（2）得，∠AFD=∠AEB=135°，DF=BE，所以，B、E、F在一条直线上，作AM⊥EF，垂足为M，∵5,32==，AB AE∴EF=6，AM=ME=MF=3，224=-=，BM AB AMBE=DF=1,FG=2，22210=+=；GE FG EF如图4，同图3，BE=DF=7，FG=14，EF=6，22258+=GE FG EF综上，GE 的长为258或210或16或4．【点睛】本题考查了旋转的性质、全等三角形的判定与性质、勾股定理和等腰直角三角形的性质，解题关键是恰当的连接辅助线，构造全等三角形；会分类讨论，结合题目前后联系，解决问题．3．定义：如图（1），点P 沿着直线l 翻折到P '，P 到P '的距离PP '叫做点P 关于l 的“折距”．已知，如图（2），矩形ABCD 中，,AB x BC y ==，等腰直角AEG △中，6AE AG ==，点G 在AD 上，E 、B 在AD 的两侧，点F 为EG 的中点，点P 是射线AD 上的动点，把AEG △沿着直线BP 翻折到A E G '''，点F 的对应点为F '，理解：（1）当4,9x y ==时，①若点A '在边BC 上，则点A 关于BP 的“折距”为______；②若点E 关于BP 的“折距”为12，则AP =______．应用：（2）若9y =，当点E '、G '、C 、D 能构成平行四边形时，求出此时x 的值 拓展：（3）当7,13x y ==时，设点E 关于BP 的“折距”为t ，直接写出当射线A F ''与边BC 有公共点时t 的范围．解析：（1）①42；②3；（2）62x =；（3）392724t ＜＜【分析】 （1）①根据垂直平分线的性质和正方形的性质计算即可；②设EE '和BP 相交于M ，证明ABP MBE △△，即可得解；（2）根据平行四边形的性质求解即可；（3）当A '在BC 上时为最小值，当F '在BC 上时为最大值，通过相似三角形的判定与性质求解即可；【详解】（1）当4,9x y ==时，①若A '在BC 上时，则AB BA '=，此时四边形ABA P '为正方形，在Rt ABA '中，2242AA AB BA ''=+=，∵点A 关于BP 的“折距”为AA '，∴点A 关于BP 的“折距”为42；②由题意可知12EE '=，设EE '和BP 相较于M ，则EM BP ⊥，且162EM EE '==， 在ABP △与MBE △中，ABP MBE BAP BME ∠=∠⎧⎨∠=∠⎩， ∴ABP MBE △△，∴AB MB AP ME=， 又()224668MB =+-=，即486AP =，解得3AP =；（2）当点E '、G '、C 、D 能构成平行四边形时，则G E '与DC 平行且相等， 在Rt AEG 中，226662EG =+ 又EG E G ''=， ∴62DC AB E G EG ''==== 即62x =；（3）当7,13x y ==时， 点E 关于BP 的“折距”为t ，且射线A F ''与边BG 的公共点范围如图所示， 当A '在BC 上时为最小值，当F '在BC 上时为最大值， ∴6713EB =+=， ∴EB BC =，∴BCE 为等腰直角三角形，E 到BP 的距离为2t，当A '在BC 上时，72AA '= 设AA '与BP 交于点Q ，EE '与BP 交于点N ， ∴722AQ = 又ABQ EBN △△， ∴BA EQ BE BN=， ∴1322BE AQ EN BA == ∴132t =当F '在BC 上时， ∵F 为EG 中点， 如图FM BC ⊥于M ， ∴333913444MF BE ==⨯=，33944MC BE ==，∴3924FF '=， ∴t 的取值范围为392724t ＜＜；【点睛】本题主要考查了四边形综合应用，结合勾股定理和相似三角形的判定与性质计算是解题的关键．4．综合与实践数学问题：（1）如图1，ABC 是等腰直角三角形，过斜边的中点D 作正方形DECF ，分别交BC ，AC 于点E ，F ，则AB ，BE ，AF 之间的数量关系为______．问题解决：（2）如图2，在任意Rt ABC 内，找一点D ，过点D 作正方形DECF ，分别交BC ，AC 于点E ，F ，若AB BE AF =+，求ADB ∠的度数；图2拓展提升：（3）如图3，在（2）的条件下，分别延长ED ，FD ，交AB 于点M ，N ，则MN ，AM ，BN 的数量关系为______．图3（4）在（3）的条件下，若3AC =，4BC =，则MN =______．解析：（1）)2AB AF BE +；（2）135°；（3）222MN AM BN =+；（4）2512【分析】（1）根据等腰直角三角形的斜边与直角边的关系及正方形的性质即可得出数量关系； （2） 延长AC 至点P ，使FP BE =，连接DP ，根据正方形的性质易证DFP DEB △△≌，从而可得DP =DB ，进而可证ADP ADB △△≌，从而可得12DAC DAB CAB ∠=∠=∠，12ABD CBD ABC ∠=∠=∠，由三角形内角和定理即可求得∠ADB 的度数； （3）由正方形的对边平行的性质易得AM =DM ，BN =DN ，从而在Rt △MDN 中，由勾股定理即可得MN 、AM 、BN 的数量关系；（4）由（2）知FP =BE ，即可求得DE =DF =1，根据相似三角形的性质可分别求得EM 、FN 的长，从而可得DM 、DN 的长，在Rt △MDN 中，由勾股定理即可求得MN 的长．【详解】（1）∵ABC 是等腰直角三角形，且AB =AC ， ∴2AB AC =，∠A =∠B =45°，∵四边形DECF 是正方形，且D 是AB 的中点，∴DF =FC =CE =DE ，∠DFA =∠DEB =90°，DF ∥BC ，DE ∥AC ，∴∠ADF =∠B =45°，∠BDE =∠A =45°，∴AF =DF ，BE =DE ，∴F 、E 分别是AC 、BC 的中点，∴CF =BE ，∴AC =AF +CF =AF +BE ， ∴()2AB AF BE =+；（2）延长AC 至点P ，使FP BE =，连接DP ．∵四边形DECF 是正方形，∴DF DE =，90DFC DEC ∠=∠=︒．∵FP BE =，90DFC DEB ∠=∠=︒，DF DE =，∴()SAS DFP DEB ≌△△．∴DP DB =．∵AB AF BE =+，AP AF FP =+，FP BE =，∴AP AB =．又∵DP DB =，AD AD =，∴()SSS ADP ADB ≌△△．∴12DAC DAB CAB ∠=∠=∠． 同理可得：12ABD CBD ABC ∠=∠=∠．∵90ACB ∠=︒，∴90CAB CBA ∠+∠=︒． ∴()1452DAB ABD CAB CBA ∠+∠=∠+∠=︒． ∴()180135ADB DAB ABD ∠=︒-∠+∠=︒．（3）∵DF ∥BC ，DE ∥AC ，∴∠CBD =∠NDB ， ∠DAC =∠ADM ，∵ABD CBD ∠=∠，DAC DAB ∠=∠，∴∠ABD =∠NDB ，∠ADM =∠DAB ，∴BN =DN ，AM =DM ．在Rt △MDN 中，由勾股定理得：22222MD DN MN AM BN ==++故答案为：222MN AM BN =+，（4）∵△ABC 是直角三角形，AC =3，BC =4，∴由勾股定理得：AB =5，设正方形DECF 的边长为x ，由（2）知，AP =AB =5，BE =FP ，CP =AP -AC =2，∵FP =CP +CF ，BE =BC -CE ，即4-x =2+x ，解得x =1，∴BE =BC -CE =3，AF =AC -CF =2，∵EM ∥AC ，FN ∥BC ，∴△BME ∽△BAC ，△AFN ∽△ACB ∴34ME BE AC BC ==，23FN AF BC AC ==， ∴94ME =，83FN =． ∵DM =ME -DE =54，DN =FN -DF =53，2512MN ==． 故答案为：2512MN =． 【点睛】 本题考查了正方形的性质，等腰三角形的性质，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理等知识，截长补短法作辅助线是本题的关键．5．（问题原型）如图，在矩形ABCD 中，对角线AC 、BD 交于点O ，以AC 为直径作O ．求证：点B 、D 在O 上．请完成上面问题的证明，写出完整的证明过程．（发现结论）矩形的四个顶点都在以该矩形对角线的交点为圆心，对角线的长为直径的圆上．（结论应用）如图，已知线段2AB=，以线段AB为对角线构造矩形ACBD．求矩形ACBD面积的最大值．（拓展延伸）如图，在正方形ABCD中，2AB=，点E、F分别为边AB、CD的中点，以线段EF为对角线构造矩形EGFH，矩形EGFH的边与正方形ABCD的对角线AC交于M、N两点，当MN的长最大时，矩形EGFH的面积为_____________________解析：问题原型：见解析；结论应用：见解析；发现结论：2；拓展延伸：2【分析】问题原型：运用矩形对角线互相平分且相等，即可求证四点共圆；结论应用：根据结论矩形面积最大时为正方形，利用对角线的长求得正方形的面积；拓展延伸：由上一问的结论，可知四边形EGFH为正方形, 证明四边形AEOH是正方形，继而求得面积【详解】解：【问题原型】∵AC为O直径，∴OA为O半径.=.令OA r∵四边形ABCE为矩形，∴AC BD =，12OA OC AC ==，.12OB OD BD == ∴OB OD OA r ===.∴点B 、D 在O 上.【结论应用】 连续CD 交AB 于点O ，过点D 作DE AB ⊥于点E .∴DE OD ≤.由【发现结论】可知，点D 在以AB 为直径的圆上，即112OD OA AB ===， ∴当1DE OD ==即AB CD ⊥时，矩形ACBD 的面积最大.2AB CD ==∴矩形ACBD 的面积最大值为22112222AB =⨯=. 【拓展延伸】 如图，连接GH ,设AC 与EF 的交点为O四边形ABCD 是正方形2AB ∴=,90BAD ADC ∠=∠=︒，//AE DF点E 、F 分别为边AB 、CD 的中点1AE EB CF FD ∴====,2EF =∴四边形AEFD 是矩形//EF AD ∴EF AB ⊥，由【结论应用】可知，2EF =时，矩形EGFH 的面积最大为2122EF = 此时四边形EGFH 为正方形，此时MN 最大，EF GH ∴⊥,112EO OF OH OG EF ===== ∴四边形AEOH 是正方形∴112AE AH AB === ∴2222112EH AE AH =++∴正方形EGFH 的面积为：22(2)2EH ==【点睛】本题考查了矩形的性质，正方形的性质与判定，灵活运用矩形，正方形的性质和判定是解题的关键．6．（概念学习）在平面直角坐标系xOy 中，O 的半径为1，若O 平移d 个单位后，使某图形上所有点在O 内或O 上，则称d 的最小值为O 对该图形的“最近覆盖距离”．例如，如图①，()(),3,04,0A B ，则O 对线段AB 的“最近覆盖距离”为3．（概念理解）（1）O 对点()3,4的“最近覆盖距离”为_ ．（2）如图②，点Р是函数24y x =+图像上一点，且O 对点Р的“最近覆盖距离”为3，则点Р的坐标为_ ．（拓展应用）（3）如图③，若一次函数4y kx =+的图像上存在点C ，使O 对点C 的“最近覆盖距离”为1，求k 的取值范围．（4）()()3,4,1D m E m +、，且42m -<<，将О对线段DE 的“最近覆盖距离”记为d ，则d 的取值范围是 ．解析：（1）4；（2）()0,4或1612,55⎛⎫-- ⎪⎝⎭；（3）3k ≥3k ≤-4）332d ≤<【分析】（1）求出点(3,4)与原点的距离，这个距离与1的差即是所求结果；（2）设点P 的坐标为(),24x x +，根据P 到圆心的距离为4及勾股定理，可得关于x 的方程，解方程即可求得点P 的坐标；（3）考虑临界状态，当OC =2时，函数图象上存在点C ，使O 对点C 的“最近覆盖距离”为1，利用三角形相似求出3k =;同理，另一个临界状态为3k =-，即可求解； （4）由题意可得DE 是一条倾斜角度为45°,长度为2的线段，可在圆上找到两条与之平行且等长的弦AB 、FG ，如果D 落在弧AF 上，或者落在弧BG 上，进而求解．【详解】（1）点(3,4)与原点的距离为22345+=，而5－1=4，则O 对点()3,4的“最近覆盖距离”为4；故答案为：4（2）由题意可知，Р到圆的最小距离为3，即Р到圆心的距离为4由点P 在直线24y x =+上，故设,2()4P x x +，则()2222416OP x x =++=解得12160,5x x ==- 故点P 的坐标为：()0,4或1612,55⎛⎫-- ⎪⎝⎭ 故答案为：()0,4或1612,55⎛⎫-- ⎪⎝⎭ （3）如图，考虑临界状态，过O 作OC ⊥DE 于C 点，当2OC =时，函数图像上存在点C ，使O 对点C 的“最近覆盖距离”为1,OCD EOD ODC EDO ∠=∠∠=∠OCD EOD ∴∆∆OC OD OE DE∴= 则12OE OC DE OD == 设,OE x =则2DE x =由勾股定理可得：()22162x x += 解得12443,333x x ==-（舍） 43,03E ⎛⎫∴- ⎪⎝⎭此时3k =．同理，另一个临界状态为3k =-经分析可知，函数相比临界状态更靠近y 轴，则存在点C3k ∴≥或3k ≤-()4332d ≤<由题意可知，DE 是一条倾斜角度为45，长度为2的线段可在圆上找到两条与之平行且等长的弦,AB FG如果D 落在弧AF 上，或者E 落在弧BG 上，则成立当12m -≤<时，E 到弧BG 的最小距离为1EO -此时34,d ≤<当41m -<<-时，E 到弧BG 的最小距离为EB此时332d <<综上332d ≤<【点睛】本题是圆的综合题，主要考查了一次函数的性质、圆的基本知识、三角形相似的判定与性质、新定义等，数形结合是本题解题的关键．7．（了解概念）在凸四边形中，若一边与它的两条邻边组成的两个内角相等，则称该四边形为邻等四边形，这条边叫做这个四边形的邻等边．（理解运用）（1）在邻等四边形ABCD 中，40A ∠=︒，60B ∠=︒，若CD 是这个邻等四边形的邻等边，则C ∠的度数为__________；（2）如图，凸四边形ABCD 中，P 为AB 边的中点，ADP PDC ∽，判断四边形ABCD 是否为邻等四边形，并证明你的结论；（拓展提升）（3）在平面直角坐标系中，AB 为邻等四边形ABCD 的邻等边，且AB 边与x 轴重合，已知(2,0)A -，(,3)C m ，(2,4)D ，若在边AB 上使DPC BAD ∠=∠的点P 有且仅有1个，则m 的值是__________．解析：（1）130°；（2）四边形ABCD 是邻等四边形，理由见解析；（3）﹣6【分析】（1）根据邻等四边形的定义即可求解；（2）由△ADP ∽△PDC ，可得AP AD PC PD =，∠DAP ＝∠DPC ，∠APD ＝∠PCD ，由P 为AB 的中点，可得AP ＝BP ，则PB AD PC PD=，可证△BPC ∽△ADP ，由相似三角形的性质得出∠A ＝∠B 即可；（3）①若点B 在点A 右侧，如图，由AB 为邻等边，则有∠DAB ＝∠ABC ＝∠DPC ，可证△ADP ∽△BPC ，可得AP BC ＝AD BP ，设点P （n ，0），由等腰直角三角形可求∠BAD ＝45°，可求B 、C 横坐标之差为3，B （m +3，0），将AP ，BP ，AD ，BC ，代入得：4232n 2+（m +1）n +2m ﹣18＝0，由题意可知n 只有一个解，可求得m ＝﹣6；②若点B 在点A 左侧，可求得∠BAD ＝135°，可证△ADP ∽△BPC ，可得AP BC ＝AD BP ，可求得B 、C 横坐标之差为34232=m ＝﹣5﹣6． 【详解】解：（1）∵CD 为邻等边，∴∠C ＝∠D ，又∵40A ∠=︒，60B ∠=︒，∴∠C ＝∠D ＝（360°﹣∠A ﹣∠B ）÷2＝130°，∴∠C ＝130°．故答案为：130°；（2）四边形ABCD 是邻等四边形，理由如下：∵△ADP ∽△PDC ， ∴AP AD PC PD=，∠DAP ＝∠DPC ，∠APD ＝∠PCD ，∠ADP ＝∠PDC ， 又∵P 为AB 的中点，∴AP ＝BP ，∴PB ADPC PD=，∴PB PCAD PD=，∵∠APD+∠BPC＝180°﹣∠DPC，∠PCD+∠PDC＝180°﹣∠DPC，且∠APD＝∠PCD，∴∠BPC＝∠PDC，∵∠ADP＝∠PDC，∴∠ADP＝∠BPC，∴△BPC∽△ADP，∴∠B＝∠A，∴四边形ABCD为邻等四边形；（3）若点B在点A右侧，如图，∵AB为邻等边，则有∠DAB＝∠ABC＝∠DPC，又∵∠ADP+∠DPA＝180°﹣∠DAB，∠BPC+∠DPA＝180°﹣∠DPC，∴∠DAB＝∠DPC，∠ADP＝∠BPC，∴△ADP∽△BPC，∴APBC ＝ADBP，设点P（n，0），∵A（﹣2，0），D（2，4），∴∠BAD＝45°，∴∠ABC＝45°，过点C作CE⊥x轴于点E，则∠CEB＝90°，∠BCE＝∠ABC＝45°，∴CE＝BE，∵点C（m，3），∴CE＝3，∴BE＝3，∴B（m+3，0），∴AP＝n+2，BP＝m+3﹣n，∴AD＝22(22)4++＝42，BC＝2233+＝32，代入APBC＝ADBP得：242332nm n+=+-，整理可得：﹣n2+（m+1）n+2m﹣18＝0，由题意可知n只有一个解，∴△＝（m+1）2+4（2m﹣18）＝0，解得：m＝﹣5±46，又∵点C在点D右侧，∴m＝﹣5+46；②若点B在点A左侧，如图，此时，∵A（﹣2，0），D（2，4），∴∠OAD＝45°，∴∠BAD＝∠ABC＝∠DPC＝135°，∵∠ADP+∠DPA＝180°﹣∠DAB，∠BPC+∠DPA＝180°﹣∠DPC，∴ADP＝∠BPC，∴△ADP∽△BPC，∴APBC ＝ADBP，由①得：B（m+3，0），C（m，3），P（n，0），AP＝﹣2﹣n，BP＝n﹣m﹣3，AD＝42BC＝32∴4232=，解得：m＝﹣6又∵点C在点D左侧，∴m＝﹣5﹣6；综上所述：m＝﹣6．【点睛】本题是相似综合题，考查新定义图形，仔细阅读题目，抓住定义中的性质，会验证新定义图形，相似三角形的判定与性质，一元二次方程根的判别式，利用相似三角形的性质构造关于n 的一元二次方程是解题关键．8．如图所示，在△ABC 中，AB BC =，D 、E 分别是边AB 、BC 上的动点，且BD BE =，连结AD 、AE ，点M 、N 、P 分别是CD 、AE 、AC 的中点，设B α∠=．（1）观察猜想①在求MN CE 的值时，小明运用从特殊到一般的方法，先令60α=︒，解题思路如下： 如图1，先由,AB BC BD BE ==，得到CE AD =，再由中位线的性质得到PM PN =， 60NPM ∠=︒，进而得出△PMN 为等边三角形，∴12MN NP CE CE ==． ②如图2，当90α=︒，仿照小明的思路求MN CE 的值； （2）探究证明如图3，试猜想MN CE 的值是否与()0180αα︒<<︒的度数有关，若有关，请用含α的式子表示出MN CE，若无关，请说明理由； （3）拓展应用如图4，2,36AC B =∠=︒，点D 、E 分别是射线AB 、CB 上的动点，且AD CE =，点M 、N 、P 分别是线段CD 、AE 、AC 的中点，当1BD =时，请直接写出MN 的长．解析：（1）②2MN CE =2）MN CE 的值与α的度数有关，sin 2MN CE α=；（3）MN 的长55-35+ 【分析】（1）②先根据线段的和差求出AD CE =，再根据中位线定理、平行线的性质得出,45PM PN APN CPM =∠=∠=︒，从而可得出90NPM ∠=︒，然后根据等腰直角三角形的性质即可得；（2）参照题（1）的方法，得出PMN 为等腰三角形和NPM ∠的度数，再利用等腰三角形的性质即可求出答案；（3）分两种情况：当点D 、E 分别是边AB 、CB 上的动点时和当点D 、E 分别是边AB 、CB的延长线上的动点时，如图（见解析），先利用等腰三角形的性质与判定得出,ABC BCE CAB AFC ∠=∠∠=∠，再根据相似三角形的判定与性质得出BC 、CE 的长，由根据等腰三角形的三线合一性得出1,182BP AC CBP ABC ⊥∠=∠=︒，从而可得sin18︒的值，最后分别利用（2）的结论即可得MN 的长．【详解】（1）②,AB BC BD BE ==∴AD CE =,90AB BC B =∠=︒∴ABC 为等腰直角三角形，45ACB CAB ∠=∠=︒∵点M 、N 、P 分别是CD 、AE 、AC 的中点11//,,//,22PN CE PN CE PM AD PM AD ∴== ,45,45PM PN APN ACB CPM CAB ∴=∠=∠=︒∠=∠=︒∴18090NPM APN CPM ∠=︒-∠-∠=︒∴PMN 为等腰直角三角形，∴222MN PN CE ==即22MN CE =； （2）MN CE的值与α的度数有关，求解过程如下： 由（1）可知，PM PN =，即PMN 为等腰三角形180180NPM APN CPM ACB CAB B α∠=︒-∠-∠=︒-∠-∠=∠=如图5，作PH MN ⊥则11,222NH MN NPH NPM α=∠=∠= 在Rt NPH 中，sin NH NPH PN∠=，即12sin 122MN CE α= 则sin 2MN CE α=；（3）依题意，分以下两种情况：①当点D 、E 分别是边AB 、CB 上的动点时如图6，作ACB ∠的角平分线交AB 边于点F ，并连结BP2,36,AC ABC AB AC =∠=︒=72ACB CAB ∴∠=∠=︒ 136,722ACE BCE ACB AFC ABC BCE ∴∠=∠=∠=︒∠=∠+∠=︒ ,ABC BCE CAB AFC ∴∠=∠∠=∠2BF CF AC ∴===，ACF ABC ~AF AC AC AB∴=，即2AC AF AB =⋅ 设==AB BC x ，则2AF AB BF x =-=-22(2)x x ∴=-解得15x 或15x =-（不符题意，舍去）即15BC =+1515CE BC BE BC BD ∴=-=-=+-=由（2）可知，36sin sin182MN CE ︒==︒ sin185sin18MN CE ∴=⋅︒=︒点P 是AC 上的中点1,182BP AC CBP ABC ∴⊥∠=∠=︒，112CP AC ==（等腰三角形的三线合一） 在Rt CBP 中，sin CP CBP BC ∠=，即151sin18415-︒==+ 51555sin18544MN --∴=︒=⨯= ②如图7，当点D 、E 分别是边AB 、CB 的延长线上的动点时同理可得：15BC =+15125CE BC BE BC BD ∴=+=+=++=+5135sin18(25)44MN CE -+∴=⋅︒=+⨯= 综上，MN 的长为554-或354+．【点睛】本题考查了中位线定理、平行线的性质、相似三角形的判定与性质、等腰三角形的性质、解直角三角形等知识点，较难的是题（3），依据题意，正确分两种情况，并结合题（2）的结论是解题关键．9．问题背景（1）如图（1），ABD △，AEC 都是等边三角形，ACD △可以由AEB △通过旋转变换得到，请写出旋转中心、旋转方向及旋转角的大小．尝试应用（2）如图（2）．在Rt ABC 中，90ACB ∠=︒，分别以AC ，AB 为边，作等边ACD △和等边ABE △，连接ED ，并延长交BC 于点F ，连接BD ．若BD BC ⊥，求DF DE的值． 拓展创新（3）如图（3）．在Rt ABC 中，90ACB ∠=︒，2AB =，将线段AC 绕点A 顺时针旋转90︒得到线段AP ，连接PB ，直接写出PB 的最大值．解析：（1）旋转中心是点A ，旋转方向是顺时针，旋转角是60︒；（2）23；（3）51．【分析】 （1）由等边三角形得出60BAD ∠=︒，60CAE ∠=︒，AD AB =，AC AE =，证明()ACD AEB SAS ≌，由旋转性质即可得；（2）证明()ADE ACB SAS ≌，由全等三角形的性质得90ADE ACB ∠=∠=︒，DE CB =，得出30BDF ∠=︒，由30直角三角形性质得12BF DF =，则可计算得答案； （3）过点A 作AE AB ⊥，且使AE =AD ，连接PE ，BE ，由直角三角形的性质求出BE 、PE 的长即可得解．【详解】解（1）∵ABD △，AEC 都是等边三角形，∴60BAD ∠=︒，60CAE ∠=︒，AD AB =，AC AE =，BAD BAC CAE BAC ∴∠+∠=∠+∠， DAC BAE ∴∠=∠，()ACD AEB SAS ∴≌，ACD ∴可以由AEB △绕点A 顺时针旋转60︒得到，即旋转中心是点A ，旋转方向是顺时针，旋转角是60︒；（2)ACD 和ABE △都是等边三角形，AC AD ∴=，AB AE =，60CAD BAE ∠=∠=︒，CAB DAE ∴∠=∠，()ADE ACB SAS ∴≌，90ADE ACB ∴∠=∠=︒，DE CB =，90ADE ∠=︒，90ADF ∴∠=︒，60ADC ACD ∠=∠=︒，30DCF CDF ∴∠=∠=︒，CF DF ∴=，BD BC ⊥，30BDF ∴∠=︒，设BF =x ，则CF =DF =2x ，DE =3x ， ∴2233DF x DE x ==； （3）90ACB ∠=︒，∴点C 在以AB 为直径的圆上运动，取AB 的中点D ，连接CD ，112CD AB ∴==， 如图，过点A 作AE AB ⊥，且使AE =AD ，连接PE ，BE ，∵将线段AC 绕点A 顺时针旋转90︒得到线段AP ，90PAC ∴∠=︒，PA =AC ．90EAD ∠=︒，PAE CAD ∴∠=∠，()CAD PAE SAS ∴≌，∴PE =CD =1．∵AB =2，AE =AD =1，∴BE =22AE AB +=2212+=5，51BP BE PE ∴≤+=+，∴BP 的最大值为5+1．【点睛】本题是几何变换的综合题，考查了旋转的性质、等边三角形的性质、全等三角形的判定与性质、勾股定理、直角三角形的性质、圆周角定理；熟练掌握旋转的性质是本题的关键． 10．（感知）如图1，在平面直角坐标系中，点C 的坐标为(0,0.5)，点A 的坐标为(1,0)，将线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ，过点B 作BM y ⊥轴，垂足为点M ，易知AOC CMB ∆∆≌，得到点B 的坐标为(0.5,1.5)．（探究）如图2，在平面直角坐标系中，点A 的坐标为(1,0)，点C 的坐标为(0,)(0)m m >，将线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ．（1）求点B 的坐标．（用含m 的代数式表示）（2）求出BC 所在直线的函数表达式．（拓展）如图3，在平面直角坐标系中，点A 的坐标为(1,0)，点C 在y 轴上，将线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ，连结BO 、BA ，则BO BA +的最小值为_______．解析：【探究】（1）点B 坐标为(,1)m m +；（2）1y x m m=+；【拓展】5． 【分析】探究:（1）证明△AOC ≌△CMB （AAS ），即可求解；（2）根据点B 的坐标为（m ，m+1），点C 坐标()0,m ，即可求解；拓展：BO+BA=2222(1)(1)(1)m m m m +++-++，BO+BA 的值，相当于求点P （m ，m ）到点M （1，-1）和点N （0，-1）的最小值，即可求解．【详解】解：探究：（1）过点B 作BM y ⊥轴，垂足为点M ．BMC 90∠∴=︒，MCB B 90∠∠∴+=︒．线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ，BCA 90CB CA ∠∴=︒=，．MCB ACO 90∠∠∴+=︒．B ACO ∠∠∴=．ACO 90∠=︒，ΔAOC ΔCMB ∴≌，MC OA,MB OC ∴==．点C 坐标()0,m ，点A 坐标()1,0，∴点B 坐标为()m,m 1+（2）∵点B 的坐标为（m ，m+1），点C 为（0，m ），设直线BC 为：y=kx+b ，1b m km b m =⎧⎨+=+⎩，解得：1k m b m ⎧=⎪⎨⎪=⎩， ∴1y x m m=+； 则BC 所在的直线为：1y x m m=+； 拓展：如图作BH ⊥OH 于H ．设点C 的坐标为（0，m ），由（1）知：OC=HB=m ，OA=HC=1，则点B （m ，1+m ），则：BO+BA=2222(1)(1)(1)m m m m +++-++，BO+BA 的值，相当于求点P （m ，m ）到点M （1，-1）和点N （0，-1）的最小值，相当于在直线y=x 上寻找一点P （m ，m ），使得点P 到M （0，-1），到N （1，-1）的距离和最小，作M 关于直线y=x 的对称点M′（-1，0），易知PM+PN=PM′+PN≥NM′，M′N=22--++=，(11)(01)5故：BO+BA的最小值为5，故答案为：5．【点睛】本题为一次函数综合题，主要考查的是三角形全等的思维拓展，其中拓展，将BO+BA的值转化点P（m，m）到点M（1，-1）和点N（0，-1）的最小值，是本题的新颖点11．（知识再现）学完《全等三角形》一章后，我们知道“斜边和一条直角边分别相等的两个直角三角形全等（简称HL定理）”是判定直角三角形全等的特有方法．（简单应用）如图（1），在△ABC中，∠BAC＝90°，AB＝AC，点D、E分别在边AC、AB上．若CE＝BD，则线段AE和线段AD的数量关系是．（拓展延伸）在△ABC中，∠BAC＝α（90°＜α＜180°），AB＝AC＝m，点D在边AC上．（1）若点E在边AB上，且CE＝BD，如图（2）所示，则线段AE与线段AD相等吗？如果相等，请给出证明；如果不相等，请说明理由．（2）若点E在BA的延长线上，且CE＝BD．试探究线段AE与线段AD的数量关系（用含有a、m的式子表示），并说明理由．解析：【简单应用】AE＝AD；【拓展延伸】（1）相等，证明见解析；（2）AE﹣AD＝2AC•cos（180°﹣α），理由见解析【分析】简单应用：证明Rt△ABD≌Rt△ACE（HL），可得结论．拓展延伸：（1）结论：AE＝AD．如图（2）中，过点C作CM⊥BA交BA的延长线于M，过点N作BN⊥CA交CA的延长线于N．证明△CAM≌△BAN（AAS），推出CM＝BN，AM ＝AN，证明Rt△CME≌Rt△BND（HL），推出EM＝DN，可得结论．（2）如图（3）中，结论：AE﹣AD＝2m•cos（180°﹣α）．在AB上取一点E′，使得BD＝CE′，则AD＝AE′．过点C作CT⊥AE于T．证明TE＝TE′，求出AT，可得结论．【详解】简单应用：解：如图（1）中，结论：AE＝AD．理由：∵∠A＝∠A＝90°，AB＝AC，BD＝CE，∴Rt△ABD≌Rt△ACE（HL），∴AD＝AE．故答案为：AE＝AD．拓展延伸：（1）结论：AE＝AD．理由：如图（2）中，过点C作CM⊥BA交BA的延长线于M，过点N作BN⊥CA交CA的延长线于N．∵∠M＝∠N＝90°，∠CAM＝∠BAN，CA＝BA，∴△CAM≌△BAN（AAS），∴CM＝BN，AM＝AN，∵∠M＝∠N＝90°，CE＝BD，CM＝BN，∴Rt△CME≌Rt△BND（HL），∴EM＝DN，∵AM＝AN，∴AE＝AD．（2）如图（3）中，结论：AE﹣AD＝2m•cos（180°﹣ ）．理由：在AB上取一点E′，使得BD＝CE′，则AD＝AE′．过点C作CT⊥AE于T．∵CE′＝BD，CE＝BD，∴CE＝CE′，∵CT⊥EE′，∴ET＝TE′，∵AT＝AC•cos（180°﹣α）＝m•cos（180°﹣α），∴AE﹣AD＝AE﹣AE′＝2AT＝2m•cos（180°﹣α）．【点睛】本题主要考查了全等三角形的性质与判定，等腰三角形的性质与判定，解直角三角形等知识，解题的关键在于能够熟练寻找全等三角形解决问题.12．问题提出（1）如图①，在△ABC中，BC＝6，D为BC上一点，AD＝4，则△ABC面积的最大值是．问题探究（2）如图②，已知矩形ABCD的周长为12，求矩形ABCD面积的最大值．问题解决（3）如图③，△ABC是葛叔叔家的菜地示意图，其中AB＝30米，BC＝40米，AC＝50米，现在他想利用周边地的情况，把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地，用来建鱼塘．已知葛叔叔欲建的鱼塘是四边形ABCD，且满足∠ADC＝60°．你认为葛叔叔的想法能否实现？若能，求出这个四边形鱼塘周长的最大值；若不能，请说明理由．解析：（1）12；（2）9；（3）能实现；170（米）．【分析】（1）当AD⊥BC时，△ABC的面积最大．（2）由题意矩形邻边之和为6，设矩形的一边为m，另一边为6﹣m，可得S＝m（6﹣m）＝﹣（m﹣3）2+9，利用二次函数的性质解决问题即可．（3）由题意，AC＝100，∠ADC＝60°，即点D在优弧ADC上运动，当点D运动到优弧ADC的中点时，四边形鱼塘面积和周长达到最大值，此时△ACD为等边三角形，计算出△ADC的面积和AD的长即可得出这个四边形鱼塘面积和周长的最大值．【详解】（1）如图①中，∵BC＝6，AD＝4，∴当AD⊥BC时，△ABC的面积最大，最大值＝1×6×4＝12．2故答案为12．（2）∵矩形的周长为12，∴邻边之和为6，设矩形的一边为m ，另一边为6﹣m ， ∴S ＝m （6﹣m ）＝﹣（m ﹣3）2+9， ∵﹣1＜0，∴m ＝3时，S 有最大值，最大值为9． （3）如图③中，∵AC ＝50米，AB ＝40米，BC ＝30米， ∴AC 2＝AB 2+BC 2 ∴∠ABC ＝90°，作△AOC ，使得∠AOC ＝120°，OA ＝OC ，以O 为圆心，OA 长为半径画⊙O ， ∵∠ADC ＝60°，∴点D 在优弧ADC 上运动，当点D 是优弧ADC 的中点时，四边形ABCD 面积取得最大值，设D ′是优弧ADC 上任意一点，连接AD ′，CD ′，延长CD ′到F ，使得D ′F ＝D ′A ，连接AF ，则∠AFC ＝30°＝12∠ADC ，∴点F 在D 为圆心DA 为半径的圆上， ∴DF ＝DA ， ∵DF +DC ≥CF ， ∴DA +DC ≥D ′A +D ′C ， ∴DA +DC +AC ≥D ′A +D ′C +AC ，∴此时四边形ADCB 的周长最大，最大值＝40+30+50+50＝170（米）． 答：这个四边形鱼塘周长的最大值为170（米）． 【点睛】本题主要是最大值的考查，求最大值，常用方法为： （1）利用平方为非负的性质求解；（2）利用三角形两边之和大于第三边求解，在求解过程中，关键在与将要求解的线段集中到一个三角形中13．（1）问题发现如图1，在OAB 和OCD 中，OA OB =，OC OD =，40AOB COD ∠=∠=︒，连接,AC BD 交于点M .填空：①ACBD的值为______；②AMB ∠的度数为______．（2）类比探究如图2，在OAB 和OCD 中，90AOB COD ∠=∠=︒，30OAB OCD ∠=∠=︒，连接AC 交BD 的延长线于点M .请判断ACBD的值及AMB ∠的度数，并说明理由； （3）拓展延伸在（2）的条件下，将OCD 绕点O 在平面内旋转，,AC BD 所在直线交于点M ，若1OD =，3OB =，请直接写出当点A 与点O D 、在同一条直线上时AD 的长．解析：（1）①1；②40︒；（2）3ACBD=90AMB ∠=︒．理由见解析；（3）2或4．【分析】（1）①证明△COA ≌△DOB （SAS ），得AC=BD ，比值为1；②由△COA ≌△DOB ，得∠CAO=∠DBO ，然后根据三角形的内角和定理先求∠OAB+∠OBA 的值，再求∠AMB 的值即可； （2）根据锐角三角比可得OD OBOC OA=，根据两边的比相等且夹角相等可得△AOC ∽△BOD ，根据相似撒尿性的性质求解即可；（3）当点A 与点O D 、在同一条直线上，有两种情况：如图3和图4，然后根据旋转的性质和勾股定理，可得AD 的长． 【详解】（1）①∵40AOB COD ∠=∠=︒， ∴∠BOD=∠AOC ， 又∵OA OB =，OC OD =， ∴△BOD ≌△AOC ， ∴BD=AC ， ∴ACBD=1； ②∵40AOB ∠=︒， ∴∠OAB+∠OBA=140°， ∵△BOD ≌△AOC ， ∴∠CAO=∠DBO ，∴∠CAO+∠OAB+∠ABM=∠DBO+∠OAB+∠ABM=∠OAB+∠OBA=140°， ∴∠AMB=40︒； （2）如图2，3ACBD=，90AMB ∠=︒．理由如下：Rt COD 中，30DCO ∠=︒，90DOC ∠=︒，3tan 303OD OC ∴=︒=， 同理得：3tan 303OB OA =︒=， OD OB OC OA∴=， 90AOB COD ∠=∠=︒， AOC BOD ∴∠=∠， AOC BOD ∴△∽△，3AC OCBD OD∴==，∠CAO=∠DBO ， ∵∠BEO+∠DBO=90°， ∴∠CAE+∠AEM=90°， ∴∠AMB=90°；（3） ∵∠A=30°，3OB =， ∴OA=tan 30OB=3． 如图3，当点D 和点A 在点O 的同侧时， ∵1OD =， ∴AD=3-2=2；如图4，当点D 和点A 在点O 的两侧时，∵1OD ，，OA=3∴AD=3+1=4．综上可知，AD的长是2或4．【点睛】本题是三角形的综合题，主要考查了三角形全等和相似的性质和判定，相似三角形的判定与性质，解直角三角形，旋转的性质，以及分类讨论的数学思想，解题的关键是能得出：△AOC∽△BOD，根据相似三角形的性质，并运用类比的思想解决问题，本题是一道比较好的题目．14．探究：小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P1（x1，y1），P2（x2，y2），可通过构造直角三角形利用图1得到结论：他还利用图2证明了线段P1P2的中点P（x，y）P的坐标公式：，．（1）请你帮小明写出中点坐标公式的证明过程；运用：（2）①已知点M（2，﹣1），N（﹣3，5），则线段MN长度为；②直接写出以点A（2，2），B（﹣2，0），C（3，﹣1），D为顶点的平行四边形顶点D 的坐标：；拓展：（3）如图3，点P（2，n）在函数（x≥0）的图象OL与x轴正半轴夹角的平分线上，请在OL、x轴上分别找出点E、F，使△PEF的周长最小，简要叙述作图方法，并求出周长的最小值．解析：（1）答案见解析；（2）①；②（﹣3，3）或（7，1）或（﹣1，﹣3）；（3）．【详解】试题分析：（1）用P1、P2的坐标分别表示出OQ和PQ的长即可证得结论；。

数学知识点小升初数学综合错题集新人教版总结----bb4a3de6-6eb3-11ec-adaf-7cb59b590d7d数学知识点小升初数学综合错题集新人教版-总结初中数学、数学课件、数学综合习题、数学教案、数学试卷综合错题集一、填空：（共21分，每项1分）1、70305880读作()，改写成用“万”作单位的数是（），省略万位后的尾数是关于（）。

2、2021年第16届广州亚运会的举办时间为2021年11月12日――11月日，那么这届亚运会要经历（）个星期还多（）天。

十二3、把2∶1化成最简整数比是()，比值是()。

83124、3÷（）=（）÷24==75%=（）折。

??5、如图中圆柱的底面半径是（），把这个圆柱的侧面展开可以得到一个长方形，这个长方形的面积是（），这个圆柱体的体积是（）。

(圆周率为π)10cm8cm555×155？156、=，=，777×()7?(___)7.1kg盐水含50g盐，占盐水的（）%。

8、78能同时被2、3、5整除，个位只能填（），百位上最大能填（）。

9、一所学校男学生与女学生的比是4：5，女学生比男学生人数多（）%。

10、一座城市地图中两地图上距离为10cm，表示实际距离30km，该幅地图的比例尺是（）。

（1）二、判断题：（共５分每题1分）1.自然数（0除外）是素数或复合数。

（）2、小于五分之四而大于五份之二的分数只有五份之三。

（）3.圆柱体的底部和高度与圆锥体相同，其体积和为36立方米，因此圆锥体为初中数学、数学课件、数学综合练习题、数学教学教案、试卷数学初中数学、数学课件、数学综合练习题、数学教学教案、试卷数学体积是9立方米。

（）4.生产的90个零件中，10个为废品，合格率为90%。

（5）“一只青蛙有四条腿、两只眼睛和一张嘴；两只青蛙有八条腿、四只眼睛、两只嘴和三只青蛙……那么青蛙的数量与腿的数量成正比。

”（）三、选择题：（５分每题1分）1、一月、二月和2022月份有。

成都嘉祥周末作业数学易错题集⼀：填空题5、⾃然数M, N满⾜：10-M=M-N=N-4，则M+N=（）。

8、有⼀个不为0的⾃然数，它的12是⼀个⽴⽅数，它的13是⼀个平⽅数，则这个数最⼩是（）。

11、⼀个分数的分⼦加上8，就可以约分为12，如果分⼦减去4，就可以约分为110，原分数的分⼦、分母同时加上同⼀个数，则可约分为12，则加上的这个数为（）。

13、⼀列⽕车驶过250⽶的隧道⽤了20秒，若将⽕车的速度提⾼⼀半，则通过330⽶隧道只⽤16秒，则这列⽕车的长为（）⽶。

14、把20%的糖⽔和30%的糖⽔混合在⼀起，想配成24%的糖⽔。

可是不⼩⼼把⽐例弄反了，则错配了的糖⽔的浓度为（）。

⼆，答题1、两数相除商9余4，如果被除数，除数都扩⼤3倍，那么被除数，除数，商，余数之和等于333，则原来的被除数是多少？2、菜地⾥的西红柿获得丰收，摘了全部的25时，装满了3筐后还有16千克不够装⼀筐，摘完其余部分后，⼜装满6筐，则共收得西红柿多少千克？3，甲⼄⼆⼈分别从⼭顶和⼭脚同时出发，沿同⼀⼭道⾏进，两⼈上⼭速度都是20⽶/分，下⼭速度都是30⽶/分，甲到达⼭脚⽴即返回，⼄到达⼭顶休息30分钟后返回，两⼈在距⼭顶480⽶处再次相遇，⼭道长多少⽶？3、分⼦、分母的乘积是2010的最简真分数有（）个。

4、n是⼀个⾮0⾃然数，12n是平⽅数，1n是⽴⽅数，则n 的最⼩值是（）。

5、所有⼗位数字和个位数字都是奇数的两位数的和是（）。

6、如右图，正六边形的⾯积为66平⽅厘⽶，三⾓形的顶点均为各边上的中点，则三⾓形的⾯积为（）。

10、甲、⼄、丙三⼈同时从A地出发去B地，结果甲⽐⼄早到5分钟，⼄⽐丙早到5分钟，已知甲每分钟⾏80⽶，丙每分钟⾏60⽶，那么⼄每分钟⾏（）⽶。

11、⼀组同学搬⼀堆砖，若每⼈搬a块，还剩下14块；若每⼈搬9块，最后⼀⼈只搬6块，这组同学共有（）⼈。

13、甲、⼄两家共养鸡106只，甲家养的鸡中，公鸡占38；⼄家养的鸡中，母鸡占511,甲、⼄两家共养母鸡（）。

四年级数学下册易错题综合训练（学习版）编制人：__________________审核人：__________________审批人：__________________编制学校：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的学习资料，如英语资料、语文资料、数学资料、物理资料、化学资料、生物资料、地理资料、历史资料、政治资料、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides various types of learning materials for everyone, such as English materials, language materials, mathematics materials, physical materials, chemical materials, biological materials, geographic materials, historical materials, political materials, other materials, etc. Please pay attention to the data format and writing method!四年级数学下册易错题综合训练易错题综合练习一、填空题1、用6、2、7三个数字组成小数部分是两位的小数，其中组成的最小的小数和最大的小数相差( )。

成都市六年级下册数学专项复习卷：易错题姓名:________ 班级:________ 成绩:________小朋友，带上你一段时间的学习成果，一起来做个自我检测吧，相信你一定是最棒的！一、填空。

（共15分） (共8题；共15分)1. （2分） (2018四上·西宁月考) 由3个十亿，5个百万和6个千组成的数，写作________;读作________。

这个数“四舍五入”到“万位”约是________万。

2. （2分）写出与下面量具有相反意义的量．方向盘顺时针转动30°．________转动30°3. （3分）(2013·铜仁) 。

________ .4. （2分） (2019五上·临河期末) 已知0.3x+8＝20，那么5x﹣90＝________．5. （2分）(2018·永川) 0.6=24：________=________%=________折=________（填分数）6. （1分）甲、乙两人每天加工零件个数的比是3：4，两人合作15天后，甲、乙两人各自加工零件的个数比是________。

7. （1分） (2019六下·泉州期中) 园林绿化队要栽一批树苗，第一天栽了总数的二成五，第二天栽了210棵，这时剩下的与已栽的棵数比是3：2．这批树苗一共有________棵．8. （2分）(2018·永安) 下面的________圆柱与左面的圆锥体积相等。

二、判断。

（8分） (共8题；共8分)9. （1分）如果一个分数的分子和分母的最大公因数是1，那么这个分数就是最简分数。

10. （1分）判断。

（1）一条直线长5厘米。

（2）线段是直线的一部分。

（3）黑板的边是一条射线。

（4）直线比射线长11. （1分） (2019五上·潍坊期中) 15除以16的商是有限小数。

（）12. （1分）折线统计图只能表示数据的变化趋势，不能体现数据的多少。

成都嘉祥外国语学校郫县分校中考数学期末规律问题数字变化类汇编一、规律问题数字变化类1．如图是一组按照某种规律摆放而成的图形，第1个图中有3条线段，第二个图中有8条线段，第三个图中有15条线，……，则第10个图中线段的条数是（ ）A ．60B ．90C ．120D ．1432．已知有理数a≠1，我们把11a -称为a 的差倒数，如： 2的差倒数是112-＝－1，－1的差倒数11(1)--＝12．如果a 1＝－2， a 2是a 1的差倒数，a 3是a 2的差倒数，a 4 是a 3的差倒数……依此类推，那么a 1＋a 2＋……＋a 100的值是（ ）A ．7.35B ．－7.5C ．5.5D ．－5.5 3．点 1A 、 2A 、 3A 、…… 、 n A （n 为正整数）都在数轴上．点 1A 在原点 O 的左边，且 1A O 1=；点 2A 在点 1A 的右边，且 21A A 2=；点 3A 在点 2A 的左边，且 32A A 3=；点 4A 在点 3A 的右边，且 43A A 4=；……，依照上述规律，点 2008A 、 2009A 所表示的数分别为（ ）A ．2008 、 2009-B ．2008- 、 2009C ．1004 、 1005-D ．1004 、 1004-4．观察下列算式：122=，224=，328=，4216=，5232=，6264=，72128=，82256=，……．根据上述算式中的规律，你认为20192的个位数字是（ ） A ．2 B ．4 C ．6 D ．85．观察下列等式：12=1，22=4，32=9，42 =16，52=25，．．．，若22222212345...n ++++++的个位数字是1（02020n <≤，且n 为整数），则n 的最大值是( )A ．2001B ．2006C ．2011D ．20196．某种细胞开始有1个，1小时后分裂成2个，2小时分裂成4个，3小时后分裂成8个，按此规律，n 小时后细胞的个数超过1000个，n 的最小值是（ ）A ．9B ．10C ．500D ．5017．如图所示的运算程序中，若开始输入的x 值为48，我们发现第1次输出的结果为24，第2次输出的结果为12，……第2019次输出的结果为（ ）A ．3B ．6C ．4D ．18．a 是不为2的有理数，我们把22a -称为a 的“哈利数”，如：3的“哈利数”是2223=--，－2的“哈利数”是()21222=--，已知13a =，2a 是1a 的“哈利数”，3a 是2a 的“哈利数”，4a 是3a 的“哈利数”，…，依次类推，则2018a =（ ）A ．3B ．-2C ．12D ．439．如图是一个按某种规律排列的数阵：根据数阵排列的规律，第n （n 是整数，且n ≥3）行从左向右数第（n ﹣2）个数是（ ）（用含n 的代数式表示）A ．21n -B ．22n -C ．23n -D ．24n - 10．小学时候大家喜欢玩的幻方游戏，老师稍加创新改成了“幻圆”游戏，现在将1-、2、3-、4、5-、6、7-、8分别填入图中的圆圈内，使横、竖以及内外两圈上的4个数字之和都相等，老师已经帮助同学们完成了部分填空，则图中+a b 的值为（ ）A ．8-或1B ．6-或3-C ．1-或4-D ．1或1- 11．如图所示，在这个数据运算程序中，若开始输入的x 的值为2，结果输出的是1，返回进行第二次运算则输出的是4-，⋯，则第2021次输出的结果是（ ）A ．6-B ．4-C ．1-D ．2-12．中国奇书《易经》中记载，远古时期，人们通过在绳子上打结来计数，即“结绳计数”．如图，一位母亲在从右到左依次排列的绳子上打结，满5进1，用来记录孩子自出生后的天数．由图可知，孩子自出生后的天数是（ ）A ．10B ．89C ．165D ．29413．观察下面由正整数组成的数阵：照此规律，按从上到下、从左到右的顺序，第51行的第1个数是（ ）A ．2500B ．2501C ．2601D ．260214．已知整数1234,,,,a a a a ⋅⋅⋅，满足条件：12132430,1,2,3,a a a a a a a ==-+=-+=-+⋅⋅⋅，依次类推2021a 的值为（ ） A ．1009- B ．1010- C ．1011- D ．2020- 15．已知整数1a ，2a ，3a ，4a ，…满足下列条件：10a =，211a a =-+，322a a =-+，433a a =-+，…以此类推，则2018a 的值为（ ）A ．－1007B ．－1008C ．－1009D ．－2018 16．记12n n s a a a =+++，令12n n s s s T n +++=，则称n T 为12,...,n a a a 这列数的“凯森和”．已知51002,...,a a a 的“凯森和”为2004，那么13，51002,...,a a a 的“凯森和”为（ ） A ．2013 B ．2015 C ．2017 D ．201917．若线段122A A =，在线段12A A 的延长线上取一点3A ，使2A 是13A A 的中点；在线段13A A 的延长线上取一点4A ，使3A 是41A A 的中点；在线段41A A 的延长线上取一点5A ，使4A 是15A A 的中点……，按这样操作下去，线段2021A A 的长度为（ ）A ．182B ．192C ．202D ．21218．探究数字“黑洞”：“黑洞”原指非常奇怪的天体，它的体积小，密度大，吸引力强，任何物体到它那里都别想出来，无独有偶，数字中也有类似的“黑洞”,满足某种条件的所有数，通过一种计算，都能被它“吸”进去，无一能逃脱它的魔掌．比如：任意找一个3的倍数，先把这个数每个数位都立方，再相加，得到一个新的数，然后把这个新数每个数位上的数字再立方，求和……，重复运算下去，就能得到一个固定的数T= ，我们称它为数字“黑洞”，T 为何具有如此魔力？通过认真的观察、分析，你一定能发现它的奥秘！此短文中的T 是（ ）A ．363B ．153C ．159D ．45619．a 是不为2的有理数，我们把称为a 的“哈利数”．如：3的“哈利数”是 ，-2的“哈利数”是， 已知，是的“哈利数”，是的“哈利数”，是的“哈利数”，…，依次类推，则=（ ）． A ．3 B ．-2 C ． D ．20．已知有理数1a ≠，我们把11a -称为a 的差倒数，如：2的差倒数是1=-112-，-1的差倒数是11=1(1)2--．如果12a =-，a 2是a 1的差倒数，a 3是a 2的差倒数，a 4是a 3的差倒数……依此类推，那么12100a a a +++的值是（ ）A ．-7.5B ．7.5C ．5.5D ．-5.5 21．一串数字的排列规律是：第一个数是2，从第二个数起每一个数与前一个数的倒数之和为1，则第2020个数是（ ）A ．12-B ．1-C ．2-D ．222．任意大于1的正整数m 的三次幂均可“分裂”成m 个连接奇数的和，如：3235=+，337911=++，3413151719=+++，…按此规律，若3m 分裂后，其中一个奇数是2021，则m 的值是（ ）A ．46B ．45C ．44D ．4323．如图所示的运算程序中，若开始输入的x 值为48，我们发现第1次输出的结果为24，第2次输出的结果为12，…第2016次输出的结果为（ ）A ．3B ．6C ．4D ．824．已知整数1a 、2a 、3a 、4a ……满足下列条件：11a =-，211a a =-+，322a a =-+，433a a =-+，……，1n n a a n +=-+（n 为正整数）依此类推，则2019a 的值为（ ）A ．1010-B ．1009-C ．1008-D ．1007-25．观察式子：13=12，13+23=(1+2)2=32，13+23+33=(1+2+3)2=62，13+23+33+43=(1+2+3+4)2=102，…，根据你发现的规律，计算53+63+73+83+93+103的结果是()A．2925 B．2025 C．3225 D．2625【参考答案】***试卷处理标记，请不要删除一、规律问题数字变化类1．C解析：C【分析】先根据前4个图得出一般性的规律，再依据规律解答即可．【详解】解：第1个图中有3=22−1条线段，第2个图中有8=32−1条线段，第3个图中有15=42−1条线段，第4个图中有24=52−1条线段，……，所以第n个图中有(n+1)2−1条线段；所以第10个图中有112−1=121-1=120条线段．故选：C【点睛】本题考查了图形的变化类规律，由简单的图形中线段的条数得出一般性的规律是解此题的关键．2．B解析：B【分析】求出数列的前4个数，从而得出这个数列以2-，13，32依次循环，且1312326-++=-，再求出这100个数中有多少个周期，从而得出答案．【详解】解：12a=-，211 1(2)3a∴==--，3131213a==-，412312a==--，⋯⋯∴这个数列以2-，13，32依次循环，且1312326-++=-，1003331……÷=，1210011533()27.562a a a ∴++⋯+=⨯--=-=-， 故选：B ．【点睛】本题考查了规律型：数字的变化类：通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．3．C解析：C【分析】先找到特殊点，根据特殊点的下标与数值的关系找到规律，数较大时，利用规律解答．【详解】解:根据题意分析可得:点A₁, A₂，A₃， .. A n 表示的数为-1，1，-2，2,-3，3,...依照上述规律，可得出结论:点的下标为奇数时，点在原点的左侧，且为下标加1除以2的相反数;点的下标为偶数时，点在原点的右侧且表示的数为点的下标数除以2;即:当n 为奇数时，n 1A 2n +=-， 当n 为偶数时，2n n A = 所以点A 2008表示的数为: 2008÷2= 1004A 2009表示的数为:- (2009+1) ÷2=-1005故选: C ．【点睛】本题考查探索与表达规律．这类题型在中考中经常出现，对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，然后找到规律．4．D解析：D【分析】根据上述等式，得到结果的末位以四个数（2，4，8，6）依次循环，而2019除以4商504余3，故得到所求式子的末位数字为8．【详解】解：根据上述等式，得到结果的末位以四个数（2，4，8，6）依次循环，∵2019÷4=504…3，∴22019的末位数字是8．故选：D【点睛】本题考查有理数的乘方运算，属于规律型试题，弄清本题的规律是解题关键．5．B解析：B【分析】通过计算得到个位数字为10个一循环，再分别验证选项中的个位数字，将符合个位数字为1的数比较大小可得．【详解】解：12=1，22=4，32=9，42 =16，52=25，62=36，72=49，82=64，92=81，102=100，112=121，122=144，∴个位数是10个数为一个循环，A、2001÷10=200...1，则200×（1+4+9+6+5+6+9+4+1+0）+1=9001，B、2006÷10=200...6，则200×（1+4+9+6+5+6+9+4+1+0）+（1+4+9+6+2+6）=9031，C、2011÷10=201...1，则201×（1+4+9+6+5+6+9+4+1+0）+1=9046，D、2019÷10=201...9，则201×（1+4+9+6+5+6+9+4+1+0）+（1+4+9+6+5+6+9+4+1）=9090，∵2001＜2006，故选B．【点睛】本题考查了数字型规律以及有理数的混合运算，解题的关键是找到个位数字为10个一循环．6．B解析：B【分析】设经过n个小时，然后根据有理数的乘方的定义列不等式，计算求出n的最小值即可．【详解】n≥，由题意得，21000∵92512=，=，1021024∴n的最小值是：10，故选：B．【点睛】本题考查了有理数的乘方，是基础题，熟记乘方的定义并列出不等式是解题的关键．7．B解析：B【分析】根据程序框图计算出前9次的输出结果，据此得出除去前2次的输出结果，后面每输出六次为一个周期循环，从而得出答案．【详解】解：∵第1次输出的结果为24，第2次输出的结果为12，第3次输出的结果为6，第4次输出的结果为3，第5次输出的结果为8，第6次输出的结果为4，第7次输出的结果为2，第8次输出的结果为1，第9次输出的结果为6，……∴除去前2次的输出结果，后面每输出六次为一个周期循环，∵（2019−2）÷6＝336…1，则第2019次输出的结果为6．故选：B．【点睛】此题考查了代数式求值，弄清题中的规律是解本题的关键．8．B解析：B【分析】分别求出数列的前5个数得出该数列每4个数为一周期循环，据此可得答案．【详解】解：∵a1＝3，∴a2＝223-＝﹣2，a3＝22(2)--＝12，a4＝2122-＝43，a5＝2423-＝3，∴该数列每4个数为一周期循环，∵2018÷4＝504……2，∴a2018＝a2＝﹣2，故选B．【点睛】本题主要考查数字的变换规律，根据题意得出该数列每4个数为一周期循环是关键．9．B解析：B【分析】观察不难发现，被开方数是从1开始的连续自然数，每一行的数据的个数是从2开始的连续偶数，求出n-1行的数据的个数，再加上n-2得到所求数的被开方数，然后写出算术平方根即可．【详解】解：前（n﹣1）行的数据的个数为2+4+6+…+2（n﹣1）=n（n﹣1），所以，第n（n是整数，且n≥3）行从左到右数第n﹣2个数的被开方数是n（n﹣1）+n﹣2=n2﹣2，所以，第n（n是整数，且n≥3）行从左到右数第n﹣2个数是22n ．故选：B．【点睛】本题考查了算术平方根，观察数据排列规律，确定出前（n-1）行的数据的个数是解题的关键．10．B解析：B【分析】由于八个数的和是4，所以需满足两个圈的和是2，横、竖的和也是2．列等式可得结论．【详解】解：设小圈上的数为c，大圈上的数为d，-1+2-3+4-5+6-7+8=4，∵横、竖以及内外两圈上的4个数字之和都相等，∴两个圈的和是2，横、竖的和也是2，则b=2-8-6-(-7)=-5，以c=2-4-6-(-5)=-3，剩下两个数为-1和2，且满足-1+2-3+4=2，∵当a=-1时，d=2，则a+b=-1-5=-6，当a=2时，d=-1，则a+b=2-5=-3，故选：B．【点睛】本题考查了有理数的加、减法的应用．解决本题的关键是知道横竖两个圈的和都是2．11．A解析：A【分析】根据题意和运算程序可以计算出前几次的输出结果，从而可以发现结果的变化特点，从而可以得到第2021次输出的结果，本题得以解决．【详解】解：由题意可得，第一次输出的结果为1，第二次输出的结果为4-，第三次输出的结果为2-，第四次输出的结果为1-，第五次输出的结果为6-，第六次输出的结果为3-，第七次输出的结果为8-，第八次输出的结果为4-，第九次输出的结果为2-，⋯，由上可得，从第二次输出结果开始，以4-，2-，1-，6-，3-，-8依次循环出现， (20211)63364-÷=⋯，∴第2021次输出的结果是6-，故选：A ．【点睛】本题考查了数字的变化类、有理数的混合运算，解题的关键是明确题意，发现输出结果的变化特点．12．D解析：D【分析】类比十进制“满十进一”，可以表示满5进1的数从左到右依次为：2×5×5×5，1×5×5，3×5，4，然后把它们相加即可．【详解】依题意，还在自出生后的天数是：2×5×5×5+1×5×5+3×5+4=250+25+15+4=294，故选：D ．【点睛】本题考查了实数运算的实际应用，解答的关键是运用类比的方法找出满5进1的规律列式计算．13．B解析：B【分析】观察这个数列知，第n 行的最后一个数是n 2，第50行的最后一个数是502=2500，进而求出第51行的第1个数．【详解】由题意可知，第n 行的最后一个数是n 2，所以第50行的最后一个数是502=2500，第51行的第1个数是2500+1=2501，故选：B ．【点睛】本题考查了规律型：数字的变化类，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．解决本题的难点在于发现第n 行的最后一个数是n 2的规律． 14．B解析：B【分析】分别计算：1234567,,,,,,a a a a a a a ⋅⋅⋅，再由具体到一般总结出规律，再利用规律解题即可得到答案．【详解】解：探究规律：10a =，2111a a =-+=-，3221a a =-+=-，4332a a =-+=-，5442a a =-+=-，6553a a =-+=-，7663a a =-+=-，……，总结规律：当n 是奇数时，结果等于12n --；n 是偶数时，结果等于2n -； 运用规律： 20212021110102a -=-=-， 故选：B ．【点睛】 本题考查的是数字类的规律探究以及列代数式，掌握规律探究的基本方法是解题的关键． 15．C解析：C【分析】根据前几个数字比较后发现：从第二个数字开始，如果顺序数为偶数，结果的数值2,n a n =-从而得到2018a 的答案．【详解】解：10,a =211011,a a =-+=-+=-322121,a a =-+=--+=-433132,a a =-+=--+=-544242,a a =-+=--+=-655253,a a =-+=--+=-766363,a a =-+=--+=-…以此类推，发现： 从第二个数字开始，如果顺序数为偶数，结果的数值是其顺序数的一半的相反数，即2,n a n =- 则2018120181009.2a =-⨯=- 故选：C ．【点睛】本题考查的是数字的变化规律型，同时考查的是绝对值的含义，有理数的加法运算，乘法运算，掌握根据前几个数字找出结果数值与顺序数之间的规律是解决本题的关键． 16．A解析：A【分析】 根据题意可知125005002004500S S S T +++==，即可求出125002004500S S S +++=⨯．再列出新的凯森和的式子，代入计算即可．【详解】 根据题意可知125005002004500S S S T +++==， ∴125002004500S S S +++=⨯．∴13，1a ，2a ，…，500a 的“凯森和”为：1250050113(13)(13)(13)501S S S T +++++++=1250013501()501S S S ⨯++++=135012004500501⨯+⨯=2013．故答案为：A．【点睛】本题考查数字的变化规律，掌握“凯森和”的概念，再找出其规律是解答本题的关键．17．B解析：B【分析】根据线段中点的定义，和两点之间的距离，找出题目中的规律，即可得到结论．【详解】由题意可知：如图写出线段的长，A1A2=2，A2是 A1A3的中点得A1A2=A2A3=2，A1A3=4，A3是 A1A4的中点得A1A3=A3A4=4，A1A4=8，A4是 A1A5的中点得A1A4=A4A5=8，……根据线段的长，找出规律，∵A1A2=2，A2A3=2=21，A3A4=4=22，A4A5=8=23，A5A6=16=24，A7A8=……，总结通项公式，∴线段 A n A n+1=2n-1（n为正整数）∴线段 A20A21=219故此题选：B【点睛】本题考查了两点间的距离，线段中点的定义，找出题目中的规律是解题的关键.18．B解析：B【详解】解：把6代入计算，第一次立方后得到216；第二次得到225；第三次得到141；第四次得到66；第五次得到432；第六次得到99；第七次得到1458；第八次得到702；第九次得到351；第十次得到153；开始重复，则T=153．故选B．19．D解析：D【详解】试题分析：=3，；；；，则这组数是以3、－2、和这四个数进行循环；则2016÷4=504，则=.考点：规律题20．A解析：A【分析】求出数列的前4个数，从而得出这个数列以2-，13，32依次循环，且1312326-++=-，再求出这100个数中有多少个周期，从而得出答案．【详解】 解：∵12a =-， ∴2111(2)3a ==--，3131213a ==-，412312a ==--，…… ∴这个数列以-2，13，32依次循环，且1312326-++=-， ∵1003331÷=， ∴121001153327.562a a a ⎛⎫+++=⨯--=-=- ⎪⎝⎭， 故选A ．【点睛】本题考查了规律型：数字的变化类：通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况． 21．D解析：D【分析】根据要求写出符合要求的数并找到数字变化的规律，利用规律求解即可．【详解】解：∵第一个数是2， 第二个数是12， 第三个数是-1，第四个数是2，…∴每三个数按照2，12，-1循环，∵2020÷3=673 (1)∴第2020个数和第1个数一致，即：2．故选：D ．【点睛】本题主要考查数字的变化规律，解决此类问题时通常需要确定数列与序数的关系或者数列的循环周期等，此题得出这列数每3个数为一周期循环是解题的关键．22．B解析：B【分析】观察可知，分裂成的奇数的个数与底数相同，然后求出到m 3的所有奇数的个数的表达式，再求出奇数2021的是从3开始的第1010个数，然后确定出1007所在的范围即可得解．【详解】解：∵底数是2的分裂成2个奇数，底数为3的分裂成3个奇数，底数为4的分裂成4个奇数，∴m 3分裂成m 个奇数，所以，到m 3的奇数的个数为：2+3+4+…+m=(2)(1)2m m +-， ∵2n+1=2021，n=1010，∴奇数2021是从3开始的第1010个奇数， ∵(442)(441)(452)(451)989,103422+⨯-+⨯-==， ∴第1010个奇数是底数为45的数的立方分裂的奇数的其中一个，即m=45．故选：B ．【点睛】本题是对数字变化规律的考查，观察出分裂的奇数的个数与底数相同是解题的关键，还要熟练掌握求和公式．23．C解析：C【分析】根据题意和题目中的运算程序，可以计算出前几次的输出结果，从而可以发现输出结果的变化特点，从而可以得到第2016次输出的结果．【详解】解：由题意可得，开始输入的x 值为48，第1次输出的结果为24，第2次输出的结果为12，第3次输出的结果为6，第4次输出的结果为3，第5次输出的结果为8，第6次输出的结果为4，第7次输出的结果为2，第8次输出的结果为1，第9次输出的结果为6，…，由上可得，输出结果从第三次开始，依次以6，3，8，4，2，1循环出现，∵（2016﹣2）÷6＝335…4，∴第2016次输出的结果为4，故选C ．【点睛】此题考查了代数式求值，通过计算找出其中的规律是解决本题的关键．24．A解析：A【分析】根据条件求出前几个数的值，再分n 是奇数时，()112n a n =-+，n 是偶数时，22n n a -=-，然后把n 的值代入进行计算即可得解． 【详解】解：a 1=-1，a 2=-|a 1+1|=-|-1+1|=0，a 3=-|a 2+2|=-|0+2|=-2，a 4=-|a 3+3|=-|-2+3|=-1，a 5=-|a 4+4|=-|-1+4|=-3，a 6=-|a 5+4|=-|-3+5|=-2，a 7=-|a 6+4|=-|-2+6|=-4…， 所以，n 是奇数时，()112n a n =-+，n 是偶数时，22n n a -=-， a 2019=12-（2019+1）=-1010， 故选：A ．【点睛】此题主要考查了数字变化规律，根据所求出的数，观察出n 为奇数与偶数时的结果的变化规律是解题的关键．25．A解析：A【分析】根据题意找到规律：()233333211234(1234)2n n n n ⎡⎤+++++⋯+=++++⋯+=⎢⎥⎣⎦即可求解．【详解】解：∵13=12，13+23=(1+2)2=32，13+23+33=(1+2+3)2=62，13+23+33+43=(1+2+3+4)2=102，…， ∴()233333211234(1234)2n n n n ⎡⎤+++++⋯+=++++⋯+=⎢⎥⎣⎦，53+63+73+83+93+103=(33333123410++++⋯+)-(33331234+++) 22 (123410)(1234)=++++⋯+-+++()()221011041422⎡⎤⎡⎤⨯+⨯+=-⎢⎥⎢⎥⎣⎦⎣⎦225510=-2925=．故选：A ．【点睛】本题考查了规律型：数字的变化类，解决本题的关键是根据数字的变化寻找规律．。

成都嘉祥外国语学校郫县分校中考数学期末规律问题算式变化类汇编一、规律问题算式变化类1．下面是按一定规律排列的一列数： 第 1 个数：11122-⎛⎫-+ ⎪⎝⎭； 第 2 个数：()()2311111113234⎡⎤⎡⎤---⎛⎫-+++⎢⎥⎢⎥ ⎪⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦； 第 3 个数：()()2311111114234⎡⎤⎡⎤---⎛⎫-+++⎢⎥⎢⎥ ⎪⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦； ⋯⋯；第 n 个数：()()()232n-111111111...1n 12342n ⎡⎤⎡⎤⎡⎤----⎛⎫-++++⎢⎥⎢⎥⎢⎥ ⎪+⎝⎭⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦； 那么在第 10 个数、第 11 个数、第 12 个数、第 13 个数中，最大的数是 ( ) A ．第 10 个数 B ．第 11 个数C ．第 12 个数D ．第 13 个数2．2020减去它的12，再减去余下的13，再减去余下的14，….依此类推，一直减到余下的12020，则最后剩下的数是（ ） A ．20202019B ．1C ．20192020D ．03．请先在草稿纸上计算下列四个式子的值：（ ） A ．351B ．350C ．325D ．3004．将2019加上它本身的12的相反数，再将这个结果加上其13的相反数，再将上述结果加上，其14的相反数，…，如此继续，操作2019次后所得的结果是（ ） A ．1B ．－1C ．20192020D ．20205．已知1x ，2x ，⋯⋯2013x 均为正数，且满足122012232013()()M x x x x x x =++++++，122013232012()()N x x x x x x =++++++，则M 与N 之间的关系是（ ）A ．M ＞NB ．M ＝NC ．M ＜ND ．无法确定6．若规定“!”是一种数学运算符号，且则的值为（ ） A ．B ．99!C ．9 900D ．2!7．观察下列各式：， ， ，…计算：3×（1×2+2×3+3×4+…+99×100）=（ ） A ．97×98×99B ．98×99×100C ．99×100×101D ．100×101×1028．一根1m 长的小棒，第一次截去它的12，第二次截去剩下的12，如此截下去，第五次后剩下的小棒的长度是（ ） A ．51()2mB ．[1－51()2]mC ．0．5mD ．[1－51()2]m9．对于正数x ，规定f(x)=1x x +，例如f(3)=34，f(13)=14，计算f(12015)+f(12014)+f(12013)+…+f(13)+f(12)+f(1)+f(2)+f(3)+…+f(2013)+f(2014)+f(2015)的结果是（ ） A ．2014 B ．2014．5 C ．2015 D ．2015．5B10．在明代的《算法统宗》中记载了利用方格进行两数相乘的一种方法，叫做“铺地锦”，如图1，计算4751⨯，将乘数47计入上行，乘数51计入右行，然后以乘数47的每位数字乘以乘数51的每位数字，将结果计入相应的格子中，最后按斜行加起来，得2397，图2用“铺地锦”法表示两个两位数相乘，则a 的值为（ ）A ．7B ．5C ．3D ．211．山西面食不仅是中华民族饮食文化的重要组成部分，也是世界的面食之根.其中，“拉面”远播世界各地.制作方法如图所示，用一根很粗的面条，把两头捏合在一起拉伸，再捏合，反复几次，这根很粗的面条就被拉成许多细的面条，第一次捏合变2根细面条，第二次捏合变4根细面条，第三次捏合变8根细面条，这样捏合到第n 次后可拉出细面条（ ）A ．2n根B ．12n +根C ．12n -根D ．112n +⎛⎫ ⎪⎝⎭根12．观察下列等式：①23﹣13＝32﹣2；②33﹣23＝52﹣6；③43﹣33＝72﹣12；④53﹣43＝92﹣20…请根据上述规律，请判断下列等式错误的是（ ） A ．20163﹣20153＝40312﹣2016×2015 B ．20173﹣20163﹣40332＝2017×2016 C ．40352﹣20183+20173＝2018×2017 D ．2018×2019﹣20183+20193＝4037213．把1，2，3，4，…，2016的每一个数的前面任意填上“＋”号或“－”号，然后将它们相加，则所得结果为( ) A ．偶数 B ．奇数C ．正数D ．有时为奇数，有时为偶数14．求1＋2＋22＋23＋…＋22020的值，可令S ＝1＋2＋22＋23＋…＋22020，则2S ＝2＋22＋23＋24＋…＋22021，因此2S －S ＝22021－1．仿照以上推理，计算出1＋2020＋20202＋20203＋…＋20202020的值为（ ）A ．2020202012020-B ．2021202012020-C ．2021202012019-D ．2020202012019-15．已知2131=+a ，2262=+a ，23103=+a ，24154=+a ……n a ，则20202010-=a a （ ） A ．2020B ．4039C ．6060D ．807916．观察式子：3211=，332212(12)3+=+=，33322123(123)6++=++=，3333221234(1234)10+++=+++=，，根据你发现的规律，计算3333335678910+++++的结果是（ ） A ．2925 B ．2025 C ．3225 D ．2625 17．观察下列式子：11223343453⨯+⨯+⨯=⨯⨯⨯，1122334454563⨯+⨯+⨯+⨯=⨯⨯⨯，112233445565673⨯+⨯+⨯+⨯+⨯=⨯⨯⨯，…探索以上式子的规律，与计算1112121318191920⨯+⨯++⨯+⨯的结果相等的算式是（ ）A ．()1192021910113⨯⨯⨯-⨯⨯B ．()11920211011123⨯⨯⨯-⨯⨯C ．()1181920910113⨯⨯⨯-⨯⨯D ．()11819201011123⨯⨯⨯-⨯⨯18．计算111111122334455667-----⨯⨯⨯⨯⨯⨯的结果为（ ）． A ．67 B ．67- C ．17- D ．1719．观察下列各式及其展开式：()2222a b a ab b +=++；()3322333a b a a b ab b +=+++；()4432234464a b a a b a b ab b +=++++；()544322345510105a b a a b a b a b ab b +=+++++…，请你猜想()11a b +的展开式第三项的系数是（ ） A ．36 B ．45C ．55D ．6620．我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”（如图所示）就是一例．这个三角形的构造法则为：两腰上的数都是1，其余每个数均为其上方左右两数之和．事实上，这个三角形给出了（a+b ）n （n 为正整数）的展开式（按a 的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应（a+b ）2=a 2+2ab+b 2展开式中各项的系数；第四行的四个数1，3，3，1，恰好对应着（a+b ）3=a 3+3a 2b+3ab 2+b 3展开式中各项的系数等等．根据上面的规律，请你猜想（a+b ）7的展开式中所有系数的和是（ ） A ．2018B ．512C ．128D ．6421．已知2221114834441004A ⎛⎫=⨯++⋯+⎪---⎝⎭，根据()21111n 3n 44n 2n 2⎛⎫=-≥ ⎪--+⎝⎭，则与A 最接近的正整数是（ ）． A ．18B ．20C ．24D ．2522．根据等式：()()2111x x x -+=-，()()23111,x x x x -++=-()()324111x x x x x -+++=-，()()4325111,x x x x x x -++++=-……的规律，则可以推算得出2021202020192222...221++++++的末位数字是（ ）A ．1B ．3C ．5D ．723．求23201312222+++++的值，可令220131222S =++++，则23201422222S =++++，因此2014221S S -=-．仿照以上推理，计算出23201315555+++++的值为（ ）A ．201451- B ．201351-C ．2014514-D ．2013514-24．观察下列各式及其展开式 (a +b )2＝a 2+2ab +b 2 (a +b )3＝a 3+3a 2b +3ab 2+b 3 (a +b )4＝a 4+4a 3b +6a 2b 2+4ab 3+b 4 (a +b )5＝a 5+5a 4b +10a 3b 2+10a 2b 3+5ab 4+b 5 ……请你猜想(2x ﹣1)8的展开式中含x 2项的系数是（ ） A ．224B ．180C ．112D ．4825．（问题背景）“整体替换法”是数学里的一种常用计算方法．利用式子的特征进行整体代换，往往能解决许多看似复杂的问题．（迁移运用）计算111211211212++++++++的值解：设原式x =，则可分析得：112x x=++根据上述方程解得：1x =2x =而原式0>，故：原式132x -+==（联系拓展）23456202222222+++++++=___________A ．2121-B ．2122-C ．2221-D ．2222-【参考答案】***试卷处理标记，请不要删除一、规律问题算式变化类 1．A 【分析】根据有理数的计算，计算第1个数、第2个数、第3个数等，总结第n 个数的规律即可得出答案．【详解】解：第个数：；第个数：；第个数：；；第个数：；n越大，第n个解析：A【分析】根据有理数的计算，计算第1个数、第2个数、第3个数等，总结第n个数的规律即可得出答案．【详解】解：第1个数：1110 22-⎛⎫-+=⎪⎝⎭；第2个数：()()2311111 11132346⎡⎤⎡⎤---⎛⎫-+++=-⎢⎥⎢⎥⎪⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦；第3个数：()()2311111 11142344⎡⎤⎡⎤---⎛⎫-+++=-⎢⎥⎢⎥⎪⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦；⋯⋯；第n个数：()()()232n-11111111 111 (1)n12342n12n⎡⎤⎡⎤⎡⎤----⎛⎫-++++=-⎢⎥⎢⎥⎢⎥⎪++⎝⎭⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦；∴n越大，第n个数越小故选：A．【点睛】本题考查有理数的计算，掌握数的规律是解题的关键．2．B【分析】根据题意，可列式2020×（1−）×（1−）×（1−）×…×（1−），先算括号里的减法，再约分即可．【详解】解：2020×（1−）×（1−）×（1−）×…×（1−）＝2020×××解析：B【分析】根据题意，可列式2020×（1−12）×（1−13）×（1−14）×…×（1−12020），先算括号里的减法，再约分即可．【详解】解：2020×（1−12）×（1−13）×（1−14）×…×（1−12020）＝2020×12×23×34…×20192020＝1．故选：B．【点睛】此题考查有理数的混合运算，首先要根据题意列式，总结规律是解题的关键．3．C【分析】通过计算前面4个式子的值，得到规律为从1开始的几个连续整数的立方和的算术平方根等于这几个连续整数的和，然后利用此规律求解．【详解】①＝1；②＝3＝1+2；③＝6＝1+2+3；解析：C【分析】通过计算前面4个式子的值，得到规律为从1开始的几个连续整数的立方和的算术平方根等于这几个连续整数的和，然后利用此规律求解．【详解】1；3＝1+2；6＝1+2+3；10＝1+2+3+4；∴＝1+2+3+…+25＝325．故选：C．【点睛】本题考查实数运算有关的规律问题，解题关键是先计算题干中的4个简单算式，得出规律后再进行复杂算式的求解．4．C【分析】根据题意易得第一次运算的结果为，第二次运算的结果为，第三次运算的结果为，第四次运算的结果为，….由此规律可进行求解．【详解】解：2019加上它本身的的相反数为：，再将这个结果加上其解析：C 【分析】根据题意易得第一次运算的结果为120192⨯，第二次运算的结果为120193⨯，第三次运算的结果为120194⨯，第四次运算的结果为201951⨯，….由此规律可进行求解． 【详解】解：2019加上它本身的12的相反数为：1120192019201922-⨯=⨯，再将这个结果加上其13的相反数为11112019201920192233⨯-⨯⨯=⨯，再将上述结果加上，其14的相反数为11112019201920193344⨯-⨯⨯=⨯，….由此规律可得第n 次的运算结果为112019n +⨯，∴第2019次后所得结果是120192019202020191⨯=+；故选C ． 【点睛】本题主要考查有理数的混合运算，熟练掌握有理数的混合运算是解题的关键．5．A 【详解】试题分析：依题意设=A ，设=BM=（A-x2013）×B ；N=A×（B-x2013）所以M-N=（A-x2013）×B- A×（B-x2013）="AB-B" x2013-AB+解析：A 【详解】试题分析：依题意设122013x x x +++=A ，设232013x x x +++=BM=（A-x 2013）×B ；N=A×（B-x 2013）所以M-N=（A-x 2013）×B- A×（B-x 2013）="AB-B" x 2013-AB+ A x 2013=（A-B ）x 2013 易知A-B=x 1＞0，x 2013＞0.则M ＞N 考点：多项式运算点评：本题难度中等，主要考查学生对多项式运算知识点的掌握．为中考常见题型，要求学生牢固掌握解题技巧．6．C 【详解】根据题意可得：100！=100×99×98×97×…×1，98！=98×97×…×1， ∴ =100×99="9" 900，故选C ．解析：C 【详解】根据题意可得：100！=100×99×98×97×…×1，98！=98×97×…×1， ∴=100×99="9" 900，故选C ．7．C 【详解】试题分析：根据给出的式子得出一般性的规律，从而得到答案. 考点：规律题解析：C 【详解】试题分析：根据给出的式子得出一般性的规律，从而得到答案. 考点：规律题8．A 【解析】试题分析：根据题意可得：第一次剩下m ，第二次剩下m ，第三次剩下m ，则第5次剩下m ． 考点：规律题解析：A 【解析】试题分析：根据题意可得：第一次剩下12m ，第二次剩下211()42=m ，第三次剩下311()82=m ，则第5次剩下51()2m ． 考点：规律题9．B 【解析】试题分析：根据题意可得：f(n)+f()=1，则原式=1×2014+=2014．5 考点：规律题解析：B 【解析】试题分析：根据题意可得：f(n)+f(1n)=1，则原式=1×2014+12=2014．5考点：规律题10．A【分析】设4a的十位数字是m，个位数字是n，根据“铺地锦”的计算方法，把方格填完整，再列出三元一次方程组，即可求解．【详解】设4a的十位数字是m，个位数字是n，由题意可知，方格里的数字，解析：A【分析】设4a的十位数字是m，个位数字是n，根据“铺地锦”的计算方法，把方格填完整，再列出三元一次方程组，即可求解．【详解】设4a的十位数字是m，个位数字是n，由题意可知，方格里的数字，如图所示，∴2116410m a an aa m n+=+⎧⎪+=-+⎨⎪=+⎩，解得：287mna=⎧⎪=⎨⎪=⎩，∴a的值为：7．故选A．【点睛】本题主要考查三元一次方程组的应用，根据等量关系，列出方程组，是解题的关键．11．A【分析】找规律，然后根据有理数的乘方的定义列出更加一般的情况即可求解. 【详解】解：第一次捏合变2根细面条，可以看成是第二次捏合变4根细面条，可以看成是第三次捏合变8根细面条，可以看成是解析：A【分析】找规律，然后根据有理数的乘方的定义列出更加一般的情况即可求解.解：第一次捏合变2根细面条，可以看成是12第二次捏合变4根细面条，可以看成是22第三次捏合变8根细面条，可以看成是32依据这个规律下去第n次捏合可拉出细面条的根数为：2n.故答案为：A.【点睛】本题借助生活中的实际例子考查了有理数的乘方的定义，理解乘方的意义是解题的关键. 12．B【分析】根据题意找出数字的变化规律，根据规律计算，判断即可．【详解】解：观察等式可以得到规律：（n+1）3﹣n3＝（2n+1）2﹣n（n+1），20163﹣20153＝40312﹣201解析：B【分析】根据题意找出数字的变化规律，根据规律计算，判断即可．【详解】解：观察等式可以得到规律：（n+1）3﹣n3＝（2n+1）2﹣n（n+1），20163﹣20153＝40312﹣2016×2015A正确，不符合题意；20173﹣20163＝40332﹣2017×2016∴20173﹣20163﹣40332＝﹣2017×2016B错误，符合题意；40352﹣20183+20173＝2018×2017C正确，不符合题意；2018×2019﹣20183+20193＝40372D正确，不符合题意；，故选B．【点睛】本题考查的是有理数的混合运算、数字的变化规律，掌握有理数的混合运算法则、正确找出数字的变化规律是解题的关键．13．A【分析】因为偶数个奇数相加，故结果是偶数．【详解】因为相邻两个数的和与差都是奇数，且是从1开始到2016，共有1008对，则所得的结果肯定是偶数个奇数相加，故结果是偶数．故选：A．【点【分析】因为偶数个奇数相加，故结果是偶数．【详解】因为相邻两个数的和与差都是奇数，且是从1开始到2016，共有1008对，则所得的结果肯定是偶数个奇数相加，故结果是偶数．故选：A ．【点睛】本题考查了有理数的加减混合运算，本题根据相邻两个数的和与差都是奇数作为突破口：当有偶数个奇数相加时，结果是偶数．14．C【分析】由题意可知S ＝ 1＋2020＋20202＋20203＋…＋20202020①，可得到2020S ＝2020＋20202＋20203＋…＋20202020＋20202021②，然后由②－① 解析：C【分析】由题意可知S ＝ 1＋2020＋20202＋20203＋…＋20202020①，可得到2020S ＝2020＋20202＋20203＋…＋20202020＋20202021②，然后由②－①，就可求出S 的值．【详解】解：设S ＝ 1＋2020＋20202＋20203＋ (20202020)则2020S ＝2020＋20202＋20203＋…＋20202020＋20202021②由②－①得：2019S ＝20202021－1 ∴2021202012019S -=． 故答案为：C ．【点晴】本题主要考查探索数与式的规律，有理数的加减混合运算．15．C【分析】先由已知等式,得出规律:,则,将代入,即可求出结果．【详解】解：．．时,．故选:C ．【点睛】此题主要考查了规律型:数字的变化类及有理数的混合运算,解题解析：C【分析】先由已知等式,得出规律:()2121n a n n n =++++++23322n n ++=,则133n n a a n +-=+,将2019n =代入,即可求出结果．【详解】解：()2121n a n n n =++++++()()21112n n n +++⎡⎤⎣⎦=+ ()()2212n n n ++=+ 223222n n n +++= 23322n n ++=． ()()2213131233222n n n n n n a a +++++++-=- ()()223131332n n n n +++--= 2236333332n n n n n ++++--= 662n += 33n =+．2019n =时,()20202019320191a a -=+32020=⨯6060=．故选:C ．【点睛】此题主要考查了规律型:数字的变化类及有理数的混合运算,解题时首先观察,分析归纳出题目中隐含的规律,然后利用规律把题目变形,从而使计算变得比较简便．16．A【分析】根据题意找到规律：即可求解．【详解】∵，，，，…，，∴．【点睛】本题主要考查了有理数的混合运算，规律型－数字变化类．此题将求的值的问题运用规律转化为求的问解析：A【分析】 根据题意找到规律：2333321123(123)(1)2n n n n ⎡⎤++++=++++=+⎢⎥⎣⎦即可求解． 【详解】∵3211=， 332212(12)3+=+=，33322123(123)6++=++=，3333221234(1234)10+++=+++=，…，33332123123()n n ++++=++++， ∴3333335678910+++++ 33333333(12310)(1234)=++++-+++ 22(12310)(1234)=++++-+++221110(101)4(41)22⎡⎤⎡⎤=⨯⨯+-⨯⨯+⎢⎥⎢⎥⎣⎦⎣⎦225510=-2925=．【点睛】本题主要考查了有理数的混合运算，规律型－数字变化类．此题将求3333335678910+++++的值的问题运用规律转化为求33333333(12310)(1234)++++-+++的问题是解题的关键．17．B【分析】根据题目中的式子，可以发现式子的变化特点，然后对所求式子变形，即可得到所求式子的值，本题得以解决．【详解】，故选：B ．【点睛】本题考查了数字的变化类，解答本题的关键是明确解析：B【分析】根据题目中的式子，可以发现式子的变化特点，然后对所求式子变形，即可得到所求式子的值，本题得以解决．【详解】1112121318191920⨯+⨯+⋯+⨯+⨯()()1223192012231011=⨯+⨯+⋯+⨯-⨯+⨯+⋯+⨯1119202110111233=⨯⨯⨯-⨯⨯⨯ ()11920211011123=⨯⨯⨯-⨯⨯， 故选：B ．本题考查了数字的变化类，解答本题的关键是明确题意，发现式子的变化特点，求出所求式子的值．18．D【分析】将式子进行变形，然后计算即可．【详解】解：==【点睛】本题考查有理数的计算，关键在于进行变形．解析：D【分析】将式子进行变形，然后计算即可．【详解】解：111111 122334455667 -----⨯⨯⨯⨯⨯⨯=11111111111 1()()()()() 22334455667 -----------=1 7【点睛】本题考查有理数的计算，关键在于进行变形．19．C【分析】利用所给展开式探求各项系数的关系，特别是上面的展开式与下面的展开式中的各项系数的关系，可推出的展开式第三项的系数．【详解】解：依据规律可得到：第三项的系数为1，第三项【分析】利用所给展开式探求各项系数的关系，特别是上面的展开式与下面的展开式中的各项系数的关系，可推出11()a b +的展开式第三项的系数．【详解】解：222()2a b a ab b +=+++=+++33223()33a b a a b ab b4322344()464a b a a b a b ab b +=++++554322345()510105a b a a b a b a b ab b +=+++++⋯⋯∴依据规律可得到：2()a b +第三项的系数为1，3()a b +第三项的系数为312=+，4()a b +第三项的系数为6123=++，⋯11()a b +第三项的系数为：10(101)123910552⨯++++⋯++==． 故选：C ．【点睛】本题考查了数字规律型，理解题意，找到系数的规律是解题的关键． 20．C【分析】仿照阅读材料中的方法将原式展开，求出系数之和即可．【详解】解：根据题意得：（a+b ）7＝a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7，系解析：C【分析】仿照阅读材料中的方法将原式展开，求出系数之和即可．【详解】解：根据题意得：（a +b ）7＝a 7+7a 6b +21a 5b 2+35a 4b 3+35a 3b 4+21a 2b 5+7ab 6+b 7，系数之和为2×（1+7+21+35）＝128，故选：C ．【点睛】此题考查了完全平方公式，以及规律型：数字的变化类，弄清“杨辉三角”中系数的规律是解本题的关键．21．D【分析】根据公式的特点把A 进行变形化简，故可求解．【详解】∵∴=≈12×2.0435=24.522≈25故选：D ．【点睛】此题主要考查数的规律计算，解题的关键是运用已知解析：D【分析】根据公式的特点把A 进行变形化简，故可求解．【详解】 ∵()21111n 3n 44n 2n 2⎛⎫=-≥ ⎪--+⎝⎭∴2221114834441004A ⎛⎫=⨯++⋯+⎪---⎝⎭ =111111111484323244242410021002⎡⎤⎛⎫⎛⎫⎛⎫⨯-+-+⋯+- ⎪ ⎪ ⎪⎢⎥-+-+-+⎝⎭⎝⎭⎝⎭⎣⎦ 1111111148145426498102⎡⎤⎛⎫⎛⎫⎛⎫=⨯-+-+⋯+- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦ 111111111121 (2345)98567102⎛⎫=⨯++++++----- ⎪⎝⎭ 111111112123499100101102⎛⎫=⨯+++---- ⎪⎝⎭≈12×2.0435=24.522≈25 故选：D ．【点睛】此题主要考查数的规律计算，解题的关键是运用已知的运算公式变形求解．22．B利用题目给出的规律：把乘（2-1）得出22022-1，研究22022的末位数字规律，进一步解决问题．【详解】解：由题目中等式的规律可得：=（2-1）×=22022-1，21解析：B【分析】利用题目给出的规律：把2021202020192222...221++++++乘（2-1）得出22022-1，研究22022的末位数字规律，进一步解决问题．【详解】解：由题目中等式的规律可得：2021202020192222...221++++++=（2-1）×2021202020192(222...221)++++++=22022-1，21的末位数字是2，22的末位数字是4，23的末位数字是8，24的末位数字是6，25的末位数字是2…，所以2n 的末位数字是以2、4、8、6四个数字一循环．2022÷4=505…2，所以22022的末位数字是4，22022-1的末位数字是3．故选：B【点睛】此题考查了平方差公式，乘方的末位数字的规律，尾数特征，注意从简单情形入手，发现规律，解决问题．23．C【分析】类比题目中所给的解题方法解答即可．【详解】解：设a=1+5+52+53+ (52013)则5a=5（1+5+52+53+…+52013）=5+52+53+…+52013+5201解析：C【分析】类比题目中所给的解题方法解答即可．解：设a=1+5+52+53+ (52013)则5a=5（1+5+52+53+…+52013）=5+52+53+…+52013+52014，∴5a-a=（5+52+53+…+52013+52014）-（1+5+52+53+…+52013）=52014-1，即a=2014514．故选：C．【点睛】本题是阅读理解题，类比题目中所给的解题方法是解决问题的基本思路．24．C【分析】观察数字规律，发现各组数据的首尾均为1，中间数字分别为上一组数据相邻两个数字之和，分别写出左边式子的指数分别为6，7，8 的等式右边各项的系数，结合括号内含x项的次数为2，即可得出答案解析：C【分析】观察数字规律，发现各组数据的首尾均为1，中间数字分别为上一组数据相邻两个数字之和，分别写出左边式子的指数分别为6，7，8 的等式右边各项的系数，结合括号内含x项的次数为2，即可得出答案．【详解】解：由所给四组式子的系数规律可得左边式子的指数分别为 6，7，8 的等式，右边各项的系数分别为：1，6，15，20，15，6，1；1，7，21，35，35，21，7，1；1，8，28，56，70，56，28，8，1；故含x2项的系数为：22×（﹣1）6×28＝112．故选：C．【点睛】本题考查了二项式展开式中的系数规律问题，发现题中所列各式的系数规律是解题的关键．25．B【分析】根据题目呈现的“整体替换法”，令，，作差即可求解．【详解】解：设，，则，故选：B．【点睛】本题为新定义类型问题的考查，解题的关键是读懂题目中“整体替换法”的概念，应用到解题解析：B【分析】根据题目呈现的“整体替换法”，令220222S =+++，23212222S =+++，作差即可求解．【详解】解：设220222S =+++，23212222S =+++， 则21222S S S =-=-， 故选：B ．【点睛】本题为新定义类型问题的考查，解题的关键是读懂题目中“整体替换法”的概念，应用到解题当中．。

成都嘉祥外国语学校八年级下 数学易错题卷5班级 ____________姓名____________1、已知212a a −是正数，则a 的取值范围____________；2、已知分式211x x +−的z 值为正整数，则整数x 的值为_____；当整数a =___ 时，分式26189a a +−的值是负整数3、如果关于x 的不等式组有且只有3个整数解，且使关于x 的分式方程=2的解为非负数的所有整数a 的和为____________4、观察分析下列方程：①，②，③；请利用它们所蕴含的规律，求关于x 的方程（n 为正整数）的根，你的答案是： ．5、.在面积为15的平行四边形ABCD 中，过点A 作AE 垂直于直线BC 于点E ，作AF 垂直于直线CD 于点F ，若AB=5，BC=6，则CE+CF 的值为 ．6、如图，直线y kx b =+经过点(12)A −−，和点(20)B −，，直线2y x =过点A ，则不等式20x kx b <+<的解集为________________________7、已知，c b a b a c a c b +=+=+求））（）（（a c c b b a abc +++的值是 8、如果关于x 的方程261x 11m x −=−−有增根，则它的增根是 。

9、如果关于x 的方程22x 12x+1-x+1m x x x−=+无解，则m 的值为 。

10、已知直线y=-2x-a 和直线y=5x+3a-1的交点在第四象限，则a 的范围为 。

11.当m 为整数_____________时，关于x 的分式方程1x−+22261m +=x x-x x 有整数解？ 12.如图，在平面直角坐标系中，R t △OAB 的顶点A 在x 轴的正半轴上．顶点B 的坐标为（3，），点C 的坐标为（，0），点P 为斜边OB 上的一个动点，则PA +PC 的最小值为__________．13．在菱形ABCD 中，AB=BD ．点E 、F 分别在AB 、AD 上，且AE=DF ．连接BF 与DE 相交于点G ，连接CG 与BD 相交于点H ．下列结论：其中正确的结论有（ ）①△AED ≌△DFB ；②S 四边形BCDG =CG 2；③CG=DG +BG ．④∠DGB=120°yO x B A14、为迎接2019年全国青运会，我市加紧城市建设的步伐，某城区对一条全长1200m的公路进行绿化带改造，计划每天完成绿化带改造任务xm，当x满足的方程为×=时，下列对这一方程所反映的数量关系描述正确的是（）A．实际每天比计划多完成改造任务300m，实际所用天数是计划的B．实际每天比计划少完成改造任务300m，计划所用天数是实际的C．实际每天比计划多完成改造任务300m，计划所用天数是实际的D．实际每天比计划少完成改造任务300m，实际所用天数是计划的15．若关于x的不等式a（x﹣1）+b（x+1）＞0的解是x＜，则关于x的不等式a（x+1）+b（x﹣1）＞0的解是．16、如图，菱形ABCD的对角线AC，BD相交于点O，AC=8cm，BD=6cm，AC上一动点P从点C出发，沿CA方向以1cm/s的速度向A运动，设点P运动时间为ts．当t等于_______时，△PCD是直角三角形．17、如图，在△ABC中，∠ABC=90°，BD为AC的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．若CF=6，AC=AF+2，则四边形BDFG的周长为_______18．如图，在五边形ABCDE中，已知∠BAE=120°，∠B=∠E=90°，AB=BC=2，AE=DE=4，在BC、DE上分别找一点M、N，则△AMN的最小周长为．19．如图，正△ABC的边长为2，以BC边上的高AB1为边作正△AB1C1，△ABC与△AB1C1公共部分的面积记为S1；再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2，△AB1C1与△AB2C2公共部分的面积记为S2；…，以此类推，则S n=．（用含n的式子表示）。

一、选择题1．一个四位数，它的千位上的数字和十位上的相同，百位上的数字和个位上的数字相同，它的个位上的数字是2，十位上的数字是个位上的4倍，这个数是（）。

A. 4242B. 8282C. 2828B解析： B【解析】【解答】个位和百位上数字都是2，十位和千位上的数字都是2×4=8，这个数是8282。

故答案为：B。

【分析】先确定十位数字和千位数字，从高位到低位写出这个数。

整数的右边起依次是个位、十位、百位、千位。

2．算式517-288的结果（）。

A. 小于200B. 等于200C. 大于200C解析： C【解析】【解答】 517-288≈500-300=200故答案为：C。

【分析】估算三位数的加减法，先把各数估成接近的整百数或整百整十数，然后再相加减，据此解答即可。

3．妈妈去超市买如表三样物品．下面哪个问题适合用估算解决？（）养生壶暖气扇学习机99元282元196元B. 收银员应收多少钱？C. 如果妈妈付给收银员600元钱，应找回多少钱？A解析： A【解析】【解答】对于选项A，妈妈准备的钱数应该为：99+282+196≈100+300+200=600（元），估算比较方便，可以进行估算；对于选项B，收银员应收的钱数必须是准确数，不能进行估算；对于选项C，妈妈付给收银员600元，应找回的钱数必须是准确数，否则对收银员和妈妈都不公平，故应找回的钱数不能进行估算。

故答案为：A。

【分析】在解决实际问题时，要明白哪些数据可以估算，哪些数据必须是准确值，题目中妈妈准备的钱数可以估算，收银员应收的钱数和应找回的钱数都必须是准确数。

4．估算576＋284，下面说法正确的是（）。

A. 它们的和比1000大一些。

B. 它们的和700小一些。

C. 576＜600，284＜300，它们的和一定小于900。

C解析： C【解析】【解答】576+284≈600+300=900故答案为：C。

【分析】根据估算方法，把两个加数分别看成整百数，都多看了，因此，估算求出的和大于实际的和。

四川省成都市嘉祥外国语学校2018-2019年度第二学期八年级（下）数学第三周易错题练习卷1. x 2−4xy −2y +x +4y 2有一个因式是x −2y ，则另一个因式是 。

2. 已知关于x 的不等式组{x −a ≥03−2x >−1的整数解共有5个，则a 的取值范围是 。

3. 若1x +2y +3z =5，3x +2y +1z =7，则1x +1y +1z = 。

4. 已知关于x 的分式方程m+1x−1=2的解为正数，则m 的取值范围是 。

5. 如果关于x 的分式方程2x x+1−m−1x 2+x =2x+1x 无解，则m 的值为 。

6. 已知：x +1x =3，则x 4x 8+x 4+1= 。

7.有四张正面分别标有数字-3，0，1，5的不透明卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数学记为a ，则使关于x 的分式方程x x ax -=+--21221 有正整数解的概率为 ．8.如果顺次连接四边形各边中点所围成的四边形是矩形，那么原来的四边形一定是（ ）A 平行四边形；B 梯形；C 对角线相等的四边形；D 对角线垂直的四边形． 9.□ABCD 中，∠DAB 的平分线AE 分对边所成两条线段长为3和5，则□ABCD 周长为 。

10.如图，菱形ABCD 中，AB=2，∠A=120°，点P ，Q ，K 分别为线段BC ，CD ，BD 上任一点，则PK+QK 的最小值为 ；11.如图，在正方形ABCD 中，E 是AB 上一点，BE=2，AE=3BE ，P 是AC 上一动点，则PB+PE 的最小值是____12.如图，在▱ABCD 中，∠DBC=45°，DE ⊥BC 于E ，BF ⊥CD 于F ，DE 、BF 交于H ，BF 、AD 的延长线交于G ，下面结论：①BD= BE ；②∠A=∠BHE ；③AB=BH ；④△BHD ∽△BDG ，⑤BH=HG ．其中正确的结论是 。

四年级数学易错题集合（一）1、写出□里的数。

□ □□F26 二7……6298 一□□二9……1□ □ □ =35 二8……3197一口□二5……2、把下而的每一组算式, 合并成综合算式73+27=10052-36=1642X 13=5461004-25=445X 16=720102 + 546=6463、用5个3和3个0按要求写出下面各数⑴一个〃零〃都不读出来;（2）只读出一个〃零〃；（3）读出两个〃零〃；（4）读出三个〃零〃。

4、每列上下为一组，第32组是（）o从小爱数学从小佥2数学…ABCDEABCDE-・5、购物屮心玩具柜购进了75个足球，每个售价20元。

全部卖出后赚了600元，每个足球的进货价格是多少元？6、皮鞋厂四月份生产皮鞋420双，平均每天生产多少双？7、苏果电器第一季度彩电的销售情况是：一月份销售258台，二月份销售339台，三月份销售222台。

第一季度平均每天销售彩电多少台？四年级数学易错题集合（二）1、□里最大能填儿？□一35〈8 Q4-27<52、填上合适的运算符号。

4 5 6 = 264 5 6 = 144 5 6 = 343、从1写到50,数字0—共写了（）个，数字2—共写了（）个。

4、一个数省略〃亿〃位后面的尾数的近似数是8亿，这个数最大是（），最小是（）,它们相差（）o5、找规律填数（1）30600、32600、34600、（）、（）。

（2）100000、99900、99800、（）、（）。

6、你能用3根小棒摆出3个角吗？请把你的想法画下來。

7、马小虎在计算除法时，把除数63错写成了36,结果得到的商是18还余8,这道题正确的商应该是多少？述余多少？8、工程队第一天修路450米，第二天修530米，还剩98米未修。

已修的长度是未修的多少倍？9、一条公路长1000米，每隔20米，安装一盏路灯，一共要安装多少盏路灯？1、与最小的八位数相邻的两个数是（）和（）。

2、10个鸟蛋重50克，100万个鸟蛋约重（）吨。

2021年成都嘉祥外国语学校小升初数学考试内容知识点总结孩子的教育始终是家长关心的头等大事，所有的家长都希望自己的孩子能够接受最好的教育，有更好的未来。

为此小升初频道为大家提供成都嘉祥外国语学校小升初数学考试内容，希望成都的同学们在备考时参考!
____年成都嘉祥外国语学校小升初数学考试内容
校内基础知识(17%)：数的认识，分数的认识，比例尺，正反比例，整除，质数合数，约数和倍数，统计知识;
计算(23%)：凑整，乘法分配律，分数四则混合运算，换元，简单裂项，解方程; 计数(7%)：图形找规律，数字找规律，枚举，简单的加乘原理;
几何(13%)：基本图形的面积，长方形和正方形，圆和扇形，圆柱的体积和表面积，三视图，展开图，梯形模型，燕尾模型，差不变原理;
行程(10%)：行程三要素关系，相遇和追及，火车过桥，比例解行程;
应用题(30%)：和差倍问题，分数应用题，比例应用题，经济问题，工程问题，列方程解应用题。

小升初考试对于同学们来说是非常重要的，为大家提供的成都嘉祥外国语学校小升初数学考试内容，希望能够满足大家的需求!同时预祝大家考入自己心目中理想的中学!。