数学物理方程学习指导书 第9章 勒让德多项式
- 格式:pdf
- 大小:206.10 KB
- 文档页数:9


勒让德多项式归一化
勒让德多项式是一类经典的正交多项式,用于描述数学和物理领域中
的各种现象和问题。
为了方便应用,我们需要将这些多项式进行归一
化处理。
勒让德多项式的归一化可以通过如下方式实现。
首先,我们需要确定
多项式中最高次幂的系数,即归一化因子。
通过求解正交条件和归一
化条件,我们可以得到这个系数的具体表达式。
以勒让德多项式P_n(x)为例,其中n代表多项式的阶数,x为自变量。
首先,我们需要确定归一化因子A_n,它的求解需要满足以下两个条件:
1. 正交条件:不同阶数的勒让德多项式在某一区间上的内积为0,即
∫(-1 to 1) P_n(x)P_m(x) dx = 0 (n ≠ m)。
这个条件保证了不同
阶数的多项式之间不存在互相干扰。
2. 归一化条件:阶数为n的勒让德多项式在区间内的归一化,即∫(-
1 to 1) [P_n(x)]^
2 dx = 1。
这个条件保证了每个多项式都有相同的
总能量。
通过求解这两个条件,我们可以得到归一化因子A_n的具体表达式。
然后,我们可以将原始的勒让德多项式除以归一化因子,即P_n(x) /
A_n,从而得到归一化后的多项式。
归一化后的勒让德多项式具有一些重要的性质和应用。
它们能够描述
电磁场、量子力学以及各种物理过程中的现象和问题。
归一化后的勒
让德多项式在实际计算中更加方便和可靠,能够提供准确的结果,并
被广泛应用于科学和工程领域。

勒让德多项式及其正交性质勒让德多项式是一种重要的数学工具,在微积分、物理学等领域都有广泛的应用。
它是一类正交多项式,具有良好的性质,可以用于解决一些特殊的数学问题。
本文将讨论勒让德多项式及其正交性质,以期读者能够深入了解这一重要数学工具。
一、勒让德多项式的定义勒让德多项式是一种定义在区间[-1,1]上的多项式函数,通常用Pn(x)表示,其中n为多项式的次数。
勒让德多项式可以通过如下公式递归地定义:P0(x) = 1P1(x) = xPn(x) = [(2n-1)xPn-1(x) - (n-1)Pn-2(x)]/n这个公式可以用来计算任意次数的勒让德多项式。
勒让德多项式的前几个函数值如下:P0(x) = 1P1(x) = xP2(x) = (3x² - 1)/2P3(x) = (5x³ - 3x)/2P4(x) = (35x⁴ - 30x² + 3)/8二、勒让德多项式的性质勒让德多项式具有许多重要的性质,其中最重要的是正交性质。
1. 正交性质勒让德多项式在区间[-1,1]上的内积可以定义为:∫[-1,1] Pn(x)Pm(x)dx如果n=m,则积分结果为2/(2n+1);如果n≠m,则积分结果为0。
也就是说,勒让德多项式之间具有正交性质。
这个性质非常重要,因为它能够使我们更方便地进行一些数学运算。
例如,计算某个函数在勒让德多项式基下的系数时,我们只需要进行一次内积计算即可。
2. 完备性质勒让德多项式在区间[-1,1]上具有完备性质。
也就是说,任何在该区间上连续的函数都可以用勒让德多项式展开,并且展开式收敛于原函数。
这个性质太过深奥,需要深入的数学知识,不在本文的讨论范围内。
3. 递推性质勒让德多项式之间具有递推性质,可以用如下公式计算高一阶的勒让德多项式:Pn+1(x) = (2n+1)xPn(x) - nPn-1(x)这个公式可以用来快速地计算任意次数的勒让德多项式。

勒让德多项式递推公式证明以勒让德多项式是数学中一类重要的特殊函数,其递推公式是证明其性质的关键。
本文将通过介绍以勒让德多项式的定义、性质和递推公式的证明,来解释这一标题。
以勒让德多项式是数学中的一类正交多项式,它们是解决物理和工程问题中的常微分方程的重要工具。
以勒让德多项式的定义如下:$$P_n(x) = \frac{1}{2^n n!} \frac{d^n}{dx^n} \left[(x^2 - 1)^n\right]$$其中,$n$为非负整数,$P_n(x)$表示以勒让德多项式的第$n$阶,$x$为自变量。
以勒让德多项式具有一系列重要的性质,如正交性、归一性等,这些性质使其在数学和物理学中得到广泛应用。
以勒让德多项式的递推公式是证明其性质的关键。
递推公式的形式如下:$$(n+1)P_{n+1}(x) = (2n+1)xP_n(x) - nP_{n-1}(x)$$下面我们来证明这个递推公式。
我们将以勒让德多项式的定义代入递推公式中,得到:$$(n+1)\left(\frac{1}{2^{n+1} (n+1)!} \frac{d^{n+1}}{dx^{n+1}} \left[(x^2 - 1)^{n+1}\right]\right) = (2n+1)x\left(\frac{1}{2^n n!} \frac{d^n}{dx^n} \left[(x^2 - 1)^n\right]\right) - n\left(\frac{1}{2^{n-1} (n-1)!} \frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right]\right) $$化简上式,可以得到:$$\frac{1}{2^{n+1} (n+1)!} \frac{d^{n+1}}{dx^{n+1}} \left[(x^2 - 1)^{n+1}\right] = \frac{2n+1}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right]$$我们将上式中的$n+1$分布到第一项中,并利用导数的链式法则进行化简,得到:$$\frac{1}{2^{n+1} (n+1)!} \frac{d}{dx}\left[(2n+1)x(x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$再次化简上式,得到:$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$继续化简上式,可以得到:$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right]$$再次化简上式,得到:$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$继续化简上式,可以得到:$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$再次化简上式,得到:$$\frac{1}{2^{n+1} (n+1)!} (2n+1)\left[x\frac{d}{dx}\left[(x^2-1)^n\right] + (x^2-1)^n\right] = \frac{(2n+1)}{2^n n!}x\frac{d^n}{dx^n} \left[(x^2 - 1)^n\right] - \frac{n}{2^{n-1} (n-1)!}\frac{d^{n-1}}{dx^{n-1}} \left[(x^2 - 1)^{n-1}\right] $$通过以上推导,我们证明了以勒让德多项式的递推公式。


勒让德多项式表示形式
勒让德多项式,又称勒让德多项式,是一种数学表达式,用来表示一个多项式的值。
它是
由法国数学家勒让德(Joseph Louis Lagrange)在1795年发明的。
勒让德多项式的表达式是一个多项式,它由一系列的系数和指数组成,每个系数和指数都
有一个特定的含义。
系数表示多项式中每一项的系数,而指数表示多项式中每一项的指数。
勒让德多项式的表达式可以用来表示一个多项式的值,它可以用来计算多项式的值,也可
以用来求解多项式的根。
它还可以用来求解多项式的导数和积分。
勒让德多项式的表达式可以用来表示一个多项式的值,它可以用来计算多项式的值,也可
以用来求解多项式的根。
它还可以用来求解多项式的导数和积分。
勒让德多项式的表达式可以用来解决许多数学问题,它可以用来解决多项式的根,也可以
用来解决多项式的导数和积分。
它还可以用来解决更复杂的数学问题,比如求解微分方程
和积分方程。
勒让德多项式的表达式是一种非常有用的数学表达式,它可以用来解决许多数学问题,比
如求解多项式的根,求解多项式的导数和积分,以及求解微分方程和积分方程。
它的表达
式简洁明了,可以让我们更容易理解多项式的值,从而更好地解决数学问题。


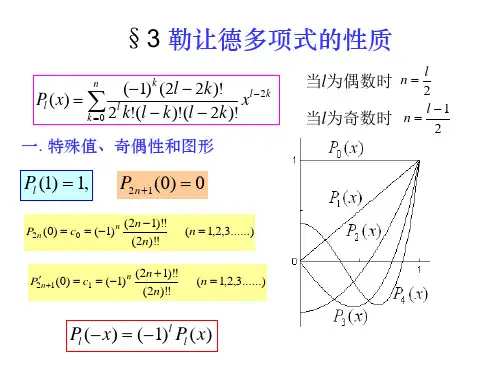
三、正交性 1 §14.2 勒让德多项式的性质用途:可计算含 pl (x 的积分。
2 ∫−1 Pl (x Pk (x dx = 2l + 1 δ kl , k , l = 0,1,2,..., (6 问: ∫ ∫ 1 2 2 P8 (x dx = ? = −1 2 ⋅ 8 + 1 17 1 0 ∫−1 P8 (x P9 (x dx = ? 1 9 2 ∫−1 xP8 (x P9 (x dx = ? = 17 ⋅ 18 + 1 2 −1 1 P 199 ( x P 300 ( x dx = ? 0四、广义傅氏展开f (x = ∑ Cl Pl (x l =0 ∞ §14.2 勒让德多项式的性质 (9 2l + 11 Cl = f ( x Pl ( x dx ∫2 −1 (10 用途: (1在物理中常需将作为表征的物理量展开为级数进行分析。
(2在求解数学物理方程时其解常是某函数的无穷级数,如稳恒电场的解,就是 Legendre级数。
五.小结一、母函数关系式二、递推公式三、正交性1 1− 2x t + t 2 §14.2 勒让德多项式的性质= ∑ Pl (x t l , t < 1 (1 l =0 ∞ 1. (l + 1Pl +1 ( x − (2l + 1x Pl ( x + l Pl−1 ( x = 0 (2 2. (2l + 1Pl (x = Pl′+1 ( x − Pl′−1 (x (3 ∫ 1 −1 Pl ( x Pk (x dx = 2 δ kl , k , l = 0,1,2,..., (6 2l + 1 ∞ 四、广义傅氏展开f ( x = ∑ Cl Pl ( x l =0 (9 2l + 1 1 Cl = f (x Pl ( x dx ∫ − 1 2 (10本节作业一.由勒让的多项式的母函数关系式推出下列递推关系: 1. (l + 1Pl +1 (x − (2l + 1x Pl ( x + l Pl −1 ( x = 0 (2 2. (2l + 1Pl (x = Pl′+1 ( x − Pl′−1 (x (3 二.P280. 2。

勒让德多项式是一类具有重要性质的正交函数,它们在数学和工程领域中有着广泛的应用。
本文将介绍勒让德多项式的定义、性质、正交关系以及其在实际问题中的应用。
一、勒让德多项式的定义勒让德多项式是勒让德微分方程的解,该微分方程形式如下:\[ (1-x^2)y''-2xy'+n(n+1)y=0 \]其中n为非负整数。
根据其定义,勒让德多项式可以通过勒让德微分方程的解出来。
勒让德多项式的具体形式可以表示为:\[ P_n(x)= \frac{1}{2^n n!} \frac{d^n}{dx^n}(x^2-1)^n \]其中n为非负整数,P_n(x)表示第n阶的勒让德多项式。
二、勒让德多项式的性质勒让德多项式具有许多重要的性质,例如:1. 勒让德多项式是正交的,即对于不同的n和m,有以下正交性质成立:\[ \int_{-1}^{1}P_n(x)P_m(x)dx=0, \quad(n\neq m) \]2. 勒让德多项式满足勒让德微分方程,这也是它的定义所在。
3. 勒让德多项式具有递推关系,即通过递推关系可以方便地计算高阶的勒让德多项式。
三、勒让德多项式的正交关系及应用勒让德多项式的正交性质在数学和工程领域中有着重要的应用。
在数学分析中,勒让德多项式的正交性质可以用来进行函数的展开和逼近,例如在傅立叶级数、泰勒级数及函数的插值逼近中。
在数值计算和数值分析中,勒让德多项式的正交特性也被广泛应用,例如在数值积分方法中,通过勒让德多项式的正交性质可以得到高效的数值积分算法。
勒让德多项式还具有广泛的物理应用,例如在量子力学中,勒让德多项式常常用来描述原子轨道的形状。
在实际问题中,勒让德多项式的正交性质为我们提供了一种简便而有效的数学工具,通过利用勒让德多项式的正交性质,我们可以更加方便地解决各种数学和工程问题。
勒让德多项式作为一类重要的正交函数,在数学和工程领域中具有着广泛的应用。
通过深入研究勒让德多项式的定义、性质、正交关系及其应用,我们可以更好地理解和运用这一类特殊的函数,从而为解决各种实际问题提供更加有效的数学工具。

课程设计报告n 阶勒让德(Legendre)多项式一、设计任务与目标n 阶勒让德(Legendre)多项式可以递归定义如下:⎪⎩⎪⎨⎧>---===--1/))(*)1()(**)12((101)(21n nx p n x p x n n xn x p n n n(1) 输入n 和x 的数值,输出此时勒让德多项式的数值。
例如输入2,1,应输出1/2。
(2)输入n 的数值, 输出此时的勒让德多项式。
例如输入2,应输出3/2 x 2 - 1/2。
本次上机实践所使用的平台和相关软件。
平台:Windows xp 相关软件:VC6.0二、方案设计与论证对于这个题目,我分析了一下,第一问是要求我要用递归方法去求最终的值,所以我在程序中编写了子函数treat ,并在主函数main 中调用,在子函数中不断调用自己本身。
第二问,由于不能按照常规来做,只能够想一些特别的方法,例如:利用字符串输出,但这种方法不行。
经老师提醒,先做好这个表达式的每一项的情况,然后再将他们整合输出,于是我选择了这个方法并向着这个方向去做,后来在网上找了相关的资料,我发现了这么一条公式:∑⎥⎦⎤⎢⎣⎡=-----=202)!2()!(!2)!22()1()(n m mn nmn x m n m n m m n x p ,这一条公式可以求出表达式的每一项,我利用四个数组,第一个数组是记录m)1(-的结果;第二个数组是记录)!2()!22(m n m n --约简后的结果;第三个数组是记录)!(!2m n m n -约简后的结果;第四个数组是记录m n 2-的结果。
最后输出每一项并整合最终的结果。
在计算)!2()!22(m n m n --之前,我采用了没有约简的方法去做,结果数值超出了我设定的int 型数据的范围,导致我只能够输出n=6的情况,n=7输出错误。
后来利用约简的方法,于是结果达到了n=8的情况。
接着我采用了double 型,结果能输出n=10的情况,但是在运行的过程中发现,输出很慢。
勒让德多项式的微分表达式勒让德多项式是高等数学中一个非常重要的概念,它是一类特殊的多项式,有着优良的数学特性,并且在实际的科学研究中被广泛应用。
它的微分表达式也被广泛采用,因为它可以表示变量的变化,并且可以更直观地体现数学模型。
本文旨在介绍勒让德多项式的微分表达式,以期对勒让德多项式的微分表达式有更深入的了解。
首先,我们需要了解勒让德多项式的定义。
勒让德多项式是一类多项式,它以带有一定规律的系数表示,其标准形式为:a_nx^n+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+...+a_1x+a_0=0 其中,n是多项式的次数,a_n, a_{n-1}, a_{n-2},…, a_1, a_0是多项式的系数。
接下来,我们来讨论勒让德多项式的微分表达式,它可以通过对多项式的每项进行微分,并根据次数进行指数变化,来得到。
下面我们来看一个例子,如多项式f(x)=x^4+2x^2-3x+4,它的微分表达式可以表示为:f’(x)=4x^3+4x-3可以看到,所得到的微分表达式只有一项,并且是对原多项式每项的指数变化、系数变化的综合反映,其公式是:f’(x)=na_nx^{n-1}+(n-1)a_{n-1}x^{n-2}+(n-2)a_{n-2}x^{n-3}+... +2a_2x+a_1此外,我们还可以使用一些特殊的技巧来求解勒让德多项式的微分表达式。
首先,无论多项式有多少项,它们都可以被写作一阶分式的形式:f(x)=a_n(x-x_1)(x-x_2)…(x-x_n)其中,a_n是多项式的系数,x_1, x_2,…, x_n是多项式中全部根的表达式,他们都可以由简化的过程得到。
按照这种形式,勒让德多项式的微分表达式可以很容易地算出。
最后,为了更直观地理解勒让德多项式的微分表达式,我们可以使用拉格朗日的偏微分法,通过对多项式的拉格朗日函数进行求导来计算多项式的微分表达式。
例如,f(x)=x^4+2x^2-3x+4应的拉格朗日函数是:L=x^4+2x^2-3x+4-l_x其中,l_x拉格朗日变量,他可以看成是多项式中的未知数,通过对拉格朗日函数进行求导可以得出:f’(x)=4x^3+4x-3这也就是我们最终求解的勒让德多项式的微分表达式了。
勒让德多项式变换
勒让德多项式是一类常见的正交多项式,它在物理学和数学领域中有广泛的应用。
勒让德多项式可以通过变换来得到不同形式的表示。
下面是一些常见的勒让德多项式变换:
1. 勒让德多项式展开为幂级数:勒让德多项式可以通过泰勒级数展开来表示。
这个展开式可以用于计算勒让德多项式的近似值。
2. 勒让德多项式的递推关系:勒让德多项式之间存在递推关系,即P_n(x) = (2n-1)xP_{n-1}(x) - (n-1)P_{n-2}(x),其中P_n(x) 表示n 阶勒让德多项式。
3. 勒让德多项式的归一化:勒让德多项式可以通过归一化来得到归一化的勒让德多项式。
归一化的勒让德多项式被广泛应用于概率密度函数和正交性的研究中。
4. 勒让德多项式的逆变换:勒让德多项式可以通过逆变换来得到原始函数的表达式。
这个逆变换可以用于将勒让德多项式转换回原始函数的形式。
这些是勒让德多项式的一些常见变换方法,它们在数学和物理学中有广泛的应用。
勒让德多项式的微分表达式
勒让德多项式是一种特殊的函数,它由最高次幂为N的N+1项组成,通常用来拟合曲线。
它和普通多项式的最大区别在于它的变量是
由不同的常数乘以指数x^n构成的,其形式如下:c(x)=a_N x^n +
a_(N-1) x^(N-1)+...+a_2 x^2 + a_1 x + a_0。
将上述表达式乘以n并将其代入原式中, 可以得出勒让德多项式
的微分表达式: c'(x)=Na_N x^(n-1)+ (N-1) a_(N-1) x ^(n-2)+…+
2a_2 x + a_1 。
对于勒让德多项式的求导,我们一般采用后面这种表达式,这也
是一种非常有效的方法,而不是一次使用n次链律法。
在使用这种表
达式之前,我们需要先记住最高次幂,即n,然后根据公式中的指数变化,从N开始,每次-1就可以得出每一项对应的指数,并且每一项前
面的系数也是可以直接把原多项式中相应系数带入即可。
因此,从上面可以看到,求勒让德多项式的导数的时候,需要我
们先找到最高次,然后根据指数的变化,再将每一项相应的系数带入,最后就可以得到她的微分表达式,这也是比较容易让人理解的一种方法。
勒让德多项式的微分表达式勒让德多项式是一种多项式的特殊形式,它的函数形式是可以用来表示微分表达式的。
它是由著名数学家勒让德几何学家首先提出的,由他十九世纪晚期提出的“笛卡尔方程”演变而来。
在几何学领域,勒让德多项式用来表达曲面函数的导数。
它可以用来表示二维和三维空间中的曲面,也称为曲面变换,因为它具有多种类型的函数生成的曲面的几何性质。
其形式如下:f(x,y)=a0+a1x+a2y+a3xy+a4x2+a5y2+a6x2y+…该多项式中的a0,a1,a2,a3等参数都是曲面上随着x、y变化而变化的常数值。
这些参数对曲面变换有重要作用,因此在使用勒让德多项式时必须将其正确地估计出来。
另一方面,勒让德多项式也可以用来表示微分表达式,它的函数形式如下:f(x)=a0+a1x+a2x2+a3x3+…该函数的导数是多项式的系数的变化,它可以用来求出函数的斜率。
对于勒让德多项式,为了求得它的导数,可以采用微积分的方法。
该方法可以帮助我们求出多项式的导数。
具体的,我们可以把勒让德多项式的函数式化为整数多项式,然后依次进行微积分计算,以获得该多项式的微分表达式。
例如,当x = 1时,从勒让德多项式可推算出其函数式为:f(x)=3+2x+x2+x3因此,对于上述函数,可以得出其导数为:f′(x)=2+2x+3x2从上面得出的结果可以看出,我们可以通过微积分的方法来解决勒让德多项式的微分表达式。
而勒让德多项式的应用广泛,它可以用于近似求解各种二阶和三阶的微分方程。
在物理学、机械工程、计算机科学等领域都可以使用勒让德多项式进行运算。
总之,勒让德多项式是一种有特殊含义的多项式,用于表示微分表达式。
它可以用来求解一些复杂的方程,并有在数学领域及其他许多领域的广泛应用。