第7章 含有互感的电路

互感电路分析一、是非题1.互感耦合线圈的同名端仅与两线圈的绕向及相对位置有关，而与电流的参考方向无关。

2.图示两互感线圈的a、c两端互为同名端，则可推断b、d也互为同名端。

3.当两互感线圈的电流同时流出同名端时，两个电流所产生磁场是互相削弱的。

4.互感电压的正负不仅与线圈的同名端有关，还与电流的参考方向有关。

5.耦合电感初、次级的电压、电流分别为u1、u2和i1、i2。

若次级电流i2为零，则次级电压u2一定为零。

6.对图示电路有。

7.对右上图示电路有。

8.图示电路中互感电压u M为参考方向，当开关S闭合瞬间，u M的真实方向与参考方向相同。

9.图示耦合电感电路中，互感电压u M为参考方向，当开关S断开瞬间，u M的真实方向与参考方向相反。

10.如图所示，当i1按图示方向流动且不断增大时，i2的实际方向如图所示。

11.对右上图示电路有：12.某匝数为N的线圈，自感为L，如果此线圈的匝数增加一倍，则其自感变为4L。

13.两个耦合电感串联，接至某正弦电压源。

这两个电感无论怎样串联都不影响电压源的电流。

1.答案(+)2.答案(+)3.答案(-)4.答案(+)5.答案(-)6.答案(-)7.答案(-)8.答案(-)9.答案(+)10.答案(-)11.答案(-)12.答案(+)13.答案(-)二、单项选择题1.两个自感系数各为L1、L2的耦合电感，其互感系数的最大值为(A)L1L2 (B)(C)L1+L2 (D)2.电路如图所示，开关S动作后时间常数最大的电路是：3.图示电路中，若已知，而不详，则电压为(A)(B)不能确定(C)(D)4.右上图示电路中、，则u1为(A)(B)(C)(D)5.图示电路中的开路电压为(A)(B)(C)(D)6.图示电路中，i S=sin(2fπt+45︒)A，f =50Hz当t =10ms时，u2为(A)正值 (B)负值 (C)零值 (D)不能确定7.电路如右上图所示，已知L1=6H，L2=3H，M=2H，则ab两端的等效电感为(A)13H (B)5H (C)7H (D)11H8.图示两互感线圈串联接于正弦交流电源，则当耦合因数k逐渐增大时，电源输出的平均功率P(A)逐渐减小 (B)逐渐增大 (C)无法确定9.两耦合线圈顺向串联时等效电感为0.7H，反向串联时等效电感为0.3H，则可确定其互感M为(A)0.1H (B)0.2H (C)0.4H (D)无法确定10.图示二端网络的等效阻抗Z ab为：(A)j1Ω (B)j2Ω (C)j3Ω11.右上图示电路，S闭合后电路的时间常数τ为(A)15ms (B)25ms (C)5ms (D)其他值12.图示电路中，开关S动作后时间常数最大的电路是：13.左下图示电路，耦合因数k=1，L1=1H，L2=1H，，则与分别为(A)10V与0V (B)10V与20V(C)-10V与0V (D)-10V与20V14.右上图示电路中，互感M=1H，电源频率ω=1rad/s，a、b两端的等效阻抗Z 为(A)j1Ω (B)0 (C)j2Ω (D)j4Ω15.图示电路中L1=1H，L2=1H，M=0.5H，C=100μF，则电路的谐振频率f0为(A)(B)(C)(D)1.答案(D)2.答案(A)3.答案(B)4.答案(C)5.答案(B)6.答案(B)7.答案(A)8.答案(A)9.答案(A)10.答案(C)11.答案(B)12.答案(C)13.答案(D)14.答案(B)15.答案(D)三、填空题1.对于L1=1H、L2=4H的耦合电感，若能实现全耦合，则互感M为____2.耦合电感的同名端与两个线圈的绕向和相对位置有关，与电流的参考方向_____________。

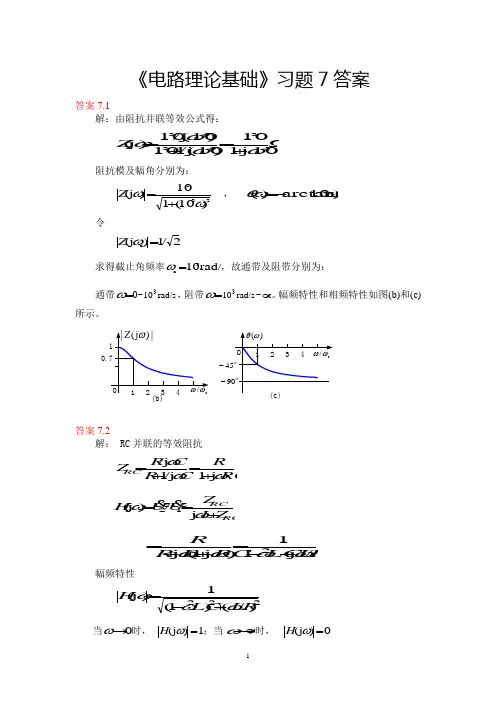
《电路理论基础》习题7答案答案7.1解：由阻抗并联等效公式得：Ω+=+=---33636310j 110)10j /(110)10j /(10)j (ωωωωZ 阻抗模及幅角分别为：233)10(110)j (ωω-+=Z ，)10arctan()(3ωωθ--=令2/1)j (c=ωZ 求得截止角频率rad/s 103c=ω，故通带及阻带分别为： 通带=ω0~rad/s 103，阻带=ωrad/s 103~∞。

幅频特性和相频特性如图(b)和(c)所示。

1234O(b)|)j (|ωZ 10.7(c)1234O)(ωθο45-ο90-c/ωωc/ωω答案7.2解： RC 并联的等效阻抗RC RC R C R Z RCωωωj 1j /1j /+=+= RCRC Z L Z U U H +==ωωj /)j (12&& RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++= 幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时， 1)j (=ωH ；当∞→ω时，0)j (=ωH所以它具有低通特性。

答案7.3解：设1111111j j 1//C R R R C R Z ωω+==， 2222222j j 1//C R R R C R Z ωω+== 由分压公式得：12122U Z Z Z U &&+= )j 1()j 1()j 1()j (11222111212C R R C R R C R R U U H ωωωω++++==&& 当R 1C 1＝R 2C 2时，得212)j (R R R H +=ω，此网络函数模及辐角均不与频率无关。

答案7.4解：因为电路处于谐振状态，故电感与电容串联电路相当于短路，因此有50S12121==+I U R R R R Ω代以Ω=1001R ，解得Ω=1002R 又因为电路处于谐振状态 ， 所以 Ω==100C L X X 故有V 5021S12=⨯+==L L L X R R I R X I U 答案7.5解：(1)根据题意，电路发生谐振时，存在下列关系：⎪⎩⎪⎨⎧======V10A1/rad/s 10/14LI U R U I LC L ωω 解得 ⎪⎩⎪⎨⎧==Ω=F 10mH 11.0μC L R 品质因数 1001.010===U U Q L（2）V 9010V 901001)(j ︒-∠=︒-∠⨯︒∠==C I U Cω&& 即有V )90cos(210︒-=t u Cω 答案9.9解：由串联谐振规律得：⎪⎪⎩⎪⎪⎨⎧===∆==Ω=RL Q Q LC R /rad/s 100/rad/s 10/1100030ωωωω 解得 ⎪⎩⎪⎨⎧==Ω=1μμC H 1100L R答案7.6解：(1)F 10034.132.0)8752(117220-⨯=⨯⨯==πωL C Qωω=∆ ， 5.3250/875/0==∆=ωωQ R L Q /0ω=， Ω=⨯⨯==65.5025.3/32.08752/0πωQ L R 谐振频率为Hz 759)14121(021c ≈⨯++-=f Q Q f Hz 1009)14121(02c2≈⨯++=f QQ f(2) 谐振时电路的平均功率为：W 071.165.502)65.502/2.23(2200=⨯==R I P 在截止频率处，电流下降至谐振电流0I 的2/1，故功率减小到0P 的一半，所以当Hz 759=f 和Hz 1009=f 时，电路平均功率均为W 535.02/0==P P (3)V 2.812.235.3=⨯===QU U U CL 答案7.7解：由谐振时阻抗为Ω310得 Ω=1000RRLC 并联电路带宽：Q/0ωω=∆（参考题9.16） 由带宽与谐振角频率及品质因数的关系得：10/0=∆=ωωQ RLC 并联电路的品质因数为10/0==G C Q ω 由上式求得：μF10)10001000/(10/100=⨯==ωG C 由C L 00/1ωω=得 H1.0H )1010/(1/15620=⨯==-C L ω答案7.8略 答案7.9解：当两线圈顺接时，等效电感H 05.0221=++=M L L L 谐振角频率s rad 10102005.011361=⨯⨯==-LC ω 取V06︒∠=U &，则谐振时的电流 A 04.0A 1050621︒∠=+︒∠=+=R R U I && 由互感的元件方程得： j124(0.4]V j100.4j20)10[(j )j (j8)V 2(0.4]V j100.4j10)5[(j )j (1212211111+=⨯+⨯+=++=+=⨯+⨯+=++=I M I L R U I M I L R U &&&&&&ωωωω两线圈电压的有效值分别为V 24.882221=+=U ，V 65.12124222=+=U 当两线圈反接时，等效电感H 01.0221'=-+=M L L L 谐振角频率rad/s 10236.2102001.01362⨯=⨯⨯=-ω j8.94(0.4A j22.36)10(j )j (2V A 4.05j )j (2222221211+=⨯Ω+=-+==⨯Ω=-+=I M I L R U I M I L R U &&&&&&ωωωω此时两线圈电压的有效值分别为V 21=U ，V 8.995.84222=+=U 答案7.10略答案7.11图示电路，V )cos(22S t u ω=，角频率rad/s 100=ω，Ω=1R ，F 1021-=C ，F 105.022-⨯=C 。

高二物理互感现象知识点互感现象是物理学中一个重要的概念，它涉及到电磁感应和电路中的能量转换。

本文将介绍高二物理课程中关于互感现象的知识点，包括定义、原理、公式和应用。

一、互感现象的定义互感现象是指两个或多个线圈或导体之间由于磁场的相互作用而产生的电动势的现象。

当电流通过一组线圈或导体时，会产生磁场，在另一组线圈或导体中感应出电动势。

这种现象是电磁感应的一种形式，可以通过互感的概念来解释。

二、互感现象的原理互感现象的原理基于法拉第电磁感应定律和楞次定律。

根据法拉第电磁感应定律，当磁通量的变化通过一个线圈时，该线圈中会产生感应电动势。

而对于互感现象，当一个线圈中的感应电动势引起电流变化时，它会通过磁场的相互作用传递到另一个线圈中，从而产生另一个感应电动势。

这个过程符合楞次定律，即感应电动势的方向会阻碍引起它的磁通量的变化。

三、互感现象的公式互感系数（M）是衡量互感现象强弱的物理量，它等于两个线圈中的磁通量变化与引起感应电动势的电流变化之间的比值。

根据这个定义，互感系数的公式为：M = (N2 * Φ2) / I1其中，N2表示第二个线圈的匝数，Φ2表示第二个线圈中的磁通量变化，I1表示第一个线圈中的电流变化。

四、互感现象的应用互感现象在电路中起着重要作用，广泛应用于变压器、感应电机、共振电路等各种电器设备和电路中。

变压器是利用互感现象来实现电能的传递和转换的设备，由两个线圈和一个铁芯构成。

感应电机则是利用互感现象来生成驱动电机转动的电动势。

共振电路中的电感和电容元件之间通过互感现象实现能量的传输和转换。

总结：高二物理课程中的互感现象是一个重要的知识点，它涉及到电磁感应和电路中的能量转换。

通过了解互感现象的定义、原理、公式和应用，我们可以更好地理解电磁现象和电路的运作原理，也能够应用互感现象来设计和优化各种电器设备和电路。

互感现象在现代科学和工程中有着广泛的应用，对我们的生活和工作产生着深远的影响。

通过深入学习和掌握互感现象的相关知识，我们可以更好地理解和应用物理学的原理，为未来的科学研究和技术创新打下坚实的基础。

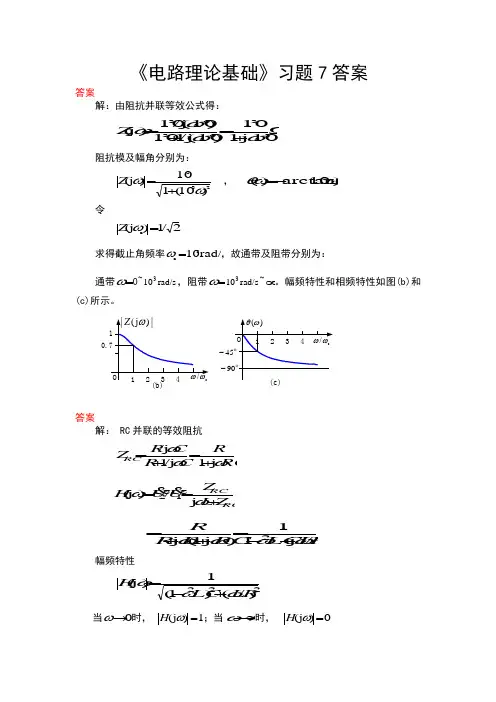
《电路理论基础》习题7答案答案解：由阻抗并联等效公式得：Ω+=+=---33636310j 110)10j /(110)10j /(10)j (ωωωωZ 阻抗模及幅角分别为：233)10(110)j (ωω-+=Z ，)10arctan()(3ωωθ--=令2/1)j (c=ωZ 求得截止角频率rad/s 103c=ω，故通带及阻带分别为： 通带=ω0~rad/s 103，阻带=ωrad/s 103~∞。

幅频特性和相频特性如图(b)和(c)所示。

--答案解： RC 并联的等效阻抗RCRC R C R Z RCωωωj 1j /1j /+=+= RCRC Z L Z U U H +==ωωj /)j (12&& RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++= 幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时， 1)j (=ωH ；当∞→ω时，0)j (=ωH所以它具有低通特性。

答案解：设1111111j j 1//C R R R C R Z ωω+==， 2222222j j 1//C R R R C R Z ωω+== 由分压公式得：12122U Z Z Z U &&+= )j 1()j 1()j 1()j (11222111212C R R C R R C R R U U H ωωωω++++==&& 当R 1C 1＝R 2C 2时，得212)j (R R R H +=ω，此网络函数模及辐角均不与频率无关。

答案解：因为电路处于谐振状态，故电感与电容串联电路相当于短路，因此有50S12121==+I U R R R R Ω代以Ω=1001R ，解得Ω=1002R 又因为电路处于谐振状态 ， 所以Ω==100C L X X 故有V 5021S12=⨯+==LL L X R R I R X I U 答案解：(1)根据题意，电路发生谐振时，存在下列关系：⎪⎩⎪⎨⎧======V10A1/rad/s 10/14LI U R U I LC L ωω 解得 ⎪⎩⎪⎨⎧==Ω=F 10mH 11.0μC L R 品质因数 1001.010===U U Q L （2）V 9010V 901001)(j ︒-∠=︒-∠⨯︒∠==C I U Cω&& 即有V )90cos(210︒-=t u Cω答案解：由串联谐振规律得：⎪⎪⎩⎪⎪⎨⎧===∆==Ω=R L Q Q LC R /rad/s 100/rad/s10/1100030ωωωω 解得 ⎪⎩⎪⎨⎧==Ω=1μμC H 1100L R答案解：(1)F 10034.132.0)8752(117220-⨯=⨯⨯==πωL C Qωω=∆ ， 5.3250/875/0==∆=ωωQ R LQ /0ω=， Ω=⨯⨯==65.5025.3/32.08752/0πωQ L R 谐振频率为Hz 759)14121(021c ≈⨯++-=f Q Q f Hz 1009)14121(02c2≈⨯++=f QQ f(2)谐振时电路的平均功率为：W 071.165.502)65.502/2.23(2200=⨯==R I P 在截止频率处，电流下降至谐振电流0I 的2/1，故功率减小到0P 的一半，所以当Hz 759=f 和Hz 1009=f 时，电路平均功率均为W 535.02/0==P P (3)V 2.812.235.3=⨯===QU U U CL 答案解：由谐振时阻抗为Ω310得 Ω=1000RRLC 并联电路带宽：Q/0ωω=∆（参考题） 由带宽与谐振角频率及品质因数的关系得：10/0=∆=ωωQ RLC 并联电路的品质因数为10/0==G C Q ω 由上式求得：μF10)10001000/(10/100=⨯==ωG C 由C L 00/1ωω=得 H1.0H )1010/(1/15620=⨯==-C L ω答案略 答案解：当两线圈顺接时，等效电感H 05.0221=++=M L L L 谐振角频率rad 10102005.011361=⨯⨯==-LC ω 取V06︒∠=U &，则谐振时的电流 A 04.0A 1050621︒∠=+︒∠=+=R R U I && 由互感的元件方程得： j124(0.4]V j100.4j20)10[(j )j (j8)V 2(0.4]V j100.4j10)5[(j )j (1212211111+=⨯+⨯+=++=+=⨯+⨯+=++=I M I L R U I M I L R U &&&&&&ωωωω两线圈电压的有效值分别为V 24.882221=+=U ，V 65.12124222=+=U 当两线圈反接时，等效电感H 01.0221'=-+=M L L L 谐振角频率rad/s 10236.2102001.01362⨯=⨯⨯=-ω j8.94(0.4A j22.36)10(j )j (2V A 4.05j )j (2222221211+=⨯Ω+=-+==⨯Ω=-+=I M I L R U I M I L R U &&&&&&ωωωω此时两线圈电压的有效值分别为V 21=U ，V 8.995.84222=+=U 答案略答案图示电路，V )cos(22S t u ω=，角频率rad/s 100=ω，Ω=1R ，F 1021-=C ，F 105.022-⨯=C 。

一、填空题1、当流过一个线圈中的电流发生变化时，在线圈本身所引起的电磁感应现象称 现象，若本线圈电流变化在相邻线圈中引起感应电压，则称为 现象。

2、当端口电压、电流为 参考方向时，自感电压取正；若端口电压、电流的参考方向 ，则自感电压为负。

3、互感电压的正负与电流的 及 端有关。

4、两个具有互感的线圈顺向串联时，其等效电感为 ；它们反向串联时，其等效电感为 。

5、两个具有互感的线圈同侧相并时，其等效电感为 ；它们异侧相并时，其等效电感为 。

6、理想变压器的理想条件是：①变压器中无 ，②耦合系数K = ，③线圈的 量和 量均为无穷大。

理想变压器具有变换 特性、变换 特性和变换 特性。

7、理想变压器次级负载阻抗折合到初级回路的反射阻抗Z 1n = 。

二、判断下列说法的正确与错误、1、由于线圈本身的电流变化而在本线圈中引起的电磁感应称为自感。

（ ）2、由同一电流引起的感应电压，其极性始终保持一致的端子称为同名端。

（ ）3、两个串联互感线圈的感应电压极性，取决于电流流向，与同名端无关。

（ ）4、顺向串联的两个互感线圈，等效电感量为它们的电感量之和。

（ ）5、同侧相并的两个互感线圈，其等效电感量比它们异侧相并时的大。

（ ）6、通过互感线圈的电流若同时流入同名端，则它们产生的感应电压彼此增强。

（ ）三、单项选择题1、符合全耦合、参数无穷大、无损耗3个条件的变压器称为（ ）A 、空芯变压器B 、理想变压器C 、实际变压器2、线圈几何尺寸确定后，其互感电压的大小正比于相邻线圈中电流的 （ ）A 、大小B 、变化量C 、变化率3、两互感线圈的耦合系数K=（ ）A 、21L L MB 、21L L MC 、21L L M 4、两互感线圈同侧相并时，其等效电感量L 同=（ ）A 、M L L M L L 221221-+-B 、2212212M L L M L L ++-C 、221221ML L M L L -+-5、两互感线圈顺向串联时，其等效电感量L 顺=（ ）A 、M L L 221-+B 、M L L ++21C 、M L L 221++6、符合无损耗、K=1和自感量、互感量均为无穷大条件的变压器是（ ）A 、理想变压器B 、全耦合变压器C 、空芯变压器。

电路互感的概念和计算公式一、电路互感的概念。

电路互感是指两个电感器件之间由于磁场的相互作用而产生的电压。

在电磁学中，电感是指电流变化时所产生的电动势。

当一个电流通过一个线圈时，会产生一个磁场，而这个磁场又会影响到另一个线圈中的电流，从而产生电动势。

这种现象就是电路互感。

电路互感是一种重要的电磁现象，它在电路中起着至关重要的作用。

在许多电子设备中，都会用到电感器件，而电路互感则是影响电感器件性能的重要因素之一。

了解电路互感的概念和计算公式，有助于我们更好地理解电路中的电磁现象，从而更好地设计和应用电子设备。

二、电路互感的计算公式。

电路互感的计算公式可以通过法拉第定律和楞次定律来推导得到。

根据法拉第定律，电路中的电动势等于电感的变化率乘以电流的变化率。

而根据楞次定律，电路中的电动势等于电感的变化率乘以磁通量的变化率。

结合这两个定律，可以得到电路互感的计算公式：M = k sqrt(L1 L2)。

其中，M表示电路互感，k表示比例系数，L1和L2分别表示两个线圈的电感。

从这个公式可以看出，电路互感与两个线圈的电感和它们之间的相对位置有关。

当两个线圈的电感增大或它们之间的距离减小时，电路互感也会增大。

而当两个线圈之间的磁场耦合程度增强时，电路互感也会增大。

因此，通过调节线圈的电感和它们之间的相对位置，可以改变电路互感的大小，从而实现对电路性能的调控。

三、电路互感的应用。

电路互感在电子设备中有着广泛的应用。

在变压器中，电路互感可以实现电压的变换。

当一个线圈中的电流发生变化时，会产生磁场，从而感应出另一个线圈中的电动势，从而实现电压的变换。

这种原理被广泛应用于变压器中，用于实现电压的升降。

此外，电路互感还可以用于电路的隔离和耦合。

在一些需要隔离的电路中，可以通过增加电路互感来实现线圈之间的电气隔离。

而在一些需要耦合的电路中，可以通过减小电路互感来实现线圈之间的电气耦合。

因此，电路互感在电子设备中有着广泛的应用。

互感的工作原理互感（Mutual Inductance）指的是两个或多个线圈之间通过电磁感应相互作用的现象。

在电路中，互感是一种重要的物理现象，它在许多电子设备和电力系统中起着关键作用。

了解互感的工作原理对于电路设计和电磁波的传输都至关重要。

一、互感的基本概念互感的基本概念是指当两个或多个线圈（或导线）彼此靠近时，通过它们之间的磁场产生电动势的现象。

当一个线圈（主线圈）的电流变化时，它所产生的磁场会穿过另一个线圈（从线圈），从而在从线圈中产生电动势。

互感的大小取决于线圈之间的位置、线圈的匝数以及电流的变化率。

二、互感的公式互感可以通过以下公式来计算：M = k * sqrt(L1 * L2)其中，M表示互感的大小，L1和L2分别表示主线圈和从线圈的自感值，k是一个介于0和1之间的系数，代表线圈之间的耦合系数。

耦合系数越大，互感效应越强。

三、互感的工作原理当主线圈中的电流变化时，通过主线圈产生的磁场穿过从线圈，从而在从线圈中产生感应电动势。

这个感应电动势会导致从线圈中的电流发生变化。

根据楞次定律（Faraday's law），感应电动势的大小与主线圈中的电流变化率成正比。

因此，通过控制主线圈中的电流变化，可以在从线圈中实现电流的放大、传输和调节等功能。

互感在很多电子设备中发挥着重要作用。

例如，变压器就是利用互感的原理来将交流电压进行降压和升压。

在变压器中，通过改变主线圈和从线圈之间的匝数比例，可以实现电压的变换。

另外，互感还广泛应用于滤波器、振荡器、放大器、调谐电路等电子设备中，为这些设备提供了优良的功率传递和信号处理能力。

四、互感的应用1. 变压器：变压器是利用互感的原理来调节电压的重要装置。

它广泛应用于电力系统和电子设备中，用于实现电压的降压、升压和隔离等功能。

2. 电感耦合无线电传输：互感也被用于无线电传输中，例如电感耦合无线电传输（Inductive Coupling Wireless Transmission）。

物理互感知识点总结一、基本概念1. 互感的定义互感是指一种物理现象，即两个电路中的电流或电压的变化会相互影响。

当一个电路中的电流或电压变化时，它会在另一个电路中引起感应电动势，从而影响该电路中的电流或电压的变化。

这种现象称之为互感。

在电路中，互感通常是由于电感元件之间的相互作用而产生的。

2. 互感的原理互感的原理是基于电磁感应定律。

根据法拉第电磁感应定律，当一个闭合电路中的磁通量发生变化时，该电路中会产生感应电动势。

而磁通量的变化可以是由于磁场强度的变化或者电路中的电流的变化所引起的。

因此，当一个电路中的电流或电压发生变化时，它会产生变化的磁场，从而在另一个电路中引起感应电动势，达到了互感的效果。

3. 互感的单位互感的单位是亨利（H），它的国际单位符号是H。

在国际单位制中，1亨利定义为当两个电流为1安培，两个匝数为1匝时，它们之间的互感为1亨利。

二、互感的影响1. 电感元件的相互彼此在电路中，当两个电感元件靠近并且相互靠近时，它们之间的互感会增加。

因为它们之间的磁通量的交联影响了磁场强度的变化，从而增大了互感的效果。

而当两个电感元件远离并且相互离开时，它们之间的互感会减小。

2. 互感的影响范围互感的影响范围主要取决于电感元件之间的距离和磁场的强度。

当电感元件之间的距离较近并且磁场较强时，互感的效果会比较显著。

而当电感元件之间的距离较远或者磁场较弱时，互感的效果会比较不明显。

3. 互感的方向互感的方向根据电流的方向来确定。

当两个电路之间的电流方向相同时，它们之间的互感是正的；当电流方向相反时，它们之间的互感是负的。

三、应用领域1. 互感器互感器是一种可以通过两个电路之间的互感效应来实现测量和监测的装置。

利用互感器，可以实现电流、电压、功率等参数的测量。

2. 变压器变压器是一种利用互感效应来实现电压变换的装置。

通过变压器，可以实现电压的升高或降低，实现电能的输送和分配。

3. 互感耦合振荡器互感耦合振荡器是一种利用互感效应来产生振荡信号的电路。