223实践与探索第三课时

2020/12/10
9
明确两点
我们曾采用待定系数法求得一次函数和反比例 函数的关系式.•但是现实生活中的数量关系是 错综复杂的,在实践中得到一些变量的对应值, 有时很难精确地判断它们是什么函数,需要我们 根据经验分析,也需要进行近似计算和修正,•建 立比较接近的函数关系式进行研究.
常用的方法是:把实践或调查中得到的一些变 量的值,通过描点得出函数的近似图象,再根据 画出的图象的特征,猜想相应的函数名称,然后 利用待定系数法求出函数关系式.
2020/12/10
10
应用提高
A
小明在做电学实验时,电路图如图所示.
R
在保持电压不变的情况下,•改换不同的电阻R,并用电流表 测量出通过不同电阻的电流I,记录结果如下:
(1)建立适当的平面直角坐标系,在坐标系中描出表格中 的各点,•并画出该函数的近似图象;
(2)观察图象,猜想I与R之间的函数关系,并求出函数 解析式;
(3)小明将一个未知电阻值的电阻串联到电路中,查得 电流表的度数为0.5安培,你知道这个电阻的电阻值吗?
2020/12/10
11
PPT教学课件
谢谢观看
Thank You For Watching
2020/12/10
12
k 2 b 10
所以y与x的函数关系式可能是：y=2x-10
(2)当y=43时，2x-10=43，解得x=26.5.
2020/12/10
7
问题情境二
为了研究某合金材料的体积V(cm3)随温 度t(℃)变化的规律,对一个用这种合金制 成的圆球测得相关数据如下:
你能否据此求出V和t的函数关系?
2020/12/10
8
客观分析

当10＜x＜25时，设y＝kx＋b(k≠0)， 将B(10，240)、C(25，150)的坐标代入y＝kx＋b中， 得1205kk＋＋bb＝＝214500，，解得kb＝＝－3060， ， ∴当10＜x＜25时，y与x之间的函数关系式为y＝－6x＋300.
A．x(x＋3)＝225 B．x(x＋16)＝225 C．(x－8)(x＋8)＝225 D．x(x－16)＝225
6．【教材改编题】两个数的和为16，积为48，则这两个数 分别是__4_，__1_2__．
7．【中考·鸡西改编】某校“研学”活动小组在一次野外实 践时，发现一种植物的主干长出若干数目的支干，每个 支干又长出同样数目的小分支，主干、支干和小分支的 总数是43，求这种植物每个支干长出的小分支个数． 解：设这种植物每个支干长出x个小分支，依题意， 得1＋x＋x2＝43，解得x1＝－7(舍去)，x2＝6. 答：这种植物每个支干长出的小分支个数是6.
A．(150＋x)(7＋x)＝950 B．(150＋20x)(7－x)＝950 C．(150＋20x)(7＋x)＝950 D．(150＋x)(7＋20x)＝950
2．【中考·宜宾】某产品每件的生产成本为50元，原定销 售价65元，经市场预测，从现在开始的第一季度销售价 格将下降10%，第二季度又将回升5%.若要使半年以后 的销售利润不变，设每个季度平均降低成本的百分率为 x，根据题意可列方程是 _6_5_×__(_1_－__1_0_%__)_×__(1_＋__5_%__)_－__5_0_(_1_－__x_)2_＝__6_5_－__5_0__.
4．【2020·桂林】参加足球联赛的每两支球队之间都要进
行两场比赛，共要比赛110场，设参加比赛的球队有x支
，根据题意，下面列出的方程正确的是( D ) A. x(12x＋1)＝110 B. x(1x－1)＝110

人们围成半圆形驱赶野马，它们被一步步逼向大门，开始奔跑起来。但就在接近大门的一刻，领头的公马又突然折身而回，箭一样地冲向人墙，人们慌不择路地躲避着，马群洪水般地泻入人墙。尘 土升腾在马圈的上空，蹄声震颤着空寂的戈壁。马群狂奔着和人群打着转，就是不肯接近那扇象征自由的大门。
2000年的秋天，野马终于迎来了奔向原野的日子。关了整整一百年的野马养殖场大门洞开了，新疆养殖场决定首次将圈养的野马放归大自然。
这天，天空如洗，阳光和煦。马场外绿草如茵，野花遍地。大门打开了，可马就是不出来，人们用嫩绿的饲草引诱，马才以怀疑的眼神一步步向大门口走来。们的心吊上了嗓子眼儿，都盼望着奔 腾的场面出现。可就在野马接近大门时，它们却放弃了美食，毅然返身走回马圈。
科研人员认识到：将这种马放归大自然是它生存的唯一选择。在即将放养的这个种群中，一只俊秀的小母马频频遭到她的父亲（头马）的攻击，小母马一接近马群，就被头马凶横而无情的撕咬，逼 得这匹发情的小母马根本无法接近野马种群。饲养人员知道，这就意味着她已“长大成人”了。由于野马种群一般都是由一匹被称为头马的公马带领，种群中小马都是的他的子女，为防止近亲繁殖，工 作人员决定让她离开种群，到其他种群找寻自己的如意郎君。后来又有几个这样的小母马，放养的日子不能再往后拖。真人app

总结词
反思、体验、成长
详细描述
个人经历是我们生活中所经历的各种事件和情境，它们塑造了我们的成长和发展。在个人经历中，实 践与探索表现为对经历的反思、体验的深入和成长的自觉。通过反思和体验，人们可以理解自己的行 为和思想，发现自己的潜力和局限，从而实现个人成长和发展。
PART 05
实践与探索的未来展望
案例三：个人经历中的实践与探索
总结词
反思、体验、成长
详细描述
个人经历是我们生活中所经历的各种事件和情境，它们塑造了我们的成长和发展。在个人经历中，实 践与探索表现为对经历的反思、体验的深入和成长的自觉。通过反思和体验，人们可以理解自己的行 为和思想，发现自己的潜力和局限，从而实现个人成长和发展。
案例三：个人经历中的实践与探索
案例二：社会调查中的实践与探索
总结词
客观、公正、深入
详细描述
社会调查是对人类社会现象进行系统研究的手段，通过收集和分析数据来了解社会的结 构和运作。在社会调查中，实践与探索表现为客观的调查设计、公正的数据收集和处理 以及深入的结论分析。通过社会调查，人们可以揭示社会现象的本质和规律，为政策制
定和社会发展提供科学依据。
实践的定义与特点
实践的定义
实践是人类有目的地改造世界的感性活动，是连接主观与客观世界的桥梁。
实践的特点
实践具有直接现实性，能够将理论转化为现实；实践具有主观能动性，能够发 挥人的主观能动性去改造世界；实践具有社会历史性，受到社会历史条件的制 约。
实践在知识学习中的作用
01
02
03
巩固理论知识
通过实践，学生可以将所 学理论知识应用于实际， 加深对知识的理解和记忆。
未来实践与探索将更加注重跨学科的知识融合， 打破传统学科界限，推动多领域合作，以解决复 杂问题。

２0１7春八年级数学下册1７．5《实践与探索(第3课时）》教案（新版)华东师大版编辑整理：尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望（201７春八年级数学下册1７.5《实践与探索（第3课时）》教案(新版）华东师大版)的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉，前进的动力。

本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017春八年级数学下册1７.5《实践与探索（第3课时)》教案(新版)华东师大版的全部内容。

１7．5 实践与探索(第3课时)(一）本课目标1。

通过描点,拟合变量之间的函数关系，导出函数的关系式，从中体会实际问题中的数学建模思想.2.了解收集数据、用描点法整理数据是猜想函数名称、利用所得函数性质解决问题的基本思想方法．（二）教学流程1。

情境导入(利用多媒体演示幻灯片）王莉同学在探索鞋码的两种长度“码”与“厘米＂之间的换算关系时，通过调查获得下表数据:((２)问43码的鞋相当于多少厘米的鞋？2.课前热身(1)用描点法画函数图象,一般分成哪几个步骤？(2）一次函数、反比例函数的图象分别具有什么特征?３.合作探究(1)整体感知为了解决上述问题,本节课我们将着重探讨通过描点，探究出函数图象的特征, 根据函数图象的特征拟合函数变量之间的关系,然后利用这个函数关系解决问题。

(２)四边互动师:利用多媒体演示幻灯片５.问题３：为了研究某合金材料的体积V(cｍ3)随温度t(℃）变化的规律,对一个用这种合金制成的圆球测得相关数据如下：能否据此求出V和t的函数关系?分析:将这些数值所对应的点在坐标系中描出.我们发现, 这些点大致位于一条直线上,可知V和t 近似地符合一次函数关系。

我们可以用一条直线去尽可能地与这些点相符合，求出近似的函数关系式。

老黄说自己的“土包子”出身，几次谈自己一个农民，还有养老金月入三千。老家的房子就是不卖，他常回村跟村民讨旧农具，准备办一个“黄家农具展览馆”，说给孙辈看看当年的样子。他说， 自己已经做不了什么，就把这作为献给时代的礼物。是啊，这份礼物的价值，无法与古董相提并论，但情怀的分量已经很重了。hg0088
大家见了小李就要“吃猪头”，胶老。果然，那日男女到茶舍道谢，手中不是提着猪头，而是一件包装精致的大红袍茶。
小李说，找不到月下老人，只好来茶舍对一屋子人表示感谢了。给一对有情人斟上茶，老海说，这是“茶为媒”。古有“花为媒”的故事，今天是茶作媒介，要把“吃猪头”的说法改一改了，就叫 “喝红袍”，大家击掌。
平时看老黄叔，大家觉得他无趣，谁知正是这“无趣”的人，有着大趣。十九世纪英国浪漫派诗人威·布莱克说，思想和力量是一种毕生的乐趣。辛弃疾说，雅志成趣。一点不假，茶可使人从雅， 雅才生出让人刮目的情趣。
有人曾担心我们茶舍无茶。这个担心，多余了。社区工作人员里有个小李，离婚两年，常没事喜欢坐在茶舍的条凳上，拿张表格，要我们填这填那，大家觉得这女孩子性情温柔，处事从容，于是我 们为之再找婆家。真成了，老张头的外甥与之年龄相仿，一说和，居然有意，皆大欢喜。不久就办了婚事。

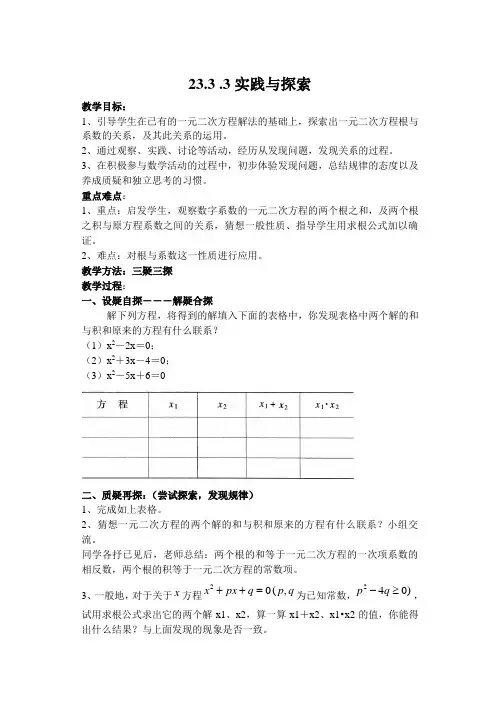
23.3 .3实践与探索教学目标：1、引导学生在已有的一元二次方程解法的基础上，探索出一元二次方程根与系数的关系，及其此关系的运用。

2、通过观察、实践、讨论等活动，经历从发现问题，发现关系的过程。

3、在积极参与数学活动的过程中，初步体验发现问题，总结规律的态度以及养成质疑和独立思考的习惯。

重点难点：1、重点：启发学生，观察数字系数的一元二次方程的两个根之和，及两个根之积与原方程系数之间的关系，猜想一般性质、指导学生用求根公式加以确证。

2、难点：对根与系数这一性质进行应用。

教学方法：三疑三探教学过程：一、设疑自探―――解疑合探解下列方程，将得到的解填入下面的表格中，你发现表格中两个解的和与积和原来的方程有什么联系？（1）x2－2x＝0；（2）x2＋3x－4＝0；（3）x2－5x＋6＝0二、质疑再探：（尝试探索，发现规律）1、完成如上表格。

2、猜想一元二次方程的两个解的和与积和原来的方程有什么联系？小组交流。

同学各抒已见后，老师总结：两个根的和等于一元二次方程的一次项系数的相反数，两个根的积等于一元二次方程的常数项。

3、一般地，对于关于x方程20(,x px q p q++=为已知常数，240)p q-≥，试用求根公式求出它的两个解x1、x2，算一算x1＋x2、x1•x2的值，你能得出什么结果？与上面发现的现象是否一致。

解：22121244b ac p qx x x x x p -=-===+===-12x x q ⋅===所以与上面猜想的结论一致。

三、拓展运用：（1）不解方程，求方程两根的和两根的积：①2310x x +-=②22410x x -+=解：①123x x +=-121x x ⋅=- ②122x x += 1212x x ⋅=-（2）已知方程2560x kx +-=的一个根是2，求它的另一个根及k 的值。

（3）不解方程，求一元二次方程22310x x +-=两个根的①平方和；②倒数和。

他们会手持一个装满经文的经转转。今生的苦难已不可改变，他们会祈祷来生不再受苦受难。带着虔诚的心，一圈圈不停地转动，转走了今生的苦难，转来了来 身的幸福。cq9传奇电子游戏跳起来
千年的草原就有千年的苦难，千年的岁月就有千年的泪水。
一条小溪发源于纳摩大峡谷，最初的源头只是几个不大的山泉，这个带着大山温度流淌的山泉，就是白龙江的源头。随后，不到2米宽的小溪流过村庄，把村庄划成了两半，成为界河，界河以南属 四川省阿坝州若尔盖县的红星镇，界河以北是甘肃省甘南州碌曲县郎木寺镇。
在这个弹丸的偏僻之地，聚集两座规模宏大的藏传格鲁派佛教寺院，虽是同派却不同支。界河南边的寺庙全称“安多达仓纳摩格尔底寺”，简称格尔底寺，建于1409年，是宗格巴大师亲传弟子所建， 年代久远，名声远扬。界河北边的寺庙全称“安多达仓纳摩赛赤寺”，简称赛赤寺，建于1748年，是格鲁派六大寺之一哲蚌寺的重要子寺，地位崇高。两寺同处一个山谷，却分属两省，隔江相望，佛号 相闻，最为奇特的是两寺均是有门无墙，所谓的门也只是两根立柱，只为标注寺名。平时，两地信徒长年生活在一起，并没有地界之限，甘南州的信众有礼佛于格尔底寺，阿坝州的信徒亦有礼佛于赛赤 寺，历经几百年，和平相处，堪称佛界奇观。
在自然和伤病面前，牧人有太多的迷惑，太多的无奈。在灾难的黑暗中，他们需要有面对苦难的勇气，超越灾难的精神。微风吹过了佛塔，仿佛听到了虔诚的佛经诵读声。长久以来，草原藏族就把 佛当成了依靠，当成了信仰，当成了精神。
若尔盖西南80公里，有一个叫达仓纳摩(亦有翻译达仓郎木)的地方，藏语翻译“虎穴仙女”一个富含寓意的名字，被人称为“佛的村庄”。