高等数学第10章 曲线积分与曲面积分

第十章 曲线积分与曲面积分 §1 对弧长的曲线积分计算公式：无论是对弧长还是对坐标的曲线积分重要的是写出曲线的参数方程若()():x x tL a t b y y t =⎧⎪≤≤⎨=⎪⎩，则()()()(,,b L af x y ds f x t y t=⎰⎰ 若()()():x x t L y y t a t b z zt =⎧⎪=≤≤⎨⎪=⎩，则()()()()(,,,,b Laf x y z ds f x t y t z t =⎰⎰ 注意：上限一定要大于下限计算下列对弧长的曲线积分（1）ds yx L ⎰+222)(，其中L 为圆周222a y x =+； 解：法一：222()Lx yds +=⎰ 22()Lads ⎰4La ds =⎰45(2)2a a a ππ== 法二：cos:02sin x a L y a θθπθ=⎧≤≤⎨=⎩，222()Lx y ds +⎰ ()()222[cos sin ]a a πθθθ=+⎰25502a d a πθπ==⎰（2）ds eLy x ⎰+22，其中L 为圆周222a y x =+，直线x y =及x 轴在第一象限内所围成的扇形的整个边界；解：()L OAABBO=++⎰⎰⎰⎰ ，其中:,00x x OA x a y =⎧≤≤⎨=⎩， cos :,0sin 4x a AB y a θπθθ=⎧≤≤⎨=⎩，:0x x BO x y x =⎧≤⎨=⎩aoA=⎰⎰01ax a e dx e ==-⎰a ABABe ds =⎰⎰ 4aa ABaee ds π==⎰（或AB⎰4πθ=⎰404aaae e ad ππθ==⎰）BO=⎰1ae ==- 故(2)24a Le a π=+-⎰（3）⎰L xds ，其中L 为抛物线122-=x y 上介于0=x 与1=x 之间的一段弧；解：由2:0121x x L x y x =⎧≤≤⎨=-⎩，得10L xds =⎰⎰32122(116)332x +==（4）⎰L ds y 2，其中L 为摆线的一拱)20)(cos 1(),sin (π≤≤-=-=t t a y t t a x ； 解：[]22(1cos )Ly ds a t π=-⎰⎰5232(1cos )t dt π=-⎰52322(2sin)2tdtπ=⎰2358sin2ta dtπ=⎰令2tθ=）3516sina dπθθ=⎰353324225632sin325315a d a aπθθ==⨯⨯=⎰（5）dsxyL⎰，其中L为圆周222ayx=+；解：利用对称性14L Lxy ds xy ds=⎰⎰，其中1cos:0sin2x aLy aθπθθ=⎧≤≤⎨=⎩1144L L Lxy ds xy ds xyds==⎰⎰⎰204(cos)(sina aπθθθ=⎰3323224cos sin2sin2a d a aππθθθθ===⎰（6）dszyx⎰Γ++1，其中Γ为曲线tex t cos=，tey t sin=，t ez=上相应于t从0变到2的弧段；解：2221dsx y zΓ++⎰=⎰22)te dt e--==-⎰（7）dsy⎰Γ，其中Γ为空间圆周：⎪⎩⎪⎨⎧==++Γxyzyx2:222.解：由2222x y zy x⎧++=⎨=⎩，得2222x z+=，令cos02xzθθπθ=⎧⎪≤≤⎨=⎪⎩故cos:cos02xyzθθθπθ⎧=⎪Γ=≤≤⎨⎪=⎩。

第十章曲线积分与曲面积分习题简答习题10—11 计算下列对弧长的曲线积分：（1）LIxds ，其中L 是圆221xy中(0,1)A 到11(,)22B 之间的一段劣弧；解:1(1)2．（2）(1)Lx y ds，其中L 是顶点为(0,0),(1,0)O A 及(0,1)B 所成三角形的边界；解:(1)322Lxyds．（3）22Lxy ds，其中L 为圆周22x yx ；解:222Lxy ds．（4）2Lx yzds ，其中L 为折线段ABCD ，这里(0,0,0)A ，(0,0,2),B (1,0,2),C (1,2,3)D ；解:2853Lx yzds ．2 求八分之一球面2221(0,0,0)xyzx y z 的边界曲线的重心，设曲线的密度1。

解故所求重心坐标为444,,333．习题10—21 设L 为xOy 面内一直线y b （b 为常数），证明xyz(0,0,0)A (0,0,2)B (1,0,2)C (1,2,3)D xyoABC(,)0LQ x y dy 。

证明：略.2 计算下列对坐标的曲线积分：（1）Lxydx ，其中L 为抛物线2yx 上从点(1,1)A 到点(1,1)B 的一段弧。

解:45Lxydx 。

（2）Ldy y xdx y x 2222)()(，其中L 是曲线x y11从对应于0x 时的点到2x 时的点的一段弧；解34)()(2222Ldyy xdxy x．（3）,Lydx xdy L 是从点(,0)A a 沿上半圆周222xya 到点(,0)B a 的一段弧；解0.Lydxxdy（4）22Lxy dyx ydx ，其中L 沿右半圆222xya 以点(0,)A a 为起点，经过点(,0)C a 到终点(0,)B a 的路径；解22Lxy dyx ydx44a 。

（5）3223Lx dx zy dy x ydz ，其中L 为从点(3,2,1)A 到点(0,0,0)B 的直线段AB ；解3223Lx dx zy dy x ydz3187874t dt。

第十章 曲线积分与曲面积分一、基本要求及重点、难点1. 基本要求(1) 了解第一类曲线积分（即对弧长的曲线积分）的概念及其物理与几何意义，并掌握其计算方法。

(2) 了解第二类曲线积分（即对坐标的曲线积分）的概念及物理意义，并掌握其计算方法，能熟练应用曲线积分计算力场沿曲线所做的功。

(3) 掌握格林公式的条件和结论，熟练掌握利用格林公式把第二类曲线积分化为二重积分的计算方法，及掌握通过添加辅助曲面利用格林公式改变积分路径的计算方法。

(4) 掌握在单连通区域上第二类曲线积分与路径无关的等价条件及其应用，会求全微分的原函数。

(5) 了解第一类曲面积分（即对面积的曲线积分）的概念及其物理与几何意义，并掌握其计算方法。

(6) 掌握高斯公式的条件与结论，并会利用高斯公式计算第二类曲面积分。

2. 重点及难点（1）重点： (a) 熟练选择适当的参数方程或坐标系将曲线积分化为定积分。

(b) 熟练掌握用投影法将曲面积分化为二重积分。

(c) 格林公式（熟练使用格林公式计算曲线积分）。

(d) 曲线积分与路径无关的概念及条件。

(e) 高斯公式（熟练使用高斯公式计算曲面积分）。

（2）难点： (a) 两类曲线积分的关系。

(b) 格林公式的灵活使用（条件、结论；辅助曲线的添加）。

(c) 高斯公式的灵活使用（条件、结论；辅助曲面的添加）。

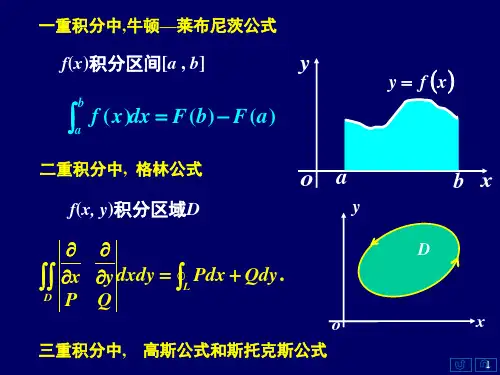
二、内容概述1、曲线积分的基本概念与性质(1) 对弧长的曲线积分（又称第一类曲线积分）定义 设(,)f x y 在x O y 面内的光滑曲线L 上有界. 第一类曲线积分为1(,)lim (,)ni i i Li f x y ds f s λξη→==∆∑⎰(见课本).Γ为空间曲线时，类似地有1(,,)lim (,,)ni i i i i f x y z ds f s λξηζΓ→==∆∑⎰.物理意义 设曲线L 的线密度为(,)x y ρ，则其质量为(,)LM x y ds ρ=⎰性质1 运算性质[] (,)(,) (,)(,)LLLf x yg x y ds f x y ds g x y ds ±=±⎰⎰⎰(,)(,)LLkf x y ds k f x y ds =⎰⎰ 其中k 为常数．性质2 对弧长的曲线积分与积分路径的走向无关，即⎰⎰-=LL ds y x f ds y x f ),(),(．性质3 对积分路径具有可加性，即12(,)(,)(,)(,)kLL L L f x y ds f x y ds f x y ds f x y ds =+++⎰⎰⎰⎰其中12k L L L L =+++．(2) 对坐标的曲线积分（又称第二类曲线积分）定义 设(,),(,)P x y Q x y 在x O y 面内的有向光滑曲线L 上有界.(,)(,)LP x y dx Q x y dy +⎰[]01lim (,)(,)ni i i i i i i P x Q y λξηξη→==∆+∆∑．Γ为空间曲线时，类似地有(,,)(,,)(,,)P x y z dx Q x y z dy R x y z dz Γ++⎰[]01lim (,,)(,,)(,,)ni i i i i i i i i i i i i P x Q y R z λξηζξηζξηζ→==∆+∆+∆∑.物理意义 变力(,) (,)F P x y i Q x y j =+沿曲线L 所作的功为(,)(,)LW P x y dx Q x y dy =+⎰．性质1 对坐标的曲线积分与积分路径的方向有关，即⎰⎰-+-=+LL dy y x Q dx y x P dy y x Q dx y x P ),(),(),(),(．性质2 对积分路径具有可加性，即1(,)(,)(,)(,)LL P x y dx Q x y dy P x y dx Q x y dy +=+⎰⎰2(,)(,)(,)(,)kL L P x y dx Q x y dy P x y dx Q x y dy +++++⎰⎰其中k L L L L +++= 21．（3）两类曲线积分之间的关系平面曲线L 上两类曲线积分有如下关系(,)(,)LP x y dx Q x y dy +⎰[(,)cos (,)cos ]LP x y Q x y ds αβ=+⎰其中),(),,(y x y x βα为平面有向曲线L 上点),(y x 处的切线向量的方向角．空间曲线Γ上两类曲线积分有如下关系(,,)(,,)(,,)P x y z dx Q x y z dy R x y z dzΓ++⎰[(,,)cos (,,)cos (,,)cos ]P x y z Q x y z R x y z ds αβγΓ=++⎰其中(,,),(,,),(,,)x y z x y z x y z αβγ为空间有向曲线Γ上点(,,)x y z 处切向量的方向角．2、曲线积分的计算公式 (1) 对弧长的曲线积分（1）设函数(,)f x y 在平面曲线: (t), (t),L x y φψ==()t αβ≤≤上连续(),()t t φψ''在区间[], αβ上连续，且22()()0t t φψ''+≠，则[ (,) (), ()Lf x y ds f t t βαφψ=⎰⎰（2）设平面曲线L 的方程为)(),(b x a x y y ≤≤=且)(x y '在区间[]b a ,上连续，则[ (,),()bLaf x y ds f x y x =⎰⎰（3）设函数),,(z y x f 在空间曲线: (), (),x t y t φψΓ==),(t z ω=(t α≤)β≤上连续，(),(),()t t t φψω'''在区间[],αβ上连续，且22()()t t φψ''+2()0t ω'+≠，则(,,)f x y z ds Γ⎰[ (), (), ()f t t t βαφψω=⎰注意 化对弧长的曲线积分为定积分时,定积分的上限一定比下限大．（2）对坐标的曲线积分(1) 设函数),(),,(y x Q y x P 在有向曲线L 上连续，L 的参数方程为:),(),(t y t x ψϕ==βα→:t ，即α为有向曲线L 的始点对应的参数值，β为其终点对应的参数值．且)(),(t t ψϕ''在以βα,为端点的区间上连续，22()()0t t φψ''+≠，则(,)(,)LP x y dx Q x y dy +⎰[] ( (), ())()( (), ()) ()P t t t Q t t t dtβαφψφφψψ''=+⎰(2) 若L 是由方程 ()y x φ=给出,L 的始点的横坐标为a ,终点的横坐标为b ,)( x ϕ具有一阶连续导数,则(,)(,)LP x y dx Q x y dy +⎰[] (, ())(, ())()baP x x Q x x x dxφφφ'=+⎰(3) 类似地,对于空间曲线:(),(),()x t y t z t φψωΓ===(,,)(,,)(,,)P x y z dx Q x y z dy R x y z dzΓ++⎰[][] (), (), ()() (), (), ()()P t t t t dt Q t t t t dtββααφψωφφψωψ''=+⎰⎰ [](), (), ()()R t t t t d t βαφψωω'+⎰ α为有向曲线Γ的始点对应的参数值，β为其终点对应的参数值．（3）二元函数的全微分求积设函数),(y x P ,),(y x Q 在单连通域G 内有连续的一阶偏导数,且xQy P ∂∂=∂∂，则Qd y P d x +在G 内为某一函数),(y x u 的全微分，且有0 (,)(,)(,)x yx y u x y P x y dx Q x y dy =+⎰⎰，(如图 (a))或 dx y x P dy y x Q y x u xx yy ⎰⎰+=00),(),(),(，(如图 (b))．3、曲线积分的有关定理定理1 (格林公式) 设闭区域D 是由分段光滑的曲线L 围成,函数),(),,(y x Q y x P 在D 上具有连续的一阶偏导数，则有dxdy y P x Q Qdy Pdx L D ⎰⎰⎰⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=+其中L 是D 的取正向的边界曲线．定理2 (平面上曲线积分与路径无关的条件) 设函数),(y x P ,),(y x Q 在单连通域G 内有连续的一阶偏导数,则以下四个条件等价①LPdx Qdy +⎰与路径无关,即LPdx Qdy +=⎰1L Pdx Qdy +⎰,其中L 、1L 为G 内具有相同始点和终点任意曲线；②⎰=+LQdy Pdx 0,其中L 为G 内的任意闭曲线;③P Q y x∂∂=∂∂在G 内恒成立; ④ (,)Pdx Qdy du x y +=,即Pdx Qdy +在G 内为某一函数(,)u x y 的全微分．4、曲面积分的基本概念与性质（1）对面积的曲面积分（又称第一类曲面积分）定义 设(,,)f x y z 在光滑曲面∑上有界.1(,,)lim (,,)niiiii f x y z dS f S λξηζ→=∑=∆∑⎰⎰(极限存在时)．物理意义 设曲面∑的面密度为(,,)x y z ρ，则其质量为(,,)M x y z dS ρ∑=⎰⎰．性质 设曲面12,(1,2,,)k i i k ∑=∑+∑++∑∑=都是光滑的,则12(,,)(,,)(,,)f x y z dS f x y z dS f x y z dS∑∑∑=+⎰⎰⎰⎰⎰⎰(,,)kf x y z dS ∑++⎰⎰（2）对坐标的曲面积分（又称第二类曲面积分）指定了侧的曲面称为有向曲面．定义 设(,,),(,,),(,,)P x y z Q x y z R x y z 在有向光滑曲面∑上有界.1(,,)lim (,,)()niiii yzi P x y z dydz P S λξηζ→=∑=∆∑⎰⎰(极限存在时)1(,,)lim (,,)()niiii zxi Q x y z dzdx Q S λξηζ→=∑=∆∑⎰⎰(极限存在时)1(,,)lim (,,)()niiii xyi R x y z dxdy R S λξηζ→=∑=∆∑⎰⎰(极限存在时)其中(,,)i i i ξηζ是任意分割有向曲面∑为n 片小曲面后,所得到的第i 片小曲面i S ∆上的任意一点,(),(),()i xy i yz i zx S S S ∆∆∆分别为i S ∆在三个坐标面上的投影.λ为n 片小曲面i S ∆(1,2,)i n =的直径中的最大者．曲面∑在点(,,)i i i ξηζ处的单位法向量为cos cos cos i i i n i j k αβγ=++()cos ,()cos ,()cos .i yz i i i zx i i i xy i i S S S S S S αβγ∆≈∆∆≈∆∆≈∆物理意义 稳定流动的不可压缩的流体（密度1=ρ），如果在点),,(z y x 处的流速是(,,) (,,)(,,)v P x y z i Q x y z j R x y z k =++,则单位时间内流过曲面∑一侧的流量为Pdydz Qdzdx Rdxdy ∑Φ=++⎰⎰．性质1 设曲面12,k ∑=∑+∑++∑则1Pdydz Qdzdx Rdxdy Pdydz Qdzdx Rdxdy∑∑++=++⎰⎰⎰⎰2.kPdydz Qdzdx Rdxdy Pdydz Qdzdx Rdxdy ∑∑+++++++⎰⎰⎰⎰性质2 设∑-表示与∑取相反侧的有向曲面，则Pdydz Qdzdx Rdxdy Pdydz Qdzdx Rdxdy -∑∑++=-++⎰⎰⎰⎰（3）两类曲面积分之间的关系空间曲面∑上的两类曲面积分有如下关系(cos cos cos )Pdydz Qdzdx Rdxdy P Q R dSαβγ∑∑++=++⎰⎰⎰⎰其中cos ,cos ,cos αβγ是有向曲面∑上点(,,)x y z 处的法向量的方向余弦．5、曲面积分的计算公式 （1）对面积的曲面积分设光滑曲面∑的方程是∑=),,(y x z z 在坐标面xoy 上的投影区域为xy D ，则(,,)f x y z dS∑⎰⎰[],,(,)xyD f x y z x y =⎰⎰ 设光滑曲面∑的方程是∑=),,(z x y y 在坐标面xoz 上的投影区域为xz D ，则(,,)f x y z dS ∑⎰⎰[],(,),xzD f x y x z z =⎰⎰设光滑曲面∑的方程是∑=),,(z y x x 在坐标面yoz 上的投影区域为yz D ，则(,,)f x y z dS ∑⎰⎰[](,),,yzD f x y z y z =⎰⎰（2）对坐标的曲面积分设光滑曲面∑的方程是∑=),,(y x z z 在坐标面xoy 上的投影区域为xy D ，取上（下）侧，则[](,,),,(,)xyD R x y z dxdy R x y z x y dxdy∑=±⎰⎰⎰⎰其中，∑取上侧时为正，∑取下侧时为负．注意 当曲面∑是母线平行于z 轴的柱面0),(=y x F 时，∑上任意一点的法向量与z 轴的夹角的余弦cos cos02πγ==，则(,,)0R x y z dxdy ∑=⎰⎰．设光滑曲面∑的方程是∑=),,(z x y y 在坐标面xoz 上的投影区域为xz D ，则(,,)Q x y z d z d x∑⎰⎰[],(,),xzD Q x y x z z dzdx =±⎰⎰∑取右侧时为正，∑取左侧为负．设光滑曲面∑的方程是(,),x x y z =∑在坐标面yoz 上的投影区域为yz D ，则(,,)P x y z dydz∑⎰⎰[](,),,yzD P x y z y z dydz =±⎰⎰∑取前侧时为正，∑取后侧为负．6、曲面积分的有关定理定理1（高斯公式） 设空间闭区域Ω是由分片光滑的闭曲面∑所围成，函数),,(),,,(),,,(z y x R z y x Q z y x P 在Ω上具有一阶连续偏导数，则有⎰⎰⎰⎰⎰∑Ω⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂=++dxdydz z R y Q x P Rdxdy Qdzdx Pdydz或⎰⎰⎰⎰⎰∑Ω⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂=++dxdydz z R y Q x P dS R Q P )cos cos cos (γβα其中∑是Ω的整个边界曲面的外侧，cos ,cos ,cos αβγ是∑上点),,(z y x 处的法向量的方向余弦．三、典型例题分析例1： 计算22x y Leds +⎰,其中L 为圆周222x y a +=,直线x y =及x 轴在第一象限内所围成的扇形的整个边界.分析 由于曲线L 分段光滑,所以先将L 分为若干光滑曲线段之和,再利用曲线积分的可加性计算曲线积分.解:22123x y LL L L eds +=++⎰⎰⎰⎰1L 的方程为 ,0y x x⎛⎫=≤≤ ⎪ ⎪⎝⎭ds ==1L dx =⎰⎰)a d e ==⎰2L 的方程为：cos ,sin ,04x a t y a t t π⎛⎫==≤≤ ⎪⎝⎭ds adt ===24 04a a L aae dt e ππ==⎰⎰3L 的方程为 0,(0)y x a =≤≤，ds dx ==.301ax a L e dx e ==-⎰⎰所以22123x y LL L L eds +=++⎰⎰⎰⎰112244a a a a aa e e e e ππ⎛⎫=-++-=+- ⎪⎝⎭例 2 ：具有连续偏导数的函数(,)f x y 应满足怎样的条件才能使曲线积分(,)()Lf x y ydx xdy +⎰与积分路径无关。

第十章 曲线积分与曲面积分一、 一、 重点两类曲面积分及两类曲面积分的计算和格林公式、高斯公式的应用 二、 二、 难点对曲面侧的理解，把对坐标的曲面积分化成二重积分，利用格林公式求非闭曲线上的第二类曲线积分，及利用高斯公式计算非闭曲面上的第二类曲面积分。

三、 三、 内容提要1． 1． 曲线（面）积分的定义：（1） （1） 第一类曲线积分∑⎰=→∆∆ni i i i LS f ds y x f 0),(lim ),(ηξλ（存在时）i S ∆表示第i 个小弧段的长度，（i i ηξ,）是i S ∆上的任一点小弧段的最大长度。

实际意义：当f(x,y)表示L 的线密度时，⎰Lds y x f ),(表示L 的质量；当f(x,y) ≡1时，⎰Lds表示L 的弧长，当f(x,y)表示位于L 上的柱面在点（x,y ）处的高时，⎰Lds y x f ),(表示此柱面的面积。

（2） （2） 第二类曲线积分]),(),([lim 1i i i ni iiiLy Q x P Qdy Pdx ∆+∆∆+∑⎰=→ηξηξλ(存在时)实际意义：设变力F =P(x,y) i +Q(x,y) j 将质点从点A 沿曲线L 移动到B 点，则F 作的功为：⎰⎰+=⋅=L L Qdy Pdx S d F W，其中S d =（dx,dy ）事实上，⎰L Pdx ，⎰L Qdy 分别是F在沿X 轴方向及Y 轴方向所作的功。

（3） （3） 第一类曲面积分∑⎰⎰=→∑∆∆ni i iiiS f ds z y x f 1),,(lim ),,(ζηξλ(存在时)i S ∆表示第i 个小块曲面的面积，（i i i ζηξ,,）为i S ∆上的任一点，λ是n 块小曲面的最大直径。

实际意义：当f(x,y ，z)表示曲面∑上点（x,y,z ）处的面密度时，⎰⎰∑ds z y x f ),,(表示曲面∑的质量，当f(x,y,z) ≡1时，⎰⎰∑ds 表示曲面∑的面积。

第十章 曲线积分与曲面积分一．曲线积分的计算 （1）基本计算1.第一类：对弧长线积分的计算(,)Lf x y ds ⎰关键是用曲线L:(),(),x t y t ϕψ=⎧⎨=⎩()t αβ≤≤做变量替换（被积函数，积分变元，积分范围）(,)[(),(,()Lf x y ds f t t βαϕψαβ=<⎰⎰例 L 为圆周221,x y +=则22xy Le ds +=⎰2e π 参数方程，曲线代入解 cos :(02)sin x L y θθπθ=⎧≤≤⎨=⎩ds d θθ==22x y Leds +=⎰202ed e πθπ=⎰例 计算2⎰L x ds ，其中2222:(0)0⎧++=>⎨-=⎩x y z a L a x y . (8分)解 由于 22222222::00⎧⎧++=+=⇒⎨⎨-=-=⎩⎩x y z a x z a L L x y x y 所以L 的参数方程可表示为:(02)sin θθπθ⎧=⎪⎪⎪=≤≤⎨⎪⎪=⎪⎩x L y t z a (3分)θθ==ds ad (2分) 故23222cos 22ππθθ==⎰⎰La a x ds ad(3分) 【例10.22】求⎰,式中L 为圆周22(0)x y ax a +=>解 L 的极坐标方程为:,(),cos 22L ds ad r a θθππθθθθ=⎧-≤≤==⎨=⎩则222cos 2a ad a ππθθ-=⋅=⎰⎰第二类：对坐标的线积分的计算 关键是用曲线L:(),(),x t y t ϕψ=⎧⎨=⎩(:)t αβ→做变量替换（被积函数，积分变元，积分范围）''(,)(,){[(),()]()[(),()]()}LP x y dx Q x y dy P t t t Q t t t dt βαϕψϕϕψψ+=+⎰⎰例 设L 为抛物线2y x =从点()0,0到()2,4一段弧，则()22Lx y dx -=⎰5615-注意微元，及参数方程的形式【例10.17】 求2L ydx xdy x +⎰，其中L 是曲线ln y x =上从点(1,0)到点(,1)e 的一段弧. 解 由ln y x =得1,ydx dy x e x==，故原式=1121002()|y y ydy e dy y e e +=+=⎰⎰⑵ 基本技巧① 利用对称性简化计算；对弧长的线积分，对称性同二重积分 例 计算3222(),Lx y ds L x y R 其中：++=⎰解：33()LLLx y ds xds y ds =+=0+⎰⎰⎰ 第一个L 关于y 对称，第二个L 关于x 对称【例10.15】 求yL xe ds ⎰，其中L 是由cos (0)sin x a ta y a t =⎧>⎨=⎩所表示的曲线上相应于233t ππ≤≤的一段弧.解 （法一）ds adt ==,故 原式=22sin sin 3333cos |0a ta ta t e adt aeππππ⋅⋅==⎰.（法二）容易看出积分弧段关于y 轴对称，而被积函数是关于变量x 的奇函数，故0y Lxe ds =⎰【例10.18】 求2()Lx y ds +⎰，其中L 为圆周222x y a +=.解 由对称性得0Lxyds =⎰，故22222()(2)()2LLLLx y ds x xy y ds x y ds xyds +=++=++⎰⎰⎰⎰2223022LLa ds a ds a a a ππ=+==⋅=⎰⎰对坐标的线积分，对称性为，当平面曲线L 是分段光滑的，关于x 对称，L 在上半平面与下半平面部分的走向相反时，若P 对y 为偶函数，则，0LPdx =⎰奇函数，则12LL Pdx Pdx =⎰⎰。

第十章 曲线积分与曲面积分一、对弧长的曲线积分（又称第一类曲线积分） 1、定义ini iiLs f ds y x f ∆ηξλ∑⎰=→=1),(lim),(， i ni i i i s f ds z y x f ∆=∑⎰=→Γ1),,(lim ),,(ζηξλ2、物理意义 线密度为),(y x ρ的曲线L 质量为ds y x M L⎰=),(ρ线密度为),,(z y x f 的曲线Γ质量为ds z y x f M ⎰Γ= ),,(3、几何意义 曲线L 的弧长=s ds L⎰，曲线Γ的弧长ds s ⎰Γ=4、若L ：k y x f =),(（常数），则ks ds k ds k ds y x f LLL===⎰⎰⎰),(5、计算（上限大于下限）（1）,(t) ,(t) :ψϕ==y x L ()βα≤≤t ，则[][][]dt t t t t f ds y x f L22)()()( ),( ),(ψϕψϕβα'+'=⎰⎰（2）L ：0()()y x x x X ψ=≤≤，则0(,)[,(XLx f x y ds f x x ψ=⎰⎰（3）L ：0()()x y y y Y ϕ=≤≤，则0(,)[(),.Y Ly f x y ds f y y ϕ=⎰⎰（4）)().(),(),(:βαωψϕ≤≤===Γt t z t y t x ，则(,,)[(),(),(()f x y z ds f t t t βαϕψωαβΓ=<⎰⎰二、对坐标的曲线积分 1、定义dy y x Q dx y x P L),(),( +⎰[]∑=→+=ni i i i iiiy Q xP 1),(),(lim∆ηξ∆ηξλdz z y x R dy z y x Q dx z y x P ),,(),,(),,(++⎰Γ[]∑=→++=n i i i i i i i i i ii iiz R y Q x P 1),,(),,(),,(lim ∆ζηξ∆ζηξ∆ζηξλ2、计算（下限对应起点，上限对应终点）（1）,(t) ,(t) :ψϕ==y x L ()βα→:t ，则(,)(,){[(),()]()[(),()]()}LP x y dx Q x y dy P t t t Q t t t dt βαϕψϕϕψψ''+=+⎰⎰（2）L ：()y x ψ=()X x t →0:，则{[,()][,()]()}bLa Pdx Qdy P x x Q x x x dx ψψψ'+=+⎰⎰（3）L ：()x y ϕ=()Y y t →0:，则{[(),]()[(),]}dLcPdx Qdy P y y y Q y y dy ϕϕϕ'+=+⎰⎰（4）):().(),(),(:βαωψϕ→===Γt t z t y t x ，则(,,)(,,)(,,)P x y z dx Q x y z dy R x y z dz Γ++⎰ {[(),(),()]()[(),(),()]()[(),(),()]()}P t t t t Q t t t t R t t t t dt βαϕψωϕϕψωψϕψωω'''=++⎰ 3、两类曲线积分之间的联系(cos cos )LLPdx Qdy P Q ds αβ+=+⎰⎰其中，(,),(,)x y x y αβ为有向曲线弧L 上点(,)x y 处的切线向量的方向角。