原码一位乘法

实验课程: 计算机组成原理实验时间:班级:姓名:学号批阅教师:硬布线实现原码一位乘法实验内容：在实验箱上用硬布线方法实现原码一位乘法实验设备：CP226组成原理实验箱实验设备介绍:CP226 模型机包括了一个标准CPU 所具备所有部件，这些部件包括：运算器ALU、累加器A、工作寄存器W、左移门L、直通门D、右移门R、寄存器组R0-R3、程序计数器PC、地址寄存器MAR、堆栈寄存器ST、中断向量寄存器IA、输入端口IN、输出端口寄存器OUT、程序存储器EM、指令寄存器IR、微程序计数器uPC、微程序存储器uM，以及中断控制电路、跳转控制电路。

其中运算器和中断控制电路以及跳转控制电路用CPLD 来实现，其它电路都是用离散的数字电路组成。

微程序控制部分也可以用组合逻辑控制来代替。

模型机为8 位机，数据总线、地址总线都为8位，但其工作原理与16位机相同。

模型机的指令码为8 位，根据指令类型的不同，可以有0 到 2 个操作数。

指令码的最低两位用来选择R0-R3 寄存器，在微程序控制方式中，用指令码做为微地址来寻址微程序存储器，找到执行该指令的微程序。

而在组合逻辑控制方式中，按时序用指令码产生相应的控制位。

在本模型机中，一条指令最多分四个状态周期，一个状态周期为一个时钟脉冲，每个状态周期产生不同的控制逻辑，实现模型机的各种功能。

模型机有24 位控制位以控制寄存器的输入、输出，选择运算器的运算功能，存储器的读写。

24 位控制位分别介绍如下：XRD ：外部设备读信号，当给出了外设的地址后，输出此信号，从指定外设读数据。

EMWR：程序存储器EM 写信号。

EMRD：程序存储器EM 读信号。

PCOE：将程序计数器PC 的值送到地址总线ABUS 上。

EMEN：将程序存储器EM 与数据总线DBUS 接通，由EMWR和EMRD决定是将DBUS 数据写到EM 中，还是从EM 读出数据送到DBUS。

IREN：将程序存储器EM 读出的数据打入指令寄存器IR 和微指令计数器uPC。

2．227/64=00011011/01000000=0.0110110=0.11011×2-1规格化浮点表示为：[27/64]原＝101，011011000[27/64]反＝110，011011000[27/64]补＝111，011011000同理：--27/64=--0.11011×2-1规格化浮点表示为：[27/64]原＝101，111011000[27/64]反＝110，100100111[27/64]补＝111，1001010002．3 模为：29=10000000002．4 不对，8421码是十进制的编码2．5浮点数的正负看尾数的符号位是1还是0浮点数能表示的数值范围取决于阶码的大小。

浮点数数值的精确度取决于尾数的长度。

2．61）不一定有N1>N2 2）正确2．7 最大的正数：0111 01111111 十进制数：（1－2－7）×27最小的正数：1001 00000001 十进制数：2－7×2－7最大的负数：1001 11111111 十进制数：--2－7×2－7最小的负数：0111 10000001 十进制数：--（1－2－7）×272．81）[x]补=00.1101 [y]补=11.0010[x+y]补＝[x]补+[y]补=11.1111无溢出x+y= －0.0001[x]补=00.1101 [--y]补=00.1110[x－y]补＝[x]补+[--y]补=01.1011 正向溢出2）[x]补=11.0101 [y]补=00.1111[x+y]补＝[x]补+[y]补=00.0100 无溢出x+y= 0.0100[x]补=11.0101 [--y]补=11.0001[x－y]补＝[x]补+[--y]补=10.0110 负向溢出3) [x]补=11.0001 [y]补=11.0100[x+y]补＝[x]补+[y]补=10.0101 负向溢出[x]补=11.0001 [--y]补=00.1100[x－y]补＝[x]补+[--y]补=11.1101 无溢出X－y=－0.00112．91）原码一位乘法|x|=00.1111 |y|=0.1110部分积乘数y n00.0000 0.1110+00.000000.0000→00.00000 0.111+00.111100.11110→00.011110 0.11+00.111101.011010→00.1011010 0.1+00.111101.1010010→00.11010010P f=x f⊕y f=1 |p|=|x|×|y|=0.11010010所以[x×y]原=1.11010010补码一位乘法[x]补=11.0001 [y]补=0.1110 [--x]补=11.0001 部分积y n y n+100.0000 0.11100→00.00000 0.1110+00.111100.11110→00.011110 0.111→00.0011110 0.11→00.00011110 0.1+11.000111.00101110[x×y]补=11.001011102）原码一位乘法|x|=00.110 |y|=0.010部分积乘数y n00.000 0.010+00.00000.000→00.0000 0.01+00.11000.1100→00.01100 0.0+00.00000.01100 0→00.001100P f=x f⊕y f=0 |p|=|x|×|y|=0.001100所以[x×y]原=0.001100补码一位乘法[x]补=11.010 [y]补=1.110 [--x]补=00.110部分积y n y n+100.000 1.1100→00.0000 1.110+00.11000.1100→00.01100 1.11→00.001100 1.1所以[x×y]补=0.0011002．101）原码两位乘法|x|=000.1011 |y|=00.0001 2|x|=001.0110部分积乘数 c000.0000 00.00010+000.1011000.1011→000.001011 0.000→000.00001011 00.0P f=x f⊕y f=1 |p|=|x|×|y|=0.00001011所以[x×y]原=1.00001011补码两位乘法[x]补=000.1011 [y]补=11.1111 [--x]补=111.0101 部分积乘数y n+1000.0000 11.11110+111.0101111.0101→111.110101 11.111→111.11110101 11.1所以[x×y]补=111.11110101 x×y=--0.000010112）原码两位乘法|x|=000.101 |y|=0.111 2|x|=001.010 [--|x| ]补=111.011 部分积乘数 c000.000 0.1110+111.011111.011→111.11011 0.11+001.010001.00011→000.100011P f=x⊕y f=0 |p|=|x|×|y|=0.100011所以[x×y]原=0.100011补码两位乘法[x]补=111.011 [y]补=1.001 [--x]补=000.101 2[--x]补=001.010 部分积乘数y n+1000.000 1.0010+111.011111.011→111.111011 1.00+001.010001.00011→000.100011所以[x×y]补=0.1000112.111) 原码不恢复余数法|x|=00.1010 |y|=00.1101 [--|y| ]补=11.0011部分积商数00.1010+11.00111101101 0←11.1010+00.110100.0111 0.1←00.1110+11.001100.0001 0.11←00.0010+11.001111.0101 0.110←01.1010+00.110111.0111 0.1100+00.110100.0100所以[x/y]原=0.1100 余数[r]原=0.0100×2—4补码不恢复余数法[x]补=00.1010 [y]补=00.1101 [--y]补=11.0011 部分积商数00.1010+11.001111.1101 0←11.1010+00.110100.0111 0.1←00.1110+11.001100.0001 0.11←00.0010+11.001111.0101 0.110←10.1010+00.110111.0111 0.1100+00.110100.0100所以[x/y]补=0.1100 余数[r]补=0.0100×2—42）原码不恢复余数法|x|=00.101 |y|=00.110 [--|y| ]补=11.010 部分积商数00.101+11.01011.111 0←11.110+00.11000.100 0.1←01.000+11.01000.010 0.11←00.100+11.01011.110 0.110+00.11000. 100所以[x/y]原=1.110 余数[r]原=1.100×2—3补码不恢复余数法[x]补=11.011 [y]补=00.110 [--y]补=11.010 部分积商数11.011+00.11000.001 1←00.010+11.01011.100 1.0←11.000+00.11011.110 1.0011.100+00.11000.010 1.001+11.01011.100所以[x/y]补=1.001+2—3=1.010 余数[r]补=1.100×2—32．121）[x]补=21101×00.100100 [y]补=21110×11.100110小阶向大阶看齐：[x]补=21110×00.010010求和：[x+y]补=21110×（00.010010＋11.100110）＝21110×11.111000 [x-y]补=21110×（00.010010＋00.011010）＝21110×00.101100 规格化：[x+y]补=21011×11.000000 浮点表示：1011，11.000000规格化：[x-y]补=21110×00.101100 浮点表示：1110，0.101100 2）[x]补=20101×11.011110 [y]补=20100×00.010110小阶向大阶看齐：[y]补=20101×00.001011求和：[x+y]补=20101×（11.011110＋00.001011）＝20101×11.101001 [x-y]补=20101×（11.011110＋11.110101）＝20101×00.010011 规格化：[x+y]补=21010×11.010010 浮点表示：1010，11. 010010规格化：[x-y]补=21010×00.100110 浮点表示：1010，00.1001102．13见教材：P702．141）1.0001011×262）0.110111*×2-62．151）串行进位方式C1=G1+P1C0G1=A1B1，P1=A1⊕B1C2=G2+P2C1G2=A2B2，P2=A2⊕B2C3=G3+P3C2G3=A3B3，P3=A3⊕B3C4=G4+P4C3G4=A4B4，P4=A4⊕B42)并行进位方式C1=G1+P1C0C2=G2+P2G1+P2P1C0C3=G3+P3G2+P3P2G1+P3P2P1C0C4= G4+P4G3+P4P3G2+P4P3P2G1+P4P3P2P1C02．16参考教材P62 32位两重进位方式的ALU和32位三重进位方式的ALU 2．17“1”。

沈阳航空工业学院课程设计报告课程设计名称：计算机组成原理课程设计课程设计题目：定点原码一位乘法器的设计院（系）：计算机学院专业：计算机科学与技术班级：4401102学号：200403011034姓名：蔡丽娇指导教师：刘泽显完成日期：2006年12月31日沈阳航空工业学院课程设计报告目录第1章总体设计方案 (1)1.1 设计原理 (1)1.2 设计思路 (1)1.3 设计环境 (2)第二章详细设计方案 (3)2.1顶层方案图的设计与实现 (3)2.1.1创建顶层图形设计文件 (3)2.1.2器件的选择与引脚锁定 (3)2.2 功能模块的设计与实现 (5)2.2.1 8位移位电路 (5)2.2.2 部分积寄存器 (7)2.2.3 乘数寄存器 (7)2.2.4 二路选择器 (8)2.2.5 计数器 (9)2.2.6 结果输出器 (11)2.3 仿真调试 (13)第3章编程下载与硬件测试 (14)3.1 编程下载 (14)3.2 硬件测试及结果分析 (14)参考文献 (15)附录（电路原理图） (16)第1章总体设计方案1.1 设计原理定点原码一位乘法器的设计主要是基于原码一位乘法的计算过成。

设计内容主要是实现输入被乘数和乘数经电路得出结果。

设计思想是：以乘数的最低位作为乘法判断位，若判断位为1，则在前次部分积（初始部分积为0）上加上被乘数，然后连同乘数一起右移一位；若判断位为0，则在前次部分积上加0，然后连同乘数一起右移一位。

重复此判断过程，直到运算n次为止(n为乘数数值部分的长度)。

1.2 设计思路原码一位乘法器主要包括ALU﹑部分积寄存器﹑乘数移位寄存器﹑被乘数寄存器和移位电路五大部分。

这五大部分就作为底层设计，其中乘数移位寄存器需要保留移出的最低位，它的最高位要接收部分积移出的最低位这两部分采用V erilog语言进行设计，顶层的乘法器采用原理图设计输入方式。

原码一位乘的数值运算中不需要考虑符号位的情况，符号位于数值位分开处理。

原码⼀位乘法1、移位操作及其意义
逻辑左移：
算术左移：
逻辑右移：
算术右移：
2、⼆进制乘法的⼿⼯计算过程
a.说明乘法可由加法实现
b.存在的问题：
*需要多输⼊的全加器（最多为n+1）
*需要长度为2n的积寄存器
*对应乘数的不同位，部分积左移次数不同
且乘法过程中总移位次数多
如何解决上述问题（改进⽅法）
*需要多输⼊的全加器（最多为n+1）
解决⽅法：基于FA的循环累加0或被乘数
*针对乘数不同位部分积左移次数不同的问题
解决⽅法：右移部分积，同时也将乘数右移，将移出的部分加⼊乘数的最左边*需要长度为2n的积寄存器
解决⽅法：从部分积和乘数寄存器取结果
3、原码⼀位乘法算法
*符号位单独参加运算，数据位取绝对值参加运算。

*运算法则：
*运算过程采⽤改进的乘法运算⽅法。

课程设计报告课程设计名称：计算机组成原理课程设计课程设计题目：定点原码一位乘法器的设计院（系）：专业：班级：学号：姓名：指导教师：完成日期：目录第1章总体设计方案 (1)1.1设计原理 (1)1.2设计思路 (2)1.3设计环境 (3)第2章详细设计方案 (5)2.1顶层方案图的设计与实现 (5)2.1.1创建顶层图形设计文件 (5)2.1.2器件的选择与引脚锁定 (5)2.1.3编译、综合、适配 (7)2.2功能模块的设计与实现 (7)2.2.1 控制器模块的设计与实现 (7)2.2.2 寄存器和与门组成的模块的设计与实现 (9)2.2.3 加法器模块的设计与实现 (11)2.2.4 寄存器模块的设计与实现 (14)2.3仿真调试 (16)第3章编程下载与硬件测试 (19)3.1编程下载 (19)3.2硬件测试及结果分析 (19)参考文献 (22)附录（电路原理图） (23)第1章总体设计方案1.1 设计原理原码一位乘，两个原码数相乘，其乘积的符号为相乘两数符号的异或值，数值则为两数绝对值之积。

例如：X的值为1101，Y的数值为1011，求X·Y数值的过程如下：即X·Y=10001111由于在计算机内多个数据一般不能同时相加，一次加法操作只能求出两数之和，因此每求得一个相加数，就与上次部分积相加每次计算时，相加数逐次向左偏移一位，由于最后的乘积位数是乘数（被乘数）的两倍，因此加法器也需增到两倍。

部分积右移时，乘数寄存器同时右移一位，所以用乘数寄存器的最低位来控制相加数取被乘数或零，同时乘数寄存器接收部分积右移出来的一位，完成运算后，部分积寄存器保存乘积的高位部分，乘数寄存器中保存乘积的低位部分。

根据人工算法可以知道，原码一位乘法的整体设计应包括乘数寄存器，被乘数寄存器，移位电路，控制器，部分积五大模块，包含一个输入、输出、控制器模块，并作为顶层设计，以上五大模块作为底层设计，采用硬件器件设计实现。

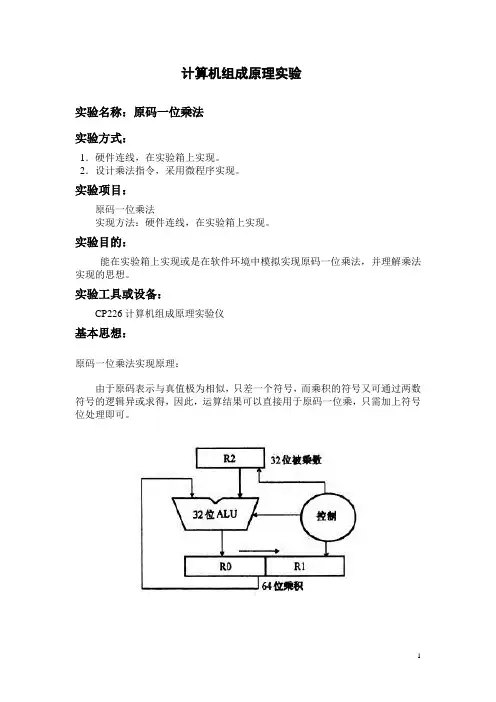
计算机组成原理实验实验名称：原码一位乘法实验方式：1．硬件连线，在实验箱上实现。

2．设计乘法指令，采用微程序实现。

实验项目：原码一位乘法实现方法：硬件连线，在实验箱上实现。

实验目的：能在实验箱上实现或是在软件环境中模拟实现原码一位乘法，并理解乘法实现的思想。

实验工具或设备：CP226计算机组成原理实验仪基本思想：原码一位乘法实现原理：由于原码表示与真值极为相似，只差一个符号，而乘积的符号又可通过两数符号的逻辑异或求得，因此，运算结果可以直接用于原码一位乘，只需加上符号位处理即可。

在实际的实验箱中8位被乘数放在R2中，运算开始时8位乘数放在R1中，运算结束时16位乘积的高位放在R0中，低位放在R1中，R0和R1串联移位。

完成这个定点原码一位乘法的运算规则可以用如下图所示的逻辑流程图表示。

在该乘法过程中，每次操作是根据乘数的一位进行操作，对于8位数的乘法，需要循环8次完成一个乘法操作，因此称为一位乘法。

下面用原码的乘法方法进行13（1101）×11（1011）的四位乘法演示。

1、在乘法开始之前，R0和R1中的初始值为0000和1011，R2中的值为1101。

2、在乘法的第一个循环中，判断R1的最低位为1，所以进入步骤1a，将R0的值0000加上R2的值1101，结果1101送人R0。

3、判断R0的末位是否为1。

如果为1，将R0和R1均右移一位，并将R1的右移结果加上1000；如果不为1，R0和R1直接右移一位（目的是将高位寄存器R0中移出的数据存放在低位寄存器R1，以实现R0 和R1的串联使用）。

其结果为（0110，1101）。

第一次循环过程结束。

第二次循环过程中，判断R1的最低位仍为1，进入步骤la，R0的值0110加1101，结果为10011。

判断R0的末位为1，将R0、R1均右移，并让R1的右移结果加上1000。

结果为（1001，1110）。

第三次循环中，因R1的最低位为0，进入步骤lb，R0加上0000为1001，判断R0的末位为1，将R0和R1均右移一位，并将R1的右移结果加上1000。

原码的一位乘总结
原码的一位乘法是指在两个用原码表示的数之间进行乘法运算。

原码是一种表示有符号整数的方法，其中最高位表示符号位，0表示正数，1表示负数。

原码的一位乘法可以通过以下步骤进行：
1.确定乘法的两个操作数，并将它们转换为原码表示。

2.对两个操作数的每一位进行相乘，得到部分积。

3.将所有的部分积相加，得到最终的乘积。

具体的步骤如下：
假设有两个操作数A和B，都用原码表示，长度为n位。

1.确定符号位：根据A和B的符号位确定结果的符号位。

如果A和B的符号位相同，则结果为正，否则为负。

2.对于第i位（i从0到n-1）：
-将A的第i位与B的第i位相乘，得到部分积Pi。

-如果A和B的符号位不同，将Pi取反（即将1变为0，0变为1）。

-将Pi左移i位（即在右边补i个0）。

3.将所有的部分积相加，得到最终的乘积。

需要注意的是，原码的一位乘法可能会出现溢出的情况。

当两个操作数相乘得到的部分积超过了原码表示的范围时，就会发生溢出。

在实际应用中，可以采用补码表示来避免这种情况的发生。

1。

2．227/64=00011011/01000000=0.0110110=0.11011×2-1＝101，011011000规格化浮点表示为：[27/64]原[27/64]反＝110，011011000[27/64]补＝111，011011000同理：--27/64=--0.11011×2-1＝101，111011000规格化浮点表示为：[27/64]原[27/64]反＝110，100100111[27/64]补＝111，1001010002．3 模为：29=10000000002．4 不对，8421码是十进制的编码2．5浮点数的正负看尾数的符号位是1还是0浮点数能表示的数值范围取决于阶码的大小。

浮点数数值的精确度取决于尾数的长度。

2．61）不一定有N1>N2 2）正确2．7 最大的正数：0111 01111111 十进制数：（1－2－7）×27最小的正数：1001 00000001 十进制数：2－7×2－7最大的负数：1001 11111111 十进制数：--2－7×2－7最小的负数：0111 10000001 十进制数：--（1－2－7）×272．81）[x]补=00.1101 [y]补=11.0010[x+y]补＝[x]补+[y]补=11.1111无溢出x+y= －0.0001[x]补=00.1101 [--y]补=00.1110[x－y]补＝[x]补+[--y]补=01.1011 正向溢出2）[x]补=11.0101 [y]补=00.1111[x+y]补＝[x]补+[y]补=00.0100 无溢出x+y= 0.0100[x]补=11.0101 [--y]补=11.0001[x－y]补＝[x]补+[--y]补=10.0110 负向溢出3) [x]补=11.0001 [y]补=11.0100[x+y]补＝[x]补+[y]补=10.0101 负向溢出[x]补=11.0001 [--y]补=00.1100[x－y]补＝[x]补+[--y]补=11.1101 无溢出X－y=－0.00112．91）原码一位乘法|x|=00.1111 |y|=0.1110部分积乘数y n00.0000 0.1110+00.000000.0000→00.00000 0.111+00.111100.11110→00.011110 0.11+00.111101.011010→00.1011010 0.1+00.111101.1010010→00.11010010P f=x f⊕y f=1 |p|=|x|×|y|=0.11010010所以[x×y]原=1.11010010补码一位乘法[x]补=11.0001 [y]补=0.1110 [--x]补=11.0001部分积y n y n+100.0000 0.11100→00.00000 0.1110+00.111100.11110→00.011110 0.111→00.0011110 0.11→00.00011110 0.1+11.000111.00101110[x×y]补=11.001011102）原码一位乘法|x|=00.110 |y|=0.010部分积乘数y n00.000 0.010+00.00000.000→00.0000 0.01+00.11000.1100→00.01100 0.0+00.00000.01100 0→00.001100P f=x f⊕y f=0 |p|=|x|×|y|=0.001100所以[x×y]原=0.001100补码一位乘法[x]补=11.010 [y]补=1.110 [--x]补=00.110部分积y n y n+100.000 1.1100→00.0000 1.110+00.11000.1100→00.01100 1.11→00.001100 1.1所以[x×y]补=0.0011002．101）原码两位乘法|x|=000.1011 |y|=00.0001 2|x|=001.0110部分积乘数c000.0000 00.00010+000.1011000.1011→000.001011 0.000→000.00001011 00.0P f=x f⊕y f=1 |p|=|x|×|y|=0.00001011所以[x×y]原=1.00001011补码两位乘法[x]补=000.1011 [y]补=11.1111 [--x]补=111.0101部分积乘数y n+1000.0000 11.11110+111.0101111.0101→111.110101 11.111→111.11110101 11.1所以[x×y]补=111.11110101 x×y=--0.000010112）原码两位乘法|x|=000.101 |y|=0.111 2|x|=001.010 [--|x| ]补=111.011部分积乘数c000.000 0.1110+111.011111.011→111.11011 0.11+001.010001.00011→000.100011P f=x⊕y f=0 |p|=|x|×|y|=0.100011所以[x×y]原=0.100011补码两位乘法[x]补=111.011 [y]补=1.001 [--x]补=000.101 2[--x]补=001.010部分积乘数y n+1000.000 1.0010+111.011111.011→111.111011 1.00+001.010001.00011→000.100011所以[x×y]补=0.1000112.111) 原码不恢复余数法|x|=00.1010 |y|=00.1101 [--|y| ]补=11.0011部分积商数00.1010+11.00111101101 0←11.1010+00.110100.0111 0.1←00.1110+11.001100.0001 0.11←00.0010+11.001111.0101 0.110←01.1010+00.110111.0111 0.1100+00.110100.0100所以[x/y]原=0.1100 余数[r]原=0.0100×2—4补码不恢复余数法[x]补=00.1010 [y]补=00.1101 [--y]补=11.0011部分积商数00.1010+11.001111.1101 0←11.1010+00.110100.0111 0.1←00.1110+11.001100.0001 0.11←00.0010+11.001111.0101 0.110←10.1010+00.110111.0111 0.1100+00.110100.0100所以[x/y]补=0.1100 余数[r]补=0.0100×2—42）原码不恢复余数法|x|=00.101 |y|=00.110 [--|y| ]补=11.010部分积商数00.101+11.01011.111 0←11.110+00.11000.100 0.1←01.000+11.01000.010 0.11←00.100+11.01011.110 0.110+00.11000. 100所以[x/y]原=1.110 余数[r]原=1.100×2—3补码不恢复余数法[x]补=11.011 [y]补=00.110 [--y]补=11.010部分积商数11.011+00.11000.001 1←00.010+11.01011.100 1.0←11.000+00.11011.110 1.00←11.100+00.11000.010 1.001+11.01011.100所以[x/y]补=1.001+2—3=1.010 余数[r]补=1.100×2—32．121）[x]补=21101×00.100100 [y]补=21110×11.100110=21110×00.010010小阶向大阶看齐：[x]补21110×（00.010010＋11.100110）＝21110×11.111000求和：[x+y]补=[x-y]补=21110×（00.010010＋00.011010）＝21110×00.10110021011×11.000000 浮点表示：1011，11.000000规格化：[x+y]补=21110×00.101100 浮点表示：1110，0.101100规格化：[x-y]补=2）[x]补=20101×11.011110 [y]补=20100×00.010110=20101×00.001011小阶向大阶看齐：[y]补20101×（11.011110＋00.001011）＝20101×11.101001求和：[x+y]补=[x-y]补=20101×（11.011110＋11.110101）＝20101×00.01001121010×11.010010 浮点表示：1010，11. 010010规格化：[x+y]补=21010×00.100110 浮点表示：1010，00.100110规格化：[x-y]补=2．13见教材：P702．141）1.0001011×262）0.110111*×2-62．151）串行进位方式C1=G1+P1C0G1=A1B1，P1=A1⊕B1C2=G2+P2C1G2=A2B2，P2=A2⊕B2C3=G3+P3C2G3=A3B3，P3=A3⊕B3C4=G4+P4C3G4=A4B4，P4=A4⊕B42)并行进位方式C1=G1+P1C0C2=G2+P2G1+P2P1C0C3=G3+P3G2+P3P2G1+P3P2P1C0C4= G4+P4G3+P4P3G2+P4P3P2G1+P4P3P2P1C02．16参考教材P62 32位两重进位方式的ALU和32位三重进位方式的ALU 2．17“1”A3B3A2 B2 A1 B1 A0 B0-。

计算机组成原理试题及答案一、填空（12分）1.某浮点数基值为2，阶符1位，阶码3位,数符1位，尾数7位，阶码和尾数均用补码表示,尾数采用规格化形式，用十进制数写出它所能表示的最大正数，非0最小正数，最大负数,最小负数。

2.变址寻址和基址寻址的区别是：在基址寻址中，基址寄存器提供，指令提供；而在变址寻址中，变址寄存器提供，指令提供.3.影响流水线性能的因素主要反映在和两个方面。

4.设机器数字长为16位（含1位符号位）。

若1次移位需10ns,一次加法需10ns，则补码除法需时间，补码BOOTH算法最多需要时间。

5.CPU从主存取出一条指令并执行该指令的时间叫,它通常包含若干个,而后者又包含若干个.组成多级时序系统。

二、名词解释(8分)1.微程序控制2.存储器带宽3.RISC4.中断隐指令及功能三、简答（18分）1。

完整的总线传输周期包括哪几个阶段？简要叙述每个阶段的工作。

2. 设主存容量为1MB，Cache容量为16KB，每字块有16个字，每字32位.(1）若Cache采用直接相联映像，求出主存地址字段中各段的位数。

(2)若Cache采用四路组相联映像，求出主存地址字段中各段的位数。

3。

某机有五个中断源，按中断响应的优先顺序由高到低为L0，L1，L2，L3，L4，现要求优先顺序改为L3，L2，L4，L0,L1,写出各中断源的屏蔽字。

4.统具备120种操作。

操作码位数固定，且具有直接、间接、立即、相对四种寻址方式。

（1)画出一地址指令格式并指出各字段的作用；（2)该指令直接寻址的最大范围；(3）一次间址的寻址范围； (4）相对寻址的寻址范围。

四、（6分）设阶码取3位,尾数取6位（均不包括符号位)，按浮点补码运算规则计算 [25169⨯] + [24)1611(-⨯］五、画出DMA 方式接口电路的基本组成框图，并说明其工作过程（以输入设备为例）。

（8分）六、（10分）设CPU 共有16根地址线，8根数据线，并用MREQ 作访存控制信号，用W R /作读写控制信号，现有下列存储芯片： RAM ：1K ×8位、2K ×4位、4K ×8位ROM ：2K ×8位、4K ×8位以及74138译码器和各种门电路（自定)，画出CPU 与存储器连接图。

定点数原码一位乘法定点数原码一位乘法是一种乘法运算的方法，它利用了二进制数的加法和移位操作来实现乘法运算。

以下是这个算法的步骤：1.将被乘数和乘数都表示为定点数，即带有符号位的纯小数。

2.将被乘数和乘数都转换为原码表示，即最高位为符号位，其余位为数值位。

3.初始化结果为0。

4.从低位到高位逐位相乘，如果该位乘积的符号与结果符号相同，则将该位乘积加到结果上，否则只做移位操作。

5.重复步骤4，直到所有位都相乘完毕。

6.对结果进行舍入或截断操作，得到最终结果。

以下是一个简单的示例：假设我们有两个定点数：被乘数为1010.101(十进制为-4.625)，乘数为1011.011(十进制为-7.25)。

按照原码一位乘法的步骤，我们可以得到以下计算过程：1.被乘数=1010.101(十进制为-4.625)2.乘数=1011.011(十进制为-7.25)3.初始化结果为0。

4.从低位到高位逐位相乘：第0位：被乘数第0位为0，乘数第0位为1，符号相同，将该位乘积加到结果上，得到0+0=0。

第1位：被乘数第1位为1，乘数第1位为1，符号相同，将该位乘积加到结果上，得到0+1*2^(-2)=0.25。

第2位：被乘数第2位为0，乘数第2位为0，符号相同，将该位乘积加到结果上，得到0.25+0=0.25。

第3位：被乘数第3位为1，乘数第3位为0，符号不同，只做移位操作，得到0.25*2=0.5。

第4位：被乘数第4位为0，乘数第4位为1，符号相同，将该位乘积加到结果上，得到0.5+0=0.5。

第5位：被乘数第5位为1，乘数第5位为1，符号相同，将该位乘积加到结果上，得到0.5+(-1)*2^(-3)=-0.25。

第6位：被乘数第6位为0，乘数第6位为0，符号相同，将该位乘积加到结果上，得到-0.25+0=-0.25。

第7位：被乘数第7位为1，乘数第7位为1，符号相同，将该位乘积加到结果上，得到-0.25+(-8)*2^(-4)=-4.875。

第六章20. 用原码一位乘、两位乘和补码一位乘（Booth 算法）、两位乘计算x ·y 。

（1）x= 0.110111，y= -0.101110；（2）x= -0.010111，y= -0.010101；（3）x= 19， y= 35；（4）x= 0.110 11， y= -0.111 01 。

解：(a) 原码一位乘:(1)[x]原=0.110111[y]原=1.101110x*=0.110111 y*=0.101110 符号位: 00X Y 011⊕=⊕=数值部分的计算：部分积 乘数y* ---------------------------------------------------------------------------------------------------------------------- 0.000000 101110 开始部分积为0+ 0.000000 乘数为0，加上0---------------------------------------------------------------------------------------------------------------------- 0.0000000.000000 0 10111 部分积右移一位，乘数右移一位+ 0.110111 乘数为1，加上X*---------------------------------------------------------------------------------------------------------------------- 0.110111 00.011011 10 1011 部分积右移一位，乘数右移一位+ 0.110111 乘数为1，加上X*--------------------------------------------------------------------------------------------------------------------- 1.010010 100.101001 010 101 部分积右移一位，乘数右移一位+ 0.110111 乘数为1，加上X*---------------------------------------------------------------------------------------------------------------------1.100000 0100.110000 0010 10+ 0.000000-------------------------------------------------------------------------------------------------------------------- 0.110000 00100.011000 00010 1 部分积右移一位，乘数右移一位+ 0.110111 乘数为1，加上X*--------------------------------------------------------------------------------------------------------------------- 1.001111 00010 右移一位0.100111 100010[x*y]原=1.100111100010(2)[x]原=1.010111[y]原=1.010101x*=0.010111 y*=0.010101 符号位: 00X Y 110⊕=⊕=数值部分的计算：部分积 乘数y*0.000000 010101 开始部分积为0+ 0.010111 乘数为1，加上X*0.0101110.001011 1 01010 部分积右移一位，乘数右移一位+ 0.000000 乘数为0，加上00.001011 10.000101 11 0101 部分积右移一位，乘数右移一位+ 0.010111 乘数为1，加上X*0.011100 110.001110 011 010 部分积右移一位，乘数右移一位+ 0.000000 乘数为0，加上00.001110 0110.000111 0011 01 部分积右移一位，乘数右移一位+ 0.010111 乘数为1，加上X*0.011110 00110.001111 00011 0 部分积右移一位，乘数右移一位+ 0.0000000.001111 000110.000111 100011故，x ·y=0.000111100011（3）[x]原=0，0001 0011[y]原=0，0010 0011x*=0001 0011 y*=0010 0011符号位: 00X Y 000⊕=⊕=数值部分的计算：部分积 乘数y*00000000 00100011 开始部分积为0+ 00010011 乘数为1，加上X* 0001001100001001 1 0010001 部分积右移一位，乘数右移一位+ 0001001100011100 100001110 01 001000 部分积右移一位，乘数右移一位 + 0000000000001110 0100000111 001 00100 部分积右移一位，乘数右移一位00000011 1001 001000000001 11001 00100000101 0011001即 0，0000 0010 1001 1001（4）x=0.11011，y=-0.11101[x]原=0.11011[y]原=1.11101x*=0.11011 y*=0.11101 符号位: 00X Y 011⊕=⊕=数值部分的计算：部分积 乘数y*0.00000 11101 开始部分积为0+ 0 .11011 乘数为1，加上X*0.110110.01101 1 1110 部分积右移一位，乘数右移一位0.00110 11 111 部分积右移一位，乘数右移一位+ 0.110111.00001 110.10000 111 11 部分积右移一位，乘数右移一位+ 0.11011 乘数为1，加上X*1.01011 1110.10101 1111 1 部分积右移一位，乘数右移一位+ 0.11011 乘数为1，加上X*1.10000 11110.11000 01111加上符号位得1.1100001111(b) 补码一位乘(Booth)当乘数y 为正数时，不管被乘数x 符号如何，都可按原码乘法的规则运算，但加和移位都必须按补码规则运算当乘数y 为负数时，把乘数的补码[y]补去掉符号位，当成一个正数与[x]补相乘，然后加上[-x]补进行校正。

原码一位乘法乘法是数学中最重要的基本运算之一，也是学习数学的重要知识，也是大学生运用数学解决问题，实现抽象思维和抽象想象的基础。

原码一位乘法，是我们经常会遇到的运算，它能够让我们快速算出乘积，也是数学运算的精髓。

原码一位乘法的原理是，通过重复进位的方式来实现一位乘法的计算，而且是一般乘法算法的关键所在。

比如说，2乘以5，它的原码乘法进位法计算过程如下：1.2乘以5，计算结果为10，然后将10除以10，取余数，即最终结果为0。

2.2乘以4，计算结果为8，然后将8除以10，取余数，即最终结果为8。

3.2乘以3，计算结果为6，然后将6除以10，取余数，即最终结果为6。

4.2乘以2，计算结果为4，然后将4除以10，取余数，即最终结果为4。

5.2乘以1，计算结果为2，然后将2除以10，取余数，即最终结果为2。

最后，可以将上述余数依次排列起来，得出最终的乘积为1082。

由于原码一位乘法的运算方法简单，而且结果容易求得，所以被广泛应用于计算机中的程序设计，尤其是在计算机科学中有着重要的地位。

尽管原码一位乘法让我们能够简单快速地计算出乘积，但是它也有一些限制，它不能处理超过一位数的乘积，也不能处理乘积过长的数字。

因此，要做更为精确的乘法计算，我们还需要用到其他算法，比如多位乘法法则。

原码一位乘法在计算机中的优势在于它可以简化计算机的运算程序，提高计算机的运算速度，减少计算机的存储空间，给用户提供更好的计算体验。

在实际应用中，原码一位乘法可以帮助我们快速算出结果，使我们在解决复杂数学问题时节省大量精力，让我们能够得出准确的结果，大大提高了工作效率。

原码一位乘法虽然有着极大的优势，但是也存在着一些缺点，例如，它不能处理超过一位数的乘法，也不能处理乘积过长的数字。

因此，我们在使用原码一位乘法时要注意其限度，最好的方式是结合不同的算法，一起运用，充分发挥它的优势，实现更加准确、更加高效的运算效果。

综上所述，原码一位乘法是数学计算中一种重要且有效的算法，它被广泛应用于计算机程序设计，可以让我们快速算出结果，提高计算机的运算效率，但是也有一些限制，要想得出更加准确、更加高效的结果，我们要将不同算法结合起来运用，把原码一位乘法发挥到最大的程度。

原码位乘法是一种基于二进制原码表示的乘法算法。

在计算机科学中，原码是二进制数的一种表示方式，最高位是符号位，0表示正，1表示负，余下的位数表示数值的绝对值。

这种乘法算法被广泛应用在数字信号处理、图像处理以及计算机图形学等领域。

以下是原码位乘法的算法步骤：
1. 将两个乘数转换为原码表示。

2. 从最低位（即最右边）开始，逐位判断乘数的每一位。

3. 如果乘数的某一位为1，则将被乘数与对应的2的幂次相乘（该幂次由当前位的位置决定），并将结果累加到总和中。

这一步实际相当于将该位的值乘以被乘数然后累加。

4. 判断完所有位之后，得到的总和即为乘积的原码表示。

5. 如果乘积的原码符号位为1，即结果为负数，需要对结果进行取反加1的运算，将其转换为补码表示。

注意：以上算法步骤描述的是基本的原码位乘法过程，实际在计算机中执行时，可能会根据具体的硬件架构进行优化改进，但从算法的基本概念和运算上仍是符合上述流程的。

例如在大部分的计算机系统中，数值在内部通常以补码形式进行存储和运算，所以实际在执行乘法运算时，会将原码转换为补码进行运算，得到的结果也是补码形式，最后再根据需要转换为原码或其他表示形式。