一元二次方程知识点总结与易错题及答案
- 格式:doc
- 大小:177.50 KB
- 文档页数:4

一元二次方程总复习考点1:一元二次方程的概念一元二次方程:只含有一个未知数,未知数的最高次数是 2,且系数不为0,这样的方程叫一元二次方程.一般形式:ax2+bx+c=0(a≠0〕。
注意:判断某方程是否为一元二次方程时,应首先将方程化为一般形式。
考点2:一元二次方程的解法1.直接开平方法:对形如(x+a〕2=b〔b≥0〕的方程两边直接开平方而转化为两个一元一次方程的方法。
x+a= ± b ∴ x1 =-a+ b x2 =-a- b2.配方法:用配方法解一元二次方程:ax2+bx+c=0(k≠0〕的一般步骤是:①化为一般形式;②移项,将常数项移到方程的右边;③化二次项系数为1,即方程两边同除以二次项系数;④配方,即方程两边都加上一次项系数的一半的平方;化原方程为(x+a〕2=b 的形式;⑤如果b≥0就可以用两边开平方来求出方程的解;如果b≤0,那么原方程无解.3.公式法:公式法是用求根公式求出一元二次方程的解的方法.它是通过配方推导出来的.一元二次方程的求根公式是x = - b ± b 2 - 4ac (b2-4ac≥0)。
步骤:①把方程转化为一般形2a式;②确定 a,b,c 的值;③求出 b2-4ac 的值,当 b2-4ac≥0时代入求根公式。
4.因式分解法:用因式分解的方法求一元二次方程的根的方法叫做因式分解法.理论根据:假设ab=0,那么 a=0 或b=0。
步骤是:①将方程右边化为 0;②将方程左边分解为两个一次因式的乘积;③令每个因式等于0,得到两个一元一次方程,解这两个一元一次方程,它们的解就是原一元二次方程的解.因式分解的方法:提公因式、公式法、十字相乘法。
5.一元二次方程的考前须知:⑴在一元二次方程的一般形式中要注意,强调a≠0.因当a=0 时,不含有二次项,即不是一元二次方程.⑵应用求根公式解一元二次方程时应注意:①先化方程为一般形式再确定a,b,c 的值;②假设b2-4ac<0,那么方程无解.⑶ 利用因式分解法解方程时,方程两边绝不能随便约去含有未知数的代数式.如-2(x+4) 2 =3〔x+4〕中,不能随便约去 x+4。

初三培优 易错 难题一元二次方程组辅导专题训练及答案一、一元二次方程1.解方程:(x+1)(x ﹣3)=﹣1.【答案】x 1x 2=1【解析】试题分析:根据方程的特点,先化为一般式,然后利用配方法求解即可.试题解析:整理得:x 2﹣2x=2,配方得:x 2﹣2x+1=3,即(x ﹣1)2=3,解得:x 1,x 2=12.已知关于x 的方程x 2﹣(2k +1)x +k 2+1=0.(1)若方程有两个不相等的实数根,求k 的取值范围;(2)若方程的两根恰好是一个矩形两邻边的长,且k =2,求该矩形的对角线L 的长.【答案】(1)k >34;(2 【解析】【分析】(1)根据关于x 的方程x 2-(2k +1)x +k 2+1=0有两个不相等的实数根,得出△>0,再解不等式即可;(2)当k=2时,原方程x 2-5x+5=0,设方程的两根是m 、n ,则矩形两邻边的长是m 、n ,利用根与系数的关系得出m+n=5,mn=5,利用完全平方公式进行变形即可求得答案.【详解】(1)∵方程x 2-(2k +1)x +k 2+1=0有两个不相等的实数根,∴Δ=[-(2k +1)]2-4×1×(k 2+1)=4k -3>0,∴k >34; (2)当k =2时,原方程为x 2-5x +5=0,设方程的两个根为m ,n ,∴m +n =5,mn =5,∴==.【点睛】本题考查了根的判别式、根与系数的关系、矩形的性质等,一元二次方程根的情况与判别式△的关系:(1)△>0时,方程有两个不相等的实数根;(2)△=0时,方程有两个相等的实数根;(3)△<0时,方程没有实数根.3.“父母恩深重,恩怜无歇时”,每年5月的第二个星期日即为母亲节,节日前夕巴蜀中学学生会计划采购一批鲜花礼盒赠送给妈妈们.(1)经过和花店卖家议价,可在原标价的基础上打八折购进,若在花店购买80个礼盒最多花费7680元,请求出每个礼盒在花店的最高标价;(用不等式解答)(2)后来学生会了解到通过“大众点评”或“美团”同城配送会在(1)中花店最高售价的基础上降价25%,学生会计划在这两个网站上分别购买相同数量的礼盒,但实际购买过程中,“大众点评”网上的购买价格比原有价格上涨52m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了920m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了152m%,求出m的值.【答案】(1)120;(2)20.【解析】试题分析:(1)本题介绍两种解法:解法一:设标价为x元,列不等式为0.8x•80≤7680,解出即可;解法二:根据单价=总价÷数量先求出1个礼盒最多花费,再除以折扣可求出每个礼盒在花店的最高标价;(2)先假设学生会计划在这两个网站上分别购买的礼盒数为a个礼盒,表示在“大众点评”网上的购买实际消费总额:120a(1﹣25%)(1+52m%),在“美团”网上的购买实际消费总额:a[120(1﹣25%)﹣920m](1+15m%);根据“在两个网站的实际消费总额比原计划的预算总额增加了152m%”列方程解出即可.试题解析:(1)解:解法一:设标价为x元,列不等式为0.8x•80≤7680,x≤120;解法二:7680÷80÷0.8=96÷0.8=120(元).答:每个礼盒在花店的最高标价是120元;(2)解:假设学生会计划在这两个网站上分别购买的礼盒数为a个礼盒,由题意得:120×0.8a(1﹣25%)(1+52m%)+a[120×0.8(1﹣25%)﹣920m](1+15m%)=120×0.8a(1﹣25%)×2(1+ 152m%),即72a(1+52m%)+a(72﹣920m)(1+15m%)=144a(1+ 152m%),整理得:0.0675m2﹣1.35m=0,m2﹣20m=0,解得:m1=0(舍),m2=20.答:m的值是20.点睛:本题是一元二次方程的应用,第二问有难度,正确表示出“大众点评”或“美团”实际消费总额是解题关键.4.有一个人患了流感,经过两轮传染后共有36人患了流感.(1)求每轮传染中平均一个人传染了几个人?(2)如果不及时控制,第三轮将又有多少人被传染?【答案】(1)5;(2)180【解析】【分析】(1)设平均一人传染了x 人,根据有一人患了流感,经过两轮传染后共有36人患了流感,列方程求解即可;(2)根据每轮传染中平均一个人传染的人数和经过两轮传染后的人数,列出算式求解即可.【详解】(1)设每轮传染中平均一个人传染了x 个人,根据题意得:x+1+(x+1)x =36,解得:x =5或x =﹣7(舍去).答:每轮传染中平均一个人传染了5个人;(2)根据题意得:5×36=180(个),答:第三轮将又有180人被传染.【点睛】本题考查一元二次方程的应用,解题的关键是能根据题意找到等量关系并列方程.5.如图,在Rt ABC V 中,90B =o ∠,10AC cm =,6BC cm =,现有两点P 、Q 的分别从点A 和点B 同时出发,沿边AB ,BC 向终点C 移动.已知点P ,Q 的速度分别为2/cm s ,1/cm s ,且当其中一点到达终点时,另一点也随之停止移动,设P ,Q 两点移动时间为xs .问是否存在这样的x ,使得四边形APQC 的面积等于216cm ?若存在,请求出此时x 的值;若不存在,请说明理由.【答案】假设不成立,四边形APQC 面积的面积不能等于216cm ,理由见解析【解析】【分析】根据题意,列出BQ 、PB 的表达式,再列出方程,判断根的情况.【详解】解:∵90B ∠=o ,10AC =,6BC =,∴8AB =.∴BQ x =,82PB x =-;假设存在x 的值,使得四边形APQC 的面积等于216cm ,则()1168821622x x ⨯⨯--=, 整理得:2480x x -+=,∵1632160=-=-<V ,∴假设不成立,四边形APQC 面积的面积不能等于216cm .【点睛】本题考查了一元二次方程的应用,熟练掌握方程根的判别方法、理解方程的意义是本题的解题关键.6.已知关于x 的一元二次方程x 2﹣6x+(2m+1)=0有实数根.(1)求m 的取值范围;(2)如果方程的两个实数根为x 1,x 2,且2x 1x 2+x 1+x 2≥20,求m 的取值范围.【答案】(1)m≤4;(2)3≤m≤4.【解析】试题分析:(1)根据判别式的意义得到△=(-6)2-4(2m+1)≥0,然后解不等式即可; (2)根据根与系数的关系得到x 1+x 2=6,x 1x 2=2m+1,再利用2x 1x 2+x 1+x 2≥20得到2(2m+1)+6≥20,然后解不等式和利用(1)中的结论可确定满足条件的m 的取值范围. 试题解析:(1)根据题意得△=(-6)2-4(2m +1)≥0,解得m ≤4;(2)根据题意得x 1+x 2=6,x 1x 2=2m +1,而2x 1x 2+x 1+x 2≥20,所以2(2m +1)+6≥20, 解得m≥3,而m≤4,所以m 的范围为3≤m≤4.7.校园空地上有一面墙,长度为20m ,用长为32m 的篱笆和这面墙围成一个矩形花圃,如图所示.(1)能围成面积是126m 2的矩形花圃吗?若能,请举例说明;若不能,请说明理由. (2)若篱笆再增加4m ,围成的矩形花圃面积能达到170m 2吗?请说明理由.【答案】(1)长为18米、宽为7米或长为14米、宽为9米;(2)若篱笆再增加4m ,围成的矩形花圃面积不能达到170m 2.【解析】【分析】(1)假设能,设AB 的长度为x 米,则BC 的长度为(32﹣2x )米,再根据矩形面积公式列方程求解即可得到答案.(2)假设能,设AB 的长度为y 米,则BC 的长度为(36﹣2y )米,再根据矩形面积公式列方程,求得方程无解,即假设不成立.【详解】(1)假设能,设AB 的长度为x 米,则BC 的长度为(32﹣2x )米,根据题意得:x(32﹣2x)=126,解得:x 1=7,x 2=9,∴32﹣2x=18或32﹣2x=14,∴假设成立,即长为18米、宽为7米或长为14米、宽为9米.(2)假设能,设AB 的长度为y 米,则BC 的长度为(36﹣2y )米,根据题意得:y(36﹣2y)=170,整理得:y 2﹣18y+85=0.∵△=(﹣18)2﹣4×1×85=﹣16<0,∴该方程无解,∴假设不成立,即若篱笆再增加4m ,围成的矩形花圃面积不能达到170m 2.8.关于x 的一元二次方程ax 2+bx+1=0.(1)当b=a+2时,利用根的判别式判断方程根的情况;(2)若方程有两个相等的实数根,写出一组满足条件的a ,b 的值,并求此时方程的根.【答案】(1)方程有两个不相等的实数根;(2)b=-2,a=1时,x 1=x 2=﹣1.【解析】【详解】分析:(1)求出根的判别式24b ac ∆=-,判断其范围,即可判断方程根的情况.(2)方程有两个相等的实数根,则240b ac ∆=-=,写出一组满足条件的a ,b 的值即可.详解:(1)解:由题意:0a ≠.∵()22242440b ac a a a ∆=-=+-=+>, ∴原方程有两个不相等的实数根.(2)答案不唯一,满足240b ac -=(0a ≠)即可,例如:解:令1a =,2b =-,则原方程为2210x x -+=,解得:121x x ==.点睛:考查一元二次方程()200++=≠ax bx c a 根的判别式24b ac ∆=-, 当240b ac ∆=->时,方程有两个不相等的实数根.当240b ac ∆=-=时,方程有两个相等的实数根.当240b ac ∆=-<时,方程没有实数根.9.如图,要利用一面墙(墙长为25米)建羊圈,用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈,求羊圈的边长AB ,BC 各为多少米?【答案】羊圈的边长AB,BC分别是20米、20米.【解析】试题分析:设AB的长度为x米,则BC的长度为(100﹣4x)米;然后根据矩形的面积公式列出方程.试题解析:设AB的长度为x米,则BC的长度为(100﹣4x)米.根据题意得(100﹣4x)x=400,解得 x1=20,x2=5.则100﹣4x=20或100﹣4x=80.∵80>25,∴x2=5舍去.即AB=20,BC=20考点:一元二次方程的应用.10.工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)求长方体底面面积为12dm2时,裁掉的正方形边长多大?【答案】裁掉的正方形的边长为2dm,底面积为12dm2.【解析】试题分析:设裁掉的正方形的边长为xdm,则制作无盖的长方体容器的长为(10-2x)dm,宽为(6-2x)dm,根据长方体底面面积为12dm2列出方程,解方程即可求得裁掉的正方形边长.试题解析:设裁掉的正方形的边长为xdm,由题意可得(10-2x)(6-2x)=12,即x2-8x+12=0,解得x=2或x=6(舍去),答:裁掉的正方形的边长为2dm,底面积为12dm2.11.已知关于x的方程x2-(m+2)x+(2m-1)=0。

方程与不等式之一元二次方程易错题汇编及答案解析一、选择题1.已知关于X 的方程x 2 +bx+a=0有一个根是-a (a ≠0),则a-b 的值为( ) A .1B .2C .-1D .0 【答案】C【解析】【分析】由一元二次方程的根与系数的关系x 1•x 2=c a、以及已知条件求出方程的另一根是-1,然后将-1代入原方程,求a-b 的值即可.【详解】∵关于x 的方程x 2+bx+a=0的一个根是-a (a≠0),∴x 1•(-a )=a ,即x 1=-1,把x 1=-1代入原方程,得:1-b+a=0,∴a-b=-1.故选C .【点睛】本题主要考查了一元二次方程的解.解题关键是根据一元二次方程的根与系数的关系确定方程的一个根.2.若代数式226(3)1x x m x ++=+-,则m =( )A .-8B .9C .8D .-9【答案】C【解析】【分析】已知等式右边利用完全平方公式化简,利用多项式相等的条件求出m 的值即可.【详解】 226(3)1x x m x ++=+-=x 2+6x+8,可得m=8,故选:C.【点睛】此题考查配方法的应用,解题关键在于掌握计算公式.3.对于一元二次方程ax 2+bx +c =0(a ≠0),下列说法:①若b =ax 2+bx +c =0一定有两个相等的实数根;②若方程ax 2+bx +c =0有两个不等的实数根,则方程x 2﹣bx +ac =0也一定有两个不等的实数根;③若c 是方程ax 2+bx +c =0的一个根,则一定有ac +b +1=0成立;④若x 0是一元二次方程ax 2+bx +c =0的根,则b 2﹣4ac =(2ax 0+b )2,其中正确的( )A .只有①②③B .只有①②④C .①②③④D .只有③④【答案】B【解析】【分析】判断上述方程的根的情况,只要看根的判别式△=-24b ac 的值的符号就可以了.④难度较大,用到了求根公式表示0x .【详解】解:①若2b ac =,方程两边平方得b 2=4ac ,即b 2﹣4ac =0,所以方程ax 2+bx +c =0一定有两个相等的实数根;②若方程ax 2+bx +c =0有两个不等的实数根,则b 2﹣4ac >0方程x 2﹣bx +ac =0中根的判别式也是b 2﹣4ac >0,所以也一定有两个不等的实数根; ③若c 是方程ax 2+bx +c =0的一个根,则一定有ac 2+bc +c =0成立,当c ≠0时ac +b +1=0成立;当c =0时ac +b +1=0不成立; ④若x 0是一元二次方程ax 2+bx +c =0的根,可得204b b ac x -±-=, 把x 0的值代入(2ax 0+b )2,可得b 2﹣4ac =(2ax 0+b )2,综上所述其中正确的①②④.故选:B .【点睛】此题主要考查了根的判别式及其应用.尤其是④难度较大,用到了求根公式表示0x ,整体代入求2204(2)b ac ax b -=+.总结:一元二次方程根的情况与判别式△的关系:(1)△0>⇔方程有两个不相等的实数根;(2)△0=⇔方程有两个相等的实数根;(3)△0<⇔方程没有实数根.4.若2245a a x -+-=,则不论取何值,一定有( )A .5x >B .5x <-C .3x ≥-D .3x ≤-【答案】D【解析】【分析】由﹣2a 2+4a ﹣5=﹣2(a ﹣1)2﹣3可得:x ≤﹣3.【详解】∵x =﹣2a 2+4a ﹣5=﹣2(a ﹣1)2﹣3≤﹣3,∴不论a 取何值,x ≤﹣3.故选D .【点睛】本题考查了配方法的应用,熟练运用配方法解答本题的关键.5.用配方法解方程2640x x ++=时,原方程变形为( )A .2(3)9x +=B .2(3)13x +=C .2(3)5x +=D .2(3)4x +=【答案】C【解析】【分析】方程整理后,配方得到结果,即可做出判断.【详解】解:方程配方得:x 2+6x+5+4-5=0,即(x+3)2=5.故选:C .【点睛】此题考查解一元二次方程-配方法,熟练掌握完全平方公式是解题的关键.6.一列自然数0,1,2,3,…,100.依次将该列数中的每一个数平方后除以100,得到一列新数.则下列结论正确的是( )A .原数与对应新数的差不可能等于零B .原数与对应新数的差,随着原数的增大而增大C .当原数与对应新数的差等于21时,原数等于30D .当原数取50时,原数与对应新数的差最大【答案】D【解析】【分析】设出原数,表示出新数,利用解方程和函数性质即可求解.【详解】解:设原数为m ,则新数为21100m , 设新数与原数的差为y 则2211100100y m m m m =-=-+, 易得,当m =0时,y =0,则A 错误 ∵10100-< 当1m 50122100b a ﹣﹣﹣===⎛⎫⨯ ⎪⎝⎭时,y 有最大值.则B 错误,D 正确. 当y =21时,21100m m -+=21解得1m =30,2m =70,则C 错误.故答案选:D .【点睛】本题以规律探究为背景,综合考查二次函数性质和解一元二次方程,解题时要注意将数字规律转化为数学符号.7.某厂四月份生产零件100万个,第二季度共生产零件282万个.设该厂五、六月份平均每月的增长率为x ,那么x 满足的方程是( )A .100(1+x )2=282B .100+100(1+x )+100(1+x )2=282C .100(1+2x )=282D .100+100(1+x )+100(1+2x )=282【答案】B【解析】【分析】主要考查增长率问题,一般增长后的量=增长前的量×(1+增长率),如果该厂五、六月份平均每月的增长率为x ,那么可以用x 分别表示五、六月份的产量,然后根据题意可得出方程.【详解】五月份的产量=100(1+x ),六月份的产量=1002(1)x +, 根据题意可得:100+100(1+x )+1002(1)x +=282.故选:B .【点睛】本题考查了由实际问题抽象出一元二次方程,增长率问题,一般形式为2(1)a x b +=,a 为起始时间的有关数量,b 为终止时间的有关数量.8.李师傅去年开了一家商店,将每个月的盈亏情况都作了记录.今年1月份开始盈利,2月份盈利2000元,4月份盈利恰好2880元,若每月盈利的平均增长率都相同,这个平均增长率是( )A .20%B .22%C .25%D .44%【答案】A【解析】【分析】设这个平均增长率为x ,根据等量关系:2月份盈利额×(1+增长率)2=4月份的盈利额列出方程求解即可.【详解】设这个平均增长率为x ,根据题意得:2000(1+x )2=2880,解得:x 1=20%,x 2=-2.2(舍去).答:这个平均增长率为20%.故选A .【点睛】此题主要考查了一元二次方程的应用,属于增长率的问题,一般公式为原来的量×(1±x )2=后来的量,其中增长用+,减少用-,难度一般.9.某型号手机原来销售单价是4000元,经过两次降价促销,现在的销售单价是2560元,若两次降价的百分率相同,则平均每次降价( )A .10%B .15%C .20%D .25%【答案】C【解析】【分析】根据原来售价是4000元,经过两次降价且降价百分率相同后销售单价为2560元,设两次降价的百分率为x ,一次降价为()40001x -,两次降价为()240001x -得出 ()240001x -=2560,算出x .【详解】解:设两次降价的百分率为x ,由题意得:4000(1﹣x )2=2560∴(1﹣x )2=256400∴1﹣x =±0.8∴x 1=1.8(舍),x 2=0.2=20%故选:C .【点睛】熟悉一元二次方程的增长率和下降率的相关题型,注意分析是一次增长(下降),还是二次增长(下降)问题.10.设α,β是方程2x 9x 10++=的两根,则()()22α2009α1β2009β1++++的值是( )A .0B .1C .2000D .4000000 【答案】D【解析】【分析】由已知方程的系数可得两根的关系(根据韦达定理或者叫根与系数的关系),再将所求代数式变形可求得代数式结果.【详解】解:∵α,β是方程2x 9x 10++=的两个实数根∴2211,910,9101αβααββ==++=++=g ∴()()()()2222α2009α1β2009β1α9α12000β9β120002000200040000004000000αβαβαβ++++=++++++===g 故选D.【点睛】(1)将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.(2)二次函数为2ax x 0(0)b c a ++=不等于的两个不同实数根:α,β满足=,b c a aαβαβ+-=g . 11.某商品原售价225元,经过连续两次降价后售价为196元,设平均每次降价的百分率为x ,则下面所列方程中正确的是( )A .22251196x (﹣)=B .21961225x (﹣)=C .22251196x (﹣)= D .21961225x (﹣)=【答案】A【解析】【分析】 可先表示出第一次降价后的价格,那么第一次降价后的价格×(1﹣降低的百分率)=225,把相应数值代入即可求解.【详解】第一次降价后的价格为225×(1﹣x ),第二次降价后的价格为225×(1﹣x )×(1﹣x ),则225(1﹣x )2=196.故选A .【点睛】本题考查了一元二次方程的应用-增长率问题.若设变化前的量为a ,变化后的量为b ,平均变化率为x ,则经过两次变化后的数量关系为a (1±x )2=b .12.某果园2011年水果产量为100吨,2013年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x ,则根据题意可列方程为( ) A .144(1﹣x )2=100 B .100(1﹣x )2=144 C .144(1+x )2=100 D .100(1+x )2=144【答案】D【解析】试题分析:2013年的产量=2011年的产量×(1+年平均增长率)2,把相关数值代入即可. 解:2012年的产量为100(1+x ),2013年的产量为100(1+x )(1+x )=100(1+x )2,即所列的方程为100(1+x )2=144,故选D .点评:考查列一元二次方程;得到2013年产量的等量关系是解决本题的关键.13.关于x的一元二次方程ax2+2x+1=0有两个不相等的实数根,那么a的取值范围是( ) A.a>1 B.a=1 C.a<1 D.a<1且a≠0【答案】D【解析】【分析】由于原方程是一元二次方程,首先应该确定的是a≠0;然后再根据原方程根的情况,利用根的判别式建立关于a的不等式,求出a的取值范围.【详解】解:由于原方程是二次方程,所以a≠0;∵原方程有两个不相等的实数根,∴△=b2-4ac=4-4a>0,解得a<1;综上,可得a≠0,且a<1;故选D.【点睛】本题考查了一元二次方程根的情况与判别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没有实数根.14.某种植基地2016年蔬菜产量为100吨,2017年比2016年产量增长8.1%,2018年比2017年产量的增长率为x,2018年底产量达到144吨,则x满足()A.100(1+x)2=144 B.100(1+8.1%)(1﹣x)=144C.100(1+8.1%)+x=144 D.100(1+8.1%)(1+x)=144【答案】D【解析】【分析】由题意知,2017年蔬菜产量为:100(1+8.1%),2018年蔬菜产量为:100(1+8.1%)(1+x),然后根据2018年底产量达到144吨列方程即可.【详解】解:∵某种植基地2016年蔬菜产量为100吨,2017年比2016年产量增长8.1%,∴2017年蔬菜产量为:100(1+8.1%),∵2018年比2017年产量的增长率为x,2018年底产量达到144吨,∴2018年蔬菜产量为:100(1+8.1%)(1+x)=144,故选D.【点睛】本题主要考查了由实际问题抽象出一元一次方程的应用,熟练掌握这些知识是解题的关键.15.已知关于x 的一元二次方程3x 2+4x ﹣5=0,下列说法正确的是( )A .方程有两个相等的实数根B .方程有两个不相等的实数根C .没有实数根D .无法确定【答案】B【解析】试题分析:先求出△=42﹣4×3×(﹣5)=76>0,即可判定方程有两个不相等的实数根.故答案选B.考点:一元二次方程根的判别式.16.已知关于x 的一元二次方程mx 2﹣(m+2)x+4m =0有两个不相等的实数根x 1,x 2.若11x +21x =4m ,则m 的值是( ) A .2B .﹣1C .2或﹣1D .不存在 【答案】A【解析】【分析】先由二次项系数非零及根的判别式△>0,得出关于m 的不等式组,解之得出m 的取值范围,再根据根与系数的关系可得出x 1+x 2=2m m +,x 1x 2=14,结合1211+x x =4m ,即可求出m 的值.【详解】∵关于x 的一元二次方程mx 2﹣(m+2)x+4m =0有两个不相等的实数根x 1、x 2, ∴()202404m m m m ≠⎧⎪⎨∆=+-⋅>⎪⎩, 解得:m >﹣1且m≠0,∵x 1、x 2是方程mx 2﹣(m+2)x+4m =0的两个实数根, ∴x 1+x 2=2m m +,x 1x 2=14, ∵1211+x x =4m ,∴214m m +=4m , ∴m=2或﹣1,∵m >﹣1,∴m=2,故选A .【点睛】本题考查了根与系数的关系、一元二次方程的定义以及根的判别式,解题的关键是:根据二次项系数非零及根的判别式△>0,找出关于m 的不等式组;牢记两根之和等于﹣b a 、两根之积等于c a.17.已知关于x 的一元二次方程20ax bx c ++=的根为2和3,则关于x 的一元二次方程20ax bx c --=的根为( ).A .2,3--B .6,1-C .2,3-D .1,6-【答案】B【解析】【分析】由2,3是一元二次方程ax 2+bx+c=0的两个实数根,可以得到如下四个等式: 2+3=-b a=-5,2×3=c a =6;再根据问题的需要,灵活变形. 【详解】 因为2和3是方程ax 2+bx+c=0的根,所以2+3=-b a ,2×3=c a ; 故一元二次方程ax 2-bx-c=0的根满足x 1x 2=-c a =-6①,x 1+x 2=-b =ab a -=5②; 将A 、B 、C 、D 的值代入①②式中,只有B 项满足.故答案选B.18.我校图书馆三月份借出图书70本,计划四、五月份共借出图书220本,设四、五月份借出的图书每月平均增长率为x ,则根据题意列出的方程是( )A .70(1+x )2=220B .70(1+x )+70(1+x )2=220C .70(1﹣x )2=220D .70+70(1+x )+70(1+x )2=220【答案】B【解析】【分析】根据题意,找出等量关系,列出方程即可.【详解】三月份借出图书70本四月份共借出图书量为70×(1+x )五月份共借出图书量为70×(1+x )2则70(1+x )+70(1+x )2=220.故选:B .【点睛】本题考查一元二次方程的应用,分析题干,列出方程是解题关键.19.关于x 的一元二次方程220x ax --=的根的情况( )A .有两个实数根B .有两个不相等的实数根C .没有实数根D .由a 的取值确定 【答案】B【解析】【分析】计算出方程的判别式为△=a 2+8,可知其大于0,可判断出方程根的情况.【详解】方程220x ax --=的判别式为280a ∆=+>,所以该方程有两个不相等的实数根, 故选:B .【点睛】本题主要考查一元二次方程根的判别式,掌握根的判别式与方程根的情况是解题的关键.20.以3和4为根的一元二次方程是( )A .27120x x -+=B .27120x x ++=C .27120x x +-=D .27120x x --=【答案】A【解析】【分析】分别求出各个选项中一元二次方程的两根之和与两根之积,进行判断即可.【详解】A 、在x 2﹣7x+12=0中,x 1+x 2=7,x 1x 2=12,此选项正确;B 、在x 2+7x+12=0中,x 1+x 2=﹣7,x 1x 2=12,此选项不正确;C 、在x 2+7x ﹣12=0中,x 1+x 2=7,x 1x 2=﹣12,此选项不正确;D、在x2﹣7x﹣12=0中,x1+x2=﹣7,x1x2=﹣12,此选项不正确;故选:A.【点睛】本题主要考查了根与系数的关系的知识,解答本题的关键是要掌握一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=ba,x1•x2=ca.。

初中数学一元二次方程知识点总结(含习题)一元二次方程知识点的总结知识结构梳理:1、概念1) 一元二次方程含有一个未知数。
2) 未知数的最高次数是2.3) 是方程。
4) 一元二次方程的一般形式是ax²+bx+c=0.2、解法1) 因式分解法,适用于能化为(x+m)(x+n)=0的一元二次方程。
2) 公式法,即把方程变形为ax²+bx+c=0的形式,一元二次方程的解为x=[-b±√(b²-4ac)]/(2a)。
3) 完全平方式,其中求根公式是(x±a)²=b,当时,方程有两个不相等的实数根。
4) 配方法,其中求根公式是(x±a)(x±b)=0,当时,方程有两个实数根。
5) 二次函数图像法,当时,方程有没有实数根。
3、应用1) 一元二次方程可用于解某些求值题。
2) 一元二次方程可用于解决实际问题的步骤包括:列方程、化简方程、解方程、检验答案。
知识点归类:考点一:一元二次方程的定义如果一个方程通过移项可以使右边为0,而左边只含有一个未知数的二次多项式,那么这样的方程叫做一元二次方程。
一元二次方程必须同时满足以下三点:①方程是整式方程。
②它只含有一个未知数。
③未知数的最高次数是2.考点二:一元二次方程的一般形式一元二次方程的一般形式为ax²+bx+c=0,其中a、b、c分别叫做二次项系数、一次项系数、常数项。
要准确找出一个一元二次方程的二次项系数、一次项系数和常数项,必须把它先化为一般形式。
考点三:解一元二次方程的方法一元二次方程的解也叫一元二次方程的根。
解一元二次方程的方法包括因式分解法、公式法、完全平方式、配方法和二次函数图像法。
解一元二次方程有四种常用方法:直接开平方法、配方法、因式分解法和公式法。
选择哪种方法要根据具体情况而定。
直接开平方法是解形如x²=a的方程的方法,解为x=±√a。
配方法是将方程的左边加上一次项系数一半的平方,再减去这个数,使得含未知数的项在一个完全平方式里,然后用因式分解法或直接开平方法解方程。

一元二次方程知识点总结与易错题及答案一元二次方程知识点总结考点一、一元二次方程1、一元二次方程:含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
2、一元二次方程的一般形式:,它的特征是:等式左边十一个关于未知数x的二次多项式,等式右边是零,其中叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。
考点二、一元二次方程的解法1、直接开平方法:利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法。
直接开平方法适用于解形如的一元二次方程。
根据平方根的定义可知,是b的平方根,当时,,,当b0时,一元二次方程有2个不相等的实数根;II当△=0时,一元二次方程有2个相同的实数根;III当△考点四、一元二次方程根与系数的关系如果方程的两个实数根是,那么,。
也就是说,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商。
考点五、一元二次方程的二次函数的关系大家已经学过二次函数(即抛物线)了,对他也有很深的了解,好像解法,在图象中表示等等,其实一元二次方程也可以用二次函数来表示,其实一元二次方程也是二次函数的一个特殊情况,就是当Y的0的时候就构成了一元二次方程了。
那如果在平面直角坐标系中表示出来,一元二次方程就是二次函数中,图象与X轴的交点。
也就是该方程的解了一元二次方程易错题一、选择题1、若关于x 的一元二次方程(m-1)x2+5x+m2-3m+2=0有一个根为0,则m的值等于()A.1B.2C.1或2D.02、巴中日报讯:今年我市小春粮油再获丰收,全市产量预计由前年的45万吨提升到50万吨,设从前年到今年我市的粮油产量年平均增长率为,则可列方程为()A.B.C.D.3、已知是关于的一元二次方程的两实数根,则的值是()A.B.C.D.4、已知a、b、c分别是三角形的三边,则(a+b)x2+2cx+(a+b)=0的根的情况是()A.没有实数根B.可能有且只有一个实数根C.有两个相等的实数根D.有两个不相等的实数根5、已知是方程的两根,且,则的值等于()A.-5B.5C.-9D.96、已知方程有一个根是,则下列代数式的值恒为常数的是()A.B.C.D.7、的估计正确的是()A.B.C.D.8、关于的一元二次方程的两个实数根分别是,且,则的值是()A.1B.12C.13D.259、(中江县初中毕业生诊断考试)某校九年级学生毕业时,每个同学都将自己的相片向全班其他同学各送一张表示留念,全班共送了2450张相片,如果全班有x名学生,根据题意,列出方程为()A.B.C.D.10、设是方程的两个实数根,则的值为()A.2006B.2007C.2008D.200911、对于一元二次方程ax2+bx+c=0(a≠0),下列说法:①若a+c=0,方程ax2+bx+c=0必有实数根;②若b+4ac<0,则方程ax2+bx+c=0一定有实数根;③若a-b+c=0,则方程ax2+bx+c=0一定有两个不等实数根;④若方程ax+bx+c=0有两个实数根,则方程cx+bx+a=0一定有两个实数根.其中正确的是()A.①②B.①③C.②③D.①③④二、填空题1、若一元二次方程x-(a+2)x+2a=0的两个实数根分别是3、b,则a+b=.3、方程(x ﹣1)(x+2)=2(x+2)的根是.4、关于x的一元二次方程ax+bx+1=0(a0)有两个相等实根,求的值为______.5、在等腰△ABC中,三边分别为a,b,c,其中a=5,若关于x的方程x+(b+2)x+6-b=0有两个相等的实数根,则△ABC的周长为_________.6、已知关于的一元二次方程x-6x-k=0(k为常数).设x,x为方程的两个实数根,且x+2x=14,则k的值为________.7、已知m、n是方程x-2003x+2004=0的两根,则(n-2004n+2005)与(m-2004m+2005)的积是.。

完整版)一元二次方程(知识点考点题型总结)一元二次方程专题复考点一、概念一元二次方程是只含有一个未知数,且未知数的最高次数是2的整式方程。
一般表达式为ax^2+bx+c=0,其中a不等于0.关于“未知数的最高次数是2”,需要注意以下三点:一是该项系数不为0;二是未知数指数为2;三是若存在某项指数为待定系数,或系数也有待定,则需建立方程或不等式加以讨论。
典型例题:例1、下列方程中是关于x的一元二次方程的是():A。
2x^2+11x-2=0B。
ax^2+bx+c=DC。
2x=x+1变式:当k时,关于x的方程kx+2x=x+3是一元二次方程。
例2、方程m+2xm+1=0是关于x的一元一次方程,求m 的值,并写出关于x的一元一次方程。
针对练:1.方程8x^2+3mx+1=0是关于x的一元二次方程,则m的值为多少?2.若方程m-2x=0是关于x的一元一次方程,求m的值,并写出关于x的一元一次方程。
3.若方程(m-1)x+m·x=1是关于x的一元二次方程,则m 的取值范围是多少?4.若方程nx+x-2x=0是一元二次方程,则下列不可能的是():A。
m=n=2B。
m=2.n=1C。
n=2.m=1D。
m=n=1考点二、方程的解方程的解是指使方程两边相等的未知数的值。
根的概念可用于求代数式的值。
典型例题:例1、已知2y+y^2-3的值为2,则4y+2y^2+1的值为多少?例2、关于x的一元二次方程(a-2)x^2+x+a-4=0的一个根为2,求a的值。
例3、已知关于x的一元二次方程ax^2+bx+c=0的系数满足a+c=b,则此方程必有一根为多少?例4、已知a,b是方程x^2-4x+m=0的两个根,b,c是方程y^2-8y+5m=0的两个根,则m的值为多少?针对练:1.已知方程x+kx-10=0的一根是2,则k为多少?另一根是多少?2.已知关于x的方程x^2+kx-2=0的一个解与方程(x+1)/(x-1)=3的解相同,求k的值,并求方程的另一个解。

一元二次方程本章内容“一元二次方程”是《课程标准》“数与代数”的重要内容,也是方程中重点内容,是学习二次函数等内容的基础,本节是本章的起始内容,主要学习下列三个内容:建立一元二次方程此内容是本节课的难点之一,在后续的内容中将继续学习,为此设计较易的[拓展应用]的例4及其变式题,[课时作业]的第6、7题。
1.一元二次方程的概念此内容是本节课的重点,是学习一元二次方程的基础,为此设计[拓展应用]的例1、例3,[当堂检测]的第1、2、4题,[课时作业]的第1—5题。
2.一元二次方程的解的含义利用方程解的含义,可求方程中的待定系数,也可由此把二次三项式变形求值,为此设计[拓展应用]的例2,[当堂检测]的第3题,[选做题]和[备选题目]的问题。
点击一:一元二次方程的定义答案:(5)针对练习。
答案:一元二次方程二次项的系数不等于零。
故m≠-3点击二:一元二次方程的一般形式元二次方程的一般形式是ax2+bx+c=0(a≠0),其中ax2是二次项,bx是一次项,c是常数项,a是二次项系数,b是一次项系数,c是常数.任何一个一元二次方程都可以通过整理转化成一般形式.由此,对于一个方程从形式上,应先将这个方程进行整理,看是否符合ax2+bx+c=0(a≠0)的一般形式.其中,尤其注意a≠0的条件,有了a≠0的条件,就能说明ax2+bx+c=0是一元二次方程.若不能确定a≠0,并且b≠0,则需分类讨论:当a≠0时,它是一元二次方程;当a=0时,它是一元一次方程.针对练习3:答案:原方程化为一般形式是:5x2+8x-2=0(若写成-5x2-8x+2=0,则不符合人们的习惯),其中二次项是5x2,二次项系数是5,一次项是8x,一次项系数是8,常数项是-2(因为一元二次方程的一般形式是三个单项式的和,所以不能漏写单项式系数的负号).点击三:一元二次方程的根的定义的意义一元二次方程的根的定义可以当作性质定理使用,即若有实数m是一元二次方程ax 2+bx +c =0(a ≠0)的根,则m 必然满足该方程,将m 代入该方程,便有am 2+bm +c =0(a ≠0);定义也可以当作判定定理使用,即若有数m 能使am 2+bm +c =0(a ≠0)成立,则m 一定是ax 2+bx +c =0的根.我们经常用定义法来解一些常规方法难以解决的问题,能收到事半功倍的效果.针对练习答案: m 3+2m 2+2009=m 3+ m 2+m 2+2009=m (m 2+ m )+ m 2+2009=m+ m 2+2009=1+2009=2010.类型之一:一元二次方程的定义例1.关于x 的方程2322+-=-mx x x mx 是一元二次方程,m 应满足什么条件? 【解析】先把这个方程变为一般形式,只要二次项的系数不为0即可.【解答】由mx 2-3x=x 2-mx+2得到(m -1)x 2+(m -3)x -2=0,所以m -1≠0,即m≠1.所以关于x 的方程2322+-=-mx x x mx 是一元二次方程,m 应满足m≠1.【点评】要特别注意二次项系数a≠0这一条件,当a=0时,上面的方程就不是一元二次方程了.当b=0或c=0时,上面的方程在a≠0的条件下,仍是一元二次方程,只不过是不完全的一元二次方程.类型之二:考查一元二次方程一般形式一元二次方程的一般形式是ax 2+bx+c=0(a 、b 、c 是已知数,a≠0),其中a 叫做二次项系数,b 叫做一次项系数c 叫做常数项.只有将方程化为一般形式之后,才能确定它的二次项系数、一次项系数和常数项.这里特别要注意各项系数的符号。

一元二次方程一、下列关于x 的方程,哪些是一元二次方程?如果不是,请在方程下写出理由。
1.(1)3522=+x ;(2)062=-x x ;(3)5=+x x ;(4)02=-x ;(5)12)3(22+=-x x x2.关于x 的方程032)4()16(22=++++-m x m x m 当m______时,是一元二次方程,当m______时,是一元一次方程。
二、关于x 的方程()()02132=+----m x m x m 是一元二次方程,则二次项是 ,一次项系数是 ,常数项是 。
三、根的判别式的运用:1.若方程2(2)2(1)0m x m x m +-++=只有一个实数根,试判断方程2(1)220m x m x m +-+-=的根的情况。
2.当m 取什么值时,关于x 的方程0)22()12(222=++++m x m x 。
(1)有两个相等实根;(2)有两个不相等的实根;(3)没有实根。
3.m 为何值时,关于x 的方程()0324122=-+++m mx x m 的根满足下列情况:(1)有两个不相等的实数;(2)有两个相等的实数根;(3)没有实数根4.当m 为什么值时,关于x 的方程01)1(2)4(22=+++-x m x m(1)有两个实数根。
(2)有实数根。
注意:题2、3的区别、题3与4的区别。
5.关于x 的一元二次方程032)1(22=--+++m m x x m 有一个根是0,求m 的值6.如果关于x 的一元二次方程2690kx x -+=有两个实数根,求k 的取值范围7.当m 为何值时,方程032)1(2=+++-m mx x m 有两个实数根8.若一元二次方程02)12(22=+-+-x x x x k 有实数根, 求k 的取值范围小结:题5—8在解题中要注意什么?9.已知关于x 的一元二次方程20x m --=有两个不相等的实数根,求m 的取值范围10.关于x 的一元二次方程2(12)10k x ---=有两个不相等的实数根,求k 的取值范围上述两题要注意什么?四、综合运用:1.已知12)1)(3(2222=++-+b a b a ,求22b a +的值.2.已知多项式22x 2xy y x y 1-+-+-的值为0,求x-y 的值3.如果012=--x x ,求2009223++-x x 的值4.若二次三项式2542+-kx x 是完全平方式,则 k 值为________.5.已知关于x 的一元二次方程02=++c bx x 的两根为2,121=-=x x ,则c bx x ++2分解因式的结果是______6.如果二次三项式k x x 2432+-在实数范围内总能分解成两个一次因式的积,求k 的取值范围7.已知关于x 的方程222(1)50x m x m ++++=有两个不相等的实数根,化简:|1|m -8.如果m 是实数,且不等式1)1(+>+m x m 的解集是x<1,那么关于x 的一元二次方程041)1(2=++-m x m mx 的根的情况如何?9.三角形的两边的长是3和4,第三边的长是方程035122=+-x x 的根,求三角形的周长10. 等腰三角形的周长是12,它的一边长是关于x 的方程2x 6x 80-+=的一个实数根,求它的腰长和底边长?11. 等腰△ABC 中,BC=8,AB,BC 的长是关于x 的方程0102=+-m x x 的两根,则三角形的周长是多少?12.已知关于方程21(21)4()02x k x k -++-=⑴求证:无论k 取何值,这个方程总有实数根; ⑵若等腰A B C ∆的一边长为4,另两边长b 、c 恰好是这个方程的两个实数根,求这个三角形的周长.。

九年级一元二次方程易错题(Word版含答案)一、初三数学一元二次方程易错题压轴题(难)1.阅读与应用:阅读1:a,b为实数,且a>0,b>0,因为()2≥0,所以a﹣2+b≥0,从而a+b≥2(当a=b时取等号).阅读2:若函数y=x+(m>0,x>0,m为常数),由阅读1结论可知:x+≥2,所以当x=,即x=时,函数y=x+的最小值为2.阅读理解上述内容,解答下列问题:问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为,周长为2(x+),求当x=时,周长的最小值为;问题2:汽车的经济时速是汽车最省油的行驶速度,某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油()L.若该汽车以每小时x公里的速度匀速行驶,1h的耗油量为yL.(1)求y关于x的函数关系式(写出自变量x的取值范围);(2)求该汽车的经济时速及经济时速的百公里耗油量.【答案】问题1:2,8;问题2:(1)y=;(2)10.【解析】【分析】(1)利用题中的不等式得到x+=4,从而得到x=2时,周长的最小值为8;(2)根据耗油总量=每公里的耗油量×行驶的速度列出函数关系式即可,经济时速就是耗油量最小的形式速度.【详解】(1)∵x+≥2=4,∴当x=时,2(x+)有最小值8.即x=2时,周长的最小值为8;故答案是:2;8;问题2:,当且仅当,即x=90时,“=”成立,所以,当x=90时,函数取得最小值9,此时,百公里耗油量为,所以,该汽车的经济时速为每小时90公里,经济时速的百公里耗油量为10L.【点睛】本题考查了配方法及反比例函数的应用,最值问题,解题的关键是读懂题目提供的材料,易错点是了解“耗油总量=每公里的耗油量×行驶的速度”,难度中等偏上.2.随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭.据某市交通部门统计,2008年底该市汽车拥有量为75万辆,而截止到2010年底,该市的汽车拥有量已达108万辆.(1)求2008年底至2010年底该市汽车拥有量的年平均增长率;(2)为了保护城市环境,缓解汽车拥堵状况,该市交通部门拟控制汽车总量,要求到2012年底全市汽车拥有量不超过125.48万辆;另据统计,从2011年初起,该市此后每年报废的汽车数量是上年底汽车拥有量的10%假设每年新增汽车数量相同,请你估算出该市从2011年初起每年新增汽车数量最多不超过多少万辆.【答案】解:(1)2008年底至2010年底该市汽车拥有量的年平均增长率是20%(2)从2011年初起每年新增汽车数量最多不超过20万辆【解析】【分析】(1)设年平均增长率x,根据等量关系“2008年底汽车拥有量×(1+年平均增长率)×(1+年平均增长率)”列出一元二次方程求得.(2)设从2011年初起每年新增汽车的数量y,根据已知得出2011年报废的车辆是2010年底拥有量×10%,推出2011年底汽车拥有量是2010年底拥有量-2011年报废的车辆=2010年拥有量×(1-10%),得出等量关系是: 2010年拥有量×(1-10%)+新增汽车数量]×(1-10%)+新增汽车数量”,列出一元一次不等式求得.【详解】解:(1)设该市汽车拥有量的年平均增长率为x.根据题意,得75(1+x)2=108,则1+x=±1.2解得x1=0.2=20%,x2=﹣2.2(不合题意,舍去).答:该市汽车拥有量的年平均增长率为20%.(2)设全市每年新增汽车数量为y万辆,则2010年底全市的汽车拥有量为(108×90%+y)万辆,2011年底全市的汽车拥有量为[(108×90%+y)×90%+y]万辆.根据题意得(108×90%+y)×90%+y≤125.48,解得y≤20.答:该市每年新增汽车数量最多不能超过20万辆.3.已知关于x 的方程24832x nx n --=和()223220x n x n -+-+=,是否存在这样的n 值,使第一个方程的两个实数根的差的平方等于第二个方程的一整数根?若存在,请求出这样的n 值;若不存在,请说明理由?【答案】存在,n=0. 【解析】 【分析】在方程①中,由一元二次方程的根与系数的关系,用含n 的式子表示出两个实数根的差的平方,把方程②分解因式,建立方程求n ,要注意n 的值要使方程②的根是整数. 【详解】 若存在n 满足题意.设x1,x2是方程①的两个根,则x 1+x 2=2n ,x 1x 2=324n +-,所以(x 1-x 2)2=4n 2+3n+2, 由方程②得,(x+n-1)[x-2(n+1)]=0, ①若4n 2+3n+2=-n+1,解得n=-12,但1-n=32不是整数,舍. ②若4n 2+3n+2=2(n+2),解得n=0或n=-14(舍), 综上所述,n=0.4.如图,∠ AOB =90°,且点A ,B 分别在反比例函数1k y x =(x <0),2ky x=(x >0)的图象上,且k 1,k 2分别是方程x 2-x -6=0的两根. (1)求k 1,k 2的值;(2)连接AB ,求tan ∠ OBA 的值.【答案】(1)k 1=-2,k 2=3. (2)tan∠OBA 6. 【解析】解:(1)∵k 1,k 2分别是方程x 2-x -6=0的两根,∴解方程x 2-x -6=0,得x 1=3,x 2=-2.结合图像可知:k 1<0,k 2>0,∴k 1=-2,k 2=3.(2)如图,过点A 作AC ⊥x 轴于点C ,过点B 作BD ⊥y 轴于点D .[来源:学&科&网Z&X&X&K]由(1)知,点A,B分别在反比例函数2yx=-(x<0),3yx=(x>0)的图象上,∴S△ACO=12×2-=1 ,S△ODB=12×3=32.∵∠AOB=90°,∴∠ AOC+∠ BOD=90°,∵∠ AOC+∠ OAC=90°,∴∠ OAC=∠ BOD.又∵∠ACO=∠ODB=90°,∴△ACO∽△ODB.∴SSACOODB∆∆=2OAOB⎛⎫⎪⎝⎭=23,∴OAOB=±6(舍负取正),即OAOB=6.∴在Rt△AOB中,tan∠OBA=OAOB=6.5.如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.(1)若点P从点A移动到点B停止,点P、Q分别从点A、C同时出发,问经过2s时P、Q 两点之间的距离是多少cm?(2)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C 同时出发,问经过多长时间P、Q两点之间的距离是10cm?(3)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?【答案】(1)2cm;(2)85s或245s;(3)经过4秒或6秒△PBQ的面积为12cm2.【解析】试题分析:(1)作PE⊥CD于E,表示出PQ的长度,利用PE2+EQ2=PQ2列出方程求解即可;(2)设x秒后,点P和点Q的距离是10cm.在Rt△PEQ中,根据勾股定理列出关于x的方程(16-5x)2=64,通过解方程即可求得x的值;(3)分类讨论:①当点P在AB上时;②当点P在BC边上;③当点P在CD边上时.试题解析:(1)过点P作PE⊥CD于E.则根据题意,得EQ=16-2×3-2×2=6(cm),PE=AD=6cm;在Rt△PEQ中,根据勾股定理,得PE2+EQ2=PQ2,即36+36=PQ2,∴2cm;∴经过2s时P、Q两点之间的距离是2;(2)设x秒后,点P和点Q的距离是10cm.(16-2x-3x)2+62=102,即(16-5x)2=64,∴16-5x=±8,∴x1=85,x2=245;∴经过85s或245sP、Q两点之间的距离是10cm;(3)连接BQ.设经过ys后△PBQ的面积为12cm2.①当0≤y≤163时,则PB=16-3y,∴12PB•BC=12,即12×(16-3y)×6=12,解得y=4;②当163<x≤223时,BP=3y-AB=3y-16,QC=2y,则1 2BP•CQ=12(3y-16)×2y=12,解得y1=6,y2=-23(舍去);③223<x≤8时,QP=CQ-PQ=22-y,则1 2QP•CB=12(22-y)×6=12,解得y=18(舍去).综上所述,经过4秒或6秒△PBQ的面积为 12cm2.考点:一元二次方程的应用.6.如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).(1)求点D的坐标.(2)求直线BC的解析式.(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.【答案】(1)D(4,7)(2)y=3944x (3)详见解析【解析】试题分析:(1)解一元二次方程求出OA、OB的长度,过点D作DE⊥y于点E,根据正方形的性质可得AD=AB,∠DAB=90°,然后求出∠ABO=∠DAE,然后利用“角角边”证明△DAE 和△ABO全等,根据全等三角形对应边相等可得DE=OA,AE=OB,再求出OE,然后写出点D的坐标即可;(2)过点C作CM⊥x轴于点M,同理求出点C的坐标,设直线BC的解析式为y=kx+b (k≠0,k、b为常数),然后利用待定系数法求一次函数解析式解答;(3)根据正方形的性质,点P与点B重合时,△PCD为等腰三角形;点P为点B关于点C 的对称点时,△PCD为等腰三角形,然后求解即可.试题解析:(1)x2﹣7x+12=0,解得x1=3,x2=4,∵OA>OB,∴OA=4,OB=3,过D作DE⊥y于点E,∵正方形ABCD,∴AD=AB,∠DAB=90°,∠DAE+∠OAB=90°,∠ABO+∠OAB=90°,∴∠ABO=∠DAE,∵DE⊥AE,∴∠AED=90°=∠AOB,∵DE⊥AE∴∠AED=90°=∠AOB,∴△DAE≌△ABO(AAS),∴DE=OA=4,AE=OB=3,∴OE=7,∴D(4,7);(2)过点C作CM⊥x轴于点M,同上可证得△BCM≌△ABO,∴CM=OB=3,BM=OA=4,∴OM=7,∴C(7,3),设直线BC的解析式为y=kx+b(k≠0,k、b为常数),代入B(3,0),C(7,3)得,,解得,∴y=x﹣;(3)存在.点P与点B重合时,P1(3,0),点P与点B关于点C对称时,P2(11,6).考点:1、解一元二次方程;2、正方形的性质;3、全等三角形的判定与性质;4、一次函数7.在等腰三角形△ABC 中,三边分别为a 、b 、c ,其中ɑ=4,若b 、c 是关于x 的方程x 2﹣(2k +1)x +4(k ﹣12)=0的两个实数根,求△ABC 的周长. 【答案】△ABC 的周长为10. 【解析】 【分析】分a 为腰长及底边长两种情况考虑:当a=4为腰长时,将x=4代入原方程可求出k 值,将k 值代入原方程可求出底边长,再利用三角形的周长公式可求出△ABC 的周长;当a=4为底边长时,由根的判别式△=0可求出k 值,将其代入原方程利用根与系数的关系可求出b+c 的值,由b+c=a 可得出此种情况不存在.综上即可得出结论. 【详解】当a =4为腰长时,将x =4代入原方程,得:()214421402k k ⎛⎫-++-= ⎪⎝⎭解得:52k = 当52k =时,原方程为x 2﹣6x +8=0, 解得:x 1=2,x 2=4,∴此时△ABC 的周长为4+4+2=10;当a =4为底长时,△=[﹣(2k +1)]2﹣4×1×4(k ﹣12)=(2k ﹣3)2=0, 解得:k =32, ∴b +c =2k +1=4. ∵b +c =4=a ,∴此时,边长为a ,b ,c 的三条线段不能围成三角形. ∴△ABC 的周长为10. 【点睛】本题考查了根的判别式、根与系数的关系、一元二次方程的解、等腰三角形的性质以及三角形的三边关系,分a 为腰长及底边长两种情况考虑是解题的关键.8.已知:如图,在平面直角坐标系中,矩形AOBC 的顶点C 的坐标是(6,4),动点P 从点A 出发,以每秒1个单位的速度沿线段AC 运动,同时动点Q 从点B 出发,以每秒2个单位的速度沿线段BO 运动,当Q 到达O 点时,P ,Q 同时停止运动,运动时间是t 秒(t >0).(1)如图1,当时间t = 秒时,四边形APQO 是矩形;(2)如图2,在P ,Q 运动过程中,当PQ =5时,时间t 等于 秒;(3)如图3,当P ,Q 运动到图中位置时,将矩形沿PQ 折叠,点A ,O 的对应点分别是D ,E ,连接OP ,OE ,此时∠POE =45°,连接PE ,求直线OE 的函数表达式.【答案】(1)t =2;(2)1或3;(3)y =12x . 【解析】 【分析】先根据题意用t 表示AP 、BQ 、PC 、OQ 的长.(1)由四边形APQO 是矩形可得AP =OQ ,列得方程即可求出t .(2)过点P 作x 轴的垂线PH ,构造直角△PQH ,求得HQ 的值.由点H 、Q 位置不同分两种情况讨论用t 表示HQ ,即列得方程求出t .根据t 的取值范围考虑t 的合理性. (3)由轴对称性质,对称轴PQ 垂直平分对应点连线OC ,得OP =PE ,QE =OQ .由∠POE =45°可得△OPE 是等腰直角三角形,∠OPE =90°,即点E 在矩形AOBC 内部,无须分类讨论.要求点E 坐标故过点E 作x 轴垂线MN ,易证△MPE ≌△AOP ,由对应边相等可用t 表示EN ,QN .在直角△ENQ 中利用勾股定理为等量关系列方程即求出t . 【详解】∵矩形AOBC 中,C (6,4) ∴OB =AC =6,BC =OA =4依题意得:AP =t ,BQ =2t (0<t≤3) ∴PC =AC ﹣AP =6﹣t ,OQ =OB ﹣BQ =6﹣2t (1)∵四边形APQO 是矩形 ∴AP =OQ ∴t =6﹣2t 解得:t =2 故答案为2.(2)过点P 作PH ⊥x 轴于点H ∴四边形APHO 是矩形∴PH =OA =4,OH =AP =t ,∠PHQ =90° ∵PQ =5∴HQ 22PQ PH 3-=①如图1,若点H 在点Q 左侧,则HQ =OQ ﹣OH =6﹣3t ∴6﹣3t =3 解得:t =1②如图2,若点H 在点Q 右侧,则HQ =OH ﹣OQ =3t ﹣6 ∴3t ﹣6=3解得:t=3故答案为1或3.(3)过点E作MN⊥x轴于点N,交AC于点M∴四边形AMNO是矩形∴MN=OA=4,ON=AM∵矩形沿PQ折叠,点A,O的对应点分别是D,E∴PQ垂直平分OE∴EQ=OQ=6﹣2t,PO=PE∵∠POE=45°∴∠PEO=∠POE=45°∴∠OPE=90°,点E在矩形AOBC内部∴∠APO+∠MPE=∠APO+∠AOP=90°∴∠MPE=∠AOP在△MPE与△AOP中PME OAP90MPE AOPPE0P︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△MPE≌△AOP(AAS)∴PM=OA=4,ME=AP=t∴ON=AM=AP+PM=t+4,EN=MN﹣ME=4﹣t∴QN=ON﹣OQ=t+4﹣(6﹣2t)=3t﹣2∵在Rt△ENQ中,EN2+QN2=EQ2∴(4﹣t)2+(3t﹣2)2=(6﹣2t)2解得:t1=﹣2(舍去),t2=43∴AM=43+4=163,EN=4﹣43=83∴点E坐标为(163,83)∴直线OE的函数表达式为y=12x.【点睛】本题考查了矩形的判定和性质,勾股定理,轴对称的性质,全等三角形的判定和性质,解一元一次和一元二次方程.在动点题中要求运动时间t的值,常规做法是用t表示相关线段,再利用线段相等或勾股定理作为等量关系列方程求值.要注意根据t 的取值范围考虑方程的解的合理性.9.已知关于x 的方程230x x a ++=①的两个实数根的倒数和等于3,且关于x 的方程2(1)320k x x a -+-=②有实数根,又k 为正整数,求代数式2216k k k -+-的值. 【答案】0.【解析】【分析】 由于关于x 的方程x 2+3x +a =0的两个实数根的倒数和等于3,利用根与系数的关系可以得到关于a 的方程求出a ,又由于关于x 的方程(k -1)x 2+3x -2a =0有实数根,分两种情况讨论,该方程可能是一次方程、有可能是一元二次方程,又k 为正整数,利用判别式可以求出k ,最后代入所求代数式计算即可求解.【详解】解:设方程①的两个实数根分别为x 1、x 2则12123940x x x x a a +-⎧⎪⎨⎪-≥⎩=== , 由条件,知12121211x x x x x x ++==3, 即33a -=,且94a ≤, 故a =-1,则方程②为(k -1)x 2+3x +2=0,Ⅰ.当k -1=0时,k =1,x =23-,则22106k k k -=+-. Ⅱ.当k -1≠0时,∆=9-8(k -1)=17-6-8k ≥0,则178k ≤, 又k 是正整数,且k ≠1,则k =2,但使2216k k k -+-无意义. 综上,代数式2216k k k -+-的值为0 【点睛】本题综合考查了根的判别式和根与系数的关系,在解方程时一定要注意所求k 的值与方程判别式的关系.要注意该方程可能是一次方程、有可能是一元二次方程,10.定南县某楼盘准备以每平方米4000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米3240元的均价开盘销售.(1)求平均每次下调的百分率;(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?【答案】(1)10%;(2)方案②【解析】试题分析:首先设下调的百分率为x,根据题意列出方程进行求解,得出答案;分别求出两种方案所需要花费的钱数,然后进行比较.试题解析:(1)设平均每次下调的百分率是x,依题意得,4000(1-x)2=3240解之得:x=0.1=10%或x=1.9(不合题意,舍去)答:平均每次下调的百分率是10%.(2)方案①实际花费=100×3240×98%=317520元方案②实际花费=100×3240-100×80=316000元∵317520>316000 ∴方案②更优惠考点:一元二次方程的应用。

《一元二次方程》知识梳理及经典例题【知识梳理】考点一、概念(1)定义:①只含有一个未知数........,并且②未知数的最高次数是.........2.,这样的③整式方程....就是一元二次方程。
(2)一般表达式:ax2+bx+c=0(a≠0)⑶难点:如何理解“未知数的最高次数是2”:①该项系数不为“0”;②未知数指数为“2”;③若存在某项指数为待定系数,或系数也有待定,则需建立方程或不等式加以讨论。
考点二、方程的解⑴概念:使方程两边相等的未知数的值,就是方程的解。
⑵应用:利用根的概念求代数式的值;考点三、解法⑴方法:①直接开方法;②因式分解法;③配方法;④公式法⑵关键点:降次类型一、直接开方法:x2=m(m≥0),⇒x=±√m对于(x+a)2=m,(ax+m)2=(bx+n)2等形式均适用直接开方法类型二、因式分解法:(x−x1)(x−x2)=0⇒x=x1,或x=x2方程特点:左边可以分解为两个一次因式的积,右边为“0”,方程形式:如(ax+m)2=(bx+n)2,(x+a)(x+b)=(x+a)(x+c),x2+2ax+a2=0类型三、配方法ax2+bx+c=0(a≠0)⇒(x+b2a )2=b2−4ac4a2在解方程中,多不用配方法;但常利用配方思想求解代数式的值或极值之类的问题。
类型四、公式法⑴条件:(a≠0,且b2−4ac≥0)⑵公式:x=−b±√b2−4ac2a,(a≠0,且b2−4ac≥0)类型五、“降次思想”的应用⑴求代数式的值;⑵解二元二次方程组。
.考点四、根的判别式b2−4ac根的判别式的作用:①定根的个数;②求待定系数的值;③应用于其它。
考点五、应用解答题⑴“握手”问题;⑵“利率”问题;⑶“几何”问题;⑷“最值”型问题;⑸“图表”类问题考点六、根与系数的关系⑴前提:对于ax2+bx+c=0而言,当满足①a≠0、②Δ≥0时,才能用韦达定理。
⑵主要内容:x1+x2=−ba ,x1x2=ca⑶应用:整体代入求值。
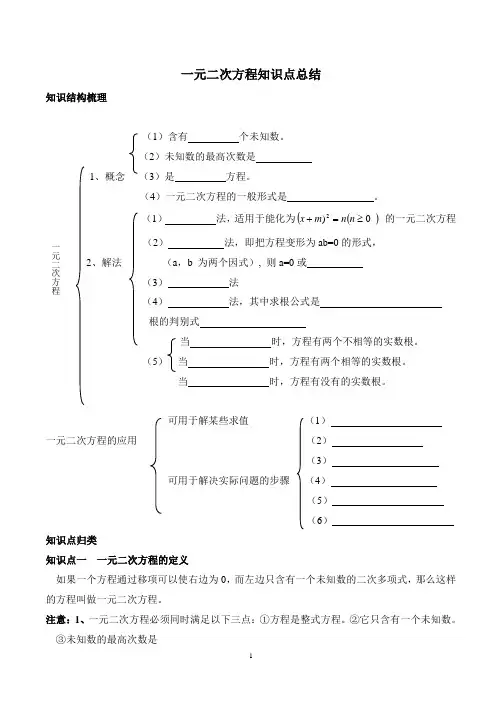
一元二次方程知识点总结知识结构梳理(1)含有 个未知数。
(2)未知数的最高次数是 1、概念 (3)是 方程。
(4)一元二次方程的一般形式是 。
(1) 法,适用于能化为)((0)2≥=+n n m x 的一元二次方程 (2) 法,即把方程变形为ab=0的形式,2、解法 (a ,b 为两个因式), 则a=0或(3) 法(4) 法,其中求根公式是 根的判别式当 时,方程有两个不相等的实数根。
(5) 当 时,方程有两个相等的实数根。
当 时,方程有没有的实数根。
可用于解某些求值 (1) 一元二次方程的应用 (2)(3)可用于解决实际问题的步骤 (4) (5)(6)知识点归类知识点一 一元二次方程的定义如果一个方程通过移项可以使右边为0,而左边只含有一个未知数的二次多项式,那么这样的方程叫做一元二次方程。
注意:1、一元二次方程必须同时满足以下三点:①方程是整式方程。
②它只含有一个未知数。
③未知数的最高次数是一元二次方程2、同时还要注意在判断时,需将方程化成一般形式。
例 下列关于x 的方程,哪些是一元二次方程?⑴3522=+x ;⑵062=-x x ;(3)5=+x x ;(4)02=-x ;(5)12)3(22+=-x x x知识点二 一元二次方程的一般形式一元二次方程的一般形式为02=++c bx ax (a ,b ,c 是已知数,0≠a )。
其中a ,b ,c 分别叫做二次项系数、一次项系数、常数项。
注意:(1)二次项、二次项系数、一次项、一次项系数,常数项都包括它前面的符号。
(2)要准确找出一个一元二次方程的二次项系数、一次项系数和常数项,必须把它先化为一般形式。
(3)形如02=++c bx ax 不一定是一元二次方程,当且仅当0≠a 时是一元二次方程。
例1 已知关于x 的方程()()021122=-+--+x m x m m 是一元二次方程时,则=m知识点三 一元二次方程的解使方程左、右两边相等的未知数的值叫做方程的解,如:当2=x 时,0232=+-x x 所以2=x 是0232=+-x x 方程的解。
中考数学一元二次方程组(大题培优易错难题)及详细答案一、一元二次方程1.已知:关于x的方程x2-4mx+4m2-1=0.(1)不解方程,判断方程的根的情况;(2)若△ABC为等腰三角形,BC=5,另外两条边是方程的根,求此三角形的周长.2【答案】(1) 有两个不相等的实数根(2)周长为13或17【解析】试题分析:(1)根据方程的系数结合根的判别式,可得出△=4>0,由此可得出:无论m 为何值,该方程总有两个不相等的实数根;(2)根据等腰三角形的性质及△>0,可得出5是方程x2﹣4mx+4m2﹣1=0的根,将x=5代入原方程可求出m值,通过解方程可得出方程的解,在利用三角形的周长公式即可求出结论.试题解析:解:(1)∵△=(﹣4m)2﹣4(4m2﹣1)=4>0,∴无论m为何值,该方程总有两个不相等的实数根.(2)∵△>0,△ABC为等腰三角形,另外两条边是方程的根,∴5是方程x2﹣4mx+4m2﹣1=0的根.将x=5代入原方程,得:25﹣20m+4m2﹣1=0,解得:m1=2,m2=3.当m=2时,原方程为x2﹣8x+15=0,解得:x1=3,x2=5.∵3、5、5能够组成三角形,∴该三角形的周长为3+5+5=13;当m=3时,原方程为x2﹣12x+35=0,解得:x1=5,x2=7.∵5、5、7能够组成三角形,∴该三角形的周长为5+5+7=17.综上所述:此三角形的周长为13或17.点睛:本题考查了根的判别式、等腰三角形的性质、三角形的三边关系以及解一元二次方程,解题的关键是:(1)牢记“当△>0时,方程有两个不相等的实数根”;(2)代入x=5求出m值.2.计算题(1)先化简,再求值:21xx-÷(1+211x-),其中x=2017.(2)已知方程x2﹣2x+m﹣3=0有两个相等的实数根,求m的值.【答案】(1)2018;(2)m=4【解析】分析:(1)根据分式的运算法则和运算顺序,先算括号里面的,再算除法,注意因式分解的作用;(2)根据一元二次方程的根的判别式求解即可.详解:(1)21xx-÷(1+211x-)=22211 11 x xx x-+÷--=()() 2211 1x xxx x+-⋅-=x+1,当x=2017时,原式=2017+1=2018(2)解:∵方程x2﹣2x+m﹣3=0有两个相等的实数根,∴△=(﹣2)2﹣4×1×(m﹣3)=0,解得,m=4点睛:此题主要考查了分式的混合运算和一元二次方程的根的判别式,关键是熟记分式方程的运算顺序和法则,注意通分约分的作用.3.解方程:233230 2121x xx x⎛⎫⎛⎫--=⎪ ⎪--⎝⎭⎝⎭.【答案】x=15或x=1【解析】【分析】设321xyx=-,则原方程变形为y2-2y-3=0, 解这个一元二次方程求y,再求x.【详解】解:设321xyx=-,则原方程变形为y2-2y-3=0.解这个方程,得y1=-1,y2=3,∴3121xx=--或3321xx=-.解得x=15或x=1.经检验:x=15或x=1都是原方程的解.∴原方程的解是x=15或x=1.【点睛】考查了还原法解分式方程,用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化,注意求出方程解后要验根.4.图1是李晨在一次课外活动中所做的问题研究:他用硬纸片做了两个三角形,分别为△ABC和△DEF,其中∠B=90°,∠A=45°,BC=,∠F=90°,∠EDF=30°, EF=2.将△DEF 的斜边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).(1)请回答李晨的问题:若CD=10,则AD= ;(2)如图2,李晨同学连接FC,编制了如下问题,请你回答:①∠FCD的最大度数为;②当FC∥AB时,AD= ;③当以线段AD、FC、BC的长度为三边长的三角形是直角三角形,且FC为斜边时,AD= ;④△FCD的面积s的取值范围是 .【答案】(1)2;(2)① 60°;②;③;④.【解析】试题分析:(1)根据等腰直角三角形的性质,求出AC的长,即可得到AD的长.(2)①当点E与点C重合时,∠FCD的角度最大,据此求解即可.②过点F作FH⊥AC于点H,应用等腰直角三角形的判定和性质,含30度角直角三角形的性质求解即可.③过点F作FH⊥AC于点H,AD=x,应用含30度角直角三角形的性质把FC用x来表示,根据勾股定理列式求解.④设AD=x,把△FCD的面积s表示为x的函数,根据x的取值范围来确定s的取值范围.试题解析:(1)∵∠B=90°,∠A=45°,BC=,∴AC=12.∵CD=10,∴AD=2.(2)①∵∠F=90°,∠EDF=30°,∴∠DEF=60°.∵当点E与点C重合时,∠FCD的角度最大,∴∠FCD的最大度数=∠DEF="60°."② 如图,过点F作FH⊥AC于点H,∵∠EDF=30°, EF=2,∴DF=. ∴DH=3,FH=.∵FC∥AB,∠A=45°,∴∠FCH="45°." ∴HC=. ∴DC=DH+HC=.∵AC=12,∴AD=.③如图,过点F作FH⊥AC于点H,设AD=x,由②知DH=3,FH=,则HC=.在Rt△CFH中,根据勾股定理,得.∵以线段AD、FC、BC的长度为三边长的三角形是直角三角形,且FC为斜边,∴,即,解得.④设AD=x,易知,即.而,当时,;当时,.∴△FCD的面积s的取值范围是.考点:1.面动平移问题;2.等腰直角三角形的判定和性质;3.平行的性质;4.含30度角直角三角形的性质;5.勾股定理;6.由实际问题列函数关系式;7.求函数值.5.解下列方程:(1)2x2-4x-1=0(配方法);(2)(x+1)2=6x+6.【答案】(1)x1=1x2=11=-1,x2=5.【解析】试题分析:(1)根据配方法解一元二次方程的方法,先移项,再加减一次项系数一半的平方,完成配方,再根据直接开平方法解方程即可;(2)根据因式分解法,先移项,再提公因式即可把方程化为ab=0的形式,然后求解即可.试题解析:(1)由题可得,x2-2x=12,∴x2-2x+1=32.∴(x-1)2=3 2 .∴x-1=.∴x1=1x2=1(2)由题可得,(x+1)2-6(x+1)=0,∴(x+1)(x+1-6)=0.∴x +1=0或x +1-6=0. ∴x 1=-1,x 2=5.6.有一个人患了流感,经过两轮传染后共有36人患了流感. (1)求每轮传染中平均一个人传染了几个人? (2)如果不及时控制,第三轮将又有多少人被传染? 【答案】(1)5;(2)180 【解析】 【分析】(1)设平均一人传染了x 人,根据有一人患了流感,经过两轮传染后共有36人患了流感,列方程求解即可;(2)根据每轮传染中平均一个人传染的人数和经过两轮传染后的人数,列出算式求解即可. 【详解】(1)设每轮传染中平均一个人传染了x 个人,根据题意得: x+1+(x+1)x =36,解得:x =5或x =﹣7(舍去).答:每轮传染中平均一个人传染了5个人; (2)根据题意得:5×36=180(个), 答:第三轮将又有180人被传染. 【点睛】本题考查一元二次方程的应用,解题的关键是能根据题意找到等量关系并列方程.7.观察下列一组方程:20x x -=①;2320x x -+=②;2560x x -+=③;27120x x -+=④;⋯它们的根有一定的规律,都是两个连续的自然数,我们称这类一元二次方程为“连根一元二次方程”.()1若2560x kx ++=也是“连根一元二次方程”,写出k 的值,并解这个一元二次方程; ()2请写出第n 个方程和它的根.【答案】(1)x 1=7,x 2=8.(2)x 1=n -1,x 2=n . 【解析】 【分析】(1)根据十字相乘的方法和“连根一元二次方程”的定义,找到56是7与8的乘积,确定k 值即可解题,(2)找到规律,十字相乘的方法即可求解. 【详解】解:(1)由题意可得k =-15,则原方程为x 2-15x +56=0,则(x -7)·(x -8)=0,解得x 1=7,x 2=8.(2)第n 个方程为x 2-(2n -1)x +n(n -1)=0,(x -n)(x -n +1)=0,解得x 1=n -1,x 2=n. 【点睛】本题考查了用因式分解法求解一元二次方程,与十字相乘联系密切,连根一元二次方程是特殊的十字相乘,中等难度,会用十字相乘解题是解题关键.8.关于x 的方程()2204kkx k x +++=有两个不相等的实数根. ()1求实数k 的取值范围;()2是否存在实数k ,使方程的两个实数根之和等于两实数根之积的算术平方根?若存在,求出k 的值;若不存在,说明理由.【答案】(1)1k >-且0k ≠;(2)不存在符合条件的实数k ,使方程的两个实数根之和等于两实数根之积的算术平方根. 【解析】 【分析】()1由于方程有两个不相等的实数根,所以它的判别式0>,由此可以得到关于k 的不等式,解不等式即可求出k 的取值范围.()2首先利用根与系数的关系,求出两根之和与两根之积,再由方程的两个实数根之和等于两实数根之积的算术平方根,可以得出关于k 的等式,解出k 值,然后判断k 值是否在()1中的取值范围内.【详解】解:()1依题意得2(2)404kk k =+-⋅>, 1k ∴>-, 又0k ≠,k ∴的取值范围是1k >-且0k ≠;()2解:不存在符合条件的实数k ,使方程的两个实数根之和等于两实数根之积的算术平方根,理由是:设方程()2204kkx k x +++=的两根分别为1x ,2x , 由根与系数的关系有:1212214k x x kx x +⎧+=-⎪⎪⎨⎪=⎪⎩,又因为方程的两个实数根之和等于两实数根之积的算术平方根,212k k +∴-=, 43k ∴=-,由()1知,1k >-,且0k ≠,43k ∴=-不符合题意,因此不存在符合条件的实数k ,使方程的两个实数根之和等于两实数根之积的算术平方根. 【点睛】本题重点考查了一元二次方程的根的判别式和根与系数的关系。
一元二次方程(一)、一元二次方程的概念1.理解并掌握一元二次方程的意义未知数个数为1,未知数的最高次数为2,整式方程,可化为一般形式;2.正确识别一元二次方程中的各项及各项的系数(1)明确只有当二次项系数0≠a 时,整式方程02=++c bx ax 才是一元二次方程。
(2)各项的确定(包括各项的系数及各项的未知数).3.一元二次方程的解的定义与检验一元二次方程的解(二)、一元二次方程的解法1.明确一元二次方程是以降次为目的,以配方法、开平方法、公式法、因式分解法等方法为手段,从而把一元二次方程转化为一元一次方程求解;2.根据方程系数的特点,熟练地选用配方法、开平方法、公式法、因式分解法等方法解一元二次方程;3.值得注意的几个问题:(1)开平方法:对于形如n x =2或)0()(2≠=+a n b ax 的一元二次方程,即一元二次方程的一边是含有未知数的一次式的平方,而另一边是一个非负数,可用开平方法求解.形如n x =2的方程的解法:当0>n 时,n x ±=;当0=n 时,021==x x ;当0<n 时,方程无实数根。
(2)配方法:通过配方的方法把一元二次方程转化为n m x =+2)(的方程,再运用开平方法求解。
配方法的一般步骤:①移项:把一元二次方程中含有未知数的项移到方程的左边,常数项移到方程的右边;②“系数化1”:根据等式的性质把二次项的系数化为1;③配方:将方程两边分别加上一次项系数一半的平方,把方程变形为n m x =+2)(的形式;④求解:若0≥n 时,方程的解为n m x ±-=,若0<n 时,方程无实数解。
(3)公式法:一元二次方程)0(02≠=++a c bx ax 的根aac b b x 242-±-= 当042>-ac b 时,方程有两个实数根,且这两个实数根不相等;当042=-ac b 时,方程有两个实数根,且这两个实数根相等,写为ab x x 221-==; 当042<-ac b 时,方程无实数根.公式法的一般步骤:①把一元二次方程化为一般式;②确定c b a ,,的值;③代入ac b 42-中计算其值,判断方程是否有实数根;④若042≥-ac b 代入求根公式求值,否则,原方程无实数根。
高中数学第二章一元二次函数方程和不等式易错题集锦单选题1、已知函数y=x−4+9x+1(x>−1),当x=a时,y取得最小值b,则a+b=()A.−3B.2C.3D.8答案:C分析:通过题意可得x+1>0,然后由基本不等式即可求得答案解:因为x>−1,所以9x+1>0,x+1>0,所以y=x−4+9x+1=x+1+9x+1−5≥2√(x+1)⋅9x+1−5=1,当且仅当x+1=9x+1即x=2时,取等号,所以y的最小值为1,所以a=2,b=1,所以a+b=3,故选:C2、已知正数x,y满足x+y=4,则xy的最大值()A. 2B.4C. 6D.8答案:B分析:直接使用基本不等式进行求解即可.因为正数x,y满足x+y=4,所以有4=x+y≥2√xy⇒√xy≤2⇒xy≤4,当且仅当x=y=2时取等号,故选:B3、不等式|5x−x2|<6的解集为()A.{x|x<2,或x>3}B.{x|−1<x<2,或3<x<6}C.{x|−1<x<6}D.{x|2<x<3}答案:B分析:按照绝对值不等式和一元二次不等式求解即可.解:∵|5x −x 2|<6,∴−6<5x −x 2<6∴{x 2−5x −6<0x 2−5x +6>0⇒{−1<x <6x 〈2或x 〉3⇒−1<x <2或3<x <6则不等式的解集为:{x|−1<x <2或3<x <6} 故选:B.4、若正数a,b 满足a +b =ab ,则a +2b 的最小值为( ) A .6B .4√2C .3+2√2D .2+2√2 答案:C分析:由a +b =ab ,可得1a +1b =1,则a +2b =(a +2b)(1a +1b ),化简后利用基本不等式可求得其最小值 因为正数a,b 满足a +b =ab , 所以1a +1b =1,所以a +2b =(a +2b)(1a +1b )=3+a b +2ba≥3+2√ab ⋅2b a=3+2√2, 当且仅当a b =2b a,即a =√2+1,b =2+√22时取等号,故选:C5、已知使不等式x 2+(a +1)x +a ≤0成立的任意一个x ,都满足不等式3x −1≤0,则实数a 的取值范围为( )A .(−∞,−13)B .(−∞,−13] C .[−13,+∞)D .(−13,+∞) 答案:C分析:使不等式x 2+(a +1)x +a ≤0成立的任意一个x ,都满足不等式3x −1≤0,则不等式x 2+(a +1)x +a ≤0的解集是(−∞,13]的子集,求出两个不等式的解集,利用集合的包含关系列不等式求解. 解:由3x −1≤0得x ≤13,因为使不等式x 2+(a +1)x +a ≤0成立的任意一个x ,都满足不等式3x −1≤0 则不等式x 2+(a +1)x +a ≤0的解集是(−∞,13]的子集,又由x 2+(a +1)x +a ≤0得(x +a )(x +1)≤0, 当a =1,x ∈{−1}⊆(−∞,13],符合;当a <1,x ∈[−1,−a ]⊆(−∞,13],则−a ≤13,∴1>a ≥−13, 当a >1,x ∈[−a,−1]⊆(−∞,13],符合, 故实数a 的取值范围为[−13,+∞).故选:C.6、设a >b >c >0,则2a 2+1ab +1a (a−b )−10ac +25c 2取得最小值时,a 的值为( ) A .√2B .2C .4D .2√5 答案:A解析:转化条件为原式=1ab +ab +1a(a−b)+a(a −b)+(a −5c)2,结合基本不等式即可得解.2a 2+1ab +1a (a −b )−10ac +25c 2 =1ab +ab +1a(a −b)+a(a −b)−ab −a(a −b)+2a 2−10ac +25c 2 =1ab +ab +1a(a −b)+a(a −b)+a 2−10ac +25c 2 =1ab +ab +1a(a −b)+a(a −b)+(a −5c)2 ≥2√1ab ⋅ab +2√1a(a−b)⋅a(a −b)+0=4,当且仅当{ab =1a(a −b)=1a =5c ,即a =√2,b =√22,c =√25时,等号成立.故选:A.小提示:易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件: (1) “一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.7、已知a >b >0,下列不等式中正确的是( ) A .ca >cb B .ab <b 2C .a −b +1a−b ≥2D .1a−1<1b−1 答案:C分析:由a >b >0,结合不等式的性质及基本不等式即可判断出结论. 解:对于选项A ,因为a >b >0,0<1a<1b,而c 的正负不确定,故A 错误;对于选项B ,因为a >b >0,所以ab >b 2,故B 错误;对于选项C ,依题意a >b >0,所以a −b >0,1a−b >0,所以a −b +1a−b ≥2√(a −b )×1a−b =2,故C 正确; 对于选项D ,因为a >b >0,a −1>b −1>−1,1a−1与1b−1正负不确定,故大小不确定,故D 错误; 故选:C.8、已知集合M ={x |−4<x <2},N ={x |x 2−x −6<0},则M ∩N = A .{x |−4<x <3}B .{x |−4<x <−2}C .{x |−2<x <2}D .{x |2<x <3} 答案:C分析:本题考查集合的交集和一元二次不等式的解法,渗透了数学运算素养.采取数轴法,利用数形结合的思想解题.由题意得,M ={x |−4<x <2},N ={x |−2<x <3},则 M ∩N ={x |−2<x <2}.故选C .小提示:不能领会交集的含义易致误,区分交集与并集的不同,交集取公共部分,并集包括二者部分. 多选题9、已知实数a >0,b >0,且满足(a −1)(b −1)=4,则下列说法正确的是( )A.ab有最小值B.ab有最大值C.a+b有最小值D.a+b有最大值答案:AC分析:已知等式化简为ab=a+b+3,利用基本不等式转化a+b,得到关于ab的不等式,研究可得ab的最值情况,转化ab,得到关于a+b的不等式,研究可得a+b的最值情况,进而作出判定.ab=a+b+3≥2√ab+3,解不等式得√ab≤−1或√ab≥3,故ab≥9,等号当且仅当a=b=3时取得,故ab有最小值9,则A对,B错;ab=a+b+3≤(a+b2)2,解不等式得a+b≤−2或a+b≥6,又a>0,b>0,故a+b≥6,当且仅当a=b=3时取等号,故a+b有最小值6,则C对,D错,故选:AC.10、(多选题)下列命题为真命题的是()A.若a>b>0,则ac2≥bc2B.若a<b<0,则a2>ab>b2C.若a>b>0且c>0,则ca2>cb2D.若a>b且1a>1b,则ab<0答案:ABD解析:由不等式的性质结合作差法,逐项判断即可得解.对于A,若a>b>0,则ac2−bc2=c2(a−b)≥0,即ac2≥bc2,故A正确;对于B,若a<b<0,则a2−ab=a(a−b)>0,ab−b2=b(a−b)>0,所以a2>ab>b2,故B正确;对于C,若a>b>0且c>0,则ca2−cb2=c(b2−a2)a2b2=c(b−a)(b+a)a2b2<0,所以ca2<cb2,故C错误;对于D,若a>b且1a >1b,则b−a<0,1a−1b=b−aab>0,所以ab<0,故D正确.故选:ABD.11、若正实数a,b满足a+b=1,则下列说法正确的是()A .ab 有最大值14B .√a +√b 有最大值√2C .1a +1b 有最小值4D .a 2+b 2有最小值√22 答案:ABC分析:由已知结合基本不等式及相关结论分别分析各选项即可判断.解:因为正实数a ,b 满足a +b =1,所以1=a +b ≥2√ab ,当且仅当a =b =12时取等号,所以ab ≤14,故ab 有最大值14,故A 正确;(√a +√b)2=a +b +2√ab =1+2√ab ≤1+2√14=2,当且仅当a =b =12时取等号,故√a +√b ≤√2,即√a +√b 有最大值√2,故B 正确; 1a+1b =a+b ab=1ab ≥4,当且仅当a =b =12时取等号,故1a +1b 有最小值4,故C 正确;a 2+b 2=(a +b )2−2ab =1−2ab ≥12,当且仅当a =b =12时取等号,所以a 2+b 2有最小值12,故D 错误. 故选:ABC .12、已知关于x 的不等式ax 2+bx +c ≥0的解集为{x |x ≤3或x ≥4},则下列结论中,正确结论的序号是( ) A .a >0B .不等式bx +c >0的解集为{x |x <−4}C .不等式cx 2−bx +a <0的解集为{x |x <−14或x >13}D .a +b +c >0答案:AD分析:由一元二次不等式的解集可确定a >0,并知ax 2+bx +c =0两根为3和4,利用韦达定理可用a 表示b,c ,由此将不等式中b,c 用a 替换后依次判断各个选项即可得到结果.对于A ,由不等式的解集可知:a >0且{−ba =3+4=7ca =3×4=12,∴b =−7a ,c =12a ,A 正确;对于B ,bx +c =−7ax +12a >0,又a >0,∴x <127,B 错误;对于C ,cx 2−bx +a =12ax 2+7ax +a <0,即12x 2+7x +1<0,解得:−13<x <−14,C 错误; 对于D ,a +b +c =a −7a +12a =6a >0,D 正确. 故选:AD.13、下列说法正确的是( )A .x +1x(x >0)的最小值是2B .2√x 2+2的最小值是√2C .2√x 2+4的最小值是2D .2−3x −4x 的最小值是2−4√3 答案:AB分析:利用基本不等式直接判断A,利用根式判断B,利用等号不成立判断C,利用特值判断D 当x >0时,x +1x≥2√x ⋅1x=2(当且仅当x =1x,即x =1时取等号),A 正确;2√x 2+2=√x 2+2,因为x 2≥0,所以2√x 2+2=√x 2+2≥√2,B 正确;2√x 2+4=2√x 2+4=√x 2+4√x 2+4≥2,当且仅当√x 2+4=√x 2+4,即x 2=−3时,等号成立,显然不成立,故C 错误;当x =1时,2−3x −4x =2−3−4=−5<2−4√3,D 错误. 故选:AB. 填空题14、已知x >54,则函数y =4x +14x−5的最小值为_______. 答案:7分析:由x >54,得4x −5>0,构造导数关系,利用基本不等式即可得到. 法一:∵x >54,∴4x −5>0,y =4x +14x−5=(4x −5)+14x−5+5≥2+5=7, 当且仅当4x −5=14x−5,即x =32时等号成立, 所以答案是:7.法二:∵x >54,令yʹ=4−4(4x−5)2=0得x =1或x =32, 当54<x <32时y′<0函数单调递减,当x >32时y′>0函数单调递增,所以当x =32时函数取得最小值为:4×32+14×32−5=7,所以答案是:7.【点晴】此题考基本不等式,属于简单题.15、已知x,y ∈(0,+∞),a ∈R ,若(x −y +sin 2α+1)(x +3y −2sin 2α)=2,则3x +y 的最小值为______. 答案:2分析:利用基本不等式即可求解.∵(x −y +sin 2α+1)(x +3y −2sin 2α)=2,∴4=(2x −2y +2sin 2α+2)(x +3y −2sin 2α)即4=(2x −2y +2sin 2α+2)(x +3y −2sin 2α) ≤(2x−2y+2sin 2α+2+x+3y−2sin 2α2)2=(3x+y+2)24,所以(3x +y +2)2≥16,解得3x +y ≥2,当且仅当2x −2y +2sin 2α+2=x +3y −2sin 2α时,取等号, 所以3x +y 的最小值为2. 所以答案是:2小提示:易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件: (1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方. 16、设a >0,b >0,给出下列不等式:①a 2+1>a ; ②(a +1a )(b +1b )≥4; ③(a +b )(1a +1b )≥4; ④a 2+9>6a . 其中恒成立的是________(填序号). 答案:①②③分析:利用做差法判断①,利用基本不等式判断②③,特殊值代入判断④即可得出结论. 由于a 2+1-a =(a −12)2+34>0,故①恒成立;由于(a +1a )(b +1b )=ab +1ab +b a +a b ≥2√ab ⋅1ab +2√b a ⋅ab =4, 当且仅当{ab =1abb a =a b 即a =b =1时等号成立,故②恒成立;由于(a +b )(1a +1b )=2+b a +a b ≥2+2√b a ×a b =4.当且仅当a b =ba ,那么a =b =1时等号成立,故③恒成立; 当a =3时,a 2+9=6a ,故④不恒成立. 综上,恒成立的是①②③. 所以答案是:①②③.小提示:本题主要考查了利用做差法和基本不等式以及特殊值代入的方法,判断不等式是否成立的问题.属于较易题. 解答题17、某旅游公司在相距为100km 的两个景点间开设了一个游船观光项目.已知游船最大时速为50km/ℎ,游船每小时使用的燃料费用与速度的平方成正比例,当游船速度为20km/ℎ时,燃料费用为每小时60元.其它费用为每小时240元,且单程的收入为6000元.(1)当游船以30km/ℎ航行时,旅游公司单程获得的利润是多少?(利润=收入−成本) (2)游船的航速为何值时,旅游公司单程获得的利润最大,最大利润是多少? 答案:(1)4750元;(2)游轮的航速应为40km/ℎ,最大利润是4800元.分析:(1)设游船的速度为v(km/ℎ),旅游公司单程获得的利润为y (元),根据利润=收入−成本建立函数关系式,所以y =6000−15v −24000v(0<v ⩽50),代入v =30km/ℎ即可求得;(2)利用基本不等式求出最大利润即可.解:(1)设游船的速度为v(km/ℎ),旅游公司单程获得的利润为y (元), 因为游船的燃料费用为每小时k ·v 2元,依题意k ·202=60,则k =320.所以y =6000−(320v 2·100v+240·100v)=6000−15v −24000v(0<v ⩽50).v =30km/ℎ时,y =4750元; (2)y =6000−15v −24000v⩽6000−2√15v ×24000v=4800,当且仅当15v =24000v,即v =40时,取等号.所以,旅游公司获得最大利润,游轮的航速应为40km/ℎ,最大利润是4800元. 18、设y =f (x )是定义在R 上的奇函数,且当x ≥0时,f (x )=2x −x 2. (1)求当x <0时,f (x )的解析式;(2)请问是否存在这样的正数a ,b ,当x ∈[a,b ]时,g (x )=f (x ),且g (x )的值域为[1b ,1a ]?若存在,求出a ,b 的值;若不存在,请说明理由.答案:(1)当x <0时,f (x )=x 2+2x (2)a =1,b =1+√52分析:(1)根据函数的奇偶性f (x )=−f (−x ),求解解析式即可;(2)根据题意,结合函数单调性,将问题转化为a ,b (0<a <b )是方程−x 2+2x =1x 的两个根的问题,进而解方程即可得答案.(1)当x <0时,−x >0,于是f (−x )=2(−x )−(−x )2=−2x −x 2. 因为y =f (x )是定义在R 上的奇函数,所以f (x )=−f (−x )=−(−2x −x 2)=2x +x 2,即f (x )=2x +x 2(x <0). (2)假设存在正实数a 、b ,当x ∈[a,b ]时,g(x)=f(x)且g(x)的值域为[1b ,1a ],根据题意,g (x )=−x 2+2x (x >0), 因为g (x )=−x 2+2x =−(x −1)2+1≤1 , 则0<1a≤1,得a ≥1.又函数g (x )在[1,+∞)上是减函数,所以{g(a)=1ag(b)=1b ,由此得到:a,b (1≤a <b )是方程−x 2+2x =1x 的两个根,解方程求得a =1,b =1+√52所以,存在正实数a =1,b =1+√52,当x ∈[a,b ]时,g(x)=f(x)且g(x)的值域为[1b ,1a ]。
一元二次方程综合一元二次方程易错题
一、填空题:
1、关于x的方程,当m 时,它是一元二次方程,当m= 时,它是一元一次方程,
2、方程的解是方程的根是
3 、若是一个完全平方式,则m为
4、关于x的一元二次方程有两个不相等的实数根,则k的取值范围 k<且k≠0
5、配方:
6、已知:方程,那么判别式的值为 -8
9、当 -6 时,方程的两根之差是7
10、若二次三项式在实数范围内不能因数分解,那么a的取值范围是
二、选择题
15、下列命题正确的是( B )
A 方程=一定无实数解 B方程若a,c同号,此方程没有实数根
C方程是一元二次方程 D方程没有数学根
三、解方程
1、 2、 3、
4、 5、 6、
四、解答题
1、证明:无论买m取何值,方程一定有两个不同的实数根。
2、关于x的方程有实数根,求k取值范围。
答:⑴.Δ=4-8-8m=-4-8m≥0
∴m≤-1/2
⑵x1x2=(m+1)/2 x1+x2=1
原不等式可改写成:
即3m+10>1 ∴m>-3 ∴m=-1或m=-2 答案由,得
∴=-,=-
故=()2-2==10
∴∴或,。
第二十一章 一元二次方程 易错必考68题(10个考点)专练易错必考题一、一元二次方程的一般形式1.(2023·全国·九年级专题练习)若关于x 的一元二次方程2(3)430m x x mx m +-+++=的常数项是6,则一次项是()A .x-B .1-C .x D .1【答案】A 【分析】根据一元二次方程定义可得36m +=,30m +¹,可得m 的值,再代入原方程,由此即可得结果.【详解】解:∵关于x 的一元二次方程2(3)430m x x mx m +-+++=的常数项是6,∴36m +=,30m +¹,解得:3m =,把3m =代入原方程可得2660x x -+=,∴一次项是x -,故选:A .【点睛】本题考查了一元二次方程的一般形式,解题的关键是熟练掌握一元二次方程的一般形式:一元二次方程的一般形式是20(0)ax bx c a ++=¹,其中,2ax 是二次项,bx 是一次项,c 是常数项.2.(2023春·八年级课时练习)将一元二次方程()11x x -=-化成()200ax bx c a ++=>的形式则a b c ++=.【答案】1【分析】直接利用一元二次方程的一般形式分析得出答案.【详解】解:将一元二次方程()11x x -=-化成一般形式20(0)ax bx c a ++=>之后,变为210x x -+=,故1,1,1a b c ==-=,1111a b c \++=-+=,故答案为:1.【点睛】此题主要考查了一元二次方程的一般形式,正确把握定义是解题关键.3.(2023·江苏·九年级假期作业)已知关于y 的一元二次方程()()223811my m my y y +-=-+,求出它各项的系数,并指出参数m 的取值范围.【答案】二次项系数是:28m -,一次项系数是:()31m --,常数项是:31m -;参数m 的取值范围是22m ¹±【分析】先将原方程化为一般式,再回答各项系数,根据“二次项系数不为零”可以求m 的取值范围.【详解】解:将原方程整理为一般形式,得:()()22383110m y m y m ---+-=,由于已知条件已指出它是一个一元二次方程,所以存在一个隐含条件280m -¹,即22m ¹±.可知它的各项系数分别是二次项系数是:28m -,一次项系数是:()31m --,常数项是:31m -.参数m 的取值范围是22m ¹±.【点睛】本题考查一元二次方程的一般式和系数、二次项系数不为零,掌握化一般式的方法是解题的关键.注意:在含参数的方程中,要认定哪个字母表示未知数,哪个字母是参数,才能正确处理有关的问题.易错必考题二、一元二次方程的解4.(2023春·吉林长春·八年级校考期末)如果关于x 的一元二次方程220ax bx ++=的一个解是1x =,则代数式2023a b --的值为( )A .2021-B .2021C .2025-D .2025【答案】D【分析】根据一元二次方程220ax bx ++=的一个解是1x =,得到20a b ++=即2a b +=-,代入计算即可.【详解】∵一元二次方程220ax bx ++=的一个解是1x =,∴20a b ++=,∴2a b +=-,∴2023202322025a b --=+=,故选D .【点睛】本题考查了一元二次方程的根,熟练掌握定义是解题的关键.5.(2023春·福建厦门·八年级厦门外国语学校校考期末)两个关于x 的一元二次方程20ax bx c ++=和20cx bx a ++=,其中a ,b ,c 是常数,且0a c +=,如果2x =是方程20ax bx c ++=的一个根,那么下列各数中,一定是方程20cx bx a ++=的根的是( )A .2B .2-C .1±D .1【答案】B【分析】利用方程根的定义去验证判断即可.【详解】∵0a ¹,0c ¹,0a c +=,∴a c=-∴1c a =-,∴20b c x x a a++=,210c b x x a a ++=,∴210b x x a +-=,210b x x a--=,∵2x =是方程20ax bx c ++=的一个根,∴2x =是方程210b x x a+-=的一个根,即32b a =-,∴2231102b x x x x a --=+-=,∴2x =-是方程210b x x a --=的一个根,即2x =-时方程20cx bx a ++=的一个根.故选:B .【点睛】本题考查了一元二次方程根的定义即使得方程两边相等的未知数的值,正确理解定义是解题的关键.6.(2023春·浙江金华·八年级统考期末)已知m 为方程2320230x x +-=的根,那么32220262023m m m +--的值为 .【答案】4046-【分析】先根据一元二次方程解的定义得到232023m m =-+,再用m 表示3m 得到()2220262023m m m +--,然后利用整体代入的方法计算.【详解】解:∵m 为方程2320230x x +-=的一个根,∴2320230m m +-=,∴232023m m =-+,∴()322220262023220262023m m m m m m +--=+--()()32023220262023m m m =-++--23620232023220262023m m m m =--++´--()33202392023m m =--+-+93202392023m m =-´-+4046=-,故答案为:4046-.【点睛】本题考查了一元二次方程的解,掌握整体代入的方法是解题关键.7.(2023春·浙江温州·八年级校考期中)已知a ,b ,c 是非零实数,关于x 的一元二次方程204c ax bx ++=,204b cx ax ++=,204a bx cx ++=,有公共解,则代数式2c a b ab b a--的值为 .【答案】2或1-【分析】设公共解为t ,根据一元二次方程根的定义得到204c at bt ++=,204b ct at ++=,204a bt ct ++=,三式相加可得:0abc ++=或12t =-,分别代入所求式可解答.【详解】解:设公共解为t ,则204c at bt ++=,204b ct at ++=,204a bt ct ++=,三式相加得()()204abc a b c t a b c t ++++++++=,即()2104a b c t t æö++++=ç÷èø,因为2211()042t t t ++=+³,所以0a b c ++=或12t =-,当0a b c ++=时,c a b =--,\原式222c a b ab--= 22222a ab b a b ab++--= 2=;当12t =-时,110424c a b -+=,110424b c a -+=,22c b a a b \=-=-,a b \=,\原式222244b ab a a b ab-+--=234b ab ab-= 22b b-= 1=-,综上,代数式2c a b ab b a--的值为2或1-.故答案为:2或1-.【点睛】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解,理解方程解的定义是解题的关键.8.(2023秋·江苏·九年级专题练习)已知x 是一元二次方程2810x x --=的实数根,求代数式24737123x x x x x +æö¸+-ç÷-+-èø的值.【答案】117【分析】利用一元二次方程的解可得出281x x -=,将其代入24737123x x x x x +æö¸+-ç÷-+-èø的化简结果中即可求出答案.【详解】解:∵x 是一元二次方程2810x x --=的实数根,∴281x x -=.24737123x x x x x +æö¸+-ç÷-+-èø()()247137233x x x x x x +=+---+-¸()()2497343x x x x x +--=¸---()()2416343x x x x x +-=¸---()()()()444343x x x x x x +-+=¸---()()()()433444x x x x x x +-=×--+-()()144x x =--21816x x =-+1116=+17∴代数式24737123x x x x x +æö¸+-ç÷-+-èø的值为117.【点睛】本题考查了一元二次方程的解、分式的化简等知识,熟练掌握一元二次方程的解的定义和分式的运算法则是解题的关键.9.(2023春·湖南长沙·八年级统考期末)请阅读下列材料:问题:已知方程210x x +-=,求一个一元二次方程,使它的根分别是已知方程根的2倍.解:设所求方程的根为y ,则2y x =,所以2y x =,把2y x =代入已知方程,得21022y y æö+-=ç÷èø;化简,得2240y y +-=;故所求方程为2240y y +-=.这种利用方程根的代换求新方程的方法,我们称为“换根法”;请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式):(1)已知方程2320x x +-=,求一个一元二次方程,使它的根分别为已知方程根的相反数;(2)已知关于x 的一元二次方程()200ax bx c a -+=¹有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.【答案】(1)2320y y --=(2)()200cy by a c -+=¹【分析】(1)设所求方程的根为y ,则y x =-,将x y =-代入已知方程2320x x +-=,化简即可得到答案;(2)设所求方程的根为y ,则1y x=,将其代入已知方程,然后化为一般形式即可得到答案.【详解】(1)解:设所求方程的根为y ,则y x =-,x y \=-,把x y =-代入已知方程2320x x +-=,得()()2320y y -+´--=,化简得,2320y y --=,\这个一元二次方程为:2320y y --=;(2)解:设所求方程的根为y ,则1y x=,y 把1x y=代入已知方程()200ax bx c a -+=¹,得2110a b c y y æö-×+=ç÷èø,去分母得,20a by cy -+=,若0c =,则20ax bx -=,于是方程()200ax bx c a -+=¹有一根为0,不符合题意,0c \¹,\所求方程为:()200cy by a c -+=¹.【点睛】本题考查了一元二次方程的解,解答该题的关键是弄清楚“换根法”的具体解题方法.易错必考题三、换元法解一元二次方程10.(2023秋·全国·九年级专题练习)若整数x ,y 使()()22221212x y x y +---=-成立,则满足条件的x ,y 的值有( )A .4对B .6对C .8对D .无数对【答案】C【分析】先化简()()22221212x y x y +---=-可得()()22221212x y x y éùéù+--+=-ëûëû,设22x y a +=,则()()1212a a --=-;然后求得a 的值,最后列举出符合题意的x ,y 的整数值即可解答.【详解】解:由()()22221212x y x y éùéù+--+=-ëûëû,设22x y a +=,则()()1212a a --=-,∴23100a a --=,即()()520a a -+=,解得:5a =或2a =-(舍弃),∴225x y +=.∴满足条件的x ,y 的整数值有:12x y =ìí=î,12x y =-ìí=î,12x y =ìí=-î,12x y =-ìí=-î,21x y =ìí=î,21x y =ìí=-î,21x y =-ìí=î,21x y =-ìí=-î,共8对.故选C .【点睛】本题主要考查了解一元二次方程、二元一次方程的解等知识点,掌握二元一次方程的解是解答本题的关键.11.(2023春·全国·八年级专题练习)用换元法解方程()()22212x x x x +++=时,如果设2x x y +=,那么原方程可变形为( )A .2120y y ++=B .2120y y --=C .2120y y -+=D .2120y y +-=【答案】D【分析】将原方程中的2x x +换成y ,再移项即可.【详解】解:根据题意,得212y y +=,即2120y y +-=;故选:D .【点睛】本题考查换元法解一元二次方程,换元法就是把某个式子看成一个整体,用一个字母去代替它,实行等量代换.12.(2023秋·全国·九年级专题练习)如果关于x 的方程20ax bx c ++=的解是11x =,23x =,那么关于y 的方程()21a y by c b -++=的解是 .【答案】12y =,24y =,【分析】根据关于x 的方程20ax bx c ++=的解是11x =,23x =,令关于y 的方程()()2110a y b y c -+-+=中1x y =-,即可得到112211y x y x -=ìí-=î,解这个方程组即可得到答案.【详解】解:∵()21a y by c b -++=,∴()()2110a y b y c -+-+=,Q 关于x 的方程20ax bx c ++=的解是11x =,23x =,令1x y =-,∴112211y x y x -=ìí-=î,∴1111y x -==或2213y x -==,解得12y =,24y =,故答案为:12y =,24y =.【点睛】本题考查换元法及一元二次方程解的定义,令关于y 的方程()()2110a y b y c -+-+=中1y x -=是解决问题的关键.13.(2023秋·全国·九年级专题练习)已知方程210210x x -+=的根为13x =,27x =,则方程2(21)10(21)210x x ---+=的根是.【答案】12x =,24x =【分析】设21x t -=,可得210210t t -+=,根据210210x x -+=的根为13x =,27x =,可得213x -=或217x -=,即可得到答案;【详解】解:设21x t -=,可得210210t t -+=,∵210210x x -+=的根为13x =,27x =,∴213x -=或217x -=,解得:12x =,24x =,故答案为12x =,24x =;【点睛】本题考查换元法求方程的解,解题的关键是设21x t -=,得到210210t t -+=,结合方程210210x x -+=的根为13x =,27x =.14.(2022秋·全国·九年级专题练习)阅读下列材料:问题:已知方程210x x +-=,求一个一元二次方程,使它的根分别是已知方程根的2倍.解:设所求方程的根为y ,则2y x =,所以2y x =,把2y x =,代入已知方程,得21022y y æö+-=ç÷èø.化简,得2240y y +-=,故所求方程为2240y y +-=这种利用方程根的代换求新方程的方法,我们称为“换根法”.请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式):(1)已知方程2210x x +-=,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为 ;(2)已知关于x 的一元二次方程()200ax bx c a ++=¹有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.【答案】(1)2210y y --=(2)20a by cy ++=()0c ¹【分析】(1)设所求方程的根为y ,则y x =-,所以x y =-,代入原方程即可得;(2)设所求方程的根为y ,则1y x =()0x ¹,于是1x y =()0y ¹,代入方程20ax bx c ++=整理即可得.【详解】(1)解:设所求方程的根为y ,则y x =-,所以x y =-,把x y =-代入方程2210x x +-=,得:2210y y --=,故答案为:2210y y --=;(2)解:设所求方程的根为y ,则1y x =()0x ¹,于是1x y=()0y ¹,把1x y =代入方程()200ax bx c a ++=¹,得2110a b c y y æöæö++=ç÷ç÷èøèø,去分母,得20a by cy ++=,若0c =,有20ax bx +=,于是,方程20ax bx c ++=有一个根为0,不合题意,∴0c ¹,故所求方程为20a by cy ++=()0c ¹.【点睛】本题主要考查一元二次方程的解,解题的关键是理解方程的解的定义和解题的方法.15.(2023秋·全国·九年级专题练习)阅读材料:为了解方程()22215140x x ---+=(),我们可以将21x -看作一个整体,设21x y -=,那么原方程可化为2540y y -+=①,解得121,4y y ==.当1y =,时,211x -=,∴22x =.∴2x =±;当4y =时,214x -=,∴25x =.∴5x =±.故原方程的解为12x =, 22x =-,35x =,45x =-.解答问题:(1)上述解题过程,在由原方程得到方程①的过程中,利用 法达到了降次的目的,体现了 的数学思想;(2)请利用以上知识解方程:()()222540x x x x +-++=;(3)请利用以上知识解方程:42340x x --=.【答案】(1)换元;转化(2)123411711715152222,,,x x x x -+---+--====(3)122,2x x ==-【分析】(1)利用换元法达到了降次的目的,体现了转化的数学思想;(2)利用换元法解方程即可;(3)利用换元法解方程即可.【详解】(1)解:利用了换元法,体现了转化思想;故答案为:换元,转化;(2)设2x x y +=,原方程可变为2540y y -+=,则()()410y y --=,∴40y -=或10y -=,∴124,1y y ==,当4y =时,24x x +=,解得1172x -±=,当1y =时,21x x +=,解得152x -±=,∴原方程的解为123411711715152222,,,x x x x -+---+--====;(3)设2y x =,原方程可变为2340y y --=,解得124,1y y ==-,∵20x ³,∴24x =,解得122,2x x ==-.【点睛】本题考查解一元二次方程.解题的关键是理解并掌握换元法解方程.易错必考题四、配方法的应用16.(2023春·山东威海·八年级统考期末)用配方法解方程2610x x --=,若配方后结果为2()x m n -=,则n 的值为( )A .10-B .10C .3-D .9【答案】B【分析】利用配方法将方程2610x x --=配成2()x m n -=,然后求出n 的值即可.【详解】∵2610x x --=,∴261x x -=,∴26919x x -+=+,即2(3)10x -=, 10n \=.故选:B .【点睛】本题主要考查了利用配方法解一元二次方程,熟练掌握配方法的步骤是解题的关键.17.(2023秋·全国·九年级专题练习)关于x 的一元二次方程新定义:若关于x 的一元二次方程:21()0a x m n -+=与22()0a x m n -+=,称为“同族二次方程”.如22(3)40x -+=与23(3)40x -+=就是“同族二次方程”.现有关于x 的一元二次方程:22(1)10x -+=与2(2)(4)80a x b x ++-+=是“同族二次方程”.那么代数式22015ax bx -++取的最大值是( )A .2020B .2021C .2022D .2023【答案】A【分析】利用“同族二次方程”定义列出关系式,再利用多项式相等的条件列出关于a 与b 的方程组,求出方程组的解得到a 与b 的值,进而利用非负数的性质确定出代数式的最大值即可.【详解】解:∵22(3)40x -+=与23(3)40x -+=就是“同族二次方程”,∴22(2)(4)8(2)(1)1a x b x a x ++-+=+-+,即22(2)(4)8(2)2(2)3a x b x a x a x a ++-+=+-+++,∴2(2)438a b a -+=-ìí+=î解得510a b =ìí=-î∴22015ax bx -++=25105201x x -+-=25(1)2020x -++,则代数式22015ax bx -++能取的最大值是2020.故选:A .【点睛】此题考查了配方法的应用,非负数的性质,以及一元二次方程的定义,弄清题中的新定义是解本题的关键.18.(2023秋·江苏·九年级专题练习)实数x 和y 满足2212521640x xy y y -+++=,则22x y -= .【答案】384【分析】将已知等式左边第三项拆项后,重新结合利用完全平方公式变形后,利用两非负数之和为0,得到两非负数分别为0,求出x 与y 的值,代入所求式子中计算,即可求出值.【详解】解:∵()()()()222222212521641236161646420x xy y y x xy y y y x y y -+++=+++-+++-==,∴60x y +=且420y -=,解得:12y =,3x =-,则22139844x y ==--,故答案为:384.【点睛】此题考查了完全平方公式的应用,熟练掌握完全平方公式是解本题的关键.19.(2023秋·全国·九年级专题练习)设m 为整数,且420m <<,方程222(23)41480x m x m m --+-+=有两个不相等的整数根,则m 的值是 .【答案】12【分析】将方程化为2(23)21x m m -+=+,根据m 为整数,且方程有两个不相等的整数根即可求解.【详解】解:222(23)(23)21x m x m m --+-=+,\[]2(23)21x m m --=+,\2(23)21x m m -+=+,Q 420m <<,92141m \<+<,\2(23)21x m m -+=±+,Q m 为整数,且方程有两个不相等的整数根,\当2125m +=时,符合题意,解得:12m =;故答案:12.【点睛】本题考查了一元二次方程的配方法,求参数的整数问题,掌握方法是解题的关键.20.(2023春·安徽池州·八年级统考期中)【阅读材料】把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.配方法在因式分解、最值问题中都有着广泛的应用.例如:①用配方法因式分解:268a a ++. ②求2611x x ++的最小值.解:原式2691a a =++- 解:原式2692x x =+++2(3)1a =+- 2(3)2x =++.()()3131a a =+-++ 2(3)0x +³Q ,()()24a a =++ 2(3)22x \++³,即2611x ++的最小值为2.请根据上述材料解决下列问题:(1)在横线上添上一个常数项使之成为完全平方式:24a a ++_______________.(2)因式分解:21232a a -+.(3)求2443x x ++的最小值.【答案】(1)4(2)(4)(8)a a --(3)2【分析】(1)根据常数项等于一次项系数的一半的平方进行配方即可;(2)将32化成364-,前三项配成完全平方式,再利用平方差公式进行因式分解即可;(3)将式子进行配方,再利用平方的非负性即可求解.【详解】(1)解:∵()22442a a a ++=+,故答案为:4;(2)解:21232a a -+【答案】(1)8;(2)见解析;(3)252【分析】(1)利用配方法把22410x x ++变形为22(1)8x ++,然后根据非负数的性质可确定代数式的最小值;(2)利用配方法得到22172()24x x x ++=++,则可判断220x x ++>,然后根据二次根式有意义的条件可判断无论x 取何实数,二次根式22x x ++都有意义;(3)利用三角形面积公式得到四边形ABCD 的面积12AC BD =××,由于10BD AC =-,则四边形ABCD 的面积()1102AC AC =××-,利用配方法得到四边形ABCD 的面积2125(5)22AC =--+,然后根据非负数的性质解决问题.【详解】解:(1)()2224102210x x x x ++=++()2221110x x =++-+ 22(1)8x =++,Q 无论x 取何实数,都有22(1)0x +³,2(1)88x \++³,即223x x ++的最小值为8;故答案为:8;(2)22172()24x x x ++=++,21()02x +³Q ,220x x \++>,\无论x 取何实数,二次根式22x x ++都有意义;(3)AC BD ^Q ,\四边形ABCD 的面积12AC BD =××,10AC BD +=Q ,10BD AC \=-,\四边形ABCD 的面积()1102AC AC =××- 2152AC AC =-+ 2125(5)22AC =--+21(5)02AC --£Q ,\当5AC =,四边形ABCD 的面积最大,最大值为252.【点睛】本题考查了配方法的应用:利用配方法把二次式变形为一个完全平方式和常数的和,然后利用非负数的性质确定代数式的最值.易错必考题五、一元二次方程中的因式分解22.(2022秋·上海普陀·八年级校考阶段练习)若关于x 的一元二次方程()221340a x x a a -+++-=的一个根是0,则a 的值是( )A .4a =-或1B .4a =-C .1a =D .0a =【答案】B【分析】根据一元二次方程的解的定义,把0x =代入()221340a x x a a -+++-=得2340a a +-=,再解关于a 的方程,然后利用一元二次方程的定义确定a 的值.【详解】解:把0x =代入()221340a x x a a -+++-=,得2340a a +-=,解得1a =或4a =-,而10a -¹,所以a 的值为4-.故选:B .【点睛】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.23.(2023秋·全国·九年级专题练习)对于两个不相等的实数a ,b ,我们规定符号{}max ,a b 表示a ,b 中的较大值,如:{}max 3,55=,因此,{}max 3,53--=-;按照这个规定,若{}2max ,35x x x x -=--,则x 的值是( )A .5B .5或16-C .1-或16-D .5或16+【答案】B【分析】根据题意进行分类讨论,当0x >时,可得2450x x --=,求出x 的值即可;当0x <时,可得2250x x --=求出x 的值即可.【详解】解:当0x >时,则0x x >>-,∴{}2max ,35x x x x x -==--,即2450x x --=,解得:125,1x x ==-(不符合题意,舍去),当0x <时,则0x x ->>,∴{}2max ,35x x x x x -=-=--,即2250x x --=,解得:116x =+(不符合题意,舍去),216x =-,综上:x 的值是5或16-,故选:B .【点睛】本题主要考查了新定义下的运算和解一元二次方程,解题的关键是正确理解题目所给新定义的运算法则,熟练掌握解一元二次方程的方法和步骤.24.(2022秋·全国·九年级专题练习)阅读下列解方程()2923x x -=-的过程,并解决相关问题.解:将方程左边分解因式,得()()()3323x x x +-=-,…第一步方程两边都除以()3x -,得32x +=,…第二步解得=1x -…第三步①第一步方程左边分解因式的方法是 ,解方程的过程从第 步开始出现错误,错误的原因是 ;②请直接写出方程的根为.【答案】 公式法 二 3x -可能为0 13x =,21x =-【分析】①根据公式法因式分解、等式的基本性质判断即可;②利用因式分解法求解即可.【详解】解:①第一步方程左边分解因式的方法是公式法,解方程的过程从第二步开始出现错误,错误的原因是:3x -可能为0,故答案为:公式法,二,3x -可能为0;②∵()2923x x -=-,∴()()()3323x x x +-=-,∴()()()33230x x x +---=,则()()310x x -+=,∴30x -=或10x +=,解得13x =,21x =-,故答案为:13x =,21x =-.【点睛】本题考查因式分解,解一元二次方程.运用平方差公式进行因式分解是解题的关键.25.(2023秋·江苏·九年级专题练习)已知:0a ¹且0b ¹,221003a b ab +-=,那么a b a b +-的值等于 .【答案】2-或2【分析】先把已知条件化为2231030a ab b -+=,再利用因式分解法得到30a b -=或30a b -=,然后把3b a =或3a b =分别代入a b a b+-中计算即可.【详解】解:∵221003a b ab +-=,即2231030a ab b -+=,∴(3)(3)0a b a b --=,∴30a b -=或30a b -=,当30a b -=时,即33,23a b a a b a a b a a ++===---;当30a b -=时,即33,23a b b b a b b b a b ++=-==-,∴a b a b+-的值等于2-或2.故答案为:2-或2.【点睛】本题考查了解一元二次方程﹣因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).26.(2022春·湖南长沙·九年级统考期末)已知关于x 的一元二次方程2430x x k -+=有实数根.(1)求k 的取值范围;(2)如果k 是符合条件的最大整数,且一元二次方程2(2)30m x x m -++-=与方程2430x x k -+=有一个相同的根,求此时m 的值.【答案】(1)43k £(2)95m =【分析】(1)一元二次方程有实数根,则0D ³,由此即可求解;(2)根据(1)中k 的取值范围求出k 的值,由此可求出方程2430x x k -+=的解,把x 的值代入一元二次方程2(2)30m x x m -++-=即可求解.【详解】(1)解:根据题意得:2(4)430k D =--´³,解得43k £,∴k 的取值范围43k £.(2)解:由(1)可知,43k £,∴k 的最大整数是1,∴方程2430x x k -+=可化为2430x x -+=,解得121,3x x ==,∵一元二次方程2(2)30m x x m -++-=与方程2430x x k -+=有一个相同的根,∴当1x =时,2130m m -++-=,解得2m =;当3x =时,(2)9330m m -´++-=,解得95m =,又20m -¹,∴95m =.【点睛】本题主要考查一元二次方程的知识,掌握一元一次方程的定义,有实根的计算方法,解一元二次方程的方法的知识是解题的关键.27.(2023春·江苏扬州·八年级统考期末)已知关于x 的一元二次方程22(21)0x m x m m -+++=.(1)求证:无论m 取何值,方程都有两个不相等的实数根;(2)如果方程的两个实数根为1x ,()212x x x >,且213x x +为整数,求整数m 所有可能的值.【答案】(1)见解析(2)4-或2-或0或2【分析】(1)根据方程的系数结合根的判别式,可得出10D =>,进而可证出方程有两个不相等的实数根;(2)解方程求出方程的两根为m ,1m +,得出11343111x m x m m ++==+++,然后利用有理数的整除性确定m 的整数值.【详解】(1)解:证明:Q 22[(21)]4()10m m m D =-+-´+=>,\无论k 取何值,方程都有两个不相等的实数根;(2)22(21)0x m x m m -+++=Q ,即()[(1)]0x m x m --+=,解得:x m =或1x m =+.\一元二次方程22(21)0x m x m m -+++=的两根为m ,1m +,12x x >Q ,11x m \=+,\11343111x m x m m ++==+++,如果311m ++为整数,则4m =-或2-或0或2,\整数m 的所有可能的值为4-或2-或0或2.【点睛】本题考查了根的判别式、解一元二次方程,解题的关键是:(1)牢记“当△0>时,方程有两个不相等的实数根”;(2)利用解方程求出m 的整数值.易错必考题六、根据一元二次方程根的情况求参数28.(2023春·内蒙古巴彦淖尔·九年级校考期中)若关于x 的一元二次方程2160x mx ++=有两个不相等的实数根,则实数m 的值可以是( )A .8B .8-C .4D .10【答案】D【分析】根据一元二次方程有两个相等的实数根,运用根的判别式进行解答即可.【详解】解:∵关于x 的一元二次方程2160x bx ++=,有两个不相等的实数根,∴22441160b ac m D =-=-´´>,∴264m >,∴8b >或8b <-,故选:D .【点睛】本题考查了一元二次方程根的判别式,熟知关于x 的一元二次方程20(0)ax bx c a ++=¹,若240b ac D =->,则原方程有两个不相等的实数根;若240b ac D =-=,则原方程有两个相等的实数根;若240b ac D =-<,则原方程没有实数根.29.(2023春·山东泰安·八年级统考期末)若关于x 的一元二次方程()22230k x x -++=有两个不相等的实数根,则k 的取值范围( )A .73k £B .73k >C .73k <且2k ¹D .73k £且2k ¹【答案】C【分析】根据一元二次方程的定义和根的判别式的意义得到 20k -¹且224(2)30,k D =--´>然后解两个不等式得到它们的公共部分即可;【详解】解:根据题意得 20k -¹ 且()2Δ24230k =--´>,解得 73k < 且 2k ¹,故选:C .【点睛】本题考查了根的判别式和一元二次方程的定义,能根据题意得出关于k 的不等式是解此题 的关键30.(2023·辽宁阜新·校联考一模)若关于x 的方程29304kx x --=有实数根,则实数k 的取值范围是( ).A .0k ¹B .1k ³-且0k ¹C .1k ³-D .1k >-且0k ¹【答案】C【分析】根据一元二次方程根的判别式即可求出答案.【详解】解:由题意可知:当0k ¹时,990k D =+³,∴1k ³-,当0k =时,原方程是一元一次方程,有实数根,∴1k ³-故选:B .【点睛】本题考查了一元二次方程20ax bx c ++= (0a a b c ¹,,,为常数)的根的判别式24b ac D =-,理解根的判别式对应的根的三种情况是解题的关键.当0D >时,方程有两个不相等的实数根;当Δ0=时,方程有两个相等的实数根;当Δ0<时,方程没有实数根.31.(2023春·广东广州·九年级统考开学考试)已知关于x 的一元二次方程()()212204a x a x a --++=没有实数根,且a 满足25113a a -<ìí-£î,则a 的取值范围是( )A .2a £-B .23a<-C .223a<-£-D .233<a<-且2a ¹【答案】C【分析】由所给方程是一元二次方程可知20a -¹,由方程没有实数根可知Δ0<,再解不等组,找出交集即可.【详解】解:Q 关于x 的一元二次方程()()212204a x a x a --++=没有实数根,\()()212426404a a a a D =+--´=+<,20a -¹,\23a <-,2a ¹,Q a 满足25113a a -<ìí-£î,由251a -<得3a <,由13a -£得2a ³-,\23a -£<,\223a<-£-,故选C .【点睛】本题考查一元二次方程的根的判别式、解不等式组,解题的关键是掌握一元二次方程的根的判别式,即Δ0<时,方程没有实数根;Δ0=时,方程有两个相等的实数根;0D >时,方程有两个不等的实数根.32.(2023秋·黑龙江哈尔滨·九年级哈尔滨市第四十七中学校考开学考试)已知关于y 的一元二次方程2230ky y -+=有实根,则k 的取值范围是 .【答案】13k £且0k ¹.【分析】根据一元二次方程的定义和根的判别式的意义得到0k ¹且△22120k =->,然后求出两不等式的公共部分即可.【详解】解:当0k ¹时,方程是一元二次方程,则△2(2)120k =--³有实数根,解得13k £且0k ¹.故答案为13k £且0k ¹.【点睛】本题主要考查了一元二次方程的定义和根与△=-24b ac 有如下关系:当△0>时,方程有两个不相等的实数根;当△0=时,方程有两个相等的实数根;当△0<时,方程无实数根.33.(2023春·浙江杭州·八年级校联考阶段练习)已知关于x 的一元一次方程360x -=与一元二次方程20x bx c ++=有一个公共解,若关于x 的一元二次方程2(36)0x bx c x ++--=有两个相等的实数解,则b c +的值为.【答案】3-【分析】先解方程360x -=得2x =,再把2x =代入方程20x bx c ++=得420b c ++=,接着根据方程有两个相等的实数解,得到2(3)4(6)0b c D =--+=,然后通过解方程组求出b 、c ,从而得到b c +的值.【详解】解:解方程360x -=得2x =,Q 关于x 的一元一次方程360x -=与一元二次方程20x bx c ++=有一个公共解,2x \=为方程20x bx c ++=的解,420b c \++=,Q 关于x 的一元二次方程2(36)0x bx c x ++--=有两个相等的实数解,\2(3)4(6)0b c D =--+=,把24c b =--代入得2(3)4(246)0b b ----+=,解得121b b ==-,当1b =-时,242c =-=-,123b c \+=--=-.故答案为:3-.【点睛】本题主要考查了一元二次方程的解与根的判别式关系:一元二次方程20(0)ax bx c a ++=¹的根与24b ac D =-有如下关系:当0D >时,方程有两个不相等的实数根;当Δ0=时,方程有两个相等的实数根;当Δ0<时,方程无实数根.34.(2023春·山东泰安·八年级校考阶段练习)已知关于x 的一元二次方程()21210a x x --+=有两个不相等的实数根,则a 的取值范围是 .【答案】2a <且1a ¹【分析】根据一元二次方程的定义结合根的判别式即可得出关于a 的一元一次不等式组,解之即可得出结论.【详解】解:Q 关于x 的一元二次方程2(1)210a x x --+=有两个不相等的实数根,\210Δ(2)4(1)0a a -¹ìí=--->î,解得:2a <且1a ¹.故答案为:2a <且1a ¹.【点睛】本题考查一元二次方程的定义、根的判别式以及解一元一次不等式组,根据一元二次方程的定义结合根的判别式列出关于a 的一元一次不等式组是解题的关键.35.(2023·辽宁抚顺·统考三模)若关于x 的方程2210kx x -+=有两个不相等的实数根,则k 的最大整数值是 .【答案】1-【分析】根据方程2210kx x -+=有两个不相等的实数根,得到()20,240k k ¹-->,确定符合题意的整数解即可.【详解】∵x 的方程2210kx x -+=有两个不相等的实数根,∴()20,240k k ¹-->,∴0,1k k ¹<,∵k 是整数,∴k 的最大整数值是1-,故答案为:1-.【点睛】本题考查了一元二次方程根的判别式,方程满足的条件,解不等式,熟练掌握根的判别式是解题的关键.36.(2022秋·上海普陀·八年级校考阶段练习)已知关于x 的方程24m x mx x m -=-.(1)有两个不相等的实数根,求m 的取值范围;(2)有两个相等的实数根,求m 的值,并求出此时方程的根;(3)有实根,求m 的最小整数值.【答案】(1)12m >-且0m ¹(2)12m =-,122x x ==-(3)0【分析】(1)分两种情况讨论:当0m =时,24m x mx x m -=-变成0x =;当0m ¹时,24m x mx x m -=-是一元二次方程,根据方程根的情况可得2Δ40b ac =->,求解即可;(2)当0m =时,24m x mx x m -=-变成0x =;当0m ¹时,24m x mx x m -=-是一元二次方程,根据方程根的情况可得2Δ40b ac =-=,求解即可;(3)当0m =时,24m x mx x m -=-变成0x =;当0m ¹时,24m x mx x m -=-是一元二次方程,根据方程根的情况可得2Δ40b ac =-³,求解即可.【详解】(1)解:24m x mx x m -=-,移项合并同类项得:2(1)04m x m x m -++=,当0m ¹时,24m x mx x m -=-是一元二次方程,由题意得:()22Δ41404m b ac m m éù=-=-+-´´>ëû,解得:12m >-;当0m =时,24m x mx x m -=-变成0x =,只有一个实数根,不符合题意;∴m 的取值范围是12m >-且0m ¹;(2)解:当0m =时,24m x mx x m -=-变成0x =,只有一个实数根,不符合题意;当0m ¹时,24m x mx x m -=-是一元二次方程,由题意得:()22Δ41404m b ac m m éù=-=-+-´´=ëû,解得:12m =-,把12m =-代入24m x mx x m -=-得:21110822x x ---=,整理得:2440x x ++=,解得:122x x ==-;(3)解:当0m =时,24m x mx x m -=-变成0x =,有一个实数根,符合题意,当0m ¹时,24m x mx x m -=-是一元二次方程,由题意得:()22Δ41404m b ac m m éù=-=-+-´´³ëû,解得:12m ³-,∴m 的最小整数值是0;【点睛】本题考查一元二次方程根的判别式,掌握24Δb ac =-与一元二次方程根的情况是解题的关键.37.(2023春·山东烟台·八年级统考期中)关于x 的一元二次方程2310kx x -+=有两个不相等的实数根.(1)求k 的取值范围.(2)是否存在k 的值,使k 为非负整数,且方程的两根均为有理数?若存在,请求出满足条件的k 的值;若不存在,请说明理由.。
一元二次方程知识点总结
考点一、一元二次方程
1、一元二次方程:含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
2、一元二次方程的一般形式:)0(02≠=++a c bx ax ,它的特征是:等式左边十一个关于未知数x 的二次 多项式,等式右边是零,其中2ax 叫做二次项,a 叫做二次项系数;bx 叫做一次项,b 叫做一次项系数;c 叫做常数项。
考点二、一元二次方程的解法
1、直接开平方法:
利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法。
直接开平方法适用于解形如b a x =+2)(的一元二次方程。
根据平方根的定义可知,a x +是b 的平方根,当0≥b 时,b a x ±=+,b a x ±-=,当b<0时,方程没有实数根。
2、配方法:
配方法的理论根据是完全平方公式2
22)(2b a b ab a +=+±,把公式中的a 看做未知数x ,并用x 代替,则有222)(2b x b bx x ±=+±。
配方法的步骤:先把常数项移到方程的右边,再把二次项的系数化为1,再同时加上1次项的系数的一半的平方,最后配成完全平方公式
3、公式法
公式法是用求根公式解一元二次方程的解的方法,它是解一元二次方程的一般方法。
一元二次方程)0(02≠=++a c bx ax 的求根公式: )04(2422≥--±-=ac b a
ac b b x 公式法的步骤:就把一元二次方程的各系数分别代入,这里二次项的系数为a ,一次项的系数为b ,常数项的系数为c 。
4、因式分解法
因式分解法就是利用因式分解的手段,求出方程的解的方法,这种方法简单易行,是解一元二次方程最常用的方法。
分解因式法的步骤:把方程右边化为0,然后看看是否能用提取公因式,公式法(这里指的是分解因式中的公式法)或十字相乘,如果可以,就可以化为乘积的形式
5、韦达定理
利用韦达定理去了解,韦达定理就是在一元二次方程中,二根之和等于-
a b ,二根之积等于a c ,也可以表示为x 1+x 2=-a b ,x 1 x 2=a
c 。
利用韦达定理,可以求出一元二次方程中的各系数,在题目中很常用。
考点三、一元二次方程根的判别式
根的判别式:
一元二次方程)0(02≠=++a c bx ax 中,ac b 42-叫做一元二次方程)0(02
≠=++a c bx ax 的根的判别式,通常用“∆”来表示,即ac b 42-=∆
I 当△>0时,一元二次方程有2个不相等的实数根;
II 当△=0时,一元二次方程有2个相同的实数根;
III 当△<0时,一元二次方程没有实数根。
考点四、一元二次方程根与系数的关系
如果方程)0(02≠=++a c bx ax 的两个实数根是21x x ,,那么a b x x -=+21,a
c x x =21。
也就是说,对于任何一个有实数根的一元二次方程,两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商。
考点五、一元二次方程的二次函数的关系
大家已经学过二次函数(即抛物线)了,对他也有很深的了解,好像解法,在图象中表示等等,其实一元二次方程也可以用二次函数来表示,其实一元二次方程也是二次函数的一个特殊情况,就是当Y 的0的时候就构成了一元二次方程了。
那如果在平面直角坐标系中表示出来,一元二次方程就是二次函数中,图象与X 轴的交点。
也就是该方程的解了
一元二次方程易错题
一、选择题
1、若关于x 的一元二次方程(m-1)x 2+5x+m 2-3m+2=0有一个根为0,则m 的值等于( )
A .1
B . 2
C . 1或2
D . 0
2、巴中日报讯:今年我市小春粮油再获丰收,全市产量预计由前年的45万吨提升到50万吨,设从前年到
今年我市的粮油产量年平均增长率为x ,则可列方程为( )
A .45250x +=
B .245(1)50x +=
C .250(1)45x -=
D .45(12)50x += 3、已知a b ,是关于x 的一元二次方程210x nx +-=的两实数根,则
b a a b +的值是( ) A .22n + B .22n -+ C .22n - D .2
2n -- 4、已知a 、b 、c 分别是三角形的三边,则(a + b)x2 + 2cx + (a + b)=0的根的情况是( )
A .没有实数根
B .可能有且只有一个实数根
C .有两个相等的实数根
D .有两个不相等的实数根
5、已知n m ,是方程0122=--x x 的两根,且8)763)(147(22=--+-n n a m m ,则a 的值等于 ( )
A .-5 B.5 C.-9 D.9
6、已知方程20x bx a ++=有一个根是(0)a a -≠,则下列代数式的值恒为常数的是( )
A .ab
B .
a b C .a b + D .a b - 7、112,022x x x x 下面对的一较小根为=--的估计正确的是 ( )
A .121-<<-x
B .011<<-x
C .101<<x
D .211<<x 8、关于x 的一元二次方程2210x mx m -+-=的两个实数根分别是12x x 、,且22127x x +=,则212()x x -的
值是( )
A .1
B .12
C .13
D .25
9、(中江县2011年初中毕业生诊断考试)某校九年级学生毕业时,每个同学都将自己的相片向全班其他同学
各送一张表示留念,全班共送了2450张相片,如果全班有x 名学生,根据题意,列出方程为( )
A . 2450)1(=-x x
B . 2450)1(=+x x
C . 2450)1(2=+x x
D . 24502
)1(=-x x 10、设a b ,是方程220090x x +-=的两个实数根,则22a a b ++的值为( )
A .2006
B .2007
C .2008
D .2009
11、对于一元二次方程ax 2+bx+c=0(a≠0),下列说法:
①若a+c=0,方程ax 2+bx+c=0必有实数根;
②若b 2
+4ac<0,则方程ax 2+bx+c=0一定有实数根;
③若a-b+c=0,则方程ax 2+bx+c=0一定有两个不等实数根;
④若方程ax 2+bx+c=0有两个实数根,则方程cx 2+bx+a=0一定有两个实数根.
其中正确的是( )
A .①②
B .①③
C .②③
D .①③④
二、填空题
1、若一元二次方程x 2-(a+2)x+2a=0的两个实数根分别是3、b ,则a+b = .
3、方程(x ﹣1)(x + 2)= 2(x + 2)的根是 .
4、关于x 的一元二次方程ax 2
+bx+1=0(a ≠0)有两个相等实根,求4-2)-(a ab 222b + 的值为___ ___. 5、在等腰△ABC 中,三边分别为a ,b ,c ,其中a=5,若关于x 的方程x 2+(b+2)x+6-b=0有两个相等的实数
根,则△ABC 的周长为_________.
6、已知关于x 的一元二次方程x 2-6x-k 2
=0(k 为常数).设x 1,x 2为方程的两个实数根,且x 1 +2x 2=14,则k 的值为________.
7、已知m 、n 是方程x 2-2003x+2004=0的两根,则(n 2-2004n+2005)与(m 2-2004m+2005)的积是 .。