09-10年度第一学期《自动控制原理》考卷A卷及答案
- 格式:doc
- 大小:870.04 KB
- 文档页数:12

《⾃动控制原理》试卷(期末A卷参考答案)试题编号:重庆邮电⼤学2009学年2学期《⾃动控制原理》试卷(期中)(A 卷)(闭卷)⼀、简答题(本⼤题共5⼩题,每⼩题4分,共20分) 1.传递函数定义及其主要性质。
答:线性定常系统在零初始条件下,输出量的拉⽒变换与输⼊量的拉⽒变换之⽐,称为传递函数。
(2分)主要性质:(每回答正确2个1分,全部正确2分)1)传递函数只适⽤于线性定常系统:由于传递函数是基于拉⽒变换,将原来的线性常系数微分⽅程从时域变换到复域,故只适⽤于线性定常系统。
2)传递函数是在零初始条件下定义的。
如果系统为⾮零初始条件,⾮零初始值V(s),则系统新的输⼊、输出关系为:Y(s)=G(s).U(s)+ V(s)3)传递函数只表⽰了系统的端⼝关系,不明显表⽰系统内部部件的信息。
因此对于同⼀个物理系统,如果描述的端⼝不同,其传递函数也可能不同;⽽不同的物理系统,其传递函数可能相同。
4)传递函数是复变量S 的有理真分式函数,分⼦多项式的次数n 低于或等于分母多项的次数m ,所有系数均为实数。
2.线性控制系统的稳定性定义。
答:如果线性控制系统在初始扰动的影响下,其动态过程随时间的推移逐渐衰减并趋于零或原平衡点,则称系统渐进稳定,简称稳定(3分),反之,如果在初始扰动下,系统的动态过程随时间的推移⽽发散,则不稳定。
(1分)3.闭环系统的零、极点位置对于时间响应性能的超调量、调节时间的有何影响?答:(1)超调量主要取决于闭环复数主导极点的衰减率21//ξξωσ-=d ,与其他闭环零、极点接近坐标原点的程度有关;(2分)(2)条件时间主要取决于靠近虚轴的闭环复数极点的实部绝对值ξωσ=,如果实数极点距离虚轴最近,并且它附近没有实数零点,则调节时间主要取决于该实数极点的模值。
(2分)4.对于⼀个给定的开环增益为o k 最⼩相位系统,说明采⽤频率⽅法和根轨迹法判断稳定性的统⼀性。
答:频率法判断系统稳定性时,当o k 较⼩时,其副相曲线在)(ωj Go 平⾯不包围(-1,j0)这点,系统稳定,随着o k 的增加,副相曲线包围(-1,j0)这点,系统不稳定。

自动控制原理试卷A(1)1.(9分)设单位负反馈系统开环零极点分布如图所示,试绘制其一般根轨迹图。
(其中-P 为开环极点,-Z ,试求系统的传递函数及单位脉冲响应。
3.(12分)当ω从0到+∞变化时的系统开环频率特性()()ωωj j H G 如题4图所示。
K 表示开环增益。
P 表示开环系统极点在右半平面上的数目。
v 表示系统含有的积分环节的个数。
试确定闭环系统稳定的K 值的范围。
4.(125.(156.(15分)某最小相位系统用串联校正,校正前后对数幅频特性渐近线分别如图中曲线(1)、(2)所示,试求校正前后和校正装置的传递函数)(),(),(21s G s G s G c ,并指出Gc (S )是什么类型的校正。
7.(15分)离散系统如下图所示,试求当采样周期分别为T=0.1秒和T=0.5秒输入)(1)23()(t t t r ⋅+=时的稳态误差。
题2图8.(12分)非线性系统线性部分的开环频率特性曲线与非线性元件负倒数描述曲线如下图所示,试判断系统稳定性,并指出)(1x N和G (j ω)的交点是否为自振点。
参考答案A(1)1、 根轨迹略,2、 传递函数)9)(4(36)(++=s s s G ;单位脉冲响应)0(2.72.7)(94≥-=--t ee t c tt 。
3、 根轨迹略。
衰减振荡时待定参数的取值范围为211+<<k ;单调衰减时待定参数的取值范围为21+≥k 。
6、校正前)101.0)(11.0(1)(1++=s s s s G ;校正后)101.0)(11.0)(1100()110(10)(1++++=s s s s s s G ;滞后校正网络)1100()110(10)(1++=s s s G 。
7、 脉冲传递函数110)(-=z T z G ,T=0.1时,2.0,1,,1==∞==*ss v p e k k p 。
T=0.5时系统不稳定。
8、 (a )系统不稳定,在A 、B 交点处会产生自振荡。


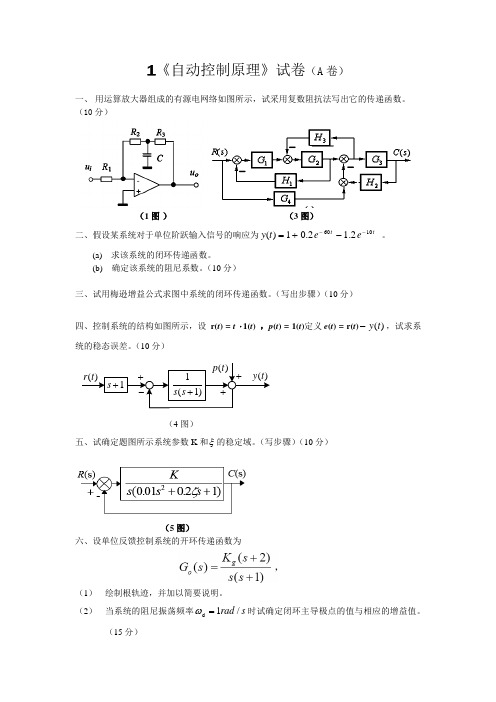
1《自动控制原理》试卷(A 卷)一、 用运算放大器组成的有源电网络如图所示,试采用复数阻抗法写出它的传递函数。
(10分)(1图 )(3图)二、假设某系统对于单位阶跃输入信号的响应为t te et y 10602.12.01)(---+= 。
(a) 求该系统的闭环传递函数。
(b) 确定该系统的阻尼系数。
(10分)三、试用梅逊增益公式求图中系统的闭环传递函数。
(写出步骤)(10分)四、控制系统的结构如图所示,设 r(t ) = t ⋅ 1(t ) ,p (t ) = 1(t )定义e (t ) = r(t ))(t y -,试求系统的稳态误差。
(10分))(t p )(t r -++)(t y 1+s )1(1+s s +(4图)五、试确定题图所示系统参数K 和ξ的稳定域。
(写步骤)(10分)(5图)六、设单位反馈控制系统的开环传递函数为(1) 绘制根轨迹,并加以简要说明。
(2) 当系统的阻尼振荡频率s rad /1d =ω时试确定闭环主导极点的值与相应的增益值。
(15分)七、最小相位系统的开环对数幅频特性的渐近线如图所示,确定系统的开环传递函数。
(10分)八、已知最小相位系统校正前后系统的折线对数幅频特性如图所示,其中Lo(ω)为校正前特性,L开(ω)为校正后特性。
(1)试作出校正装置的对数幅频特性Lc(ω)(折线);(2)试写出校正装置的传递函数Gc(s);(3)计算校正后系统的相位裕度γ。
(15分)cp为s右半平面上的开环根的个数,v为开九、设开环系统的奈氏曲线如下图所示,其中,环积分环节的个数,试判别闭环系统的稳定性。
(10分)(a)(b)2《自动控制原理》试卷(B 卷)一、 求下图所示系统的传递函数)(/)(0s U s U i 。
(10分)(1图) (3图)二、假设某系统对于单位阶跃输入信号的响应为t t e e t y 10602.12.01)(---+= 。
(a) 求该系统的闭环传递函数。

1《自动控制原理》试卷(A 卷)一、 用运算放大器组成的有源电网络如图所示,试采用复数阻抗法写出它的传递函数。
(10分)(1图 )(3图)二、假设某系统对于单位阶跃输入信号的响应为t t e e t y 10602.12.01)(---+= 。
(a) 求该系统的闭环传递函数。
(b) 确定该系统的阻尼系数。
(10分)三、试用梅逊增益公式求图中系统的闭环传递函数。
(写出步骤)(10分)四、控制系统的结构如图所示,设 r(t ) = t ⋅ 1(t ) ,p (t ) = 1(t )定义e (t ) = r(t ))(t y -,试求系统的稳态误差。
(10分)(4图)五、试确定题图所示系统参数K 和ξ的稳定域。
(写步骤)(10分)(5图)六、设单位反馈控制系统的开环传递函数为(1) 绘制根轨迹,并加以简要说明。
(2) 当系统的阻尼振荡频率s rad /1d =ω时试确定闭环主导极点的值与相应的增益值。
(15分)七、最小相位系统的开环对数幅频特性的渐近线如图所示,确定系统的开环传递函数。
(10分)八、已知最小相位系统校正前后系统的折线对数幅频特性如图所示,其中Lo(ω)为校正前特性,L开(ω)为校正后特性。
(1)试作出校正装置的对数幅频特性Lc(ω)(折线);(2)试写出校正装置的传递函数Gc(s);(3)计算校正后系统的相位裕度γ。
(15分)cp为s右半平面上的开环根的个数,v为开九、设开环系统的奈氏曲线如下图所示,其中,环积分环节的个数,试判别闭环系统的稳定性。
(10分)(a)(b)2《自动控制原理》试卷(B 卷)一、 求下图所示系统的传递函数)(/)(0s U s U i 。
(10分)(1图) (3图)二、假设某系统对于单位阶跃输入信号的响应为t t e e t y 10602.12.01)(---+= 。
(a) 求该系统的闭环传递函数。
(b) 确定该系统的阻尼系数。
(10分)三、系统的信号流图如图所示,求输出C (S )的表达式。
自动控制原理:参考答案及评分标准一、单项选择题(每小题1分,共20分)1. 系统和输入已知,求输出并对动态特性进行研究,称为(C)A. 系统综合B.系统辨识C.系统分析D.系统设计2. 惯性环节和积分环节的频率特性在(A )上相等。
A. 幅频特性的斜率B.最小幅值C.相位变化率D.穿越频率3. 通过测量输出量,产生一个与输出信号存在确定函数比例关系值的元件称为(C)A.比较元件B.给定元件C.反馈元件D.放大元件4. 3从0变化到时,延迟环节频率特性极坐标图为(A )A.圆B.半圆C椭圆 D.双曲线5. 当忽略电动机的电枢电感后,以电动机的转速为输出变量,电枢电压为输入变量时,电动机可看作一个(B )A.比例环节B.微分环节C.积分环节D.惯性环节6.若系统的开环传递函数为10s(5s 2)则它的开环增益为(A.1B.2C.5D.107.二阶系统的传递函数G(s)5~2s 2s 5则该系统是(A.临界阻尼系统B.欠阻尼系统8. 若保持二阶系统的Z不变,提咼3n,A.提高上升时间和峰值时间C.提高上升时间和调整时间9. 一阶微分环节G(s) 1 Ts,当频率A. 45 °B.-45°10. 最小相位系统的开环增益越大,其(A.振荡次数越多C. 过阻尼系统D.零阻尼系统则可以(B )B. 减少上升时间和峰值时间D. 减少上升时间和超调量卡时,则相频特性G(j )为(A )C. 90 °D.- 90°D )B. 稳定裕量越大D. 稳态误差越小11设系统的特征方程为D s s4 8s3217s 16s 50,则此系统(A )A.稳定B.临界稳定C.不稳定D.稳定性不确定。
12某单位反馈系统的开环传递函数为: G ss(s 1)(s 5),当k= ( C )时,闭环系统临界稳定。
B.20 C.30 D.4013.设系统的特征方程为Ds 3s310s 5s2s 2 0,则此系统中包含正实部特征的个数有(C )A.0B.1C.2D.316.稳态误差e ss 与误差信号E (s )的函数关系为(B )A.(-3,x )B.(0宀)C.(- x ,-3)D.(-3,0)20.在直流电动机调速系统中,霍尔传感器是用作( B )反馈的传感器。
课程名称: 自动控制理论 (A/B 卷 闭卷)试卷A一、填空题(每空 1 分,共15分)1、反馈控制又称偏差控制,其控制作用是通过 与反馈量的差值进行的。
2、复合控制有两种基本形式:即按 的前馈复合控制和按 的前馈复合控制。
3、两个传递函数分别为G 1(s)与G 2(s)的环节,以并联方式连接,其等效传递函数为()G s ,则G(s)为 (用G 1(s)与G 2(s) 表示)。
4、典型二阶系统极点分布如图1所示,则无阻尼自然频率=n ω ,阻尼比=ξ ,该系统的特征方程为 ,该系统的单位阶跃响应曲线为 。
5、若某系统的单位脉冲响应为0.20.5()105t t g t e e --=+,则该系统的传递函数G(s)为 。
6、根轨迹起始于 ,终止于 。
7、设某最小相位系统的相频特性为101()()90()tg tg T ϕωτωω--=--,则该系统的开环传递函数为 。
8、PI 控制器的输入-输出关系的时域表达式是 , 其相应的传递函数为 ,由于积分环节的引入,可以改善系统的 性能。
二、选择题(每题 2 分,共20分)1、采用负反馈形式连接后,则 ( )A 、一定能使闭环系统稳定;B 、系统动态性能一定会提高;C 、一定能使干扰引起的误差逐渐减小,最后完全消除;D 、需要调整系统的结构参数,才能改善系统性能。
2、下列哪种措施对提高系统的稳定性没有效果 ( )。
A 、增加开环极点;B 、在积分环节外加单位负反馈;C 、增加开环零点;D 、引入串联超前校正装置。
3、系统特征方程为 0632)(23=+++=s s s s D ,则系统 ( )A 、稳定;B 、单位阶跃响应曲线为单调指数上升;C 、临界稳定;D 、右半平面闭环极点数2=Z 。
4、系统在2)(t t r =作用下的稳态误差∞=ss e ,说明 ( )A 、 型别2<v ;B 、系统不稳定;C 、 输入幅值过大;D 、闭环传递函数中有一个积分环节。
⾃动控制原理科⽬考试题A卷(开卷)及答案级(学⽣填写):姓名:学号:命题:审题:审批: ------------------------------------------- 密 ---------------------------- 封 --------------------------- 线 ----------------------------------------------------------- (答题不能超出密封装订线)2009~2010学年第⼀学期控制⼯程基础科⽬考试题A 卷(开卷))(1s G------------------------------------------------------ 密 ---------------------------- 封 --------------------------- 线 ----------------------------------------------------------- 班级(学⽣填写):姓名:学号:3、6. 为2型系统,p K =∞, v K = ∞, a K =K=20当输⼊r( t )分别为1( t )、t 和t 2时,e ss 分别为0,0,1/10 ;当r(t)=1( t )+ t + t 2时,根据线性系统的叠加原理,e ss =0+0+1/10=1/10 。
1. 求下图所⽰电路的传递函数及微分⽅程(10分))1(11)()(212122Cs R R R R Cs R Cs R s U s U r c +-=+-= ; r 2c 1c21u R u R dtdu CR R -=+ 。
1、求下图所⽰电路的传递函数及微分⽅程(8分)。
⼀系统的开环传递函数为 G(S)H(S)=100/(10s+1)(2s+1)(0.2s+1) (1)绘制渐近对数幅频曲线图。
1)7. 试分别⽤幂级数法、部分分式法求以下函数的z 反变换并求x (3):(9分))2)(1()(--=z z zz X1)幂级数法+++-+--+--+-+---------------3213232121211127314151421767693232323z z z z z z z z z z z z z z z zz z,.....7)3(,3)2(,1)1(,0)0()(...73)2)(1()(0321=====+++=--=∑∞=----x x x x z k x z z z z z zz X k k2)、部分分式法21)2)(1(1)(-+--=--=z z z z z z X 11 21)(-+--=z zz z z X k z z z z z z 2]2[,1]1[11=- =- -- e(kT)=-1+2ke *(t)=e (0)δ(t )+e (T )δ(t -T )+e (2T )δ(t -2T )+…=0+1δ(t -T )+3δ(t -2T )+ 7δ(t -3T )+…⼀.填空题1、单输⼊单输出;线性定常系统。
安徽大学2009 —2010 学年第一 学期《自动控制理论》考试试卷(A 卷)(闭卷 时间120分钟)一、化简题(共15分)系统的结构图如图所示,试求该系统的闭环传递函数)()(s R s C 。
题 号一二三四五六七总分得 分阅卷人院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------得分得分二、简答题(共15分)设PI 控制系统如图所示,1K 是待定系数,ξ=0.2,n ω=86.6。
2(2)n n s s ωξω+R1C-1K s(1)用劳斯判据判断系统稳定时,请问1K 的取值范围?(5分)(2)若要求闭环系统的极点全部位于s=-1垂线之左,请问1K 的取值范围?(5分) (3)当输入21()2r t t=时,且1K =17.3时,请计算稳态误差值?(5分)三、绘图题(共15分)已知某单位反馈系统的开环传递函数 )2)(1(2)()(*++=s s s Ks H s G1. 试绘制其根轨迹图(10分)2. 确定系统稳定时的*K 值范围(5分)得分四、判断题(共15分) 已知系统开环传递函数为(1)()()(1)K s G s H s s Ts τ-+=+;,,0K T τ>试概略绘制系统的奈奎斯特曲线,并讨论系统的稳定性。
得分得分答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------五、设计题(共15分)设单位反馈系统的开环传递函数为:()(0.21)(0.06251)KG s s s s =++若要求校正后系统的静态速度误差系数40v K ≥,相角裕度为50︒,试设计串联校正装置。
并画出校正前后系统的Bode 图。
六、计算题(共10分)已知控制系统的结构图如下,其中已知量2121,,,T T k k 均大于零。
为提高系统的控制精度,使系统由Ⅰ型提高到Ⅲ型,加入了前馈校正1)(22++=s T bsas s G c ,试求b a ,值。
[已知)()()(t c t r t e -=]R (s ) k 1s (T 1s +1)k 2 E (s )122++s T bs asC (s )得分七、计算题(共15分)设离散系统如下图所示,其中ZOH 为零阶保持器,0.1,1T s K == 1. 试求静态误差系数 (5分)2. 求系统在t t r =)(作用下的稳态误差*()e ∞ (5分)3. 求系统的单位阶跃响应)(nT c (5分)答 题 勿 超 装 订 线 ------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------得分p v a K K K 、、安徽大学2009 —2010学年第 一学期《 自动控制理论》(A 卷)考试试题参考答案及评分标准一、系统的结构图如图所示,试求该系统的闭环传递函数)()(s R s C 。
解:图中有2条前向通路,5个回路,,,,112321211=∆==∆=G P G G P,,,,,22135342132212121H G H G L G L G G L H G G L H G L =-=-=-=-=,)(154321L L L L L ++++-=∆ 则有∆∆+∆=2211)()(P P s R s C2213321221123211H G H G G G G H G G H G G G G -+++++=二、(1)闭环传递函数为 21132223211()75007500()234.675007500n n n n s K s K s s s s K s s s K ωζωωω++Φ==++++++特征方程为321()34.6750075000D s s s s K =+++=列劳斯表如下:3210s s s s11134.634.67500750034.67500K K ⨯-1750075000K根据劳斯判据得到:1034.6K <<时,系统稳定。
(2)令s=s 1-1代入到原特征方程,得到新的特征方程:321111()(1)34.6(1)7500(1)75000D s s s s K =-+-+-+=整理得:321111()34.67433.875007466.40D s s s s K =+++-=()列劳斯表如下:3210ss ss11131.631.67433.875007466.431.675007466.4K K ⨯---()17433.875007466.4K -根据劳斯判据得到:1032.3K <<时,闭环系统的极点全部位于s=-1垂线之左。
(3)31()R s s =,单位反馈系统的误差传递函数()1()e s s Φ=-Φ故2321(34.6)()34.675007500s s e s s s s K +Φ=+++2332001320111(34.6)()lim ()()lim 34.675007500(34.6)34.61lim7500375034.675007500s s s s s E s sR s e s s s s s s K s K s s s K →→→+=Φ=++++===+++三、1.绘制根轨迹的典型步骤如下:(1) 开环极点为0,-1,-2,见图,它们是根轨迹各分支上的起点。
由于开环无有限零点,故根轨迹各分支都将趋向无穷。
(2) 一共有三个分支。
且根轨迹是对称实轴的。
(3) 定根轨迹的渐近线。
三根分支的渐近线方向,可按式(4-9)来求,即3)12()12(ππϕ+±=-+±=k m n k a (,2,1=k )因为当k 值变化时,相角值是重复出现的,所以渐近线不相同的相角值只有60o ,-60o 和180o 。
因此,该系统有三条渐近线,其中相角等于1800的一条是负实轴。
渐近线与实轴的交点按式(4-8)求,即131211-=--=-=--==∑∑m n mi zm n ni piia σ该渐近线如图中的细虚线所示。
(4) 确定实轴上的根轨迹。
在原点与-1点间,以及-2点的左边都有根轨迹。
(5) 确定分离点。
在实轴上,原点与-1点间的根轨迹分支是从原点和-1点出发的,最后必然会相遇而离开实轴。
分离点可按式计算,即0)2(1)1(11=--+--+s s s解得 423.0-=s 和577.1-=s因为10->>s ,所以分离点必然是423.0-=s (由于在-1和-2间实轴上没有根轨迹,故577.1-=s 显然不是要求的分离点)。
(6) 确定根轨迹与虚轴的交点。
应用劳斯稳定判据,可以确定这些交点。
因为所讨论的系统特征方程式为:0223*23=+++K s s s所以其劳斯阵列为:s 3 1 2s 2 3*2Ks 1 326*K - s 0 *2K使第一列中s 1项等于零,则求得*K 值为3*=K 。
解由s 2行得到的辅助方程063232*2=+=+s K s可求得根轨迹与虚轴的交点 2j s ±= 虚轴上交点的频率为2±=ω,与交点相应的增益值为3*=K 。
2.系统稳定时满足:30*<<K5.0=ζj ω× × ×5.0=ζ四、(1)奈奎斯特曲线系统开环频率特性为:222[()(1)]()()(1)K T j T G j H j T τωτωωωωω-+--=+开环幅相曲线的起点:(0),(0)90A ϕ++=∞=-︒终点:()0,()270A ϕ∞=∞=-︒与实轴的交点:令虚部为零,解得1()()xx x T G j H j K ωτωωτ⎧=⎪⎨⎪=-⎩因为()ϕω从90-︒单调递减至270-︒,故幅相曲线在第Ⅱ与第Ⅲ象限间变化。
开环概略幅相曲线如图所示实线。
由于系统是Ⅰ型系统,故还需从(0)(0)G j H j ++逆时针补画半径无穷大,圆心角为90-︒的圆弧,如图所示虚线。
K τ-ω(0)(0)G j H j ++j(2)稳定性讨论:由奈奎斯特判据ZP R =-,而0P =,当0R =时,得0Z =,系统稳定,此时1K τ<;1K τ=时,系统临界稳定;1K τ>时,系统不稳定。
五、(1)开环增益K 的确定:0lim ()40v s K sG s K →==≥,可取40K =,故待校正系统的开环传递函数为: 4040()(0.21)(0.06251)(/51)(/161)G s s s s s s s ==++++(2)校正前:5*4014.14c ω==900.20.062522c c arctg arctg γωω=︒--=-︒可知系统不稳定。
若选超前校正,可知校正后系统的''c ω会大于14.14,而原系统在16ω=之后相角下降很快,因此,可选滞后校正一试。
(3)选择''c ω:考虑''50555γ=︒+︒=︒,其中5︒为考虑滞后校正的滞后角度。
由:''900.20.062555c c arctg arctg γωω=︒--=︒,可计算在 2.4c ω=处有(2.4)55.83γ=︒,因此,可取:'' 2.4c ω=(4)确定滞后校正的参数b 和T 。
由:20lg ('')0c b L ω+=,可求得2.40.0640b ==由:10.1''c bT ω=,可求得69.44T =,由此可得:1/0.241()1/0.0141c bTs s G s Ts s ++==++(5)经验算,相角裕度满足要求。
六、由系统的结构以及已知参量)()()(t c t r t e -=得)()1(1)1)(1()()1()()()()(1212122121s R s T s k k s T s T s bs as k s T s k k s R s C s R s E +++++++-=-=)()1()1)(1()()1)(1()()1()1)(1()()1()()(2212122212212122221s R s T k k s T s T s bs as k s T s T s s R s T k k s T s T s bs as k s T k k s R s E +++++-++=+++++++-=要使系统的控制精度由由Ⅰ型提高到Ⅲ型,则有当221)(tt r =时,系统的稳态误差为0即:212222213210322121222100)1()(1*)1()1)(1()()1)(1()(k k s s b k s ak T T s T T s s T k k s T s T s bs as k s T s T s s s sE e s s s ss -+-++=+++++-++==→→→要使0=ss e ,则有⎩⎨⎧=-=-+0102221b k ak T T 成立,解得⎪⎪⎩⎪⎪⎨⎧=+=22211k b k T T a或者,求其等效开环传递函数,使复合校正后系统具有Ⅲ型控制精度,令分母的s 及s 平方项系数为零,得到同样结果七、1. 系统开环脉冲传递函数为⎥⎦⎤⎢⎣⎡------=⎥⎦⎤⎢⎣⎡+-=----))(1()1()1()1()1(1)1()(2121T T e z z z e z Tz z s s Z z z G 将1.0=T 代入并整理得[]11110.005(0.9)()(1)(0.905)0.005(0.9)lim 1()lim 1(1)(0.905)0.005(0.9)lim(1)()lim(1)0.1(1)(0.905)0p z z v z z a z G z z z z K G z z z z K z G z z z z K →→→→+=--⎡⎤+=+=+=∞⎢⎥--⎣⎦+=-=-=--=2.待求稳态误差()1v Te K ∞==3.)905.0)(1()9667.0(00484.011)1(1)1()(11.021+-+=⎥⎦⎤⎢⎣⎡----=⎥⎦⎤⎢⎣⎡+⋅-===---z z z e z e z T K s s Z K z z G K T T T901.09.1)9667.0(00484.0)(1)()(211.0+-+=+=Φ==z z z z G z G z K T901.0801.29.2)9667.0(00484.01901.09.1)9667.0(00484.0)()()(2322-+-+=-⋅+-+=⋅Φ=z z z z z z z z z z z R z z C1234560.004840.01870.04070.070.1060.148z z z z z z Λ------=++++++*()0.00484()0.0187(2)0.0407(3)0.07(4)0.106(5)0.148(6)c t t T t T t T t T t T t T δδδδδδΛ=-+-+-+-+-+-+。