第八章 北航 材料力学 全部课件 习题答案

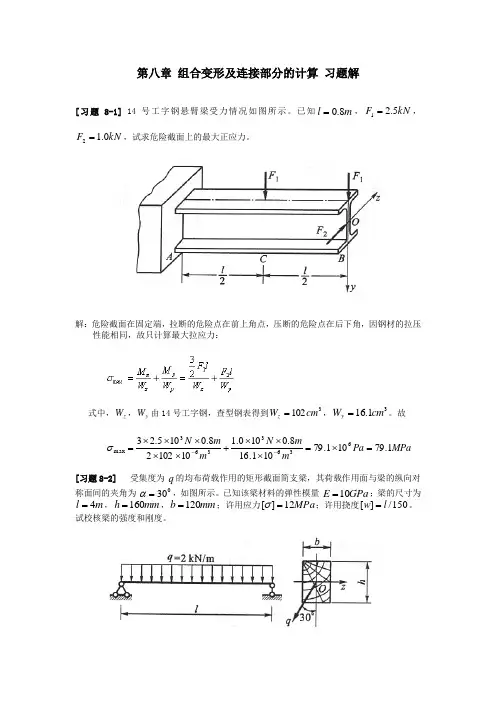
第八章 组合变形及连接部分的计算 习题解[习题8-1] 14号工字钢悬臂梁受力情况如图所示。

已知m l 8.0=，kN F 5.21=，kN F 0.12=，试求危险截面上的最大正应力。

解：危险截面在固定端，拉断的危险点在前上角点，压断的危险点在后下角，因钢材的拉压性能相同，故只计算最大拉应力：式中，z W ，y W 由14号工字钢，查型钢表得到3102cm W z =，31.16cm W y =。

故MPa Pa mm N m m N 1.79101.79101.168.0100.11010228.0105.236363363max=⨯=⨯⨯⨯+⨯⨯⨯⨯⨯=--σ [习题8-2] 受集度为 q 的均布荷载作用的矩形截面简支梁，其荷载作用面与梁的纵向对称面间的夹角为 030=α，如图所示。

已知该梁材料的弹性模量 GPa E 10=；梁的尺寸为m l 4=，mm h 160=，mm b 120=；许用应力MPa 12][=σ；许用挠度150/][l w =。

试校核梁的强度和刚度。

解：（1）强度校核)/(732.1866.0230cos 0m kN q q y =⨯== （正y 方向↓）)/(15.0230sin 0m kN q q z =⨯== （负z 方向←）)(464.34732.1818122m kN l q M y zmaz ⋅=⨯⨯== 出现在跨中截面)(241818122m kN l q M z ymaz ⋅=⨯⨯== 出现在跨中截面)(5120001601206161322mm bh W z =⨯⨯==)(3840001201606161322mm hb W y =⨯⨯==最大拉应力出现在左下角点上：yy z z W M W M maxmax max +=σ MPa mmmm N mm mm N 974.1138400010251200010464.33636max=⋅⨯+⋅⨯=σ因为 MPa 974.11max =σ，MPa 12][=σ，即：][max σσ<所以 满足正应力强度条件，即不会拉断或压断，亦即强度上是安全的。

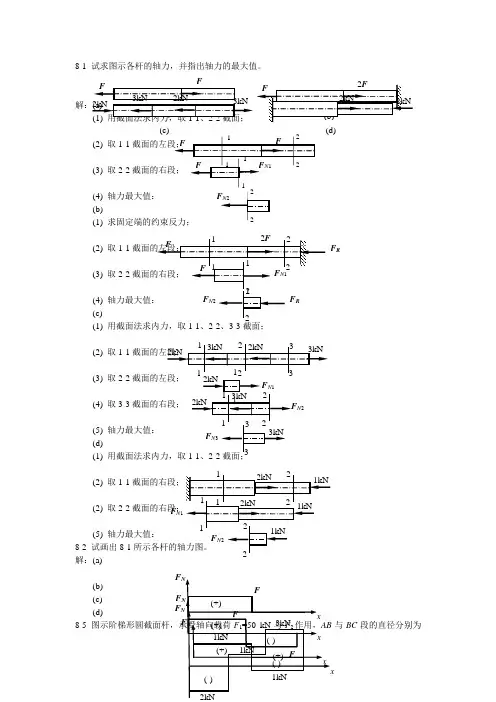
8-1 试求图示各杆的轴力，并指出轴力的最大值。

(2) 取1-1(3) 取2-2(4) 轴力最大值： (b)(1) 求固定端的约束反力； (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力，取1-1、2-2、3-3截面；(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段；(5) 轴力最大值： (d)(1) 用截面法求内力，取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值： 8-2 试画出8-1解：(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求载荷F 2之值。

解：(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求BC 段的直径。

解：(1)用截面法求出1-1、2-2截面的轴力；(2) 求1-1、2-2截面的正应力，利用正应力相同；8-7 图示木杆，承受轴向载荷F =10 kN 作用，杆的横截面面积A =1000 mm 2，粘接面的方位角θ= 450，试计算该截面上的正应力与切应力，并画出应力的方向。

解：(1) (2) 8-14 2=20 mm ，两杆F =80 kN 作用，试校核桁架的强度。

解：(1) 对节点A(2) 列平衡方程 解得： (2) 8-15 图示桁架，杆1A 处承受铅直方向的载荷F 作用，F =50 kN ，钢的许用应力[σS ] =160 MPa ，木的许用应力[σW ] =10 MPa 。

解：(1) 对节点A (2) 84 mm 。

8-16 题8-14解：(1) 由8-14得到的关系；(2) 取[F ]=97.1 kN 。

8-18 图示阶梯形杆A 2=100 mm 2，E =200GPa ，试计算杆AC 的轴向变形 解：(1) (2) AC 8-22 图示桁架，杆1与杆2的横截面面积与材料均相同，在节点A 处承受载荷F 作用。

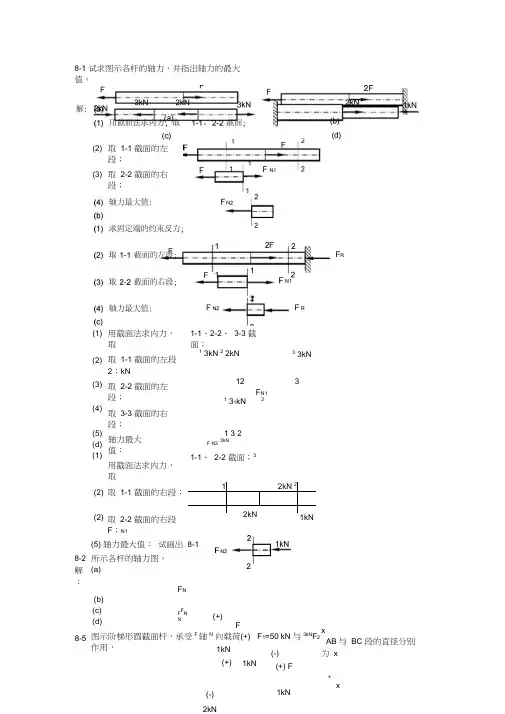
xx8-1 试求图示各杆的轴力，并指出轴力的最大值。

取 1-1 截面的左段；(2) (3) F N1取 2-2 截面的右段；F R用截面法求内力，取1-1、2-2、 3-3 截面；(1) (2) (3) (4)(5)(d)(1)取 1-1 截面的左段2；kN 取 2-2 截面的左段；取 3-3 截面的右段；轴力最大值： 用截面法求内力，取13kN 2 2kN33kN12 3F N11 31kN 21 32 F N33kN1-1、 2-2 截面；38-2 解：8-5 (2) (2) 取 1-1 截面的右段； 取 2-2 截面的右段F ；N112kN 22kN(5) 轴力最大值： 试画出 8-1所示各杆的轴力图。

(a) (b) (c) (d)F NF FN N(+)F图示阶梯形圆截面杆，承受F 轴N 向载荷(+) F 1=50 kN 与3kNF 2作用， 1kN (+) 1kN(-)(+) Fx AB 与 BC 段的直径分别为 x (-)1kN2kNd 1=20 mm 和 d 2=30 mm ，如欲使 AB 与 BC 段横截面上的正应力相同，试求载荷 F 2 之值。

(2) 求 1-1、 2-2 截面的正应力，利用正应力相同；8-7 图示木杆，承受轴向载荷 F=10 kN 作用，杆的横截面面积 A=1000 mm 2，粘接面的方位 角θ= 450，试计算该截面上的正应力与切应力，并画出应力的方向。

l 1l 2解： (1) 用截面法求 AB 、 BC 段的轴力；(2) 分段计F 算个杆向变形；FAC 杆缩短。

2F8-22 图示桁架，杆 1与A 杆 2的横截面面积与材料均相B 同，在节点 A 处承受C 载荷 F 作用。

从解： 8-6 解： (1) 用截面法求出 F 11-1、2-2 截面的轴力；(2) 求 1-1、 2-2 截面的正应A 力 ，利用正应力相B 同 ；题 8-5 图所示圆截面杆，已知载荷 1F 1=200 kN ，F 2=1020 kN ，CAB 段的直径 d 1=40 mm ，如 欲使 AB 与 BC 段横截面上的正应力相同，试求 BC 段的直径。

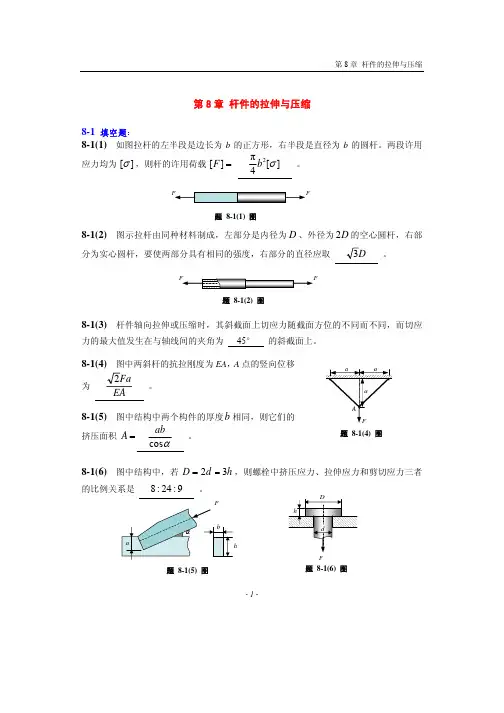
- 1 -第8章 杆件的拉伸与压缩8-1 填空题：8-1(1) 如图拉杆的左半段是边长为b 的正方形，右半段是直径为b 的圆杆。

两段许用应力均为 ][σ，则杆的许用荷载 =][F ][4π2σb 。

8-1(2) 图示拉杆由同种材料制成，左部分是内径为D 、外径为D 2的空心圆杆，右部分为实心圆杆，要使两部分具有相同的强度，右部分的直径应取 D3 。

8-1(3) 杆件轴向拉伸或压缩时，其斜截面上切应力随截面方位的不同而不同，而切应力的最大值发生在与轴线间的夹角为 45° 的斜截面上。

8-1(4) 图中两斜杆的抗拉刚度为EA ，A 点的竖向位移为EAFa 2 。

8-1(5) 图中结构中两个构件的厚度b 相同，则它们的挤压面积 =A αcos ab。

8-1(6) 图中结构中，若 h d D 32==，则螺栓中挤压应力、拉伸应力和剪切应力三者的比例关系是 9:24:8 。

题 8-1(5) 图题 8-1(1) 图题 8-1(2) 图题 8-1(6)图F题 8-1(4) 图- 2 -分析：222bs 3π4)(π4d F d D F =−=σ， 2tπ4d F =σ， 22π3πd F hd F ==τ，故有 9:24:883:1:31::tbs ==τσσ。

8-2 单选题：8-2(1) 图示的等截面杆左端承受集中力，右端承受均布力，杆件处于平衡状态。

1、3两个截面分别靠近两端，2截面则离端部较远。

关于1、2、3这三个截面上的正应力的下列描述中，正确的是 C 。

A ．三个截面上的正应力都是均布的 B ．1、2两个截面上的正应力才是均布的 C ．2、3两个截面上的正应力才是均布的 D ．1、3两个截面上的正应力才是均布的8-2(2) 若图示两杆的材料可以在铸铁和钢中选择，那么，综合强度和经济性两方面的因素， C 更为合理。

A ．两杆均选钢 B ．两杆均选铸铁C ．① 号杆选钢，② 号杆选铸铁D ．① 号杆选铸铁，② 号杆选钢8-2(3) 图示承受轴向荷载的悬臂梁中，在加载前的一条斜直线KK 在加载过程中所发生的变化是 D 。

材料力学_北京航空航天大学中国大学mooc课后章节答案期末考试题库2023年
1.一直杆轴向受拉压，横截面上只有轴力没有剪力，故横截面上只有正应力没
有切应力。

答案:
错误
2.一空心圆截面直杆，轴向受拉，其横截面内径变小。

答案:
正确
3.静不定结构中的压杆失稳之后，若外载荷继续增加，该压杆的轴向压力保持
不变（按照小挠度理论），但是压杆两端相对位移增加，可能导致其压弯组合破坏。

答案:
正确
4.利用对称性简化结构受力与变形分析，本质是直接确定结构对称面上的某些
内力与位移。

答案:
正确
5.如图所示两端固定阶梯型钢杆AC，左右两段长度相等，横截面面积
，当环境温度升高时，判断中间截面B的移动方向。

答案:
向右移动
6.组合梁的两种受载情况(1)和(2)如图所示。

下列结论中正确的是。

答案:
两者的Q图、M图均不同。

7.如图所示两端铰支等截面梁受均布荷载q作用，中央截面C处有弹簧支座，
其弹性系数为K。

以下4项判断中，正确的是。

(1) 该梁为一度静不定梁。

(2) 若解除中央截面C处的弹簧支座，则相应的变形协调条件是C截面向下
的挠度等于弹簧的压缩量。

(3) 若弹性系数，则中央支座相当于可动铰支座。

(4) 若，则梁AB相当于简支梁。

答案:
全部正确。

8.如图所示为T字形截面梁AD的横截面与弯矩图，z轴为形心轴，B截面和
C截面的弯矩大小相等、符号相反，则有。

答案:
最大拉应力位于截面C，最大压应力位于截面B。

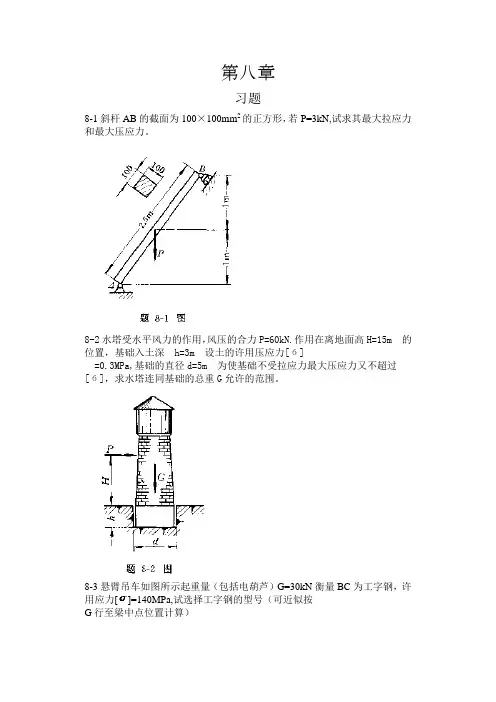
第八章习题8-1斜杆AB的截面为100×100mm2的正方形，若P=3kN,试求其最大拉应力和最大压应力。

8-2水塔受水平风力的作用，风压的合力P=60kN.作用在离地面高H=15m 的位置，基础入土深h=3m 设土的许用压应力[б]=0.3MPa,基础的直径d=5m 为使基础不受拉应力最大压应力又不超过[б]，求水塔连同基础的总重G允许的范围。

8-3悬臂吊车如图所示起重量（包括电葫芦）G=30kN衡量BC 为工字钢，许用应力[]=140MPa,试选择工字钢的型号（可近似按G行至梁中点位置计算）8-4如图所示，已知，偏心距，竖杆的矩形截面尺寸材料是3号钢，，规定安全系数=1.5。

试校核竖杆的强度。

8-5 若在正方形截面短柱的中间处开一个槽，使截面面积减小为原截面面积的一半，问最大压应力将比不开槽时增大几倍？8-6 图示一矩形截面杆，用应变片测得杆件上、下表面的轴向应变分别为材料的弹性模量。

（1）试绘制横截面的正应力分布图。

（2）求拉力P及其偏心距e的数值。

8-7 一矩形截面短柱，受图示偏心压力P作用，已知许用拉应力许用压应力求许用压力。

8-8 加热炉炉门的升降装置如图所示。

轴AB的直径d=4cm，CD为的矩形截面杆，材料都是Q235钢，已知力P=200N。

（1）试求杆CD的最大正应力；（2）求轴AB的工作安全系数。

提示：CD杆是压缩与弯曲的组合变形问题。

AB轴是弯曲与扭转的组合变形构件，E处是危险截面，M=154.5N*m,T=173.2N*m。

8-9 一轴上装有两个圆轮如图所示，P、Q两力分别作用于两轮上并处于平衡状态。

圆轴直径d=110mm，=60Mpa，试按照第四强度理论确定许用载荷。

8-10 铁道路标的圆信号板，装在外径D=60mm的空心圆柱上。

若信号板上作用的最大风载的强度p=2kPa,已知，试按第三强度理论选定空心柱的壁厚。

8-11 一传动轴其尺寸如图所示，传递的功率P=7kW，转速，齿轮I上的啮合力与齿轮结圆切线成的夹角，皮带轮Ⅱ上的两胶带平行，拉力为和，且。

《材料力学》课后习题答案详细在学习《材料力学》这门课程时，课后习题是巩固知识、加深理解的重要环节。

一份详细准确的课后习题答案，不仅能够帮助我们检验自己的学习成果，还能在遇到困惑时提供清晰的思路和正确的解法。

首先，让我们来谈谈材料力学中一些常见的概念和原理。

材料力学主要研究物体在受力作用下的变形、内力以及应力等情况。

例如，拉伸和压缩是常见的受力形式。

当一根杆件受到轴向拉力时，它会沿轴向伸长，同时横截面积会减小；而受到轴向压力时，则会沿轴向缩短，横截面积可能增大。

在这个过程中，我们需要计算内力、应力和应变，以评估杆件的强度和稳定性。

以一道典型的拉伸习题为例。

假设有一根圆截面的直杆，直径为d，长度为 L，受到轴向拉力 F 的作用。

我们首先需要计算横截面上的正应力。

根据公式，正应力等于内力除以横截面积。

内力就是所受的拉力 F，横截面积为πd²/4。

所以，正应力σ ＝ 4F ／（πd²) 。

接下来，计算杆的伸长量。

根据胡克定律，伸长量ΔL ＝ FL ／（EA) ，其中 E是材料的弹性模量，A 是横截面积。

再来看一道关于弯曲的习题。

有一矩形截面的梁，宽度为 b，高度为 h，承受一个集中力 P 作用在梁的中点。

这时候，我们需要计算梁横截面上的最大正应力。

通过分析可以知道，最大正应力出现在梁的上边缘或下边缘。

根据弯曲正应力公式，最大正应力σmax ＝ Mymax ／I ，其中 M 是弯矩，ymax 是离中性轴最远的距离，I 是惯性矩。

对于矩形截面，惯性矩 I ＝ bh³/12 。

在解答扭转习题时，也有相应的方法和公式。

例如，对于一个圆轴扭转的问题，我们要计算切应力和扭转角。

切应力的分布规律是沿半径线性分布，最大切应力在圆轴的外表面。

扭转角则可以通过公式计算得出。

在处理组合变形的习题时，情况会稍微复杂一些。

可能同时存在拉伸（压缩）、弯曲和扭转等多种变形。

这时候，需要分别计算每种变形引起的应力和应变，然后根据叠加原理进行综合分析。