非寿险费率厘定的索赔频率预测模型及其应用
- 格式:pdf
- 大小:553.60 KB
- 文档页数:6


车险费率厘定的索赔概率预测模型及其比较分析
卢志义;蔡静
【期刊名称】《河北工业大学学报》
【年(卷),期】2017(046)003
【摘要】广义线性模型和广义可加模型作为经典线性模型的扩展,近年来在非寿险精算中得到了广泛的应用.本文在对2种模型进行简介的基础上,将驾驶员的性别、车型等8个变量作为费率因子,分别建立了车险索赔发生概率估计的广义线性模型和广义可加模型,并选取瑞典瓦萨(Wasa)保险公司的车险数据对2种模型的估计效果进行比较分析.结果表明,对于离散型费率因子占绝大多数的车险数据,广义可加模型并不具有明显的优势.因此,在车险费率厘定实务中,若离散型费率因子较多,应选择结构相对简单的广义线性模型.
【总页数】7页(P56-62)
【作者】卢志义;蔡静
【作者单位】天津商业大学理学院,天津300134;天津商业大学理学院,天津300134
【正文语种】中文
【中图分类】F224.7;O212
【相关文献】
1.非寿险费率厘定的索赔频率预测模型及其应用 [J], 孟生旺;徐昕
2.面板数据下的线性混合模型及其在车险费率厘定中的应用 [J], 张连增;王皎
3.基于Tweedie类分布的广义可加模型在车险费率厘定中的应用 [J], 孙维伟
4.大额索赔条件下的车险费率厘定 [J], 张连增;王缔
5.P2P租车平台商业车险费率厘定方法与实证研究 [J], 肖陆祇;肖陆镝;杜平;刘小西
因版权原因,仅展示原文概要,查看原文内容请购买。


非寿险产品费率厘定精算准则目录第一章总则 (1)第二章原则与方法 (1)第三章风险因素 (4)第四章监控及报告 (7)第一章总则第一条为加强对保险公司非寿险产品费率厘定的监督管理,确保保险公司稳健经营和偿付能力充足,保护被保险人利益,根据《中华人民共和国保险法》和《保险公司管理规定》制定本指导原则。
第二条本指导原则所称保险公司,是指在中华人民共和国境内依法设立的经营财产保险业务的中资保险公司、中外合资保险公司、外资独资保险公司以及外国保险公司分支公司。
第三条凡是经营非寿险产品业务的保险公司,应当按照保险监督管理机构的规定,遵循非寿险精算的原理、方法和谨慎性原则,合理厘定非寿险产品费率。
第四条当本指导原则与任何法律法规或保险监督管理机构对于费率厘定的要求有所冲突时,应遵守法律法规或保险监督管理机构的规定。
因遵守法律或监管部门的规定而无法遵守本指导原则的规定,不属于违反本指导原则。
第二章原则与方法第五条经营非寿险产品业务,应该建立费率的管理制度,费率厘定的流程及配备相关的精算专业人员和必要地软硬件设备。
第六条费率厘定时应满足以下原则(一)费率是对未来风险转移成本的估计值。
(二)费率应反映所有风险转移的成本。
(三)费率应反映个体风险转移的成本。
(四)费率应当是合理的、适当的、充分的,并且是公平的。
第七条费率厘定过程中,除了考虑纯风险损失外,还需要考虑包括信用风险、操作风险等在内的各类风险。
除精算外,也应该听取承保、理赔、销售、法律、财务等领域专业人员的意见和建议。
第八条费率厘定应考虑其变化趋势:必须考虑过去的和未来的索赔成本、索赔频率、风险暴露、费用和保费的变化。
推荐使用动态财务分析,即在各变量互相关联的前提下,考虑未来的行为与环境的变化,进行预测分析。
第九条费率厘定时,需要考虑投保人、被保险人或相关人员的心理承受能力及经济支付能力。
第十条应当考虑到法律环境、经济环境和政府监管行为的变化对未来风险的影响。


分位数回归在非寿险产品费率厘定中的应用
郭念国;徐昕
【期刊名称】《统计与决策》
【年(卷),期】2010()24
【摘要】文章首先分析了非寿险产品费率厘定中的零索赔额现象;指出了线性回归模型和广义线性模型在非寿险产品费率厘定中存在的问题和不足;分析了分位数回归模型在非寿险产品费率厘定中的优点,并结合实例,给出了实证分析。
结果表明,分位数回归模型更能从整体上反映出费率厘定变量之间的关系及其对索赔额的影响。
【总页数】3页(P28-30)
【关键词】费率厘定;线性回归模型;广义线性模型;分位数回归
【作者】郭念国;徐昕
【作者单位】中国人民大学统计学院;河南工业大学理学院;中国保险监督管理委员会博士后科研工作站
【正文语种】中文
【中图分类】O212.1;F840.65
【相关文献】
1.广义线性混合模型及其在非寿险信度费率厘定中的应用 [J], 康萌萌
2.对非寿险级别费率厘定过程中损失率法的探究——基于同整体费率厘定的比较分析 [J], 汤志云
3.非寿险费率厘定中的分类费率因子研究 [J], 张俊岭;张俊峰
4.基于中位数回归模型非寿险精算中费率因子的显著性判别分析 [J], 郭念国
5.Copula函数在非寿险费率厘定中的应用 [J], 郭莲丽;李建勋
因版权原因,仅展示原文概要,查看原文内容请购买。

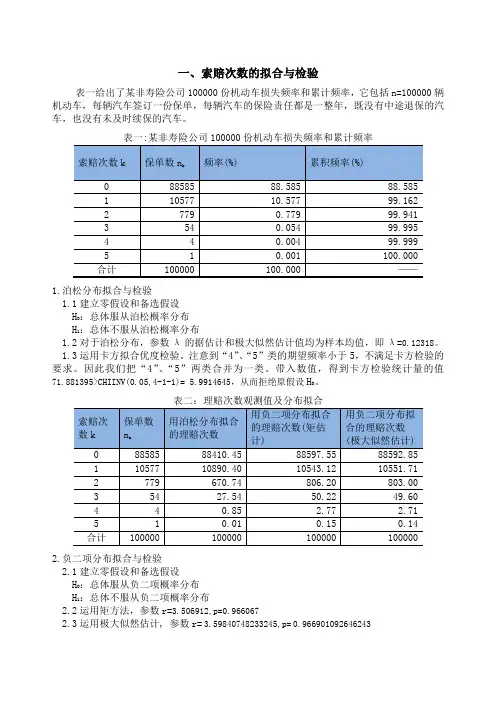
一、索赔次数的拟合与检验表一给出了某非寿险公司100000份机动车损失频率和累计频率,它包括n=100000辆机动车,每辆汽车签订一份保单,每辆汽车的保险责任都是一整年,既没有中途退保的汽车,也没有未及时续保的汽车。
1.泊松分布拟合与检验1.1建立零假设和备选假设H0:总体服从泊松概率分布H1:总体不服从泊松概率分布1.2对于泊松分布,参数λ的据估计和极大似然估计值均为样本均值,即λ=0.12318。
1.3运用卡方拟合优度检验。
注意到“4”、“5”类的期望频率小于5,不满足卡方检验的要求。
因此我们把“4”、“5”两类合并为一类。
带入数值,得到卡方检验统计量的值71.881395>CHIINV(0.05,4-1-1)= 5.9914645,从而拒绝原假设H0。
2.负二项分布拟合与检验2.1建立零假设和备选假设H0:总体服从负二项概率分布H1:总体不服从负二项概率分布2.2运用矩方法,参数r=3.506912,p=0.9660672.3运用极大似然估计, 参数r=3.59840748233245,p=0.966901092646243每个理赔次数类别下的期望频数=样本容量*理论频率,由此我们可以计算出负二项分布拟合的期望理赔频数,结果如表二所示。
与前相同,我们把“4”、“5”两类合并为一类。
带入数值,得到卡方检验统计量的值1.1365479<CHIINV(0.05,4-2-1)= 3.8414591,从而接受原假设H0。
显然,负二项分布是一个更优的结果。
Excel计算结果如下所示:二、损失分布的拟合与检验如下表所示, 给出了某非寿险公司近几年来的损失分布记录:3030 3120 9960 690 15660 6060 60605160 8160 2310 2970 1110 11460 15602310 9100 14910 360 435 3360 33606045 11760 6960 7860 660 1725 756012060 510 3960 3660 3210 8760 119552 3000 6000 8 0.228571 7.62E-053 6000 9000 8 0.228571 7.62E-054 9000 120005 0.142857 4.76E-055 12000 16000 3 0.085714 2.14E-05合计35画出频率分布直方图:1.对数正态分布拟合1.1对数正态分布拟合(矩估计法)建立零假设和备选假设H0:总体服从对数正态分布H1:总体不服从对数正态分布用K—S0.152400666,查表的显著性水平0.05下的临界值为0.22425,从而我们不能拒绝原假设H0,用对数正态分布拟合是合理的。

第五章经验费率厘定本章主要内容一、引言二、信度的含义三、有限波动信度四、贝叶斯方法五、一致最精确信度六、NCD系统例:假设某保险公司开发一新险种,保单组合由10位投保人构成。
开始,由于没有任何理赔经验数据,只能先验地假定他们具有相似的风险水平。
然后假定每一投保人每年至多引发一次理赔,且理赔额为1。
最初,根据同行业的损失水平,估计这一保单组合的保费为0.2,我们称这种保费为先验保费,或集体保费。
这样的估计是否符合实际情形,需要经验数据来验证。
为了搜集足够的理赔数据,保险公司连续追踪十年,采集的全部数据显示于下表。
请分析下表的数据,说明保费收取是否合理,该如何改进。
(1)总体平均理赔额为23/100=0.23。
(2)投保人9和1的理赔记录明显偏高,0.7与0.6的比例足以认为这二人的风险水平要劣于集体的风险水平;(3)投保人7、8和10无理赔记录,表明他们的风险水平又优于集体的风险水平。
经验费率厘定就是非寿险精算中用于消除风险子集的非同质性而发展起来的一类方法。
这些方法主要包括两大类:一类是在保险年度开始前,根据被保险人最近几个保险年度的理赔经验确定下一个保险年度的续期保费。
另一类是在保险年度末,根据被保险人当年的理赔经验来调整他在当年已经交纳的保险费。
二、信度与保费保费的构成)pure premium ⎧⎪⎧⎨⎨⎪⎩⎩纯保费(保险费完全附加保费(应付难以预料的确定性赔付)附加保费费用附加(支付经营费用,代理费用,税金等)纯保费是保险公司为了支付该保单在保险期间的期望赔付成本而收取的保险费。
可以分成两种情况考虑:(1)个别保单情形: ()i i p E C =,其中i p 表示第i 份保单的纯保费,()i E C 表示该保单的期望赔付成本。
(2)保单组合的情形设有N个同质的保单在观察时期内发生理赔,每一份保单的纯保费可以表示为()E SpN=, 其中()E S表示保单组合的总理赔额的期望,如200辆汽车总理赔额的期望为80000美元,则保费为80000400 200=⏹经验估费所谓经验费率厘定,就是在确定投保人的保费时,要考虑个人的理赔经验。

保险费制定的预测模型介绍随着社会的不断发展和进步,保险行业越来越成为人们生活中必不可少的部分。
保险公司需要根据风险进行保险费的制定,确定适当的价值水平。
然而,不同的保险公司采用的保险费率制定方法不同,其依赖的因素也不尽相同。
因此,开发方法来对保险费的制定进行预测是必不可少的。
本文将介绍一种预测保险费制定的预测模型——时间序列模型。
时间序列模型是一种分析数据变化趋势的方法,能够提供对未来数据值的预测。
在保险领域中,时间序列模型可以利用历史保险数据,预测未来保险费水平。
时间序列模型由三个重要的组成部分构成,即趋势(trend)、季节性(seasonality)和随机性(randomness)。
趋势是指数据值随着时间的推移而发生的持续性变化,季节性是指周期性变化的部分,而随机性则是指无规律变化的部分。
利用这些基本元素,我们可以建立时间序列模型来预测未来的保险费水平。
在建立时间序列模型时,我们需要首先确定时序数据中是否存在趋势、季节性和随机性。
如果存在以上三种元素,我们就可以根据时序数据中的趋势、季节性和随机性,建立相应的预测模型。
一般来说,我们可以采用一些方法来建立预测模型。
例如,我们可以利用平均值、加权平均值或指数平滑法等,来进行较为粗糙的预测。
这些方法的只能考虑到保险费制定的简单趋势,而没有考虑到可能存在的季节性和随机性,因此,它们的预测精度相对较低。
如果我们需要更加精确地预测未来保险费水平,我们可以采用较为复杂的时间序列预测方法,如“ARIMA模型”或“季节性ARIMA模型”。
这些方法可以更好地考虑到趋势、季节性和随机性因素,提高预测精度。
最后,我们还需要说明的是,预测模型并非万无一失,它所建立的预测结果是具有不确定性的,因此,我们还需要进行预测误差分析,防止其误导经营决策。
总之,时间序列模型是一种有效的预测保险费制定的方法。
它可以更好地考虑到不同因素的影响,提高预测精度,为保险公司的发展提供重要的决策支持。

互联网大数据时代的到来,为保险业的改革和发展创造了难得的机遇,保险业是数据依赖型企业,精算师的工作也是建立在数据分析的基础上,近年来互联网大数据不仅为精算师提供了方便的分析工具,也在改变着现有的精算技能和方法。
数据量的增加及获取难度的降低,为“预测模型”的建立提供了保障。
传统精算技术碰上大数据时代,撞出了许多火花,预测模型也越来越多地为精算师所使用。
保险业正值供给侧改革,费率市场化为公司转型和结构调整创造了空间,科学运用预测模型,为公司实现销售创新、差异化定价和精准风险管理等提供了重要的技术支持。
一、预测模型的使用传统的精算技术利用大数法则计算平均值,只能在静态环境下较低的维度来量化风险,很难充分地反映风险的复杂性,一旦未来环境变化因素变多,对结果的预测效果将会大打折扣。
而且对于一些具有高度相关性的数据缺乏甄别作用。
随着技术的发展,数据数量的增加以及获取难度的降低,目前精算师越来越多地采用预测模型的方法来分析结果,预测模型建模其实是一个多变量统计方法。
与传统精算方式相比,采用预测模型建模的方式有如下优势:∙可以有效消除单变量所造成的偏差;∙是一种能有效使用数据的方式;∙得到的不仅仅是平均值,更是一个体现出不确定性的统计结果;能更好的体现不同变量间的联系。
二、如何建立预测模型预测模型一般先根据结果的需要收集原始数据,将尽可能多维度的数据收集起来,理解数据,清洗数据,并根据需要把数据变形或拓展。
挑选有用的数据作为自变量,然后再利用模型将因变量和自变量联系起来,常用的有广义线性模型(Generalized Linear Model),决策树模型(Classification and Regression Tree)等。
建立模型之后还需要通过如双向提升图,累计收益图,实际/预测之比等的不同方式评估模型,验证有效后执行,从而在今后利用自变量信息直接通过模型计算出需要的结果。
三、预测模型运用举例(一)保证续保定期寿险退保率预测保证续保定期寿险,一般以10年期,20年期为主,在10年或20年这段保费固定期内每年缴纳固定的保费,过了固定期后可以不经过核保直接保证续保,有的可以续保成另一个10年期或20年期保证续保定期寿险,有的可以续保成每年续保定期寿险(Annually Renewable Term,以下简称ART)。