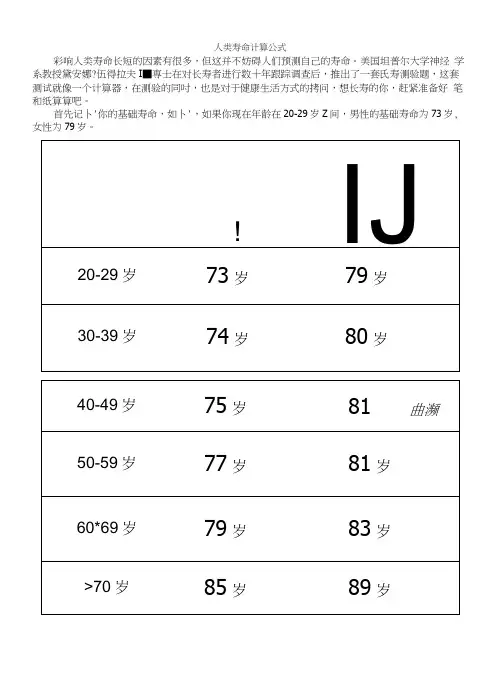
关于TM寿命推算方法
- 格式:doc
- 大小:524.50 KB
- 文档页数:6


预测寿命的计算公式
预测寿命可以使用以下一些计算公式:
1. 人均寿命计算公式:人均寿命=总寿命/人口数量。
其中,总寿命可以是某个国家、地区或全球的总年寿命,人口数量是指相应的人口总数。
2. 生命表法计算公式:生命表法根据不同年龄段的死亡率,预测一个人在不同年龄段的存活概率。
根据具体的生命表,可以计算出一个人出生后在某个年龄段存活的概率。
3. 危险系数法计算公式:危险系数法基于某一特定年龄段的死亡率,通过统计方法预测出未来某一特定年龄段的死亡率。
根据预测的死亡率,可以计算出未来某一特定年龄的预期寿命。
需要注意的是,以上的计算公式只是一种估计寿命的方法,实际的寿命受到多种因素的影响,包括遗传因素、生活方式、环境等。
因此,使用这些公式只能作为一种参考,不能准确预测个体的寿命。

关于TM21 LED寿命推算方法1、基础知识IES LM-80-08是用于测量LED光源光通维持率的方法,被广泛用于描述LED的光衰特性,LED器件生产厂家提供的LM-80-08测试报告(ES认可的测试机构测试)采用的数据都来至于持续测试6000h或更多时间内的测试数据,然而对于被测产品LM-80-08并没有很好的定义对于收集到的数据,如何被实际用于确定LED的有效寿命。
TM-21是Energy Star标准的技术备忘,补充了根据LM-80-08测试过程中获得的数据,来进行超出老化时间的寿命推算的方法。
额定光通维持寿命是指LED光源的光输出相对于初始光输出达到某一给定百分比所经过的运行时间,这个值被定义为Lp,p为给定的百分比值,业界常用LED光输出下降至初始光输出的70%所经过的时间来定义LED的寿命,LED达到其额定光通维持寿命取决于很多变量,包括运行温度、驱动电流、产品结构的设计和材料特性。
2、样品规模及测试数据采集对于从LM80报告中获得的所有针对某一特定产品的壳温、驱动电流等数据,都应用于流明维持寿命推算,推荐的样品规模集最小为20 pcs,并可以在流明维持寿命推算中,相对于寿命测试持续时间,LED推算寿命最大不超过6倍测试时间。
任何样品规模的改变都将导致不确定度及流明维持寿命推算的时间间隔的改变,对于样品规模为10~19pcs的情况,LED推算寿命最大不超过倍测试时间。
不支持样品规模小于10pcs的寿命推算。
从目前各厂家提供的LM80报告来看,样品规模多为20 pcs或25 pcs。
目前LM80 6000h报告中数据的采集时间间隔多为1000h,且很多厂家持续测试时间已超6000H,超6000H的附加测量可以提高流明维持寿命推算的准确性。
3、流明维持寿命推算方法目前LM80报告中采用最多的是对采集到的数据进行曲线拟合,以推算光通维持率衰减至70%所经历的时间,这个时间就是LED的流明维持寿命。

预测寿命的计算公式(一)预测寿命的计算公式1. 年龄预测公式•人类寿命计算公式•个体寿命计算公式2. 健康指数计算公式•常见健康指数计算公式•个体健康指数计算公式3. 寿命预测公式•基本寿命预测公式•个体寿命预测公式1. 年龄预测公式人类寿命计算公式人类寿命可以根据年龄预测公式进行估算。
一种常用的人类寿命计算公式是:寿命 = 平均寿命 - 实际年龄其中,平均寿命是指人群在一定时间内的平均寿命,实际年龄是指个体的实际年龄。
举个例子,如果平均寿命为80岁,而某个人的实际年龄为50岁,则该人的预测寿命为:寿命 = 80 - 50 = 30岁个体寿命计算公式个体的寿命也可以根据年龄预测公式进行预测,但需要考虑个体的各项关键因素。
一个简单的个体寿命计算公式如下:寿命 = 平均寿命 - 实际年龄 + 健康指数其中,平均寿命同样是指人群在一定时间内的平均寿命,实际年龄是指个体的实际年龄,健康指数是衡量个体健康程度的量化指标。
2. 健康指数计算公式常见健康指数计算公式健康指数是评估个体健康状况的重要指标之一。
常见的健康指数计算公式包括:•BMI(身体质量指数)计算公式:BMI = 体重(kg)/ 身高(m^2)•悬崖指数计算公式:悬崖指数 = (年龄 - 30) *•健康生活方式指数计算公式:健康生活方式指数 = 运动时间(小时) + 睡眠时间(小时) + 饮食均衡指数个体健康指数计算公式个体的健康指数可以根据其特定情况进行计算。
一个常见的个体健康指数计算公式如下:健康指数 = 基础健康指数 + 遗传因素调整 + 环境因素调整其中,基础健康指数是个体在没有其他调整因素的情况下的健康指数,遗传因素调整和环境因素调整分别是根据遗传因素和环境因素对基础健康指数进行调整得出的量化指标。
3. 寿命预测公式基本寿命预测公式基本寿命预测公式是预测人群寿命的常用模型之一。
一个简单的基本寿命预测公式如下:寿命 = 人均预期寿命 + 其他调整因素其中,人均预期寿命是指人群在一定时间内的平均寿命,其他调整因素可以包括基因、环境等对寿命产生影响的因素。

人的平均寿命计算方法_平均寿命计算公式一览如何计算人的平均寿命我们经常看到报纸上说中国人的平均寿命是多少多少。
前不久中国科学院院士钟南山严正指出我国人均寿命远没达到75岁,原因是计算的方法不对。
但他没有告诉我们正确的计算方法,以及他计算出的结果。
所谓人均75岁,即平均每个人的预期寿命为75岁。
我们以75岁为基数,凡是寿命低于75岁的,其岁数差额总和必须与寿命大于75岁人的岁数差额总和相等。
假如寿命低于75岁的人数是总人口的X1,他们平均寿命与75岁的差额为Y1,而寿命大于75的人数为总人口的X2,他们的平均寿命与75岁的差额为Y2,则X1Y1=X2Y2。
一般来说,X1与X2的和就是总人口的数量。
当X1=X2=50%时,则Y2=Y1。
设Y1=10岁,则寿命大于75岁的人平均寿命与75岁的差额Y2也应该为10岁,就是说现在应该看到大约有一半的人的寿命大于75岁,且平均寿命在85岁左右,超过85岁,乃到100多岁的人应该比比皆是。
显然,这与事实相差太远。
那么如何估算某个瞬间人的平均寿命,才能尽可能与事实相符呢?这的确是个很困难的事。
因为不断有人出生,有人死亡,活着的还能活多久?都难以估算。
下面,我试着给出几种计算方法,供大家参考。
一、对固定人群平均寿命的计算即将这固定人群的所有人的寿命总和除以这批人总人数,就得这批人的平均寿命。
例:某张姓家族(自一对夫妻开始繁衍),自1908年到2007年,100年间全部死亡人数(包括嫁出的张姓姑娘,不包括娶进张家的外姓媳妇)为100人,这些亡人的寿命总和为5873岁,则可得出该张姓家族100年来的家族平均寿命:S=5873÷100=58.73(岁)其中S为平均寿命,下同。
诸位读者也不妨用此法对自己的家族计算一下本家族的平均寿命,时间跨度越大,计算出的数字越准确。
大家可以将计算出来的结果都汇集到本文楼下,就可以从侧面看出我国过去一段时期的人均寿命了。
二、对固定时间段出生的人群平均寿命的计算即将这固定时间段里出生的所有人的最终寿命加在一起,除以全体人数,就得出这期间人的平均寿命。

电容寿命计算公式RIFA、Nichicon、Rubycon的电解电容计算公式电解电容寿命计算是电容电路设计的最关键的一步,它直接考量电容的设计寿命,电容寿命主要受到温度的影响,所以在设计时候考虑到热源和风道,是提高电容寿命的有效方式,在设计时尽量让电容远离热源,通风好,有时利用强制风冷的方式,尽量让电容工作于低温情况下。
关于电容的寿命计算步骤这里不详述,请参考“电解电容寿命设计步骤”一文,以下主要介绍 rifa , nichicon ,Rubycon 电容寿命得计算公式。
1、 nichicon 的电解电容寿命计算公式nichicon 的电解电容寿命计算公式分为两种: a 、大封装电解电容( large can type ); b 、小封装( miniature type )的电容,以下针对两种电容分别列出其计算公式。
A、 large can type电容结算公式如下:其中:Ln: 估算之寿命(在环境温度 Tn 和总纹波 In )Lo: 在最大允许工作温度 To 和最大允许工作纹波 Im 条件下的额定寿命To: 最大允许工作温度Tn: 环境温度to: 在最大允许工作温度 To 和最大允许工作纹波电流 Im 条件下内部温升量Im : 在最大允许工作温度 To 条件下的最大允许工作纹波电流有效值(在标准频率条件下的正弦波) In : 实际应用的纹波电流有效值Δ tn: 在环境温度 Tn 和纹波电流 In 条件下致使的内部温升K: 因纹波损耗引起温升的加速系数( Tn 从实际应用环境获得, In 根据其规格书中的纹波系数将实际纹波有效值归一到标准频率上的有效值。
其它参数可从规格书中得到)以上公式给出的是一个基本寿命与环境温度函数、热点温度及纹波电流函数之积。
其内部温升Δ tn 估算并非由电阻损耗计算方式,而是提供了一个参考点值和相应的比例转换公式。
此公式关键点是归一到标准频率的等效电流有效值In 的求解。

中国平均寿命计算方法2篇第一篇:中国平均寿命计算方法中国的平均寿命是指中国人口平均预期寿命,即在出生时预计的平均寿命。
计算中国平均寿命的方式有多种,其中常用的两种方法是年龄段法和人群法。
年龄段法是一种常用且简单的方法。
这种方法通过对人口年龄段进行统计和比较,计算得出平均寿命。
一般来说,它将人口根据不同年龄段划分,并统计每个年龄段的人口数量。
然后,根据每个年龄段的死亡率来推算该年龄段的平均寿命。
最后,将每个年龄段的平均寿命加权平均,得出整个人口的平均预期寿命。
这种方法简单直观,是中国计算平均寿命的主要方式之一。
人群法是另一种常用的计算平均寿命的方法。
这种方法以一定集团或区域的特定人群为研究对象,通过长期追踪观察其生存状况来计算平均寿命。
一般来说,人群法选取一定数量的代表性个体,对他们的出生和死亡情况进行记录和统计。
然后,根据这些数据,计算这个人群的平均寿命。
这种方法更加精确,能够反映具体区域或群体的寿命水平。
这两种方法虽然有所不同,但都能够为我们提供有关中国平均寿命的重要数据。
通过对中国平均寿命的计算,我们可以了解中国人口的整体寿命水平,并为国家的人口政策和社会发展提供重要参考。
第二篇:中国平均寿命计算方法计算中国平均寿命是了解中国人口健康状况的重要课题之一。
除了以上提到的年龄段法和人群法,还有其他一些计算平均寿命的方法。
其中,还有健康调查法。
这种方法通常通过对一定数量的人口进行问卷调查和健康检查,了解他们的健康状况和寿命情况。
根据这些数据,可以计算出该人群的平均寿命。
这种方法能够更加全面地了解人口的健康状况,对制定健康政策和提升人群健康水平有重要意义。
此外,还有生命周期法。
这种方法通过对从出生到死亡的整个生命周期进行研究和分析,计算出平均寿命。
这种方法能够更加全面地了解每个年龄段的死亡率和寿命情况,对制定针对不同年龄段的健康政策具有重要意义。
除了以上提到的方法,还有其他一些计算平均寿命的方式。
无论是何种方法,计算中国平均寿命都需要收集大量的人口数据,并进行科学的统计和分析。

人类寿命三种计算方法关于《人类寿命三种计算方法》,是我们特意为大家整理的,希望对大家有所帮助。
长寿是我们每个人都所希望的,但对于如何做才能长寿,每个人都有着自己的观点,你知道中国人平均寿命是多少岁吗?中国男人与女人的平均寿命相关多少呢?今天小编就带大家一起来了解下关于寿命与长寿的知识。
有专家说,人体的自然性命有三种计算方法:一种是按性成熟期的8至10倍计算,人体的性成熟期是14至15岁,寿命该是112至150岁;第二是按生长期的5至7倍计算,人的生长期一般是20至25年,寿命该是100至175岁;三是按细胞分裂乘50至55次来计算,细胞每2.4年分裂一次,寿命该是120至132岁。
按上述计算,人人都应活过百岁,但百岁老人仍是今来稀。
世界上迄今活过200岁的有两人:男的是英国人卡恩,活209岁;女的是南美的玛卡兰殊,活203岁。
影响寿命的因素有14项第一是遗传,长寿父母与短寿父母基因的影响可延寿或折寿达20年。
第二是生态环境,空气清新、气候宜人与空气污浊、噪音超标的生活环境也可延寿和折寿20年。
第三,家庭美满与否也可加减寿命10年。
第四,烟瘾大,常酗酒,折寿20年。
第五,饮食与运动,合理饮食与适当运动延寿20年,反之,折寿16年。
第六,心胸开朗,豁达大度,延寿10年;心情恶劣,好发脾气,折寿10年。
第七,睡眠良好与否,增减8年。
第八,性生活适度,延寿5年,荒淫无度,折寿10年。
这些数字分析,当然颇有道理,也算是老生常谈。
但有一项谈及性别的,说男性应减2年,女性则增4年,大概是基于世界上长寿女性往往比男性为多,而以男性为中心的社会,男的所受压力较大之故。
影响人类寿命十大因素科学家研究认为,人的生理寿命是100-160岁。
但是,有诸多因素影响生理寿命,下面是10个最重要的相关因素。
体质强壮的人不一定比体弱多病者长寿,这是因为体弱多病者对某些病有一定的抗病能力,而且了解自身薄弱环节,有相应的保健措施;而强壮的人则往往忽视自己的身体。

平均预期寿命及常用的计算法副主任医师郝建国山东冠县疾病预防控制中心人口平均预期寿命(Life expectancy)是指假若当前的分年龄死亡率保持不变,同一时期出生的人预期能继续生存的平均年数。
它以当前分年龄死亡率为基础计算,但实际上,死亡率是不断变化的,因此,平均预期寿命是一个假定的指标。
这个指标与性别、年龄、种族有着紧密的联系,因此常常需要分别计算。
平均预期寿命是我们最常用的预期寿命指标,它表明了新出生人口平均预期可存活的年数,是度量人口健康状况的一个重要的指标。
寿命的长短受两方面的制约。
一方面,社会经济条件、卫生医疗水平限制着人们的寿命,所以不同的社会,不同的时期,寿命的长短有着很大的差别;另一方面,由于体质、遗传因素、生活条件等个人差异,也使每个人的寿命长短相差悬殊。
因此,虽然难以预测具体某个人的寿命有多长,但可以通过科学的方法计算并告知在一定的死亡水平下,预期每个人出生时平均可存活的年数。
这就是人口平均预期寿命。
一、计算方法人口平均预期寿命的计算要用到一连串的数学公式。
如果用文字来描述,则计算人口平均预期寿命的方法就是:对同时出生的一批人进行追踪调查,分别记下他们在各年龄段的死亡人数直至最后一个人的寿命结束,然后根据这一批人活到各种不同年龄的人数来计算人口的平均寿命。
用这批人的平均寿命来假设一代人的平均寿命即为平均预期寿命。
由于事实上要跟踪同时出生的一批人的整个完整的生命过程有很大的困难,在实际计算时,往往可以利用同一年各年龄人口的死亡率水平,来代替同一代人在不同年龄的死亡率水平,然后计算出各年龄人口的平均生存人数,由此推算出这一年的人口平均预期寿命。
因此,人口的平均预期寿命与同时代的死亡率水平有关。
1、人口老龄化指标反证法:我们可以通过人口老龄化指标(65岁以上的人口在7%以上)反证法,来推断一个国家或地区的平均寿命。
设平均寿命为“L”,总人口为单位“1”,每一岁所占总人口比例为“x”, x=(1 / L)×100。

LEDLM-80PL LED光通量维持率及老化寿命测试系统是根据IES-LM-80,1IES0LM-82,TM-12, GB2312-80等CIE和IEC标准设计制造。
LED有着寿命长的2特点,但是根据使用条件和驱动电流的不同,LED有5W或5W以上不等的使用寿3命。
不同于传统的光源,LED的不会瞬间熄灭,而是慢慢的光衰。
因此,LM-80 4标准中引入了L70,L50等概念。
51)L70 (小时):光衰至70%光通量时所用的时间。
62)L50(小时):光衰至50%光通量时所用的时间。
7功能:81)记录光通量随时间的变化曲线,及色参数随时间的变化曲线。
92)通过测试记录较短时间的光衰数据,推算出LED的寿命时间。
10LED有5W个小时以上的理论寿命,如果按照传统的测试方法需要测试5W个11小时,这显然是不可取的。
所以LEDLM-80PL引用了阿伦尼斯模型,公式如下:121、P=P0exp(-βt)132、β=β 0 IFexp(-Ea/KTj)14式中:P0为初试光通量。
P为加温加电后的光通量;β为某一温15度的衰退系数。
t为某一温度下的加电工作时间;β0为常数;Ea为激活能;K 16为波耳兹曼常数;IF为工作电流;T j为结温171819首先我们以每1000小时光衰推断寿命。
20例如:假定1000小时光衰光衰率为n%,21由公式1可得50%光衰公式:t=1000*ln0.5/ln(1-n%)22由公式1可得30%光衰公式:t=1000*ln0.7/ln(1-n%)232425所以我们可以得到:2627温度(温度指LED灯底部与电路板接触处表面温度,在散热条件充28分时即为环境温度,350mA使用时结温比环境温度高15摄氏度)对于测试结果29会有很大影响,我们可以用公式2来推断不同温度下的LED寿命,假定已知某种30LED温度T1(摄氏度)时的寿命为t1,温度T2(摄氏度)时的寿命为t2,由公31式2可得温度T3条件下的寿命t3为:32t3=t1*exp{(ln(t2/t1)/[1/(T2+15+273)-1/(T1+15+273)] *33[1/(T3+15+273)-1/(T1+15+273)]}343536然后可以得到在不同温度下50%与30%光衰时间:37项85°C(h)70°C(h)50°C(h)25°C(h)目L(58312.95041422756.57306100144.3113833055.6622 0)L(34277.6212711709.92251531.576428668.0953 0)38光衰指数曲线:3940在1000小时之前光通量变化很多情况下是先升后降,因此TM-21要求100041小时以前的数据不用于曲线拟合,而仅采用最后5000小时的数据进行曲线拟合。
期望寿命计算公式及例题期望寿命是指在出生时预期的平均寿命,是一个国家或地区的人口统计学指标,也是衡量一个国家或地区人民生活水平和医疗水平的重要指标之一。
计算期望寿命的公式可以帮助我们更好地了解人口的生存状况和社会的发展水平。
本文将介绍期望寿命的计算公式及例题,帮助读者更好地理解这一概念。
首先,让我们来看一下期望寿命的计算公式。
期望寿命的计算公式是:\[E(x) = \sum_{i=0}^{n} l_{x+i}\]其中,E(x)代表期望寿命,l代表年龄的存活人数,x代表年龄,n代表最大年龄。
这个公式的意思是,将每个年龄段的存活人数相加,然后除以总人口数,就可以得到期望寿命。
接下来,让我们通过一个例题来看一下期望寿命的计算方法。
假设某国有以下年龄段的存活人数:0岁,1000000人。
1岁,990000人。
2岁,980000人。
3岁,970000人。
4岁,960000人。
5岁,950000人。
假设这个国家的总人口数为2000000人。
我们可以使用期望寿命的计算公式来计算这个国家的期望寿命。
首先,我们需要计算每个年龄段的存活人数占总人口数的比例。
然后将这些比例相加,就可以得到期望寿命。
0岁的存活人数占总人口数的比例为1000000/2000000=0.5。
1岁的存活人数占总人口数的比例为990000/2000000=0.495。
2岁的存活人数占总人口数的比例为980000/2000000=0.49。
3岁的存活人数占总人口数的比例为970000/2000000=0.485。
4岁的存活人数占总人口数的比例为960000/2000000=0.48。
5岁的存活人数占总人口数的比例为950000/2000000=0.475。
将这些比例相加,得到期望寿命:E(x) = 0.5 + 0.495 + 0.49 + 0.485 + 0.48 + 0.475 = 2.925。
所以,这个国家的期望寿命为2.925岁。
通过这个例题,我们可以看到期望寿命的计算方法。
平均预期寿命及常用的计算法人口平均预期寿命(Life expectancy)是指假若当前的分年龄死亡率保持不变,同一时期出生的人预期能继续生存的平均年数。
它以当前分年龄死亡率为基础计算,但实际上,死亡率是持续变化的,所以,平均预期寿命是一个假定的指标。
这个指标与性别、年龄、种族有着紧密的联系,所以常常需要分别计算。
平均预期寿命是我们最常用的预期寿命指标,它表明了新出生人口平均预期可存活的年数,是度量人口健康状况的一个重要的指标。
寿命的长短受两方面的制约。
一方面,社会经济条件、卫生医疗水平限制着人们的寿命,所以不同的社会,不同的时期,寿命的长短有着很大的差别;另一方面,因为体质、遗传因素、生活条件等个人差异,也使每个人的寿命长短相差悬殊。
所以,虽然难以预测具体某个人的寿命有多长,但能够通过科学的方法计算并告知在一定的死亡水平下,预期每个人出生时平均可存活的年数。
这就是人口平均预期寿命。
人口平均预期寿命的计算要用到一连串的数学公式。
如果用文字来描述,则计算人口平均预期寿命的方法就是:对同时出生的一批人实行追踪调查,分别记下他们在各年龄段的死亡人数直至最后一个人的寿命结束,然后根据这个批人活到各种不同年龄的人数来计算人口的平均寿命。
用这批人的平均寿命来假设一代人的平均寿命即为平均预期寿命。
因为事实上要跟踪同时出生的一批人的整个完整的生命过程有很大的困难,在实际计算时,往往能够利用同一年各年龄人口的死亡率水平,来代替同一代人在不同年龄的死亡率水平,然后计算出各年龄人口的平均生存人数,由此推算出这个年的人口平均预期寿命。
所以,人口的平均预期寿命与同时代的死亡率水平相关。
1、人口老龄化指标反证法:我们能够通过人口老龄化指标(65岁以上的人口在7%以上)反证法,来推断一个国家或地区的平均寿命。
设平均寿命为“L”,总人口为单位“1”,每一岁所占总人口比例为“x”, x=(1 / L)×100。
这样,我们每给定一个L的值,就可计算出一个对应的x值、60和65岁以上人群所占的比例(%)。
人口平均预期寿命的常用计算法
以下是几种常用的计算人口平均预期寿命的方法:
1.最简单的方法是根据已知的出生率和死亡率来计算预期寿命。
首先需要获得相关的人口统计数据,包括出生率和死亡率。
然后,根据这些数据,可以使用一些公式来计算出预期寿命。
假设出生率为B,死亡率为D,那么预期寿命E可以通过以下公式计算:E=1/(D-B)
使用这种方法计算的预期寿命通常是以年为单位的平均寿命。
2.人口平均预期寿命也可以通过构建生命表来计算。
生命表是一个记录不同年龄组人口死亡率和存活率的统计工具。
它通常使用年龄组进行分类,并根据人口统计数据和死亡数据计算出预期寿命。
生命表可以提供详细的年龄组别的死亡率和存活率数据,使得可以更加准确地计算出预期寿命。
通过对生命表进行分析,可以确定不同年龄组的平均寿命,进而计算出人口平均预期寿命。
使用Kaplan-Meier估计,可以从一组有时限的生存数据中计算出人口平均预期寿命。
该方法考虑了个体在不同时间点上生存的概率,并据此计算出预期寿命。
这些是计算人口平均预期寿命的几种常用方法。
选择哪种方法取决于数据的可用性和特定领域的要求。
无论使用哪种方法,预计寿命都是一个重要的指标,可以用于评估健康和社会福利水平,并制定相应的政策和规划。
平均生命年限计算公式生命年限是指一个人在出生时能够活到的平均年龄。
它是一个重要的指标,可以帮助人们了解一个国家或地区的整体健康水平和生活质量。
通过计算公式,我们可以更好地了解生命年限的情况,并采取相应的措施来改善人们的生活。
生命年限的计算公式通常是基于一些基本的健康和生活指标。
这些指标包括但不限于,平均寿命、婴儿死亡率、疾病发病率、医疗资源分配等。
通过这些指标的分析和计算,可以得出一个地区或国家的平均生命年限。
计算公式通常由一系列的参数和变量组成。
这些参数和变量包括但不限于,出生率、死亡率、人口增长率、医疗资源投入、环境因素等。
通过对这些参数和变量的测量和分析,可以得出一个相对准确的生命年限。
通常来说,生命年限的计算公式可以分为几个步骤。
首先,需要收集和整理相关的数据,包括人口统计数据、医疗卫生数据、环境数据等。
然后,需要对这些数据进行分析,得出一些基本的指标和参数。
接下来,可以利用这些指标和参数来建立一个数学模型,通过这个模型来计算生命年限。
最后,需要对计算结果进行验证和修正,以确保其准确性和可靠性。
生命年限的计算公式可以帮助政府和社会组织更好地了解人口的健康状况和生活质量。
通过对生命年限的计算,可以及时发现和解决一些健康和生活方面的问题。
比如,如果一个地区的生命年限较低,可能意味着该地区存在较严重的健康问题,需要采取相应的措施来改善人们的生活。
又如,如果一个地区的生命年限较高,可能意味着该地区的健康和生活水平较高,可以作为其他地区的借鉴和参考。
在实际的应用中,生命年限的计算公式可以根据不同的需求和情况进行调整和改进。
比如,可以根据地区的特点和环境的变化来修正一些参数和变量,以提高计算结果的准确性和可靠性。
又如,可以根据不同的目的和目标来设计不同的计算模型,以满足不同的需求和情况。
总之,生命年限的计算公式是一个重要的工具,可以帮助人们更好地了解人口的健康状况和生活质量。
通过对生命年限的计算,可以及时发现和解决一些健康和生活方面的问题,为改善人们的生活做出贡献。
人类寿命计算公式出炉啦人类寿命一直是人们关注的焦点之一。
随着医学技术的不断进步和人们生活水平的提高,人类的寿命也在不断延长。
而关于人类寿命的计算公式也一直是科学家们探讨的话题之一。
最近,一项以人类寿命为基础的计算公式终于出炉了。
这个公式是由一群来自世界各地的科学家们经过多年的研究和实验得出的。
他们通过对世界各地的人类寿命数据进行了大量的分析和统计,最终得出了这个公式。
这个公式不仅可以用来预测人类的寿命,还可以用来研究人类寿命与各种因素之间的关系,对人类健康和长寿有着重要的意义。
这个公式的核心是人类寿命与遗传因素、生活方式和环境因素之间的关系。
通过对大量的数据进行分析,科学家们发现,人类寿命与遗传因素有着密切的关系。
一些基因可以影响人类的寿命,而这些基因又受到环境因素和生活方式的影响。
比如,一些人天生就拥有长寿基因,但如果他们过于糟糕的生活方式,也会影响到他们的寿命。
因此,这个公式不仅考虑了遗传因素,还考虑了生活方式和环境因素对人类寿命的影响。
这个公式的具体形式是,L = G + (E + H) / 2,其中L代表人类的寿命,G代表遗传因素对寿命的影响,E代表生活方式对寿命的影响,H代表环境因素对寿命的影响。
通过这个公式,科学家们可以预测一个人的寿命,并且可以通过调整生活方式和改善环境来延长人类的寿命。
这个公式的出炉对人类的健康和长寿有着重要的意义。
首先,它可以帮助人们更好地了解自己的寿命,并且可以通过调整生活方式和改善环境来延长寿命。
其次,它可以帮助医生更好地预测疾病的发生和发展,从而更好地进行治疗和预防。
最后,它还可以帮助政府和社会制定更科学的健康政策,促进人类的健康和长寿。
当然,这个公式还有一些局限性,比如它只是一个统计模型,并不能完全准确地预测一个人的寿命。
而且,人类的寿命受到很多因素的影响,不仅仅是遗传因素、生活方式和环境因素。
因此,科学家们还需要不断地进行研究和实验,来完善这个公式,使其更加准确和全面。
人的寿命大限推算方法
人类的极限寿命可以通过人体的细胞分裂次数来计算出来,人体内的细胞,一生中大概能分裂50次,每次细胞分裂的周期一般在2-3年,按照这个分裂次数和周期来算,人类的极限寿命能够达到120岁。
人的寿命大限推算方法
发育正常的男女一般在15周岁时就已经达到性成熟,这一周期的7-9倍就是人类寿命的极限,用这种方法我们可以算出人类的极限寿命在105岁到135岁。
根据我国统计局公布的数字,我国人均寿命是76岁,远远达不到寿命极限的标准,影响寿命的因素有很多,除了饮食、生活习惯和环境因素外,还有一些外因。
早期社会人类的平均寿命只能够达到45岁左右,但是随着社会的发展,医学的发达,人类的平均寿命已经有了大幅度的提高,有的人类甚至能够活到百岁以上。
关于TM21 LED寿命推算方法
1、基础知识
IES LM-80-08是用于测量LED光源光通维持率的方法,被广泛用于描述LED的光衰特性,LED器件生产厂家提供的LM-80-08测试报告(ES认可的测试机构测试)采用的数据都来至于持续测试6000h或更多时间内的测试数据,然而对于被测产品LM-80-08并没有很好的定义对于收集到的数据,如何被实际用于确定LED的有效寿命。
TM-21是Energy Star标准的技术备忘,补充了根据LM-80-08测试过程中获得的数据,来进行超出老化时间的寿命推算的方法。
额定光通维持寿命是指LED光源的光输出相对于初始光输出达到某一给定百分比所经过的运行时间,这个值被定义为Lp,p为给定的百分比值,业界常用LED光输出下降至初始光输出的70%所经过的时间来定义LED的寿命,LED达到其额定光通维持寿命取决于很多变量,包括运行温度、驱动电流、产品结构的设计和材料特性。
2、样品规模及测试数据采集
对于从LM80报告中获得的所有针对某一特定产品的壳温、驱动电流等数据,都应用于流明维持寿命推算,推荐的样品规模集最小为20 pcs,并可以在流明维持寿命推算中,相对于寿命测试持续时间,LED推算寿命最大不超过6倍测试时间。
任何样品规模的改变都将导致不确定度及流明维持寿命推算的时间间隔的改变,对于样品规模为10~19pcs的情况,LED推算寿命最大不超过5.5倍测试时间。
不支持样品规模小于10pcs的寿命推算。
从目前各厂家提供的LM80报告来看,样品规模多为20 pcs或25 pcs。
目前LM80 6000h报告中数据的采集时间间隔多为1000h,且很多厂家持续测试时间已超6000H,超6000H的附加测量可以提高流明维持寿命推算的准确性。
3、流明维持寿命推算方法
目前LM80报告中采用最多的是对采集到的数据进行曲线拟合,以推算光通维持率衰减至70%所经历的时间,这个时间就是LED的流明维持寿命。
同样的曲线拟合方法,可以用来推算未来某个时间节点的光通量。
对于LM80报告中每一组被测单元所采集的温度及驱动电流数据,都应单独用该方法进行曲线拟合。
首先我们得对每一组里面相同测试时间点里的每一个规范化数据进行平均。
假设持续测试时间为T,对于LM80 6000h数据,对于其数据集用于曲线拟合的数据点应该是1000h到6000h,对于少于1000h的数据不应用于曲线拟合;从6000h到10000h,对于其数据集用于曲线拟合的数据应该是最后5000h的数据;对于持续测试时间大于10000h的数据集,在总体测量时间50%点以后的数据集都应用于曲线拟合,换句话说,在T/2到T之间的数据都应用于曲线拟合,例如持续测试时间为11000H,则5500h到11000h的测试数据都应用于曲线拟合,如果没有T/2这个节点的测试数据,那么上一个最近时间点的测试数据就应该包含在用于曲线拟合的数据集内,如持续测试时间11000h,每1000h采集一次数据,那么用于曲线拟合的数据集应为5000h到11000h。
4、曲线拟合方法
对各数据采集时间点的数据的平均值按照指数最小二乘法进行曲线拟合。
LED随时间的光衰减可以用e指数关系表示φ(t)=B exp(-at),φ(t)为归一化的光通维持率,t为持续测试的时间,B为最小二乘法曲线拟合派生出的初始化常数,a为最小二乘法曲线拟合派生出的衰退系数。
LED光衰至初始光通量70%所用时间的推算公式为(光衰减e指数关系两边同时取ln):
当a>0时,指数拟合曲线会衰减至零,L70为正值;当a<0时,指数拟合曲线会随着时间的增加而增加,L70为负值。
当L70值落在测试LM80持续测试时间内的某一个时间节点时,则L70值应为通过最接近于该点的两个测试节点之间的线性插值获得,且该值的优先级高于通过以上公式预测获得的值。
下面就以亿光5630B @2700K/150mA/85℃下的LM80测试数据为例进行曲线拟合说明:
LM80测试数据如下:
我们可以在matlab中使用cftool命令对所获得的数据进行e指数拟合,程序如下:
x=[1000 2000 3000 4000 5000 6000];
y=[0.9890 0.9821 0.9743 0.9635 0.9546 0.9304];
cftool;
运行程序,会弹出曲线拟合工具界面,点data读入x值、y值,creat data set,将各测试点数据读入图中
点fitting,在type of fit下选择Exponential,点击a*exp(b*x),点击apply,可得出a值和b值以及拟合曲线。
从而我们可得出中的B=1.005,a=1.139e-005,带入可算出L70为31752 H,我们可近似认为可以达到32000h的寿命,与LM80报告中的推算值一致。
5、结果的修正
修正系数为n,总测试时间为T,L70为推测寿命
10~19 pcs样品修正系数为n=5.5;
20 pcs及以上样品修正系数为n=6;
当 0<L70<n*T 时最后表述预测结果为实际推测值L70;
当L70>n*T时最后表述预测结果为实际推测值n*T;
当L70<0时最后表述预测结果为n*T,并且任何测试时间外的的推算值都归
为最近测试点的值。
综上,那么亿光5630B @2700K/150mA/85℃下的寿命推测值为32000h,符合0<L70<n*T的条件(20pcs样品,n*T应为36000h),那么我们可以表述此条件下5630的寿命为32000h。
6、温度插值计算
当实际使用温度与LM80报告中的测试温度(55℃、85℃或生产厂家指定的第三个温度)不同时,可采用下列方法来预测寿命,运行条件因相同或降低(如驱动电流)。
插值前提:Ts1<Ts<Ts2
其中Ts1为LM80报告中相对于实际使用温度较低的测试值,Ts2为报告中相对于实际使用温度较高的测试值。
关于衰退系数我们引入阿列纽斯方程,
a=a0I f exp(-Ea/KTs)
其中a为衰退系数,a0为衰退常数,I f为驱动电流,Ea为材料激活能(ev),K为波尔茨曼常数(8.62x10-5ev/K),Ts为实际使用焊盘温度(单位为K)。
对于相同电流下(或降低)实际使用温度介于Ts1和Ts2之间,我们需要通过如下温度插值法来推算光通维持寿命,其中a1为Ts1温度下的衰退系数,a2为Ts2温度下的衰退系数(可直接由曲线拟合派生出):
首先我们得算出Ts1和Ts2之间的实际使用温度下的衰退系数as:
a1= a0I f exp(-Ea/KTs1)
a2= a0I f exp(-Ea/KTs2)
由上面两式两边同时取ln,再相减,我们可以得出Ea/K=(ln a1-ln a2)/(1/Ts2-1/Ts1),再代入a1和Ts1(a2和Ts2也可)得:
a0I f=a1*exp(Ea/KTs1)
综上,我们可以计算出Ts温度下的衰退系数:
as=a1*exp(Ea/KTS1)*exp((ln a2-ln a1)/(Ts*(1/Ts2-1/Ts1)))关于初始化常数
Bs=√(B1*B2)
其中B1为较低温度Ts1的拟合初始化常数,B2为较高温度Ts2的拟合初始化常数
将Bs、as,代入可推算出实际使用温度Ts下(电流与LM80报告相同或更低)的L70 寿命。
同样可以计算出Ts温度下时间t时的光通量φ(t)=B exp(-at)。
阿列纽斯方程只适用于a1、a2均为正数时的L70推算,当有一个为正数时,则寿命推算值应为LM80报告中某一测试温度下的L70值,当两个全部为负时,则寿命应为6倍测试时间(对于样品数量为10~19pcs时为5.5倍)。
对于实际使用温度高于LM80报告中测试的最高温度时,不能做L70推算,对于实际使用温度低于LM80报告中较低的测试温度时,应根据LM80报告中较低温度的测试数据来推算L70的值。
陈小康
2013.12.09
深圳市九洲光电科技有限公司。