标准击实试验的曲线拟合方法

一、课程设计题目： 对于函数 xex x f --=)(从00=x 开始，取步长1.0=h 的20个数据点，求五次最小二乘拟合多项式5522105)()()()(x x a x x a x x a a x P -++-+-+= 其中 ∑===1995.020i ix x 二、原理分析 （1）最小二乘法的提法当数据量大且由实验提供时，不宜要求近似曲线）（x y φ=严格地经过所有数据点),(i i y x ，亦即不应要求拟合函数）（x ϕ在i x 处的偏差（又称残差）i i i y x -=)(φδ(i=1,2,…,m)都严格的等于零，但是，为了使近似曲线能尽量反应所给数据点的变化趋势，要求偏差i δ适当的小还是必要的，达到这一目标的途径很多，例如，可以通过使最大偏差i δmax 最小来实现，也可以通过使偏差绝对值之和∑ii δ最小来实现……，考虑到计算方便等因素，通常用使得偏差平方和∑ii 2δ最小（成为最小二乘原则）来实现。

按最小二乘原则选择近似函数的方法称为最小二乘法。

用最小二乘法求近似函数的问题可以归结为：对于给定数据),(i i y x(i=1,2,…,m)，要求在某个函数类Φ中寻求一个函数）（x *ϕ，使[][]21)(21*)()(min ∑∑=Φ∈=-=-mi iix mi iiy x y x ϕϕϕ（1-1） 其中）（x ϕ为函数类Φ中任意函数。

（1）确定函数类Φ，即确定）（x ϕ的形式。

这不是一个单纯的数学问题，还与其他领域的一些专业知识有关。

在数学上，通常的做法是将数据点),(i i y x 描绘在坐标纸上，然后根据这些点的分布情况来选择的）（x ϕ形式。

（2）球最小二乘法的解，即求满足条件（1-1）的近似函数）（x *ϕ。

（3）最小二乘法的实验原理 设）（x ϕ具有如下形式）（x ϕ=F),,,,10x a a a n ⋅⋅⋅（ （1-2） 其中n<m, k a (k=0,1,…,n)是待定参数，求具有这种形式的最小二乘解的实质，就是要适当选择k a =*k a (k=0,1,…,n)，使相应的函数 ),,,,()(**1*0*x a a a x n ⋅⋅⋅=ϕ （1-3） 满足条件（1-1），也就是说，点),,,(**1*0n a a a ⋅⋅⋅是多元函数 []211010),,,,),,,∑=-⋅⋅⋅=⋅⋅⋅mi i i n n y x a a a F a a a s （（的极小点，从而使**1*0,,,n a a a ⋅⋅⋅满足方程组0S=∂∂ka ，(k=0,1,…,n) （1-4） 因此，可以通过解上述方程组（称为法方程组）来求取*k a (k=0,1,…,n)，以便获得最小二乘解。

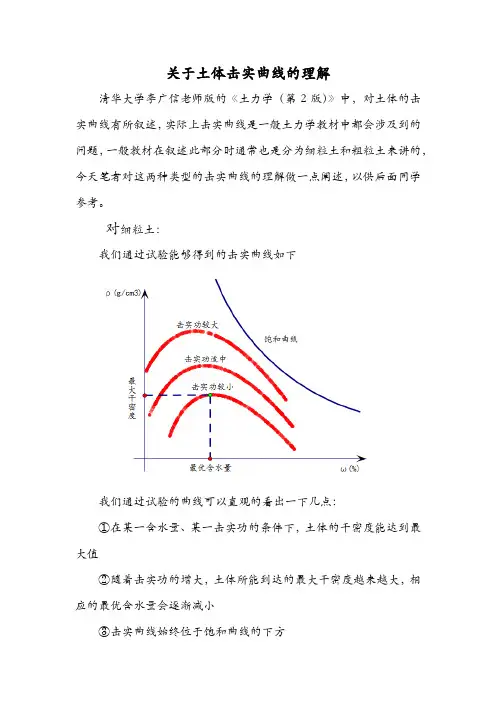
关于土体击实曲线的理解清华大学李广信老师版的《土力学（第2版）》中，对土体的击实曲线有所叙述，实际上击实曲线是一般土力学教材中都会涉及到的问题，一般教材在叙述此部分时通常也是分为细粒土和粗粒土来讲的，今天笔者对这两种类型的击实曲线的理解做一点阐述，以供后面同学参考。

对细粒土：我们通过试验能够得到的击实曲线如下我们通过试验的曲线可以直观的看出一下几点：①在某一含水量、某一击实功的条件下，土体的干密度能达到最大值②随着击实功的增大，土体所能到达的最大干密度越来越大，相应的最优含水量会逐渐减小③击实曲线始终位于饱和曲线的下方对于上述的三点是我们直接从试验曲线中直观的得到的结论，下面我们对这三点结论给出一些阐述： 首先，我们先来理解饱和曲线，关于含水量=w s m m ω和干密度s d m Vρ=中，对任一土体，在s m 不变的情况下，水含量的多少会影响在不限制压实条件下最终的V 值，即我们假定（注意是假定！），在压实过程中，我们有手段或者措施对土体实现100%的压实，那么随着水的增多，压实后土体的剩余体积就在增大，最终如下图，也就是饱和曲线但是！但是！现实的情况并非如此，也就是说我们不可能有充分的手段对土体进行100%的击实，事实上在试验中我们反而要控制变量，即我们只能付出一定量的功来对土体进行压实，我们还是来定量分析下，下图的土颗粒，我们假设只用100J 进行压实（这里的100焦耳只是一个定性的概念，即指100个单位的能量）当无水加入时，我们假设土体在100J 的作用下体积压实了5个单位，此时压实功的效率为55%/100J =个,此时的干密度500.5395d ρ==。

当有10%的水加入时，体积压实了15个单位，此时功的效率为1515%/100J =个，相应的干密度500.58885d ρ== 再加入10%的水时，体积压实了20个单位，此时功的效率为2020%/100J =个，相应的干密度500.6380d ρ== 当再加入10%水时，由于水的继续增多，在土颗粒内形成封闭的气泡，会降低功的利用率，体积的压实会下降！此时体积由于封闭气泡的存在，体积只被压实了15个单位，功的利用率1515%/100J =个，相应的干密度500.58885d ρ==，以此类推，当水的含量继续增加时，压实功的利用率会进一步的降低，从而不能得到更大的干密度。

击实曲线与理论饱和线在学习粘性土压实特性时，会遇到黏性土击实曲线和理论饱和线两条曲线。

学生在理解理论饱和线的物理含义，以及理论饱和线和击实曲线的关系时往往会遇到一定的困难。

因此，本文将对这一知识点进行扩展讲解。

图1即为常见的黏性土击实曲线和理论饱和线的关系图，黏性土的击实曲线反映的是：在一定击实功作用下，黏性土的干密度随含水率变化关系。

曲线中存在一个最优含水率，与之对应的是最大干密度。

黏性土的击实曲线是一条试验曲线，其数据点来自击实试验，通过数据的拟合可以得到一条光滑曲线。

粘性土的击实曲线反映出黏性土的击实特性。

在一定击实功作用下，当含水率较少时，黏土颗粒之间水膜的润滑作用不足，颗粒之间不易错动，土体不易被压实；当含水率较高时，颗粒间水膜润滑作用充足，但土体孔隙中水体不易被挤出而占据较多的孔隙空间，土体仍然不易被压实。

只有当土体含水率达到该击实功作用下的最优含水率时，黏土颗粒之间既有一定的润滑作用，水分也没有挤占太多的孔隙空间，土体可以达到该击实功作用下的最大干密度。

图1典型击实曲线与理论饱和线位置关系图当击实功变化时，黏性土的最优含水率也会相应变化。

因为较大的击实功可以抵抗较大的粒间错动阻力，使土颗粒相互错动形成更紧密的排列，从而达到压实的目的。

因此，当击实功增大，最优含水率会相应减小；击实功减小，最优含水率会相应增大。

并且，同一种土，击实功越大，所能达到的最大干密度也越大。

理论饱和线描述的是饱和含水率和干密度的函数关系，是一条理论曲线，而非试验曲线，与最大干密度没有必然联系。

理论饱和线的函数关系可以由三相草图进行推导。

理论饱和线中的干密度必大于击实曲线中相同含水率对应的干密度。

因为理论饱和线中对应的点表征的是土体处于饱和状态，而击实曲线中对应的点表征的是土体处于非饱和状态。

同一土体在相同含水率下，饱和状态肯定更密实，具有更大的干密度。

理论饱和线的含义：1，对应于纵坐标任一干密度做一水平线，与理论饱和线相交的点对应的横坐标含水率就是该土在该干密度下的饱和含水率。

曲线拟合的数值计算方法实验【摘要】实际工作中，变量间未必都有线性关系，如服药后血药浓度与时间的关系；疾病疗效与疗程长短的关系；毒物剂量与致死率的关系等常呈曲线关系。

曲线拟合（curve fitting）是指选择适当的曲线类型来拟合观测数据，并用拟合的曲线方程分析两变量间的关系。

曲线直线化是曲线拟合的重要手段之一。

对于某些非线性的资料可以通过简单的变量变换使之直线化，这样就可以按最小二乘法原理求出变换后变量的直线方程，在实际工作中常利用此直线方程绘制资料的标准工作曲线，同时根据需要可将此直线方程还原为曲线方程，实现对资料的曲线拟合。

常用的曲线拟合有最小二乘法拟合、幂函数拟合、对数函数拟合、线性插值、三次样条插值、端点约束。

关键词曲线拟合、最小二乘法拟合、幂函数拟合、对数函数拟合、线性插值、三次样条插值、端点约束一、实验目的1.掌握曲线拟合方式及其常用函数指数函数、幂函数、对数函数的拟合。

2.掌握最小二乘法、线性插值、三次样条插值、端点约束等。

3.掌握实现曲线拟合的编程技巧。

二、实验原理1.曲线拟合曲线拟合是平面上离散点组所表示的坐标之间的函数关系的一种数据处理方法。

用解析表达式逼近离散数据的一种方法。

在科学实验或社会活动中，通过实验或观测得到量x与y的一组数据对（X i，Y i)（i=1，2，...m），其中各X i 是彼此不同的。

人们希望用一类与数据的背景材料规律相适应的解析表达式，y=f(x，c）来反映量x与y之间的依赖关系，即在一定意义下“最佳”地逼近或拟合已知数据。

f(x，c)常称作拟合模型，式中c=(c1，c2，…c n)是一些待定参数。

当c在f中线性出现时，称为线性模型，否则称为非线性模型。

有许多衡量拟合优度的标准，最常用的一种做法是选择参数c使得拟合模型与实际观测值在各点的残差(或离差)，c）-f （f y e k k k =的加权平方和达到最小，此时所求曲线称作在加权最小二乘意义下对数据的拟合曲线。

击实实验报告标准击实试验报告贵XX大学学生实验报告xxx五——xxx六学年度第一学期材料与建筑工程学院三年级专业土木工程班级课程名称土力学试验组别组员成绩 XX大学学生实验报告实验项目名称_ _击实试验_________ 组长 _______ 组别同组学生实验时间_20XX_年_X月_X日指导教师 _______ 实验报告需包含以下内容：①实验目的与原理；②主要实验仪器及设备；③实验步骤；④实验数据及处理；⑤实验结论；⑥其它；⑦思考题（一）实验目的与原理1.实验目的击实实验的目的是测定试样在一定击实次数下或某种压实功能下的干密度与含水率之间的关系，从而确定土的最大干密度和最优含水率。

2.试验原理土在一定的压实效应下，若含水率不同，则密度也会不同。

当压实功能和压实方法不变时，土的密度随含水率的增加而增加，但当含水率增大到一定程度后，土的密度反而减小，这是因为细粒土在含水率较低时，颗粒表面形成薄膜水，摩擦力大，不易压实；当含水率继续增加时，颗粒表面结合水膜渐渐加厚，其润滑作用也增大。

在外力作用下，容易移动，易于压实；而继续增加水量，只会增加土的孔隙体积，从而使干密度降低。

能使土体达到最大干密度的含水率称为最优含水率。

（二）主要实验仪器及设备1.击实仪：由击实筒、击锤及导筒组成。

本次实验选用轻型击实仪。

2.天平：称量200g，最小分度值0.01g；称量500g，最小分度值1.0g。

3.台秤：称量10kg，最小分度值5g。

4.圆孔筛：孔径为40mm、20mm和5mm标准筛各一个。

5.试样推出器：本实验用修土刀和刮土刀从击实筒中取出试样。

6.烘箱。

7.其他：喷水设备、碾土器、盛土盘、修土刀、平直尺、量筒和保湿设备等。

（三）实验步骤1.试样制备（湿法制备）① 称取天然含水率的代表性土体碾散，按要求过筛，将筛下的土样拌匀，并测定其含水率。

② 根据土样的塑限预估最佳含水率，按干法制备的原则选择至少5个含水率试样，分别将天然含水率土样风干或加水进行制备，并让制备好的土样喷洒的水分能均匀分布。

实验10 曲线拟合和插值运算一． 实验目的学会MATLAB 软件中软件拟合与插值运算的方法。

二． 实验内容与要求在生产和科学实验中，自变量x 与因变量y=f(x)的关系式有时不能直接写出表达式，而只能得到函数在若干个点的函数值或导数值。

当要求知道观测点之外的函数值时，需要估计函数值在该点的值。

要根据观测点的值，构造一个比较简单的函数y=t (x),使函数在观测点的值等于已知的数值或导数值，寻找这样的函数t(x),办法是很多的。

根据测量数据的类型有如下两种处理观测数据的方法。

（1） 测量值是准确的，没有误差，一般用插值。

（2） 测量值与真实值有误差，一般用曲线拟合。

MATLAB 中提供了众多的数据处理命令，有插值命令，拟合命令。

1.曲线拟合已知离散点上的数据集[(1x ,1y ),………(n x ,n y )]，求得一解析函数y=f (x),使f(x)在原离散点i x 上尽可能接近给定i y 的值，之一过程叫曲线拟合。

最常用的的曲线拟合是最小二乘法曲线拟合，拟合结果可使误差的平方和最小，即使求使21|()|n i ii f x y =-∑ 最小的f(x).格式：p=polyfit(x,Y ,n).说明：求出已知数据x,Y 的n 阶拟合多项式f(x)的系数p ，x 必须是单调的。

[例 1.9]>>x=[0.5,1.0,1.5,2.0,2.5,3.0]; %给出数据点的x 值>>y=[1.75,2.45,3.81,4.80,7.00,8.60]; %给出数据点的y 值>>p=polyfit (x,y,2); %求出二阶拟合多项式f(x)的系数>>x1=0.5:0.05:3.0; %给出x 在0.5~3.0之间的离散值>>y1=polyval(p,1x ); %求出f(x)在1x 的值>>plot(x,y,‟*r ‟, 11,x y ‟-b ‟) %比较拟合曲线效果计算结果为：p=0.5614 0.8287 1.1560即用f(x)=0.56142x +0.8287x+1.1560拟合已知数据，拟合曲线效果如图所示。

巧用Excel软件处理击实试验数据并绘制曲线效果图永利(新疆生产建设兵团农二师勘测新疆库尔勒市841000)【摘要】应用Excel对击实试验数据成果进行简化处理，绘制击实曲线图，并利用Excel强大的分析计算功能，求解出曲线的趋势方程及相关系数，进一步求解出最优含水率和最大干密度，简化了绘制曲线的烦琐工作，同时减少手工绘图的误差。

本文对此作了详细介绍。

【关键词】Excel 击实试验曲线饱和趋势方程相关系数最大干密度最优含水率饱和度1 前言土的击实试验是衡量土的压实性的一项很重要指标，在铁路、公路、桥梁、机场、水利（水库坝体）等工程建设的填方地基设计中都是必不可少的。

此外，土的渗透、压缩、剪切等试验在一定程度上又是由击实试验来控制的。

所以击实试验的成果对设计、施工以至于工程造价都会带来影响。

土在外力作用下（碾压或夯实），孔隙度变小，密度增加，强度提高，压缩性及渗透性降低，使土的工程性质得到改善。

而土的压实性就是指在一定的含水量条件下，以人工或机械的办法，使土能够达到某种密实程度的性能。

土的压实强度与含水量、压实功能和压实方法有着密切的关系。

当压实功能和压实方法不变时，则土的干密度随含水量的增加而增加；当干密度达到某一最大值后，含水量的继续增加反而使干密度减小。

此时干密度的最大值称为最大干密度，其相应的含水量称为最优含水量。

击实试验的目的，就是模拟工地压实条件，用标准击实的方法，测定在某种压实功能下土的含水量和干密度的关系，确定土的最优含水量和相应的最大干密度，以求用最小的压实功能，得到符合工程要求的密实度。

图1 击实试验计算和曲线效果图长期以来，工作在试验场所的技术人员面对大量击实试验数据，采用手工描点，曲线尺绘图的办法，不仅工作量大烦琐，并且极易受个人因素影响，得出的试验结果可信度比较差，不同程度地困绕着工程技术人员。

目前计算机已经普及，但专业绘制击实效果图的软件并不多见，且有的软件在输入数据时相对较为复杂。

标准击实试验干密度和含水率的数值分析方法发布者：中煤30处王玥明中煤三建试验检测有限责任公司李桂云发布时间：2006-11-17 10:29:00内容摘要关键词:击实试验;最大干密度;最佳含水率;数值分析摘要：在土木工程建设基础回填及公路填方路基工程中，土的最大干密度和最佳含水量是工程施工质量控制的两个重要因素，是回填土压实度的主要判定指标。

规范推荐通过绘制- 曲线图的求解方法，实验数据计算而得数据大多是离散的，因而曲线的任意性空间较大，在大多数情况下存在人为误差，不能绘制出合理的标准曲线，本文提出了利用最小二乘法求解拟合方程并绘制逼近曲线，从而理论求解最大干密度和最佳含水量。

正文文字大小：大中小前言压实度是控制公路工程质量的主要技术指标之一,压实度可靠的一个重要前提就是要求最大干密度准确并与测点实际干密度相对应.做标准击实试验的目的是为了获取填筑土的最大干密度和相应的最佳含水量, 按照《公路土工试验规程》（JTJ051）的规定，土的最大干密度和最佳含水量是根据击实试验结果，手工绘制- 曲线图，按曲线的峰值点来确定。

而此项试验的结果受人为因素影响较大, 往往因不同试验人员的经验、对数据的处理方法、绘制比例等，导致求解的最大干密度和最佳含水量结果差异较大，得出的标准密度往往偏离其真实值，以至于施工中出现压实度总是不合格或压实度大于100%的现象。

不能正确指导施工，从而引起质量事故。

笔者结合工程实例, 对上述击实试验数据处理和绘图存在的问题，结合数值分析原理和工科数学求极值的方法，提出了按最小二乘原则确定对应试验数据的拟合曲线，从而为理论求解最大干密度和最佳含水量提供了依据，并给示例进行计算。

1 击实试验数据处理的常规方法分析1．1《公路土工试验规程》规定以干密度为纵坐标,含水量为横坐标,绘制干密度及含水率的关系曲线,曲线上的峰值点坐标分别为最大干密度和最优含水率(图#).如果曲线不能绘制出明显的峰值点,应进行补点或重做.但在试验过程中存在两个问题:同一组试验数据,可以绘制出明显的峰值点,也可以绘制不出明显的峰值点,这样将导致不同的人在处理数据时对是否需要重做或补点有不同的判断.同时,同一组试验数据,不同的人会绘制出不同的曲线,导致最大干密度和最优含水率产生偏差,而这些误差正是在处理数据时无法避免的。

巧用Excel软件处理击实试验数据并绘制曲线效果图图1 击实试验计算和曲线效果图长期以来，工作在试验场所的技术人员面对大量击实试验数据，采用手工描点，曲线尺绘图的办法，不仅工作量大烦琐，并且极易受个人因素影响，得出的试验结果可信度比较差，不同程度地困绕着工程技术人员。

目前计算机已经普及，但专业绘制击实效果图的软件并不多见，且有的软件在输入数据时相对较为复杂。

若使用AutoCAD绘制，由点连线，既不精确也很麻烦。

笔者利用Excel处理试验数据，并绘制击实曲线图（该图为矢量图，可任意放大缩小，便于试验人员对比观察），最终求解出试验结果。

利用Excel表格还可以对试验中的异常值加以分析补充或剔除。

本文介绍了这一方法和操作过程，抛砖引玉，请同行指点。

本文实例是采用南实处型击实仪（定体积法）对粒径小于5mm的土样试验后所得数据的分析处理。

其他类型土的物理力学数据，可采用公式校正的方法，达到试验目的。

2 数据的采集与输入首先新建Excel文件，制作各种表头项目，如图1所示。

利用Excel的表格功能输入表头“击实试验计算&曲线效果图”，居中后设定字体大小并合并单元格（以下类似）。

在表头下方各行分别输入调配含水量(%)、干密度、土的饱和含水率(%)、湿密度、击实筒+土重(g)、击实筒体积(cm3)、土的比重等。

其他表项如图依次类推。

制作完后输入本试验中的常量，如筒的重量、体积，水的密度等，再输入试验所得土的比重，不同调配含水量及其相应的击实筒+土重。

然后根据公式：湿密度=（（击实筒+土重）-击实筒重）/击实筒体积（1）如表中B7=(B8-B9)/B10干密度=湿密度/（1+0.01×调配含水量）（2）如表中B5 =B7/(1+B4×0.01)土的饱和含水率=（4℃水的密度/土的干密度-1/土样比重）×100 （3）如表中B6 =(E10/B5-1/E9) ×100其余的相应表格项可按住ctrl键用鼠标拖动的办法依次产生或输入类似公式。

物理实验中的数据处理与曲线拟合方法研究在物理实验中，数据处理是一个至关重要的环节。

通过对实验数据的处理和分析，可以获得更加准确的结果，并且可以得到实验中所关注的物理规律和规律之间的关系。

而曲线拟合则是数据处理中常用的一种方法，通过将实验数据与已知的数学模型进行比较，来确定物理规律和参数之间的关系。

本文将探讨物理实验中常见的数据处理方法和曲线拟合技术。

一、数据处理方法1.平均值与标准偏差平均值是最常见的统计量之一，可以将多次实验的结果进行平均，以减小由于实验误差带来的随机误差。

标准偏差则是衡量实验数据的离散程度，即通过测量数据的离散程度来提供数据的精确度和可靠性。

在数据处理中，平均值和标准偏差经常用于误差分析和对比实验结果的稳定性。

2.直线拟合直线拟合是一种常见的数据处理方法，适用于已知数据和一个已知的数学模型。

通过将已知数据点与一条直线进行比较，可以确定直线的斜率和截距，进而得到与实验规律和参数之间的关系。

直线拟合在物理实验中常用于测量物理量之间的线性关系，如牛顿第二定律中的质量和重力之间的关系。

3.二次曲线拟合二次曲线拟合是一种常用的非线性拟合方法，适用于已知数据和一个已知的二次曲线模型。

通过将已知数据点与一个二次曲线进行比较，可以确定曲线的系数，进而得到与实验规律和参数之间的关系。

二次曲线拟合在物理实验中常用于研究非线性关系，如弹簧的伸缩关系和周期性运动的位移-时间关系。

二、曲线拟合方法1.最小二乘法最小二乘法是一种常用的曲线拟合方法，通过求解最小二乘问题，确定拟合曲线与实验数据之间的最小残差平方和。

最小二乘法对应于用一个函数来逼近已知数据点的问题，是一种求解最优解的数学方法。

在物理实验中，最小二乘法广泛用于拟合直线、曲线和函数。

2.非线性最小二乘法非线性最小二乘法是一种适用于非线性拟合的曲线拟合方法，通过求解非线性最小二乘问题，确定拟合曲线与实验数据之间的最小残差平方和。

与线性最小二乘法类似，非线性最小二乘法也是一种求解最优解的数学方法。

击实试验拟合绘图及其极值的求取
吴彩虹
【期刊名称】《安徽建筑》
【年(卷),期】2003(010)003
【摘要】利用切比雪夫曲线拟合原理,对击实试验所得 5点进行多次拟合,得到关于含水量 W多项式,并绘制曲线;根据所得多项式ρ (ω )=a0+ a1ω 1+ a2ω 2+ a3ω 3+ a4ω 4+ a5ω 5在区间单峰值,极值点处的一阶导数为零的特点,由此求最大干密度和最优含水量.
【总页数】1页(P58)
【作者】吴彩虹
【作者单位】安徽省水利水电勘测设计院
【正文语种】中文
【中图分类】TU4
【相关文献】
1.确定标准击实试验极值的一种数值分析方法 [J], 王驰;许民哲
2.分别用耿贝尔(Gumbel)极值分布和广义(GEV)极值分布拟合五华县降水极值 [J], 赵立
3.击实试验拟合绘图及其极值的求取 [J], 吴彩虹
4.利用回归和数值分析求取击实试验极值的方法探讨 [J], 丁百湛;王美芹;霍飞;陈海新
5.刍议土工标准击实试验最大干密度的求取 [J], 张旭
因版权原因，仅展示原文概要，查看原文内容请购买。

击实试验数据的数值分析方法摘要：对于公路填方路基工程，土的最大干密度和最佳含水量是路基施工质量控制的两个重要因素，是路基填土压实度的主要判定指标。

规范推荐通过绘制- 曲线图的求解方法，因曲线的任意性空间较大，容易引起人为误差。

为此，本文结合数值分析原理，提出了按最小二乘原则求解击实试验数据的拟合曲线，从而为理论求解最大干密度和最佳含水量提供了依据。

在实践运用中，将其移植到EXECL或相关程序中，极大提高了工作效率和减少人为误差，具有一定的推广应用价值。

关键词：道路工程；数值分析；最大干密度；最佳含水量；最小二乘；曲线拟合0 前言对于公路填方路基工程，土压实是最重要的工作，填方路堤的质量主要由路基土的压实度来判断的。

按照公路工程施工技术规范的规定，土的最大干密度和最佳含水量是路基施工质量控制的两重要因素，是路基填土压实度的主要判定指标。

按照《公路土工试验规程》（JTJ051）的规定，土的最大干密度和最佳含水量是根据击实试验结果，手工绘制- 曲线图，按曲线的峰值点来确定和。

从各公路项目的试验结果调查分析来看，这种采用击实曲线求解的方法，往往因不同试验人员的经验、对数据的处理方法、绘制比例等，导致求解的最大干密度和最佳含水量结果差异较大。

这种差异主要是因为绘制- 曲线的任意性空间较大容易引起人为误差所致。

针对上述击实试验数据处理存在的问题，本文结合数值分析原理，提出了按最小二乘原则确定对应试验数据的拟合曲线，从而为理论求解最大干密度和最佳含水量提供了依据，并给示例进行计算。

1 数值分析原理1.1曲线拟合原理设在直角坐标系中给定对数据（即相应和的坐标）①其中。

又选定个在区间[ ]上连续且在点集上线性无关的基函数，其中。

问题是要在曲线族②中寻找一曲线按照最小二乘原则去拟合击实试验数据①，用所得的拟合曲线去代替击实试验数据①所反映的函数关系。

因数据①是在试验室通过击实试验测量计算所得的最佳含水量和最大干密度，一般在试验中总会带有观测误差，因此不必要求曲线一定要通过数据①表示的所有点。

曲线拟合方法概述工业设计 张静 1014201056引言：在现代图形造型技术中，曲线拟合是一个重要的部分，是曲面拟合的基础。

现着重对最小二乘法、移动最小二乘法、NURBS 三次曲线拟合法和基于RBF 曲线拟合法进行比较,论述这几种方法的原理及其算法，基于实例分析了上述几种拟合方法的特性，以分析拟合方法的适用场合，从而为图形造型中曲线拟合的方法选用作出更好的选择。

1 曲线拟合的概念在许多对实验数据处理的问题中，经常需要寻找自变量和对应因变量之间的函数关系，有的变量关系可以根据问题的物理背景，通过理论推导的方法加以求解，得到相应关系式.但绝大多数的函数关系却很复杂，不容易通过理论推导得到相关的表达式,在这种情况下，就需要采用曲线拟合的方法来求解变量之间的函数关系式。

曲线拟合（Curve Fitting),是用连续曲线近似地刻画或比拟平面上离散点组所表示的坐标之问的函数关系的一种数据处理方法。

在科学实验或社会活动中，通过实验或观测得到量x 与y 的一组数据对（x i ，y i ),i =1，2,3…,m ，其中各x i 是彼此不同的。

人们希望用一类与数据的规律相吻合的解析表达式y =f （x)来反映量x 与y 之间的依赖关系。

即在一定意义下“最佳”地逼近或拟合已知数据。

f(x)称作拟合函数,似的图像称作拟合曲线。

2 曲线拟合的方法2。

1最小二乘法最小二乘法通过最小化误差的平方和寻找数据的最佳函数匹配，是进行曲线拟合的一种早期使用的方法 一般最小二乘法的拟合函数是一元二次，可一元多次，也可多元多次。

该方法是通过求出数据点到拟合函数的距离和最小的拟合函数进行拟合的方法令f （x ）=ax 2+bx+c ，计算数据点到该函数所表示的曲线的距离和最小 即：δ=∑-=n i y x f i i 02))((对上式求导，使其等于0，则可以求出f(x ）的系数a ，b,c ,从而求解出拟合函数。

2。

2 移动最小二乘法移动最小二乘法在最小二乘法的基础上进行了较大的改进，通过引入紧支概念（即影响区域，数据点一定范围内的节点对该点的拟合函数值有影响），选取适合的权函数，算出拟合函数来替代最小二乘法中的拟合函数 从而有更高的拟合精度及更好的拟合光滑度。