八年级数学上册习题集

初二数学上册不等式练习题一、基础练习1. 解下列不等式，并将解表示在数轴上：a) 3x + 7 < 10b) 2 - 5x ≥ 12. 计算下列不等式组成的区间的并集，并用数轴表示出来：a) 1 < x ≤ 3b) -4 ≤ x < -13. 如果 x + 2 < x - 3，问该不等式是否有解，为什么？4. 解下列不等式，并将解表示在数轴上：a) |x - 4| < 2b) -3x + 5 > 2x + 15. 解下列关于 x 的不等式，并将解表示在数轴上：a) x(x - 2) > 0b) (x - 3)(x - 5) ≤ 0二、综合练习1. 解下列关于 x 的不等式组，并将解表示在数轴上：a) (x - 3)(x - 4) > 0b) (2x - 3)(x + 1) ≥ 0c) x(x - 2)(x + 1) ≤ 02. 某校初二年级共有 180 名学生，已知男生人数超过女生人数的40%，求男生人数的范围。

3. 某公司的年收入是 300 万元以上，假设每年收入增长不少于 10% ，求 n 年后的最小年收入。

4. 已知两个不等式：2x - 3 < y ≤ 5x + 1 和 3y + 2 > 4x + 5，解该不等式组。

三、应用题1. 小明买了一辆自行车，已知原价为 2000 元，商场正在搞促销活动，每天降价 10%，问过了多少天后，自行车价格降到 1000 元以下？2. 某公交车站至某大厦，全程约 20 公里。

已知 7:00 时公交车从车站发车，每分钟行驶速度为 3 公里，而 7:30 时某早班车从大厦出发，每分钟行驶速度为 4 公里。

问早班车何时追上公交车？3. 某航班 8:00 从 A 市起飞，前往 B 市，航程 800 公里。

同时，一列动车列车 8:05 从 B 市开往 A 市，时速为 180 公里/小时。

问几点钟两车相遇？4. 甲、乙两人玩掷骰子游戏，假设出现的点数加起来是 x，已知甲的点数不能小于 3 ，乙的点数不能大于 9 。

1、如图：在△ABC中,∠C=2∠B,AD是△ABC的角平分线,∠1=∠B,试说明AB=AC+CD2、如图,AD是∠BAC的角平分线，DE⊥AB垂足为E，DF⊥AC，垂足为点F，且BD=CD 求证：BE＝CF3、如图，点B和点C分别为∠MAN两边上的点，AB=AC。

（1）按下列语句画出图形：①AD⊥BC，垂足为D；②∠BCN的平分线CE与AD的延长线交于点E；③连结BE；（2）在完成（1）后不添加线段和字母的情况下，请你写出除△ABD≌△ACD外的两对全等三角形：____≌____，____≌____；（3）并选择其中的一对全等三角形予以证明。

已知：AB=AC，AD⊥BC，CE平分∠BCN，求证：△ADB≌△ADC；△BDE≌△CDE。

AB D CM NE4、如图，PB、PC分别是△ABC的外角平分线且相交于点P.求证：点P在∠A的平分线上AB CP5、如图，△ABC中，p是角平分线AD，BE的交点. 求证：点p在∠C的平分线上6、下列说法中，错误的是（）A．三角形任意两个角的平分线的交点在三角形的内部B．三角形两个角的平分线的交点到三边的距离相等C．三角形两个角的平分线的交点在第三个角的平分线上D．三角形任意两个角的平分线的交点到三个顶点的距离相等7、如图在三角形ABC中BM=MC∠ABM=∠ACM求证AM平分∠BAC8、如图，AP、CP分别是△ABC外角∠MAC与∠NCA的平分线，它们相交于点P，PD⊥BM于点D，PF⊥BN于点F．求证：BP为∠MBN的平分线。

9、如图，在∠AOB的两边OA，OB上分别取OM=ON，OD=OE，DN和EM相交于点C．求证：点C在∠AOB 的平分线上．10、如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC.（1）若连接AM，则AM是否平分∠BAD？请你证明你的结论；（2）线段DM与AM有怎样的位置关系？请说明理由．11、八（1）班同学上数学活动课，利用角尺平分一个角（如图所示）．设计了如下方案：（Ⅰ）∠AOB是一个任意角，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线．（Ⅱ）∠AOB是一个任意角，在边OA、OB上分别取OM=ON，将角尺的直角顶点P介于射线OA、OB之间，移动角尺使角尺两边相同的刻度与M、N重合，即PM=PN，过角尺顶点P的射线OP就是∠AOB的平分线．（1）方案（Ⅰ）、方案（Ⅱ）是否可行？若可行，请证明；若不可行，请说明理由；（2）在方案（Ⅰ）PM=PN的情况下，继续移动角尺，同时使PM⊥OA，PN⊥OB．此方案是否可行？请说明理由．12、如图，P是∠BAC内的一点，PE⊥AB，PF⊥AC，垂足分别为点E，F，AE=AF。

三角形一、填空题1．如果三角形的一个角等于其它两个角的差，则这个三角形是______三角形．2．已知△ABC中，AD⊥BC于D，AE为∠A的平分线，且∠B=35°，∠C=65°，则∠DAE 的度数为_____ ．3．三角形中最大的内角不能小于_____，两个外角的和必大于_____ ．4．三角形ABC中，∠A=40°，顶点C处的外角为110°，那么∠B＝_____ ．5．锐角三角形任意两锐角的和必大于_____．6．三角形的三个外角都大于和它相邻的内角，则这个三角形为 _____ 三角形．7．在三角形ABC中，已知∠A＝80°，∠B＝50°，那么∠C 的度数是．8．已知∠A=12∠B=3∠C ，则∠A= ．9．已知，如图7-1，∠ACD＝130°，∠A＝∠B，那么∠A的度数是．10．如图7-2，根据图形填空：（1）AD是△ABC中∠BAC的角平分线，则∠＝∠＝∠．（2）AE是△ABC中线，则＝＝．（3）AF是△ABC的高，则∠＝∠＝90°．11．如图7-3所示，图中有个三角形，个直角三角形．12．在四边形的四个外角中，最多有个钝角，最多有个锐角，最多有个直角．13．四边形ABCD中，若∠A+∠B=∠C+∠D，若∠C=2∠D，则∠C＝．14．一个多边形的每个外角都为30°，则这个多边形的边数为；一个多边形的每个内角都为135°，则这个多边形的边数为．15．某足球场需铺设草皮，现有正三角形、正四边形、正五边形、正六边形、正八边形、正十边形6种形状的草皮，请你帮助工人师傅选择两种草皮来铺设足球场，可供选择的两种组合是．16．若一个n边形的边数增加一倍，则内角和将．17．在一个顶点处，若此正n边形的内角和为，则此正多边形可以铺满地面．18．如图7-4，BC⊥ED于O，∠A=27°，∠D=20°，则∠B= ，∠ACB= ．图7-1 图7-2 图7-3图7-4 图7-519．如图7-5，由平面上五个点A 、B 、C 、D 、E 连结而成，则∠A +∠B +∠C +∠D +∠E = ．20．以长度为5cm 、7cm 、9cm 、13cm 的线段中的三条为边，能够组成三角形的情况有 种，分别是 ．二、选择题21．已知三角形ABC 的三个内角满足关系∠B ＋∠C =3∠A ，则此三角形（ ）．A ．一定有一个内角为45°B ．一定有一个内角为60°C ．一定是直角三角形D ．一定是钝角三角形22．如果一个三角形的三个外角之比为2：3：4，则与之对应的三个内角度数之比为（ ）．A ．4：3：2B ．3：2：4C ．5：3：1D ．3：1：523．三角形中至少有一个内角大于或等于（ ）．A ．45°B ．55°C ．60°D ．65°24．如图7-6，下列说法中错误的是（ ）．A ．∠1不是三角形ABC 的外角B ．∠B <∠1＋∠2C ．∠ACD 是三角形ABC 的外角D ．∠ACD >∠A +∠B25．如图7-7，C 在AB 的延长线上，CE ⊥AF 于E ，交FB 于D ，若∠F =40°，∠C =20°，则∠FBA 的度数为（ ）．A ．50°B ．60°C ．70°D ．80°26．下列叙述中错误的一项是（ ）．A ．三角形的中线、角平分线、高都是线段．B ．三角形的三条高线中至少存在一条在三角形内部．C ．只有一条高在三角形内部的三角形一定是钝角三角形．D ．三角形的三条角平分线都在三角形内部．27．下列长度的三条线段中，能组成三角形的是（ ）． A ．1，5，7 B ．3，4，7 C ．7，4，1 D ．5，5，528．如果三角形的两边长为3和5，那么第三边长可以是下面的（ ）．A ．1B ．9C ．3D ．1029．三条线段a ＝5，b ＝3，c 的值为整数，由a 、b 、c 为边可组成三角形（ ）．A ．1个B ．3个C ．5个D ．无数个30．四边形的四个内角可以都是（ ）．A ．锐角B ．直角C ．钝角D ．以上答案都不对31．下列判断中正确的是（ ）．图7-6 图7-7A ．四边形的外角和大于内角和B ．若多边形边数从3增加到n （n 为大于3的自然数），它们外角和的度数不变C ．一个多边形的内角中，锐角的个数可以任意多D ．一个多边形的内角和为1880°32．一个五边形有三个角是直角，另两个角都等于n ，则n 的值为（ ）．A ．108°B ．125°C ．135°D ．150°33．多边形每一个内角都等于150°，则从此多边形一个顶点发出的对角线有（ ）．A ．7条B ．8条C ．9条D ．10条34．如图7-9，三角形ABC 中，D 为BC 上的一点，且S △ABD =S △ADC ，则AD 为（ ）．A ．高B ．角平分线C ．中线D ．不能确定35．如图7-10，已知∠1＝∠2，则AH 必为三角形ABC 的（ ）．A ．角平分线B ．中线C ．一角的平分线D ．角平分线所在射线36．现有长度分别为2cm 、4cm 、6cm 、8cm 的木棒，从中任取三根，能组成三角形的个数为（ ）．A ． 1B ． 2C ． 3D ． 437．如图7-11，三角形ABC 中，AD 平分∠BAC ，EG ⊥AD ，且分别交AB 、AD 、AC 及BC 的延长线于点E 、H 、F 、G ，下列四个式子中正确的是（ ）38．如图7-12，在三角形ABC 中，∠1＝∠2，G 为AD 的中点，延长BG 交AC 于E ．F 为AB 上的一点，CF ⊥AD 于H ．下列判断正确的有（ ）．（1）AD 是三角形ABE 的角平分线． （2）BE 是三角形ABD 边AD 上的中线．（3）CH 为三角形ACD 边AD 上的高．A ．1个B ．2个C ．3个D ．0个三、解答题39．如图，在三角形ABC 中，∠B ＝∠C ，D 是BC 上一点，且FD ⊥BC ，DE ⊥AB ，∠AFD ＝140°，你能求出∠EDF 的度数吗？40．如图，有甲、乙、丙、丁四个小岛，甲、乙、丙在同一条直线上，而且乙、丙在甲的正东方，丁岛在丙岛的正北方，甲岛在丁岛的南偏西52°方向，乙岛在丁岛的南偏东40°方向．那图7-9 图7-10 图7-11 图7-12么，丁岛分别在甲岛和乙岛的什么方向？41．如图，已知三角形ABC的三个内角平分线交于点I，IH⊥BC于H，试比较∠CIH和∠BID 的大小．42．如图，在三角形ABC中，AD⊥BC，BE⊥AC，CF⊥AB，BC=16，AD＝3，BE=4，CF=6，你能求出三角形ABC的周长吗？43．如图，在三角形ABC中，AD是BC边上的中线，三角形ABD的周长比三角形ACD的周长小5，你能求出AC与AB的边长的差吗？44．已知等腰三角形的周长是16cm．（1）若其中一边长为4cm，求另外两边的长；（2）若其中一边长为6cm，求另外两边长；（3）若三边长都是整数，求三角形各边的长．45．如图，四边形ABCD中，∠A＝∠C=90°，BE平分∠ABC，DF平分∠ADC，试问BE 与DF平行吗？为什么？46．某同学在计算多边形的内角和时，得到的答案是1125°，老师指出他少加了一个内角的度数，你知道这个同学计算的是几边形的内角和吗？他少加的那个内角的度数是多少？47．把边长为2cm的正方形剪成四个一样的直角三角形，如图所示．请用这四个直角三角形拼成符合下列条件的图形：（1）不是正方形的菱形；（2）不是正方形的长方形；（3）梯形；（4）不是长方形、菱形的的平行四边形．48．下面是数学课堂的一个学习片段，阅读后，请回答下面的问题：学习等腰三角形有关内容后，张老师请同学们交流讨论这样一个问题．“已知等腰三角形ABC的角A等于30°，请你求出其余两角”．同学们经过片刻的思考与交流后，李明同学举手说: “其余两角是30°和120°”；王华同学说：“其余两角是75°和75°．” 还有一些同学也提出了自己的看法…（1）假如你也在课堂中, 你的意见如何? 为什么？（2）通过上面数学问题的讨论, 你有什么感受？（用一句话表示）49．如图，凸六边形ABCDEF的六个角都是120°，边长AB＝2cm，BC=8cm，CD＝11cm，DE＝6cm，你能求出这个六边形的周长吗？参考解析：一、填空题1．直角2．15°3．60°，180°4．70°5．90°6．锐角7．∠C＝180°－80°－50°＝50°．8．设∠A的度数为x．则∠B＝2x，∠C＝x．所以x＋2x＋x＝180°，解得x＝54°．所以∠A＝54°．9．∠A＝∠B＝∠ACD＝65°．10．（1）BAD，CAD，BAC；（2）BE，CE，BC；（3）AFB，AFC．11．解：有5个三角形，分别是△ABD，△ADE，△CDE，△ADC，△ABC；有4个直角三角形，分别是△ABD，△ADE，△CDE，△ADC．12．3，2，413．120°14．12，815．正三角形和正四边形、正三角形和正六边形、正四边形和正八边形中任选两种即可．16．增加（n－4）×180°17．360°或720°或180°18．解：因为∠BED＝∠A＋∠D=47°，所以∠B＝180°－90°－47°＝43°．所以∠BCD＝27°＋43°＝70°．所以∠ACB＝180°－70°＝110°．19．解：连结BC，如图，则∠DBC＋∠ECB＝∠D+∠E．所以∠A+∠B+∠C+∠D+∠E＝∠A+∠B+∠C+∠DBC＋∠ECB＝180°．20．解：有3种．分别以长为5cm，7cm，9cm；7cm，9cm13cm；5cm，9cm，13cm的线段为边能组成三角形．二、选择题21．A22．C23．C24．D25．C26．C27．D28．C29．C30．B31．B32．C33．C34．C（点拨：可能会错选A或B．有的同学一看到面积就认为与高相关，故错选A；有的同学认为平分内角必平分三角形的面积，故错选B．其实，因为△ABD与△ACD同高h，又S△ABD=S△ADC，即BD×h=·CD×h，所以，BD=CD，由此可知，AD为三角形ABC中BC边的中线．）35．D（点拨：可能会错选A或选C．错选A的同学，只注重平分内角而忽视了三角形的角平分线为一线段这一条件；而错选C的同学，实质上与错选A的同学犯的是同一个错误，显然这里“角平分线”与“一角的平分线”是一个意思，因为前提条件是说“AH必为三角形ABC 的”．）36．A（点拨：由三角形的三边关系知：若长度分别为2cm、4cm、6cm，不可以组成三角形；若长度分别为4cm、6cm、8cm，则可以组成三角形；若长度分别为2cm、4cm、8cm，则不可以组成三角形；若长度分别为2cm、6cm、8cm，则不可以组成三角形．即分别为2cm、4cm、6cm、8cm的木棒，从中任取三根，能组成三角形的个数为1，故应选A．）37．C（点拨：因为EG⊥AD，交点为H，AD平分∠BAC，所以在直角三角形AHE中，∠1＝90°－，在三角形ABC中，易知∠BAC＝180°－（∠2＋∠3），所以∠1＝90°－［180°－（∠2＋∠3）］=（∠3+∠2）．又因为∠1是三角形EBG的外角，所以∠1＝∠2＋∠G．所以∠G＝∠1－∠2＝（∠3+∠2）－∠2＝（∠3－∠2）．）38．A（点拨：由∠1＝∠2，知AD平分∠BAE，但AD不是三角形ABE内的线段，所以（1）不正确；同理，BE虽然经过三角形ABD边AD的中点G，但BE不是三角形ABD内的线段，故（2）不正确；由于CH⊥AD于H，故CH是三角形ACD边AD上的高，（3）正确．应选A．）三、解答题39．解析：要想求∠EDF的度数，我们可以利用平角定义，只要能求出∠EDB即可．而∠EDB 在三角形BDE中，只要能求出∠B就可以利用三角形内角和求∠EDB．而∠B又等于∠C，题中告诉了三角形DFC的一个外角∠AFD＝140°，所以我们能得出∠C的度数．解：因为∠AFD是三角形DCF的一个外角．所以∠AFD=∠C+∠FDC．即140°＝∠C＋90°．解得∠C＝50°．所以∠B＝∠C＝50°．所以∠EDB＝180°－90°－50°＝40°．所以∠FDE＝180°－90°－40°＝50°．40．解析：我们可以用字母代替甲、乙、丙、丁，用角度代表方向．把题中数据与图形一一对应，利用各方向的关系可求出丁岛分别在甲岛和乙岛的方向．解：设甲岛处的位置为A，乙岛处的位置为B，丙岛处的位置为D，丁岛处的位置为C．如图：因为丁岛在丙岛的正北方，所以CD⊥AB．因为甲岛在丁岛的南偏西52°方向，所以∠ACD＝52°．所以∠CAD＝180°-90°-52°＝38°．所以丁岛在甲岛的东偏北38°方向．因为乙岛在丁岛的南偏东40°方向，所以∠BCD=40°．所以∠CBD＝180°-90°-40°＝50°．所以丁岛在乙岛的西偏北50°方向．41．解析：利用角平分线的性质解．解：因为AI、BI、CI为三角形ABC的角平分线，所以∠BAD=∠BAC，∠ABI=∠ABC，∠HCI=∠ACB．所以∠BAD＋∠ABI+∠HCI=∠BAC+∠ABC+∠ACB＝（∠BAC+∠ABC+∠ACB）＝×180°＝90°．所以∠BAD＋∠ABI＝90°－∠HCI．又因为∠BAD＋∠ABI＝∠BID，90°－∠HCI＝∠CIH，所以∠BID＝∠CIH．所以∠BID和∠CIH是相等的关系．42．解析：本题已知一边长和三条高，我们可以利用三角形的面积公式求得另外两边长，三边相加即可得到三角形的周长．解：由三角形面积公式可得S△ABC＝BC×AD＝AC×BE，即16×3＝4×AC，所以AC＝12．由三角形面积公式可得S△ABC＝BC×AD＝AB×CF，即16×3＝6×AB．所以AB＝8．所以三角形ABC的周长为16+12+8＝36．43．解析：本题要求AC与AB的边长的差，且AC与AB的长度都不知道，不少同学感到无从下手．其实，只要我们仔细分析分析题中条件：三角形ABD的周长比三角形ACD的周长小5，即AC-AB+CD-BD=5，又AD是BC边上的中线，所以BD=CD．所以AC-AB=5．解：AC-AB=5．44．解析：在第（1）和第（2）问中，没有说明所给边长是腰长还是底边长，因此我们要进行分类讨论．在第（3）问中，只给出了三边长都是整数，而此三角形又是等腰三角形，所以其最长边小于8cm，我们可以用列表法一一列出各组边长．解：（1）如果腰长为4cm，则底边长为16-4-4＝8cm．三边长为4cm，4cm，8cm，不符合三角形三边关系定理．所以应该是底边长为4cm．所以腰长为（16-4）÷2＝6cm．三边长为4cm，6cm，6cm，符合三角形三边关系定理，所以另外两边长都为6cm．（2）如果腰长为6cm，则底边长为16-6-6＝4cm．三边长为4cm，6cm，6cm，符合三角形三边关系定理．所以另外两边长分别为6cm和4cm．如果底边长为6cm，则腰长为（16-6）÷2＝5cm．三边长为6cm，5cm，5cm，符合三角形三边关系定理，所以另外两边长都为5cm．（3）因为周长为16cm，且三边都是整数，所以三角形的最长边不会超过8cm且是等腰三角形，我们可用列表法，求出其各边长如下：7cm，7cm，2cm；6cm，5cm，5cm；6cm，6cm，4cm，共有这三种情况．45．解析：要想BE与DF平行，就要找平行的条件．题中只给出了∠A＝∠C=90°，BE平分∠ABC，DF平分∠ADC．那么我们是利用同位角相等呢还是利用同旁内角互补？经过仔细观察图形我们知道∠BFD是三角形ADF的外角，则∠BFD＝∠A+∠ADF．而∠ADF是∠ADC的一半，∠ABE是∠ABC的一半，所以我们选择用同旁内角互补来证平行．解：BE与DF平行．理由如下：由n边形内角和公式可得四边形内角和为（4-2）×180°＝360°．因为∠A＝∠C=90°，所以∠ADC+∠ABC=180°．因为BE平分∠ABC，DF平分∠ADC，所以∠ADF＝∠ADC，∠ABE＝∠ABC．因为∠BFD是三角形ADF的外角，所以∠BFD＝∠A+∠ADF．所以∠BFD＋∠ABE＝∠A+∠ADC＋∠ABC＝∠A+（∠ADC+∠ABC）＝90°＋90°＝180°．所以BE与DF平行．46．解析：我们发现1125°不能被180°整除，所以老师说少加了一个角的度数．我们可设少加的度数为x，利用整除求解．解：设少加的度数为x．则1125°＝180°×7-135°．因为0°<x<180°，所以x＝135°．所以此多边形的内角和为1125°+135°＝1260°．设多边形的边数为n，则（n－2）×180°＝1260°，解得n＝9．所以此多边形是九边形，少加的那个内角的度数是135°．47．解析：题中告诉了我们按要求拼成．解：如图：48．解析：本题首先要求考生在阅读数学课堂的一个学习片断后，对两名学生的说法提出自己的看法，这时考生应抓住题中条件“等腰三角形ABC的角A等于30°”这个不确定条件进行分析研究．当∠A是顶角时，设底角是α，∴30°+α+α=180°，α=75°，∴其余两底角是75°和75°．当∠A是底角时，设顶角是β，∴30°+30°+β=180°，β=120°，∴其余两角是30°和120°．由此说明李明和王华两同学都犯了以偏概全的答题的错误．对于第（2）问应在第（1）问的解答的基础上，可总结出“根据图形位置关系，实施分类讨论思想方法解多解型问题”，“考虑问题要全面”等．小结：三角形的中线、角平分线、高（线）是三角形中三条十分重要的线段，初学者常因不能准确理解其概念的实质内涵，而出现这样或那样的错误，现举例分析如下，以达到亡羊补牢或未雨绸缪的目的．49．解析：要求六边形的周长，必须先求出边EF和AF的长．由六边形ABCDEF的六个角都是120°，可知六边形的每一个外角的度数都是60°，如图4，如果延长BA，得到的∠PAF=60°，延长EF，得到的∠PFA=60°，两条直线相交形成三角形APF，在三角形APF 中，∠P的度数为180°－60°－60°＝60°，因此三角形APF是等边三角形．同样的道理，我们分别延长AB、DC，交于点G，那么三角形BGC为等边三角形．分别延长FE、CD交于点H，则三角形DHE也是等边三角形．所以∠P=∠G=∠H=60°．所以三角形GHP也是等边三角形．于是我们得到三角形APF、三角形BGC、三角形DHE、三角形GHP四个等边三角形．于是就把多边形的问题转化为和等边三角形有关的问题．利用等边三角形的三边相等的性质，可以轻松的求出AF和EF的长，从而求出六边形ABCDEF的周长．解：如图4，分别作直线AB、CD、EF的延长线使它们交于点G、H、P．因为六边形ABCDEF的六个角都是120°，所以六边形ABCDEF的每一个外角的度数都是60°．所以三角形APF、三角形BGC、三角形DHE、三角形GHP都是等边三角形．所以GC=BC=8cm，DH=DE＝6cm．所以GH=8＋11＋6＝25cm，FA=PA=PG-AB-BG=25-2-8＝15cm，EF=PH-PF-EH=25-15-6＝4cm．所以六边形的周长为2＋8+11+6+4+15＝46cm．多边形及其内角和一、选择题:(每小题3分,共24分)1.一个多边形的外角中,钝角的个数不可能是( )A.1个B.2个C.3个D.4个2.不能作为正多边形的内角的度数的是( )A.120°B.(12847)° C.144° D.145°3.若一个多边形的各内角都相等,则一个内角与一个外角的度数之比不可能是( )A.2:1B.1:1C.5:2D.5:44.一个多边形的内角中,锐角的个数最多有( )A.3个B.4个C.5个D.6个5.四边形中,如果有一组对角都是直角,那么另一组对角可能( )A.都是钝角;B.都是锐角C.是一个锐角、一个钝角D.是一个锐角、一个直角6.若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( )A.十三边形B.十二边形C.十一边形D.十边形7.若一个多边形共有十四条对角线,则它是( )A.六边形B.七边形C.八边形D.九边形8.若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为( )A.90°B.105°C.130°D.120°二、填空题:(每小题3分,共15分)1.多边形的内角中,最多有________个直角.2.从n边形的一个顶点出发,最多可以引______条对角线, 这些对角线可以将这个多边形分成________个三角形.3.如果一个多边形的每一个内角都相等,且每一个内角都大于135°, 那么这个多边形的边数最少为________.4.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比为9:2,则这个多边形的边数为_________.5.每个内角都为144°的多边形为_________边形.三、基础训练:(每小题12分,共24分)1.如图所示,用火柴杆摆出一系列三角形图案,按这种方式摆下去,当摆到20层(n=20)时,需要多少根火柴?2.一个多边形的每一个外角都等于24°,求这个多边形的边数.四、提高训练:(共15分)一个多边形的每一个内角都相等,一个内角与一个外角的度数之比为m:n,其中m,n是互质的正整数,求这个多边形的边数(用m,n表示)及n的值.五、探索发现:(共18分)从n边形的一个顶点出发,最多可以引多少条条对角线?请你总结一下n边形共有多少条对角线.六、中考题与竞赛题:(共4分)若一个多边形的内角和等于1080°,则这个多边形的边数是( )A.9B.8C.7D.6答案:一、1.D 2.D 3.D 4.A 5.C 6.A 7.B 8.C二、1.4 2.(n-3) (n-2) 3.9 4.11 5.十三、1.630根 2.15四、边数为2()m nn+,n=1或2.五、(n-3)(3)2n n-条六、B.多边形练习题一、判断题．1．当多边形边数增加时，它的内角和也随着增加．（）n=3 n=2n=12．当多边形边数增加时．它的外角和也随着增加．（）3．三角形的外角和与一多边形的外角和相等．（）4．从n边形一个顶点出发，可以引出（n一2）条对角线，得到（n一2）个三角形．（）5．四边形的四个内角至少有一个角不小于直角．（）二、填空题．1．一个多边形的每一个外角都等于30°，则这个多边形为边形．2．一个多边形的每个内角都等于135°，则这个多边形为边形．3．内角和等于外角和的多边形是边形．4．内角和为1440°的多边形是．5．一个多边形的内角的度数从小到大排列时，恰好依次增加相同的度数，其中最小角为100°，最大的是140°，那么这个多边形是边形．6．若多边形内角和等于外角和的3倍，则这个多边形是边形．7．五边形的对角线有条，它们内角和为．8．一个多边形的内角和为4320°，则它的边数为．9．多边形每个内角都相等，内角和为720°，则它的每一个外角为．10．四边形的∠A、∠B、∠C、∠D的外角之比为1：2：3：4，那么∠A：∠B：∠C：∠D= ．11．四边形的四个内角中，直角最多有个，钝角最多有个，锐角最多有个．12．如果一个多边形的边数增加一条，那么这个多边形的内角和增加，外角和增加．三、选择题．1．多边形的每个外角与它相邻内角的关系是（）A．互为余角 B．互为邻补角 C．两个角相等 D．外角大于内角2．若n边形每个内角都等于150°，那么这个n边形是（）A．九边形 B．十边形 C．十一边形 D．十二边形3．一个多边形的内角和为720°，那么这个多边形的对角线条数为（）A．6条 B．7条 C．8条 D．9条4．随着多边形的边数n的增加，它的外角和（）A．增加 B．减小 C．不变 D．不定5．若多边形的外角和等于内角和的和，它的边数是（）A．3 B．4 C．5 D．76．一个多边形的内角和是1800°，那么这个多边形是（）A．五边形 B．八边形 C．十边形 D．十二边形7．一个多边形每个内角为108°，则这个多边形（）A．四边形 B，五边形 C．六边形 D．七边形8，一个多边形每个外角都是60°，这个多边形的外角和为（）A．180° B．360° C．720° D．1080°9．n边形的n个内角中锐角最多有（）个．A．1个 B．2个 C．3个 D．4个10．多边形的内角和为它的外角和的4倍，这个多边形是（）A．八边形 B．九边形 C．十边形 D，十一边形四、解答题．1．一个多边形少一个内角的度数和为2300°．（1）求它的边数；（2）求少的那个内角的度数．2．一个八边形每一个顶点可以引几条对角线？它共有多少条对角线？n 边形呢？3．已知多边形的内角和为其外角和的5倍，求这个多边形的边数．4．若一个多边形每个外角都等于它相邻的内角的21，求这个多边形的边数．5．多边形的一个内角的外角与其余内角的和为600°，求这个多边形的边数．6．n 边形的内角和与外角和互比为13：2，求n ．7．五边形ABCDE 的各内角都相等，且AE ＝DE ，AD ∥CB 吗？8．将五边形砍去一个角，得到的是怎样的图形？9．四边形ABCD 中，∠A+∠B=210°，∠C ＝4∠D ．求：∠C 或∠D 的度数．10．在四边形ABCD 中，AB ＝AC ＝AD ，∠DAC ＝2∠BAC ．求证：∠DBC ＝2∠BDC ．。

数学初二数学习题集题目一：整数的运算1. 计算：(-5) + 7 - (-2) + (-9) + 112. 将以下小数用分数表示：0.25, 0.6, -0.75, -3.23. 求以下两个数的积的相反数：-3（2/3）和-4（4/5）题目二：代数的基本概念1. 判断以下哪些是代数式，哪些是算式：3x + y, 4 + 2 = 6, 3 + 2y = 82. 用适当的数值代入变量，求解以下方程：a) 2x + 5 = 17b) 3y - 8 = 7题目三：平面图形的性质与计算1. 给出三角形ABC的三条边长分别为5cm, 8cm, 10cm，判断该三角形的类型并说明理由。

2. 已知平行四边形ABCD中，AB = 3cm，BC = 5cm，求对角线BD的长度。

3. 给出一个梯形ABCD，已知AD平行BC，AB = 6cm，BC = 9cm，CD = 12cm，求AD的长度。

题目四：数据的统计与分析1. 对以下一组数据进行频数统计，并绘制频数直方图：2, 2, 3, 4, 4, 4, 5, 5, 5, 5, 6, 6, 7, 8, 8, 9, 102. 某班级20位学生的数学成绩如下：78, 85, 92, 80, 88, 89, 76, 81, 95, 84, 79, 93, 87, 90, 83, 86, 91, 85, 88, 94a) 求该班级的平均数b) 求该班级的中位数c) 求该班级的众数题目五：概率与统计1. 一枚硬币抛掷3次，计算出现3次正面朝上的概率。

2. 一副标准扑克牌中，红桃牌有13张，从中抽取5张牌，计算抽到全是红桃牌的概率。

3. 某农场有100头奶牛，统计数据显示，每头奶牛生第二胎是公牛的概率为0.5，如果第二胎是母牛，则生第三胎是公牛的概率为0.4。

根据这些数据，计算该农场最终会有多少头公牛。

题目六：几何体的计算1. 给定一个正方体的棱长为3cm，求其体积和表面积。

2. 某房间的长、宽、高分别为4m，3m，2.5m，求其体积。

新版人教版八年级数学上册全册习题集目录1. 第一章：整数2. 第二章：有理数3. 第三章：代数式4. 第四章：图形的认识5. 第五章：图形的性质6. 第六章：相交线与平行线7. 第七章：三角形8. 第八章：全等三角形9. 第九章：五边形与多边形10. 第十章：集合第一章：整数本章介绍整数的概念、整数之间的大小比较、整数的加减法运算以及整数的乘法运算。

通过题练，加深对整数概念的理解，并掌握整数的运算方法和技巧。

第二章：有理数本章介绍有理数的概念、有理数之间的大小比较、有理数的加减法运算以及有理数的乘除法运算。

通过题练，巩固对有理数概念的掌握，提高有理数运算的能力。

第三章：代数式本章介绍代数式的概念、代数式的计算与化简、代数式的值、代数式的应用等内容。

通过题练，培养代数思维能力，掌握代数式的运算技巧。

第四章：图形的认识本章介绍图形的基本概念和常见图形的性质。

通过题练，加深对图形认识的理解，掌握图形的命名、计算面积和周长的方法。

第五章：图形的性质本章介绍圆和与圆有关的性质，以及相似图形的性质。

通过题练，加深对圆和相似图形性质的理解，提高解决相关问题的能力。

第六章：相交线与平行线本章介绍平行线和相交线的性质，以及平行线与相交线间夹角和对应角的关系。

通过题练，掌握平行线和相交线的性质，提高几何问题的解决能力。

第七章：三角形本章介绍三角形的定义、分类和性质，以及三角形的角平分线和垂线的性质。

通过题练，加深对三角形性质的理解，提高解决相关问题的能力。

第八章：全等三角形本章介绍全等三角形的概念和性质，以及全等三角形的判定方法。

通过题练，掌握全等三角形的判定和应用，提高解决相关问题的能力。

第九章：五边形与多边形本章介绍五边形和多边形的定义、分类和性质，以及多边形的内角和外角的关系。

通过题练，加深对五边形和多边形性质的理解，提高解决相关问题的能力。

第十章：集合本章介绍集合及其表示方法、集合的运算和集合的应用。

通过题练，培养集合思维能力，巩固对集合概念的掌握。

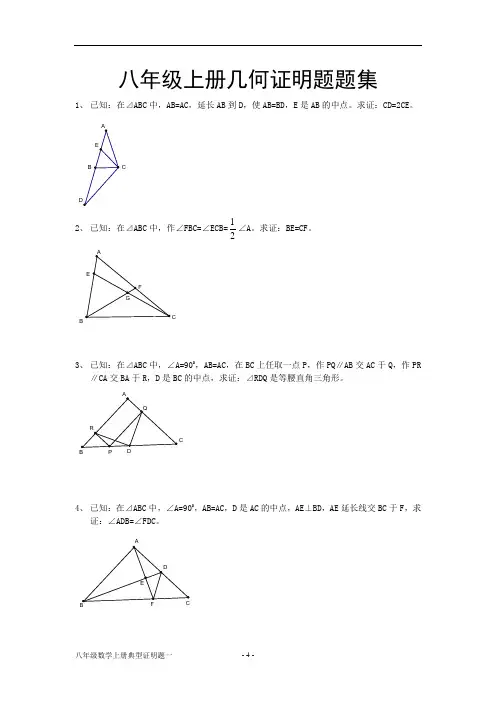
C八年级上册几何证明题题集1、 已知：在⊿ABC 中，AB=AC ，延长AB 到D ，使AB=BD ，E 是AB 的中点。

求证：CD=2CE 。

2、 已知：在⊿ABC 中，作∠FBC=∠ECB=21∠A 。

求证：BE=CF 。

B3、 已知：在⊿ABC 中，∠A=900，AB=AC ，在BC 上任取一点P ，作PQ ∥AB 交AC 于Q ，作PR∥CA 交BA 于R ，D 是BC 的中点，求证：⊿RDQ 是等腰直角三角形。

CB4、 已知：在⊿ABC 中，∠A=900，AB=AC ，D 是AC 的中点，AE ⊥BD ，AE 延长线交BC 于F ，求证：∠ADB=∠FDC 。

ABB DCA B C DE P 图 ⑴5、如图甲，Rt ∆ABC 中，AB=AC ，点D 、E 是线段AC 上两动点，且AD=EC ，AM ⊥BD ，垂足为M ，AM 的延长线交BC 于点N ，直线BD 与直线NE 相交于点F 。

（1）试判断∆DEF 的形状，并加以证明。

（2）如图乙，若点D 、E 是直线AC 上两动点，其他条件不变，试判断∆DEF 的形状，并加以证明。

6、已知：在⊿ABC 中BD 、CE 是高，在BD 、CE 或其延长线上分别截取BM=AC 、CN=AB ，求证：MA ⊥NA 。

7、已知：如图(1)，在△ABC 中，BP 、CP 分别平分∠ABC 和∠ACB ，DE 过点P 交AB 于D ，交AC 于E ，且DE ∥BC ．求证：DE －DB=EC ．①②③图88、△ABC为正三角形，点M是射线BC上任意一点，点N是射线CA上任意一点，且BM=CN，直线BN与AM相交于Q点，就下面给出的三种情况，如图8中的①②③，先用量角器分别测量∠BQM的大小，然后猜测∠BQM等于多少度．并利用图③证明你的结论．9、在Rt△ABC中，AB＝AC，∠BAC=90°，O为BC的中点。

(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系(不要求证明)；(2)如果点M、N分别在线段AB、AC上移动，在移动中保持AN＝BM，请判断△OMN的形状，并证明你的结论。

初二上学期数学练习题在初二上学期，数学是一门重要的学科，它帮助我们培养逻辑思维和解决问题的能力。

下面是一些初二上学期数学练习题，帮助同学们巩固所学的知识，并提升数学解题能力。

1. 判断题：（每题2分，共10个小题）( ) 1. 两个互质的数的最大公因数一定是1。

( ) 2. 分子比分母小的真分数一定小于1。

( ) 3. 两个相交的直线一定共有一个交点。

( ) 4. 正方形是长方形的一种特殊情况。

( ) 5. 对称轴将图形分为两个对称的部分。

2. 选择题：（每题3分，共15个小题）( ) 1. 下列哪个数是无理数？A. 4B. -3C. 2.5D. √5( ) 2. 下列哪个点不在坐标图中？A. (2, 3)B. (-5, 0)C. (0, 0)D. (1, -1)( ) 3. 若1/2 ÷ a = 2/3，则a的值为多少？A. 1B. 3/4C. 3/2D. 4/3( ) 4. 解方程2x + 3 = 7的解是：A. x = 2B. x = 3C. x = 5D. x = 7( ) 5. 一个立方体的体积是64立方厘米，它的边长是多少？A. 2 cmB. 4 cmC. 6 cmD. 8 cm3. 计算题：（每题5分，共3个小题）1) 计算：20 ÷ (4 - 2) + 5 × 2 = ?2) 某员工的每小时工资是30元，他这个月工作了20天，每天工作8小时，应发工资是多少？3) 一个数字的十分之一加上三分之一等于2，这个数字是多少？4. 解答题：（每题15分，共2个小题）1) 分解因数：将36分解为两个不同的质数之积。

2) 已知两个直角边的长分别是3cm和4cm，求斜边的长。

5. 应用题：（每题20分，共2个小题）1) 一袋米重4.5千克，小明买了9袋米，问他买了多少千克的米？2) 小华每天骑自行车去上学，单程用时30分钟，来回用时1小时。

如果每天骑行的距离是12公里，求小华骑自行车的平均速度。

C第一章 勾股定理评估试卷（1）一、选择题（每小题3分，共30分）1. 直角三角形一直角边长为12，另两条边长均为自然数，则其周长为( ). （A ）30 （B ）28 （C ）56 （D ）不能确定2. 直角三角形的斜边比一直角边长2 cm ，另一直角边长为6 cm ，则它的斜边长 （A ）4 cm （B ）8 cm （C ）10 cm（D ）12 cm3. 已知一个Rt △的两边长分别为3和4，则第三边长的平方是（ ） （A ）25（B ）14（C ）7（D ）7或254. 等腰三角形的腰长为10,底长为12,则其底边上的高为( ) （A ）13 （B ）8 （C ）25 （D ）645. 五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（ ）715242520715202425157252024257202415(A)(B)(C)(D)6. 将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( )（A ） 钝角三角形 （B ） 锐角三角形 （C ） 直角三角形 （D ） 等腰三角形. 7. 如图小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( ) （A ） 25 （B ） 12.5 （C ） 9 （D ） 8.58. 三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( ) （A ） 等边三角形 （B ） 钝角三角形 （C ） 直角三角形 （D ） 锐角三角形.9.△ABC 是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°，AC=30米，AB=50米，如果要在这块空地上种植草皮，按每平方米草皮a 元计算，那么共需要资金（ ）.（A ）50a 元 （B ）600a 元 （C ）1200a 元 （D ）1500a 元10.如图，AB ⊥CD 于B ，△ABD 和△BCE 都是等腰直角三角形，如果CD=17，BE=5，那么AC 的长为（ ）. （A ）12 （B ）7 （C ）5 （D ）135米3米（第10题） （第11题） （第14题）二、填空题（每小题3分，24分）11. 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要____________米. 12. 在直角三角形ABC 中，斜边AB =2，则222AB AC BC ++=______. 13. 直角三角形的三边长为连续偶数，则其周长为 .14. 如图，在△ABC 中，∠C=90°，BC=3，AC=4.以斜边AB 为直径作半圆，则这个半圆的面积是____________.（第15题） （第16题） （第17题）15. 如图，校园内有两棵树，相距12米，一棵树高13米，另一棵树高8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞___________米.16. 如图，△ABC 中，∠C =90°，AB 垂直平分线交BC 于D 若BC =8，AD =5，则AC 等于______________.17. 如图，四边形ABCD 是正方形，AE 垂直于BE ，且AE =3，BE =4，阴影部分的面积是______.18. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边和长为7cm,则正方形A ，B ，C ，D 的面积之和为___________cm 2.三、解答题（每小题8分，共40分）19. 11世纪的一位阿拉伯数学家曾提出一个“鸟儿捉鱼”的问题：EABCDBDE ABCD第18题图7cm“小溪边长着两棵棕榈树，恰好隔岸相望.一棵树高是30肘尺（肘尺是古代的长度单位），另外一棵高20肘尺；两棵棕榈树的树干间的距离是50肘尺.每棵树的树顶上都停着一只鸟.忽然，两只鸟同时看见棕榈树间的水面上游出一条鱼，它们立刻飞去抓鱼，并且同时到达目标.问这条鱼出现的地方离开比较高的棕榈树的树跟有多远？20. 如图，已知一等腰三角形的周长是16，底边上的高是4.求这个三角形各边的长.21. 如图，A、B两个小集镇在河流CD的同侧，分别到河的距离为AC=10千米，BD=30千米，且CD=30千米，现在要在河边建一自来水厂，向A、B两镇供水，铺设水管的费用为每千米3万，请你在河流CD上选择水厂的位置M，使铺设水管的费用最节省，并求出总费用是多少？22. 如图所示的一块地，∠ADC=90°，AD=12m，CD=9m，AB=39m，BC=36m，求这块地的面积。

初二上册数学第一章习题1．填空：(1)如图3，已知AD∥BC，AD＝CB，要用边角边公理证明△ABC≌△CDA，需要三个条件，这三个条件中，已具有两个条件，一是AD＝CB(已知)，二是( )＝( )；还需要一个条件( )＝( )(这个条件可以证得吗)．(2)如图4，已知AB＝AC，AD＝AE，∠1＝∠2，要用边角边公理证明△ABD≌ACE，需要满足的三个条件中，已具有两个条件：( )＝( )，( )＝( )；还需要一个条件（）=（）(这个条件可以证得吗)．2、已知：AD∥BC，AD＝ CB(如图3)．求证：△ADC≌△CBA．3、已知：点A、F、E、C在同一条直线上， AF＝CE，BE∥DF，BE＝DF．求证：△ADF ≌△CBE．4、如图19.2.4，在△ABC中，AB＝AC，AD平分∠BAC，求证：△ABD≌△ACD．图19.2.45、如图所示, 根据题目条件，判断下面的三角形是否全等． （1） AC ＝DF ， ∠C ＝∠F ， BC ＝EF ； （2） BC ＝BD ， ∠ABC ＝∠ABD ．6、小兰做了一个如图所示的风筝，其中∠EDH=∠FDH, ED=FD ，将上述条件标注在图中，小明不用测量就能知道EH=FH 吗7、点M 是等腰梯形ABCD 底边AB 的中点，求证DM=CM ，∠ADM ＝∠BCM ．8、如图,已知AC 和BD 相交于O,且BO ＝DO,AO ＝CO,下列判断正确的是（ ） A ．只能证明△AOB ≌△CODB ．只能证明△AOD ≌△COBC ．只能证明△AOB ≌△COBD ．能证明△AOB ≌△COD 和△AOD ≌△COBHE FDOBD9、如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是（）A．甲和乙Ｂ．乙和丙Ｃ．只有乙Ｄ．只有丙10．如图,已知MB＝ND,∠MBA＝∠NDC,下列不能判定△ABM≌△CDN的条件是（）A．∠M＝∠N B．AB＝CD C．AM＝CN D．AM∥CN11、某同学把一块三角形的玻璃打碎也成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是（）A．带①去B．带②去C．带③去D．带①和②去12、下列条件不可以判定两个直角三角形全等的是（）A．两条直角边对应相等B．两个锐角对应相等C．一条直角边和它所对的锐角对应相等D．一个锐角和锐角所对的直角边对应相等13、如图,是一个三角形测平架,已知AB＝AC,在BC的中点D挂一个重锤,自然下垂．调整架身,使点A恰好在重锤线上,AD和BC的关系为＿＿＿＿14．已知如图,AE＝AC,AB＝AD,∠EAB＝∠CAD,试说明:∠B＝∠D15、如图,已知线段AB、CD相交于点O,AD、CB的延长线交于点E,OA=OC,EA=EC,请说明∠A=∠C.16、沿矩形ABCD的对角线BD翻折△ABD得△A/BD,A/D交BC于F,如图所示,△BDF是何种三角形请说明理由.17、已知：如图1，AB＝AC，F、E分别是AB、AC的中点．求证：△ABE≌△ACF．18、下列说法正确的是( )A. 有两边和一个角相等的两个三角形全等B. 两条直角边对应相等的两个直角三角形全等C. 三角形的一条中线把三角形分成的两个小三角形全等D. 有两边和其中一边的对角对应相等的两个三角形全等19、下列说法错误的是( )A. 有两角和其中一角的对边对应相等的两个三角形全等B. 全等三角形对应的角平分线相等C. 斜边和一个锐角分别相等的两个直角三角形全等D. 在△ABC和△A’B’C’中, 若AB=BC=CA, A’B’=B’C’=C’A’, 则△ABC≌△A’B’C’20、在下列各组的条件中, 不能判定△ABC和△DEF全等的是( )A. AB=DE, ∠B=∠E, ∠C=∠F B、AC=DF, BC=DE, ∠C=∠DC. AB=EF, ∠A=∠E, ∠B=∠F D、∠A=∠F, ∠B=∠E, AC=DE21、根据下列各组的条件, 能判定△ABC≌△A’B’C’的是( )A. AB=A’B’, BC=B’C’, ∠A=∠A’B. ∠A=∠A’, ∠C=∠C’, AC=A’C’C. AB=A’B’, S△ABC=S△A’B’C’D. ∠A=∠A’, ∠B=∠B’, ∠C=∠C’22、如图所示, 将两根钢条AA’、BB’的中点O连在一起, 使AA’、BB’可以绕着点O自由旋转, 就做成了一个测量工件, 则A’B’的长等于内槽宽AB, 那么判定△OAB ≌△OA’B’的理由是( )A. 边角边B. 角边角C. 边边边D. 角角边23、下列条件中不能作出惟一直角三角形的是( )A. 已知两个锐角B. 已知一条直角边和一个锐角C. 已知两条直角边D. 已知一条直角边和斜边二. 填空题24、△ABC≌△A’B’C’, AB=24, S△A’B’C’=180, 则△ABC中AB边上的高是_______________.25、如图, 在△ABC和△ABD中, ∠C=∠D=900, 要使△ABC≌△ABD, 还需增加一个条件是___________________.(25) (26) (27)26、如图, 线段AC和BD相交于O点, 且OA=OC, AE29、如果△ABC≌△DEF, 且△ABC 的周长是100cm, A、B分别与D、E对应, 且AB=30cm, DF=25cm, 那么BC的长为_____三. 解答题30、.如图所示, 已知AB=DC, AE=DF, CE=BF, 试说明: AF=DE.31、如图有两个长度相同的滑梯, 左边滑梯的高度AC与右边滑梯水平方向的长度DF 相等, 两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系33、. 如图, 已知点A、C、B、D在同一直线上, AM=CN, BM=DN, ∠M=∠N, 试说明: AC=BD.一、耐心填一填1．在△ABC 和A B C '''△中，AB A B ''=，A A '=∠∠，要使ABC A B C '''△≌△，则需增加的条件为______．（写一个即可） 2．已知ABC DEF △≌△，5cm BC EF ==，△ABC 的面积是220cm ，那么△DEF 中EF 边上的高是______cm ．3．如图1，如果AB ∥CD ，AD ∥BC ，E ，F 为AC 上的点，AE ＝CF ， 图中全等的三角形有__对．4．如图2，已知AD ，BC 相交于O 点，AB AC =，BD CD =，写出图中另一对相等的线段______．5．如图3，AB ∥DE ，AB DE =，AE ，BD 相交于C 点，在BC ，CD 上分别取M ，N 两点，使AM EN =，则AM 和EN 一定平行，这个说法正确吗答：______．6．如图4，点D ，E 是BC 上两点，且=AB AC ，=AD AE ，要使ABE ACD △≌△，根据SSS 的判定方法还需要给出的条件是______或______．7．7、如图5，AB ，CD 相交于点O ，AD ＝CB ，请你补充一个条件，使得△AOD ≌△COB ．你补充的条件是______．8、如图18，△ABC 中，∠C ＝90°，AD 平分∠BAC ，AB ＝5，CD ＝2，则△ABD 的面积是______．二、精心选一选 1．下列命题中，错误的是（ ） A ．全等三角形对应边上的中线相等B ．面积相等的两个三角形是全等三角形C ．全等三角形对应边上的高线相等D ．全等三角形对应角的平分线相等3．如图7，PD ⊥AB ，PE ⊥AC ，垂足分别为D ，E ，且=PD PE ，判定△APD 与△APE 全等的理由不应该是（ ）A ．SASB ．AASC ．SSSD ．HLA DE C 图1 BF A D EC图3B AD O C 图2 B AE C图4 B A D C图7B P EADEC 图8 BF O ADECB图9F A D O C B 图5A D CB 图18E 1 BADC24．如图8，已知AB ，CD 相交于O 点，AOC BOD △≌△，E ，F 分别在OA ，OB 上，要使EOC FOD △≌△，添加的一个条件不可以是（ ） A ．∠OCE ＝∠ODF B ．∠CEA ＝∠DFB C ．CE ＝DF D ．OE ＝OF5．如图9，在△ABC 中，AB ＝AC ，AD 是ABC △的角平分线，DE AB DF AC ⊥⊥，，垂足分别为E ，F ．则下列四个结论：①AD 上任意一点到点C ，B 的距离相等；②AD 上任意一点到边AB ，AC 的距离相等；③BD ＝CD ，AD ⊥BC ；④∠BDE ＝∠CDF ．其中，正确的个数为 （ ）A ．1个B ．2个C ．3个D ．4个6．△ABC 中，AB ＝AC ，三条高AD ，BE ，CF 相交于O ，那么图10中全等的三角形有（ ） A ．5对 B ．6对 C ．7对 D ．8对三、用心想一想 1、如图，∠B ＝∠E ，AB ＝EF ，BD ＝EC ，那么△ABC 与 △FED 全等吗为什么2、如图，已知AB=AD ，AC=AE ，∠1=∠2，求证：BC=DE3、如图11是一个测平架，AB ＝AC ，在BC 中点D 挂一个重锤，自然下垂，使用时调整架身，使点A 恰好在重锤线上，就说明此时BC 处于水平位置，你能说明其中的道理吗AD图11AD E C B图10 F4、已知:如图13，A F C D ，，，四点在同一直线上，AF ＝CD ，AB ∥DE ，且=AB DE ． 求证：（1）ABC DEF △≌△；（2）CBF FEC ∠∠．5、如图14，AC ＝AE ，∠BAM ＝∠BND ＝∠EAC ， 图中是否存在与△ABE 全等的三角形并证明．6、如图，已知AC ⊥AB ，DB ⊥AB ，AC ＝BE ，AE ＝BD ，试猜想线段CE 与DE 的大小与位置关系，并证明你的结论.A DF CB 图E ADMCB 图14 E NA CEDB。

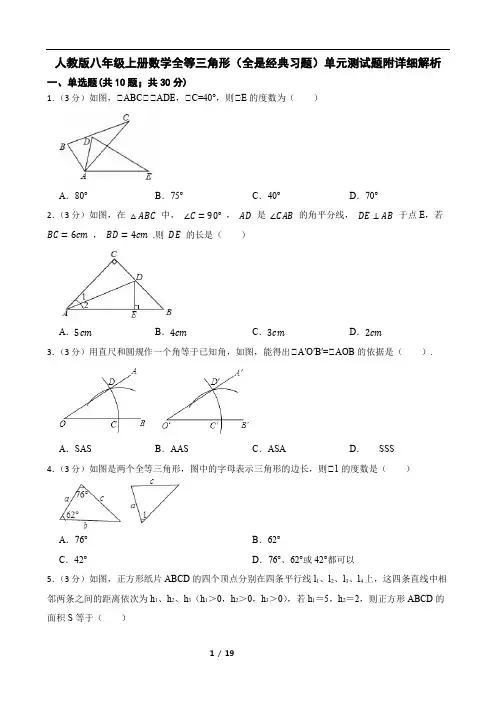
人教版八年级上册数学全等三角形（全是经典习题）单元测试题附详细解析一、单选题(共10题；共30分)1．（3分）如图，△ABC△△ADE，△C=40°，则△E的度数为（）A．80°B．75°C．40°D．70°2．（3分）如图，在△ABC中，∠C=90°，AD是∠CAB的角平分线，DE⊥AB于点E，若BC=6cm，BD=4cm.则DE的长是（）A．5cm B．4cm C．3cm D．2cm3．（3分）用直尺和圆规作一个角等于已知角，如图，能得出△A′O′B′=△AOB的依据是（）.A．SAS B．AAS C．ASA D．SSS4．（3分）如图是两个全等三角形，图中的字母表示三角形的边长，则△1的度数是（）A．76°B．62°C．42°D．76°、62°或42°都可以5．（3分）如图，正方形纸片ABCD的四个顶点分别在四条平行线l1、l2、l3、l4上，这四条直线中相邻两条之间的距离依次为h1、h2、h3（h1＞0，h2＞0，h3＞0），若h1＝5，h2＝2，则正方形ABCD的面积S等于（）A．34B．89C．74D．1096．（3分）下列说法正确的是（）A．周长相等的两个三角形全等B．面积相等的两个三角形全等C．三个角对应相等的两个三角形全等D．三条边对应相等的两个三角形全等7．（3分）如图，直线l1，l2，l3表示三条公路。

现要建造一个洗手台P，使P到三条公路的距离都相等，则洗手台P可选择的点有（）A．一处B．二处C．三处D．四处8．（3分）如图，一块玻璃被打碎成三块，如果要去玻璃店配一块完全一样的玻璃，那么最合理的办法是（）A．带①去B．带②去C．带③去D．带①②③去9．（3分）如图，若要用“HL”证明Rt△ABC△Rt△ABD，则还需补充的条件是（）A．AC=AD或BC=BD B．AC=AD且BC=BDC．△BAC=△BAD D．以上都不对10．（3分）如图，边长为5的大正方形ABCD是由四个全等的直角三角形和一个小正方形EFGH组成，连结AF并延长交CD于点M.若AH＝GH，则CM的长为（）A．12B．34C．1D．54二、填空题(共5题；共15分)11．（3分）如图所示，AB=AC，AD=AE，△BAC=△DAE，△1=25°，△2=30°，则△3=．12．（3分）如图，△ABC的三边AB、BC、CA的长分别为30、40、15，点P是三条角平分线的交点，将△ABC分成三个三角形，则SΔAPB︰SΔBPC︰SΔCPA等于13．（3分）如图，AB⊥BC，AD⊥DC，请你添加一个条件，利用“HL”，证明Rt△ABC≌Rt△ADC.14．（3分）如图，△AOB=30°，OP平分△AOB，PD△OB于D，PC△OB交OA于C，若PC=10，则PD=．15．（3分）如图，C 为线段AE 上一动点（不与A、E 重合），在AE 同侧分别作等边△ABC 和等边△CDE，AD 与BE 交于点O，AD 与BC 交于点P，BE 与CD 交于点Q，连接PQ，以下五个结论：①AD=BE；②PQ△AE；③AP=BQ；④DE=DP；⑤△AOB=60°，其中正确的结论是（把你认为正确的结论的序号都填上）．三、解答题(共11题；共75分)16．（5分）如图，点E，F在BC上，BE＝CF，△A＝△D ，△B＝△C．求证：△ABF△△DCE。

第一章一、填空题（每小题3分，共27分） 1．如果△ABC 和△DEF 全等,△DEF 和△GHI 全等，则△ABC 和△GHI _一定全等， 如果△ABC 和△DEF 不全等，△DEF 和△GHI 全等，则△ABC 和△GHI __全等．(填“一定”或“不一定”或“一定不”） 2．如图1，△ABC ≌△ADE ，∠B ＝100°，∠BAC ＝30°，那么∠AED ＝__．3．△ABC 中,∠BAC ∶∠ACB ∶∠ABC ＝4∶3∶2，且△ABC ≌△DEF ,则∠DEF ＝____． 4．如图2,BE ，CD 是△ABC 的高，且BD ＝EC ，判定△BCD ≌△CBE 的依据是“__”．5．如图3,AB ，CD 相交于点O ,AD ＝CB ，请你补充一个条件，使得△AOD ≌△COB ．你补充的条件是 _ ． 6．如图4，AC ，BD 相交于点O ，AC ＝BD ，AB ＝CD ，写出图中两对相等的角____．7．如图5,△ABC 中，∠C ＝90°，AD 平分∠BAC ，AB ＝5，CD ＝2，则△ABD 的面积是______．8．地基在同一水平面上，高度相同的两幢楼上分别住着甲、乙两位同学，有一天，甲对乙说：“从我住的这幢楼的底部到你住的那幢楼的顶部的直线距离,等于从你住的那幢楼的底部到我住的这幢楼的顶部的直线距离．"你认为甲的话正确吗?答：____．9．如图6，直线AE ∥BD ,点C 在BD 上，若AE ＝4，BD ＝8，△ABD 的面积为16，则ACE △的面积为__． 二、选择题（每小题3分，共24分） 1．如图7,P 是∠BAC 的平分线AD 上一点，PE ⊥AB 于E ,PF ⊥AC 于F ，下列结论中不正确的是（ )A ．PE PF = B ．AE AF = C ．△APE ≌△APF D ．AP PE PF =+2．下列说法中：①如果两个三角形可以依据“AAS"来判定全等,那么一定也可以依据“ASA ”来判定它们全等；②如果两个三角形都和第三个三角形不全等,那么这两个三角形也一定不全等；③要判断两个三角形全等,给出的条件中至少要有一对边对应相等．正确的是（ )A ．①和②B ．②和③C ．①和③D ．①②③3．如图8， AD 是ABC △的中线，E ，F 分别是AD 和AD 延长线上的点，且DE DF =，连结BF ，CE ．下列说法:①CE ＝BF ；②△ABD 和△ACD 面积相等；③BF ∥CE ；④△BDF ≌△CDE ．其中正确的有( )A ．1个 B ．2个 C ．3个 D ．4个4．直角三角形斜边上的中线把直角三角形分成的两个三角形的关系是（ ） A ．形状相同 B ．周长相等 C ．面积相等 D ．全等 5．如图9，AD AE =,= = =100 =70BD CE ADB AEC BAE ︒︒，，∠∠∠,下列结论错误的是( ）A ．△ABE ≌△ACD B ．△ABD ≌△ACE C ．∠DAE =40° D ．∠C =30°6．已知:如图10,在△ABC 中，AB ＝AC ，D 是BC 的中点，DE ⊥AB 于E ，DF ⊥AC 于F ，则图中共有全等三角形（ ） A ．5对 B ．4对 C ．3对 D ．2对A D EC B 图1 AD E C B 图2A D O CB 图3 A DO C B 图4 A D C B 图5ADC B 图6E A D C B 图7E FADCB图8 E F A D OC B 图9A DE C B 图10F G A EC 图11B A ′ E ′D7．将一张长方形纸片按如图11所示的方式折叠，BC BD ，为折痕，则CBD ∠的度数为( )A ．60°B ．75°C ．90°D ．95° 8．根据下列已知条件，能惟一画出△ABC 的是（ )A ．AB ＝3,BC ＝4，CA ＝8 B ．AB ＝4，BC ＝3,∠A ＝30° C ．∠A ＝60°，∠B ＝45°，AB ＝4D ．∠C ＝90°，AB ＝6 三、解答题 (本大题共69分) 1．（本题8分）请你用三角板、圆规或量角器等工具,画∠POQ ＝60°，在它的边OP 上截取OA ＝50mm ，OQ 上截取OB ＝70mm ，连结AB ，画∠AOB 的平分线与AB 交于点C ，并量出AC 和O C 的长 ．（结果精确到1mm ，不要求写画法)．2．（本题10分)已知：如图12，AB ＝CD ，DE ⊥AC ,BF ⊥AC ，E ，F 是垂足,DE BF =．求证：（1)AF CE =;（2）AB CD ∥．3．（本题11分）如图13,工人师傅要检查人字梁的∠B 和∠C 是否相等，但他手边没有量角器,只有一个刻度尺．他是这样操作的:①分别在BA 和CA 上取BE CG =；②在BC 上取BD CF =；③量出DE 的长a 米，FG 的长b 米．如果a b =，则说明∠B 和∠C 是相等的．他的这种做法合理吗？为什么?4．（本题12分）填空，完成下列证明过程． 如图14,ABC △中，∠B ＝∠C ，D,E ，F 分别在AB ,BC ，AC 上，且BD CE =，=DEF B ∠∠ 求证：=ED EF ． 证明：∵∠DEC ＝∠B ＋∠BDE （ ），又∵∠DEF ＝∠B （已知）, ∴∠______＝∠______（等式性质）．在△EBD 与△FCE 中，∠______＝∠______(已证），______＝______（已知）,∠B ＝∠C （已知)，∴EBD FCE △≌△( )． ∴ED ＝EF （ )．5．(本题13分)如图15,O 为码头，A ,B 两个灯塔与码头的距离相等，OA ，OB 为海岸线，一轮船从码头开出,计划沿∠AOB 的平分线航行，航行途中，测得轮船与灯塔A ,B 的距离相等，此时轮船有没有偏离航线?画出图形并说明你的理由．6．（本题15分）如图16，把△ABC 纸片沿DE 折叠,当点A 落在四边形BCDE 内部时， （1)写出图中一对全等的三角形，并写出它们的所有对应角；（2）设AED ∠的度数为x ，∠ADE 的度数为y ,那么∠1，∠2 的度数分别是多少？（用含有x 或y 的代数式表示） (3)∠A 与∠1+∠2之间有一种数量关系始终保持不变，请找出这个规律．A D E CB 图12 F AD E C B图13 F G A D E C B图14 F图15A DEC B图16 A ′ 21ABDEFA轴对称一．选择题1.下列图形中,不是轴对称图形的是（ ） A ．H B 。

小学数学八年级上册练习题本文将从小学数学八年级上册练习题的角度，为大家提供一份详细的解答。

以下是题目的具体练习内容：1. 计算下列各组数的平均数：(1) 15，18，21，24(2) 3.5，4.2，5.9，6.7，7.1(3) 17，18，22.5，27.5解答：(1) 平均数 = (15 + 18 + 21 + 24) ÷ 4 = 78 ÷ 4 = 19.5(2) 平均数 = (3.5 + 4.2 + 5.9 + 6.7 + 7.1) ÷ 5 = 27.4 ÷ 5 = 5.48(3) 平均数 = (17 + 18 + 22.5 + 27.5) ÷ 4 = 85 ÷ 4 = 21.252. 一个长方形的长比宽多5，长和宽的和是36，求长和宽各是多少？解答：设长为x，宽为y，则由题目可得以下方程：x = y + 5 （长比宽多5）x + y = 36 （长和宽的和是36）解方程组：将第一个方程中的x代入第二个方程：（y + 5）+ y = 362y + 5 = 362y = 36 - 52y = 31y = 31 ÷ 2y = 15.5将y的值代入第一个方程求得x的值：x = 15.5 + 5x = 20.5所以长为20.5，宽为15.5。

3. 一个长方体的长、宽和高分别为3cm、4cm和5cm，求其总表面积和体积。

解答：总表面积 = 2 × (长×宽 + 宽×高 + 长×高)= 2 × (3×4 + 4×5 + 3×5)= 2 × (12 + 20 + 15)= 2 × 47= 94cm²体积 = 长×宽×高= 3×4×5= 60cm³4. 某电器商店购进一批电视机，每台成本价为3000元，商店准备在售价的基础上上涨20%，求每台电视机的售价是多少？如果商店希望每台电视机的利润为400元，应该以多少的售价出售？解答：(1) 上涨20%后的售价：售价 = 成本价 + 成本价 ×上涨百分比= 3000 + 3000 × 0.2= 3000 + 600= 3600元每台电视机的售价为3600元。

初二年级数学上册练习题大全集一、整数运算1. 计算下列各式的值：a) (-3) + 2b) 5 - (-7)c) (-4) × 3d) (-15) ÷ 52. 在数轴上标出下列各数，并写出其相反数：a) 4b) -7c) 0d) -1/23. 判断下列各式是否正确：a) 7 - (-7) = 14b) -5 + 2 = -3c) -8 × (-3) = 24d) -21 ÷ 7 = 3二、分数运算1. 将下列各分数化为最简形式：a) 16/32b) 24/36c) 12/20d) 28/352. 将下列各分数化为小数：a) 3/4b) 2/5c) 7/8d) 5/63. 计算下列各式的值：a) 1/3 + 2/3b) 3/5 - 1/5c) 1/8 × 4/5d) 5/6 ÷ 2/3三、代数表达式1. 给出下列各代数表达式的值：a) 2x - 3, 当 x = 4b) 3y + 5, 当 y = -2c) x^2 + y^2, 当 x = -3, y = 2d) 4x - 2y, 当 x = 1, y = -22. 求下列各代数表达式的值：（用合适的数填空）a) 2x - 5, 当 x = 2, y = 3b) 3xy + 4y, 当 x = -1, y = -2四、几何图形1. 计算下列各图形的面积：a) 长方形，长为4cm，宽为7cmb) 正方形，边长为6cmc) 圆形，半径为5cm2. 求下列各图形的周长：a) 长方形，长为8cm，宽为5cmb) 正方形，边长为9cmc) 圆形，半径为4cm五、方程式与不等式1. 解下列各方程式：a) 2x + 3 = 7b) 4y - 8 = 12c) 5(x - 3) = 152. 判断下列各不等式的真假：a) 3x + 2 > 5, 当 x = 1b) 7 - 4y ≤ 21, 当 y = 2c) 2(x - 3) ≥ 8, 当 x = 5六、比例1. 计算下列各组数的比例：a) 2:5b) 4:3c) 10:82. 列出与下列各组数成比例的数：a) 1:3b) 2:8c) 5:15七、平均数1. 计算下列各组数的平均数：a) 5, 8, 12, 6, 10b) 20, 14, 18, 242. 如果平均年龄是15岁，且有5个人，他们的年龄分别是16岁、18岁、14岁、12岁和13岁，求最小和最大年龄。

八年级上册数学练习册1．解：原式=a2a4=a2+4=a6，故选：B．2．解：∵x2+2mx+9是一个完全平方式，∴m=±3，故选：B．3. 解：∵（x1）2=（x+7）（x7），∴x22x+1=x249，解得x=25，∴ = =5，∴ 的平方根是± ．故选D．4．解：A、原式=x2+y2，不符合平方差公式的特点；B、第一个数是2x，第二个数是y，积的项应是4xy，不符合完全平方公式的特点；C、正确；D、两个平方项应同号．故选C．5. 解：∵a3b+ab32a2b+2ab2=7ab8，ab（a2+b2）2ab（ab）=7ab8，ab（a22ab+b2）2ab（ab）+2a2b27ab+8=0，ab（ab）22ab（ab）+2a2b27ab+8=0，ab[（ab）22（ab）+1]+2（a2b24ab+4）=0，ab（ab1）2+2（ab2）2=0，∵a、b均为正数，∴ab＞0，∴ab1=0，ab2=0，即ab=1，ab=2，解方程，解得a=2、b=1，a=1、b=2（不合题意，舍去），∴a2b2=41=3．故选B．6．解：∵（x2）（x+b）=x2+bx2x2b=x2+（b2）x2b=x2ax1，∴b2=a，2b=1，∴b=0.5，a=1.5，∴a+b=2．故选A．7．解：设这个正多边形是正n边形，根据题意得：（n2）×180°÷n=144°，解得：n=10．故选：B．8. 解：图中全等三角形有：△ABO≌△ADO、△ABO≌△CDO，△ABO≌△CBO；△AOD≌△COD，△AOD≌△COB；△DOC≌△BOC；△ABD≌△CBD，△ABC≌△ADC，共8对．故选C．9．解：根据角平分线的性质，（3）的依据是到角的两边的距离相等的点在角平分线上，故选B．10．解：根据题意可知等腰三角形的三边可能是4，4，9或4，9，9∵4+4＜9，故4，4，9不能构成三角形，应舍去4+9＞9，故4，9，9能构成三角形∴它的周长是4+9+9=22故选D．11．解：如上图：①OA为等腰三角形底边，符合符合条件的动点P有一个；②OA为等腰三角形一条腰，符合符合条件的动点P有三个．综上所述，符合条件的点P的个数共4个．故选C．12．解：∵AE⊥AB且AE=AB，EF⊥FH，BG⊥FH∠EAB=∠EFA=∠BGA=90°，∠EAF+∠BAG=90°，∠ABG+∠BAG=90°∠EAF=∠ABG，∴AE=AB，∠EFA=∠AGB，∠EAF=∠ABG△EFA≌△ABG∴AF=BG，AG=EF．同理证得△BGC≌△DHC得GC=DH，CH=BG．故FH=FA+AG+GC+CH=3+6+4+3=16故S= （6+4）×163×46×3=50．故选A．二．填空题（共6小题）13．已知a+b=2，则a2b2+4b的值为 4 ．解：∵a+b=2，∴a2b2+4b，=（a+b）（ab）+4b，=2（ab）+4b，=2a+2b，=2（a+b），=2×2，=4．14．计算：（a3）2+a5的结果是 a6+a5 ．解：（a3）2+a5=a3×2+a5=a6+a5．15．若2x3+x212x+k有一个因式为2x+1，则k为 6 ．解：2x3+x212x+k=（2x+1）（x26），∴k=6，16．一个多边形的每个外角都等于72°，则这个多边形的边数为 5 ．解：多边形的边数是：360÷72=5．17．如图所示，AB=DB，∠ABD=∠CBE，请你添加一个适当的条件∠BDE=∠BAC ，使△ABC≌△DBE．（只需添加一个即可）解：∵∠ABD=∠CBE，∴∠ABD+∠ABE=∠CBE+∠ABE，即∠ABC=∠DBE，∵AB=DB，∴①用“角边角”，需添加∠BDE=∠BAC，②用“边角边”，需添加BE=BC，③用“角角边”，需添加∠ACB=∠DEB．故答案为：∠BDE=∠BAC或BE=BC或∠ACB=∠DEB．（写出一个即可）18．如图，直线a∥b，△ABC是等边三角形，点A在直线a上，边BC在直线b上，把△ABC沿BC方向平移BC的一半得到△A′B′C′（如图①）；继续以上的平移得到图②，再继续以上的平移得到图③，…；请问在第100个图形中等边三角形的个数是 400 ．解：如图①∵△ABC是等边三角形，∴AB=BC=AC，∵A′B′∥AB，BB′=B′C= BC，∴B′O= AB，CO= AC，∴△B′OC是等边三角形，同理阴影的三角形都是等边三角形．又观察图可得，第1个图形中大等边三角形有2个，小等边三角形有2个，第2个图形中大等边三角形有4个，小等边三角形有4个，第3个图形中大等边三角形有6个，小等边三角形有6个，…依次可得第n个图形中大等边三角形有2n个，小等边三角形有2n个．故第100个图形中等边三角形的个数是：2×100+2×100=400．三．解答题（共8小题）19．运用乘法公式计算：（1）1997×2023；（2）（3a+2b）（3a+2b）；（3）（2b3a）（3a2b）．解：（1）原式=（20233）×（2023+3）=2023232=40000009=3999991；（2）原式=（2b）2（3a）2=4b29a2；（3）原式=（3a）2（2b）2=9a24b2．20．分解因式：33a210a解：（1） x2y8y，= y（x216），= y（x+4）（x4）；（2）a33a210a，=a（a23a10），=a（a+2）（a5）．(2) [八年级上册数学练习册]高中数学三角函数练习题及答案一、选择题1．探索如图所呈现的规律，判断2 013至2 014箭头的方向是() 图1－2－3【解析】观察题图可知0到3为一个周期，则从2 013到2 014对应着1到2到3.【答案】 B2．－330是()A．第一象限角 B．第二象限角C．第三象限角 D．第四象限角【解析】－330＝30＋(－1)360，则－330是第一象限角．【答案】 A3．把－1 485转化为＋k360，kZ)的形式是()A．45－4360 B．－45－4360C．－45－5360 D．315－5360【解析】－1 485＝－5360＋315，故选D.【答案】 D4．(2023济南高一检测)若是第四象限的角，则180－是() A．第一象限的角 B．第二象限的角C．第三象限的角 D．第四象限的角【解析】∵是第四象限的角，k360－90k360，kZ，－k360＋180180－－k360＋270，kZ，180－是第三象限的角．【答案】 C5．在直角坐标系中，若与的终边互相垂直，则与的关系为()A．＝＋90B．＝90C．＝＋90－k360D．＝90＋k360【解析】∵与的终边互相垂直，故－＝90＋k360，kZ，＝90＋k360，kZ. 【答案】 D二、填空题6．，两角的终边互为反向延长线，且＝－120，则＝________.【解析】依题意知，的终边与60角终边相同，＝k360＋60，kZ.【答案】 k360＋60，kZ7．是第三象限角，则2是第________象限角．【解析】∵k360＋180k360＋270，kZk180＋90k180＋135，kZ当k＝2n(nZ)时，n360＋90n360＋135，kZ，2是第二象限角，当k＝2n＋1(nZ)时，n360＋270n360＋315，nZ2是第四象限角．【答案】二或四8．与610角终边相同的角表示为________．【解析】与610角终边相同的角为n360＋610＝n360＋360＋250＝(n＋1)360＋250＝k360＋250(kZ，nZ)．【答案】 k360＋250(kZ)三、解答题9．若一弹簧振子相对平衡位置的位移x(cm)与时间t(s)的函数关系如图所示，图1－2－4(1)求该函数的周期；(2)求t＝10.5 s时该弹簧振子相对平衡位置的位移．【解】 (1)由题图可知，该函数的周期为4 s.(2)设本题中位移与时间的函数关系为x＝f(t)，由函数的周期为4 s，可知f(10.5)＝f(2.5＋24)＝f(2.5)＝－8(cm)，故t＝10.5 s时弹簧振子相对平衡位置的位移为－8 cm.图1－2－510．如图所示，试表示终边落在阴影区域的角．【解】在0～360范围中，终边落在指定区域的角是0或315360，转化为－360～360范围内，终边落在指定区域的角是－4545，故满足条件的角的集合为{|－45＋k36045＋k360，kZ}．11．在与530终边相同的角中，求满足下列条件的角．(1)最大的负角；(2)最小的正角；(3)－720到－360的角．【解】与530终边相同的角为k360＋530，kZ.(1)由－360＜k360＋530＜0，且kZ可得k＝－2，故所求的最大负角为－190.(2)由0＜k360＋530＜360且kZ可得k＝－1，故所求的最小正角为170(3)由－720k360＋530－360且kZ得k＝－3，故所求的角为－550.(3) [八年级上册数学练习册]数学配套练习册答案配套练习册的作业最好当天完成。

第4页1、图中有几个三角形用符号表示这些三角形。

B C2、下列长度的三条线段能否组成三角形为什么（1）3,4,8；（2）5,6,11；（3）5,6,10.5页有什么不同这三条△ABC的边BC上的高AD在各自三角1、如图，（1）（2）和（3）中的三个B形的什么位置你能说出其中的规律吗B DC B(D) CD B C2、填空：（1）如下页图（1），AD，BE，CF是△ABC的三条中线，则AB=2____，BD=____，AE=1/2____.(2)如下页图（2），AD，BE，CF是△ABC的三条角平分线，则∠1=____，∠3=1/2____，∠ACB=2____，AAF FEE习题1、图中有几个三角形用符号表示这些三角形。

B D E C2、长为10,7,5,3的四根木条，选其中三根组成三角形，有几种选法为什么（1） （2）（3）4、 如图，在△ABC 中，AE 是中线，AD 是角平分线，AF 是高。

填空： （1） BE=____＝1/2____.（2） ∠(3)∠AFB=____=90° (4)B E D FC 5、 选择题。

下列图形中有稳定性的是（）A 、正方形B 、长方形C 、直角三角形D 、平行四边形 12页例1 如图，在△ABC 中，∠BAC =40°, ∠B = 75°，AD 是△ABC 的角平分线．求∠ADB 的度数．CDA B例2：如图,C 岛在A 岛的北偏东50°方向，B 岛在A 岛的北偏东80°方向，C 岛在B 岛的北偏西40°方向。

求下面各题.13页1.如图,从A 处观测C 处时仰角∠CAD ＝30°,从B 处观测C 处时仰角∠CBD ＝45°.从C 处观测A 、B 两处时视角∠ACB 是多少 DBCE北2.如图，一种滑翔伞的形状是左右对称的四边形ABCD，其中∠A=150°，,∠B=∠D=40°,求∠C的度数。

八年级数学上册《第十五章整数指数幂》练习题附答案-人教版一、选择题1.下列运算正确的是( )A.3x2+2x3=5x5B.(π﹣3.14)0=0C.3﹣2=﹣6D.(x3)2=x62.计算(－1)0＋|－2|的结果是 ( )A.－3B.1C.－1D.33.下列运算正确的是( )A.2a＋3a＝5a2B.＝﹣5C.a3•a4＝a12D.(π﹣3)0＝14.计算(﹣2)0＋9÷(﹣3)的结果是( )A.﹣1B.﹣2C.﹣3D.﹣45.2﹣3可以表示为( )A.22÷25B.25÷22C.22×25D.(﹣2)×(﹣2)×(﹣2)6.科学家可以使用冷冻显微术以高分辨率测定溶液中的生物分子结构，使用此技术测定细菌蛋白结构的分辨率达到0.22纳米，也就是0.000 000 000 22米.将0.000 000 000 22用科学记数法表示为( )A.0.22×10﹣9B.2.2×10﹣10C.22×10﹣11D.0.22×10﹣87.已知a＝2﹣2，b＝(3﹣1)0，c＝(﹣1)3，则a，b，c的大小关系是( )A.a＞b＞cB.b＞a＞cC.c＞a＞bD.b＞c＞a8.计算(﹣3a﹣1)﹣2的结果是( )A.6a2B. 19a2 C.-19a2 D.9a29.计算x3y(x－1y)－2的结果为( )A.x5yB.yx5C.y5x2D.x5y210.计算(a2)3＋a2·a3－a2÷a－3的结果是( )A.2a5－aB.2a5－1aC.a5D.a6二、填空题11.若|a|－2=(a－3)0，则a=________.12.已知﹣(x ﹣1)0有意义，则x 的取值范围是 . 13.若(x ﹣12)0没有意义，则x ﹣2的值为____. 14.计算：(﹣2xy ﹣1)﹣3＝ .15.已知0.003×0.005=1.5×10n ，则n 的值是________.16.对实数a 、b ，定义运算☆如下：a ☆b=，例如：2☆3=2﹣3=18 则计算：[2☆(﹣4)]☆1= .三、解答题17.化简：(﹣3)0＋(﹣12)﹣2÷|﹣2|.18.化简：(﹣12)﹣1﹣2＋(π﹣3.14)0﹣(﹣2)﹣3；19.化简：4a 2b ÷(b 2a )﹣2· a b 2；20.化简：(2x －3y 2)－2÷(x －2y)3；21.已知式子（x －1）－12x －3＋(x －2)0有意义，求x 的取值范围.22.据测算，4万粒芝麻的质量约为160克，那么1粒芝麻的质量约为多少？(单位：千克，用科学记数法表示)23.一块900 mm2的芯片上能集成10亿个元件.(1)每个这样的元件约占多少平方毫米？(2)每个这样的元件约占多少m2?参考答案1.D2.D3.D.4.B5.A6.B.7.B.8.B9.A10.D11.答案为：－3.12.答案为：x ≠2且x ≠1.13.答案为：414.答案为：﹣y 38x 3.15.答案为：－516.答案为：16.17.解：原式＝1＋2＝3.18.解：原式＝﹣238.19.解：原式=ab.20.解：原式＝14x 6y －4÷x －6y 3＝x 124y 7.21.解：由题意得：⎩⎨⎧2x －3≠0，x －2≠0，x －1≠0， 解得⎩⎪⎨⎪⎧x ≠32，x ≠2，x ≠1.∴x≠32且x≠2且x≠1.22.解：160÷40 000=0.004(克)=4×10－6(千克).23.解：(1)10亿=10×108=109，∴900÷109=9×10－7(mm2).(2)1 m2=106 mm2，9×10－7÷106=9×10－13(m2).。

初二年级数学上册练习题大全集一、整数的加减运算1. 计算下列各题：a) (-4) + 7 =b) 3 + (-8) =c) (-5) + (-6) =d) 10 - (-3) =e) 8 - 3 =f) (-7) - 4 =2. 求下列各题的差：a) 12 - (-5) =b) 8 - 12 =c) (-6) - 3 =d) (-8) - (-9) =e) (-3) - (-7) =f) 0 - (-2) =3. 计算下列各题，并说明答案的正负性：a) (-3) + 4 + (-2) =b) 6 - (-4) - 1 =c) (-10) - 5 + 2 =d) 9 - (-7) + (-3) =e) (-1) - (-4) - (-6) =f) 8 + (-3) - (-9) =二、分数的加减运算1. 将下列各题化为相同分母的分数，并计算结果：a) 3/4 + 1/6 =b) 2/3 - 1/5 =c) 7/8 + 2/9 =d) 5/6 - 1/3 =e) 2/5 + 3/10 =f) 3/7 - 1/7 =2. 以最简形式计算下列各题：a) 2/3 + 4/9 - 1/6 =b) 1/4 - 1/5 + 3/10 =c) 3/5 + 4/7 - 2/9 =d) 2/3 - 1/2 - 5/6 =e) 4/5 + 3/10 - 1/2 =f) 1/8 - 1/4 + 1/2 =三、代数式的化简和计算1. 化简下列代数式：a) 3x - 2x + 5x =b) -2y + 4y - y + 3y =c) 5a - 3a + 7a - a =d) -4b - (-2b) - 3b =e) 6c - 2c - 4c + 3c =f) 2m - m + 3m - 4m =2. 计算下列各题的值，并说明结果的正负性：a) 2x + 3y - x + 5y =b) -4a - 3b - (-a) + b =c) 5m - 2n + (-m) - 3n =d) -7p + 3q - (-2p) + 4q =e) 6x - 3y - 4x + y =f) -5a + 2b - (-3a) + 4b =四、几何图形的性质与计算1. 已知矩形ABCD，AB = 8 cm，AD = 6 cm。