下载文档原格式
实验报告实验名称：机器学习:线性支持向量机算法实现学员: 张麻子学号: *＊***＊＊**** 培养类型：硕士年级：专业：所属学院：计算机学院指导教员：＊＊＊＊** 职称：副教授实验室:实验日期:ﻬ一、实验目得与要求实验目得:验证SVM(支持向量机）机器学习算法学习情况要求：自主完成。
二、实验内容与原理支持向量机（Support Ｖecｔｏr Maｃｈine,SVM）得基本模型就是在特征空间上找到最佳得分离超平面使得训练集上正负样本间隔最大。
SVＭ就是用来解决二分类问题得有监督学习算法。
通过引入了核方法之后SVM也可以用来解决非线性问题。
但本次实验只针对线性二分类问题。
ＳVM算法分割原则：最小间距最大化，即找距离分割超平面最近得有效点距离超平面距离与最大。
对于线性问题：假设存在超平面可最优分割样本集为两类,则样本集到超平面距离为：需压求取：由于该问题为对偶问题，可变换为:可用拉格朗日乘数法求解。
但由于本实验中得数据集不可以完美得分为两类，即存在躁点。
可引入正则化参数Ｃ,用来调节模型得复杂度与训练误差。
作出对应得拉格朗日乘式：对应得ＫKT条件为：故得出需求解得对偶问题:本次实验使用python编译器，编写程序，数据集共有２７０个案例，挑选其中70％作为训练数据,剩下30％作为测试数据。
进行了两个实验,一个就是取Ｃ值为１，直接进行ＳＶM训练;另外一个就是利用交叉验证方法,求取在前面情况下得最优Ｃ值.三、实验器材实验环境:windowｓ7操作系统+pytｈon编译器。
四、实验数据(关键源码附后)实验数据:来自ＵCI机器学习数据库,以Hｅart Disease数据集为例。
五、操作方法与实验步骤１、选取Ｃ＝1，训练比例７：3，利用pyｔｈon库sｋleａrｎ下得SVM（)函数进行训练,后对测试集进行测试；2、选取训练比例7：3，Ｃ＝nｐ、linspace（０、０001，1，30)}。
利用交叉验证方法求出Ｃ值得最优解。
机器学习实验报告小结引言本次实验旨在通过机器学习算法解决一个二分类问题，并评估各种机器学习模型的性能。
我们首先收集了一个包含大量样本和标签的数据集，然后使用不同的机器学习算法进行训练和测试。
通过实验的结果，我们得出了一些结论并提出了一些建议。
实验方法数据集我们使用了一个包含N个样本的数据集，每个样本包含M个特征和一个二分类标签。
我们将数据集按照7:3的比例划分为训练集和测试集。
特征选择在进行实验之前，我们进行了特征选择，选择了与目标变量相关性最高的M1个特征，以避免维度灾难和降低计算复杂度。
机器学习模型我们使用了以下几种机器学习模型进行实验：1. 逻辑回归2. 决策树3. 支持向量机4. 随机森林5. 神经网络模型训练和评估使用训练集对每个模型进行训练，并在测试集上进行性能评估。
评估指标包括准确率、精确率、召回率和F1-score等。
实验结果模型性能比较在测试集上，不同模型的性能如下：模型准确率精确率召回率F1-score-逻辑回归0.85 0.86 0.84 0.85决策树0.82 0.80 0.85 0.82支持向量机0.84 0.83 0.86 0.85随机森林0.86 0.87 0.85 0.86神经网络0.89 0.88 0.90 0.89从上表可以看出，神经网络模型在准确率、精确率、召回率和F1-score等指标上均取得了最佳性能，其次是随机森林模型。
逻辑回归模型的性能相对较差。
模型优化针对神经网络模型，我们进行了一些优化措施：1. 调整超参数：我们通过调整神经网络的层数、节点数、激活函数和优化算法等参数，以提高模型的性能。
2. 特征工程：我们尝试了不同的特征组合和变换，以提高模型对数据的拟合能力。
3. 数据增强：我们通过对训练集进行数据增强，如随机旋转、翻转和裁剪等操作，以扩大训练样本数量。
经过优化后，神经网络模型在测试集上的性能得到了进一步提升，准确率达到了0.91，且稳定性也有所提高。
机器学习算法性能评估实验报告一、实验背景在当今数字化和智能化的时代，机器学习算法在各个领域都发挥着重要作用，从图像识别、自然语言处理到医疗诊断和金融预测等。
然而，不同的机器学习算法在处理不同类型的数据和问题时，其性能表现可能会有很大的差异。
因此，对机器学习算法进行性能评估是至关重要的，它可以帮助我们选择最适合特定任务的算法，并对算法进行优化和改进。
二、实验目的本实验的主要目的是对几种常见的机器学习算法在不同数据集上的性能进行评估和比较，包括决策树、支持向量机、朴素贝叶斯和随机森林。
通过实验，我们希望回答以下几个问题：1、不同算法在不同数据集上的准确性、召回率和 F1 值等性能指标的表现如何？2、算法的性能是否受到数据集特征（如数据规模、特征数量、类别分布等）的影响？3、如何根据数据集的特点选择合适的机器学习算法？三、实验数据集为了全面评估机器学习算法的性能，我们选择了三个具有不同特点的数据集：1、鸢尾花数据集（Iris Dataset）：这是一个经典的数据集，包含150 个样本，每个样本有 4 个特征，分别是花萼长度、花萼宽度、花瓣长度和花瓣宽度，共分为 3 个类别（鸢尾花的品种）。
2、乳腺癌威斯康星数据集（Breast Cancer Wisconsin Dataset）：该数据集包含 569 个样本，每个样本有 30 个特征，用于诊断乳腺肿瘤是良性还是恶性。
3、 MNIST 手写数字数据集：这是一个大型的数据集，包含 60000个训练样本和10000 个测试样本，每个样本是一个28x28 的灰度图像，代表 0 到 9 中的一个数字。
四、实验方法1、数据预处理对于鸢尾花数据集和乳腺癌威斯康星数据集，我们首先对数据进行了标准化处理，以使每个特征的均值为 0，标准差为 1。
对于 MNIST 数据集，我们将图像像素值归一化到 0 到 1 之间，并将标签进行独热编码。
2、算法实现我们使用 Python 中的 Scikitlearn 库实现了决策树、支持向量机、朴素贝叶斯和随机森林算法。
第1篇一、实验背景随着大数据时代的到来，机器学习技术在各个领域得到了广泛应用。
本实验旨在通过实际操作，掌握机器学习建模的基本流程，包括数据预处理、特征选择、模型选择、模型训练和模型评估等步骤。
通过实验，我们将深入理解不同机器学习算法的原理和应用，提高解决实际问题的能力。
二、实验目标1. 熟悉Python编程语言，掌握机器学习相关库的使用，如scikit-learn、pandas等。
2. 掌握数据预处理、特征选择、模型选择、模型训练和模型评估等机器学习建模的基本步骤。
3. 熟悉常见机器学习算法，如线性回归、逻辑回归、决策树、支持向量机、K最近邻等。
4. 能够根据实际问题选择合适的机器学习算法，并优化模型参数，提高模型性能。
三、实验环境1. 操作系统：Windows 102. 编程语言：Python3.83. 机器学习库：scikit-learn 0.24.2、pandas 1.3.4四、实验数据本实验使用鸢尾花数据集（Iris dataset），该数据集包含150个样本，每个样本有4个特征（花瓣长度、花瓣宽度、花萼长度、花萼宽度）和1个标签（类别），共有3个类别。
五、实验步骤1. 数据导入与预处理首先，使用pandas库导入鸢尾花数据集，并对数据进行初步查看。
然后，对数据进行标准化处理，将特征值缩放到[0, 1]范围内。
```pythonimport pandas as pdfrom sklearn import datasets导入鸢尾花数据集iris = datasets.load_iris()X = iris.datay = iris.target标准化处理from sklearn.preprocessing import StandardScalerscaler = StandardScaler()X = scaler.fit_transform(X)```2. 特征选择使用特征重要性方法进行特征选择，选择与标签相关性较高的特征。
上机名称：基于Python的机器学习算法应用一、实验目的1. 理解机器学习的基本概念和常用算法；2. 掌握Python编程语言在机器学习中的应用；3. 通过实际案例，提升对机器学习算法的理解和运用能力。
二、实验环境1. 操作系统：Windows 102. 编程语言：Python3.73. 开发工具：PyCharm4. 机器学习库：scikit-learn三、实验内容本次实验主要分为以下几个部分：1. 数据预处理2. 特征选择3. 模型训练与评估4. 模型优化与调参四、实验步骤1. 数据预处理（1）数据导入：首先，我们需要导入实验所需要的数据集。
本实验以鸢尾花数据集为例，使用scikit-learn库中的datasets模块进行导入。
```pythonfrom sklearn.datasets import load_irisiris = load_iris()X = iris.datay = iris.target```（2）数据可视化：为了更好地理解数据分布情况，我们可以对数据进行可视化展示。
```pythonimport matplotlib.pyplot as pltplt.scatter(X[:, 0], X[:, 1], c=y)plt.xlabel('Sepal length')plt.ylabel('Sepal width')plt.title('Iris Dataset')plt.show()```2. 特征选择特征选择是机器学习中的一个重要步骤，有助于提高模型的准确率和减少计算复杂度。
在本实验中，我们使用递归特征消除（Recursive Feature Elimination，RFE）方法进行特征选择。
```pythonfrom sklearn.feature_selection import RFEfrom sklearn.linear_model import LogisticRegressionmodel = LogisticRegression()rfe = RFE(model, n_features_to_select=2)fit = rfe.fit(X, y)print("Selected features: %s" % fit.support_)print("Selected feature scores: %s" % fit.ranking_)3. 模型训练与评估接下来，我们对筛选后的特征进行模型训练和评估。
机器学习实验报告（2）研究⽣机器学习与数据挖掘第⼀部分：实验综述1.实验⽬的：1.发掘数据集⼤⼩和C4.5的关系2.属性个数对该关系的影响2.实验思路：要求⽐较数据集⼤⼩和C4.5精度的关系，以及属性个数对此关系的影响。
本实验中采⽤了两种思路，思路⼀是：使⽤同类实例的训练集和测试集，当分析训练集⼤⼩与C4.5精度的关系时，对训练集进⾏多次随机采样，并建⽴基于采样得到的新的训练集的模型，采⽤固定的测试集测试模型精度。
记录并⽐较得出结论；分析测试集与C4.5精度的关系时；基于相同的训练集，对测试集多次采样，以不同⼤⼩的测试集测试模型精度，记录⽐较得出结论。
思路⼆是：使⽤⼀个数据集，采⽤带筛选器的分类器，对处理后的数据进⾏10重交叉验证，记录所得精度，修改筛选器的抽样⽐率，得到不同的数据集，重复实验，⽐较得最后的结论。
采⽤多组数据集进⾏重复实验，归纳得出概括性结论。
本实验中第⼀⼆实验采⽤思路⼀，第三个实验采⽤思路⼆（重复实践了实验⼀）。
3.使⽤数据记录如下：hayes-roth_train.arffhayes-roth_test.arffkdd_JapaneseVowels_train.arffkdd_JapaneseVowels_test.arffsegment-challenge.arffsegment-test.arffmonks-problems-3_test.arffmonks-problems-3spectf_test.arffspectf_train.arffdermatology.arffsplice.arffspectrometer.arffarrhythmia.arffhypothyroid.arff4.使⽤分类器：实验⼀⼆使⽤：weka.classifiers.trees.J48-C0.25-M2实验三使⽤：weka.classifiers.meta.FilteredClassifier-F"weka.filters.unsupervised.attribute.RandomSubset-N*-S1"-W weka.classifiers.trees.J48 ---C0.25-M2注：*为可修改值5.实验参考原理：1)模型精度的影响因素模型的表现出了与学习算法有关，还与类的分布，误分类代价以及训练集和测试集的⼤⼩有关。
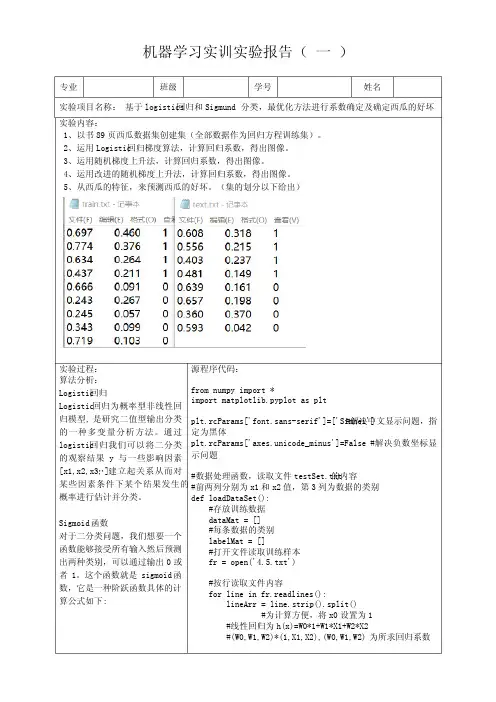
机器学习实训实验报告（ 一 ）专业 班级 学号 姓名实验项目名称： 基于logistics回归和Sigmund分类，最优化方法进行系数确定及确定西瓜的好坏实验内容：1、以书89页西瓜数据集创建集（全部数据作为回归方程训练集）。
2、运用Logistic回归梯度算法，计算回归系数，得出图像。
3、运用随机梯度上升法，计算回归系数，得出图像。
4、运用改进的随机梯度上升法，计算回归系数，得出图像。
5、从西瓜的特征，来预测西瓜的好坏。
（集的划分以下给出）实验过程：算法分析：Logistic回归Logistic回归为概率型非线性回归模型, 是研究二值型输出分类的一种多变量分析方法。
通过logistic回归我们可以将二分类的观察结果y与一些影响因素[x1,x2,x3,…]建立起关系从而对某些因素条件下某个结果发生的概率进行估计并分类。
Sigmoid函数对于二分类问题，我们想要一个函数能够接受所有输入然后预测出两种类别，可以通过输出0或者1。
这个函数就是sigmoid函数，它是一种阶跃函数具体的计算公式如下: 源程序代码：from numpy import *import matplotlib.pyplot as pltplt.rcParams['font.sans-serif']=['Simhei']#解决中文显示问题，指定为黑体plt.rcParams['axes.unicode_minus']=False#解决负数坐标显示问题#数据处理函数，读取文件testSet.txt的内容#前两列分别为x1和x2值，第3列为数据的类别def loadDataSet():#存放训练数据dataMat = []#每条数据的类别labelMat = []#打开文件读取训练样本fr = open('4.5.txt')#按行读取文件内容for line in fr.readlines():lineArr = line.strip().split()#为计算方便，将x0设置为1#线性回归为h(x)=W0*1+W1*X1+W2*X2#(W0,W1,W2)*(1,X1,X2),(W0,W1,W2)为所求回归系数Sigmoid函数的性质: 当x为0时，Sigmoid函数值为0.5，随着x的增大对应的Sigmoid值将逼近于1; 而随着x的减小, Sigmoid 函数会趋近于0。
人工智能的机器学习实习报告机器学习实习报告一、引言机器学习是人工智能领域的关键技术之一，其目的是通过让机器能够从大量数据中自动学习和改进，来实现人类无法完成的任务。
本实习报告将介绍我在人工智能公司实习期间，参与的机器学习项目。
二、项目背景和目标在实习期间，我参与了一个图像识别项目。
该项目的背景是，公司的客户希望开发一种能够自动识别和分类图像的软件。
为了实现这一目标，我们团队利用机器学习算法，从大量的图像数据中构建了一个强大的图像分类模型。
三、数据收集和预处理为了构建这个模型，我们首先需要收集大量的图像数据。
我们从各种渠道搜集了具有不同特征和类别的图像，并进行了数据的预处理工作。
预处理包括图像的降噪、裁剪和大小调整等操作，以确保模型训练的数据质量和一致性。
四、模型选择和训练在选择模型方面，我们考虑了多种经典的机器学习算法，如支持向量机（SVM）、决策树和神经网络等。
通过实验和对比，我们最终选择了卷积神经网络（CNN）作为我们的模型。
CNN在图像分类方面表现卓越，能够准确地识别不同的图像特征。
在模型训练阶段，我们使用了大量的图像数据作为输入，并将其分为训练集和验证集。
通过多次迭代训练和调整网络参数，我们不断提高模型的准确性和泛化能力。
最终，我们得到了一个优秀的图像分类模型。
五、模型评估和改进为了评估我们的模型，我们使用测试集对其进行了验证和评测。
我们比较了模型的预测结果与真实标签之间的差异，并计算了准确率、召回率和F1值等指标。
通过评估结果，我们发现模型在大部分图像上都表现出色，但在某些特殊场景下存在一定的识别误差。
针对这些问题，我们对模型进行了改进和优化。
我们尝试了增加训练数据、调整网络结构、改进数据预处理等方法，以进一步提高模型的性能。
经过数次迭代和改进，我们成功降低了模型的误差率，准确度得到了显著提升。
六、实际应用和展望在项目结束后，我们将开发的图像识别系统应用于客户的实际场景中。
通过与客户的合作和反馈，我们不断改进和优化系统，以满足客户的需求。
机器学习算法实习报告第一章：引言机器学习是人工智能领域的一个重要分支，通过获取和分析大量数据，利用算法来帮助机器自动学习并提高性能。
本报告旨在总结我在机器学习算法实习中的经验和收获。
第二章：实习背景在此章节中，我将介绍所在实习机构以及实习项目的背景和目标。
同时，我还会简要介绍机器学习算法的应用领域和意义，以便读者能够更好地了解本文的主题。
第三章：实习过程这一章节将详细描述我在实习期间所进行的具体工作和实践经验。
我会列举常用的机器学习算法，并逐一分析其原理和应用场景。
同时，我还会介绍我所参与的机器学习项目的实际案例，包括数据采集、特征选择、模型训练与评估等环节，并提供相应的实验结果和分析。
第四章：实习心得与收获在这一章节中，我将总结整个实习过程中的心得与收获。
我会谈论我对机器学习算法的认识和理解的提高，以及在项目中遇到的挑战和解决方案。
同时，我还会分享我在与团队合作和沟通中所积累的经验和技巧，以及对未来在机器学习领域的发展的展望。
第五章：实习总结最后，本章将对整个实习经历进行总结。
我会回顾我在实习中所取得的成果和进展，并对自己的表现进行自我评价。
同时，我还会对未来深入研究和应用机器学习算法的方向提出建议，并总结本报告的主要观点和论点。
结语通过这次实习，我不仅仅熟悉了常见的机器学习算法，还学会了如何在实际项目中应用这些算法解决实际问题。
实习过程中的挑战和困难也让我获得了成长和提升。
我相信这次实习经历将对我的职业发展产生积极的影响，并为我未来的学习和研究提供坚实的基础。
参考文献[1] Mitchell, T. Machine Learning. McGraw-Hill Education, 1997.[2] Hastie, T., Tibshirani, R., & Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer, 2009.[3] Bishop, C. M. Pattern Recognition and Machine Learning. Springer, 2006.（此为虚构文章，仅供参考）。
机器学习与数据科学实习报告一、实习背景在机器学习与数据科学领域，实习是提升个人能力和职业发展的重要途径之一。
通过实践应用机器学习的知识和技术，我有机会在实际项目中运用数据科学的方法，有效地解决实际问题。
二、实习目标在这次实习中，我的主要目标是掌握机器学习和数据科学的基本原理和技术。
通过实际项目的实践，我希望能够熟练运用机器学习算法进行数据分析和预测建模，并能够将模型应用于实际的业务场景中。
此外，我还希望能够提升自己的数据处理和数据可视化能力，以便更好地分析和展示数据。
三、实习内容1. 数据收集与清洗在实习开始时，我首先需要收集相关的数据集，并对数据进行初步的清洗工作。
这包括去除异常值和缺失值，对数据进行标准化和归一化，以便后续的分析和建模工作。
2. 数据探索与可视化接下来，我将对数据进行探索性分析，了解数据的分布和特征。
我将使用统计方法和可视化工具对数据进行可视化分析，以便更好地理解数据。
通过这一步骤，我可以发现数据中存在的潜在问题，并为后续的建模工作做好准备。
3. 特征工程与建模在数据探索的基础上，我将进行特征工程的工作，包括特征选择、特征转换和特征提取等。
通过对特征的优化和处理，可以提高后续建模的效果。
然后，我将选择合适的机器学习算法，如决策树、支持向量机或神经网络等，进行模型的训练和优化。
4. 模型评估与改进在模型建立完成后，我将进行模型的评估工作。
通过指标评价和交叉验证等方法，评估模型的性能和准确度。
如果模型不满足需求，我将根据评估结果对模型进行改进和调参，以提高模型的稳定性和预测能力。
5. 结果展示与报告最后，我将根据实际需求对模型结果进行展示和应用。
通过数据可视化和报告撰写，我将向公司内部和外部的利益相关者汇报实习成果和应用效果。
四、实习收获与总结通过这次实习，我对机器学习和数据科学有了更深入的理解和实践经验。
我掌握了数据处理、数据分析和建模的基本流程和技术方法。
我也意识到了机器学习和数据科学在实际项目中的重要性和应用潜力。
基于AutoEncoder原理和L_BFGS 优化算法实现手写数字识别目录1 神经网络基本概念 (3)1.1概述 (3)1.2 神经网络模型 (4)2 AutoEncoder原理 (5)2.1 反向传播算法 (5)2.2 Softmax回归 (7)2.3 Stacked AutoEncoder (8)2.4 微调过程 (9)2.5 Sparse AutoEncoder (9)2.6 Denoise AutoEncoder (10)3 L_BFGS算法 (11)3.1基本原理 (11)3.2算法流程 (16)3.3算法收敛性分析： (19)4 基于AutoEncoder的手写数字识别 (19)4.1 MNIST数据库 (19)4.2 模型训练 (20)4.3 模型测试 (20)5 实验结果及分析： (20)5.1 AutoEncoder (21)5.2 Sparse AutoEncoder (21)5.3 Denoise AutoEncoder (22)5.4 实验结果汇总及分析 (23)6 参考资料 (25)AutoEncoder 实现手写数字识别1 神经网络基本概念1.1概述神经网络是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。
这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。
神经网络由多个神经元构成，下图就是单个神经元的图1所示：图1 神经元模型这个神经元是以123,,x x x 以及截距1+为输入值的运算单元，其输出为3,()()()T W b i i i h x f W x f W x b ===+∑，其中函数()f ⋅被称作“激活函数”。
在本次试验中，我们选用sigmoid 函数作为激活函数()f ⋅图2 sigmoid 函数图像1.2 神经网络模型神经网络就是将许多个单一的神经元联结在一起，这样，一个神经元的输出就可以是另一个神经元的输入。
例如，下图就是一个简单的神经网络：图3 神经网络示意图我们用()l i a 第l 层第i 单元的激活值（输出值）。
当1l =时，()l i i a x =，也就是第i 个输入值。
对于给定的参数集合,W b ，神经网络就可以按照函数,()W b h x 来计算输出结果。
以上述模型为例，计算步骤如下: (2)(1)(1)(1)(1)11111221331(2)(1)(1)(1)(1)22112222332(2)(1)(1)(1)(1)33113223333(3)(2)(2)(2)(2)(2)(2)(2),11111221331()()()()()W b a f W x W x W x b a f W x W x W x b a f W x W x W x b h x a f W a W a W a b =+++=+++=+++==+++(2)我们用()l i z 表示第第l 层第i 单元输入加权和（包括偏置），这样我们对上式就可以得到一种更加简洁的表示法：(2)(1)(1)(2)(2)(3)(2)(2)(2)(3)(3),()()()W b z W x b a f z z W a b h x a f z =+==+== (3)上述的计算步骤叫作前向传播。
给定第l 层的激活值()l a 后，第1l +层的激活值(1)l a +就可以按照下面步骤计算得到：(1)()()()(1)(1)()l l l l l l z W a b a f z +++=+= (4)2 AutoEncoder 原理2.1 反向传播算法自编码（AutoEncoder ）神经网络是一种无监督的学习算法，它使用了反向传播算法，让目标值等于输入值，例如输入值为训练样本集合(1)(2)(3){,,}x x x ，则我们的输出值()()i i y x =。
下图是一个自编码神经网络的示例：图4 单隐层神经网络自编码神经网络的主要参数是连接权重W 和偏置b ，我们尝试利用自编码神经网络学习一个,()W b h x x =，也就是说我们尝试逼近一个恒等函数，从而使得输出ˆx 接近于输入x 。
假设我们有一个固定样本集(1)(1)()(){(,),,(,)}m m x y x y ，它包含m 个样例。
对于单个样例(,)x y ，其代价函数为：这是一个方差代价函数。
给定一个包含m 个样例的数据集，我们可以定义整体代价函数为：以上公式中的第一项(,)J W b 是一个均方差项。
第二项是一个规则化项（也叫权重衰减项），其目的是减小权重的幅度，防止过度拟合。
我们的目标是针对参数W 和b 来求其函数(,)J W b 的最小值。
为了求解神经网络，我们将每一个参数()l ij W 和()l i b 初始化为一个很小的、接近于0的随机数，之后对目标函数求最优解。
梯度下降法中每一次迭代都是按照如下公式对参数W 和b 进行更新：其中α是学习速率。
更新参数W 和b的关键步骤是计算偏导数。
而反向传播算法是计算偏导数的一种有效方法。
整体代价函数(,)J W b 的偏导数为：反向传播算法的思路是：给定一个样例(,)x y ，我们首先进行前向传导算法，得到23,,L L 的激活值，包括输出层l n L 的输出值,()W b h x 。
之后，针对第l 层的每一个节点i ，我们计算出其“残差”()l i δ，该残差表明了该节点对最终输出值得误差产证了多少影响。
残差的定义如下：对于1,2,3,,2l l l l n n n =---的各个层，第l 层的第i 个节点的残差计算方法如下：1()()(1)()1()l s l l l l i ji j i j W f z δδ++=⎛⎫'= ⎪⎝⎭∑ (10)需要我们计算的偏导数就可以写成下面的形式：总的来说，利用向量化的表示，反向传播算法可以表示成以下几个步骤：1. 进行前馈传导计算，利用前向传导公式，得到23,,L L 直至输出层l n L 的激活值。
2. 对于第l n 层（输出层），计算出残差：()()()()()l l l n n n y a f z δ'=--⋅ (12)3. 对于1,2,3,,2l l l l n n n =---的各个层 ()()()(1)()()()l l T l l W f z δδ+'=⋅(13) 4. 计算最终需要的偏导数值： ()()(1)()(1)(,;,)()(,;,)l l l l TW l b J W b x y a J W b x y δδ++∇=∇= (14)5. 根据公式（7）更新权重参数： ()()()()()()(,;,)(,;,)l l l l W l l b W W J W b x y b b J W b x y ∆=∆+∇∆=∆+∇ (15)2.2 Softmax 回归Softmax 回归模型是logistic 回归模型在多分类问题上的推广。
在logistic 回归中，训练集由m 个已标记的样本构成：{}(1)(1)()()(,),,(,)m m x y x y ，其中输入特征()1i n x +∈ℜ。
由于logistic 回归是针对二分类问题的，因此类标记{}()0,1i y ∈。
假设函数如下：我们的目的就是训练模型参数θ，使其能够最小化代价函数：而在Softmax 回归中，类标签y 可以取k 个不同的值。
因此对于训练集{}(1)(1)()()(,),,(,)m m x y x y ，我们有{}()1,2,,i y k ∈，所以假设函数()h x θ形式如下： (i)()2|;)|;)T K x i x k x θθθ⎥=⎥⎥⎥⎥⎥⎦=⎦其中112,,,n k θθθ+∈ℜ是模型参数。
Softmax 回归算法的代价函数如下：{()1i y j ⎤⎥=∑∑ 其中{}1⋅是示性函数。
为了限制Softmax 回归在描述对象时候出现过拟合现象，我们加入了权重衰减项2102k n iji j λθ==∑∑来修改代价函数，则整个代价函数变为： 经过这个权重衰减后(0)λ>，代价函数就变成了严格的凸函数，这样就可以保证得到唯一解。
此时的Hessian 矩阵变为可逆矩阵，并且因为()J θ是凸函数，L -BFGS 等算法可以保证收敛到全局最优解。
2.3 Stacked AutoEncoder栈式自编码神经网络（Stacked AutoEncoder ）是一个由多层自编码神经网络组成的神经网络，其前一层的自编码神经网络的输出作为厚一层自编码神经网络的输入。
对于一个n 层的栈式自编码神经网络，假定用(,1)(,2)(,1)(,2),,,k k k k W W b b 表示第k 个自编码神经网络的(1)(2)(1)(2),,,W W b b 参数，那么该栈式自编码神经网络的编码过程就是，按照从前向后的顺序徐行每一层自编码神经网络的编码步骤： ()()(1)(,1)()(,1)()l l l l l l a f z z W a b +==+ (22)一种比较好的获取栈式自编码神经网络参数的方法是采用逐层贪婪训练法进行训练。
即利用原始输入来训练网络的第一层，得到其参数(1,1)(1,2)(1,1)(1,2),,,W W b b ；然后网络的第一层将原始输入转化为由隐层单元激活值组成的向量A ，接着把A 作为第二层的输入，继续训练得到第二层的参数(2,1)(2,2)(2,1)(2,2),,,W W b b ，最后对后面的各层采用同样的策略训练参数。
2.4 微调过程微调（fine -tuning ）是深度学习中的常用策略，可以大幅提神一个展示自编码神经网络的性能表现。
从更高的视角来讲，微调将栈式自编码神经网络的所有层视为一个模型，网络中所有的权重只都可以被优化。
在栈式的自编码神经网络中，微调的实现主要分为以下几个步骤：1. 对于输出层（l n 层），我们使用的是Softmax 回归分类器，该层的残差为： ()()()()l l n l n n a J f z δ'=-∇⋅ (23)其中()T J I P θ∇=-，其中I 为输入数据对应的类别标签，P 为条件概率向量。
2. 对于1,2,3,,2l l l l n n n =---的各个层，利用公式（13），（14），（15），（16）计算残差，更新参数。
2.5 Sparse AutoEncoder稀疏自编码神经网络（Sparse AutoEncoder ）的稀疏性可以被解释如下。
如果当神经元的输出接近于1的时候我们认为它是被激活的，而输出接近于0的时候认为它是被抑制的，那么是的神经元大部分的时候都是被抑制的限制被称作稀疏性限制。
令(2)()1ˆ()i j j a x m ρ⎡⎤=⎣⎦表示隐层神经元j 的平均活跃度。
