五年级上册数学平行四边形经典错题

（苏教版）五年级数学上册平行四边形面积的计算及答案（一）一、填空（1）4.5平方米（）平方分米 2400平方厘米（）平方分米（2）一个平行四边形的底是9分米，高是底的2倍，它的面积是（）平方分米。

（3）一个平行四边形的底是12厘米，面积是156平方厘米，高是（）厘米。

（4）一块平行四边形钢板，底是1.5米，高是1.2米，如果每平方米钢板重23.5千克，这块钢板重（）千克。

二、判断题。

（1）平行四边形的面积等于长方形面积。

（）（2）一个平行四边形的底是5分米，高是20厘米，面积是100平方分米。

（）（3）一个平行四边形面积是42平方米，高是6米，底是7米。

（）三、评议。

下面是四个平行四边形，小红认为它们的面积都是6平方厘米，你认为对吗？（单位：厘米）四、已知下图中正方形的周长为36厘米，求平行四边形的面积。

提高题1.有一块平行四边形的钢板底边长1.8米，高0.4米，这种钢板每平方米重10.2千克，这块钢板有多少千克？2.下图是平行四边形钢板，在这块钢板上要截下一个最大的正方形钢板，剩下边角料的面积是多少？参考答案一、填空。

（1）450 24 （2）162 （3）13 （4）42.3二、判断题。

（1）（×）（2）（×）（3）（√）三、评议。

下面是四个平行四边形，小红认为它们的面积都是6平方厘米，你认为对吗？（单位：厘米）（√）（×）（√）（×）四、已知下图中正方形的周长为36厘米，求平行四边形的面积。

36÷4＝9（厘米）9×9＝81（平方厘米）提高题。

1.先求出平行四边形的面积：1.8×0.4＝0.72（平方米）0.72×10.2＝7.344（千克）2.知道平行四边形的面积是56平方分米，则高为7分米，一个最大的正方形，7×7＝49（平方分米）56－49＝7（平方分米）。

五年级上册数学错题整理一、小数乘法部分1. 题目：0.25×0.4的积是（）。

错误答案：1题目解析：计算小数乘法时，先按照整数乘法算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点。

0.25×0.4，先算25×4 = 100，0.25有两位小数，0.4有一位小数，共三位小数，所以积应该是0.1。

2. 题目：一个数乘0.8的积比45个0.6少7，这个数是多少？错误答案：（45×0.6 7）÷0.8=(27 7)÷0.8 = 20÷0.8 = 250题目解析：45个0.6是45×0.6 = 27，积比27少7，那么这个积是277=20，一个数乘0.8等于20，所以这个数是20÷0.8 = 25。

错误答案中把20÷0.8算错了。

二、小数除法部分1. 题目：1.8÷0.36 =（）错误答案：0.5题目解析：根据商不变的性质，把被除数和除数同时扩大100倍，变成180÷36 = 5。

错误答案是把除法当成乘法计算了。

2. 题目：5.63÷6.1的商保留两位小数是（）。

错误答案：0.92295题目解析：先计算5.63÷6.1≈0.92295，题目要求保留两位小数，看第三位小数是2，根据四舍五入，应该舍去，所以正确答案是0.92。

三、简易方程部分1. 题目：3x+5 = 20，求x的值。

错误答案：3x+5 = 20，3x=20 + 5，3x = 25，x = 25÷3，x = 8.333...题目解析：解方程时，等式两边同时进行相同的运算。

3x+5 = 20，应该是等式两边同时减去5，得到3x=20 5，3x = 15，x = 5。

2. 题目：一个数的3倍比这个数的2倍多10，这个数是多少？（设这个数为x）错误答案：3x+2x = 10，5x = 10，x = 2题目解析：根据题意，应该是3x 2x = 10，x = 10。

五年级数学多边形面积常错经典题一、填空。

1.一个平行四边形的底是14厘米，高是9厘米，它的面积是（）；与它等底等高的三角形面积是（）.2.工地上有一堆钢管，横截面是一个梯形，已知最上面一层有2根，最下面一层有12根，共堆了 11 层，这堆钢管共有（）根。

3.一个三角形比与它等底等高的平行四边的面积少30平方厘米，则这个三角形的面积是（）。

4.一个三角形的面积是4.5平方分米，底是5分米，高是（）分米。

5.一个等边三角形的周长是18厘米，高是3.6厘米，它的面积是（）平方厘米。

6.在推导平行四边形面积计算公式时，可把平行四边形通过割补平移转化为（）形去推导，推导三角形面积计算公式时，可把两个完全一样的三角形拼成一个（）形去推导，推导梯形面积计算公式时，可把两个完全一样的梯形拼成一个（）形进行推导。

7.直角三角形的两条直角边长分别为3厘米和4厘米，这个直角三角形面积是（）平方厘米。

8.一个三角形的底边长扩大2倍，高不变，扩大后的三角形面积比原来三角形面积扩大（）倍。

9. 一个三角形的面积是25平方厘米，和它等底等高的平行四边形的面积是（）平方厘米。

10.平行四边形的底长16米，高是12米，它的面积是（）平方米。

11.在一个长9厘米，周长26厘米的长方形内画一个最大的三角形，这个三角形的面积是（）平方厘米。

12.三角形的底扩大3倍，高扩大2倍，面积扩大（）倍。

13.一个三角形与梯形的高相等，它们的面积也相等。

那梯形的上底与下底的和等于三角形（）的长度。

14.右图中阴影部分的面积是15平方厘米，长方形的面积是（）平方厘米。

15.一个平行四边形的底是6厘米，高是14厘米，它的面积是（）平方厘米，与它等底等高的三角形面积是（）平方厘米。

16.如图，每个方格的边长为1厘米，这只小鱼的面积是（）平方厘米。

17.有一个长方形长15厘米，宽8厘米，另一直角梯形上底长7厘米，下底长6厘米，高8厘米，将它们拼成一个梯形，梯形的面积是（）平方厘米。

五年级数学三角形平行四边形面积常错经典题练习一一、填空。

1．在推导平行四边形面积计算公式时，可把平行四边形通过割补平移转化为( )形去推导，推导三角形面积计算公式时，可把两个完全一样的三角形拼成一个( )形去推导，推导梯形面积计算公式时，可把两个完全一样的梯形拼成一个( )形进行推导。

2、一个平行四边形的底是14厘米，高是9厘米，它的面积是（）；与它等底等高的三角形面积是（）.3．工地上有一堆钢管，横截面是一个梯形，已知最上面一层有2根，最下面一层有12根，共堆了11层，这堆钢管共有（）根。

4．一个三角形比与它等底等高的平行四边的面积少30平方厘米，则这个三角形的面积是（）。

5．一个三角形的面积是45平方分米，底是18分米，高是（）分米。

6．一个等边三角形的周长是18厘米，高是36厘米，它的面积是（）平方厘米。

7、直角三角形的两条直角边长分别为3厘米和4厘米，这个直角三角形面积是( )平方厘米。

8、一个三角形的底边长扩大2倍，高不变，扩大后的三角形面积比原来三角形面积扩大( )倍。

二、判定题1．两个面积相等的三角形，一定能拼成一个平行四边形.（）2．平行四边形的面积等于一个三角形面积的2倍.（）3．两个完全一样的梯形，能拼成一个平行四边形.（）4．把一个长方形的框架挤压成一个平行四边形，面积减少了.（）5．两个三角形面积相等，底和高也一定相等。

（）6.平行四边形面积等于长方形面积。

( )7.等底等高的三角形可拼成一个平行四边形。

( )8.只要知道梯形的两底之和的长度和它的高，就可以求出它的面积。

( )9.两个周长相等的等边三角形，面积必相等。

( )三、选择题1．等边三角形一定是 _______ 三角形.[ ]A．锐角； B．直角； C．钝角2.两个完全一样的锐角三角形，可以拼成一个 ________[ ]A．长方形； B．正方形； C．平行四边形； D．梯形3．把一个平行四边形任意分割成两个梯形，这两个梯形中 ________总是相等的.[ ]A．高； B．面积； C．上下两底的和练习二一、填空。

苏教版五年级数学上册易错题一、计算公式1、平行四边形的面积=底×高平行四边形的底=面积÷高平行四边形的高=面积÷底（等底等高的平行四边形面积相等）2、三角形的面积=底×高÷2三角形的底=面积×2÷高三角形的高=面积×2÷底（等底等高的三角形面积相等）3、梯形的面积=（上底+下底）×高÷2梯形的高=面积×2÷（上底+下底）梯形的上底=面积×2÷高－下底梯形的下底=面积×2÷高－上底4、计算圆木、钢管堆根数公式：总根数=（顶层根数+底层根数）×层数÷2 层数=底层根数－顶层根数+15、三角形是等底等高的平行四边形面积的一半；三角形与平行四边形等积（面积）等底，则高是平行四边形高的2倍；三角形与平行四边形等积（面积）等高，则底是平行四边形底的2倍。

6、 1公顷=10000平方米 1平方千米=1000000平方米=100公顷（画图、组合图形、不规则图形）二、判断1、一个数不是正数就是负数。

（）2、+20米和-20米所表示的距离是一样的。

（）3、三角形面积是平行四边形面积的一半。

（）4、两个面积相等的三角形一定可以拼成一个平行四边形。

（）5、两个面积相等的三角形，它们的底和高也一定相等。

（）6、在小数点后面填上0或去掉0，这个数的大小不变。

（）7、在小数的末尾填上0，小数的大小不变，但计数单位变了。

（）8、近似数2.60要比近似数2.6更精确一些。

（）三、填空及解决问题1、把9、+7、-7、-3、0按从小到大的顺序排列（）。

2、一盒牛奶包装上写着“净重250±5克”，这盒牛奶的标准重是（），最重不超过（）克，最轻不低于（）克。

3、一天凌晨的气温是-5ºC，中午比凌晨上升了2 ºC，中午的气温是（）。

五年级上册错题整理填空。

1、一瓶矿泉水的外包装上标有“净含量250ml±3ml”，说明这瓶矿泉水的净含量最多（）ml，最少（）ml。

2、把一个平行四边形通过剪、移、拼的方法拼成一个长方形，面积（），周长（）。

把一个平行四边形框架拉成一个长方形，面积（），周长（）。

3、一个平行四边形的底是9cm，高是18cm，它的面积是（）cm2，与它等底等高的三角形的面积是（）cm2。

4、一个梯形上底是12cm，下底是20cm，高是30cm，面积是（）cm2。

5、一块平行四边形地，底长30米，高20米，这块地的面积是（）。

6、一个三角形的面积是72平方厘米，底是36厘米，高是（）厘米。

7、一块梯形装饰板，上底6分米，下底10分米，高1米。

装饰板的两面都要涂油漆，涂油漆的面积是（）平方分米。

8、在面积是42平方米的平行四边形内画一个最大的三角形，三角形的面积是（）。

9、把一个长8米，宽5米的长方形分成完全一样的直角梯形，如果每个梯形上、下底之和是8米，那么梯形的高是（）米。

判断。

1、在+4，—6,0,9，—0.08,20.56，—3中，一共有4个整数。

（） 42、把一个平行四边形木框拉成长方形侯，周长和面积都不会变。

（）3、一个平行四边形，底16cm，高10cm。

如果它的底增加1cm，高减少1cm，那么面积将保持不变。

（）4、平行四边形的面积一定等于三角形面积的2倍。

（）5、一个三角形的高延长到原来的4倍，面积就是原来的2倍。

（）选择题。

1、把两个完全一样的直角三角形拼成一个长方形，已知直角三角形的两条直角边分别是3分米、2分米，拼成的长方形面积是（）平方分米。

A.12B.6C.3。

五年级上册数学错题漫画一、错题漫画1。

题目：一个平行四边形的底是5分米，高是3分米，它的面积是（）平方分米。

小明的答案是16平方分米。

解析：1. 首先根据平行四边形的面积公式：S = 底×高。

2. 已知底是5分米，高是3分米，那么面积S=5×3 = 15平方分米。

3. 小明可能是把平行四边形的面积计算当成了求周长，(5 + 3)×2=16，这是错误的概念。

二、错题漫画2。

题目：一个三角形的面积是24平方厘米，底是8厘米，高是（）厘米。

小红的答案是3厘米。

解析：1. 根据三角形的面积公式S=(1)/(2)×底×高。

2. 已知面积S = 24平方厘米，底b = 8厘米，将公式变形为高=2S÷底。

3. 则高h=2×24÷8 = 6厘米。

4. 小红可能是直接用面积除以底，没有乘2，所以得出了错误答案。

题目：在1 - 20的自然数中，既是奇数又是合数的数有（）。

小刚写的是9和15，但是漏写了。

解析：1. 奇数是不能被2整除的数，合数是除了能被1和本身整除外，还能被其他数（0除外）整除的自然数。

2. 在1 - 20中，奇数有1、3、5、7、9、11、13、15、17、19；合数有4、6、8、9、10、12、14、15、16、18、20。

3. 既是奇数又是合数的数有9、15，小刚写对了这两个数，但可能忽略了检查是否完整。

四、错题漫画4。

题目：把5米长的绳子平均分成8段，每段长（）米，每段占全长的（）。

小李的答案：每段长(8)/(5)米，每段占全长的(5)/(8)。

解析：1. 把5米长的绳子平均分成8段，求每段长多少米，用总长度除以段数，即5÷8=(5)/(8)米。

2. 求每段占全长的几分之几，把全长看作单位“1”，平均分成8段，每段就占全长的(1)/(8)。

3. 小李把每段的长度和每段占全长的比例弄反了。

题目：一个数既是6的倍数，又是48的因数，这个数可能是（）。

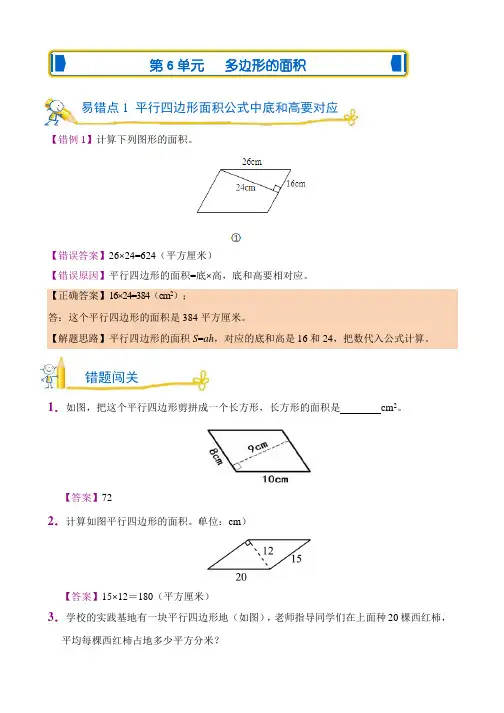
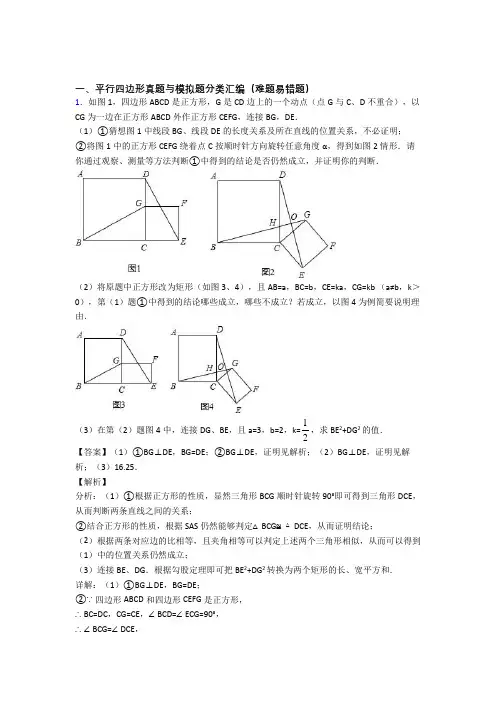
一、平行四边形真题与模拟题分类汇编（难题易错题）1．如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．（1）①猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系，不必证明；②将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α，得到如图2情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立，并证明你的判断．（2）将原题中正方形改为矩形（如图3、4），且AB=a，BC=b，CE=ka，CG=kb （a≠b，k＞0），第（1）题①中得到的结论哪些成立，哪些不成立？若成立，以图4为例简要说明理由．（3）在第（2）题图4中，连接DG、BE，且a=3，b=2，k=12，求BE2+DG2的值．【答案】（1）①BG⊥DE，BG=DE；②BG⊥DE，证明见解析；（2）BG⊥DE，证明见解析；（3）16.25．【解析】分析：（1）①根据正方形的性质，显然三角形BCG顺时针旋转90°即可得到三角形DCE，从而判断两条直线之间的关系；②结合正方形的性质，根据SAS仍然能够判定△BCG≌△DCE，从而证明结论；（2）根据两条对应边的比相等，且夹角相等可以判定上述两个三角形相似，从而可以得到（1）中的位置关系仍然成立；（3）连接BE、DG．根据勾股定理即可把BE2+DG2转换为两个矩形的长、宽平方和．详解：（1）①BG⊥DE，BG=DE；②∵四边形ABCD和四边形CEFG是正方形，∴BC=DC，CG=CE，∠BCD=∠ECG=90°，∴∠BCG=∠DCE，∴△BCG≌△DCE，∴BG=DE，∠CBG=∠CDE，又∵∠CBG+∠BHC=90°，∴∠CDE+∠DHG=90°，∴BG⊥DE．（2）∵AB=a，BC=b，CE=ka，CG=kb，∴BC CG b==，DC CE a又∵∠BCG=∠DCE，∴△BCG∽△DCE，∴∠CBG=∠CDE，又∵∠CBG+∠BHC=90°，∴∠CDE+∠DHG=90°，∴BG⊥DE．（3）连接BE、DG．根据题意，得AB=3，BC=2，CE=1.5，CG=1，∵BG⊥DE，∠BCD=∠ECG=90°∴BE2+DG2=BO2+OE2+DO2+OG2=BC2+CD2+CE2+CG2=9+4+2.25+1=16.25．点睛：此题综合运用了全等三角形的判定和性质、相似三角形的判定和性质以及勾股定理．2．在△ABC中，AB=BC，点O是AC的中点，点P是AC上的一个动点（点P不与点A，O，C重合）．过点A，点C作直线BP的垂线，垂足分别为点E和点F，连接OE，OF．（1）如图1，请直接写出线段OE与OF的数量关系；（2）如图2，当∠ABC=90°时，请判断线段OE与OF之间的数量关系和位置关系，并说明理由（3）若|CF﹣AE|=2，3△POF为等腰三角形时，请直接写出线段OP的长．【答案】（1）OF =OE；（2）OF⊥EK，OF=OE，理由见解析；（3）OP的长为62或233.【解析】【分析】（1）如图1中，延长EO交CF于K，证明△AOE≌△COK，从而可得OE=OK，再根据直角三角形斜边中线等于斜边一半即可得OF=OE；（2）如图2中，延长EO交CF于K，由已知证明△ABE≌△BCF，△AOE≌△COK，继而可证得△EFK是等腰直角三角形，由等腰直角三角形的性质即可得OF⊥EK，OF=OE；（3）分点P在AO上与CO上两种情况分别画图进行解答即可得.【详解】（1）如图1中，延长EO交CF于K，∵AE⊥BE，CF⊥BE，∴AE∥CK，∴∠EAO=∠KCO，∵OA=OC，∠AOE=∠COK，∴△AOE≌△COK，∴OE=OK，∵△EFK是直角三角形，∴OF=12EK=OE；（2）如图2中，延长EO交CF于K，∵∠ABC=∠AEB=∠CFB=90°，∴∠ABE+∠BAE=90°，∠ABE+∠CBF=90°，∴∠BAE=∠CBF，∵AB=BC，∴△ABE≌△BCF，∴BE=CF，AE=BF，∵△AOE≌△COK，∴AE=CK，OE=OK，∴FK=EF，∴△EFK是等腰直角三角形，∴OF⊥EK，OF=OE；（3）如图3中，点P在线段AO上，延长EO交CF于K，作PH⊥OF于H，∵|CF﹣AE|=2，EF=23，AE=CK，∴FK=2，在Rt△EFK中，tan∠FEK=3，∴∠FEK=30°，∠EKF=60°，∴EK=2FK=4，OF=12EK=2，∵△OPF是等腰三角形，观察图形可知，只有OF=FP=2，在Rt△PHF中，PH=12PF=1，HF=3，OH=2﹣3，∴OP=()2212362+-=-.如图4中，点P在线段OC上，当PO=PF时，∠POF=∠PFO=30°，∴∠BOP=90°，∴323综上所述：OP6223.【点睛】本题考查了全等三角形的判定与性质、直角三角形斜边中线等于斜边一半、等腰直角三角形的判定与性质、解直角三角形等，综合性较强，正确添加辅助线是解题的关键.3．如图所示，矩形ABCD中，点E在CB的延长线上，使CE＝AC，连接AE，点F是AE的中点，连接BF、DF，求证：BF⊥DF．【答案】见解析.【解析】【分析】延长BF，交DA的延长线于点M，连接BD，进而求证△AFM≌△EFB，得AM=BE，FB=FM，即可求得BC+BE=AD+AM，进而求得BD=BM，根据等腰三角形三线合一的性质即可求证BF⊥DF．【详解】延长BF，交DA的延长线于点M，连接BD．∵四边形ABCD是矩形，∴MD∥BC，∴∠AMF=∠EBF，∠E=∠MAF，又FA=FE，∴△AFM≌△EFB，∴AM=BE，FB=FM．∵矩形ABCD中，∴AC=BD，AD=BC，∴BC+BE=AD+AM，即CE=MD．∵CE=AC，∴AC=CE= BD =DM．∵FB=FM，∴BF⊥DF．【点睛】本题考查了矩形的性质，全等三角形的判定和对应边相等的性质，等腰三角形三线合一的性质，本题中求证DB=DM是解题的关键．4．如图，在正方形ABCD中，对角线AC与BD交于点O，在Rt△PFE中，∠EPF=90°，点E、F分别在边AD、AB上．（1）如图1，若点P与点O重合：①求证：AF=DE；②若正方形的边长为3，当∠DOE=15°时，求线段EF的长；（2）如图2，若Rt△PFE的顶点P在线段OB上移动（不与点O、B重合），当BD=3BP 时，证明：PE=2PF．【答案】（1）①证明见解析，②22；（2）证明见解析.【解析】【分析】（1）①根据正方形的性质和旋转的性质即可证得：△AOF ≌△DOE 根据全等三角形的性质证明； ②作OG ⊥AB 于G ，根据余弦的概念求出OF 的长，根据勾股定理求值即可；（2）首先过点P 作HP ⊥BD 交AB 于点H ，根据相似三角形的判定和性质求出PE 与PF 的数量关系．【详解】（1）①证明：∵四边形ABCD 是正方形，∴OA=OD ，∠OAF=∠ODE=45°，∠AOD=90°，∴∠AOE+∠DOE=90°，∵∠EPF=90°，∴∠AOF+∠AOE=90°，∴∠DOE=∠AOF ，在△AOF 和△DOE 中，OAF ODE OA ODAOF DOE ＝＝＝∠∠⎧⎪⎨⎪∠∠⎩， ∴△AOF ≌△DOE ，∴AF=DE ；②解：过点O 作OG ⊥AB 于G ，∵正方形的边长为3∴OG=123∵∠DOE=15°，△AOF ≌△DOE ，∴∠AOF=15°，∴∠FOG=45°-15°=30°，∴OF=OG cos DOG ∠=2， ∴EF=22=22OF OE +；（2）证明：如图2，过点P 作HP ⊥BD 交AB 于点H ，则△HPB 为等腰直角三角形，∠HPD=90°，∴HP=BP ，∵BD=3BP ，∴PD=2BP ，∴PD=2HP ，又∵∠HPF+∠HPE=90°，∠DPE+∠HPE=90°，∴∠HPF=∠DPE ，又∵∠BHP=∠EDP=45°，∴△PHF ∽△PDE ，∴12PF PH PE PD ==， ∴PE=2PF ．【点睛】 此题属于四边形的综合题．考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质以及勾股定理．注意准确作出辅助线是解此题的关键．5．如图，已知矩形ABCD 中，E 是AD 上一点，F 是AB 上的一点，EF ⊥EC ，且EF ＝EC ． （1）求证：△AEF ≌△DCE ．（2）若DE ＝4cm ，矩形ABCD 的周长为32cm ，求AE 的长．【答案】（1）证明见解析；（2）6cm.【解析】分析：（1）根据EF⊥CE，求证∠AEF=∠ECD．再利用AAS即可求证△AEF≌△DCE．（2）利用全等三角形的性质，对应边相等，再根据矩形ABCD的周长为32cm，即可求得AE的长.详解：（1）证明：∵EF⊥CE，∴∠FEC=90°，∴∠AEF+∠DEC=90°，而∠ECD+∠DEC=90°，∴∠AEF=∠ECD．在Rt△AEF和Rt△DEC中，∠FAE=∠EDC=90°，∠AEF=∠ECD，EF=EC．∴△AEF≌△DCE．（2）解：∵△AEF≌△DCE．AE=CD．AD=AE+4．∵矩形ABCD的周长为32cm，∴2（AE+AE+4）=32．解得，AE=6（cm）．答：AE的长为6cm．点睛：此题主要考查学生对全等三角形的判定与性质和矩形的性质等知识点的理解和掌握，难易程度适中，是一道很典型的题目．6．如图，在正方形ABCD中，点G在对角线BD上（不与点B，D重合），GE⊥DC于点E，GF⊥BC于点F，连结AG．（1）写出线段AG，GE，GF长度之间的数量关系，并说明理由；（2）若正方形ABCD的边长为1，∠AGF=105°，求线段BG的长．【答案】（1）AG2=GE2+GF2（2）【解析】试题分析：（1）结论：AG2=GE2+GF2．只要证明GA=GC，四边形EGFC是矩形，推出GE=CF，在Rt△GFC中，利用勾股定理即可证明；（2）作BN⊥AG于N，在BN上截取一点M，使得AM=BM．设AN=x．易证AM=BM=2x，MN=x，在Rt△ABN中，根据AB2=AN2+BN2，可得1=x2+（2x+x）2，解得x=，推出BN=，再根据BG=BN÷cos30°即可解决问题.试题解析：（1）结论：AG2=GE2+GF2．理由：连接CG．∵四边形ABCD是正方形，∴A、C关于对角线BD对称，∵点G在BD上，∴GA=GC，∵GE⊥DC于点E，GF⊥BC于点F，∴∠GEC=∠ECF=∠CFG=90°，∴四边形EGFC是矩形，∴CF=GE，在Rt△GFC中，∵CG2=GF2+CF2，∴AG2=GF2+GE2．（2）作BN⊥AG于N，在BN上截取一点M，使得AM=BM．设AN=x．∵∠AGF=105°，∠FBG=∠FGB=∠ABG=45°，∴∠AGB=60°，∠GBN=30°，∠ABM=∠MAB=15°，∴∠AMN=30°，∴AM=BM=2x，MN=x，在Rt△ABN中，∵AB2=AN2+BN2，∴1=x2+（2x+x）2，解得x=，∴BN=，∴BG=BN÷cos30°=．考点：1、正方形的性质，2、矩形的判定和性质，3、勾股定理，4、直角三角形30度的性质7．问题探究（1）如图①，已知正方形ABCD的边长为4．点M和N分别是边BC、CD上两点，且BM ＝CN，连接AM和BN，交于点P．猜想AM与BN的位置关系，并证明你的结论．（2）如图②，已知正方形ABCD的边长为4．点M和N分别从点B、C同时出发，以相同的速度沿BC、CD方向向终点C和D运动．连接AM和BN，交于点P，求△APB周长的最大值；问题解决（3）如图③，AC为边长为23的菱形ABCD的对角线，∠ABC＝60°．点M和N分别从点B、C同时出发，以相同的速度沿BC、CA向终点C和A运动．连接AM和BN，交于点P．求△APB周长的最大值．【答案】（1）AM⊥BN，证明见解析；（2）△APB周长的最大值4+42；（3）△PAB的周长最大值=23+4．【解析】试题分析：根据全等三角形的判定SAS证明△ABM≌△BCN，即可证得AM⊥BN；（2）如图②，以AB为斜边向外作等腰直角△AEB，∠AEB=90°，作EF⊥PA于E，作EG⊥PB于G，连接EP，证明PA+PB=2EF，求出EF的最大值即可；（3）如图③，延长DA到K，使得AK=AB，则△ABK是等边三角形，连接PK，取PH=PB，证明PA+PB=PK，求出PK的最大值即可.试题解析：（1）结论：AM⊥BN．理由：如图①中，∵四边形ABCD是正方形，∴AB=BC，∠ABM=∠BCN=90°，∵BM=CN，∴△ABM≌△BCN，∴∠BAM=∠CBN，∵∠CBN+∠ABN=90°，∴∠ABN+∠BAM=90°，∴∠APB=90°，∴AM⊥BN．（2）如图②中，以AB为斜边向外作等腰直角三角形△AEB，∠AEB=90°，作EF⊥PA于E，作EG⊥PB于G，连接EP．∵∠EFP=∠FPG=∠G=90°，∴四边形EFPG是矩形，∴∠FEG=∠AEB=90°，∴∠AEF=∠BEG，∵EA=EB，∠EFA=∠G=90°，∴△AEF≌△BEG，∴EF=EG，AF=BG，∴四边形EFPG是正方形，∴PA+PB=PF+AF+PG﹣BG=2PF=2EF，∵EF≤AE，∴EF的最大值=AE=2，∴△APB周长的最大值=4+4．（3）如图③中，延长DA到K，使得AK=AB，则△ABK是等边三角形，连接PK，取PH=PB．∵AB=BC，∠ABM=∠BCN，BM=CN，∴△ABM≌△BCN，∴∠BAM=∠CBN，∴∠A PN=∠BAM+∠ABP=∠CBN+∠ABN=60°，∴∠APB=120°，∵∠AKB=60°，∴∠AKB+∠APB=180°，∴A、K、B、P四点共圆，∴∠BPH=∠KAB=60°，∵PH=PB，∴△PBH是等边三角形，∴∠KBA=∠HBP，BH=BP，∴∠KBH=∠ABP，∵BK=BA，∴△KBH≌△ABP，∴HK=AP，∴PA+PB=KH+PH=PK，∴PK的值最大时，△APB的周长最大，∴当PK是△ABK外接圆的直径时，PK的值最大，最大值为4，∴△PAB的周长最大值=2+4．8．如图，抛物线y=mx2+2mx+n经过A（﹣3，0），C（0，﹣32）两点，与x轴交于另一点B．（1）求经过A，B，C三点的抛物线的解析式；（2）过点C作CE∥x轴交抛物线于点E，写出点E的坐标，并求AC、BE的交点F的坐标（3）若抛物线的顶点为D，连结DC、DE，四边形CDEF是否为菱形？若是，请证明；若不是，请说明理由．【答案】（1）y=12x2+x﹣32；（2）F点坐标为（﹣1，﹣1）；（3）四边形CDEF是菱形．证明见解析【解析】【分析】将A、C点的坐标代入抛物线的解析式中，通过联立方程组求得该抛物线的解析式；根据（1）题所得的抛物线的解析式，可确定抛物线的对称轴方程以及B、C点的坐标，由CE∥x轴，可知C、E关于对称轴对称。

小学数学人教版五年级上册五年级数学多边形面积常错经典题一、填空（每空1分，共13分）3．一个平行四边形的底是14厘米，高是9厘米，它的面积是（）；与它等底等高的三角形面积是（）.5．工地上有一堆钢管，横截面是一个梯形，已知最上面一层有2根，最下面一层有12根，共堆了11层，这堆钢管共有（）根。

6．一个三角形比与它等底等高的平行四边的面积少30平方厘米，则这个三角形的面积是（）。

7．一个三角形的面积是4.5平方分米，底是5分米，高是（）分米。

8．一个等边三角形的周长是18厘米，高是3.6厘米，它的面积是（）平方厘米。

二、判定题（每题2分，共10分）1．两个面积相等的三角形，一定能拼成一个平行四边形.（）2．平行四边形的面积等于一个三角形面积的2倍.（）3．两个完全一样的梯形，能拼成一个平行四边形.（）4．把一个长方形的框架挤压成一个平行四边形，面积减少了.（）5．两个三角形面积相等，底和高也一定相等。

（）三、选择题（每题2分，共8分）1．等边三角形一定是_______ 三角形.[ ]A．锐角；B．直角；C．钝角2.两个完全一样的锐角三角形，可以拼成一个________[ ]A．长方形；B．正方形；C．平行四边形；D．梯形3．把一个平行四边形任意分割成两个梯形，这两个梯形中________总是相等的.[ ]A．高；B．面积；C．上下两底的和、填空。

1．在推导平行四边形面积计算公式时，可把平行四边形通过割补平移转化为( )形去推导，推导三角形面积计算公式时，可把两个完全一样的三角形拼成一个( )形去推导，推导梯形面积计算公式时，可把两个完全一样的梯形拼成一个( )形进行推导。

4．直角三角形的两条直角边长分别为3厘米和4厘米，这个直角三角形面积是( )平方厘米。

7．一个三角形的底边长扩大2倍，高不变，扩大后的三角形面积比原来三角形面积扩大( )倍。

三、判断题。

1．平行四边形面积等于长方形面积。

( )2．等底等高的三角形可拼成一个平行四边形。

苏教版（一）五年级数学上册易错题一、计算公式1、平行四边形的面积=底×高平行四边形的底=面积÷高平行四边形的高=面积÷底（等底等高的平行四边形面积相等）2、三角形的面积=底×高÷2三角形的底=面积×2÷高三角形的高=面积×2÷底（等底等高的三角形面积相等）3、梯形的面积=（上底+下底）×高÷2梯形的高=面积×2÷（上底+下底）梯形的上底=面积×2÷高－下底梯形的下底=面积×2÷高－上底4、计算圆木、钢管堆根数公式：总根数=（顶层根数+底层根数）×层数÷2层数=底层根数－顶层根数+15、三角形是等底等高的平行四边形面积的一半；三角形与平行四边形等积（面积）等底，则高是平行四边形高的2倍；三角形与平行四边形等积（面积）等高，则底是平行四边形底的2倍。

6、1公顷=10000平方米 1平方千米=1000000平方米=100公顷（画图、组合图形、不规则图形）二、判断1、一个数不是正数就是负数。

（）2、+20米和-20米所表示的距离是一样的。

（）3、三角形面积是平行四边形面积的一半。

（）4、两个面积相等的三角形一定可以拼成一个平行四边形。

（）5、两个面积相等的三角形，它们的底和高也一定相等。

（）6、在小数点后面填上0或去掉0，这个数的大小不变。

（）7、在小数的末尾填上0，小数的大小不变，但计数单位变了。

（）8、近似数2.60要比近似数2.6更精确一些。

（）三、填空及解决问题1、把9、+7、-7、-3、0按从小到大的顺序排列（）。

2、一盒牛奶包装上写着“净重250±5克”，这盒牛奶的重是（），最重不超过（）克，最轻不低于（）克。

3、一天凌晨的气温是-5ºC，中午比凌晨上升了2ºC，中午的气温是（）。

一、填空题（1-6题每空1分，7-14题每空2分）1.把一个平行四边形沿着（）剪开，可以将它拼成一个（），转化后图形的（）和（）相当于平行四边形的（）和（）。

2.两个（）的三角形可以拼成一个平行四边形，拼成的图形的底是三角形的底的（）倍，高是三角形的高的（）倍，拼成图形的面积是每个三角形面积的（）倍。

3.两个（）的梯形可以拼成一个平行四边形，平行四边形的底等于梯形的（），平行四边形的高等于梯形的（），梯形的面积是平行四边形的（）。

4.一个三角形的面积是12平方米，底是4米，它的高是（）分米。

5.一个平行四边形相邻的两条边分别是5厘米和4.6厘米，高是4.8厘米，它的面积是（）。

6.5224公顷=（）平方米=（）平方千米814.2平方厘米=（）平方分米=（）平方毫米7.一个等腰直角三角形的直角边都是8厘米，斜边上的高是6厘米，它的面积是（）。

8.一个直角三角形的三条边分别是6厘米，8厘米，10厘米，它的面积是（）平方分米。

9.一个直角三角形的三条边分别是3厘米，4厘米，6厘米，它斜边上的高是（）。

10.图10中，甲三角形的面积为48平方厘米，乙三角形的面积占整个平行四边形面积的六分之一，乙三角形的面积是（），平行四边形的面积是（）。

图10 图1211.一个梯形的上底是下底的4倍，如果将下底延长5厘米，就成了一个平行四边形，这个梯形的上底是（）厘米，下底是（）厘米。

12. 图12中，有（）个梯形，有（）平行四边形。

二，判断题（每题2分）1.平行四边形的面积是三角形面积的2倍。

（）2.三角形的面积是它同底等高的平行四边形面积的一半。

（）3.长方形是特殊的平行四边形，正方形又是特殊的长方形。

（）4.把推拉门做成平行四边形是因为平行四边形具有稳定性。

（）三、选择题（每题2.5分）1.用木条钉成的长方形拉成一个平行四边形，它的面积（），它的周长（）。

A、不变B、变大C、变小D、无法确定2．一个三角形的底扩大3倍，高扩大3倍，它的面积（），它的周长（）。

五年级上册数学错题一、小数乘法部分1. 题目：0.25×0.4 = 1解析：这是小数乘法计算错误。

计算小数乘法时，先按照整数乘法算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点。

0.25×0.4，先算25×4 = 100，0.25有两位小数，0.4有一位小数，共三位小数，所以积应该是0.1。

2. 题目：1.2×1.3 = 15.6解析：按照小数乘法计算方法，12×13 = 156，1.2有一位小数，1.3也有一位小数，共两位小数，正确结果应该是1.56。

二、小数除法部分1. 题目：3.6÷0.4 = 90解析：在计算3.6÷0.4时，根据商不变的性质，将被除数和除数同时扩大10倍，变为36÷4 = 9，而不是90。

2. 题目：2.5÷0.5 = 0.5解析：2.5÷0.5，同样将被除数和除数同时扩大10倍变为25÷5 = 5，而不是0.5。

三、简易方程部分1. 题目：3x+5 = 14，解得x = 3解析：先根据等式的性质，方程两边同时减5，得到3x = 14 5 = 9，再两边同时除以3，解得x = 3，这是正确的。

如果解得错误，比如解得x = 2，错误原因是在计算3x = 9时，错误地将9÷3算成了2。

2. 题目：2(x 3)=10，解得x = 8解析：先将方程左边展开得到2x-6 = 10，然后方程两边同时加6，得到2x = 16，再两边同时除以2，解得x = 8。

如果解得错误，可能是在展开2(x 3)时算错，或者后续计算步骤出错。

四、多边形的面积部分1. 题目：一个平行四边形的底是5厘米，高是3厘米，它的面积是15平方厘米。

如果把底扩大到原来的2倍，高不变，面积是30平方厘米。

如果把高扩大到原来的3倍，底不变，面积是45平方厘米。

如果底和高都扩大到原来的2倍，面积是60平方厘米。

（完整word版）五年级上册数学平行四边形经典错题
平行四边形的面积错题
1、填一填
（1）1.25平方千米=（125）公顷=（1250000 ）平方米（2）把一个平行四边形转化（拼接）成长方形，它的面积与原来的平行四边形的面积（相等）。

转化后长方形的长与平行四边形的（底）相等，宽与平行四边形的（高）相等。

（3）把一个平行四边形框架拉成长方形，它的面积与原来的平行四边形的面积（变大）。

（4）等底等高的三角形面积是平行四边形的面积（一半）2、判断
（1）形状不同的两个平行四边形面积一定不相等（×）（2）周长相等的两个平行四边形面积一定相等（×）
（3）知道一个平行四边形的底和其对应的高的长度就能求出它的面积（√）
（4）等底等高的两个三角形能拼成一个平行四边形。

（×）计算三角形、平行四边形和梯形一定要带公式计算！
3、有一个平行四边形的面积是56平方厘米，底是7厘米，高是多少厘米？
56÷7=8（平方厘米）
4、一块平行四边形的菜地，底是25米，底比高多11米，每平方米收白菜8千克，这块地共收白菜多少千克？
25×（25-11）×8=2800（千克）
5、一个平行四边形的果园，底是30米，高是15米，种了90棵梨树，平均每棵梨树占地多少平方米？
30×15÷90=5（平方米）
6、一块平行四边形的铁皮的周长是82厘米，一条底长是16厘米，这条底上的高是20厘米，求另一条底上的高是多少厘米？
面积：16×20=320（平方厘米）另一条底：82÷2-16=25（厘米）320÷25=12.8（厘米）。

《平行四边形》单元五三错题一、填空题1 .在同一平面内，两条直线的位置关系是（ ）或（ ）。

2 .在同一平面内，过直线外一点能画（）条直线与这条直线互相平行, 能画（）条直线与这条直线互相垂直。

3 .在同一平面内，如果两条直线都与另一条直线互相垂直，那么这两条直 线（）。

4 .操场两边的直线跑道是互相平行的，在跑道之间画 垂直线段AB. CDo 量得线段AC 的长度为87米，线段AB 的长度为73米，线段CD 长（）米。

在两条直线跑道 之间可以画出（）条与线段AB 等长的线段。

5 .把一个平行四边形拉成长方形后，长方形的宽（ 长边上的高。

（填“大于”“小于”或“等于”）6. 一个等腰梯形上底长3米，下底的长度是上底的2倍，其中一条腰长4 米。

这个等腰梯形的周长是（ ）米。

7 .如右图，如果把一个平行四边形沿高剪成两个梯 形，那么这两个梯形的周长之和比原来平行四边形周长 多（）厘米。

8 .下面图形中各有几个平行四边形？（）个。

二、选择题1 .张大爷开垦了一块长方形花圃（如图长方形ABCD ）,他已经做好了围 绕花圃四周的篱笆，但是由于场地限制，只能把长方形花圃改成平行四边 形（如图平行四边形AEFD ）,那么张大爷做好的篱笆就（）。

A.长了B.正好够用C.短了D.无法判断2 .关于平行四边形，下面说法正确的有（）个。

①两组对边分别平行；②邻边相等；③对边相等；④对角相等；⑤过它的 一个顶点可以画无数条高；⑥具有稳定性。

姓名:）平行四边形较 7厘米3 .把一个长方形框架拉成一个平行四边形框架后，它的周长（A.变短了B.变长了C.不变D.无法判断4 .下面是运动会中四名运动员掷铅球的情况，（）的成绩最好。

A.小瑞B.小辉 < *C.小杰D.小明 示瑞一示％ 小杰吮 5 .把一张长方形纸沿一个方向连续对折两次后展开，三条折痕（）A.互相平行B.互相垂直C.相交D.可能互相平行，也可能互相垂直 三、判断题（正确的打“ ，错误的打"x” ）1 .汉字“云”中既含有互相平行的线段又含有互相垂直的线段。

第11讲平行四边形的面积（讲义）小学数学五年级上册易错专项练（知识梳理+易错汇总+易错精讲+易错专练）1.平行四边形面积计算公式的推导。

把平行四边形通过割补法变成长方形，通过长方形面积计算公式确定平行四边形面积计算公式。

2.平行四边形的面积计算公式。

平行四边形的面积＝底×高。

如果用S表示平行四边形的面积，用a表示平行四边形的底,用h表示平行四边形的高,那么平行四边形面积的计算公式可以写成S＝ah。

1.用数方格的方法计算面积时，不满一格的按半格计算。

2.判断两个平行四边形的面积是否相等，应根据它们的底和高的具体情况进行判断。

3.平行四边形的面积与它的底和高有关，底扩大到原来的n倍（n≠0），高缩小到原来的 n 分之一，面积不变。

4.求平行四边形的面积，先要找到底和与其相对应的高，再计算。

【易错一】一个平行四边形相邻两条边分别是6厘米、4厘米，量得一条边上的高为5厘米，这个平行四边形的面积是（）平方厘米。

A．24 B．42 C．20 D．30【解题思路】根据平行四边形的特点可知，底边上的高一定小于另一条斜边，所以高为5厘米对应的底为4厘米，利用面积公式计算即可。

【完整解答】5×4＝20（平方厘米）故答案为：C【易错点】此题的解题关键是根据平行四边形的特征确定高和底边长，利用平行四边形的面积公式求解。

【易错二】一个平行四边形的面积是120平方分米，如果它的高扩大到原来的3倍，底不变，它的面积是( )平方分米。

【解题思路】根据平行四边形的面积S＝ah，根据积的变化规律知：一个因数不变，另一个因数扩大到原来的几倍，积也扩大到原来的几倍，可知底不变，高扩大到原来的3倍，积也扩大到原来的3倍，据此解答。

【完整解答】120×3＝360（平方分米）【易错点】本题主要考查了学生根据平行四边形面积公式和积的变化规律解答问题的能力。

【易错三】如图，如果把这个平行四边形的底增加2厘米，高减少2厘米，面积会发生什么变化？【解题思路】把这个平行四边形的底增加2厘米，高减少2厘米，则底是4＋2＝6（厘米），高是4－2＝2（厘米）。