- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设
t t
t
0 TP dt fTP 1 f TP dt
f 0,1 权系数
则
a PTP a E fTE 1 f
0 aP
1 f a E
a fT 1 f a T
0 TE W W 0 P
W
1 f
q wds
j j 1 j
n
引入记号
w n ds j H ij w ds c i n j
j i j i
Gij
j
wds
则
H u G q
ij j ij j 1 j 1
n
n
j
或写成矩阵形式
a.常数单元(1节点)
取单元中点为节点,则
u const q const
b.线性单元(2节点) 取单元两端点为节点,则
j 1 1 j1
2 j 1 1 j2 2 u j u1j1 u 2j 2
q j q1j1 q 2j 2
令
Ke Kw aE , aW x E x w a P a E aW , b S x
则
a PTP a E TE aW TW b d
或
aPTP
a
nbT
b d
足标nb表示相邻节点.
d 或d 标准形式
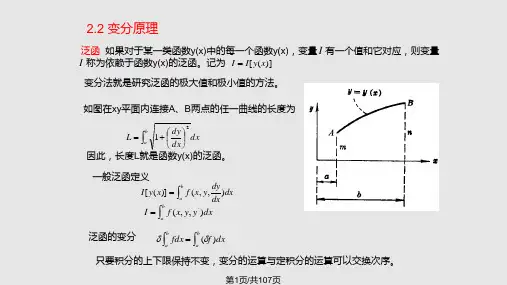
将分成j 1,2,..., n个直线段称为单元。 u 设待求函数u及导数q 的逼近函数为 n
u q x y
j j
ji ui
j j j
j j
j i j x i j
u ÷ n
j i j q i j
j i j y i j
第五章
边界元法、有限体积法和有限分析法
一、边界元法(Boundary Element Method或BEM) 基本思想:将控制微分方程转化为边界积分方程, 再用有限元法来处理边界积分方程。 特点: 1.区域内满足微分方程,边界上近似满足边界条件。 2.维数减少一个,可以简化计算。 3.精度一般高于有限元法。 4.系数矩阵不对称并为满阵,需要解析函数的基本解, 目前主要适用于线性问题。
u i 点i处未知函数值。 ci 依赖于点i处边界几何形状的函数, 若i在区域内,则ci 1 1 若i在光滑边界上,则ci 2
(d)式也可写为为
w u ci u u ds wds e n n
i
3.数值离散
(1)边界上剖分和插值
由(c)
u 2 wd u i d u i
则(a)式变为
w w u u u ds u ds q wds wds n n n
i 2
1
2
1
说明:内点的函数值可用边界上的函数值及其 法向导数值沿区域的边界积分来表示。
满足(c)式的解称为基本解。对于各向同性介质
Gij H ij
解方程组后,则全部边界上u,q为已知, 再求出区域内任意点u值为
u
i
u H q G
j ij j j 1 j 1
n
n
ij
二、有限体积法(Finite Volume Method或FVM)
1.基本思想:
将计算区域划分为一系列不重复的控制体积, 使每个网格点周围有一个控制体积,将待解的微分 方程对每一个控制体积积分,便得出一组离散方程。
0 TW
式中
0 a P faE faW a P
KE aE x e aW
0 aP
KW x W
c p x
t
三、有限分析法(Finite Analytic Method或FAM)
1.基本思想: 划分子区域,在子区域中求局部解析解。 导出一个代数方程,将节点值联系起来,将所有
B
m 1
1m
sinh m y B2 m cosh m y sin m y k
n m n , m 特征值 2h 2k A1n,A2 n,B1n,B2 n 傅立叶系数
以中心节点代入
uP cECuEC cWC uWC cNC u NC cSC uSC cSW uSW cSE uSE cNE u NE cNW u NW
2.数值离散的一般步骤
例:一维热传导问题
d dT K S 0 a dx dx
K---热传导系数 T---温度 S---单位体积内热量的产生率
P,E,W----节点 e,w---控制体交界面(一般为中点)
设y,z方向为单位厚度,则控制体体积为
将(a)式对该控制体积分
取h=k=1
n
n 2
则边中点与角点
C EC C NC CWC C SC
n 1
sin n n 1 1 0.205 35 3 n cos n sin n n 2 1 1 n 0.044 685 3 n cos n
2
w u u wd q wds u u ds n n
2
1
而
2
u w u wd wds u ds n n
wud
2
代入上式得
wud
ux, y f f E y , fW y , f S x , f N x , x, y, h, k , g
如内节点P
u P c EC u EC cWC uWC c NC u NC ... c SW u SW c SE u SE c P g P
u u
1
u n
q
2
当近似解不要求满足边界条件时,由格林公式可得:
2u 2u ud u q uds u u u ds x 2 y 2 n n 2 1
引入权函数w=δu代入上式
(3)代数方程的建立
对单元中心节点P(i,j)有
uij ci 1, j ui 1, j ci 1, j ui 1, j ci , j 1ui , j 1 ... ci 1, j 1ui 1, j 1 ci 1, j ui 1, j ci , j g i , j
1.边界积分方程的建立
例:Laplace方程
u
2
u
2
x
2
u
2
y
2
0
(在Ω内)
u u u q n
(在Γ1上)
(在Γ2上)
其伽辽金方程为
Lu pud
2u 2u 2 ud 0 x 2 y
源项的处理: 设
S S c S PTP S c 常数部分 S P TP的常数部分
于是
a P a E aW S P x b S c x
标准形式不变。
3.非恒定问题的处理
T T c p K t x x c p 定压比热
局部解析解汇集在一起求解。
2.一般原理 设微分方程
Lu g
(1) 网格划分 由相邻四个网格构成一个单元。
E,W,S,N,C-----东,南,西,北,中
(2)单元分析解
假设:边界条件近似为
f E y a0 a1 y a2 y 2
系数a0,a1,a2由东边NE,NC,SE节点的f值确定。 用分离变量法求线性微分方程的解析解
H u G q
将已知值
u,q
等代入,整理成代数方程组形式
ij x j
U
j 1
n
bi
式中
xj
q1 , q2 ,... qn , u n 1 , u n 2 ,...u n T
1 1
bij
H
j 1
n1
ij u j
j n1 1
G
n
ij q j
U ij
x 11
dT dT K K Sdx 0 b dx e dx w w
e
在节点间T值的插值变化规律为: (1)阶梯形剖面 节点上的T值为该点周围控制体内的数值。 但dT/dx在w,e上无定义。
(2)分段线性剖面
K e TE TP K w TP Tw S x 0 c xe xw S S对于控制体的平均值
2
u w w q wds wds u ds u ds n n n
2
1
2
1
--------(a)
称为边界元出发方程。
若选权函数w满足 2 w 0
而不要求满足边界条件时,则
2
u w w q wds wds u ds u ds b n n n
1
2
1
选择另一权函数w,使其对区域内任一点i满足
2 w i 0 c 1 Diracdelta 函数 0
i
(在i点) (不在i点处)
则
u w d u wd u
2 i 2
i
u i 未知函数u在i点的值