西北工业大学-《827信号与系统》-基础提高-第6讲

目　录2014年西北工业大学827信号与系统考研真题（回忆版）2011年西北工业大学432信号与系统（A）考研真题2010年西北工业大学827信号与系统（A）考研真题2009年西北工业大学信号与系统（B）考研真题2008年西北工业大学827信号与系统（A）考研真题2007年西北工业大学432信号与系统（A）考研真题2006年西北工业大学432信号与系统（A）考研真题2005年西北工业大学信号与系统考研真题2004年西北工业大学432信号与系统考研真题2003年西北工业大学432信号与系统考研真题2002年西北工业大学536信号与系统考研真题版）西北工业大学201!年攻波硕士学位删究生入学专试试题试题名称：信号与系统（A ）说 明：明节答迎•律七在答题维上科目代码：432 第I 页共』页—、口o 分）系统如图1-1欧不，请何该系统是若为：即KI 的？ <4分）以｝因果的？（4分〉线性的？ C4^J E ）时求先的，《4分） 壬）稳定的？ 3分〉；并蚀分别说叫厕的-二、f 15分）某螃性时不变系统当轿人叫，）肘,扎亨状态痢应为:fP [|.,（心话别如园3-2.圈3-3和国3足所:芥.⑴ 用图解法求Y （»； <12分，f2）吗招丫口心的散学表达式.I分）COSift^r七』-广5｝宙+门-]1-<“"奸丁），成中T 为常数L 试利用脂积的性质求彼系玩的冲噩响应h ⑴、"20分旧物系统如图3-1所示,系统输入』。

的敏业叶变换F （j*》以及11J 问>y(t)~X(t)COSr» £I 顷九｝乘法器西北工业大学2011年攻读硕士学位研究生入学君试试题试题名称「信号与系统(A)科目代码：432说呱所有答题一供吗在答题纸上弟2页兵4弟图3-3叫、HQ分)图4-【区示系统.r.U)=12V，LTH,O1F.R,=3Q.R^2Q b R.1Q.坤升美s断升时.搦电捋已经处干起余*1o时.升美sfflrr：求s件］mm<i)总两端电压的客状态响曲.％(“m林(2)R,两端电翼的零输入响应.5>16分此西北工业大学20]I年攻读硕士学在研究生入学考试试题试题名称：信导与系统（A）科目代码：432说明：所有答魅•律”在答逅纸上第3页共，1页图4-]五」20分）在连瓣时间系统中.RG电路可以构成将通滤波嚣:在抽样素统中.可以利用也容的充放电特性来构成吓关电容滤波器■图5-1-个开美屯容就波簪的原理小摄图，屯容CI和C2两靖的起始电压为零,如果在nT时茉，开美黝接通,英咻而百订十9虬开关$1断开，维接通＜n^0）t电容Cl和C2的充放电时间近小于「（1）对于激励*和响晌写出侔IS-1所示系统的爸分方程：门3图5-1西北工业大学20】I年攻读硕士学位研究生入学考试拭题试题名称，信号与系统（对科目代码：432说明：所亏答.腿神写在答题纸上第』讯其4训F若粉入代耳浏卜叫），求系统的零状态响应孔曲丁）槌分L六、＜20分〕已知:.y J jj）-6）].-u（ji+6}"W（Jt+l）-求;J1J s(n)=i<14)⑵而出序列瓦皿（65»七、"。

西北工业大学《827 信号与系统》习题解析 第 1 讲第 一 章信号与系统的基本概念1 －1 画出下列各信号的波形： (1)f 1 ( t ) ＝ (2 －e －t )U ( t )；(2)f 2 ( t ) ＝e －t cos10πt ×[U ( t －1) －U ( t －2) ] 。

1 －2 已知各信号的波形如图题 1 －2 所示，试写出它们各自的函数式。

1 －3 写出图题 1 －3 所示各信号的函数表达式。

(图见视频)1 －4 画出下列各信号的波形：(1) f 1 ( t ) ＝U ( t 2 －1)； (2) f 2 ( t ) ＝ ( t －1)U ( t 2 －1)； (3) f 3 ( t ) ＝U ( t 2 －5t ＋6)； (4)f 4 ( t ) ＝U ( sin πt ) 。

1 －5 判断下列各信号是否为周期信号，若是周期信号，求其周期 T 。

1) f 1 ( t ) ＝ 2 cos (2t －) 2) f 2 ( t ) ＝ [ sin ( t －) ]3) f 3 ( t ) ＝ 3 cos2πtU ( t ) 1 －6 化简下列各式： (1)jt －wδ(2τ－1)d τ1； (2)[ cos ( t ＋)( δ(t ))]； (3)jw －w[ cost δ(t ) ] sintdt 。

1 －7 求下列积分： (1)jw cos [ ω( t －3) δ(t －2)] dt ；(2)jδ(t ＋3)dt ；(3) jwe －2t δ(t 0 －t )dt 。

— 1 —21－8试求图题1－8中各信号一阶导数的波形，并写出其函数表达式，其中f3( t) ＝cos t[ U( t) －U( t－5) ] 。

1－9已知信号f() 的波形如图题1－9所示，试画出y( t) ＝f(t＋1)U( －t)的波形。

1－10已知信号f( t)的波形如图题1－10所示，试画出信号与信号的波形。

西北工业大学-《827信号与系统》-基础提高-第1、2讲第1讲第一章信号与系统的基本概念(一）1.1 信号的描述及其分类信息、消息与信号信息是组成客观物质世界的三大要素，对其处理和传输具有非常重要的意义。

信息一般以一定的物理形式表现为消息；消息一般不便于直接传输，常借助于转换设备转换为便于传输的电信号。

消息是信号的具体内容，信号则是消息的便于传送的表现形式。

信号常用的表现形式为：函数、图形、数据。

1.2 信号的分类：1.确定信号、随机信号确定信号：由确定时间函数描述的信号。

在某已确定时刻，信号有确定的值；随机信号：信号是时间的随机函数。

在某已确定时刻，信号的值不确定； 2.连续信号与离散信号连续信号：除若干不连续点外，自变量的取值是连续的；模拟信号：自变量和函数值都连续的信号；离散信号：自变量的取值是离散的；数字信号：自变量和函数值都是离散的。

3. 周期信号和非周期信号 4.能量信号和功率信号5.有时限信号与无时限信号6.有始信号与有终信号7.因果信号与非因果信号1.3 常用的连续信号及时域特性一、正弦信号f(t)=A m cos(ωt+?) (-∞<t<="" p="">3、三要素：角频率ω，最大值A m ，初相位?πωπ=== 212f f T T二、直流信号f(t)=A (-∞<t<∞)< p="">三、单位阶跃信号>?><000100()()100t t t U t U t t t t t非因果信号→因果信号四、单位门信号（时限信号）τττ?-<<=1()220其余t G t练习：用单位阶跃表示门信号五、单位冲激信号δ?∞==?≠?0()00t t t δδ+-∞-∞==??00()()1t dt t dt→=ττ0δ(t)δ(t)lim δ?∞=?-=?()0t t A t t t tδ?∞=-?+=?≠??000()0t t A t t t t单位冲激信号性质：δδδδδ∞-∞==-=?1.f (t)(t)f (0)(t)2.f (t )(t )dt f (0)3.(t )(t )讨论：δδδδδ∞-∞-=-+-=--=?0000000()()()()()()()()()t t t t f t t t f t t t f t t t dt f t δδ=14.(at )(t)a t ?=?=?1at xdt dx a()()δδδττ-∞==U t t ()()()()t与关系：dU t t dtU t d强度：a>0δδ∞∞-∞-∞==?11()()at dt x dx a a 强度：a<0 δδδδ∞-∞-∞∞-∞∞∞-∞==- ==1()()1()11()at dt x dxa x dxa x dx aaδδ-=- -==000t 115.(at t )(t )a aat t xdt dx a强度：a>0δδ∞∞-∞-∞-==?011()()at t dt x dx a aδ6.[f (t)]（1）f(t)=0，有n 个不相等的根，t 1，t 2，…t n ，且'≠= ()0(1,2,)i i f t t n 则δδ==-'∑11[()]()()ni ii f t t t f t （2）f(t)=0，有重根，δ[()]f t 无意义。

专业课基础提高课程第8讲第四章连续系统频域分析-傅立叶变换（一）第四章 连续系统频域分析用傅立叶变换求零状态稳定系统的响应及研究稳定系统的功能。

4-1 引言一、定义系统函数定义：()()()Y j H j F j ωωω=（1）h(t)的傅立叶变换；（2）描述系统频率特性；（3）取决于系统本身。

二、计算1)()()j t H j h t e dt ωω∞--∞=⎰ ()2)()()Y j H j F j ωωω=3)()()p j H j H p ωω== 4)()H j ω=响应相量激励相量4-2 系统对非正弦周期信号的响应一、基本信号j t e W 通过线性系统对于一个单位冲激响应为()h t 的线性时不变系统，若激励信号为：二、正弦信号通过线性系统3、非正弦周期信号通过线性系统（1）方法一：用谐波分析方法（叠加定理）（2）方法二：傅立叶变换（频域分析法）结论：周期信号作用于线性系统，其响应也为周期信号；周期激励信号的频谱为冲激序列，其响应频谱也为冲激序列。

4-3 系统对非周期信号的响应专业课基础提高课程第9讲第四章连续系统频域分析-傅立叶变换（二）4-4 频域系统函数一、定义系统函数H(jw)的定义为：()()()Y jw H jw F jw = 二、H(jw)的物理意义从上式可以看出H(jw)是系统单位冲激响应的频谱函数。

反之有：()()jwt h t H jw e dw ¥-?=ò可以看出H(jw)是将h(t)分解为无穷多个指数信号之和时，其相应的频率密度函数。

三、 H(jw)的求法1) 当给定激励与零状态响应时，根据定义求解2)当已知系统单位冲激响应时，对其求解傅里叶变换即可3)当给定系统的电路模型时，用相量法求解4)当给定系统的数学模型(微分方程)时，用傅里叶变换法求解四、系统频率特性五、应用举例4-5 信号通过线性系统不失真条件信号失真：线性失真：幅度失真、相位失真非线性失真：产生新的频率成分一、时域：二、频域：4-6 理想低通滤波器及其响应滤波器：使一部分频率范围的信号通过，而另一部分信号得以抑制的系统。

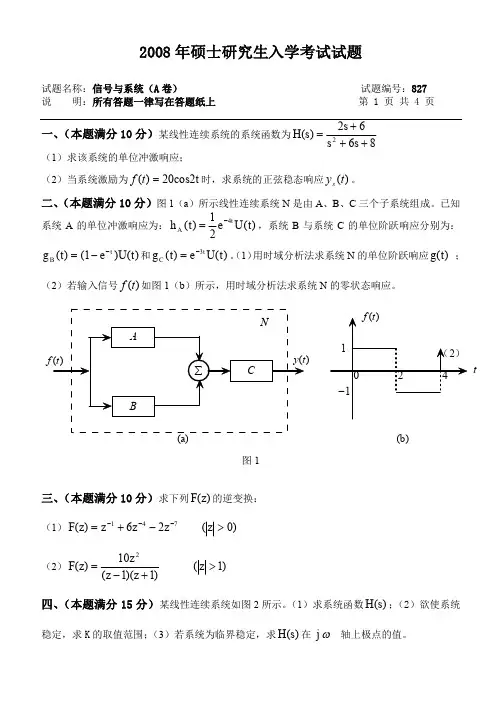
西北工业大学《827信号与系统》重难点解析第1讲第一章信号与系统的基本概念一、信号的主要分类(1)连续时间信号：自变量的取值是连续的离散时间信号：自变量的取值是离散的(2)周期信号：具有周期性，且是无始无终信号非周期信号：不具有周期性(3)因果信号：t＜0时，f( t) ＝0；t＞0时，f( t) ≠0的信号非因果信号：t＞0时，f( t) ＝0的信号(4)功率信号：平均功率为有限值，能量趋近于无穷；能量信号：平均功率为0，能量为有限值的信号注意：(1)两个连续周期信号的和不一定是周期信号，只有当这两个信号的周期比为有理数时，该信号才是周期信号，且周期为原信号周期的最小公倍数；(2)直流信号和有界的周期信号均为功率信号；阶跃信号和有始周期信号也是功率信号；有界的非周期信号均为能量信号；无界的周期信号和无界的非周期信号均为非功率非能量信号。

一个信号只能是功率信号和能量信号两者之一，不会两者都是，但可以两者都不是，也就是非周期非能量信号。

【例1】判断下列各信号是否为周期信号后，若为周期信号，求出其周期。

(1)f( t) ＝cos8t－sin12t(2)f(k) ＝cos k＋2sin2πk解：(1) T1＝＝T2＝＝由于＝，故f( t)为周期信号，其周期为T1和T2的最小公倍数，即T＝(2) cos k为周期信号，N1＝＝842π2π故f(k)为周期信号，为N1和N2的最小公倍数，即N＝8个间隔2cos2πk为周期信号，N2＝＝1三、δ(t )和 δ′( t ) 函数的性质【例 2】 (3t －2)[ δ(t ) ＋ δ(t －2) ]dtt 2 －2t ＋ 3) δ＇( t －2)dt(3t －2) δ(t －2)dt＝ －2 ＋ (3 ×2 －2) ＝ 2(2) 原式 ＝ － ( t 2 ＋ 3 －2t ) ＇ t ＝2 ＝ － (2t －2) t ＝2 ＝ －2四、系统的分类(1)线性系统：同时满足齐次性和叠加性的系统 非线性系统：不能同时满足以上两个条件的系统 (2)时不变系统：满足时不变的系统 时变系统：不满足时不变的系统(3)因果系统：响应不产生激励之前的系统 非因果系统：响应产生于激励之前的系统(4)稳定系统：系统的激励有界，响应也有界的系统 非稳定系统：系统的激励有界，响应无界的系统【例 3】 已知系统：a ：y ( t ) ＝2f ( t ) ＋3 b ：y ( t ) ＝f (2t ) c ：y ( t ) ＝f ( －t ) d ：y ( t ) ＝tf ( t ) 试判断上述哪些系统满足下列条件： (1)不是线性系统的是： (2)不是稳定系统的是： (3)不是时不变系统的是： (4)不是因果系统的是：解：(1) a (2)d (3)b ，c ，d (4)b ，c五、线性时不变系统的性质f ( t ) →y ( t )，f 1 ( t ) →y 1 ( t )，f 2 ( t ) →y 2 ( t )， A 1，A 2，A 为任意常数，常见性质如下： 1．齐次性：Af ( t ) →Ay ( t )2．叠加性：f 1 ( t ) ＋f 2 ( t ) →y 1 ( t ) ＋y 2 ( t )5 555西北工业大学《827 信号与系统》重难点解析3．线性：A 1f 1 ( t ) ＋A 2f 2 ( t ) →A 1 y 1 ( t ) ＋A 2 y 2 ( t ) 4．时不变性：f ( t －τ) →y ( t －τ) 5．微分性：→6．积分性：)d τ→)d τ【例 4】 一阶系统的初始状态为 y (0 － )，激励与响应分别为f ( t )，y ( t ) 。

2014西工大信号与系统827回忆版
信号与系统今年的出题是60分的小型大题，每题六分，和90分的综合大题，每题十五分大概写写，具体题号忘了
一
给定电路求自然频率及微分方程
将Sa（t）分解成cos（t）的基本形式
求离散信号的卷积和求连续信号的卷积
求信号能量
判断系统等价不等价分析线性时不变
有些基本题忘了，其他的都比较基础吧。

二
给定sgnt函数和sa（t）求两信号卷积后的值
给定信号流图求z域稳定，系统函数，和稳态响应
给定系统框图，用状态变量分析稳定
求系统初值和终值。

这个题出的很巧妙
电路s域分析
s域抽样和z域离散互换很有难度。