材料力学习题册

材料力学习题册参考答案材料力学习题册参考答案（无计算题）第1章：轴向拉伸与压缩一：1（ABE ）2（ABD ）3（DE ）4（AEB ）5（C ）6（ＣＥ）７（ABD ）8（C ）9（BD ）10（ADE ）11（ACE ）12（D ）13（CE ）14（D ）15（ＡＢ）１６（BE ）17（D ）二：1对2错3错4错5对6对7错8错9错10错11错12错13对14错15错三：1：钢铸铁 2：比例极限p σ 弹性极限e σ 屈服极限s σ 强度极限b σ3.横截面 45度斜截面4. εσE =， EAFl l =5.强度，刚度，稳定性；6.轴向拉伸（或压缩）；7. llb b ?μ?=8. 1MPa=106 N/m 2 =1012 N/mm 2 9. 抵抗伸缩弹性变形，加载方式 10. 正正、剪 11.极限应力 12. >5% <5% 13. 破坏s σ b σ 14.强度校核截面设计荷载设计15. 线弹性变形弹性变形 16.拉应力 45度 17.无明显屈服阶段的塑性材料力学性能参考答案：1. A 2. C 3. C 4. C 5. C 6. 5d ; 10d 7. 弹塑8. s2s 9. 0.1 10. 压缩11. b 0.4σ 12. <；< 剪切挤压答案：一：1.（C ），2.（B ），3.（A ），二：1. 2bh db 2. b(d+a) bc 3. 4a δ a 2 4. F第2章：扭转一：1.（B ） 2.（C D ） 3.（C D ） 4. （C ） 5. （A E ） 6. （A ）7. （D ）8. （B D ） 9.（C ） 10. （B ） 11.（D ） 12.（C ）13.（B ）14.（A ） 15.（A E ）二：1错 2对 3对 4错 5错 6 对三：1. 垂直 2. 扭矩剪应力 3.最外缘为零4. p ττ< 抗扭刚度材料抵抗扭转变形的能力5. 不变不变增大一倍6. 1.5879τ7.实心空心圆8. 3241)(α- 9. m ax m in αττ= 10. 长边的中点中心角点 11.形成回路（剪力流）第3章：平面图形的几何性质一：1.（C ），2.（A ），3.（C ），4.（C ），5.（A ），6.（C ），7.（C ），8.（A ），9.（D ）二：1）. 1；无穷多；2）4)4/5(a ； 3），84p R I π=p 4z y I 16R I I ===π4）12/312bh I I z z ==；5）)/(/H 6bh 6BH W 32z -= 6）12/)(2211h b bh I I I I z y z y +=+=+；7）各分部图形对同一轴静矩8）两轴交点的极惯性矩；9）距形心最近的；10）惯性主轴；11）图形对其惯性积为零三：1：64/πd 114； 2.（0 , 14.09cm ）(a 22，a 62)3： 4447.9cm 4， 4：0.00686d 4 ，5: 77500 mm 4 ;6: 64640039.110 23.410C C C C y y z z I I mm I I mm ==?==?第4章：弯曲内力一：1.（A B ）2.（D ）3.（B ）4.（A B E ）5.（A B D ）6.（ACE ） 7.（ABDE ） 8.（ABE ）9. （D ） 10. （D ） 11.（ACBE ） 12.（D ） 13.（ABCDE ）二：1错 2错 3错 4对 5错 6对 7对三：1. 以弯曲变形 2.集中力 3. KNm 2512M .max =4. m KN 2q = 向下 KN 9P = 向上5.中性轴6.荷载支撑力7. 小8. 悬臂简支外伸9. 零第5章：弯曲应力一：1（ＡＢＤ）２．（C ）3.（BE ）4.（A ）5.（C ）6.（C ）7.（B ）8.（C ）9.（BC ）二：1对 2错 3错 4 对 5 错 6错 7 对三：1.满足强度要求更经济、更省料2. 变成曲面，既不伸长也不缩短3.中性轴4.形心主轴5.最大正应力6.剪力方向7.相等8.平面弯曲发生在最大弯矩处9.平面弯曲第6章：弯曲变形一：1（B ），2（B ），3（A ），4（D ），5（C ），6（A ），7（C ），8（B ），9（A ）10（B ），11（A ）二：1对2错3错4错5错6对7错8错9错10对11错12对三：1.（转角小量:θθtan ≈）（未考虑高阶小量对曲率的影响）2. 挠曲线采用近似微分方程导致的。

练习1 绪论及基本概念1-1 是非题（1）材料力学是研究构件承载能力的一门学科。

（ 是 ）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。

（是 ）（3）构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。

（ 是 ） （4）应力是内力分布集度。

（是 ）（5）材料力学主要研究构件弹性范围内的小变形问题。

（是 ） （6）若物体产生位移，则必定同时产生变形。

（非 ） （7）各向同性假设认为，材料沿各个方向具有相同的变形。

（F ）（8）均匀性假设认为，材料内部各点的力学性质是相同的。

（是）：（9）根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。

（非） （10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。

（非 ）1-2 填空题（1）根据材料的主要性质对材料作如下三个基本假设：连续性假设 、均匀性假设 、 各向同性假设 。

（2）工程中的 强度 ，是指构件抵抗破坏的能力； 刚度 ，是指构件抵抗变形的能力。

（3）保证构件正常或安全工作的基本要求包括 强度 ， 刚度 ，和 稳定性 三个方面。

，（4）图示构件中，杆1发生 拉伸 变形，杆2发生 压缩 变形， 杆3发生 弯曲 变形。

（5）认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为 连续性假设 。

根据这一假设构件的应力，应变和位移就可以用坐标的 连续 函数来表示。

（6）图示结构中，杆1发生 弯曲 变形，构件2发生 剪切 变形，杆件3发生 弯曲与轴向压缩组合。

变形。

（7）解除外力后，能完全消失的变形称为 弹性变形 ，不能消失而残余的的那部分变形称为 塑性变形 。

（8）根据小变形条件，可以认为构件的变形远小于其原始尺寸。

1-3 选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。

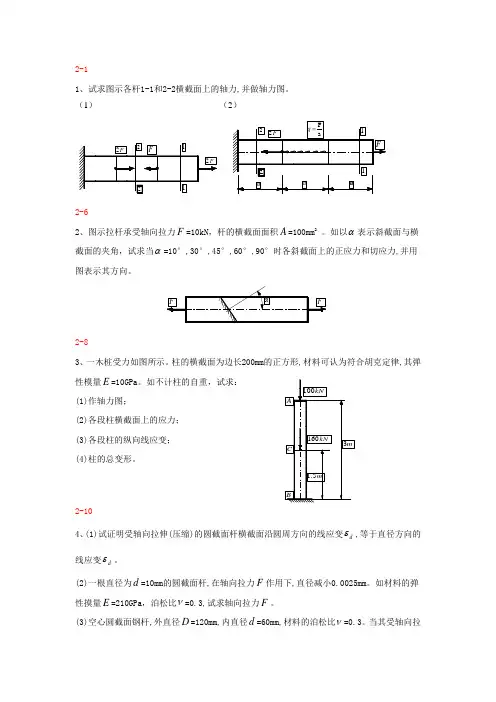
2-11、试求图示各杆1-1和2-2横截面上的轴力,并做轴力图。

（1） （2）2-62、图示拉杆承受轴向拉力F =10kN ，杆的横截面面积A =100mm 2。

如以α表示斜截面与横截面的夹角，试求当α=10°,30°,45°,60°,90°时各斜截面上的正应力和切应力,并用图表示其方向。

2-83、一木桩受力如图所示。

柱的横截面为边长200mm 的正方形,材料可认为符合胡克定律,其弹性模量E =10GPa 。

如不计柱的自重，试求：(1)作轴力图；(2)各段柱横截面上的应力； (3)各段柱的纵向线应变；(4)柱的总变形。

2-104、(1)试证明受轴向拉伸(压缩)的圆截面杆横截面沿圆周方向的线应变d ε,等于直径方向的线应变d ε。

(2)一根直径为d =10mm 的圆截面杆,在轴向拉力F 作用下,直径减小0.0025mm 。

如材料的弹性摸量E =210GPa ，泊松比ν=0.3,试求轴向拉力F 。

(3)空心圆截面钢杆,外直径D =120mm,内直径d =60mm,材料的泊松比ν=0.3。

当其受轴向拉伸时, 已知纵向线应变ε=0.001,试求其变形后的壁厚δ。

2-145、图示A和B两点之间原有水平方向的一根直径d=1mm的钢丝,在钢丝的中点C加一竖直荷载F。

已知钢丝产生的线应变为ε=0.0035,其材料的弹性模量E=210GPa，钢丝的自重不计。

试求：(1) 钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律)；(2) 钢丝在C点下降的距离∆；(3) 荷载F的值。

2-196、简易起重设备的计算简图如图所示.一直斜杆AB应用两根63mm×40mm×4mm不等边角钢组[σ=170MPa。

试问在提起重量为P=15kN的重物时,斜杆AB是否满足强度成,钢的许用应力]条件?2-217、一结构受力如图所示,杆件AB,AD均由两根等边角钢组成。

班级姓名学号110 kN 20 kN 第1章材料力学的基本概念第2章轴向拉伸和压缩2-1试用截面法计算图示杆件各段的轴力，并画轴力图。

2-2图示等截面直杆由钢杆与铜杆CD在C处粘接而成。

直杆各部分的直径均为d=36mm,受力如图所示。

若不考虑杆的自重，试求4C段和4D段杆的轴向变形量2-4螺旋压紧装置如图所示。

现己知工件所受的压紧力为F=4kNo装置中旋紧螺栓螺纹的内径Ji = 13.8nuii;固定螺栓内径t/2= 17311U11O两根螺栓材料相同，其许用应力A材料力学习题册2班级 姓名 学号31-1截而利2-5现场施工所用起重机吊环由两根侧臂组成（图小，三处均为狡链连接。

每一侧臂AB 和都由两根矩形截面杆所组成（图b ）。

已知起重载荷F P =1200 kN, 每根矩形杆截面尺寸比例b/h=0・3,材料的许用应力0]=78.5MPa 。

试设计矩形杆的截2-6图示结构中BC 和AC 都是圆截面直杆，直径均为d=20mm,材料都是Q235钢, 其许用应力[<r] = 157MPao 试求该结构的许可载荷。

材料力学习题册第3章扭转3—4变截面轴受力如图所示，图中尺寸单位为mm。

若己知Mj = 1765N・m, Me2 = 1171N m,材料的切变模量G=80.4 GPa,试求：（1）轴内最大切应力，并指出其作用位置。

（2）轴的最大相对扭转角3-5图示实心圆轴承受外加扭转力偶，其力偶矩Me=3 kN m,图中尺寸单位为mm。

试求：（1）轴横截面上的最大切应力。

（2）轴横截面上半径r=15nmi以内部分承受的扭矩所占全部横截面上扭矩的白分比。

（3）去掉r =15nun以内部分，横截面上的最大切应力增加的百分比。

45班级姓名学号3-6同轴线的芯轴AB与轴套CD,在D处二者无接触，而在C处焊成一体。

轴的4 端承受扭转力偶作用，如图所示。

己知轴直径d =66 mm,轴套外直径£）=80 nun,厚度5=6 mm；材料的许用切应力[r] = 60 MPa o试求结构所能承受的最大外力偶矩。

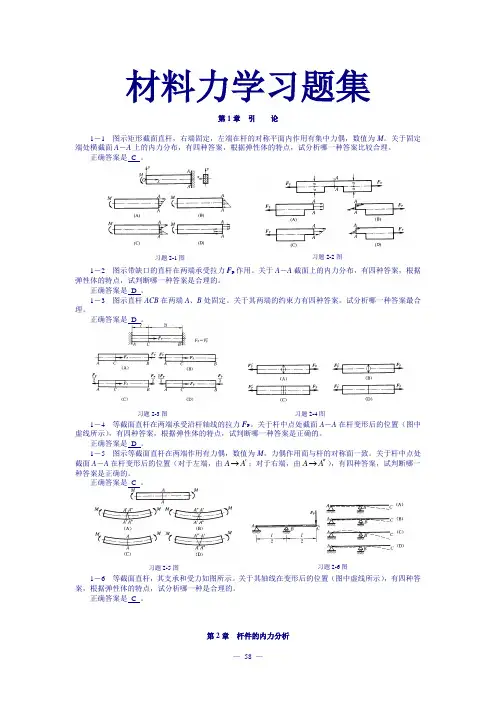
习题2-1图 习题2-2图习题2-3图 习题2-4图 习题2-5图 习题2-6图 材料力学习题集第1章 引 论1－1 图示矩形截面直杆，右端固定，左端在杆的对称平面内作用有集中力偶，数值为M 。

关于固定端处横截面A －A 上的内力分布，有四种答案，根据弹性体的特点，试分析哪一种答案比较合理。

正确答案是 C 。

1－2 图示带缺口的直杆在两端承受拉力F P 作用。

关于A －A 截面上的内力分布，有四种答案，根据弹性体的特点，试判断哪一种答案是合理的。

正确答案是 D 。

1－3 图示直杆ACB 在两端A 、B 处固定。

关于其两端的约束力有四种答案。

试分析哪一种答案最合理。

正确答案是 D 。

1－4 等截面直杆在两端承受沿杆轴线的拉力F P 。

关于杆中点处截面A －A 在杆变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试判断哪一种答案是正确的。

正确答案是 D 。

1－5 图示等截面直杆在两端作用有力偶，数值为M ，力偶作用面与杆的对称面一致。

关于杆中点处截面A －A 在杆变形后的位置（对于左端，由A A '→；对于右端，由A A ''→），有四种答案，试判断哪一种答案是正确的。

正确答案是 C 。

1－6 等截面直杆，其支承和受力如图所示。

关于其轴线在变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试分析哪一种是合理的。

正确答案是 C 。

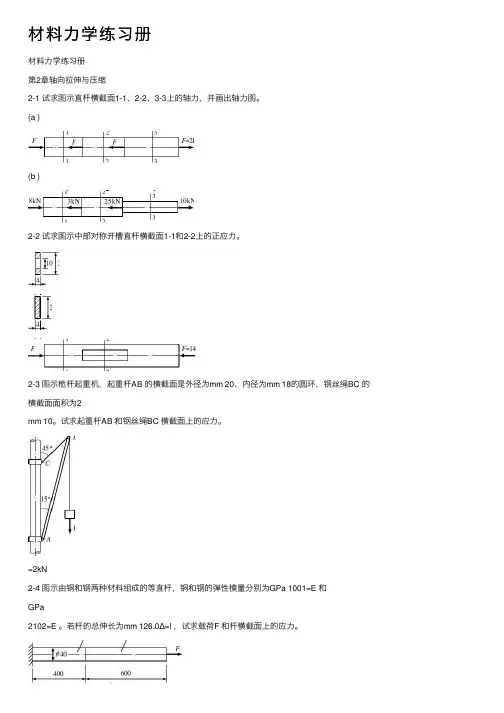
第2章 杆件的内力分析习题2-1图习题2-2图习题2-3图习题2-4图2－1 平衡微分方程中的正负号由哪些因素所确定？简支梁受力及Ox 坐标取向如图所示。

试分析下列平衡微分方程中哪一个是正确的。

（A d Q F d M（B （C （D 2－2 对于图示承受均布载荷q 的简支梁，其弯矩图凸凹性与哪些因素相关？试判断下列四种答案中。

2－3 已知梁的剪力图以及a 、e 截面上的弯矩M a 和M e ，如图所示。

为确定b M 、M ，现有下列四种答案，试分析哪一种 （A （B （C （D 之间剪力图的面积，以此类推。

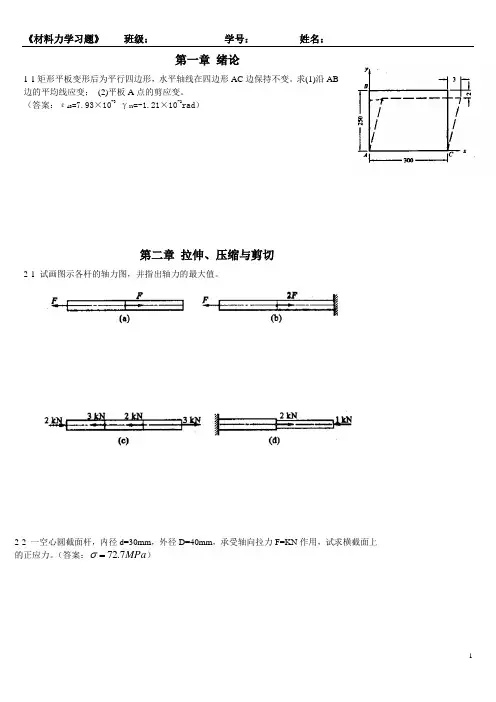
材料⼒学练习册材料⼒学练习册第2章轴向拉伸与压缩2-1 试求图⽰直杆横截⾯1-1、2-2、3-3上的轴⼒，并画出轴⼒图。

(a )(b )2-2 试求图⽰中部对称开槽直杆横截⾯1-1和2-2上的正应⼒。

2-3 图⽰桅杆起重机，起重杆AB 的横截⾯是外径为mm 20、内径为mm 18的圆环，钢丝绳BC 的横截⾯⾯积为2mm 10。

试求起重杆AB 和钢丝绳BC 横截⾯上的应⼒。

=2kN2-4 图⽰由铜和钢两种材料组成的等直杆，铜和钢的弹性模量分别为GPa 1001=E 和GPa2102=E 。

若杆的总伸长为mm 126.0Δ=l ，试求载荷F 和杆横截⾯上的应⼒。

2-5 图⽰阶梯形钢杆，材料的弹性模量GPa 200=E ，试求杆横截⾯上的最⼤正应⼒和杆的总伸长。

2-6 图⽰电⼦秤的传感器为⼀空⼼圆筒形结构，圆筒材料的弹性模量GPa 200=E 。

在秤某⼀沿圆筒轴向作⽤的重物时，测得筒壁产⽣的轴向线应变6108.49-?-=ε。

试求此重物的重量P 。

第3章材料的⼒学性质拉压杆的强度计算3-1 图⽰⽔压机，若两根⽴柱材料的许⽤应⼒为MPa 80][=σ，试校核⽴柱的强度。

3-2 图⽰油缸盖与缸体采⽤6个螺栓连接。

已知油缸内径mm350=D ，油压MPa 1=p 。

若螺栓材料的许⽤应⼒MPa 40][=σ，试求螺栓的内径。

3-3 图⽰铰接结构由杆AB 和AC 组成，杆AC 的长度为杆AB 长度的两倍，横截⾯⾯积均为2mm 200=A 。

两杆的材料相同，许⽤应⼒MPa 160][=σ][F3-4 承受轴⼒kN 160N =F 作⽤的等截⾯直杆，若任⼀截⾯上的切应⼒不超过MPa 80，试求此杆的最⼩横截⾯⾯积。

3-5 试求图⽰等直杆AB 各段内的轴⼒。

a3-6 图⽰结构的横梁AB 可视为刚体，杆1、2和3的横截⾯⾯积均为A ，各杆的材料相同，许⽤应⼒为][σ。

试求许⽤载荷][F 。

3-7 图⽰铰接正⽅形结构，各杆的材料均为铸铁，其许⽤压应⼒与许⽤拉应⼒的⽐值为3][][t c =σσ，各杆的横截⾯⾯积均为A 。

第一章 绪论1-1矩形平板变形后为平行四边形，水平轴线在四边形AC 边保持不变。

求(1)沿AB边的平均线应变； (2)平板A 点的剪应变。

（答案：εAB =7.93×10-3 γXY =-1.21×10-2rad ）第二章 拉伸、压缩与剪切2-1 试画图示各杆的轴力图，并指出轴力的最大值。

2-2 一空心圆截面杆，内径d=30mm ，外径D=40mm ，承受轴向拉力F=KN 作用，试求横截面上的正应力。

（答案：MPa 7.72=σ）2-3 题2－1 c 所示杆，若该杆的横截面面积A=502m m ，试计算杆内的最大拉应力与最大压应力（答案：MPa t 60max ,=σ MPa c 40max ,=σ）2.4图示轴向受拉等截面杆，横截面面积A=5002m m ，载荷F=50KN 。

试求图示截面m-m 上的正应力与切应力，以及杆内的最大正应力与最大切应力。

（答案：MPa MPa MPa MPa 50 ; 100 ; 24.49 ; 32.41max max ==-==τστσαα）2.5如图所示，杆件受轴向载荷F 作用。

该杆由两根木杆粘接而成，若欲使粘接面上的正应力为其切应力的二倍，则粘接面的方位角θ应为何值（答案： 6.26=θ）2.6 等直杆受力如图所示，试求各杆段中截面上的轴力，并绘出轴力图。

2.7某材料的应力－应变曲线如图所示，图中还同时画出了低应变去区的详图，试确定材料的弹性模量E 、屈服极限s σ、强度极限b σ、与伸长率δ，并判断该材料属于何种类型（塑性或脆性材料）。

2.8某材料的应力－应变曲线如图所示，试根据该曲线确定： （1）材料的弹性模量E 、比例极限P σ与屈服极限2.0σ; （2）当应力增加到MPa 350=σ时，材料的正应变ε， 以及相应的弹性应变e ε与塑性应变p ε2.9图示桁架，杆1与杆2的横截面均为圆形，直径分别为d1=30mm 与d2＝20mm ，两杆材料相同，许用应力[]σ＝160MPa ，该桁架在节点A 处承受铅垂方向的载荷F=80KN 作用。

F12312练习 1 绪论及基本概念1-1 是非题（1） 材料力学是研究构件承载能力的一门学科。

（ 是 ）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。

（是）（3） 构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。

（ 是 ） （4） 应力是内力分布集度。

（是 ）（5） 材料力学主要研究构件弹性范围内的小变形问题。

（是 ） （6） 若物体产生位移，则必定同时产生变形。

（非 ） （7） 各向同性假设认为，材料沿各个方向具有相同的变形。

（F ） （8） 均匀性假设认为，材料内部各点的力学性质是相同的。

（是）（9） 根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。

（非） （10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。

（非 ）1-2 填空题（1） 根据材料的主要性质对材料作如下三个基本假设：连续性假设、均匀性假设 、各向同性假设 。

（2） 工程中的强度 ，是指构件抵抗破坏的能力； 刚度 ，是指构件抵抗变形的能力。

（3） 保证构件正常或安全工作的基本要求包括 强度 ， 刚度 ，和 稳定性三个方面。

3（4） 图示构件中，杆 1 发生 拉伸 变形，杆 2 发生 压缩 变形，杆 3 发生 弯曲 变形。

（5） 认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为 连续性假设。

根据这一假设构件的应力，应变和位移就可以用坐标的 连续 函数来表示。

（6） 图示结构中，杆 1 发生 弯曲变形，构件 2发生 剪切 变形，杆件 3 发生 弯曲与轴向压缩组合。

变形。

（7） 解除外力后，能完全消失的变形称为 弹性变形，不能消失而残余的的那部分变形称为 塑性变形 。

（8） 根据 小变形 条件，可以认为构件的变形远 小于 其原始尺寸。

1-3选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。

3第一章 绪论一、选择题1.关于确定截面内力的截面法的适用范围，有下列四种说法：【D.适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普通情况。

2.关于下列结论的正确性：【C 1.同一截面上正应力τσ与剪应力必须相互垂直3.同一截面上各点的剪应力必相互平行。

】3.下列结论中那个是正确的：【B.若物体各点均无位移，则该物体必定无变形】4.根据各向同性假设，可认为构件的下列量中的某一种量在各方向都相同：【B 材料的弹性常数】5.根据均匀性假设，可认为构件的下列量中的某个量在各点处都相同：【C 材料的弹性常数】6.关于下列结论：【C 1.应变分为线应变ε和切应变γ 2.应变为无量纲量 3.若物体的各部分均无变形，则物体内各点的应变均为零】7.单元体受力后，变形如图虚线所示，则切应变γ为【B 2α】二、填空题1.根据材料的主要性能作如下三个基本假设 连续性假设 ， 均匀性假设 和 各向同性假设 。

2.构件的承载能力包括强度、刚度和稳定性三个方面。

3.图示结构中，杆1发生轴向拉伸变形，杆2发生轴向压缩变形，杆3发生弯曲变形。

4.图示为构件内A 点处取出的单元体，构件受力后单元体的位置为虚线表示，则称dx du /为A 点沿x 方向的线应变，dy dv /为【A 点沿y 方向的线应变】，)(21a a +为【A 在xy 平面内的角应变】。

5.认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为连续性假设。

根据这一假设，构件的应力、应变和位移就可以用坐标的连续性函数来表示。

6.在拉（压）杆斜截面上某点处分布内力集度称为应力(或全应力），它沿着截面法线方向的分量称为正应力，而沿截面切线方向的分量称为切应力。

第二章杆件的内力分析一、选择题1.单位宽度的薄壁圆环受力如图所示，p 为径向压强，其n-n 截面上的内力N F 有四个答案：【B 2/pD 】2.梁的内力符号与坐标系的关系是：【B 剪力、弯矩符号与坐标系无关】3.梁的受载情况对于中央截面为反对称（如图）。