材料力学例题
- 格式：pdf
- 大小：3.94 MB
- 文档页数：23
下载文档原格式
合集下载
材料力学例题
C
0.75m 1m
A
D 1.5m
B
F
横梁BC为刚杆，自重Q＝2KN，力P＝10KN可在横 梁BC上自由移动。AB杆的许用应力为[σ]=100MP ａ，设计AB杆的横截面面积。如果AB杆采用直径 为10毫米的细丝，需要几根？
P C
30°
Ｂ
• [例] 长为 L=2m 的圆杆受均布力偶 m=20Nm/m 的作用，如图，若杆的内外径之比为 =0.8 ，
例题 空心圆杆AB和CD杆焊接成整体结构，受力如图.AB杆的外径 D=140mm，内外 径之比α= d/D=0.8，材料的许用应力[] = 160MPa。试用第三强度理论校核AB杆的 强度。 解:（1）外力分析 将力向AB杆的B截面形心简化得
10kN
0.8m A
B D
F 25kN
M e 15 1 . 4 10 0 . 6 15 kN m
G=80GPa ，许用剪应力 []=30MPa，试设计杆
的外径；若[]=2º /m ，试校核此杆的刚度，并
求右端面转角。
[例题] 某传动轴设计要求转速n = 500 r / min，输入功率P1 = 500 马力， 输出功率分别 P2 = 200马力及 P3 = 300马力，已 知：G=80GPa ，[ ]=70M Pa，[ ]=1º /m ，试确定： ①AB 段直径 d1和 BC 段直径 d2 ？ ②若全轴选同一直径，应为多少？ ③主动轮与从动轮如何安排,轴的受力合理？ P2 A 500 B 400 P3 C
y Me A x B l/2 F1
F2
D F2 D M e C ( F1 F 2 ) 2 2 20 F2 kN 3 F 20kN
轴产生扭转和垂直纵向对称面内的平 面弯曲
0.75m 1m
A
D 1.5m
B
F
横梁BC为刚杆，自重Q＝2KN，力P＝10KN可在横 梁BC上自由移动。AB杆的许用应力为[σ]=100MP ａ，设计AB杆的横截面面积。如果AB杆采用直径 为10毫米的细丝，需要几根？
P C
30°
Ｂ
• [例] 长为 L=2m 的圆杆受均布力偶 m=20Nm/m 的作用，如图，若杆的内外径之比为 =0.8 ，
例题 空心圆杆AB和CD杆焊接成整体结构，受力如图.AB杆的外径 D=140mm，内外 径之比α= d/D=0.8，材料的许用应力[] = 160MPa。试用第三强度理论校核AB杆的 强度。 解:（1）外力分析 将力向AB杆的B截面形心简化得
10kN
0.8m A
B D
F 25kN
M e 15 1 . 4 10 0 . 6 15 kN m
G=80GPa ，许用剪应力 []=30MPa，试设计杆
的外径；若[]=2º /m ，试校核此杆的刚度，并
求右端面转角。
[例题] 某传动轴设计要求转速n = 500 r / min，输入功率P1 = 500 马力， 输出功率分别 P2 = 200马力及 P3 = 300马力，已 知：G=80GPa ，[ ]=70M Pa，[ ]=1º /m ，试确定： ①AB 段直径 d1和 BC 段直径 d2 ？ ②若全轴选同一直径，应为多少？ ③主动轮与从动轮如何安排,轴的受力合理？ P2 A 500 B 400 P3 C
y Me A x B l/2 F1
F2
D F2 D M e C ( F1 F 2 ) 2 2 20 F2 kN 3 F 20kN
轴产生扭转和垂直纵向对称面内的平 面弯曲
材料力学典型例题及解析 12.冲击问题典型习题解析
击构件瞬间的速度为 υ
，只须将前面（a）式右端改为
1 2
⋅
Pυ2 g
= Vε
，即可导出 kd
=
υ2 。 g∆st
（4）、前面推导过程中，冲击物的势能取为 Ep = P(h + ∆d ) ，一般情况下 ∆d << h ，可将其忽
略，取 Ep = Ph ，读者可仿照上面推导一下，并讨论忽略后对 kd 有什么影响。
所以本问题的动载荷因数为： kd
=
∆d ∆st
=1+
1+ 2h = 1+ ∆st
1+
2
× 440 ×10 −3 2 ×10 −3 m
m
= 22
讨论：（1）、在线弹性范围内，载荷、变形、应变、应力之间都是线性关系，也就是说，当
外载荷被放大 kd 倍，则变形、应力、应变也同样被放大 kd 倍。所以有σ d = kdσ st 。有了 kd 很
动能完全转化为橡皮筋的应变能。即 Ek = Vε 。
解：设小球离开木拍瞬间速度为υ ，则其动能 Ek
=
1 2பைடு நூலகம்
W g
υ 2 ；而橡皮筋被拉至最长时应变能
Vε
=
1 2
F ⋅ ∆L ，其中
F
为小球速度为零时橡皮筋所受拉力。由于假设橡皮筋为线弹性变形，
3
所以 F
=σ
A
=
Eε
A=
∆L L0
EA ，于是Vε
=
∆d
=
∆d ∆st
P 。定义
∆d ∆st
= kd 为动载荷因数，则有
Fd P
=
∆d ∆st
= σd σ st
工程力学---材料力学第七章-梁弯曲时位移计算与刚度设计经典例题及详解
P
B C
l 2 l 2
A
x
P 解：AC段：M ( x ) x 2 y P EIy x 2 A P 2 EIy x C x 4 l 2 P 3 EIy x Cx D 12
P
B C
l 2
x
由边界条件： x 0时，y 0
l 由对称条件： x 时，y 0 2
梁的转角方程和挠曲线方程分别为：
最大转角和最大挠度分别为：
11qa max A 1 x1 0 6 EI 19qa 4 ymax y2 x2 2 a 8EI
3
例5：图示变截面梁悬臂梁，试用积分法
求A端的挠度 P
I
2I
l
fA 解： AC段 0 x l
B
P 3 2 EIy x C2 x D2 6
由边界条件： x l时,y=0, =0
得：
C2
1 1 Pl 2 , D2 Pl 3 2 3
l x 时,yC左 =yC右 , C左 = C右 由连续条件： 2
5 3 2 C1 Pl , D1 Pl 3 16 16
由连续条件： x1 x2 a时, y1 y2 , y1 y2
由边界条件： x1 0时, y1 0
0 x 2 a 时 , y 由对称条件： 2 2
得 D1 0
C1 C2 得 D1 D2
11 3 得 C2 qa 6
qa 1 (11a 2 3 x12 ) 0 x1 a 6 EI q 2 [3ax2 2 ( x2 a)3 11a 3 a x2 2a 6 EI qa y1 (11a 2 x1 x13 ) 0 x1 a 6 EI q y2 [4ax23 ( x2 a) 4 44a 3 x2 ] a x2 2a 24 EI
材料力学考试典型题目
2
(4)
Fx 2 EIw Flx C1 (3) 2 2 3 Flx Fx EIw C 1x C 2 2 6 边界条件 x 0, w 0
x 0, w 0
(4)
将边界条件代入（3）（4）两式中,可得 C1 0 梁的转角方程和挠曲线方程分别为
C2 0
ql 2 q 3 EIw x x C 4 6
ql 3 q 4 EIw x x Cx D 12 24
边界条件x=0 和 x=l时, w
0
x
q
wmax B
梁的转角方程和挠曲线方程 A 分别为
A
l
B
q 2 3 3 (6lx 4 x l ) 24 EI qx w (2lx 2 x 3 l 3 ) 24 EI
FN 3 l3 -4 1.58 10 m uB ΔlCD Δl BC -0.3mm EA3
-4
Δl AD Δl AB Δl BC ΔlCD -0.47 10 mm
例题5 图示等直杆,已知直径d=40mm,a=400mm,材料的剪切弹性
模量G=80GPa，DB=1°. 试求：
x= l , M = 0
M 0
+
Mb l
梁上集中力偶作用处左、右两侧
FRA
A a
M
FRB
C b l B
横截面上的弯矩值(图)发生突变，其
突变值等于集中力偶矩的数值.此处 剪力图没有变化.
M /l
+ +
Mb l
Ma l
例题1 图示一抗弯刚度为 EI 的悬臂梁, 在自由端受一集中力 F 作用.试求梁的挠曲线方程和转角方程, 并确定其最大挠度 wmax 和最大转角 max w
材料力学复习例题
1 P 2 3 P
t
P
d
t
P/4
1
2
3
工程力学教程电子教案
20
1
2
3 P
3板(杆)拉伸强度计算 板 杆 拉伸强度计算
σ max =
FN P = (b 2 d )t Amin
3
1 110 × 10 = = 200 MPa ≥ [σ ] 4 (8 . 5 1 .6 × 2 ) × 1 × 10
P/4
一拉伸压缩 1,轴力图 2,强度条件应用:校核,设计,计算 3,低碳钢拉伸实验,应力-应变曲线 4,连接件强度:剪切,挤压实用计算
例题
30 kN A B 3 30 kN A 2
3
B 2
作轴力图. 要作ABCD杆的 作轴力图. 解:要作 杆的 20 kN 20 kN 轴力图, 轴力图,则需分别将 C D AB,BC,CD杆的轴 杆的轴 20 kN 1 20kN 力求出来.分别作截 力求出来. x 1 面1-1,2-2,3-3,如 , , , D C 20kN 左图所示. 左图所示. F
Me B
(a)
(b)
图示为一受集中荷载F作用的简支 图示为一受集中荷载 作用的简支 试作其剪力图和弯矩图. 梁.试作其剪力图和弯矩图. a F b 根据整体平衡, 解:根据整体平衡,求 A B 得支座约束力 C FA FB x FA=Fb/l, FB=Fa/l
例
梁上的集中荷载将 梁分为AC和 两段 两段, 梁分为 和CB两段, 根据每段内任意横截面 左侧分离体的受力图容 易看出, 易看出,两段的内力方 程不会相同. 程不会相同.
σ x1 σ x2
σ x3
FNx1 400 × 10 3 = = 160 × 10 6 Pa = 160MPa = 6 A1 2500 × 10 FNx 2 -100 × 10 3 = = -40 × 10 6 Pa = -40MPa = A2 2500 × 10 6
t
P
d
t
P/4
1
2
3
工程力学教程电子教案
20
1
2
3 P
3板(杆)拉伸强度计算 板 杆 拉伸强度计算
σ max =
FN P = (b 2 d )t Amin
3
1 110 × 10 = = 200 MPa ≥ [σ ] 4 (8 . 5 1 .6 × 2 ) × 1 × 10
P/4
一拉伸压缩 1,轴力图 2,强度条件应用:校核,设计,计算 3,低碳钢拉伸实验,应力-应变曲线 4,连接件强度:剪切,挤压实用计算
例题
30 kN A B 3 30 kN A 2
3
B 2
作轴力图. 要作ABCD杆的 作轴力图. 解:要作 杆的 20 kN 20 kN 轴力图, 轴力图,则需分别将 C D AB,BC,CD杆的轴 杆的轴 20 kN 1 20kN 力求出来.分别作截 力求出来. x 1 面1-1,2-2,3-3,如 , , , D C 20kN 左图所示. 左图所示. F
Me B
(a)
(b)
图示为一受集中荷载F作用的简支 图示为一受集中荷载 作用的简支 试作其剪力图和弯矩图. 梁.试作其剪力图和弯矩图. a F b 根据整体平衡, 解:根据整体平衡,求 A B 得支座约束力 C FA FB x FA=Fb/l, FB=Fa/l
例
梁上的集中荷载将 梁分为AC和 两段 两段, 梁分为 和CB两段, 根据每段内任意横截面 左侧分离体的受力图容 易看出, 易看出,两段的内力方 程不会相同. 程不会相同.
σ x1 σ x2
σ x3
FNx1 400 × 10 3 = = 160 × 10 6 Pa = 160MPa = 6 A1 2500 × 10 FNx 2 -100 × 10 3 = = -40 × 10 6 Pa = -40MPa = A2 2500 × 10 6
工程力学---材料力学(第七章- 梁弯曲时位移计算与刚度设计)经典例题及详解
得： D 0
Pl 2 得： C 16
AC段梁的转角方程和挠曲线方程分别为：
P 2 2 (4 x l ) 16 EI Px y (4 x 2 3 l 2 ) 48 EI
y
P
B
A
x
l 2
C
l 2
x
最大转角和最大挠度分别为：
max A B
ymax y
q 7qa 8k 384 EI
3
q/2
B C
q/2
A B C
顺时针
q/2
例16：图示梁Ｂ处为弹性支座，弹簧刚 度
EI k 求C端挠度fC。 2a 3
q
A
EI k
B
C
2a
a
解：(1)梁不变形，仅弹簧变形引起的C点挠度为 4 3 qa 3qa B处反力=qa fC 1 2 k EI
q
B
x
l
由边界条件： x 0时，y 0
x l时，y 0
得：
ql 3 C , D0 24
梁的转角方程和挠曲线方程分别为：
y
q 2 3 3 (6lx 4 x l ) 24 EI
q
x
A qx y (2lx 2 x 3 l 3 ) 24 EI
ql 3 24 EI
A a a
q
B C
a
qa 12 EI
顺时针
3 3
P=qa
A B
P=qa
m=qɑ²/2
qa qa C B 6 EI 4 EI
4
顺时针
B
q
C
qa 5qa fC B a 8EI 24 EI
06材料力学
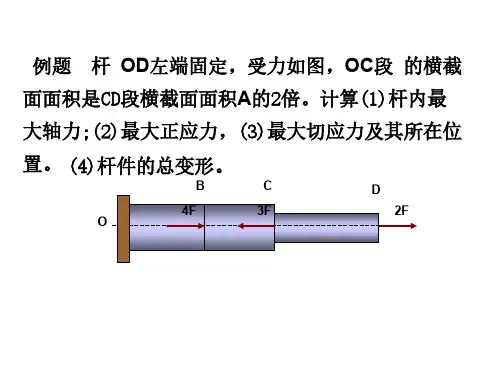
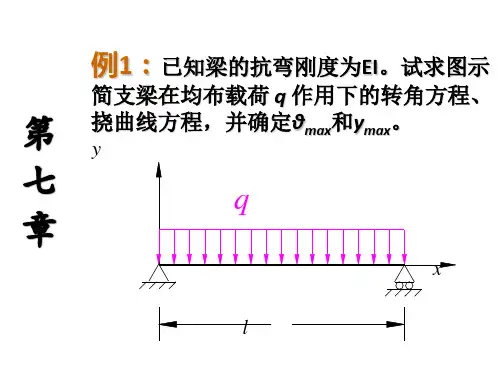
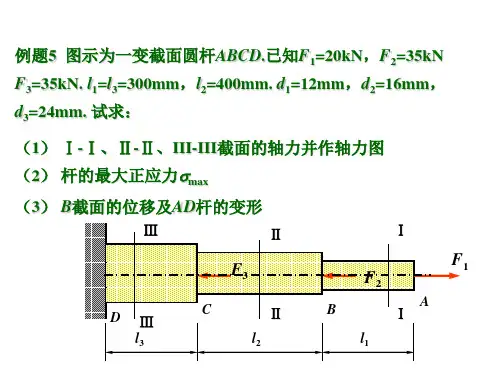
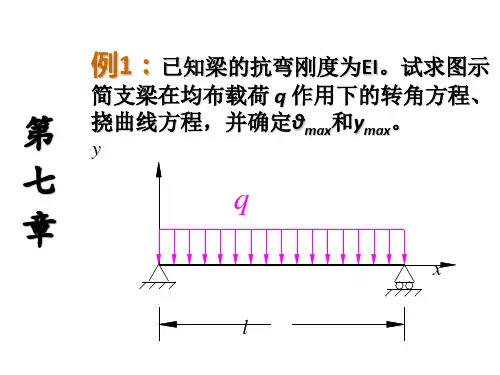
注册土木工程师（港口与航道工程）执业资格考试培训讲稿基础考试：上午4小时120道题每题1分其中材料力学15道题平均每道题用时2分钟。
01年结构考题：拉压2 剪切1 扭转2 截面性质3 弯曲内力2 弯曲正应力3 弯曲变形（含超）2 应力状态强度理论 1 组合变形 2 稳定 102年岩土考题：拉压3 剪切1 扭转2 截面性质2 弯曲内力2 弯曲正应力1 弯曲变形（含超）1 应力状态强度理论 2 组合变形 1 稳定 102年结构考题：拉压3 剪切1 扭转1 截面性质2 弯曲内力2 弯曲正应力2 弯曲变形（含超）1 应力状态强度理论 2 组合变形 1 稳定 2全部是选择题，计算量小根据考试特点复习时应：基本概念要清楚，基本公式和定义要记牢，解题方法要熟练，要培养快速反应能力一、基本概念内力：构件在外力作用下发生变形，引起构件内部各质点之间产生的附加内力（简称内力）。
应力：截面内一点处内力的分布集度。
单位是：N/m2（Pa）、N/mm2（MPa）等。
应力可分为正应力σ和剪应力τ（剪应力）。
位移：构件内任一点由其原来位置到其新位置的连线称为该点的线位移。
构件内某一线段（或平面）由原始位置所转过的角度称为该线段（或平面）的角位移。
变形：构件形状的改变。
应变：构件内任一点处的变形程度。
应变又可分为线应变ε和剪应变γ，均为无量纲量。
线应变ε表示变形前构件内任一点处的一条微线段,变形后的长度改变量与其原始长度之比。
剪应变γ表示过构件内任一点的两个互相垂直的微线段，变形后两个微线段的角度改变量。
例题0 单元体变形后的形状如图中虚线所示，则A点的剪应变是( )。
(A) O，2γ，２γ (B) γ，γ，２γ(C) γ，２γ，２γ (D) O，γ，２γ例题0图答案：D二、四种基本变形的内力、应力及强度、变形1、内力拉压内力：轴力N扭转内力M T弯曲内力Q、M关键点内力的正负号，内力图的画法重点弯曲内力（因拉压、扭转内力较简单）熟练利用剪力、弯矩与分布力的微分关系及其图形的规律判断内力图的正确性。
材料力学例题
B
DC
1
3
2
A
B
DC
1
3
2
A
1 32
A
Δl1
Δl3
F
A'
A'
变形几何方程为 Δl1 Δl3 cos
物理方程为
Δl1
FN1l1 EA1
Δl3
FN3l cos
E3 A3
（3）补充方程
FN1
FN 3
EA E3 A3
cos2
（4）联立平衡方程与补充方程求解 B
DC
FN1 FN2
FN1 cos FN2 cos FN3 F 0
d
[] = 60MPa ,许用挤压应力为 [bs]= 200MPa .试校核销钉的
强度.
F
B
A
d1
d d1
F
解: （1）销钉受力如图b所示
F
剪切面
F
d
F
F
2
2
挤压面
d
B
A
d1
d d1
F
（2）校核剪切强度
剪切面
F
由截面法得两个面上的剪力
FS
F 2
d
剪切面积为 A d 2
4
FS 51MPa
3
2
1
l
a
a
B
C
A
F
解：（1） 平衡方程
Fx 0 Fx 0 l
3 a
2 a
1
Fy 0
B
C
A
FN1 FN2 FN3 F 0
MB 0
F FN3
FN2
FN1
3 a
2 a
1
工程力学材料力学-知识点-及典型例题
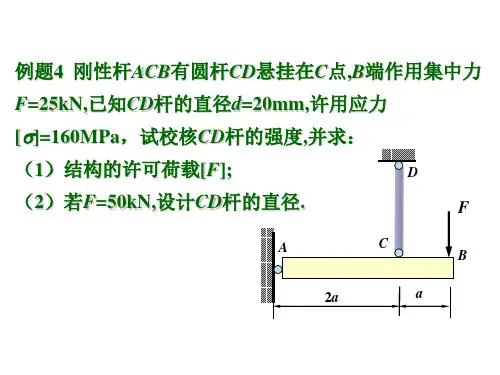
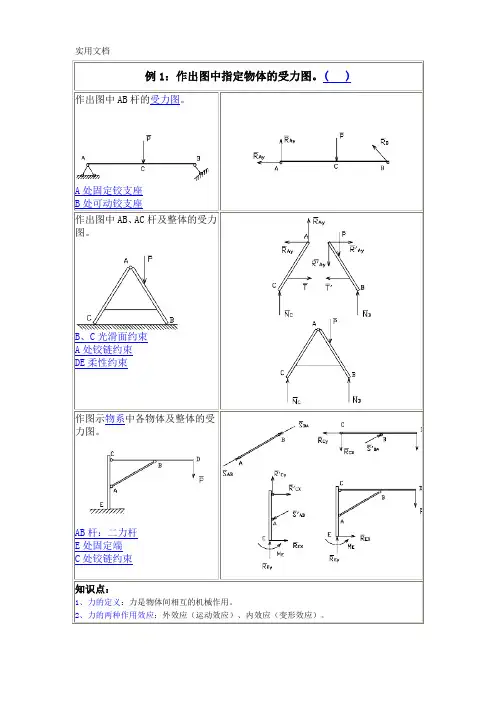
作出图中AB杆的受力图。
A处固定铰支座B处可动铰支座作出图中AB、AC杆及整体的受力图。
B、C光滑面约束A处铰链约束DE柔性约束作图示物系中各物体及整体的受力图。
AB杆：二力杆E处固定端C处铰链约束（1）运动效应：力使物体的机械运动状态发生变化的效应。
（2）变形效应：力使物体的形状发生和尺寸改变的效应。
3、力的三要素：力的大小、方向、作用点。
4、力的表示方法：（1）力是矢量，在图示力时，常用一带箭头的线段来表示力；（注意表明力的方向和力的作用点！）（2）在书写力时，力矢量用加黑的字母或大写字母上打一横线表示，如F、G、F1等等。
5、约束的概念：对物体的运动起限制作用的装置。
6、约束力（约束反力）：约束作用于被约束物体上的力。
约束力的方向总是与约束所能限制的运动方向相反。
约束力的作用点，在约束与被约束物体的接处7、主动力：使物体产生运动或运动趋势的力。
作用于被约束物体上的除约束力以外的其它力。
8、柔性约束：如绳索、链条、胶带等。
(1)约束的特点：只能限制物体原柔索伸长方向的运动。
(2)约束反力的特点：约束反力沿柔索的中心线作用，离开被约束物体。
（）9、光滑接触面：物体放置在光滑的地面或搁置在光滑的槽体内。
（1）约束的特点：两物体的接触表面上的摩擦力忽略不计，视为光滑接触面约束。
被约束的物体可以沿接触面滑动，但不能沿接触面的公法线方向压入接触面。
（2）约束反力的特点：光滑接触面的约束反力沿接触面的公法线，通过接触点，指向被约束物体。
（）10、铰链约束：两个带有圆孔的物体，用光滑的圆柱型销钉相连接。
约束反力的特点:是方向未定的一个力；一般用一对正交的力来表示，指向假定。
（）11、固定铰支座（1）约束的构造特点：把中间铰约束中的某一个构件换成支座，并与基础固定在一起，则构成了固定铰支座约束。
（2）约束反力的特点：固定铰支座的约束反力同中间铰的一样，也是方向未定的一个力；用一对正交的力来表示，指向假定。
()12、可动铰支座（1）约束的构造特点把固定铰支座的底部安放若干滚子，并与支撑连接则构成活动铰链支座约束，又称锟轴支座。
材料力学例题及解题指导
图 2-8 解：设在荷载 G 作用下，横梁移动到 AB位置（图 2-8b），则杆 1 的缩短量为 l1，而杆 2、3 的伸长量为 l2、l3。取横梁 AB 为分离体，如图 2-8c，其上除荷载 G 外，还有轴力 N1、N2、N3 以及 X。由于假设 1 杆缩短，2、3 杆伸长，故应将 N1 设为压力，而 N2、N3 设 为拉力。 (1) 平衡方程
例题及解题指导
图 3.6
例 2-5 图 3-6 所示螺钉承受轴向拉力 F，已知许可切 应力[]和拉伸许可应力[]之间的关系为：[]=0.6[]，许 可 挤 压 应 力 [bs] 和 拉 伸 许 可 应 力 [] 之 间 的 关 系 为 ： [bs]=2[]。试建立 D，d，t 三者间的合理比值。
解：(1) 螺钉的拉伸强度
时单位杆长的分布力 q＝A1，此处 是材料单位体积的重量即容重。将 q 代入上式得到
l A l2 Al l Gl
2EA 2EA 2EA 此处 G＝Al 是整个杆的重量。上式表明等直杆自重引起的总伸长等于全部重量集中于 下端时伸长的一半。
解题指导：对于轴力为变数的杆，利用虎克定律计算杆件轴向变
N1 得正号说明原先假设拉力是正确的， 同时也就表明轴力是正的。AB 段内任一截 面的轴力都等于+6kN。 再求 BC 段轴力，在 BC 段任一截面 2-2 处 将杆件截开，仍考察左段（图 2-5c），在截 面上仍设正的轴力 N 2，由 X＝0 得
－6＋18＋N2＝0
N2＝－12kN
N2 得负号说明原先假设拉力是不对的
解：根据强度条件式(4-6)得出：
10
d 3 16MT 3 16 7.64 106 109mm
[ ]
30
11
再根据刚度条件式(4-9b )得出：
材料力学典型例题与详解(经典题目)
G = [σ ]A(l) − F
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18，或 1.33∶1.09∶1。 讨论：计算结果表明，采用等强度石柱时最节省材料，这是因为这种设计使得各截面的正应 力均达到许用应力，使材料得到充分利用。 3 滑轮结构如图，AB 杆为钢材，截面为圆形，直径 d = 20 mm ，许用应力 [σ ] = 160 MPa ，BC 杆为木材，截面为方形，边长 a = 60 mm ，许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解：1、计算 1-1 截面轴力：从 1-1 截面将杆截成两段，研究上半段。设截面上轴力为 FN1 ，
为压力（见图 b），则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重，大
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18，或 1.33∶1.09∶1。 讨论：计算结果表明，采用等强度石柱时最节省材料，这是因为这种设计使得各截面的正应 力均达到许用应力，使材料得到充分利用。 3 滑轮结构如图，AB 杆为钢材，截面为圆形，直径 d = 20 mm ，许用应力 [σ ] = 160 MPa ，BC 杆为木材，截面为方形，边长 a = 60 mm ，许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解：1、计算 1-1 截面轴力：从 1-1 截面将杆截成两段，研究上半段。设截面上轴力为 FN1 ，
为压力（见图 b），则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重，大
材料力学典型例题及解析7.应力应变状态典型习题解析
应力、应变状态分析典型习题解析1 已知矩形截面梁，某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。
绘出表示1、2、3及4点应力状态的微体，并求出各点的主应力。
b = 60 mm ，h = 100 mm 。
解题分析：从图中可分析1、4点是单向应力状态，2点在中性轴上为纯剪切应力状态，31取平行和垂直与梁横截面的六个平面，构成微体。
则各点处的应力状态如图示。
2、梁截面惯性矩为点微体上既有正应力又有切应力。
解：、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==）bh I z 1点处弯曲正应力（压应力）MPa 100Pa 10100m10500m 1050m N 101064833−=×=×××⋅×==−−z I My σ1点为单向压缩受力状态，所以021==σσ，MPa 1003−=σ2点为纯剪切应力状态，MPa 30Pa 1030m10100602N1012036263=×=×××××=−τ（向下）容易得到，MPa 301=σ，02=σ，MPa303−=σ3点为一般平面应力状态弯曲正应力MPa50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−z I My σ弯曲切应力σ14τ2F S =120 kN题图1中性轴324hστ25 mm 31b M =10 kN·mσ3150 mm 1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−zz bI S F τMPa6.8MPa6.58Pa)10522()2Pa 1050(2Pa 1050)2(22626622minmax −=×+×±×=+−±+=x y x yx τσσσσσσ所以 MPa 6.581=σ，02=σ，MPa 6.83−=σ4点为单向拉伸应力状态，拉伸正应力的大小与1点相等。
工程力学材料力学_知识点_及典型例题
该理论认为，塑性破坏主要是由畸变能密度引起的。变形后，变形固体存在变形能，变形能包括形状改变的变形能（畸变能）和体积改变的变形能。单位体积畸变能称为畸变能密度。在复杂应力情况下，若危险点的畸变能密度超过材料单向拉伸时材料的许可畸变能密度，则强度不足。根据畸变能密度的计算公式导出强度条件为：
说明：一、二强度理论适用于脆断破坏，三、四强度理论适用于塑性破坏。上述四个强度理论的强度条件中，不等式右面部分就是相应的强度理论所对应的相当应力。
5、应力状态分类
（１）、只有一个主应力不为零的应力状态，称为单向应力状态。也称为简单应力状态。
（２）、两个主应力不为零的应力状态，称为二向应力状态。
（３）、三个主应力全不为零的应力状态，称为三向应力状态。
单向应力状态和二向应力状态又称为平面应力状态。
二向应力状态和三向应力状态又称为复杂应力状态。
6、平面应力状态任一斜截面上正应力和切应力公式为：
11、轴向拉压杆横截面上正应力的计算公式：
12、极限应力（σu）：材料失效时的应力。
塑性材料的极限应力是屈服极限（σs）；脆性材料的极限应力是强度极限（σb）。
13、许用应力[σ]：保证构件安全工作，材料许可承担的最大应力。
其中：n---安全系数
14、安全系数：为保证构件具有一定安全贮备而选取的一个大于1的系数。安全系数越大构件越安全，但越不经济。
知识点：
1、剪切的受力特点：构件受到一对大小相等、方向相反、作用线相隔很近的平行力作用。
2、剪切的变形特点：沿平行两力作用线之间的面发生相对错动。发生相对错动的面称为剪切面。
剪切变形是工程实际中常见的一种基本变形。常出现于联接件中，如：铆钉联接、螺栓联接、销钉联接、键联接、榫头联接等等。
说明：一、二强度理论适用于脆断破坏，三、四强度理论适用于塑性破坏。上述四个强度理论的强度条件中，不等式右面部分就是相应的强度理论所对应的相当应力。
5、应力状态分类
（１）、只有一个主应力不为零的应力状态，称为单向应力状态。也称为简单应力状态。
（２）、两个主应力不为零的应力状态，称为二向应力状态。
（３）、三个主应力全不为零的应力状态，称为三向应力状态。
单向应力状态和二向应力状态又称为平面应力状态。
二向应力状态和三向应力状态又称为复杂应力状态。
6、平面应力状态任一斜截面上正应力和切应力公式为：
11、轴向拉压杆横截面上正应力的计算公式：
12、极限应力（σu）：材料失效时的应力。
塑性材料的极限应力是屈服极限（σs）；脆性材料的极限应力是强度极限（σb）。
13、许用应力[σ]：保证构件安全工作，材料许可承担的最大应力。
其中：n---安全系数
14、安全系数：为保证构件具有一定安全贮备而选取的一个大于1的系数。安全系数越大构件越安全，但越不经济。
知识点：
1、剪切的受力特点：构件受到一对大小相等、方向相反、作用线相隔很近的平行力作用。
2、剪切的变形特点：沿平行两力作用线之间的面发生相对错动。发生相对错动的面称为剪切面。
剪切变形是工程实际中常见的一种基本变形。常出现于联接件中，如：铆钉联接、螺栓联接、销钉联接、键联接、榫头联接等等。
材料力学习题
材料力学习题材料力学是工程学和物理学的重要基础学科，它研究材料在外力作用下的力学性能和变形规律。
掌握材料力学的基本理论和方法对于工程技术人员来说至关重要。
下面我们来看一些材料力学的习题，通过解题来加深对材料力学知识的理解。
1. 一根长为L的钢杆，横截面积为A，受到拉力F，求钢杆的伸长量。
解，根据胡克定律，材料的伸长量与受力成正比。
伸长量ΔL与拉力F的关系可以用公式表示为ΔL = FL/EA，其中E为杨氏模量，A为横截面积。
根据公式，我们可以计算出钢杆的伸长量。
2. 一根长度为L的铜棒，横截面积为A，受到拉力F，求铜棒的伸长量。
解，根据胡克定律，材料的伸长量与受力成正比。
伸长量ΔL与拉力F的关系可以用公式表示为ΔL = FL/EA，其中E为杨氏模量，A为横截面积。
由于铜和钢的杨氏模量不同，因此需要根据铜的杨氏模量和横截面积来计算铜棒的伸长量。
3. 一根长为L的橡胶棒，横截面积为A，受到拉力F，求橡胶棒的伸长量。
解，橡胶是一种具有较大的拉伸变形能力的材料，其伸长量与拉力之间的关系并不符合胡克定律。
橡胶的拉伸性能可以用应力-应变曲线来描述，根据橡胶的应力-应变曲线可以计算出橡胶棒的伸长量。
4. 一根长度为L的钢丝，横截面积为A，受到拉力F，求钢丝的应力。
解，钢丝的应力可以用公式表示为σ = F/A，其中F为拉力，A为横截面积。
根据这个公式，我们可以计算出钢丝的应力。
5. 一根长度为L的铝棒，横截面积为A，受到拉力F，求铝棒的应力。
解，铝和钢的杨氏模量不同，因此铝棒的应力需要根据铝的杨氏模量和横截面积来计算。
通过以上习题的解答，我们可以加深对材料力学的理解，掌握材料在外力作用下的力学性能和变形规律。
希望大家能够通过练习，提高对材料力学知识的掌握程度，为工程实践提供坚实的理论基础。
材料力学典型例题及解析 1.拉伸应力典型习题解析
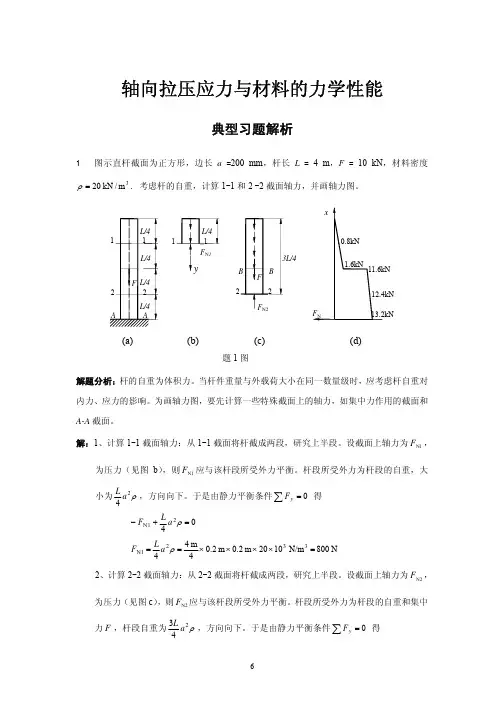
轴向拉压应力与材料的力学性能典型习题解析1 图示直杆截面为正方形，边长a =200 mm ，杆长L = 4 m ，F = 10 kN ，材料密度3m /kN 20=ρ. 考虑杆的自重，计算1-1和2 -2截面轴力，并画轴力图。
解题分析：杆的自重为体积力。
当杆件重量与外载荷大小在同一数量级时，应考虑杆自重对内力、应力的影响。
为画轴力图，要先计算一些特殊截面上的轴力，如集中力作用的截面和A-A 截面。
解：1、计算1-1截面轴力：从1-1截面将杆截成两段，研究上半段。
设截面上轴力为1N F ，为压力（见图b ），则1N F 应与该杆段所受外力平衡。
杆段所受外力为杆段的自重，大小为ρ24a L ，方向向下。
于是由静力平衡条件∑=0y F 得 042N1=+−ρa L F N 800N/m 1020m 2.0m 2.04m 44332N1=××××==ρa L F 2、计算2-2截面轴力：从2-2截面将杆截成两段，研究上半段。
设截面上轴力为N2F ，为压力（见图c ），则N2F 应与该杆段所受外力平衡。
杆段所受外力为杆段的自重和集中力F ，杆段自重为ρ243a L ，方向向下。
于是由静力平衡条件∑=0y F 得(c)(a) (b)题1图(d)kN 12.4N 104.12N/m 1020m 2.0m 2.04m43N 10104333332N2=×=×××××+×=+=ρa L F F 3、计算集中力F 作用截面上的轴力：首先将杆沿力F 作用截面（B-B ）上侧截开，设截面上轴力为压力+B F N ，研究上半部分杆段。
由于只受本身重量作用，所以由静力平衡条件得F 作用截面上侧轴力为kN 1.6N 106.1N/m 1020)m 2.0(2m 4233322N =×=×××==+ρa L F B 然后将杆沿F 作用截面（B-B ）下侧截开，设截面上轴力为压力−B F N ，研究上半部分杆段。
材料力学典型例题及解析 6.弯曲变形典型习题解析
弯曲变形典型习题解析1 试用积分法写出图示梁的挠曲轴方程，说明用什么条件决定方程中积分常数，画出挠曲轴大致形状。
图中C 为中间铰。
为已知。
I E解题分析：梁上中间铰处，左、右挠度相等，转角不相等。
解：设支反力为，如图示。
yB A yA FM F、、1、建立各段挠曲轴近似微分方程并积分 将梁分为AC 、CB 、BD 段。
AC 段 a x ≤≤10挠曲轴近似微分方程 11x FM w I E yA A ⋅−=′′转角方程1211'12C x Fx Mw IE yA A+−= (a) 挠度方程1113121162D x C x F x M w I E y A A ++−=(b)CB 段 )(2b a x a +≤≤挠曲轴近似微分方程2"2x FMw I E yA A ⋅−=转角方程 222222C x F xM w I E yA A+−=′(c)挠度方程2223222262D x C xFx M w I E yA A++−= (d)BD 段 l x b a ≤≤+3)(挠曲轴近似微分方程[])(333b a x Fx FM w I E yB yA A+−+−=′′转角方程[]32323332)(2C b a x F x F x M w I E yB yA A++−+−=′ (e) 挠度方程[]33333332336)(62D x C b a x FxFxM w I E yB yA A+++−+−= (f)2、确定积分常数共有6个积分常数。
需要6个位移边界条件和光滑连续条件。
332211D C D C D C 、、、、、题1图M A边界条件：，代入(b)得 01=x 01=w 01=D (g)0'1=w 代入(a)得 01=C(h)b a x +=2，02=w (i)连续条件： ， a x x ==2121w w =(j) b a x x +==32， 32w w ′=′ (k) 32w w =(l)联立(i)、(j)、(k)、(l)，可求出。
材料力学经典例题
Ip R
称为抗扭截面 系数(模量 模量)， 系数 模量 ， 单位： 单位：mm3。
Nm mm
3
MT = W p
=10 MPa
3
五、Ip和Wp公式
π D4
32
工程上采用空心截面构件：提高强度， 工程上采用空心截面构件：提高强度，节约 材料， 材料，重量轻 结构轻便，应用广泛。 结构轻便，应用广泛。
Ip =
例题2.4 例题2.4 油缸盖与缸体采用6个螺栓连接。已知油缸内径 油缸盖与缸体采用6个螺栓连接。 D=350mm，油压p=1MPa 螺栓许用应力[σ]=40MPa p=1MPa。 [σ]=40MPa， D=350mm，油压p=1MPa。螺栓许用应力[σ]=40MPa， 求螺栓的内径。 求螺栓的内径。 解： 油缸盖受到的力 F = D 2 p
目录
FN 1 = 2 F1 ≤ [σ ] A1
失效、 §2.7 失效、安全因数和强度计算
3、根据水平杆的强度，求许可载荷 根据水平杆的强度， 查表得水平杆AB的面积为A2=2×12.74cm2 =2×
FN 2 = − FN 1 cos α = − 3F
FN 2 = 3F2 ≤ [σ ] A2
FN 1
（kN·m） ）
MT
2. 校核强度
MT1 10×103 ×16 ×103 = 50.9MPa＜ [τ] (τmax )1 = W = π×1003 p1
MT2 3×103 ×16 τmax ) 2 = = ×103 = 70.7 MPa ＞ [τ] ( Wp2 π×603
MT1 180 10×103 ×32 180 ⋅ = ⋅ = 0.7 o m ＜[θ] θ1 = GIp1 π 80×109 ×π×1004 ×10−12 π MT2 180 3×103 ×32 3 180 ⋅ = ×10 ⋅ = 1.7 o m ＞[θ] θ2 = GIp2 π 80×π×604 π
材料力学典型例题及解析 5.弯曲应力典型习题解析
q
h1
h2
A
Ｂ
b l
题3图
解题分析：两板叠放在一起，在均布载荷 q 作用下，两梁一起变形，在任一截面上，两者弯 曲时接触面的曲率相等。小变形情况下，近似认为两者中性层的曲率相等。根据该条件，可 计算出各梁分别承担的弯矩。然后再分别计算两梁的最大应力。两板胶合在一起时，按一个 梁计算。 解：1、计算两板简单叠放在一起时的最大应力
= 0.5 m 2q ≤ σ Wz
解得 q ≤ W z [σ ] = 49 ×10−6 m 3 ×160 ×106 Pa = 15 680 N/m = 15.68 kN/m
0.5 m2
0.5 m2
3、BD 杆的强度条件
BD 杆横截面上各点拉伸正应力相同，强度条件为
σ
≤ [σ ] 或σ = F NBD =
F
Ay
=
3m 4
q
，
F
By
=
9m 4Leabharlann q2、梁的强度条件
画梁的弯矩图如图 b。显然，B 截面为危险截面。 M B = 0.5 m2 q ，查表知 10 号工 字钢 W z = 49 ×10−6 m 3 ，于是 B 截面上弯曲正应力强度条件为
[ ] [ ] σ m a x ≤ σ
或
σ ma x
=
M max Wz
=
I I
1 2
M
2
=( h1)3 h2
M
2
=
1M 8
2
梁中间截面弯矩为
M
=
M
1
+
M
2
=
1 ql 8
2
于是
M
1
=
1 72
材料力学各单元的题
[4] 图示杆件受到大小相等的四个轴向力P的作用。其中 ____段的变形为零。
A、AB
B、AC
C、AD
D、BC
[5] 设一阶梯形杆的轴力沿杆轴是变化的，则在发生破坏 的截面上___。 A、外力一定最大，且面积一定最小 B、轴力一定最大，且面积一定最小 C、轴力不一定最大，但面积一定最小 D、轴力与面积之比一定最大
C
a
F
FNAB FNBC
B F
求BC杆的正应力
BC
FNBC 17.32 103 ABC 602
4.8 N mm 2 4.8 MPa
例题2-4 图示为一变截面圆杆ABCD。已知F1=20kN， F2=35kN，F3=35kN。l1=l3=300mm，l2=400mm。d1=12mm， d2=16mm，d3=24mm。E=210GPa 试求： (1) Ⅰ-Ⅰ、Ⅱ-Ⅱ、Ⅲ-Ⅲ 截面的轴力并作轴力图 (2) 杆的最大正应力max (3) B 截面的位移及AD 杆的变形
[1]设低碳钢拉伸试件工作段的初始横截面积为 A0 ，试件被拉 断后，断口的横截面积为A，试件断裂前所能承受的最大荷载 为 Pb ，则下列结论中____是正确的。
Pb A、材料的强度极限 b A0 P B、材料的强度极限 b b A
C、当试件工作段中的应力达到强度极限 b 的瞬时。试件的 横截面积为A．
[8] 下列结论中正确的是（ ） A. 内力是应力的代数和 B. 应力是内力的平均值 C. 应力是内力的集度 D. 内力必大于应力 [9] 长度和横截面面积均相同的两杆，一为钢杆，一为铝
杆，在相同的拉力作用下（ ）
A. 铝杆的应力和钢杆相同，而变形大于钢杆 B. 铝杆的应力和钢杆相同，而变形小于钢杆
材料力学计算题库完整
实用文档第一章绪论【例 1-1 】钻床如图1-6a 所示，在载荷P 作用下，试确定截面m-m上的内力。
【解】（ 1）沿 m-m 截面假想地将钻床分成两部分。
取m-m 截面以上部分进行研究（图1-6b ），并以截面的形心O为原点。
选取坐标系如图所示。
（ 2）为保持上部的平衡，m-m 截面上必然有通过点O的内力 N 和绕点 O的力偶矩M。
（ 3）由平衡条件∴【例 1-2 】图 1-9a 所示为一矩形截面薄板受均布力p 作用，已知边长=400mm，受力后沿 x 方向均匀伸长=0.05mm。
试求板中 a 点沿 x 方向的正应变。
【解】由于矩形截面薄板沿x 方向均匀受力，可认为板内各点沿x 方向具有正应力与正实用文档应变，且处处相同，所以平均应变即 a 点沿 x 方向的正应变。
x 方向【例 1-3 】图 1-9b 所示为一嵌于四连杆机构内的薄方板，b=250mm。
若在 p 力作用下CD杆下移b=0.025，试求薄板中 a 点的剪应变。
【解】由于薄方板变形受四连杆机构的制约，可认为板中各点均产生剪应变，且处处相同。
第二章拉伸、压缩与剪切【例题 2.1 】一等直杆所受外力如图 2. 1 (a)所示，试求各段截面上的轴力，并作杆的轴力图。
解：在 AB段范围内任一横截面处将杆截开，取左段为脱离体( 如图 2. 1 (b)所示)，假定轴力 F N1为拉力 ( 以后轴力都按拉力假设) ，由平衡方程F x0 ， F N1300得F N130kN结果为正值，故 F N1为拉力。
同理，可求得BC段内任一横截面上的轴力( 如图 2. 1 (c)所示)为F N230 4070(kN)在求 CD段内的轴力时，将杆截开后取右段为脱离体( 如图 2. 1 (d)所示)，因为右段杆上包含的外力较少。
由平衡方程F x0 ，F N330 200.得F N330 20 10(kN)结果为负值，说明 F N3 为压力。
同理，可得段内任一横截面上的轴力F N4 为DEF N4 20kN30kN 40kN80kN30kN 20kN(a)40kN 80kN 30kN 20kN30kNA (a)CDEB20kN30kN40kN80kN30kN(b) 30kN (a)A (a)BC DE40kN 80kN F30kN20kN30kN40kN 80kN 30kN 30kN20kNCDE(a)B30kN30kN(b) 40kN A F N1(a)(c)BD F N2EA30kN C(b)40kN(b)FABC D30kN20kN30kN80kNE30kN30kN(c)40kNF N2(b)F N330kN 20kN30kN(a)F(d)F 30kN40kN(b)F N2(c) BCDE30kN20kN30kNA(d)F N340kNF N2(c)30kN(c)30kN (b)e)F N420kN40kN(d)20kN(c)F N2 FF N330kN(d)30kN (e)F N370kN 30kN 20kN F N420kN(d) (c)F N3 40kN 30kN F N2 20kN(e) 30kN70kN20kN(f)(d)20kN F N4 (e)FN420kNN3 70kN30kN(e)(d)(f)F20kN 30kN20kN20kNF N470kN10kN30kN(f)20kN70kN(f) (e) 30kN(e) 20kN FN410kN20kN(f)30kN70kN20kN10kN10kN(f)30kN 10kN20kN10kN(f)图 2.1 例题 2.1 图【例题 2.2 】 一正方形截面的阶梯形砖柱，其受力情况、各段长度及横截面尺寸如图 2.8(a) 所示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（1）能用欧拉公式时压杆的最小长度； （2）当压杆长度为上述最小长度的 3/4 时，压杆的临界应力.
已知： E = 200 GPa， p= 200 MPa ， s = 240 MPa ，用直
线公式时，a = 304 MPa， b =1.12 MPa.
已知托架D处承受载荷 F=10KN。AB杆外径 D=50mm，内径d=40mm， E=200GPa。λ1=100， [nst]=3。
传动轴的直径为ｄ＝40毫米，皮带轮的直径分别为：右侧轮直 径D1＝200毫米，右侧轮D2＝120毫米，皮带的张力为F1＝2F2 ＝4KN，F3＝2F4。轴的许用应力为：[σ]＝100MPａ，用第三 强度理论校核轴的强度。
例题 外径 D = 50 mm，内径 d = 40 mm 的钢管，两端铰支， 材料为 Q235钢，承受轴向压力 F. 试求
A
B
L=4m
例 铸铁梁的截面为T字形，截面对形心轴的惯性矩为 I zc 40.3106 m4 ，已知材料许用拉应力 [ ] 40MPa
许用压应力为 [ ] 100MPa 试校核梁的正应力强度。
P=20KN q=10KN/m
61
zc
2m
3m
1m
139
已知倒T型截面对形心主惯性轴的惯性矩为 Izc=10-5m4， 悬臂梁的尺寸及受力如图，铸铁材料的许用拉应力为
径d2=200mm。设许用应力 =100 Mpa，试按第四强度理论求
轴的直径。
z
5kN
3.64kN
10kN
A
C
B
Dx
y
1.82kN
300mm 300mm 100mm
传动轴的直径为ｄ＝40毫米，左端的皮带轮直径为D1＝150毫米， 右端的皮带轮直径为D2＝100毫米，皮带的张力为F1＝2F2＝4KN， F3＝2F4。轴的许用应力为：[σ]＝80MPa，用第三强度理论校核轴 的强度。
10kN
0.8m
D
A
B
F 25kN
15kN
M e 15 1.4 10 0.6 15kN m
AB杆为扭转和平面弯曲的组合变形
C
F
A
Ｍe
B
例题 传动轴如图所示.在A处作用一个外力偶矩Me=1kN·m,皮带轮直径D=300mm,皮带 轮紧边拉力为F1,松边拉力为F2.且F1=2F2,l=200mm,轴的许用应力[]=160MPa.试用第 三强度理论设计轴的直径
例题 杆 OD左端固定，受力如图，OC段 的横截
面面积是CD段横截面面积A的2倍。计算(1)杆内最
大轴力;(2)最大正应力，(3)最大切应力及其所在位
置。 (4)杆件的总变形。
B
C
4F
3F
O
D 2F
例：已知AB大梁为刚体，拉杆直径d=2cm,E=200GPa, []=160MPa.求：(1)许可载荷[F],（2）B点位移。
的作用，如图，若杆的内外径之比为 =0.8 ， G=80GPa ，许用剪应力 []=30MPa，试设计杆 的外径；若[]=2º/m ，试校核此杆的刚度，并
求右端面转角。
[例题] 某传动轴设计要求转速n = 500 r / min，输入功率P1 = 500 马力， 输出功率分别 P2 = 200马力及 P3 = 300马力，已
40MPa，许用压应力 80MPa，要求：① 绘制梁的内 力图； ②校核梁的弯曲正应力强度。
例题 空心圆杆AB和CD杆焊接成整体结构，受力如图.AB杆的外径 D=140mm，内外 径之比α= d/D=0.8，材料的许用应力[] = 160MPa。试用第三强度理论校核AB杆的 强度。
解:（1）外力分析 将力向AB杆的B截面形心简化得
解:1、外力分析：
y
将力向轴的形心简化
Me
x
M eC
( F1
F2 )
D 2
F2 D 2
z
A
B
F2
20 kN 3
l/2 F1 F2 l/2
F 20kN
Me
MeC
轴产生扭转和垂直纵向对称面内的平 面弯曲
F=3F2
例题 图示一钢制实心圆轴，轴上的齿轮C上作用有铅垂切向力 5 kN，径向力 1.82 kN；齿轮 D上作用有水平切向力10 kN，径向 力 3.64 kN。齿轮 C 的节圆直径 d1 = 400 mm，齿轮 D 的节圆直
知：G=80GPa ，[ ]=70M Pa，[ ]=1º/m ，试确定：
①AB 段直径 d1和 BC 段直径 d2 ？ ②若全轴选同一直径，应为多少？
③主动轮与从动轮如何安排,轴的受力合理？
P1 A
P2 B
500
P3
C 400
等截面传动轴的转速为n＝191转/分，由A轮输入的 功率为8KW，由B、C、D各轮输出的功率分别为 3KW，1KW，4KW。已知轴的许用剪应力为[τ]＝ 60MPa，剪变模量为G＝80GPa，许用转角为
[]=20/m。要求：首先合理安排各轮的位置，然后
绘出轴的内力图，确定轴的直径D。
200cm
200cm
200cm
例题：一简支梁受力如图所示。已知 [ ] 12MPa ，空心圆截面
的内外径之比 d 0.8 ，试选择截面直径D；若外径D增加 一倍，比值不变，D则载荷 q 可增加到多大？
q=0.5KN/m
校核AB杆的稳定性
例题 油缸活塞直经 D = 65mm，油压 p =1.2MPa.活塞杆长度
l=1250mm，材料为35钢，s =220MPa，E = 210GPa，[nst] =
6.试确定活塞杆的直经.
D
p
活塞
活塞杆 d
例题 AB的直径 d=40mm，长 l=800mm，两端可视为铰支. 材
料为Q235钢，弹性模量 E = 200GPa. 比例极限p =200MPa，屈 服极限 s=240MPa，由AB杆的稳定条件求[F]. （若用直线式 a
= 304 MPa， b =1.12 MPa ）
0.6
0.3
B C
F
A
例题 简易起重架由两圆钢杆组成，杆AB：d2 30mm ，杆 AC：d1 20mm ,两杆材料均为Q235钢, E 200GPa, s 240MPa 1 100, 2 60 ,规定的强度安全系数ns 2，稳定安全系 数 nst 3 ，试确定起重机架的最大起重量 Fmax 。
C
0.75m A
D
B
1m
1.5m
F
横梁BC为刚杆，自重Q＝2KN，力P＝10KN可在横 梁BC上自由移动。AB杆的许用应力为[σ]=100MP ａ，设计AB杆的横截面面积。如果AB杆采用直径 为10毫米的细丝，需要几根？
P C
20Nm/m
已知： E = 200 GPa， p= 200 MPa ， s = 240 MPa ，用直
线公式时，a = 304 MPa， b =1.12 MPa.
已知托架D处承受载荷 F=10KN。AB杆外径 D=50mm，内径d=40mm， E=200GPa。λ1=100， [nst]=3。
传动轴的直径为ｄ＝40毫米，皮带轮的直径分别为：右侧轮直 径D1＝200毫米，右侧轮D2＝120毫米，皮带的张力为F1＝2F2 ＝4KN，F3＝2F4。轴的许用应力为：[σ]＝100MPａ，用第三 强度理论校核轴的强度。
例题 外径 D = 50 mm，内径 d = 40 mm 的钢管，两端铰支， 材料为 Q235钢，承受轴向压力 F. 试求
A
B
L=4m
例 铸铁梁的截面为T字形，截面对形心轴的惯性矩为 I zc 40.3106 m4 ，已知材料许用拉应力 [ ] 40MPa
许用压应力为 [ ] 100MPa 试校核梁的正应力强度。
P=20KN q=10KN/m
61
zc
2m
3m
1m
139
已知倒T型截面对形心主惯性轴的惯性矩为 Izc=10-5m4， 悬臂梁的尺寸及受力如图，铸铁材料的许用拉应力为
径d2=200mm。设许用应力 =100 Mpa，试按第四强度理论求
轴的直径。
z
5kN
3.64kN
10kN
A
C
B
Dx
y
1.82kN
300mm 300mm 100mm
传动轴的直径为ｄ＝40毫米，左端的皮带轮直径为D1＝150毫米， 右端的皮带轮直径为D2＝100毫米，皮带的张力为F1＝2F2＝4KN， F3＝2F4。轴的许用应力为：[σ]＝80MPa，用第三强度理论校核轴 的强度。
10kN
0.8m
D
A
B
F 25kN
15kN
M e 15 1.4 10 0.6 15kN m
AB杆为扭转和平面弯曲的组合变形
C
F
A
Ｍe
B
例题 传动轴如图所示.在A处作用一个外力偶矩Me=1kN·m,皮带轮直径D=300mm,皮带 轮紧边拉力为F1,松边拉力为F2.且F1=2F2,l=200mm,轴的许用应力[]=160MPa.试用第 三强度理论设计轴的直径
例题 杆 OD左端固定，受力如图，OC段 的横截
面面积是CD段横截面面积A的2倍。计算(1)杆内最
大轴力;(2)最大正应力，(3)最大切应力及其所在位
置。 (4)杆件的总变形。
B
C
4F
3F
O
D 2F
例：已知AB大梁为刚体，拉杆直径d=2cm,E=200GPa, []=160MPa.求：(1)许可载荷[F],（2）B点位移。
的作用，如图，若杆的内外径之比为 =0.8 ， G=80GPa ，许用剪应力 []=30MPa，试设计杆 的外径；若[]=2º/m ，试校核此杆的刚度，并
求右端面转角。
[例题] 某传动轴设计要求转速n = 500 r / min，输入功率P1 = 500 马力， 输出功率分别 P2 = 200马力及 P3 = 300马力，已
40MPa，许用压应力 80MPa，要求：① 绘制梁的内 力图； ②校核梁的弯曲正应力强度。
例题 空心圆杆AB和CD杆焊接成整体结构，受力如图.AB杆的外径 D=140mm，内外 径之比α= d/D=0.8，材料的许用应力[] = 160MPa。试用第三强度理论校核AB杆的 强度。
解:（1）外力分析 将力向AB杆的B截面形心简化得
解:1、外力分析：
y
将力向轴的形心简化
Me
x
M eC
( F1
F2 )
D 2
F2 D 2
z
A
B
F2
20 kN 3
l/2 F1 F2 l/2
F 20kN
Me
MeC
轴产生扭转和垂直纵向对称面内的平 面弯曲
F=3F2
例题 图示一钢制实心圆轴，轴上的齿轮C上作用有铅垂切向力 5 kN，径向力 1.82 kN；齿轮 D上作用有水平切向力10 kN，径向 力 3.64 kN。齿轮 C 的节圆直径 d1 = 400 mm，齿轮 D 的节圆直
知：G=80GPa ，[ ]=70M Pa，[ ]=1º/m ，试确定：
①AB 段直径 d1和 BC 段直径 d2 ？ ②若全轴选同一直径，应为多少？
③主动轮与从动轮如何安排,轴的受力合理？
P1 A
P2 B
500
P3
C 400
等截面传动轴的转速为n＝191转/分，由A轮输入的 功率为8KW，由B、C、D各轮输出的功率分别为 3KW，1KW，4KW。已知轴的许用剪应力为[τ]＝ 60MPa，剪变模量为G＝80GPa，许用转角为
[]=20/m。要求：首先合理安排各轮的位置，然后
绘出轴的内力图，确定轴的直径D。
200cm
200cm
200cm
例题：一简支梁受力如图所示。已知 [ ] 12MPa ，空心圆截面
的内外径之比 d 0.8 ，试选择截面直径D；若外径D增加 一倍，比值不变，D则载荷 q 可增加到多大？
q=0.5KN/m
校核AB杆的稳定性
例题 油缸活塞直经 D = 65mm，油压 p =1.2MPa.活塞杆长度
l=1250mm，材料为35钢，s =220MPa，E = 210GPa，[nst] =
6.试确定活塞杆的直经.
D
p
活塞
活塞杆 d
例题 AB的直径 d=40mm，长 l=800mm，两端可视为铰支. 材
料为Q235钢，弹性模量 E = 200GPa. 比例极限p =200MPa，屈 服极限 s=240MPa，由AB杆的稳定条件求[F]. （若用直线式 a
= 304 MPa， b =1.12 MPa ）
0.6
0.3
B C
F
A
例题 简易起重架由两圆钢杆组成，杆AB：d2 30mm ，杆 AC：d1 20mm ,两杆材料均为Q235钢, E 200GPa, s 240MPa 1 100, 2 60 ,规定的强度安全系数ns 2，稳定安全系 数 nst 3 ，试确定起重机架的最大起重量 Fmax 。
C
0.75m A
D
B
1m
1.5m
F
横梁BC为刚杆，自重Q＝2KN，力P＝10KN可在横 梁BC上自由移动。AB杆的许用应力为[σ]=100MP ａ，设计AB杆的横截面面积。如果AB杆采用直径 为10毫米的细丝，需要几根？
P C
20Nm/m