贝叶斯博弈与贝叶斯Nash均衡
- 格式:pdf
- 大小:1.07 MB
- 文档页数:99


一:子博弈精炼纳什均衡在给出子博弈精炼Nash均衡的正式定义之前,我们需要先介绍“子博弈”这个概念。
子博弈(sub game):由一个单结信息集X开始的与所有该决策结的后续结(包括终点结)组成的,能够自成一个博弈的原博弈的一部分。
即给定“历史”,每一个行动选择开始至博弈结束构成了的一个博弈,称为原动态博弈的一个“子博弈”。
子博弈可以作为一个独立的博弈进行分析,并且与原博弈具有相同的信息结构。
为了叙述方便,一般用表示博弈树中开始于决策结的子博弈。
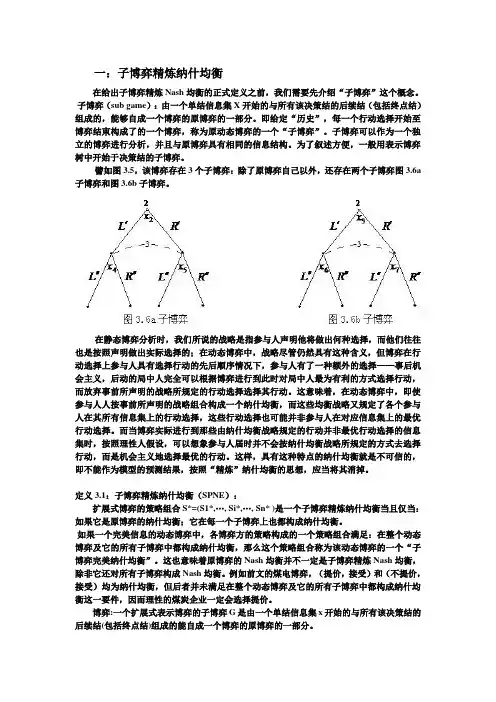
譬如图3.5,该博弈存在3个子博弈:除了原博弈自己以外,还存在两个子博弈图3.6a 子博弈和图3.6b子博弈。
在静态博弈分析时,我们所说的战略是指参与人声明他将做出何种选择,而他们往往也是按照声明做出实际选择的;在动态博弈中,战略尽管仍然具有这种含义,但博弈在行动选择上参与人具有选择行动的先后顺序情况下,参与人有了一种额外的选择——事后机会主义,后动的局中人完全可以根据博弈进行到此时对局中人最为有利的方式选择行动,而放弃事前所声明的战略所规定的行动选择选择其行动。
这意味着,在动态博弈中,即使参与人人按事前所声明的战略组合构成一个纳什均衡,而这些均衡战略又规定了各个参与人在其所有信息集上的行动选择,这些行动选择也可能并非参与人在对应信息集上的最优行动选择。
而当博弈实际进行到那些由纳什均衡战略规定的行动并非最优行动选择的信息集时,按照理性人假设,可以想象参与人届时并不会按纳什均衡战略所规定的方式去选择行动,而是机会主义地选择最优的行动。
这样,具有这种特点的纳什均衡就是不可信的,即不能作为模型的预测结果,按照“精炼”纳什均衡的思想,应当将其消掉。
定义3.1:子博弈精炼纳什均衡(SPNE):扩展式博弈的策略组合 S*=(S1*,…, Si*,…, Sn* )是一个子博弈精炼纳什均衡当且仅当:如果它是原博弈的纳什均衡;它在每一个子博弈上也都构成纳什均衡。
如果一个完美信息的动态博弈中,各博弈方的策略构成的一个策略组合满足:在整个动态博弈及它的所有子博弈中都构成纳什均衡,那么这个策略组合称为该动态博弈的一个“子博弈完美纳什均衡”。



博弈论的主要均衡概念及其比较【摘要】均衡概念是构成整个博弈论的基石,对博弈论均衡概念的透彻理解将对博弈论的学习打下良好的基础。
本文首先将博弈划分为不同的类型,并对主要的均衡概念进行了数学描述,最后对不同的均衡概念进行了比较。
【关键词】博弈论;纳什均衡;重复博弈博弈论在现代经济学中占据着相当重要的位置,在微观经济学的本科教学环节中,如果将博弈论这一部分排除在外,那么教学内容是不完整的,并且和现代微观经济学的发展严重脱节。
但是由于课时以及学生接受能力的限制,对博弈论的内容进行全面深入地讲解难以做到,因此,将博弈论的基本概念和方法清晰地向本科学生进行展示就显得十分重要了。
在博弈论的基本概念当中,最重要的当属博弈均衡的概念,这些概念的掌握有助于学生把握博弈论的整体框架,并对博弈论的后续学习至关重要。
因此,本文将主要的博弈均衡概念进行分类和表述,并对不同的博弈概念进行比较,以期对博弈论的教学有所助益。
一、博弈的主要类型博弈构成的基本要素包括:1、参与人(1~N);2、各个参与人各自可选择的行动集合Ai={ai};3、参与人i的策略Si,给定信息集,该策略决定在博弈的每一阶段他选择的行动;4、参与人的收益Ui (S1,S2…SN)。
依据不同的分类标准,博弈可以被划分为不同的类型。
1、静态博弈、动态博弈和重复博弈博弈各方同时选择策略的博弈称为静态博弈,如猜硬币、投标等,静态博弈一般可以用支付矩阵来表达。
动态博弈是指博弈各方按照一定的先后次序进行策略的选择,典型的例子如对弈,动态博弈一般可以用“博弈树”来表达。
Game Theory 中文翻译为博弈论也是分别用静态和动态博弈的典型代表博彩和对弈的简称而来。
重复博弈是指同一个博弈(静态或动态)反复进行所构成的博弈过程,如体育比赛中的多局赛制等。
2、完全信息和不完全信息博弈完全信息博弈是指每个参与人都了解其他参与人的收益函数的博弈,不完全信息博弈是指参与人并不完全了解其他参与人收益函数的博弈。
一:子博弈精炼纳什均衡在给出子博弈精炼Nash均衡的正式定义之前,我们需要先介绍“子博弈〞这个概念。
子博弈〔sub game〕:由一个单结信息集X开始的与所有该决策结的后续结〔包括终点结〕组成的,能够自成一个博弈的原博弈的一局部。
即给定“历史〞,每一个行动选择开始至博弈完毕构成了的一个博弈,称为原动态博弈的一个“子博弈〞。
子博弈可以作为一个独立的博弈进展分析,并且与原博弈具有一样的信息结构。
为了表达方便,一般用表示博弈树中开始于决策结的子博弈。
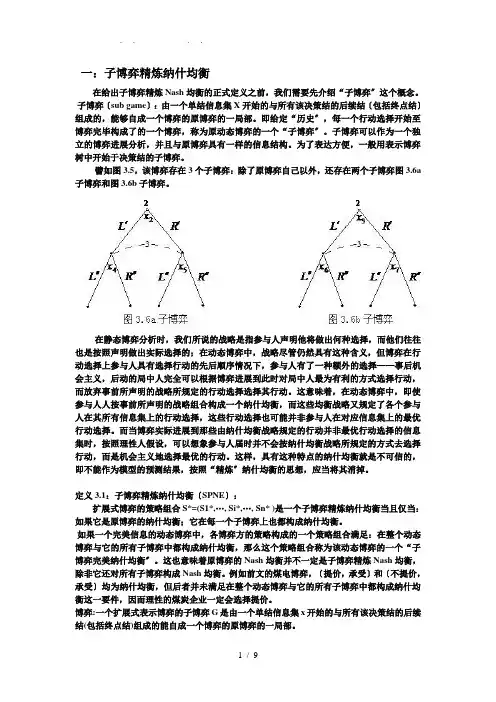
譬如图3.5,该博弈存在3个子博弈:除了原博弈自己以外,还存在两个子博弈图3.6a 子博弈和图3.6b子博弈。
在静态博弈分析时,我们所说的战略是指参与人声明他将做出何种选择,而他们往往也是按照声明做出实际选择的;在动态博弈中,战略尽管仍然具有这种含义,但博弈在行动选择上参与人具有选择行动的先后顺序情况下,参与人有了一种额外的选择——事后机会主义,后动的局中人完全可以根据博弈进展到此时对局中人最为有利的方式选择行动,而放弃事前所声明的战略所规定的行动选择选择其行动。
这意味着,在动态博弈中,即使参与人人按事前所声明的战略组合构成一个纳什均衡,而这些均衡战略又规定了各个参与人在其所有信息集上的行动选择,这些行动选择也可能并非参与人在对应信息集上的最优行动选择。
而当博弈实际进展到那些由纳什均衡战略规定的行动并非最优行动选择的信息集时,按照理性人假设,可以想象参与人届时并不会按纳什均衡战略所规定的方式去选择行动,而是机会主义地选择最优的行动。
这样,具有这种特点的纳什均衡就是不可信的,即不能作为模型的预测结果,按照“精炼〞纳什均衡的思想,应当将其消掉。
定义3.1:子博弈精炼纳什均衡〔SPNE〕:扩展式博弈的策略组合 S*=(S1*,…, Si*,…, Sn* )是一个子博弈精炼纳什均衡当且仅当:如果它是原博弈的纳什均衡;它在每一个子博弈上也都构成纳什均衡。
如果一个完美信息的动态博弈中,各博弈方的策略构成的一个策略组合满足:在整个动态博弈与它的所有子博弈中都构成纳什均衡,那么这个策略组合称为该动态博弈的一个“子博弈完美纳什均衡〞。


贝叶斯博弈模型1. 引言贝叶斯博弈模型是一种重要的博弈模型之一,它可以用于解决多方参与的决策问题。
本文将先介绍贝叶斯博弈的基本概念和数学公式,然后利用一个具体案例来说明贝叶斯博弈的应用。
2. 贝叶斯博弈的基本概念贝叶斯博弈是一类博弈模型,其中参与者的信息不完全。
与传统的博弈模型不同,贝叶斯博弈模型中参与者的决策被视为一个随机变量,而不是唯一确定的策略。
参与者在制定决策时,需要考虑其他参与者的信息和策略。
在贝叶斯博弈中,参与者的信息受到随机变量的影响。
这些随机变量可能来自于环境、其他参与者的行为或其他因素。
每个参与者都有一个先验信念,即他们在未观察到其他参与者的策略和收益时的信念。
参与者在不断观察和收集信息的同时更新自己的信念,从而制定更为准确的策略。
贝叶斯博弈模型的核心是博弈的贝叶斯纳什均衡。
贝叶斯纳什均衡是一组随机策略,其中每个参与者的策略都是最优的,即使其他参与者的策略是未知的。
换句话说,贝叶斯纳什均衡是参与者在自己的信息不完全的情况下,最优策略的概率分布。
3. 贝叶斯博弈的数学公式在贝叶斯博弈中,每个参与者都有一个随机变量Ai表示他的私有信息。
公共信息O也是一个随机变量,表示所有参与者都知道的信息。
参与者对于公共信息的信念被表示为对O的后验分布P(O|A1,…,An)。
参与者的策略S是一个函数,它映射Ai和O到应该采取的行动。
贝叶斯博弈的收益函数表示参与者的收益是他的策略和其他参与者的策略的函数。
每个参与者都希望最大化自己的期望收益。
因此,每个参与者的目标是找到使他的后验预期收益最大化的策略。
假设有N个参与者,第i个参与者的策略为Si(Ai,O),则贝叶斯纳什均衡定义为每个参与者的策略Si(Ai,O)都使得其他参与者的策略Si-1(A1,O) ~ Si-1(Ai-1,O)的条件下他的收益最大化。
换句话说,对于所有i∈{1,2,…,N},Si(Ai,O)都是贝叶斯纳什均衡当且仅当:E[S1(A1,O)|A1]≥E[S1(A1’,O)|A1] (1)······E[SN(AN,O)|AN]≥E[SN(AN’,O)|AN] (2)式(1)和式(2)表示每个参与者的策略都是其他参与者的策略的反应。

贝叶斯纳什均衡例题假设有两家企业摘要:1.贝叶斯纳什均衡的概述2.贝叶斯纳什均衡的例题:两家企业的博弈3.贝叶斯纳什均衡的应用范围正文:一、贝叶斯纳什均衡的概述贝叶斯纳什均衡(Bayesian Nash Equilibrium)是一种博弈论中的概念,指的是在给定自己的特征和其他局中人特征的概率分布的情况下,每个局中人选择策略使自己的期望支付达到最大化,也就是说,没有人有积极性选择其他策略。
在这种均衡状态下,每个参与者都认为自己的选择是最佳的,因为其他参与者也作出了相同的选择。
二、贝叶斯纳什均衡的例题:两家企业的博弈假设有两家企业A 和B,它们分别面临市场进入与否的决策。
企业A 可以选择进入或不进入市场,企业B 也可以选择进入或不进入市场。
两个企业的收益取决于它们各自的决策以及对方企业的决策。
如果企业A 进入市场,企业B 选择阻挠的概率为x,此时企业A 的收益为-10;如果企业A 进入市场,企业B 不阻挠的概率为1-x,此时企业A 的收益为40。
同样,如果企业B 进入市场,企业A 选择阻挠的收益为-10,企业B 不阻挠的收益为40。
在这个博弈过程中,企业A 和企业B 都希望最大化自己的收益。
因此,它们需要根据对方的决策来选择自己的最优策略。
在贝叶斯纳什均衡状态下,企业A 和企业B 都选择了能使自己收益最大化的策略,此时没有人有积极性选择其他策略。
三、贝叶斯纳什均衡的应用范围贝叶斯纳什均衡是一种理论分析工具,它可以帮助我们在不确定性条件下,预测和分析各个参与者的决策行为。
在实际应用中,贝叶斯纳什均衡可以用于解决许多经济、社会和政治领域的问题,例如价格博弈、专利竞争、国际贸易等。

第十二章贝叶斯纳什均衡及其精炼前两章讨论的是完全信息条件下的博弈,给出了博弈的基本分析框架。
本章将讨论不完全信息下的博弈行为,包括不完全信息静态博弈和不完全信息动态博弈。
12.1不完全信息博弈与贝叶斯纳什均衡一、不完全信息博弈完全信息博弈指博弈中的参与人对所有其他参与人的支付(偏好)函数有完全的了解,并且支付函数是所有参与人的共同知识(common knowledge)的博弈。
反之,不满足完全信息博弈假设的博弈称为不完全信息博弈。
二、海萨尼(Harsanyi)转换在博弈中,信息不完全使得博弈参与人必须预测其他参与人的类型。
至于“类型”概念,以两个企业博弈的例子说明。
假设参与人1为在位者企业,参与人2为进入者企业。
进入者依据在位者的生产成本高低选择是否进入该行业,高则进,低则不进。
但是进入者不知道在位者的成本是高还是低。
因此,进入者必须预测在位者的成本“类型”,究竟是高成本的还是低成本的。
海萨尼提出通过引入“自然”概念解决这个问题。
即由自然实现行动,确定其他参与人的类型,从而转换成我们已讨论过的扩展式动态博弈结构。
即通过自然选择类型,实现不完全信息向完全信息的转换,我们称之为海萨尼转换。
在本例中,通过自然选择在位者的成本类型,进入者再针对高成本或低成本进行是否进入的博弈决策。
应当指出,通过自然选择类型的划分,不仅是针对支付函数而言的,其包括参与人所拥有的所有个人信息,如战略空间和信息集等等。
通过上述分析可知道,不完全信息意味着,至少有一个参与人拥有多种类型,否则就成为完全信息博弈。
用表示参与人的一个特定类型,表示参i θi i Θ与人所有可能类型的集合,,并假定i i i Θ∈θ取自某个客观的分布函数。
n i i 1}{=θ),,(1n P θθL为简化起见,假定只有参与人本人观察到自i 己的类型,其他人都不能察到。
但依据海萨尼i θi θ公理,我们假定分布函数是所有参与),,(1n P θθL 人的共同知识,就是说,在博弈开始时,所有参与人关于自然行动的信念是相同的。