八年级上册青岛版《数学配套练习册》答案

1.1 全等三角形一、选择题1．△ABC≌△BAD，A和B，C和D是对应点，∠CAB的对应角是（）A．∠DAB B．∠DBA C．∠DBC D．∠CAD2．下列说法正确的是（）A．面积相等的两个图形是全等图形B．周长相等的两个图形是全等图形C．所有正方形都是全等图形D．能够完全重合的两个图形是全等图形3．在△ABC中，∠A=∠B，若与△ABC全等的三角形中有一个角为90°，则△ABC中等于90°的角是（）A．∠A B．∠B C．∠C D．∠B或∠C4．如图，在A，B，C，D，E，F几个区域中，其中全等图形的对数为（）（第4题图）A．1 B．2 C．3 D．45．有下列说法：①能够完全重合的两个三角形是全等三角形；②一个图形经过平移、翻折、旋转后，位置变化了，但形状、大小没有改变，即平移、翻折、旋转前后的两个图形是全等形；③面积相等的两个三角形是全等三角形；④全等三角形的周长相等；⑤全等三角形的对应边相等，对应角相等．其中正确的个数是（）A．1B．2 C．3 D．46．有下列图形：①两个正方形；②每边长都是1cm的两个四边形；③每边都是2cm的两个三角形；④半径都是1.5cm的两个圆．其中是一对全等图形的有（）A．1个B．2个C．3个D．4个二．填空题7．请观察图中的5组图案，其中是全等形的是（填序号）．（第7题图）8．如图，△ABC≌△ADE，则AB=．若∠BAE=120°，∠BAD=40°，则∠BAC=°．（第8题图）（第9题图）9．如图，BE交AD于点C，△ABC≌△DEC，则∠A=，∠E=，∠BCA=，AB=，BC=，AC=，点C的对应点是点，AB∥，若AB⊥BE，则DE BE．10．如图，△ABC≌△DEF，若AB=7cm，BC=8cm，AC=6cm，BE=5cm，则EC=cm，△DEF的周长=cm．（第10题图）三、解答题11．已知△ABC≌△FED，若△ABC的周长为32，AB=8，BC=12，求FD的长．12．已知△ABC≌△DEF，∠A=85゜，∠B=60゜，AB=8，EH=5．求∠DFE的度数及DH的长．（第12题图）13．如图，一块土地上共有20棵果树，要把它们平均分给四个小组去种植，并且要求每个小组分得的果树组成的图形、形状大小要相同，应该怎样分？（第13题图）答案一、1. B【分析】∵△ABC≌△BAD，A和B，C和D是对应点，∴∠CAB=∠DBA．故选B．2. D【分析】A．面积相等，但图形不一定能完全重合，故错误；B．周长相等的两个图形不一定能完全重合，故错误；C．正方形的面积不相等，也不是全等形，故错误；D．符合全等形的概念，故正确．故选D．3. C【分析】∵与△ABC全等的三角形中有一个角为90°，∠A=∠B，∴∠C=90°．故选C．4. C【分析】观察图形，根据全等的概念可知，图中A与D，E与F，B与C能够重合，是全等形，共3对．故选C．5. D【分析】①能够完全重合的两个三角形是全等三角形，故正确；②一个图形经过平移、翻折、旋转后，位置变化了，但形状、大小没有改变，即平移、翻折、旋转前后的两个图形是全等形，故正确；③面积相等的两个三角形不一定是全等三角形，故错误；④全等三角形的周长相等，故正确；⑤全等三角形的对应边相等，对应角相等，故正确．故正确的有4个．故选D．6. B【分析】①两个正方形是相似图形，但不一定全等，故不符合题意；②每边长都是1cm 的两个四边形是菱形，其内角不一定对应相等，故不符合题意；③每边都是2cm的两个三角形是两个全等的等边三角形，故不符合题意；④半径都是1.5cm的两个圆是全等形，故符合题意．故选B．二、7.（1）（4）（5）8.AD，80【分析】∵△ABC≌△ADE，∴AB=AD，∠BAC=∠DAE，∴∠BAC-∠DAC=∠DAE-∠DAC，∴∠BAD=∠CAE．∵∠BAD=40°，∴∠CAE=40°．∵∠BAE=120°，∴∠BAC=∠BAE-∠CAE=80°．9. ∠D，∠B，∠ECD，DE，EC，DC，C，DE，⊥【分析】△ABC≌△DEC，则∠A=∠D，∠E=∠B，∠BCA=∠ECD，AB=DE，BC=EC，AC=DC，点C的对应点是点C，AB∥DE，若AB⊥BE，则DE⊥BE．10. 3，21【分析】∵AB=7cm，BC=8cm，AC=6cm，∴EC=BC-BE=8-5=3（cm），△ABC的周长是21cm．∵△ABC≌△DEF，∴△DEF的周长=△ABC的周长=21cm．三、11. 解：∵△ABC的周长为32，AB=8，BC=12，∴AC=32-8-12=12．∵△ABC≌△FED，∴FD=AC=12．12. 解：∵△ABC≌△DEF，∠A=85°，∠B=60°，AB=8，EH=5，∴∠D=∠A=85°，∠DEF=∠B=60°，DE=AB=8，∴∠DFE=180°-∠D-∠DEF=35°，DH=DE-EH=8-5=3．13. 解：如答图．（第13题答图）。

青岛版数学练习册八年级上册参考答案1.11.略.2.DE,∠EDB，∠E.3.略.4.B5.C6.AB=AC,BE=CD,AE=AD,∠BAE=∠CAD7.AB∥EF,BC∥ED.8.(1)2a+2b;(2)2a+3b;(3)当n为偶数时，n2(a+b);当n为奇数时，n-12a+n+12b.1.2第1课时1.D2.C3.(1)AD=AE;(2)∠ADB=∠AEC.4.∠1=∠25.△ABC≌△FDE(SAS)6.AB∥CD.因为△ABO≌△CDO(SAS).∠A=∠C.7.BE=CD.因为△ABE≌△ACD(SAS).第2课时1.B2.D3.(1)∠ADE=∠ACB；(2)∠E=∠B.4.△ABD≌△BAC(AAS)5.(1)相等，因为△ABE≌△CBD(ASA);(2)DF=EF,因为△ADF≌△CEF(ASA).6.相等，因为△ABC≌△ADC(AAS).7.(1)△ADC≌△AEB;(2)AC=AB,DC=EB,BD=EC;∠ABE=∠ACD,∠BDO=∠CEO,∠BOD=∠COE.第3课时1.B2.C3.110°4.BC的中点.因为△ABD≌△ACD(SSS).5.正确.因为△DEH≌△DFH(SSS).6.全等.因为△ABD≌△ACD(SSS).∠BAF=∠CAF.7.相等，因为△ABO≌△ACO(SSS).1.3第1课时1~6(略).7.作∠AOB=∠α,延长BO，在BO上取一点C，则∠AOC即为所求.8.作∠AOB=∠α,以OB为边，在∠AOB的外部作∠BOC=∠β；再以OA为边，在∠AOC的内部作∠AOD=∠γ,则∠DOC即为所求.第2课时1.略.2.（1）略;（2）全等(SAS).3.作BC=a-b;分别以点B、C为圆心，a为半径画弧，两弧交于点A;连接AB，AC，△ABC即为所求.4.分四种情况：（1）顶角为∠α,腰长为a;(2)底角为∠α，底边为a;(3)顶角为∠α，底边为a;(4)底角为∠α，腰长为a.((3),(4)暂不作).第3课时1.四种：SSS,SAS,ASA,AAS.2.作线段AB;作∠BAD=∠α,在∠BAD同侧作∠ABE=∠B;AD与BE相交于点C.△ABC即为所求.3.作∠γ=∠α+∠β;作∠γ的外角∠γ′;作△ABC,使AB=c.∠A=∠γ′，∠B=∠α.4.作∠γ=180°-∠β；作△ABC,使BC=a,∠B=∠α,∠C=∠γ.第一章综合练习1.A2.C3.C4.AB=DC或∠ACB=∠DBC或∠A=∠D.5.△ACD≌△BDC,△ABC ≌△BAC.6.△ABC≌△CDE(AAS)7.4分钟8.△BOC′≌△B′OC(AAS)9.略10.相等.△BCF≌△EDF(SAS).△ABF≌△AEF(SSS)检测站1.B2.B3.20°4.∠BCD5.相等.△ABP≌△ACP（SSS）,△PDB≌△PEC(AAS).6.略2.11~3.略.4.B5.C6.(1)(2)(4)7.20°;30°.8.略2.2第1课时1~2.略3.C4.D5.略6.66°7.（1）AA′∥CC′∥BB′,且AA′⊥MN,BB′⊥MN,CC′⊥MN.(2)5 cm8.(1)DE⊥AF;(2)略.第2课时1.(-2,-3),(2,3).2.3,-43.(3,2)4.B5~6.略7.（1）(-a,b);(2)当n=4k+1时，在第一象限，n=4k+2时，在第四象限，n=4k+3时，在第三象限，n=4(n+1)时，在第二象限，k为非负整数.2.31~3.略.4.B5.C.6.略.7.4条.8.略.2.4第1课时1.略.2.CM=DM,CE=DE.3.C4.∠A=∠B,∠ACD=∠BCD,∠ADC=∠BDC.5~6.略.7.连接BM,PB＜PM+MB，∵MB=MA，∴PB＜PA.第2课时1.作一条线段的垂直平分线2.D3~5.略.6.分别作点A关于OM，ON的对称点D，E.连接DE，分别交OM，ON于点B，C.连接AB，AC，则△ABC 的周长最小.2.51.略.2.103.D4.C5.作∠AOB的平分线交MN于点P.则P即为所示.6.（1）DE=DC,AE=BE,BE=BC;(2)7.7.（1）△ADO≌△AEO(AAS),△BOD≌△COE(ASA),OB=OC;(2)∠1=∠2.8.4处.三条直线围成的三角形的三内角平分线的交点，及任一内角平分线与其他两个角的外角平分线的交点.2.6第1课时1.略.2.35°,35°.3.50°,80°或65°,65°.4.C5.B6.∠EBC=36°,∠C=∠BEC=72°.7.△ACD≌ABD(SSS),∠CAG=∠BAG.AG 是等腰三角ABC的顶角平分线.∴AD垂直平分BC.8.99°第2课时1.略.2.△ABE,△ECD,△EBC.3.C4.△DBE是等腰三角形.因为∠B=∠C=∠DEB.5.△AED是等腰三角，因为∠EAD=∠BAD=∠ADE.6~7.略.第3课时1.略.2.1，3.3.C4.△ADE是等边三角形.因为三个角都等于60°.5.略.6.任两边的垂直平分线的交点即为点O.7.BE=DC.因为△ADC≌△ABE(SAS).第二章综合练习1.GH,∠E,EO.1.B(4,-3);C(-4,3);6;8.3.24.45.64°;58°.6.D7.C8.A9.A10.(1)AB=AD,AE=AC,BC=DE,BF=DF,EF=CF;∠BAC=∠DAE,∠B=∠D,∠C=∠E,∠BAE=∠DAC,∠EAF=∠CAF,∠BFE=∠DFC,∠BAF=∠DAF.(2)△AEF与△ACF，△ABF与△ADF都关于直线MN成轴对称.11.△ABC 与△A′B′C′关于y轴对称.12.△ACE≌△DCB（SAS）.AE=BD.又∠HGE=∠CGB.∠HEG=∠CBG.∠HGE+∠HEG=∠CGB+∠CBG=90°.∠EHG=90°.AE⊥BD.13.4个.①以BC为底边的等腰三角形可作1个;②以BC为腰的等腰三角形可作3个.检测站1.60°2.AP;PC,AP;∠CAP.3.1；7.4.55°,55°或70°,40°.5.AC,∠C,△ABD.6.B7.B8.B9.D10.A11.略.12.∠BAC=60°,∠C=90°,∠B=30°.13.∵△ABC≌△BAD.∠CAB=∠DBA,∴△EBA是等腰三角形.14.（1）5;(2)80°.15.∠ACD=180°-A2,∠BCE=180°-B2,∠ACB=90°.∴∠ACD+∠BCE=90°+∠DCE.∠DCE=45°.3.1第1课时1.B≠0；B=0;A=0且B≠0.2.≠23.1,0.4.B5.D6.B7.x=-1且y≠08.19.ba-5;400.10.a=-1.11.略.12.n+13n-2第2课时1.略2.（1）2abc2;(2)xy(x+y);(3)a(a+b);(4)2x(x+y).3.A4.C5.B6.x ≠1且x≠07.当a≠0时，a2a=12;当m≠0，n≠0时，n2mn=nm.8.M=-3x(a+x)2;x≠0,-a,a.9.5a2-1030a2-2a3.21.略.2.2a(b-a)3.C4.C5.B6.(1)3y2x;(2)-1(x-y)2;(3)a+22-a;(4)2a2a -3b.7.-78.a-b+ca+b+c9.略.3.31~3.略.4.(1)-1ab;(2)ab18c;(3)4yx;(4)4yx.5.D6.C7.(1)a+1;(2)-b3x;( 3)xy2;(4)aa+b8.-139.略.3.41.略.2.6a2b2,ab,3b,2a.3.(x+2)(x-2)24.D5.D6.2b24a2b2c2,3ac324a2 b2c2;(2)5(a-b)215a(a+b)(a-b),3(a+b)215(a+b)(a-b);(3)3x-2y(3x +2y)(3x-2y),2(3x+2y)(3x-2y);(4)(x+1)2(x-1)(x+1)2,x(x-1)(x+1)(x-1)(x+1)2,x-1(x-1)(x+1)2.7 .(m-n)2m-n,-mnm-n.8.cyz(b-c)(c-a)xyz(a-b)(b-c)(c-a),axz(a-b) (c-a)xyz(a-b)(b-c)(c-a),bxy(a-b)(b-c)xyz(a-b)(b-c)(c-a). 9.(1)把前一个分式的分子，分母同乘-a2b即得下一个分式;(2)-a12b8a13b6.(3)（-1）na2n-2bn+1(-1)n+1a2n-1bn-1.3.5第1课时1.略.2.（1）-b2a;(3)2aa-b.3.C4.D5.(1)y2x;(2)x+2;(3)3.6.(1)2+x;(2)3abb-a.7.x+2.8.原式=1.第2课时1.略.2.b2-4c4a3.-4(x+2)(x-2)4.C5.D6.D7.(1)3c3-4a2b12ab2c2;(2)6x2+xy+7y242x2y2;(3)2mn-m2n2-m2.8.-659.(1)11-a;(2)x2.10.1(x-1)(x-2),1(x-2)(x-3),1(x-3)(x-4),1x-100.第3课时1.C2.D3.B4.(1)a-bb;(2)x+2.5.126.∵ca+b＜1.∴c2(a+b)2＜ca+b3.6第1课时1.(1)7x4y;(2)b2a;(3)2x-y;(4)a+ba-b2.ala+b,ala+b.3.23;49;13.4.A5.C6.(1)2;(2)2;(3)4.7.68.(1)xyx+y(天);(2)甲：myx+y(元),乙：mxx+y(元).9.（1）ba;(2)b-10a-10,b+10a+10;(3)b-10a-10＜ba＜b+10a+10.第2课时1.略.2.8∶93.124.245.C6.D7.8a38.a-b=-39.260 mm10.5211.-5.第3课时1.略.2.2∶33.33124.1 m5.10∶15∶216.D7.B8.x∶y∶z=(a+b)2∶(a2-b2)∶(a-b)29.34a,a,54a.10.6,8,10.11.63人，192人，45人.3.7第1课时1.略.2.去分母，将分式方程转化为整式方程求解，然后验根.3.-124.-325.B6.B7.D8.30x-2-30x=12.9.(1)x=4;(2)x=0.10.m=-1 8711.(1)x=5;(2)a=6.第5个方程;（3）1+x2x=n+1x,x=2n+1.第2课时1.略.2.无解3.C4.B5.不正确，错在第3步，没有检验;方程无解.6.(1)x=3;(2)无解;（3）无解；（4）无解.7.a=-58.(1)①x=1;②x=2;③x=3;(2)方程1x-2-1x-3=1x-5-1x-6的解为x=4;方程1x+2-1x+1=1x-1-2x-2的解为x=0.第3课时1.略.2.12010-x-12010=33.16+1x=13.4.D5.(1)设去年每间屋的租金为x元，9.6x=10.2x+500;(2)8 000元.6.4 km/h7.37.5 km/h8.1.5 t9.(1)设预定工期为x天，4x+xx+5=1,x=20（天）.(2)采取联合施工4天，然后由乙单独施工的方案省工程费.第三章综合练习1.a≠32；x=-1.2.m=3,m≠1.3.24.125.a∶b=b∶c,c∶b=b∶a,ac=b26.127.3∶4∶58.39.C10.C11.A12.D13.B14.D15.616.a+b=0.17.(1)-5y2ax;(2)-x3y ;(3)2xy;(4)3x+1;(5)1681x4y4;(6)2a2b2;(7)a-3a2-13;(8)-1a+1.18.(1）-715;(2)310.19.S1∶S2=1∶220.21821.(1)无解;（2）x=1912;(3)x=-2;(4)无解.22.应提高60 km/h23.(1)x ≠-1，0，1；（2）原式=1.24.1次清洗.残留农药比为11+y;分两次清洗后，残留农药比为：4（2+）2，11+y-4(2+y)2=y2(1+y)(2+y)2＞0.第2种方案好.检测站1.x≠32,x=-23.2.x≠0且x≠-53.164.295.326.D7.C8.B9.B10.相等11.（1）mn-m;(2)ab;(3)2x-1x.12.11-x;-1.13.(1)x=4;(2)无解;(3)x=2.14.a=-115.14516.3617.28天4.1第1课时1~2.略.3.3.44.C5.B6.总产量1 757 t;平均产量8.53 t.7.9 000 m3 8.a·10%+b·15%+c·5%a+b+c (a,b,c为甲、乙、丙三种汽油原价) 第2课时1.820，920，320.2.86 km/h3.C4.(1)甲；（2）乙.5.9.9%6.(1)1.84 kg;(2)3 312 kg.4.21.略.2.94.53.C4.x=225.平均数：1 626，中位数1 680.6.26 cm7.9或108.（1）85.5;(2)41人;（3）高低分悬殊大.4.3第1课时1.2;1与2.2.7与83.B4.平均数、中位数、众数都是21岁5.平均数为2,中位数是3，众数是1.6.（1）3个；（2）32 000个.7.（1）甲组：平均数80，中位数80，众数90；乙组：平均数80.2，中位数80，众数70;（2）略.第2课时1.72.A3.平均数13千瓦时，中位数22.5千瓦时，众数10千瓦时.4.（1）众数55 min,中位数55 min;(2)平均数为55 min.符合学校的要求.5.甲当选4.41~2.略.3.(1)平均直径都是20 mm;(2)小明.4.乙地;甲地温差比乙地大.5.（1）平均身高都是178 cm;(2)图略.甲队整齐.6.(1)x甲=1.69 m,x乙=1.68 m;(2)图略.甲比较稳定.4.5第1课时1.1.22.10,26.3.10,1.8.4.A5.D6.S2甲=0.055,S2乙=0.105;果农甲.7.（1）x=3,S2=2;(2)x=13,S2=2；(3)x=30,S2=200.8.（1）xA=0，S2A=2.29;(2)取-2,-1,0,3,0;xB=0,S2B=2.8.第2课时1.乙2.D3.（1）略;(2)大刚的平均数为13.35,方差为0.004;小亮的平均数为13.3，方差为0.02.大刚成绩好.4.（1）x苹果=8，x香蕉=8，S2苹果=9，S2香蕉=1.333；（2）略;（3）9月份多进苹果.5.S2=1n［(x1-x)2+(x2-x)2+…+(xn-x)2］=1n［x21+x22+…+x2n-2x(x1+x2+…+xn)+nx2］=1n［x21+x22+…+x2n-2nx(x1+x2+…+xnn+nx2)］=1n［x21+x22+…+x2n-nx2］.4.61.C2.略3.甲4.相差75.x甲=178,S2甲=0.6;x乙=178,S2乙=1.8.6.(1)x甲=200.8,S2甲=7.96;x乙=201.5,S2乙=38.05;(2)甲. 第四章综合练习1.1.62 m2.8,8,8,1.23.20,18,184.4,3.5.b＞a＞c6.C7.D8.C9.(1)甲组：x甲=3.中位数2，众数1，S2甲=7.67;乙组：x乙=3,中位数3，众数3，S2乙=1.67;(2)乙组.10.（1）x=2 135.7(元),众数为800元，中位数为1 600元；（2）略.11.（1）x=2,众数为3，中位数为2;（2）68人.12.（1）22℃；（2）20.8℃;(3)146天.13.乙成绩稳定检测站1.2.12元2.23.64.31.8℃,4.965.D6.C7.D8.90.6分9.(1)x甲=5.6 cm,S2甲=1.84,x乙=5.6 cm,S2乙=1.04.(2)乙苗长的比较整齐.10.（1）x甲=7，S2甲=0.4,x乙=7,S2乙=2.8;(2)甲.11.612.（1）甲班：平均分24，方差5.4;乙班中位数24,众数21，方差19.8;(2)甲班42人，乙班36人;（3）甲班.综合与实践略.5.11~2.略.3.面积相等的三角形，是全等三角形，假.4.D5.D6.B7~9.略.5.21.略.2.不正确.如正方形与菱形.3.小亮不对；小莹说法正确.4.不正确.如2≠-2,但22=(-2)2.5.不正确;t=20t1+30t220+30.5.31~3.略.4.C5.直角定义;余角定义;对顶角相等；等量代换；余角定义.6.（1）C,E,F,G;(2)E;(3)K;(4)略.7.C5.41.B2.C3.（1）∠D；内错角相等，两直线平行；（2）∠DEC；AB∥DE.同位角相等，两直线平行.4.已知：∠CBE;两直线平行，同位角相等;已知,∠CBE;等量代换；内错角相等，两直线平行.5.略.6.（1）如果两个角相等，那么这两个角是同角或等角的补角.真命题；（2）如果三角形中有两个角是锐角,那么第三个角是钝角，假命题，如∠A=80°，∠B=70°，∠C=30°.7.（1）延长AE与CD相交于点G.∵AB∥EF.∴∠A+∠AEF=180°.∵AB∥CD,∴∠A+∠G=180°.∴∠A+∠AEF=∠A+∠G,∠AEF=∠G.∴EF∥CD;(2)360°.5.5第1课时1.略.2.C3.D4.∠B=∠C,∠AOB=∠DOC.5.∠1＞∠ACB＞∠26.略.7.(1)∠A逐渐减小,∠B,∠C逐渐变大;若点A向下运动,变化相反;(2)α=β+γ.5.5第2课时1.(1)∠B=∠DAC;(2)∠A=∠D;∠CGE+∠B=180°.2.D3.B4.略.5.∠1=∠C+∠CDE,∠2=∠C+∠CED,∠1+∠2=180°.6.(1)∠EFD=90°-∠FED=12(∠A+∠B+∠C)-(∠B+12∠A)=12(∠C-∠B);(2)不变.5.6第1课时1.D2.C3.（1）BC=EF或BE=CF；（2）∠A=∠D；（3）∠C=∠F.4.（1）△ABE≌△DCF(SAS),△ABF≌△DCE(SAS),△BEF≌△CFE;(2)略.5.△AFC≌△BED(ASA)6.取EF的中点M，连接GM，并延长交FH于点N.GN 分别交AD,BC于点P,Q.△PEM≌△QFM.沿GN将道路取直即可.第2课时1.平行2.90°3.B4.D5.∵∠ABD=∠ADB,∴∠CBD=∠CDB.∴BC=DC.6.△ABD与△ACD都是等腰三角形，BD=AD=DC.7.△ABD≌△ACE（SAS）.∠A=∠CAE=60°.∴△ADE为等边三角形.8.∵△AEB≌△BDA(ASA).∴AE=BD,EB=DA,CE=CD,EF=DF.AF=BF.第3课时1.=2.①②③3.A4.略.5.△ABD≌△AED(SAS),∴AB=AE.DC=AB+BD=AE+DE,DC=DE+EC,∴AE=EC.∴点E在线段AC的垂直平分线上.6.（1）∠A≠∠C.因为△ABD与△CBD不全等；（2）∠A＞∠C.因为AB ＜BC，在BC上取BA′=BA.△ABD≌△A′BD.∠A=∠BA′D.∠BA′D＞∠C,∴∠A＞∠C；(3)当AB=CB时.∠A=∠C;当AB＜BC时，∠A＞∠C；当AB＞BC时，∠A＜∠C.第4课时1.OA=OB.2.=.三角形的三内角平分线相交于一点.3.B4.B5.△ADE≌△ADF.AE=AD.△AEF为等腰三角形.6.△BEO≌△BFO（AAS）,△BED≌△BFD（SAS）.△EOD≌△FOD（SSS）或(SAS).7.DE=BD-CE.由DE∥BC.∠BOD=∠OBC=∠OBD.∴BD=OD.又∠OCE=∠OCF=∠BOC+∠OBC=∠BOC+∠BOE=∠COE.∴CE=OE.DE=OD-OE=BD-CE.第5课时1.AB=AD或BC=DC（HL）2.D3.B4.作直线MN，过MN上一点D作MN的垂线l;在直线l上截取DA=h;以A为圆心，a为半径画弧交MN于点B，C两点;连接AB，AC.△ABC即为所求.5.连接AC.Rt△ABC≌RtADC(HL).∴BC=DC.Rt△BCE≌Rt△DCF(HL).6.连接AF，BF.△AEF≌△BEF△AFC≌△BFD(SAS).7.(1)Rt△OBD≌Rt△OCE(HL);(2)Rt△OBD≌△OCE(HL);(3)相等.第五章综合练习1.A2.C3.D4.B5.D6.略.7.120°8.∠2=∠1.∴∠2=∠C,AB∥CD.9.延长EF交BC于点G.∵∠2=∠4，∴AB∥EF.∠3=∠B=∠EGC.∴DE∥BC.∴∠AED=∠ACB.10.∠ABE=∠FBD,∠ABE+∠AEB=90°,∠FBD+∠AFE=90°.∴∠AEB=∠AFE.∴AE=AF.11.△ACE≌△BDE(AAS),∴EC=ED.12.(1)∠D=∠AEC(同角的余角相等).△ACE≌△CBD.∴AE=CD;(2)BD=CE=12AC=6 cm.13.(1)Rt△ADE≌Rt△ADF;(2)DB=DC,Rt△DBE≌Rt△DCF(HL).14.(1)略;（2）连接BD.∠DBC=12∠B=30°.∵∠CDE=∠CED.∴∠CED=12∠ACB=30°.∴△DBE为等腰三角形.∵DM⊥BE,∴BM=EM.15.△BPD≌△BDC(SAS),△BCD≌△ACD(SSS).∠P=∠BCD=∠ACD=12∠ACB=30°.16.(1)作DF⊥AB，垂足为点E.AC=AE,DE=DC.∵∠B=∠A=45°,∴BE=DE.∴AB=AE+BE=AC+CD.(2)(1)中的等量关系仍成立.∵∠ACB＞∠B,∴AB ＞AC.在AB上截取AG=AC.分别作DF⊥AC,DE⊥AB.△DCF≌△DGE.∵∠EGD=∠C=2∠B.∴∠B=∠BDG.BG=DG=DC.∴AB=AG+GB=AC+CD.检测站1.A2.C3.C4.三;△ODG≌△OEG,△DPG≌△EPG;△ODP≌△OEP,HL或AAS.5.略.6.FA=FD,∠ADF=∠DAF=∠DAC+∠CAF.∵∠DAC=∠BAD.∴∠B=∠ADF-∠BAD=∠DAF-∠DAC=∠CAF.7.(1)略；（2）∵CA=CE,∴∠CAE=∠E.∵∠ACB=∠CAE+∠E=2∠E,∠ACB=2∠BCD,∴∠E=∠BCD.CD∥AE.8.(1)①③或②③;（2）略.9.(1)△ABQ≌△PBC;(3)∠MBN=60°,△ABM≌△PBN(ASA).BM=BN.∴△BMN为等边三角形.∠MNB=∠QBC.MN∥AC.总复习题1.(3,4)，等腰2.-53.50°,60°,70°.4.略.5.5，5.6.D7.C8.D9.B10.D11.(1)11-x;(2)x2-xy-2y23xy2;(3)-(1-m)2;(4) 1-a.12.32°13.-314.设每天修x m,3 600x-3 6001.8x=20.x=80 m.15.(1)中位数12℃,众数11℃;(2)1.143.16.分别作FG⊥BC,FM⊥AD,FN⊥AE,垂足分别为点G，M，N.FM=FG=FN.17.∵∠BAD=∠BDA,∴AB=DB=CD.∵BE=DE,∴△ABE≌△ADE.AB=AD,△ABD为等边三角形.连接CF.△AEC≌△FEC.∵∠ACF=60°,∴△AFC为等边三角形.∴AF=AC,AE=12AC.18.延长BO交AC于点D.∠BOC=110°.19.作CF⊥AC，交AD延长线于点 F.∵∠BAC=90°，AD⊥BM.∴∠ABM=∠MAE.∵AB=AC,∴△ABM≌△CFA.∠1=∠F.AM=CF.∵AM=CM,∴CF=CM.∠FCD=45°=∠MCD.∴△FCD≌△MCD(SAS).∠2=∠F=∠1.总检测站1.a-12.(1)SSS;(2)SAS;(3)HL.3.5,5,5.25.4.4,3.5.△ABC≌△ABD,△ACE≌△ADE,△CEB≌△DEB.6.C7.D8.D9.D10.B11.113 850 kg 12.(1)x=-2;(2)无解.13.30 m14.∵△ABE≌△ACE,∴BE=CE,BD=CD.△BDE≌△CDE(SSS).15.(1)①②③④,①③②④,①④②③,②③①④,②④①③.(2)略.≤≥＜＞×≠÷′△∠°αβ⊥∥∵∴△≌△S△ACC′1.2.3.4.5.6.7.8.9.10.。

5.6.1 几何证明举例1. 如图，玻璃三角板摔成三块，现在到玻璃店在配一块同样大小的三角板，最省事的方( ）A. 带①去B. 带②去C. 带③去D.带①②③去2. 如图，已知∠1=∠2，则不一定能使△ABD ≌△ACD 的条件是（ ）A. AB=ACB. BD=CDC. ∠B=∠CD.∠BDA=∠CDA3. 如图，给出下列四组条件：①AB DE BC EF AC DF ===，，；②AB DE B E BC EF =∠=∠=，，；③B E BC EF C F ∠=∠=∠=∠，，；④AB DE AC DF B E ==∠=∠，，．其中，能使ABC DEF △≌△的条件共有（ ）A ．1组B ．2组C ．3组D ．4组4.如图，90E F ∠=∠=，B C ∠=∠，AE AF =，结论：①EM FN =；②CD DN =； ③FAN EAM ∠=∠； ④ACN ABM △≌△．其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个第1题图 第2题图 第3题图5. 如图，在下列条件中，不能证明△ABD≌△ACD的是（）A.BD=DC，AB=ACB.∠ADB=∠ADC，BD=DCC.∠B=∠C，∠BAD=∠CADD.∠B=∠C，BD=DC6. 如图，已知△ABC的六个元素，则下列甲、乙、丙三个三角形中和△ABC全等的图形是7.如图，△ABC中，BD=EC，∠ADB=∠AEC，∠B=∠C，则∠CAE= .8. 如图，点B、E、F、C在同一直线上,已知∠A =∠D，∠B =∠C，要使△ABF≌△DCE，以“AAS”需要补充的一个条件是（写出一个即可）．9. 已知：如图，∠ABC=∠DCB，BD、CA分别是∠ABC、∠DCB的平分线．求证：AB=DC AEFBCDMN10．如图，已知AD 是△ABC 的角平分线，在不添加任何辅助线的前提下，要使△AED ≌△AFD ，需添加一个条件是：_______________，并给予证明.参考答案1. C2. B3.C4.C5.D6.乙和丙7. ∠BAD8. AF=DE 或BF=CE 或BE=CF9. 证明：在△ABC 与△DCB 中(ABC DCB ACB DBCBC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩已知）（公共边） ∴△ABC ≌△DCB∴AB=DC10. 解法一：添加条件：AE ＝AF ，证明：在△AED 与△AFD 中，∵AE ＝AF ，∠EAD ＝∠FAD ，AD ＝AD ，∴△AED ≌△AFD （SAS ）.解法二：添加条件：∠EDA ＝∠FDA ，证明：在△AED 与△AFD 中，∵∠EAD ＝∠FAD ，AD ＝AD ，∠EDA ＝∠FDA∴△AED ≌△AFD （ASA ）.。

青岛版数学配套练习册答案八上【练习一：数与式】1. 计算下列各题：(1) (-2) × 3 = -6(2) (-3)² = 9(3) 5 - (-3) = 8(4) 4 × (-2) - 3 = -112. 化简下列各题：(1) 3x - 2x + 5 = x + 5(2) 4y + 3y - 2y = 5y3. 求下列方程的解：(1) 2x - 3 = 7，解得 x = 5(2) 3x + 4 = 2x - 1，解得 x = -5【练习二：方程与不等式】1. 解一元一次方程：(1) x + 6 = 11，解得 x = 5(2) 3x - 9 = 6，解得 x = 72. 解一元一次不等式：(1) 2x + 5 > 3，解得 x > -1(2) 4 - 3x ≥ 1，解得x ≤ 1【练习三：函数】1. 根据函数的定义域，求下列函数的值域：(1) f(x) = x²，值域为[0, +∞)(2) g(x) = 2x - 3，值域为 (-∞, +∞)2. 判断下列函数的单调性：(1) f(x) = x³，为增函数(2) g(x) = -x² + 2，为减函数在(0, +∞)，增函数在 (-∞, 0)【练习四：几何】1. 已知三角形ABC，∠A = 60°，AB = 8，AC = 6，求BC的长度：BC = √(8² + 6² - 2 × 8 × 6 × cos(60°)) = √(64 + 36 - 48) = √522. 已知圆的半径为5，求圆的面积：面积= π× 半径² = 25π【练习五：统计与概率】1. 某班级有50名学生，随机抽取5名学生进行数学测试，求这5名学生的平均分超过90分的概率。

（此题需要具体数据，无法给出具体答案）2. 抛一枚均匀硬币两次，求正面朝上的次数为1的概率。

4.5 方差一、选择题1.在方差的计算公式：s 2=101［（x 1-15）2+（x 2-15）2+…+（x 10-15）2］中，10，15分别表示（）A.数据的个数和方差B.平均数和数据的个数C.数据的个数和平均数D.数据的方差和平均数2.如果一组数据：3，4，5，6，5，7，那么这组数据的方差是（） A.35 B. 21 C.34D.323.下列选项能够反映一组数据离散程度的统计量是（）A.平均数B.中位数C.众数D.方差4.甲、乙两学生在军训打靶训练中，打靶的总次数相同，且所中环数的平均数也相同，但甲的成绩比乙的成绩稳定，那么两者的方差的大小关系是（）A.s 2甲<s 2乙B.s 2甲>s 2乙C.s 2甲=s 2乙D.不能确定5.要判断小强同学的数学考试成绩是否稳定，那么需要知道他最近几次数学考试成绩 的（）A.方差B.众数C.平均数D.中位数6.某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验，它们平均亩产量分别是x 甲=610千克，x 乙=608千克，亩产量的方差分别是s 2甲=29.6，s 2乙=2.7，则下列推广种植两种小麦的最佳决策是（）A.甲的平均亩产量较高，推广甲B.甲、乙的平均亩产量相差不多，均可推广C.甲的平均亩产量较高，且亩产量比较稳定，应推广甲D.甲、乙的平均亩产量相差不多，但乙的亩产量比较稳定，应推广乙7. 若一组数据x 1，x 2，…，x n 的方差是3，则另一组数据x 1+5，x 2+5，…，x n +5的方差是（）A.3B.8C.9D.14二、填空题8.已知甲、乙两个品种棉花的纤维长度的平均数相等，若甲种棉花的纤维长度的方差 s 2甲=1.327 5，乙种棉花的纤维长度的方差s 2乙=1.877 5，则甲、乙两种棉花质量较好的 是_______种.9.市运会举行射击比赛，某校射击队从甲、乙、丙、丁四人中选拔一人参赛，在选拔赛中,每人射击10次，计算他们10发成绩的平均数（环）及方差如下表.请你根据表中数据选一人参加比赛，最合适的人选是_______.10. 甲、乙、丙三人进行飞镖比赛，如果他们每人五次投得的成绩如图，那么三人中成绩最稳定的是_______.（第10题图）11. 如果一组数据5，8，10，x，9的众数是8，那么这组数据的方差是_______.三、解答题12. 为了考察甲、乙两种玉米的生长情况，在相同的时间，将它们种在同一块实验田里，经过一段时间后，分别抽取了10株幼苗，测得苗高如下（单位：cm）：甲：8，12，8，10，13，7，12，11，10，9；乙：11，9，7，7，12，10，11，12，13，8．（1）哪种玉米的高度相对较高？（2）哪种玉米的幼苗长得比较整齐？13. 已知A组数据如下：0，1，-2，-1，0，-1，3.（1）求A组数据的平均数；（2）从A组数据中选取5个数据，记这5个数据为B组数据.要求B组数据满足两个条件：①它的平均数与A组数据的平均数相等；②它的方差比A组数据的方差大.你选取的B组数据是__________，请说明理由.14. 七年级一班和二班各推选10名同学进行投篮比赛，按照比赛规则，每人各投了10个球，两个班选手的进球数统计如下表，请根据表中数据回答问题.（1）分别求一班和二班选手进球数的平均数、众数和中位数.（2）如果要从这两个班中选出一个班代表年级参加学校的投篮比赛，争取夺得总进球数团体第一名，你认为应该选择哪个班？如果要争取个人进球数进入学校前三名，你认为应该选择哪个班？答案一、1.C 2.A 3.D 4.A 5.A 6.D 7.A二、8.甲 9.丙 10.乙 11.2.8三、12. 解：（1）甲组数据的平均数=101×（8+12+8+10+13+7+12+11+10+9）=10； 乙组数据的平均数=101×（11+9+7+7+12+10+11+12+13+8）=10． 则两种玉米的高度相当．（2）s 2甲=101×［（8-10）2+（12-10）2+…+（9-10）2］=3.6； s 2乙=101×［（11-10）2+（9-10）2+…+（8-10）2］=4.2. 因为s 2甲<s 2乙，所以甲玉米幼苗长得比较整齐．13. 解：（1）x A =71×（0+1-2-1+0-1+3）=0. （2）1，-2，-1，-1，3. 因为x B =51×（1-2-1-1+3）=0，所以x A =x B . 因为s 2A =71×（02+12+22+12+02+12+32）=716，s 2B =51×（12+22+12+12+32）=516， 所以s 2B >s 2A .即数据1，-2，-1，-1，3符合题意.14. 解：（1）一班：7，7，7；二班：7，7，7.（2）一班的方差s 21=2.6，二班的方差s 22=1.4.如果想夺得团体第一名，二班选手水平发挥更稳定，那么应该选择二班；一班前三名选手的成绩更突出，如果要争取个人进球数进入学校前三名，那么应该选择一班.。

八年级上册青岛版数学配套练习册答案Prepared on 21 November 2021青岛版数学练习册八年级上册参考答案1.11.略.2.DE,∠EDB，∠E.3.略.4.B5.C6.AB=AC,BE=CD,AE=AD,∠BAE=∠CAD7.AB∥EF,BC∥∠ADB=∠AEC.4.∠1=∠25.△ABC≌△FDE(SAS)6.AB∥CD.因为△ABO≌△CDO(SAS).∠A=∠△ABE≌△ACD(SAS).第2课时∠ADE=∠ACB；(2)∠E=∠B.4.△ABD≌△BAC(AAS)5.(1)相等，因为△ABE≌△CBD(ASA);(2)DF=EF,因为△ADF≌△CEF(ASA).6.相等，因为△ABC≌△ADC(AAS).7.(1)△ADC≌△AEB;(2)AC=AB,DC=EB,BD=EC;∠ABE=∠ACD,∠BDO=∠CEO,∠BOD=∠COE.第3课时°4.BC的中点.因为△ABD≌△ACD(SSS).5.正确.因为△DEH≌△DFH(SSS).6.全等.因为△ABD≌△ACD(SSS).∠BAF=∠CAF.7.相等，因为△ABO≌△ACO(SSS).1.3第1课时1~6(略).7.作∠AOB=∠α,延长BO，在BO上取一点C，则∠AOC即为所求.8.作∠AOB=∠α,以OB为边，在∠AOB的外部作∠BOC=∠β；再以OA为边，在∠AOC的内部作∠AOD=∠γ,则∠DOC即为所求.第2课时1.略.2.（1）略;（2）全等(SAS).3.作BC=a-b;分别以点B、C为圆心，a为半径画弧，两弧交于点A;连接AB，AC，△ABC即为所求.4.分四种情况：（1）顶角为∠α,腰长为a;(2)底角为∠α，底边为a;(3)顶角为∠α，底边为a;(4)底角为∠α，腰长为a.((3),(4)暂不作).第3课时1.四种：SSS,SAS,ASA,AAS.2.作线段AB;作∠BAD=∠α,在∠BAD同侧作∠ABE=∠B;AD与BE相交于点C.△ABC即为所求.3.作∠γ=∠α+∠β;作∠γ的外角∠γ′;作△ABC,使AB=c.∠A=∠γ′，∠B=∠α.4.作∠γ=180°-∠β；作△ABC,使BC=a,∠B=∠α,∠C=∠γ.第一章综合练习∠ACB=∠DBC或∠A=∠D.5.△ACD≌△BDC,△ABC≌△BAC.6.△ABC≌△CDE(AAS)7.4分钟8.△BOC′≌△B′OC(AAS)9.略10.相等.△BCF≌△EDF(SAS).△ABF≌△AEF(SSS)检测站°4.∠BCD5.相等.△ABP≌△ACP（SSS）,△PDB≌△PEC(AAS).6.略2.1°;30°.8.略2.2第1课时°7.（1）AA′∥CC′∥BB′,且AA′⊥MN,BB′⊥MN,CC′⊥MN.(2)5 cm8.(1)DE⊥AF;(2)略.第2课时1.(-2,-3),(2,3).2.3,-43.(3,2)4.B5~6.略7.（1）(-a,b);(2)当n=4k+1时，在第一象限，n=4k+2时，在第四象限，n=4k+3时，在第三象限，n=4(n+1)时，在第二象限，k 为非负整数.2.32.4第1课时∠A=∠B,∠ACD=∠BCD,∠ADC=∠BDC.5~6.略.7.连接BM,PB＜PM+MB，∵MB=MA，∴PB＜PA.第2课时1.作一条线段的垂直平分线2.D3~5.略.6.分别作点A关于OM，ON的对称点D，E.连接DE，分别交OM，ON于点B，C.连接AB，AC，则△ABC的周长最小.2.5∠AOB的平分线交MN于点P.则P即为所示.6.（1）DE=DC,AE=BE,BE=BC;(2)7.7.（1）△ADO≌△AEO(AAS),△BOD≌△COE(ASA),OB=OC;(2)∠1=∠2.6第1课时1.略.2.35°,35°.3.50°,80°或65°,65°.4.C5.B6.∠EBC=36°,∠C=∠BEC=72°.7.△ACD≌ABD(SSS),∠CAG=∠BAG.AG 是等腰三角ABC的顶角平分线.∴°第2课时1.略.2.△ABE,△ECD,△△DBE是等腰三角形.因为∠B=∠C=∠DEB.5.△AED是等腰三角，因为∠EAD=∠BAD=∠ADE.6~7.略.第3课时△ADE是等边三角形.因为三个角都等于60°△ADC≌△ABE(SAS).第二章综合练习1.GH,∠°;58°∠BAC=∠DAE,∠B=∠D,∠C=∠E,∠BAE=∠DAC,∠EAF=∠CAF,∠BFE=∠DFC,∠BAF=∠DAF.(2)△AEF与△ACF，△ABF与△ADF都关于直线MN成轴对称.11.△ABC与△A′B′C′关于y轴对称.12.△ACE≌△DCB（SAS）.AE=BD.又∠HGE=∠CGB.∠HEG=∠CBG.∠HGE+∠HEG=∠CGB+∠CBG=90°.∠EHG=90°.AE⊥①以BC为底边的等腰三角形可作1个;②以BC为腰的等腰三角形可作3个.检测站1.60°2.AP;PC,AP;∠°,55°或70°,40°.5.AC,∠C,△10.A11.略.12.∠BAC=60°,∠C=90°,∠B=30°.13.∵△ABC≌△BAD.∠CAB=∠DBA,∴△EBA是等腰三角形.14.（1）5;(2)80°.15.∠ACD=180°-A2,∠BCE=180°-B2,∠ACB=90°.∴∠ACD+∠BCE=90°+∠DCE.∠DCE=45°.3.1第1课时1.B≠0；B=0;A=0且B≠0.2.≠≠10.a=-1.11.略.12.n+13n-2第2课时≠1且x≠07.当a≠0时，a2a=12;当m≠0，n≠≠3.28.a-b+ca+b+c9.略.3.33.49.(1)把前一个分式的分子，分母同乘-a2b即得下一个分式;(2)-a12b8a13b6.(3)（-1）na2n-2bn+1(-1)n+1a2n-1bn-1.3.5第1课时第2课时7.(1)3c3-4a2b12ab2c2;(2)6x2+xy+7y242x2y2;(3)2mn-m2n2-m2.8.-659.(1)11-a;(2)x2.10.1(x-1)(x-2),1(x-2)(x-3),1(x-3)(x-4),1x-100.第3课时6.∵ca+b＜1.∴c2(a+b)2＜ca+b3.6第1课时1.(1)7x4y;(2)b2a;(3)2x-y;(4)a+ba-b2.ala+b,ala+b.8.(1)xyx+y(天);(2)甲：myx+y(元),乙：mxx+y(元).9.（1）ba;(2)b-10a-10,b+10a+10;(3)b-10a-10＜ba＜b+10a+10.第2课时1.略.2.8∶8.a-b=-39.260 mm10.5211.-5.第3课时1.略.2.2∶33.33124.1 m5.10∶15∶∶y∶z=(a+b)2∶(a2-b2)∶3.7第1课时11.(1)x=5;(2)a=6.第5个方程;（3）1+x2x=n+1x,x=2n+1.第2课时（4）无解.7.a=-58.(1)①x=1;②x=2;③x=3;(2)方程1x-2-1x-3=1x-5-1x-6的解为x=4;方程1x+2-1x+1=1x-1-2x-2的解为x=0.第3课时1.略.2.12010-x-12010=33.16+1x=13.4.D5.(1)设去年每间屋的租金为x元，9.6x=10.2x+500;(2)8 000元.6.4 km/h7.37.5 km/h8.1.5 t9.(1)设预定工期为x天，4x+xx+5=1,x=20（天）.(2)采取联合施工4天，然后由乙单独施工的方案省工程费.第三章综合练习1.a≠≠5.a∶b=b∶c,c∶b=b∶a,ac=b26.127.3∶4∶∶S2=1∶220.21821.(1)无解;（2）x=1912;(3)x=-2;(4)无解.22.应提高60km/h23.(1)x≠检测站1.x≠32,x=-23.2.x≠0且x≠4.1第1课时8.a·10%+b·15%+c·5%a+b+c (a,b,c为甲、乙、丙三种汽油原价)第2课时4.24.3第1课时第2课时4.41~2.略.3.(1)平均直径都是20 mm;(2)小明.4.乙地;甲地温差比乙地大.5.（1）平均身高都是178 cm;(2)图略.甲队整齐.6.(1)x甲=1.69 m,x乙=1.68 m;(2)图略.甲比较稳定.4.5第1课时第2课时1.乙2.D3.（1）略;(2)大刚的平均数为13.35,方差为0.004;小亮的平均数为13.3，方差为0.02.大刚成绩好.4.（1）x苹果=8，x香蕉=8，S2苹果=9，S2香蕉=1.333；（2）略;（3）9月份多进苹果.5.S2=1n［(x1-x)2+(x2-x)2+…+(xn-x)2］=1n［x21+x22+…+x2n-2x(x1+x2+…+xn)+nx2］=1n［x21+x22+…+x2n-2nx(x1+x2+…+xnn+nx2)］=1n［x21+x22+…+x2n-nx2］.4.6第四章综合练习℃；（2）20.8℃;(3)146天.13.乙成绩稳定检测站℃12.（1）甲班：平均分24，方差5.4;乙班中位数24,众数21，方差19.8;(2)甲班42人，乙班36人;（3）甲班.综合与实践略.5.15.21.略.2.不正确.如正方形与菱形.3.小亮不对；小莹说法正确.4.不正确.如2≠-2,但22=(-2)2.5.不正确;t=20t1+30t220+30.5.31~3.略.4.C5.直角定义;余角定义;对顶角相等；等量代换；余角定义.6.（1）C,E,F,G;(2)E;(3)K;(4)略.7.C5.4∠D；内错角相等，两直线平行；（2）∠DEC；AB∥DE.同位角相等，两直线平行.4.已知：∠CBE;两直线平行，同位角相等;已知,∠CBE;等量代换；内错角相等，两直线平行.5.略.6.（1）如果两个角相等，那么这两个角是同角或等角的补角.真命题；（2）如果三角形中有两个角是锐角,那么第三个角是钝角，假命题，如∠A=80°，∠B=70°，∠C=30°.7.（1）延长AE与CD相交于点G.∵AB∥EF.∴∠A+∠AEF=180°.∵AB∥CD,∴∠A+∠G=180°.∴∠A+∠AEF=∠A+∠G,∠AEF=∠G.∴EF∥CD;(2)360°.5.5第1课时∠B=∠C,∠AOB=∠DOC.5.∠1＞∠ACB＞∠26.略.7.(1)∠A逐渐减小,∠B,∠C逐渐变大;若点A向下运动,变化相反;(2)α=β+γ.5.5第2课时1.(1)∠B=∠DAC;(2)∠A=∠D;∠CGE+∠B=180°∠1=∠C+∠CDE,∠2=∠C+∠CED,∠1+∠2=180°.6.(1)∠EFD=90°-∠FED=12(∠A+∠B+∠C)-(∠B+12∠A)=12(∠C-∠B);(2)不变.5.6第1课时∠A=∠D；（3）∠C=∠F.4.（1）△ABE≌△DCF(SAS),△ABF≌△DCE(SAS),△BEF≌△CFE;(2)略.5.△AFC≌△BED(ASA)6.取EF的中点M，连接GM，并延长交FH于点N.GN分别交AD,BC于点P,Q.△PEM≌△QFM.沿GN将道路取直即可.第2课时1.平行2.90°∵∠ABD=∠ADB,∴∠CBD=∠CDB.∴BC=DC.6.△ABD与△ACD都是等腰三角形，BD=AD=DC.7.△ABD≌△ACE（SAS）.∠A=∠CAE=60°.∴△ADE为等边三角形.8.∵△AEB≌△BDA(ASA).∴AE=BD,EB=DA,CE=CD,EF=DF.AF=BF.第3课时1.=2.①②③3.A4.略.5.△ABD≌△AED(SAS),∴AB=AE.DC=AB+BD=AE+DE,DC=DE+EC,∴AE=EC.∴点E在线段AC的垂直平分线上.6.（1）∠A≠∠C.因为△ABD与△CBD不全等；（2）∠A＞∠C.因为AB＜BC，在BC上取BA′=BA.△ABD≌△A′BD.∠A=∠BA′D.∠BA′D ＞∠C,∴∠A＞∠C；(3)当AB=CB时.∠A=∠C;当AB＜BC时，∠A＞∠C；当AB＞BC时，∠A＜∠C.第4课时△ADE≌△ADF.AE=AD.△AEF为等腰三角形.6.△BEO≌△BFO（AAS）,△BED≌△BFD（SAS）.△EOD≌△FOD（SSS）或(SAS).7.DE=BD-CE.由DE∥BC.∠BOD=∠OBC=∠OBD.∴BD=OD.又∠OCE=∠OCF=∠BOC+∠OBC=∠BOC+∠BOE=∠COE.∴CE=OE.DE=OD-OE=BD-CE.第5课时△ABC即为所求.5.连接AC.Rt△ABC≌RtADC(HL).∴BC=DC.Rt△BCE≌Rt△DCF(HL).6.连接AF，BF.△AEF≌△BEF△AFC≌△BFD(SAS).7.(1)Rt△OBD≌Rt△OCE(HL);(2)Rt△OBD≌△OCE(HL);(3)相等.第五章综合练习°8.∠2=∠1.∴∠2=∠C,AB∥CD.9.延长EF交BC于点G.∵∠2=∠4，∴AB∥EF.∠3=∠B=∠EGC.∴DE∥BC.∴∠AED=∠ACB.10.∠ABE=∠FBD,∠ABE+∠AEB=90°,∠FBD+∠AFE=90°.∴∠AEB=∠AFE.∴AE=AF.11.△ACE≌△BDE(AAS),∴EC=ED.12.(1)∠D=∠AEC(同角的余角相等).△ACE≌△CBD.∴AE=CD;(2)BD=CE=12AC=6 cm.13.(1)Rt△ADE≌Rt△ADF;(2)DB=DC,Rt△DBE≌Rt△DCF(HL).14.(1)略;（2）连接BD.∠DBC=12∠B=30°.∵∠CDE=∠CED.∴∠CED=12∠ACB=30°.∴△DBE为等腰三角形.∵DM⊥BE,∴BM=EM.15.△BPD≌△BDC(SAS),△BCD≌△ACD(SSS).∠P=∠BCD=∠ACD=12∠ACB=30°.16.(1)作DF⊥AB，垂足为点E.AC=AE,DE=DC.∵∠B=∠A=45°,∴BE=DE.∴AB=AE+BE=AC+CD.(2)(1)中的等量关系仍成立.∵∠ACB＞∠B,∴AB＞AC.在AB上截取AG=AC.分别作DF⊥AC,DE⊥AB.△DCF≌△DGE.∵∠EGD=∠C=2∠B.∴∠B=∠BDG.BG=DG=DC.∴AB=AG+GB=AC+CD.检测站△ODG≌△OEG,△DPG≌△EPG;△ODP≌△OEP,HL或AAS.5.略.6.FA=FD,∠ADF=∠DAF=∠DAC+∠CAF.∵∠DAC=∠BAD.∴∠B=∠ADF-∠BAD=∠DAF-∠DAC=∠CAF.7.(1)略；（2）∵CA=CE,∴∠CAE=∠E.∵∠ACB=∠CAE+∠E=2∠E,∠ACB=2∠BCD,∴∠E=∠BCD.CD∥AE.8.(1)①③或②③;（2）略.9.(1)△ABQ≌△PBC;(3)∠MBN=60°,△ABM≌△PBN(ASA).BM=BN.∴△BMN为等边三角形.∠MNB=∠QBC.MN∥AC.总复习题1.(3,4)，等腰2.-53.50°,60°,70°°13.-314.设每天修x m,3 600x-3 6001.8x=20.x=80 m.15.(1)中位数12℃,众数11℃⊥BC,FM⊥AD,FN⊥AE,垂足分别为点G，M，N.FM=FG=FN.17.∵∠BAD=∠BDA,∴AB=DB=CD.∵BE=DE,∴△ABE≌△ADE.AB=AD,△ABD为等边三角形.连接CF.△AEC≌△FEC.∵∠ACF=60°,∴△AFC为等边三角形.∴AF=AC,AE=12AC.18.延长BO交AC于点D.∠BOC=110°.19.作CF⊥AC，交AD延长线于点F.∵∠BAC=90°，AD⊥BM.∴∠ABM=∠MAE.∵AB=AC,∴△ABM≌△CFA.∠1=∠F.AM=CF.∵AM=CM,∴CF=CM.∠FCD=45°=∠MCD.∴△FCD≌△MCD(SAS).∠2=∠F=∠1.总检测站△ABC≌△ABD,△ACE≌△ADE,△CEB≌△12.(1)x=-2;(2)无解.13.30 m14.∵△ABE≌△ACE,∴BE=CE,BD=CD.△BDE≌△CDE(SSS).15.(1)①②③④,①③②④,①④②③,②③①④,②④①③.(2)略.≤≥＜＞×≠÷′△∠°αβ⊥∥∵∴△≌△S△ACC′。

3.6 比和比例一、选择题1．如果43=y x ，那么下列等式不成立的是（ ） A ．73=+y x x B ．41=-y y x C ．4343=++y x D ．4x =3y 2．如果a ，b 是不等于0的实数，2a =3b ，那么下列等式正确的是（ ）A ．32=b aB ．23=b aC ．34=+b b aD ．35=+b b a 3．如果5x =6y ，那么下列结论正确的是（ ）A ．x ：6=y ：5B ．x ：5=y ：6C ．x =5，y =6D ．x =6，y =54．下列线段能成比例的是（ ）A ．3cm ，6cm ，8cm ，9cmB ．3cm ，5cm ，6cm ，9cmC ．3cm ，6cm ，7cm ，9cmD ．3cm ，6cm ，9cm ，18cm5．已知线段a ，b ，c ，d ，如果ab =cd ，那么下列式子一定正确的是 （ ）A ．d b c a =B ．c b d a =C ．d b c a =D ．dc b a = 二、填空题6．若a ，b ，c 满足643c b a ==，a ，b ，c 都不为0，则b c b a -+= ． 7．若32===f e d c b a ，则fd be c a 3232+-+-= ． 8．已知线段a =4，b =1，如果线段c 是线段a ，b 的比例中项，那么c = ．三、解答题9．已知032≠=b a ，求b ab ab a b a 2222---的值． 10．已知非零实数a ，b ，c 满足13125c b a ==，且a +b =34，求c 的值． 11．已知线段x ，y ，z 满足x +y +z =54，且432z y x ==，求x ，y ，z 的值． 12．已知线段a =0.3m ，b =60cm ，c =12dm ．（1）求线段a 与线段b 的比．（2）如果线段a ，b ，c ，d 成比例，求线段d 的长．（3）b 是a 和c 的比例中项吗？为什么？答案一、1．B 【分析】A ．∵43=y x ，∴73=+y x x ，故此选项不符合题意；B ．∵43=y x ，∴41-=-y y x ，故此选项符合题意；C ．∵43=y x ，∴4343=++y x ，故此选项不符合题意；D ．∵43=y x ，∴4x =3y ， 故此选项不符合题意．故选B ．2．B 【分析】A ．由32=b a 得，3a =2b ，故此选项错误；B ．由23=b a 得，2a =3b ，故此选项正确；C ．由34=+b b a 得，3（a +b ）=4b ，整理得，3a =b ，故此选项错误；D ．由35=+b b a 得，3（a +b ）=5b ，整理得，3a =2b ，故此选项错误．故选B ．3．A 【分析】∵5x =6y ，∴56y x =，故选项A 正确．故选A ． 4．D 【分析】根据如果其中两条线段的乘积等于另外两条线段的乘积，那么四条线段叫成比例线段．所给选项中，只有D 符合，3×18=6×9．故选D ．5．C 【分析】∵ab =cd ，且c ≠0，b ≠0，∴d b c a =．故选C ． 二、6．27【分析】设643c b a ===k ，则a =3k ，b =4k ，c =6k ．把a =3k ，b =4k ，c =6k 代入，得b c b a -+=k k k k 4643-+=27． 7．32【分析】∵32===f e d c b a ，∴b =1.5a ，d =1.5c ，f =1.5e ．∴f d b e c a 3232+-+-=e c a e c a 5.435.132+-+-=32． 8．2【分析】根据比例中项的概念结合比例的基本性质，得比例中项的平方等于两条线段的乘积．则c 2=4×1，解得c =±2（线段是正数，负值舍去），故c =2．三、9.解：∵032≠=b a ， ∴设a =2x ，b =3x ，则原式=x x x x x x x x 932322223222-⨯⨯⨯-⨯⨯-=-1+4=3． 10．解：设13125c b a ===k （k ≠0）， 则a =5k ，b =12k ，c =13k ．∵a +b =34，∴5k +12k =34，解得k =2．∴c =13k =13×2=26．11．解：设432z y x ===k （k ≠0），则x =2k ，y =3k ，z =4k ．∵x +y +z =54，∴2k +3k +4k =54，解得k =6． ∴x =2×6=12，y =3×6=18，z =4×6=24．12．解：（1）∵a =0.3m=30cm ，b =60cm ， ∴a ：b =30：60=1：2．（2）∵线段a ，b ，c ，d 是成比例线段， ∴dc b a =． ∵c =12dm=120cm ， ∴d12021=，∴d =240cm ． （3）是．理由如下：∵b 2=3600，ac =30×120=3600， ∴b 2=ac ，∴b 是a 和c 的比例中项．。

2.6 等腰三角形一、选择题1. 下列说法正确的是（）A. 等腰三角形的高、中线、角平分线互相重合B. 顶角相等的两个等腰三角形全等C. 等腰三角形一边不可以是另一边的两倍D. 等腰三角形的两个底角相等2. 已知∠AOB=30°，点P在∠AOB的内部，P1与P关于OB对称，P2与P关于OA对称，则P，P1，P2三点构成的三角形是（）A. 直角三角形B. 钝角三角形C. 等腰三角形D. 等边三角形3. 等腰三角形的对称轴，最多可以有（）A. 1条B. 3条C. 6条D. 无数条4. 下列判断不正确的是（）A. 等腰三角形的两底角相等B. 等腰三角形的两腰相等C. 等边三角形的三个内角都是60°D. 两个内角分别为120°，40°的三角形是等腰三角形5. 下列轴对称图形中对称轴最多的是（）A. 等腰直角三角形B. 正方形C. 有一个角为60°的等腰三角形D. 圆二、填空题6. 若等腰三角形的一个角是110°，则它的底角为_______°．7. 若等腰三角形的腰长是6，底边长为3，则周长为__________．8. 若等腰三角形的一个底角为50°，则此等腰三角形的顶角为_________．9. 在△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A=________°．10. 若等腰三角形的周长为13cm，其中一边长为5cm，则该等腰三角形的腰长为_____cm．11. 若等腰三角形一腰上的中线把这个三角形的周长分成15和12，则这个三角形的底边长为_________．12. 腰长为12㎝，底角为15°的等腰三角形的面积为________cm2．答案一、1. D【分析】A．等腰三角形的高、中线、角平分线互相重合，错误；B．顶角相等的两个三角形全等，错误；C．等腰三角形一边不可以是另一边的两倍，错误，D．等腰三角形的两个底角相等，正确．故选D．2. D【分析】根据轴对称的性质，进行轴对称变换时对应线段相等，对应角相等，即OP1= OP=OP2，∠P1OB=∠BOP，∠POA=∠AOP2，则∠P1OP2=∠P1OB+∠BOP+∠POA+∠AOP2= 2（∠BOP+∠POA）=2∠AOB=60°．已知两边相等且一个内角为60°的三角形为等边三角形．故选D.3. B【分析】一般等腰三角形有一条，即底边上的中线所在直线；若是特殊的等腰三角形即等边三角形，则有三条，即每条边上的中线所在直线．故选B．4. D【分析】根据等腰三角形的性质可知，等腰三角形的两腰相等，两底角相等；根据等边三角形的性质可知，三个内角都相等，都等于60°；根据三角形的内角和为180°可知，两个内角分别为120°，40°的三角形的第三个角为20°，不是等腰三角形.故选D.5. D【分析】根据轴对称图形的特点可知，等腰直角三角形只有一条对称轴，是底边上的中线所在的直线；正方形有四条对称轴，是两条对角线所在直线和两对边的中点所在的直线；有一个角为60°的等腰三角形是等边三角形，则有三条对称轴，是三边的中垂线；圆有无数条对称轴，是直径所在的直线.故选D.二、6. 35【分析】①当这个角是顶角时，底角=（180°-110°）÷2=35°；②当这个角是底角时，另一个底角为110°．因为110°+110°=240°，不符合三角形的内角和定理，所以舍去．7. 15【分析】根据等腰三角形的特点可知，其三边长分别为6，6，3，因此周长为6+6+3=15.8. 80°【分析】先根据等腰三角形的两底角相等可知，两底角分别为50°，50°．再根据三角形的内角和可得等腰三角形的顶角为80°.9. 4或3 【分析】当5cm是等腰三角形的底边长时，则其腰长是（13-5）÷2=4（cm），能够组成三角形；当5cm是等腰三角形的腰时，则其底边是13-5×2=3（cm），能够组成三角形．10. 36°【分析】如答图，设∠A=x．∵AD=BD，∴∠ABD=∠A=x.∵BD=BC，∴∠BCD=∠BDC=∠ABD+∠A=2x.∵AB=AC，∴∠ABC=∠BCD=2x，∴∠DBC=x.∵x+2x+2x=180°，∴x=36°，∴∠A=36°.（第10题答图）11. 7或11【分析】设这个等腰三角形为△ABC，AB，AC是腰，BC是底边，BD是AC上的中线，如答图.分两种情况：①AB+AD =15，CD+BC=12.∵AD=CD=AC=AB，∴AB+AB =15，∴AB=10，∴10×+BC =12，∴BC=7.∵10+10=20 >17，∴可以构成三角形（三角形两边之和大于第三边），此时底边长为7.②AB+AD =12，CD+BC =15.∵AD=CD=AC=AB，∴AB+AB=12，∴AB=8，∴8×+BC=15，∴BC=11.∵8+8=16>11，∴可以构成三角形（三角形两边之和大于第三边），此时底边长为11.（第11题答图）12. 36【分析】如答图，△ABC是等腰三角形，且∠BAC=∠B=15°，AC=BC=12cm．过点A 作DA⊥BC的延长线于点D．因为在Rt△ADC中，∠DCA=30°，AC=12cm，所以DA=AC= 6（cm）．所以根据三角形的面积公式，得S△ABC=BC DA=36（cm2）．（第12题答图）。

读书破万卷下笔如有神青岛版数学练习册八年级上册参考答案1.11.略.2.DE,∠EDB，∠E.3.略.4.B5.C6.AB=AC,BE=CD,AE=AD,∠BAE=∠CAD7.AB∥EF,BC∥ED.8.(1)2a+2b;(2)2a+3b;(3)当n为偶数时，n2(a+b);当n为奇数时，n-12a+n+12b.1.2第1课时1.D2.C3.(1)AD=AE;(2)∠ADB=∠AEC.4.∠1=∠25.△ABC≌△FDE(SAS)6.AB∥CD.因为△ABO≌△CDO(SAS).∠A=∠C.7.BE=CD.因为△ABE≌△ACD(SAS).第2课时1.B2.D3.(1)∠ADE=∠ACB；(2)∠E=∠B.4.△ABD≌△BAC(AAS)5.(1)相等，因为△ABE≌△CBD(ASA);(2)DF=EF,因为△ADF≌△CEF(ASA).6.相等，因为△ABC≌△ADC(AAS).7.(1)△ADC≌△AEB;(2)AC=AB,DC=EB,BD=EC;∠ABE=∠ACD,∠BDO=∠CEO,∠BOD=∠COE.第3课时1.B2.C3.110°4.BC的中点.因为△ABD≌△ACD(SSS).5.正确.因为△DEH≌△DFH(SSS).6.全等.因为△ABD≌△ACD(SSS).∠BAF=∠CAF.7.相等，因为△ABO≌△ACO(SSS).1.3第1课时即为AOC，则∠C上取一点BO，在BO延长,α∠AOB=作∠).7.略1~6(读书破万卷下笔如有神所求.8.作∠AOB=∠α,以OB为边，在∠AOB的外部作∠BOC=∠β；再以OA为边，在∠AOC的内部作∠AOD=∠γ,则∠DOC即为所求.第2课时1.略.2.（1）略;（2）全等(SAS).3.作BC=a-b;分别以点B、C为圆心，a为半径画弧，两弧交于点A;连接AB，AC，△ABC即为所求.4.分四种情况：（1）顶角为∠α,腰长为a;(2)底角为∠α，底边为a;(3)顶角为∠α，底边为a;(4)底角为∠α，腰长为a.((3),(4)暂不作). 第3课时1.四种：SSS,SAS,ASA,AAS.2.作线段AB;作∠BAD=∠α,在∠BAD同侧作∠ABE=∠B;AD与BE相交于点C.△ABC即为所求.3.作∠γ=∠α+∠β;作∠γ的外角∠γ′;作△ABC,使AB=c.∠A=∠γ′，∠B=∠α.4.作∠γ=180°-∠β；作△ABC,使BC=a,∠B=∠α,∠C=∠γ. 第一章综合练习1.A2.C3.C4.AB=DC或∠ACB=∠DBC或∠A=∠D.5.△ACD≌△BDC,△ABC≌△BAC.6.△ABC≌△CDE(AAS)7.4分钟8.△BOC′≌△B′OC(AAS)9.略10.相等.△BCF≌△EDF(SAS).△ABF≌△AEF(SSS)检测站1.B2.B3.20°4.∠BCD5.相等.△ABP≌△ACP（SSS）,△PDB≌△PEC(AAS).6.略2.1.°;30°.4.B5.C6.(1)(2)(4)7.20略1~3.读书破万卷下笔如有神8.略2.2第1课时1~2.略3.C4.D5.略6.66°7.（1）AA′∥CC′∥BB′,且AA′⊥MN,BB′⊥MN,CC′⊥MN.(2)5 cm8.(1)DE⊥AF;(2)略.第2课时1.(-2,-3),(2,3).2.3,-43.(3,2)4.B5~6.略7.（1）(-a,b);(2)当n=4k+1时，在第一象限，n=4k+2时，在第四象限，n=4k+3时，在第三象限，n=4(n+1)时，在第二象限，k 为非负整数.2.31~3.略.4.B5.C.6.略.7.4条.8.略.2.4第1课时1.略.2.CM=DM,CE=DE.3.C4.∠A=∠B,∠ACD=∠BCD,∠ADC=∠BDC.5~6.略.7.连接BM,PB＜PM+MB，∵MB=MA，∴PB＜PA.第2课时1.作一条线段的垂直平分线2.D3~5.略.6.分别作点A关于OM，ON的对称点D，E.连接DE，分别交OM，ON于点B，C.连接AB，AC，则△ABC的周长最小.2.51.略.2.103.D4.C5.作∠AOB的平分线交MN于点P.则P即为所示.6.（1）DE=DC,AE=BE,BE=BC;(2)7.7.（1）△ADO≌△AEO(AAS),△BOD ≌三条直线围成的三角形的三.处2.8.4∠1=∠COE(ASA),OB=OC;(2)△．读书破万卷下笔如有神内角平分线的交点，及任一内角平分线与其他两个角的外角平分线的交点.2.6第1课时1.略.2.35°,35°.3.50°,80°或65°,65°.4.C5.B6.∠EBC=36°,∠C=∠BEC=72°.7.△ACD≌ABD(SSS),∠CAG=∠BAG.AG是等腰三角ABC的顶角平分线.∴AD垂直平分BC.8.99°第2课时1.略.2.△ABE,△ECD,△EBC.3.C4.△DBE是等腰三角形.因为∠B=∠C=∠DEB.5.△AED是等腰三角，因为∠EAD=∠BAD=∠ADE.6~7.略. 第3课时1.略.2.1，3.3.C4.△ADE是等边三角形.因为三个角都等于60°.5.略.6.任两边的垂直平分线的交点即为点O.7.BE=DC.因为△ADC≌△ABE(SAS).第二章综合练习1.GH,∠E,EO.1.B(4,-3);C(-4,3);6;8.3.24.45.64°;58°.6.D7.C8.A9.A10 .(1)AB=AD,AE=AC,BC=DE,BF=DF,EF=CF;∠BAC=∠DAE,∠B=∠D,∠C=∠E,∠BAE=∠DAC,∠EAF=∠CAF,∠BFE=∠DFC,∠BAF=∠DAF. (2)△AEF与△ACF，△ABF与△ADF都关于直线MN成轴对称.11.△ABC与△A′B′C′关于y轴对称.12.△ACE≌△DCB（SAS）.AE=BD.又∠HGE=∠CGB.∠HEG=∠CBG.∠HGE+∠HEG=∠CGB+∠CBG=90°.∠②;个1为底边的等腰三角形可作BC①以.个BD.13.4⊥.AE°EHG=90．读书破万卷下笔如有神以BC为腰的等腰三角形可作3个.检测站1.60°2.AP;PC,AP;∠CAP.3.1；7.4.55°,55°或70°,40°.5.AC,∠C,△ABD.6.B7.B8.B9.D10.A11.略.12.∠BAC=60°,∠C=90°,∠B=30°.13.∵△ABC≌△BAD.∠CAB=∠DBA,∴△EBA是等腰三角形.14.（1）5;(2)80°.15.∠ACD=180°-A2,∠BCE=180°-B2,∠ACB=90°.∴∠ACD+∠BCE=90°+∠DCE.∠DCE=45°.3.1第1课时1.B≠0；B=0;A=0且B≠0.2.≠23.1,0.4.B5.D6.B7.x=-1且y≠08.19.ba-5;400.10.a=-1.11.略.12.n+13n-2第2课时1.略2.（1）2abc2;(2)xy(x+y);(3)a(a+b);(4)2x(x+y).3.A4.C5.B6.x ≠1且x≠07.当a≠0时，a2a=12;当m≠0，n≠0时，n2mn=nm.8.M=-3x(a+x)2;x≠0,-a,a.9.5a2-1030a2-2a3.21.略.2.2a(b-a)3.C4.C5.B6.(1)3y2x;(2)-1(x-y)2;(3)a+22-a;(4)2a2a-3b.7.-78.a-b+ca+b+c9.略.3.3读书破万卷下笔如有神1~3.略.4.(1)-1ab;(2)ab18c;(3)4yx;(4)4yx.5.D6.C7.(1)a+1;(2)-b3x;(3)xy2;(4)aa+b8.-139.略.3.41.略.2.6a2b2,ab,3b,2a.3.(x+2)(x-2)24.D5.D6.2b24a2b2c2,3ac324a 2b2c2;(2)5(a-b)215a(a+b)(a-b),3(a+b)215(a+b)(a-b);(3)3x-2y( 3x+2y)(3x-2y),2(3x+2y)(3x-2y);(4)(x+1)2(x-1)(x+1)2,x(x-1)(x+1)(x-1)(x+1)2,x-1(x-1)(x+1)2.7.(m-n)2m-n,-mnm-n.8.cyz(b-c)(c-a)xyz(a-b)(b-c)(c-a),axz(a-b)(c-a)xyz(a-b)(b-c)(c-a),bxy(a-b)(b-c)xyz(a-b)(b-c)(c-a).9.(1)把前一个分式的分子，分母同乘-a2b即得下一个分式;(2)-a12b8a13b6.(3)（-1）na2n-2bn+1(-1)n+1a2n-1bn-1.3.5第1课时1.略.2.（1）-b2a;(3)2aa-b.3.C4.D5.(1)y2x;(2)x+2;(3)3.6.(1)2+x;(2)3abb-a .7.x+2.8.原式=1.第2课时1.略.2.b2-4c4a3.-4(x+2)(x-2)4.C5.D6.D7.(1)3c3-4a2b12ab2c2;(2)6x2+xy+7y242x2y2;(3)2mn-m2n2-m2.8.-659.(1)11-a;(2)x2.10.1(x-1)(x-2),1(x-2)(x-3),1(x-3)(x-4),1x-100.读书破万卷下笔如有神第3课时1.C2.D3.B4.(1)a-bb;(2)x+2.5.126.∵ca+b＜1.∴c2(a+b)2＜ca+b3.6第1课时1.(1)7x4y;(2)b2a;(3)2x-y;(4)a+ba-b2.ala+b,ala+b.3.23;49;13.4.A5.C6.(1)2;(2)2;(3)4.7.68.(1)xyx+y(天);(2)甲：myx+y(元),乙：mxx+y(元).9.（1）ba;(2)b-10a-10,b+10a+10;(3)b-10a-10＜ba＜b+10a+10.第2课时1.略.2.8∶93.124.245.C6.D7.8a38.a-b=-39.260 mm10.5211.-5.第3课时1.略.2.2∶33.33124.1 m5.10∶15∶216.D7.B8.x∶y∶z=(a+b)2∶(a2-b2)∶(a-b)29.34a,a,54a.10.6,8,10.11.63人，192人，45人.3.7第1课时1.略.2.去分母，将分式方程转化为整式方程求解，然后验根.3.-124.-325.B6.B7.D8.30x-2-30x=12.9.(1)x=4;(2)x=0.10.m=-18711.(1)x=5;(2)a=6.第5个方程;（3）1+x2x=n+1x,x=2n+1.第2课时1.略.2.无解3.C4.B5.不正确，错在第3步，没有检验;方程无）无解；3（;无解.6.(1)x=3;(2)解．读书破万卷下笔如有神（4）无解.7.a=-58.(1)①x=1;②x=2;③x=3;(2)方程1x-2-1x-3=1x-5-1x-6的解为x=4;方程1x+2-1x+1=1x-1-2x-2的解为x=0.第3课时1.略.2.12010-x-12010=33.16+1x=13.4.D5.(1)设去年每间屋的租金为x元，9.6x=10.2x+500;(2)8 000元.6.4 km/h7.37.5 km/h8.1.5 t9.(1)设预定工期为x天，4x+xx+5=1,x=20（天）.(2)采取联合施工4天，然后由乙单独施工的方案省工程费.第三章综合练习1.a≠32；x=-1.2.m=3,m≠1.3.24.125.a∶b=b∶c,c∶b=b∶a,ac=b26.127.3∶4∶58.39.C10.C11.A12.D13.B14.D15.616.a+b=0.17.(1)-5y2ax;(2)-x3 y;(3)2xy;(4)3x+1;(5)1681x4y4;(6)2a2b2;(7)a-3a2-13;(8)-1a+1.18.(1）220.218S2=1∶-715;(2)310.19.S1∶km/h23.(1)x60 无解.22.应提高）21.(1)无解;（2x=1912;(3)x=-2;(4)分两次清残留农药比为11+y;）原式2=1.24.1次清洗.1-1≠，0，；（0.＞，11+y-4(2+y)2=y2(1+y)(2+y)224洗后，残留农药比为：（2+）. 2种方案好第检测站-53.164.29≠x且0≠32,x=-23.2.x≠1.x读书破万卷下笔如有神5.326.D7.C8.B9.B10.相等11.（1）mn-m;(2)ab;(3)2x-1x.12.11-x;-1.13.(1)x=4;(2)无解;(3)x=2.14.a=-115.14516.3617.28天4.1第1课时1~2.略.3.3.44.C5.B6.总产量1 757 t;平均产量8.53 t.7.9 000 m3 8.a·10%+b·15%+c·5%a+b+c (a,b,c为甲、乙、丙三种汽油原价) 第2课时1.820，920，320.2.86 km/h3.C4.(1)甲；（2）乙.5.9.9%6.(1)1.84 kg;(2)3 312 kg.4.21.略.2.94.53.C4.x=225.平均数：1 626，中位数1 680.6.26 cm7.9或108.（1）85.5;(2)41人;（3）高低分悬殊大.4.3第1课时1.2;1与2.2.7与83.B4.平均数、中位数、众数都是21岁5.平均数为2,中位数是3，众数是1.6.（1）3个；（2）32 000个.7.（1）甲组：平均数80，中位数80，众数90；乙组：平均数80.2，中位数80，众数70;（2）略.第2课时1.72.A3.平均数13千瓦时，中位数22.5千瓦时，众数10千瓦时.4.（1）众数55 min,中位数55 min;(2)平均数为55 min.符合学校的要求.5.甲当选4.4读书破万卷下笔如有神1~2.略.3.(1)平均直径都是20 mm;(2)小明.4.乙地;甲地温差比乙地大.5.（1）平均身高都是178 cm;(2)图略.甲队整齐.6.(1)x甲=1.69 m,x乙=1.68 m;(2)图略.甲比较稳定.4.5第1课时1.1.22.10,26.3.10,1.8.4.A5.D6.S2甲=0.055,S2乙=0.105;果农甲.7.（1）x=3,S2=2;(2)x=13,S2=2；(3)x=30,S2=200.8.（1）xA=0，S2A=2.29;(2)取-2,-1,0,3,0;xB=0,S2B=2.8.第2课时1.乙2.D3.（1）略;(2)大刚的平均数为13.35,方差为0.004;小亮的平均数为13.3，方差为0.02.大刚成绩好.4.（1）x苹果=8，x香蕉=8，S2苹果=9，S2香蕉=1.333；（2）略;（3）9月份多进苹果.5.S2=1n［(x1-x)2+(x2-x)2+…+(xn-x)2］=1n［x21+x22+…+x2n-2x(x1+x2+…+xn)+nx2］=1n［x21+x22+…+x2n-2nx(x1+x2+…+xnn+nx2)］=1n［x21+x22+…+x2n-nx2］.4.61.C2.略3.甲4.相差75.x甲=178,S2甲=0.6;x乙=178,S2乙=1.8.6.(1)x甲=200.8,S2甲=7.96;x乙=201.5,S2乙=38.05;(2)甲. 第四章综合练习1.1.62 m2.8,8,8,1.23.20,18,184.4,3.5.b＞a＞c6.C7.D8.C9.(1)甲组：x甲=3.中位数2，众数1，S2甲=7.67;乙组：x乙=3,中位数3，众数3，S2乙=1.67;(2)乙组.10.（1）x=2 x=2,）1（.11.）略2（元；6001 元，中位数为800众数为),元135.7(读书破万卷下笔如有神众数为3，中位数为2;（2）68人.12.（1）22℃；（2）20.8℃;(3)146天.13.乙成绩稳定检测站1.2.12元2.23.64.31.8℃,4.965.D6.C7.D8.90.6分9.(1)x甲=5.6 cm,S2甲=1.84,x乙=5.6 cm,S2乙=1.04.(2)乙苗长的比较整齐.10.（1）x甲=7，S2甲=0.4,x乙=7,S2乙=2.8;(2)甲.11.612.（1）甲班：平均分24，方差5.4;乙班中位数24,众数21，方差19.8;(2)甲班42人，乙班36人;（3）甲班.综合与实践略.5.11~2.略.3.面积相等的三角形，是全等三角形，假.4.D5.D6.B7~9.略.5.21.略.2.不正确.如正方形与菱形.3.小亮不对；小莹说法正确.4.不正确.如2≠-2,但22=(-2)2.5.不正确;t=20t1+30t220+30.5.31~3.略.4.C5.直角定义;余角定义;对顶角相等；等量代换；余角定义.6.（1）C,E,F,G;(2)E;(3)K;(4)略.7.C5.4DE.∥AB；DEC）∠2（；内错角相等，两直线平行；D）∠1（1.B2.C3.读书破万卷下笔如有神同位角相等，两直线平行.4.已知：∠CBE;两直线平行，同位角相等;已知,∠CBE;等量代换；内错角相等，两直线平行.5.略.6.（1）如果两个角相等，那么这两个角是同角或等角的补角.真命题；（2）如果三角形中有两个角是锐角,那么第三个角是钝角，假命题，如∠A=80°，∠B=70°，∠C=30°.7.（1）延长AE与CD相交于点G.∵AB∥EF.∴∠A+∠AEF=180°.∵AB∥CD,∴∠A+∠G=180°.∴∠A+∠AEF=∠A+∠G,∠AEF=∠G.∴EF∥CD;(2)360°.5.5第1课时1.略.2.C3.D4.∠B=∠C,∠AOB=∠DOC.5.∠1＞∠ACB＞∠26.略.7.(1)∠A逐渐减小,∠B,∠C逐渐变大;若点A向下运动,变化相反;(2)α=β+γ.5.5第2课时1.(1)∠B=∠DAC;(2)∠A=∠D;∠CGE+∠B=180°.2.D3.B4.略.5.∠1=∠C+∠CDE,∠2=∠C+∠CED,∠1+∠2=180°.6.(1)∠EFD=90°-∠FED=12(∠A+∠B+∠C)-(∠B+12∠A)=12(∠C-∠B);(2)不变.5.6第1课时1.D2.C3.（1）BC=EF或BE=CF；（2）∠A=∠D；（3）∠C=∠F.4.（1）△ABE≌△DCF(SAS),△ABF≌△DCE(SAS),△BEF≌△CFE;(2)略.5.△AFC≌△BED(ASA)6.取EF的中点M，连接GM，并延长交FH于点N.GN 分别交AD,BC于点P,Q.△PEM≌△QFM.沿GN将道路取直即可.第2课时BC=DC.6.∴CDB.∠CBD=∴∠ADB,∠ABD=∵∠3.B4.D5.°2.90平行1.读书破万卷下笔如有神△ABD与△ACD都是等腰三角形，BD=AD=DC.7.△ABD≌△ACE（SAS）.∠A=∠CAE=60°.∴△ADE为等边三角形.8.∵△AEB≌△BDA(ASA).∴AE=BD,EB=DA,CE=CD,EF=DF.AF=BF.第3课时1.=2.①②③3.A4.略.5.△ABD≌△AED(SAS),∴AB=AE.DC=AB+BD=AE+DE,DC=DE+EC,∴AE=EC.∴点E在线段AC的垂直平分线上.6.（1）∠A≠∠C.因为△ABD与△CBD不全等；（2）∠A＞∠C.因为AB＜BC，在BC上取BA′=BA.△ABD≌△A′BD.∠A=∠BA′D.∠BA′D ＞∠C,∴∠A＞∠C；(3)当AB=CB时.∠A=∠C;当AB＜BC时，∠A＞∠C；当AB＞BC时，∠A＜∠C.第4课时1.OA=OB.2.=.三角形的三内角平分线相交于一点.3.B4.B5.△ADE≌△ADF.AE=AD.△AEF为等腰三角形.6.△BEO≌△BFO（AAS）,△BED≌△BFD（SAS）.△EOD≌△FOD（SSS）或(SAS).7.DE=BD-CE.由DE∥BC.∠BOD=∠OBC=∠OBD.∴BD=OD.又∠OCE=∠OCF=∠BOC+∠OBC=∠BOC+∠BOE=∠COE.∴CE=OE.DE=OD-OE=BD-CE.第5课时1.AB=AD或BC=DC（HL）2.D3.B4.作直线MN，过MN上一点D作MN的垂线l;在直线l上截取DA=h;以A为圆心，a为半径画弧交MN于点B，C两点;连接AB，AC.△ABC即为所求.5.连接AC.Rt△ABC≌RtADC(HL).∴BC=DC.Rt△BCE≌Rt△DCF(HL).6.连接AF，BF.△AEF≌△BEF读书破万卷下笔如有神AFC≌△BFD(SAS).7.(1)Rt△OBD≌Rt△OCE(HL);(2)Rt△OBD≌△OCE(HL);(3)相等.第五章综合练习1.A2.C3.D4.B5.D6.略.7.120°8.∠2=∠1.∴∠2=∠C,AB∥CD.9.延长EF交BC于点G.∵∠2=∠4，∴AB∥EF.∠3=∠B=∠EGC.∴DE∥BC.∴∠AED=∠ACB.10.∠ABE=∠FBD,∠ABE+∠AEB=90°,∠FBD+∠AFE=90°.∴∠AEB=∠AFE.∴AE=AF.11.△ACE≌△BDE(AAS),∴EC=ED.12.(1)∠D=∠AEC(同角的余角相等).△ACE≌△CBD.∴AE=CD;(2)BD=CE=12AC=6cm.13.(1)Rt△ADE≌Rt△ADF;(2)DB=DC,Rt△DBE≌Rt△DCF(HL).14.(1)略;（2）连接BD.∠DBC=12∠B=30°.∵∠CDE=∠CED.∴∠CED=12∠ACB=30°.∴△DBE为等腰三角形.∵DM⊥BE,∴BM=EM.15.△BPD≌△BDC(SAS),△BCD≌△ACD(SSS).∠P=∠BCD=∠ACD=12∠ACB=30°.16.(1)作DF⊥AB，垂足为点E.AC=AE,DE=DC.∵∠B=∠A=45°,∴BE=DE.∴AB=AE+BE=AC+CD.(2)(1)中的等量关系仍成立.∵∠ACB＞∠B,∴AB＞AC.在AB上截取AG=AC.分别作DF⊥AC,DE⊥AB.△DCF≌△DGE.∵∠EGD=∠C=2∠B.∴∠B=∠BDG.BG=DG=DC.∴AB=AG+GB=AC+CD. 检测站1.A2.C3.C4.三;△ODG≌△OEG,△DPG≌△EPG;△ODP≌△OEP,HL或AAS.5.略.6.FA=FD,∠ADF=∠DAF=∠DAC+∠CAF.∵∠DAC=∠BAD.∴∠B=∠ADF-∠BAD=∠DAF-∠DAC=∠CAF.7.(1)略；（2）∵CA=CE,∴∠CAE=∥BCD.CD∠E=∴∠BCD,∠ACB=2∠E,∠E=2∠CAE+∠ACB=∵∠E.∠．读书破万卷下笔如有神AE.8.(1)①③或②③;（2）略.9.(1)△ABQ≌△PBC;(3)∠MBN=60°,△ABM≌△PBN(ASA).BM=BN.∴△BMN为等边三角形.∠MNB=∠QBC.MN∥AC.总复习题1.(3,4)，等腰2.-53.50°,60°,70°.4.略.5.5，5.6.D7.C8.D9.B10.D11.(1)11-x;(2)x2-xy-2y23xy2;(3)-(1-m)2;(4)1-a.12.32°13.-314.设每天修x m,3 600x-3 6001.8x=20.x=80 m.15.(1)中位数12℃,众数11℃;(2)1.143.16.分别作FG⊥BC,FM⊥AD,FN⊥AE,垂足分别为点G，M，N.FM=FG=FN.17.∵∠BAD=∠BDA,∴AB=DB=CD.∵BE=DE,∴△ABE≌△ADE.AB=AD,△ABD为等边三角形.连接CF.△AEC≌△FEC.∵∠ACF=60°,∴△AFC为等边三角形.∴AF=AC,AE=12AC.18.延长BO交AC于点D.∠BOC=110°.19.作CF⊥AC，交AD延长线于点F.∵∠BAC=90°，AD⊥BM.∴∠ABM=∠MAE.∵AB=AC,∴△ABM≌△CFA.∠1=∠F.AM=CF.∵AM=CM,∴CF=CM.∠FCD=45°=∠MCD.∴△FCD≌△MCD(SAS).∠2=∠F=∠1.总检测站1.a-12.(1)SSS;(2)SAS;(3)HL.3.5,5,5.25.4.4,3.5.△ABC≌△ABD,△ACE≌△ADE,△CEB≌△DEB.6.C7.D8.D9.D10.B11.113 850 kg 12.(1)x=-2;(2)无解.13.30 m14.∵△ABE≌△ACE,∴BE=CE,BD=CD.△BDE≌△CDE(SSS).15.(1),,,,读书破万卷下笔如有神③.(2)略.′ACC△S⊥∥∵∴△≌△βα1.2.3.4.5.6.7.8.9.10.。

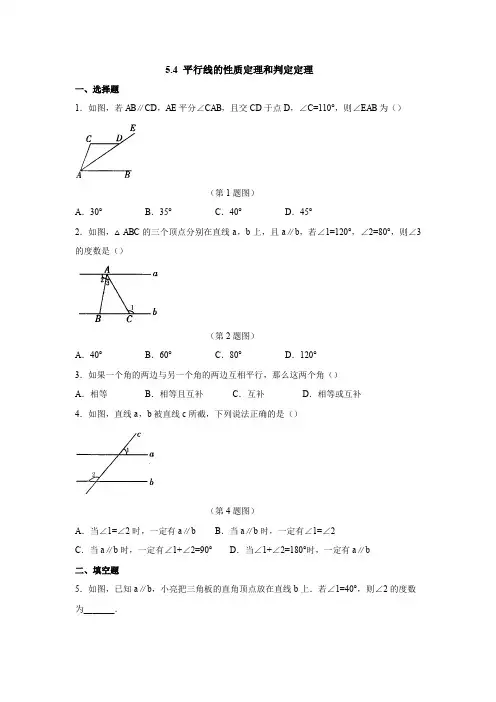
5.4 平行线的性质定理和判定定理一、选择题1．如图，若AB∥CD，AE平分∠CAB，且交CD于点D，∠C=110°，则∠EAB为（）（第1题图）A．30°B．35°C．40°D．45°2．如图，△ABC的三个顶点分别在直线a，b上，且a∥b，若∠1=120°，∠2=80°，则∠3的度数是（）（第2题图）A．40°B．60°C．80°D．120°3．如果一个角的两边与另一个角的两边互相平行，那么这两个角（）A．相等B．相等且互补C．互补D．相等或互补4．如图，直线a，b被直线c所截，下列说法正确的是（）（第4题图）A．当∠1=∠2时，一定有a∥b B．当a∥b时，一定有∠1=∠2C．当a∥b时，一定有∠1+∠2=90°D．当∠1+∠2=180°时，一定有a∥b二、填空题5．如图，已知a∥b，小亮把三角板的直角顶点放在直线b上．若∠1=40°，则∠2的度数为_______．（第5题图）（第6题图）6．如图，AB∥CD，∠A=25°，∠C=45°，则∠E的度数是_______．7．如图，在△ABC中，DE∥BC，∠A=45°，∠C=70°，则∠ADE=_______．（第7题图）（第8题图）8．如图，把矩形ABCD沿EF对折后使两部分重合，若∠1=50°，则∠AEF=_______．9．如图，将三角尺的直角顶点放在直线a上，a∥b，∠1=50°，∠2=60°，则∠3的度数为_______°．（第9题图）三、解答题10．（1）判断下列推理过程是否正确，如有错误请予改正：如图①．∵∠B=70°（已知），∠CFE=70°（已知），∴∠B=∠CFE（同位角相等）．∴AB∥CF（两直线平行）．∴∠BAF=∠CF A（内错角相等）．①②（第10题图）（2）请把下列证明过程补充完整：已知：如图②，DE∥BC，BE平分∠ABC．求证：∠1=∠3．证明：∵BE平分∠ABC（已知），∴∠1=_______（______________）．又∵DE∥BC（已知），∴∠2=_______ （______________）．∴∠1=∠3（________________）．11．如图，AD∥BC，∠B=∠C．求证：AD平分∠EAC．（第11题图）12．（1）如图，直线c，d分别被直线a，b所截，且∠3+∠4=180°，求证：∠2+∠5=180°．（2）在（1）的证明过程中，你运用了哪两个互为逆命题的真命题？（第12题图）13．如图，已知AB∥CD，∠ABE和∠CDE的平分线相交于点F，∠E=140°，求∠BFD的度数．（第13题图）答案一、1．B 2．A 3．D 4．D二、5．50° 6．70° 7．65° 8．115° 9．70 三、10．解：（1）“同位角相等”改为“等量代换”；“两直线平行”改为“同位角相等，两直线平行”；“内错角相等”改为“两直线平行，内错角相等”．（2）∠2；角平分线的定义；∠3；两直线平行，同位角相等；等量代换．11．证明：因为AD ∥BC ，所以∠EAD =∠B ，∠CAD =∠C ．又因为∠B =∠C ，所以∠EAD =∠CAD ，所以AD 平分∠EAC ．12．（1）证明：因为∠3+∠4=180°，所以c ∥d ，所以∠1+∠2=180°．又因为∠1=∠5，所以∠2+∠5=180°．（2）运用了“同旁内角互补，两直线平行”和“两直线平行，同旁内角互补”两个互为逆命题的真命题．13．解：如答图，过点G 作EG ∥AB ，则∠ABE +∠BEG =180°，∠GED +∠CDE =180°．所以∠ABE +∠BEG +∠GED +∠CDE =360°，即∠ABE +∠E +∠CDE =360°．因为∠E =140°，所以∠ABE +∠CDE =220°．因为∠ABE 和∠CDE 的平分线相交于点F ，所以∠FBE +∠FDE =21（∠ABE +∠CDE ）=110°． 又因为∠FBE +∠FDE +∠E +∠BFD=360°，所以∠BFD =110°．（第13题答图）。

青岛版数学练习册八上答案青岛版数学练习册八年级上册答案【练习一：实数的概念和性质】1. 判断题：实数包括有理数和无理数。

（√）2. 选择题：下列哪个数是有理数？A. πB. √2C. 0.33333（无限循环小数）D. √3答案：C3. 填空题：若a是有理数，b是无理数，则a+b是____。

答案：实数【练习二：代数式的运算】1. 计算题：计算下列代数式的值。

(1) (3x - 2y) - (4x + 5y)答案：-x - 7y(2) (2a + 3b)(2a - 3b)答案：4a² - 9b²2. 应用题：若x = 1，y = -1，计算下列代数式的值。

(1) 2x + 3y答案：-1(2) (x - y)²答案：4【练习三：一次方程和不等式】1. 解方程题：解下列一次方程。

(1) 3x - 5 = 2x + 4答案：x = 9(2) 2x + 3 = 5x - 7答案：x = 52. 解不等式题：解下列不等式。

(1) 2x + 5 > 3x - 2答案：x < 7(2) 3x - 4 ≤ 2x + 6答案：x ≥ 10【练习四：几何图形的性质】1. 选择题：下列哪个图形是轴对称图形？A. 三角形B. 圆形C. 正方形D. 五边形答案：B和C2. 填空题：若一个正方形的边长为a，则其面积为____。

答案：a²【练习五：函数及其图像】1. 判断题：一次函数的图像是一条直线。

（√）2. 选择题：下列哪个函数是一次函数？A. y = x²B. y = 2x + 3C. y = 1/xD. y = |x|答案：B【结束语】通过以上练习，同学们应该对八年级上册数学的基本概念、运算规则、方程解法、不等式解法以及几何图形和函数图像有了更深入的理解。

希望这些练习能帮助大家巩固知识点，提高解题能力。

如果在学习过程中遇到任何问题，欢迎随时向老师或同学求助。

2.3 轴对称图形一、选择题1．下图中的四个图案，是轴对称图形的有（）A．4个B．3个C．2个D．1个2．分别以直线l为对称轴，所作轴对称图形错误的是（）A B C D 3．如图的图形属于轴对称图形的个数是（）（第3题图）A．4 B．3 C．2 D．14．如图的图案是轴对称图形的有（）（第4题图）A．1个B．2个C．3个D．4个5．如图的扑克牌，是轴对称图形的有（）（第5题图）A．4张B．3张C．2张D．0张6．下列图形不是轴对称图形的是（）A．一条线段B．一个角C．一个平行四边形D．一个等腰梯形7．下面给出的每幅图形中的两个图案是轴对称的是（）A B C D二、填空题8．如图，将标号为A，B，C，D的正方形沿图中虚线剪开后拼成标号为P，Q，M，N的四个轴对称图形，请对号入座．P与对应，Q与对应，M与对应，N与对应．9．如图是一个风筝的图案，它是轴对称图形，量得∠B=20°，则∠E=．（第9题图）10．如图是一个风筝的图案，它是轴对称图形，EF是对称轴．∠A=90°，∠AED=130°，∠C=45°，则∠BFC的度数为．（第10题图）11．如图，一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔，如果一个球按图中的方向被击出（球可以经过多次反射），那么该球最后将落入号球袋．（第11题图）三、解答题12．判断下列图形是否为轴对称图形，如果是，画出它的对称轴．13．把如图图形补成以直线l为对称轴的轴对称图形．（第13题图）14．如图，五边形ABCDE是轴对称图形，线段AF所在的直线为对称轴，找出图中所有相等的线段和相等的角．（第14题图）答案一、1．A【分析】根据轴对称图形的概念知，这四个图形全是轴对称图形．故选A．2．C【分析】根据轴对称的定义可得C沿l对折不能重合．故选C．3．C【分析】根据轴对称图形的性质得出从左起第1，3个图形是轴对称图形，故属于轴对称图形的个数是2．故选C．4．B【分析】第一个不是轴对称图形；第二个是轴对称图形；第三个不是轴对称图形；第四个是轴对称图形，则是轴对称图形的有2个．故选B．5．D【分析】根据轴对称图形的概念知，这四张扑克都不是轴对称图形．故选D．6．C【分析】A．一条线段，是轴对称图形，不符合题意；B．一个角，是轴对称图形，不符合题意；C．一个平行四边形，不是轴对称图形，符合题意；D．一个等腰梯形，是轴对称图形，不符合题意．故选C．7．A【分析】A．是轴对称图形，故符合题意；B．不是轴对称图形，故不符合题意；C．不是轴对称图形，故不符合题意；D．不是轴对称图形，故不符合题意．故选A．二、8．B，C，A，D9．20°【分析】∵风筝的图案是轴对称图形，∴∠E=∠B=20°．10．140°【分析】如答图．∵一个风筝的图案，它是轴对称图形，EF是对称轴．∠A=90°，∠AED=130°，∠C=45°，∴∠D=90°，∠MED=65°，∴∠DEF=115°，∴∠CFN=360°-115°-90°-45°=110°，∴∠BFC的度数为2×（180°-110°）=140°．（第10题答图）11. 1【分析】如答图，该球最后将落入1号球袋．（第11题答图）三、12．解：如答图．（第12题答图）13．解：如答图．14. 解：相等的线段：AB=AE，CB=DE，CF=DF；相等的角：∠B=∠E，∠C=∠D，∠BAF=∠EAF，∠AFD=∠AFC．。

青岛版八年级上册数学课后练习题答案
推荐文章
北师大版八年级下册数学练习题答案热度：八年级下册数学练习题及答案热度：八年级数学上册竞赛练习题含答案热度：8年级下册数学课后练习题答案热度：浙教版八年级上数学期末练习题热度：心专才能绣得花，心静才能织得麻。

专心才能做好八年级数学课本习题。

小编整理了关于八年级上册青岛版数学课后练习题答案，希望对大家有帮助!
八年级上册青岛版数学课后练习题答案(一)
第11页练习
1、解：全等.
理由：因为AB = DC，∠ABC = ∠DCB，BC = CB，
所以利用“SAS”可以判定△ABC ≌ △DCB.
2、解：全等.
理由：因为AB = AD，∠A = ∠A，AE = AC，
所以可以利用“SAS”判定△ABE ≌ △ADC.
八年级上册青岛版数学课后练习题答案(二)
第16页练习
1、解：(1)全等，因为这两个等腰三角形的三条边分别相等.
(2)不一定，因为这两个三角形的底不一定相等，顶角也不一定相等.
(3)全等，因为这两个等边三角形的三条边分别相等.
2、解：∠A = ∠C.
因为在△ABD与△CBD中，AB = CB，AD = CD，且BD为公共边，
所以△ABD ≌ △CBD，所以∠A = ∠C.
3、解：如厂房顶人字架，自行车架等是利用三角形的稳定性;电动推拉门等是利用四边形的不稳定性.
八年级上册青岛版数学课后练习题答案(三)
第20页练习
八年级上册数学课后习题答案。

2.6.3 等腰三角形1．正△ABC 的两条角平分线BD 和CE 交于点I ，则∠BIC 等于（ ）A ．60°B ．90°C ．120°D ．150°2．下列三角形：①有两个角等于60°；②有一个角等于60°的等腰三角形；•③三个外角（每个顶点处各取一个外角）都相等的三角形；•④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有（ ）A ．①②③B ．①②④C ．①③D ．①②③④3．如图，D 、E 、F 分别是等边△ABC 各边上的点，且AD=BE=CF ，则△DEF •的形状是（ ）A ．等边三角形B ．腰和底边不相等的等腰三角形C ．直角三角形D ．不等边三角形E DCAB F21E D C A B4．Rt △ABC 中，CD 是斜边AB 上的高，∠B=30°，AD=2cm ，则AB 的长度是（ ）A ．2cmB ．4cmC ．8cmD ．16cm5．如图，E 是等边△ABC 中AC 边上的点，∠1=∠2，BE=CD ，则对△ADE 的形状最准备的判断是（ ）A ．等腰三角形B ．等边三角形C ．不等边三角形D ．不能确定形状6．△ABC 中，AB=AC ，∠A=∠C ，则∠B=_______．7．已知AD 是等边△ABC 的高，BE 是AC 边的中线，AD 与BE 交于点F ，则∠AFE=______．8．等边三角形是轴对称图形，它有______条对称轴，分别是_____________．9．△ABC 中，∠B=∠C=15°，AB=2cm ，CD ⊥AB 交BA 的延长线于点D ，•则CD •的长度是_______．10．如图，△ABC 中，AB=AC ，∠BAC=120°，AD ⊥AC 交BC•于点D ，•求证：•BC=3AD. D CAB参考答案1．C 2．D 3．A 4．C 5．B6．60°7．60°8．三；三边的垂直平分线9．1cm 10．∵AB=AC，∠BAC=120°，∴∠B=∠C=30°，∴在Rt△ADC中CD=•2AD，•∵∠BAC=120°，∴∠BAD=120°-90°=30°，∴∠B=∠BAD，∴AD=BD，∴BC=3AD。

1.2怎样判定三角形全等一、选择题1．如图，在∠AOB的两边上截取AO=BO，OC=OD，连接AD，BC交于点P，连接OP，则下列结论正确的是（）①△APC≌△BPD ②△ADO≌△BCO ③△AOP≌△BOP ④△OCP≌△ODP．（第1题图）A．①②③④ B．①②③C．②③④D．①③④2．下列说法不正确的是（）A．有两条边和它们的夹角对应相等的两个三角形全等B．有三个角对应相等的两个三角形全等C．有两个角及其中一角的对边对应相等的两个三角形全等D．有三条边对应相等的两个三角形全等3．如图，已知AB∥CD，AB=3，BC=4，要使△ABC≌△CDA，则需（）A．AD=4 B．DC=3 C．AC=3 D．BD=4（第3题图）（第4题图）4．如图，AC与BD相交于点P，AP=DP，则需要“SAS”证明△APB≌△DPC，还需添加的条件是（）A．BA=CD B．PB=PC C．∠A=∠D D．∠APB=∠DPC5．如图，在△ABD和△ACE中．AB=AC，AD=AE，如果由“SAS”可以判定△ABD≌△ACE，则需补充条件（）A．∠EAD=∠BAC B．∠B=∠C C．∠D=∠E D．∠EAB=∠CAD（第5题图）（第6题图）6．小明不小心把三角形的玻璃摔碎成3块，现在要去玻璃店配一块完全一样的玻璃，他最省事的是带（）去．A．①B．②C．③D．①和③二、填空题7．如图，在△ABC中，∠B=∠C，D，E，F分别是AB，BC，AC上的点，BD=CE，如果补充条件（填一个条件即可），那么可以判定△BDE≌△CEF．（第7题图）（第8题图）8．如图，填空：（填SSS、SAS、ASA或AAS）（1）已知BD=CE，CD=BE，利用可以判定△BCD≌△CBE；（2）已知AD=AE，∠ADB=∠AEC，利用可以判定△ABD≌△ACE；（3）已知OE=OD，OB=OC，利用可以判定△BOE≌△COD；（4）已知∠BEC=∠CDB，∠BCE=∠CBD，利用可以判定△BCE≌△CBD．三、解答题9．如图，AB=AD，BC=CD，∠ABC=∠ADC．求证：OB=OD．（第9题图）10．如图，已知AD，AF分别是两个钝角△ABC和△ABE的高，如果AD=AF，AC=AE．求证：BC=BE．（第10题图）（第11题图）11．如图，沿AC方向开山修路，为了加快施工进度，要在山的另一面同时施工，工人师傅在AC上取一点B，在小山外取一点D，连接BD并延长，使DF=BD，过F点作AB的平行线MF，连接MD并延长，在延长线上取一点E，使DE=DM，在E点开工就能使A，C，E 成一条直线，你知道其中的道理吗？12．如固，为了修筑一条公路，需测量出被大石头阻挡的∠BAC的大小，为此，小张师傅便在直线AC上取点D，使AC=CD，在BC的延长线上取点E，使BC=CE，连接DE，只要测出∠D的度数，则可知∠A的度数等于∠D的度数．请说明理由．（第12题图）13．已知，如图，在△ABC中，∠B=2∠C，AD是△ABC的角平分线，请说明AC=AB+BD．（第13题图）14．如图，AB=DE，AF=DC，BC⊥AD，EF⊥AD，垂足分别为C，F，AD与BE相交于点O．猜想：点O为哪些线段的中点？选择一种结论证明．（第14题图）答案一、1. A 【分析】∵AO =BO ，OC =OD ，∠O =∠O ，∴△ADO ≌△BCO （SAS ），故②正确． ∴∠COP =∠DOP ．∵OC =OD ，OP =OP ，∴△OCP ≌△ODP （SAS ），故④正确．∴PC =PD ． ∵∠CAP =∠DBP ，∠CP A =∠DPB ，∴△APC ≌△BPD （AAS ），故①正确．∴P A =PB ． ∵AO =BO ，OP =OP ，∴△AOP ≌△BOP （SSS ），故③正确．故选A ．2. B 【分析】A ．正确，符合判定SAS ；B ．不正确，全等三角形的判定必须有边的参与；C ．正确，符合判定AAS ；D ．正确，符合判定SSS ．故选B ．3. B 【分析】∵AB ∥CD ，∴∠BAC =∠DCA ．∵AB =3，DC =3，∴AB =DC ．∵AC =CA ， ∴△ABC ≌△CDA （SAS ）．故选B ．4. B 【分析】在△APB 和△DPC 中，当⎪⎩⎪⎨⎧=∠=∠=PC PB DPC APB DP AP ，，时，△APB ≌△DPC ，∴需要“SAS ”证明△APB ≌△DPC ，还需添加的条件是PB =PC ．故选B ．5. A 【分析】补充∠EAD =∠BAC ．∵∠EAD =∠BAC ，∴∠EAD +∠DAC =∠BAC +∠DAC ，即∠EAC =∠DAB ．在△AEC 和△ADB 中，⎪⎩⎪⎨⎧=∠=∠=，，，AC AC DAB EAC AD AE ∴△ABD ≌△ACE （SAS ）．故选A ．6. C 【分析】第一块，仅保留了原三角形的一个角和部分边，不符合任何判定方法；第二块，仅保留了原三角形的一部分边，所以该块不行；第三块，不但保留了原三角形的两个角还保留了其中一个边，所以符合ASA 判定，所以应该拿这块去．故选C ．二、7. BE =FC 【分析】补充条件BE =FC ．∵在△BDE 和△CEF 中，⎪⎩⎪⎨⎧=∠=∠=，，，FC EB C B EC DB ∴△BDE ≌△CEF （SAS ）．8. SSS ，ASA ，SAS ，AAS 【分析】（1）∵BD =CE ，CD =BE ，BC 为公共边，∴△BCD ≌△CBE （SSS ）；（2）∵AD =AE ，∠ADB =∠AEC ，∠A 为公共角，∴△ABD ≌△ACE （ASA ）；（3）∵OE =OD ，OB =OC ，∠BOE =∠COD （对顶角相等），∴△BOE ≌△COD （SAS ）；（4）∵∠BEC =∠CDB ，∠BCE =∠CBD ，BC 为公共边，∴△BCE ≌△CBD （AAS ）． 三、9.证明：在△ABC 和△ADC 中，∵AB =AD ，BC =CD ，AC 是公共边，∴△ABC ≌△ADC （SSS ），∴∠DCO =∠BCO ．在△BCO 和△DCO 中，∵BC =CD ，CO 是公共边，∠DCO =∠BCO ，∴△BCO ≌△DCO （SAS ），∴OB =OD （全等三角形对应边相等）．10. 证明：∵AD ，AF 分别是两个钝角△ABC 和△ABE 的高，且AD =AF ，AC=AE ， ∴Rt △ADC ≌Rt △AFE （HL ），∴CD =EF ．∵AD =AF ，AB =AB ，∴Rt △ABD ≌Rt △ABF （HL ）．∴BD =BF ．∴BD -CD =BF -EF ，即BC =BE ．11. 解：∵在△BDE 和△FDM 中，⎪⎩⎪⎨⎧=∠=∠=，，，DM DE FDM BDE DF BD∴△BDE ≌△FDM （SAS ），∴∠BEM =∠FME ，∴BE ∥MF ．∵AB ∥MF ，∴A ，C ，E 三点在一条直线上．12. 解：在△ABC 和△DEC 中，⎪⎩⎪⎨⎧=∠=∠=，，，EC BC DCE ACB CD AC∴△ABC ≌△DE C （SAS ），∴∠A=∠D ，∴测出∠D 的度数，即可得知∠A 的度数．13. 解：（方法一）如答图（1），在AC 上截取AE =AB ，连接DE ．∵AD 是△ABC 的角平分线，∴∠BAD =∠EAD ．在△BAD 和△EAD 中，⎪⎩⎪⎨⎧=∠=∠=，，，AE AB EAD BAD AD AD∴△BAD ≌△EAD ，∴BD =DE ，∠B =∠AED ．∵∠B =2∠C ，∠AED =∠C +∠EDC ，∴∠C =∠EDC ，∴DE =EC =BD ，∴AC =AE +CE =AB +BD ．（方法二）如答图（2），延长AB 到点F ，使AF =AC ，连接DF ．∵在△F AD 和△CAD 中，⎪⎩⎪⎨⎧=∠=∠=，，，AD AD CAD FAD AC AF∴△F AD ≌△CAD ，∴∠C =∠F ．∵∠ABC =2∠C ，∠ABC =∠F +∠BDF ，∴∠F =∠BDF ，∴BD =BF ，∴AC =AF =AB +BD ．（1） （2）（第13题答图）14. 解：O 为线段EB ，线段FC ，线段AD 的中点．证明如下： ∵AF =CD ，∴AF +FC =CD +FC ，即AC=DF ．∵BC ⊥AD ，EF ⊥AD ，∴∠ACB =∠DFE =90°．∴在Rt △ACB 和Rt △DFE 中，⎩⎨⎧==，，DF AC DE AB ∴Rt △ACB ≌Rt △DFE （HL ），∴EF =BC ．在△EFO 和△BCO 中，⎪⎩⎪⎨⎧=∠=∠∠=∠，，，BC EF BOC EOF BCO EOF∴△EFO ≌△BCO ，∴OE =OB ，即O 是线段BE 中点．。

青岛版初二上册数学练习题数学是一门重要的学科，对于学生的学习和发展起着至关重要的作用。

为了帮助初二学生提高数学能力，青岛版初二上册设计了一系列的数学练习题。

本文将围绕这些练习题展开讨论，帮助学生更好地理解和应用数学知识。

第一节选择题在初二上册数学练习题中，选择题占据了较大的比例。

这些题目要求学生根据题干和选项，选择正确的答案。

以下是一道典型的选择题：【题目】已知a + 3 = 8，则a的值是多少？A. 4B. 5C. 8D. 11【解析】根据题干可得a = 8 - 3 = 5，因此答案为B选项。

通过解答选择题，学生可以巩固基本的运算和推理能力，同时也培养了他们的逻辑思维和解决问题的能力。

第二节计算题除了选择题，初二上册的数学练习题还包括了大量的计算题。

这些题目要求学生进行运算，并给出准确的结果。

以下是一道典型的计算题：【题目】计算3.4 × 2.6的结果，保留一位小数。

【解析】根据乘法的运算法则，我们有3.4 × 2.6 = 8.84，因此结果是8.8（保留一位小数）。

通过解答计算题，学生可以熟练掌握基本的运算方法，提高他们的计算速度和准确性。

第三节应用题初二上册的数学练习题还涉及到了一些实际问题的应用题。

这些题目要求学生将抽象的数学概念应用到实际情境中，并解决实际问题。

以下是一道典型的应用题：【题目】某商场搞促销活动，原价为300元的商品现以折扣价200元出售，请计算折扣率是多少？【解析】首先，我们计算折扣额为300 - 200 = 100元。

然后，我们可以计算折扣率为折扣额除以原价，即100 / 300 ≈ 0.3333。

换算成百分数，折扣率约为33.33%。

通过解答应用题，学生可以发现数学在现实生活中的重要性，并培养他们解决实际问题的能力。

第四节证明题除了选择题、计算题和应用题，初二上册的数学练习题还包含了一些证明题。

这些题目要求学生通过逻辑推理和数学推导，证明一些数学结论。