直线 圆 线性规划

直线与圆◆知识点归纳 直线与方程 1.直线的倾斜角规定：当直线l 与x 轴平行或重合时，它的倾斜角为0 范围：直线的倾斜角α的取值范围为),0[π 2.斜率：)2(tan πα≠=a k ，R k ∈斜率公式：经过两点),(111y x P ，),(222y x P )(21x x ≠的直线的斜率公式为121221x x y y k P P --=3.直线方程的几种形式能力提升斜率应用例1.已知函数)1(log )(2+=x x f 且0>>>c b a ，则cc f b b f a a f )(,)(,)(的大小关系例2.已知实数y x ,满足)11(222≤≤-+-=x x x y ，试求23++x y 的最大值和最小值两直线位置关系 两条直线的位置关系设两直线的方程分别为：222111:b x k y l +=或0:22221111=++C y B x A l ；当21k k ≠或1221B A B A ≠时它们相交，交点坐标为方程组⎩⎨⎧+=+=2211b x k y b x k y 或⎩⎨⎧=++=++00222111C y B x A C y B x A直线间的夹角：①若θ为1l 到2l 的角，12121tan k k k k +-=θ或21211221tan B B A A B A B A +-=θ；②若θ为1l 和2l 的夹角，则12121tan k k k k +-=θ或21211221tan B B A A B A B A +-=θ；③当0121=+k k 或02121=+B B A A o直线1l 到2l 的角θ与1l 和2l 的夹角α：)2(πθθα≤=或)2(πθθπα>-=；距离问题1.平面上两点间的距离公式),(),,(222111y x P y x P 则 )()(121221y y x x P P -+-=2.点到直线距离公式点),(00y x P 到直线0:=++C By Ax l 的距离为：2200BA CBy Ax d +++=3.两平行线间的距离公式已知两条平行线直线1l 和2l 的一般式方程为1l ：01=++C By Ax ，2l ：02=++C By Ax ，则1l 与2l 的距离为2221BA C C d +-=4.直线系方程:若两条直线1l ：0111=++C y B x A ，2l ：0222=++C y B x A 有交点，则过1l 与2l 交点的直线系方程为)(111C y B x A ++＋0)(222=++C y B x A λ或)(222C y B x A +++0)(111=++C y B x A λ (λ为常数)对称问题1.中点坐标公式：已知点),(),,(2211y x B y x A ，则B A ,中点),(y x H 的坐标公式为⎪⎪⎩⎪⎪⎨⎧+=+=222121y y y x x x点),(00y x P 关于),(b a A 的对称点为)2,2(00y b x a Q --，直线关于点对称问题可以化为点关于点对称问题。

高中数学直线和圆知识点复习总结
1.直线方程⑴点斜式；⑵斜截式；⑶截距式；⑷两点式；⑸一般式(A，B不全为0)。

(直线的方向向量，法向量）
2.求解线性规划问题的步骤是：(1)列约束条件；(2)作可行域，写目标函数；(3)确定目标函数的最优解。

3.两条直线的位置关系：
4.直线系。

5.几个公式⑴设A(x1，y1)、B(x2，y2)、C(x3，y3)，⊿ABC的重心G是：()；⑵点P(x0，y0)到直线Ax+By+C=0的距离：；⑶两条平行线Ax+By+C1=0与Ax+By+C2=0的距离是；
6.圆的方程：⑴标准方程：①；②。

⑵一般方程：(注：Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆A=C0且B=0且D2+E2-4AF
7.圆的方程的求法：⑴待定系数法；⑵几何法；⑶圆系法。

8.圆系：⑴；注：当时表示两圆交线。

⑵。

9.点、直线与圆的位置关系：(主要掌握几何法)⑴点与圆的位置关系：(表示点到圆心的距离)①点在圆上；②点在圆内；③点在圆外。

⑵直线与圆的位置关系：(表示圆心到直线的距离)①相切；②相交；③相离。

⑶圆与圆的位置关系：(表示圆心距，表示两圆半径，且)①相离；②外切；③相交；④内切；⑤内含。

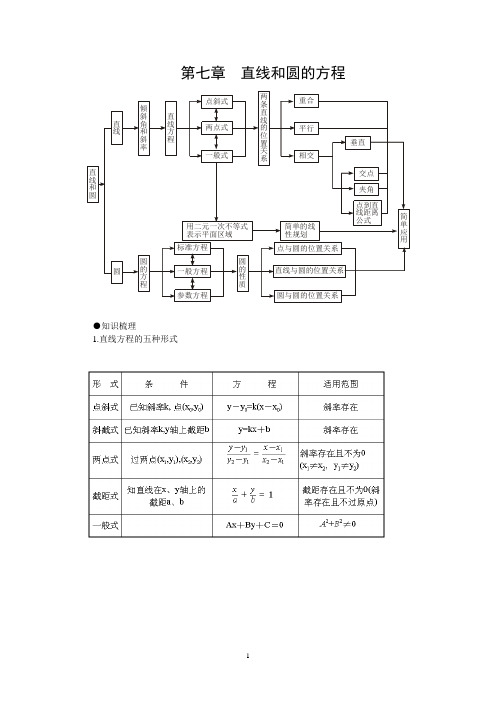
第七章直线和圆的方程●知识梳理1.直线方程的五种形式2.直线的倾斜角、斜率及直线的方向向量及位置关系:（1）直线的倾斜角在平面直角坐标系中，对于一条与x 轴相交的直线，如果把x 轴绕着交点按逆时针方向旋转到和直线重合时所转的最小正角记为α，那么α就叫做直线的倾斜角.直线和x 轴平行或重合时，直线的倾斜角为0°,直线倾斜角取值范围0°≤α＜180°. （2）直线的斜率倾斜角α不是90°的直线，它的倾斜角的正切叫做这条直线的斜率，常用k 表示，即k =tan α（α≠90°）.倾斜角是90°的直线没有斜率；倾斜角不是90°的直线都有斜率，其取值范围是（－∞，+∞）.（4）求直线斜率的方法①定义法：已知直线的倾斜角为α，且α≠90°，则斜率k =tan α.②公式法：已知直线过两点P 1（x 1，y 1）、P 2（x 2，y 2），且x 1≠x 2，则斜率k =1212x x y y --.平面直角坐标系内，每一条直线都有倾斜角，但不是每一条直线都有斜率. 对于直线上任意两点P 1（x 1，y 1）、P 2（x 2，y 2），当x 1=x 2时，直线斜率k 不存在，倾斜角α=90°；当x 1≠x 2时，直线斜率存在，是一实数，并且k ≥0时，α=arctan k ，k ＜0时，α=π+arctan k .（5）到角与夹角：若直线l 1, l 2的斜率分别为k 1, k 2，将l 1绕它们的交点逆时针旋转到与l 2重合所转过的最小正角叫l 1到l 2的角；l 1与l 2所成的角中不超过900的正角叫两者的夹角。

若记到角为θ，夹角为α，则tan θ=21121k k k k +-,tan α=21121k k k k +-.（6）平行与垂直：若直线l 1与l 2的斜率分别为k 1, k 2。

且两者不重合，则l 1//l 2的充要条件是k 1=k 2；l 1⊥l 2的充要条件是k 1k 2=-1。

线性规划与圆线性规划是一种数学优化方法，用于解决一类特定的优化问题。

它的目标是在给定的约束条件下，找到使目标函数取得最大（或最小）值的变量值。

而圆是一个具有特殊几何形状的闭合曲线，由一定半径的点构成。

线性规划与圆的关系主要体现在以下几个方面：1. 圆的方程在解决与圆相关的问题时，首先需要了解圆的方程。

圆的标准方程可表示为(x-a)^2 + (y-b)^2 = r^2，其中(a,b)为圆心的坐标，r为半径的长度。

通过这个方程，可以确定圆上的任意一点的坐标。

2. 圆与线的关系线性规划中的约束条件通常以线的形式表示。

与圆相关的线性约束可以是直线、射线或线段。

在求解线性规划问题时，需要确定线与圆的关系，即判断线是否与圆相交、相切或不相交。

这可以通过计算线与圆的方程得出。

3. 圆的最优解线性规划的目标是找到使目标函数取得最大（或最小）值的变量值。

在与圆相关的线性规划问题中，如果圆是目标函数的约束条件之一，那么最优解可能存在于圆上的某个点。

通过求解线性规划问题，可以确定目标函数在圆上取得最优解的点的坐标。

4. 圆的优化问题除了作为约束条件，圆本身也可以成为一个优化问题的目标。

例如，给定一个圆心和一组点，可以通过线性规划方法确定半径的长度，使得圆能够包含尽可能多的点。

这种情况下，线性规划的目标函数是最大化圆内点的数量，约束条件是圆心和点之间的距离。

综上所述，线性规划与圆有着密切的关系。

通过合理地应用线性规划方法，可以解决与圆相关的优化问题，包括确定圆的位置、判断线与圆的关系以及优化圆的半径等。

这种方法不仅可以应用于数学领域，还可以在工程、经济、物流等实际问题中得到广泛应用。

高三数学直线和圆的方程——直线与圆、圆与圆的位置关系苏教版【本讲教育信息】一. 教学内容：直线和圆的方程——直线与圆、圆与圆的位置关系二. 本周教学目标：1. 掌握直线和圆的位置关系、圆与圆的位置关系等知识，能够从代数特征（解或讨论方程组）或几何性质去考虑2. 会运用半径长、半径、弦心距构成的直角三角形减少运算量三. 本周知识要点：1. 研究圆与直线的位置关系最常用的方法：①判别式法；②考查圆心到直线的距离与半径的大小关系。

直线0=++C By Ax 与圆222)()(r b y a x =-+-的位置关系有三种，若22BA CBb Aa d +++=，则0<∆⇔⇔>相离r d ；0=∆⇔⇔=相切r d ；0>∆⇔⇔<相交r d2. 两圆位置关系的判定方法设两圆圆心分别为O 1，O 2，半径分别为r 1，r 2，d O O =21 ①条公切线外离421⇔⇔+>r r d ②条公切线外切321⇔⇔+=r r d③条公切线相交22121⇔⇔+<<-r r d r r ④条公切线内切121⇔⇔-=r r d ⑤无公切线内含⇔⇔-<<210r r d3. 直线和圆相切：这类问题主要是求圆的切线方程求圆的切线方程主要可分为已知斜率k 或已知直线上一点两种情况，而已知直线上一点又可分为已知圆上一点和圆外一点两种情况。

①过圆上一点的切线方程：圆),(00222y x P r y x 的以=+为切点的切线方程是200r y y x x =+。

当点00(,)P x y 在圆外时，200r y y x x =+表示切点弦的方程。

一般地，曲线)(00022y x P F Ey Dx Cy Ax ，的以点=++-+为切点的切线方程是：0220000=++⋅++⋅-+F y y E x x D y Cy x Ax 。

当点00(,)P x y 在圆外时，0220000=++⋅++⋅-+F y y E x x D y Cy x Ax 表示切点弦的方程。

卜一、线性规划、直线与圆的方程（必修二）第一部分线性规划1.已知点（x, y ）所在的可行域如图 2所示•若要使目标函数z =ax ■ y 取得最大值的最优解有无数多个，则1 5 A • 4 B • - C • - D432x — y —2 兰02.若实数x, y 满足不等式组’则2x - y 的最大值是（B ）x 30, y -0-A . 5B . 6C . 7D . 8"x - y + 8 K 03.设一元二次不等式组2x y -14乞0所表示的平面区域为 M,使函数y =a x 的图象过x 2y -19 _0区域M 的a 取值范围是(D ) A. [2,.10] B . [ ..10, 9] C . (2, 9)4.在“家电下乡”活动中，某厂要将 100台洗衣机运往邻近的乡镇•现有4辆甲型货车和8辆乙型货车可供使用•每辆甲型货车运输费用400元，可装洗衣机20台；每辆乙型货车运输费用300元，可装洗衣机10台.若每辆车至多只运一次，则该厂所花的最少运输费用为 （B ）a 的值为（D ）3 5DxA.2000 元B.2200 元C.2400 元D.2800 元y 沁x y _26.已知点P （x, y ）满足约束条件 y- 3x -6，则z = x - 2y 的最大值是（2y ■ x 的最小值为（D ）x - y 2 丄 010 .如果实数x, y 满足条件 y • 2 _ 0 ，那么z =2x - y 的最小值为 _______________ 。

答案：-6。

x y 2 岂 0x_2,y _1, 所表示的平面区域为 M 若曲线 x 2y -6 _0经过区域M 则实数m 的取值范围是（D ）3「33A. （-口） B .15,：：C .,15） D. [—,15]5 •设二元一次不等式组x 2 「my 2 二 1 总(A ) -3(B ) -2(C) -1(D ) 27.如果实数 A. 2x - y 1 _0x 、y 满足条件 y • 1 _ 0 ，那么2x - y 的最大值为（x y 1 乞 0C.-3&在平面直角坐标系中，不等式组（一；为常数）表示的平面区域的面积是 4,则A . 2B . -2 C.-4x _09.设x, y 满足约束条件 y _ x，则4x 3y 叮2x 2y 3 x 1取值范围是（D ）A.[1,5]B.[2,6]C. [3,10]D.[3,11]x y 2 亠 011.设x, y 满足约束条件 』x+2y+1兰0，贝V z=(x+1)2+(y- 2)2的最小值是 ________________y >016答案：1653x —y —6 辽0,12.设x , y 满足约束条件 x 「y ^2_0,若目标函数z=ax+by(a . 0 , b 0 )的最大值为 x 亠0, y 丄0. 1 312,则丄的最小值为a 2b第二部分直线与圆的方程:•，且 sin ：：£ 亠 cos, - 0，则 a, b 满足(D )2.经过抛物线y 2 =4x 的焦点，且方向向量为 a =（1厂2）的直线I 的方程是（B ）A. x-2y-1=0 B . 2x y-2=0 C. x 2y_1=0D. 2x-y-2=03 .直线x - y • m =0与圆x 2 • y 2 -2x -1 = 0有两个不同交点的一个充分不必要条件是 （C ） A . -3 m ：： 1 B . -4 m ：： 2 C . 0 :: m :: 1 D . m 14.若圆x 2 + y 2— 4x —4y — 10= 0上至少有三个不同的点到直线 则直线l 的倾斜角的范围是(B )5.已知直线l 与直线x-y-1 = 0垂直，则I 的倾斜角〉=—. 1352 26.与直线x - y - 4 =0和圆x y • 2x -2y =0都相切的半径最小的圆的方程是 _________ .答案：(x-1)2+(y+1)2=2答案:25 121.设直线ax by • c = 0的倾斜角为 A . a b =1 Bab=0 D . a-b = 0l : ax + by = 0的距离为2 2 ,A .[二-]B12 4-益 52] C- F 7D . [0,-]27.已知圆C ： x 2 y 2 Dx Ey • 3 = 0 ,圆C 关于直线x • y ―仁0对称，圆心在第二象限， 半径为.2 .⑴求圆C 的方程；⑵已知不过原点的直线I 与圆C 相切，且在x 轴、y 轴上的截距相等，求直线 I 的方程。

高考数学中的线性规划基本概念介绍在高中数学中，我们接触到了许多不同的数学知识，其中很重要的一项便是线性规划。

在高考数学考试中，线性规划占据了相当重要的位置，成为众多学生备战高考的重要课程。

本文将为大家介绍一下高考数学中的线性规划基本概念。

一、线性规划的含义与基本形式所谓线性规划，就是针对一定的线性约束条件和线性目标函数，找到一个可行解，使得目标函数取得最大值或最小值。

具体来说，我们可以把线性规划形式表示为以下三个部分：第一部分：目标函数。

实际应用中，我们需要通过目标函数来描述最优解的性质。

第二部分：约束条件。

约束条件按照不同的形式可以分为等式约束和不等式约束。

等式约束通常包括一些限制条件，例如生产的成本、材料、人工等费用等；而不等式约束则包括一些限制条件，例如工艺上的限制、质量上的限制等等。

第三部分：变量范围。

变量范围是针对线性规划中的所有变量进行限制，例如生产量、工作量等等。

变量的范围通常以非负数的形式进行限制。

二、线性规划的图形解释在图形表示中，我们可以把约束条件和目标函数分别绘制在平面直角坐标系上。

具体来说，约束条件的图像形式通常为一些直线或者凸多边形，而目标函数的图像则大多为一条直线。

设二维实数集合$$S = {(x,y)\mid x,y \in R}$$为平面直角坐标系上的点集。

设集合$$P = {(x,y)\mid a_{1}x+b_{1}y\le c_{1},a_{2}x+b_{2}y\le c_{2}}$$ 其中a1,b1,c1,a2,b2,c2均为常数，为x 轴和y轴上的两条直线。

则P就是由这两个约束条件限制而成的平面直角坐标系中的点集。

同时，一元线性规划问题中最常见的约束条件就是不等式约束。

在平面直角坐标系中，这些不等式约束通常形成一个封闭凸多边形，我们将其称之为约束多边形。

因此，在二元问题中，问题的可行解便是在该多边形中的可行点，即使得目标函数取得最小值或最大值的点。

三、线性规划的解法与应用在现实生活中，线性规划具有广泛的应用范围，例如经济学、管理学等学科领域。

直线与圆的方程一、直线的方程 1、倾斜角：，范围0≤α＜π，x l //轴或与x 轴重合时，α=00。

2、斜率： k=tan α α与κ的关系：α=0⇔κ=0已知L 上两点P 1（x 1,y 1） 0＜α＜02>⇔k πP 2（x 2,y 2） α=κπ⇔2不存在`⇒k=1212x x y y -- 022<⇔<<κππ当1x =2x 时，α=900，κ不存在。

当0≥κ时，α=arctank ，κ＜0时，α=π+arctank 3、截距（略）曲线过原点⇔横纵截距都为0。

几种特殊位置的直线 ①x 轴：y=0 ②y 轴：x=0 ③平行于x 轴：y=b!④平行于y 轴：x=a ⑤过原点：y=kx两个重要结论：①平面内任何一条直线的方程都是关于x 、y 的二元一次方程。

②任何一个关于x 、y 的二元一次方程都表示一条直线。

5、直线系：（1）共点直线系方程：p 0（x 0,y 0）为定值，k 为参数y-y 0=k （x-x 0） '特别：y=kx+b ，表示过（0、b ）的直线系（不含y 轴）（2）平行直线系：①y=kx+b ，k 为定值，b 为参数。

②AX+BY+入=0表示与Ax+By+C=0 平行的直线系 ③BX-AY+入=0表示与AX+BY+C 垂直的直线系（3）过L 1,L 2交点的直线系A 1x+B 1y+C 1+入（A 2X+B 2Y+C 2）=0（不含L2） 6、三点共线的判定：①AC BC AB =+，②K AB =K BC ，③写出过其中两点的方程，再验证第三点在直线上。

二、两直线的位置关系（说明：当直线平行于坐标轴时，要单独考虑） 2、L 1 到L 2的角为0，则12121tan k k k k •+-=θ（121-≠k k ）3、夹角：12121tan kk k k +-=θ4、点到直线距离：2200BA c By Ax d +++=（已知点（p 0(x 0,y 0)，L ：AX+BY+C=0）①两行平线间距离：L 1=AX+BY+C 1=0 L 2：AX+BY+C 2=0⇒2221B A c c d +-=②与AX+BY+C=0平行且距离为d 的直线方程为Ax+By+C ±022=+B A d③与AX+BY+C 1=0和AX+BY+C 2=0平行且距离相等的直线方程是0221=+++C C BY AX 5、对称：（1）点关于点对称：p(x 1,y 1)关于M （x 0,y 0）的对称)2,2(1010Y Y X X P --'：（2）点关于线的对称：设p(a 、b)一般方法：如图：(思路1)设P 点关于L 的对称点为P 0(x 0,y 0) 则Kpp 0﹡K L =－1P , P 0中点满足L 方程:解出P 0(x 0,y 0)（思路2）写出过P ⊥L 的垂线方程，先求垂足，然后用中点坐标公式求出P 0(x 0,y 0)的坐标。

线性规划知识点线性规划是一种数学优化方法，用于解决线性约束条件下的最优化问题。

它在各个领域中都有广泛的应用，包括经济学、管理学、工程学等。

一、线性规划的基本概念1. 目标函数：线性规划的目标是最大化或者最小化一个线性函数，称为目标函数。

目标函数通常表示为Z = c1x1 + c2x2 + ... + cnxn，其中ci为系数，xi为变量。

2. 约束条件：线性规划的解必须满足一系列线性约束条件。

约束条件通常表示为a1x1 + a2x2 + ... + anx ≤ b，其中ai为系数，b为常数。

3. 变量：线性规划中的变量是需要优化的未知数，通常表示为x1, x2, ..., xn。

4. 可行解：满足所有约束条件的解称为可行解。

5. 最优解：在所有可行解中，使目标函数达到最大或者最小值的解称为最优解。

二、线性规划的求解方法1. 图形法：对于二维线性规划问题，可以使用图形法求解。

首先绘制约束条件的直线，然后确定可行域，最后在可行域中找到使目标函数最大或者最小的解。

2. 单纯形法：对于高维线性规划问题，通常使用单纯形法求解。

单纯形法是一种迭代算法，通过不断挪移到更优的解来寻觅最优解。

3. 整数规划：当变量需要取整数值时，称为整数规划。

整数规划问题通常较难求解，可以使用分支定界法等方法进行求解。

三、线性规划的应用1. 生产计划：线性规划可以用于确定最佳的生产计划，包括生产数量、原材料采购等。

2. 仓储管理：线性规划可以用于优化仓储管理，包括货物的存放位置、调度等。

3. 运输问题：线性规划可以用于解决运输问题，包括货物的调度、最佳路径选择等。

4. 金融投资：线性规划可以用于优化投资组合，确定最佳的资产配置方案。

5. 能源管理：线性规划可以用于能源管理，包括能源生产、分配等。

四、线性规划的局限性1. 线性假设：线性规划假设目标函数和约束条件都是线性的，这在某些实际问题中可能不成立。

2. 单一目标：线性规划只能优化一个目标函数，对于多目标问题需要进行权衡和转化。