动点问题的函数图象

专题02 动点问题中的函数图象及规律探索问题一、基础知识点综述动点问题中函数图象的题目的解决方法是：先根据动点运动规律找出所求与动点运动之间的关系，进而获取相应函数的解析式及函数值变化规律，达到求解的目的.考查的重点是分段函数解析式的求解.探索规律问题通常用归纳法，即从简单到复杂，从特殊到一般，这类题目考查的是学生的观察与归纳能力，注意从特殊到一般的归纳方法.二、主要思想方法分类讨论、数学归纳.三、精品例题解析例1. （2019·达州改编）如图，边长都为4的正方形ABCD和正三角形EFG如图放置，AB与EF在同一条直线上，且A点与F点重合，现将△EFG沿AB方向以每秒1个单位的速度匀速运动，当点F与B重合时停止. 在这个运动过程中，正方形ABCD与△EFG重叠部分的面积S与运动时间t的函数解析式是【答案】()220224t242tSt⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩.【解析】解：(1)(2)当0≤t≤2时，如图（1）所示，由题意知：∠HF A=60°，∠AHF=30°，CCEAF =t ，AH,12S AF AH =⨯⨯=)2122tt =； 当2<t ≤4时，如图（2）所示，由题意知：∠E =60°，∠AHE =30°， AF =t ，AE =4-t , AH)4t -EFG EFA S S S =-△△())2144t 4t 42⎤=⨯---⎦()24t 2=-综上所述，()22024t 242t S t ⎧≤≤⎪⎪=⎨⎪-<≤⎪⎩例2. （2019·自贡）均匀的向一个容器内注水，在注满水的过程中，水面的高度h 与时间t 的函数关系如图所示，则该容器是下列四个中的（）【答案】D .【解析】解：A 为圆柱体，其函数图象应为一条直线，故不合题意；B 选项下面粗上面细，其函数图象是一条折线，且后半段的变化速率较慢（图象较缓），故不合题意；C 选项函数图象应为一条曲线，故不合题意；D 选项下面细上面粗，其函数图象是一条折线，且后半段的变化速率较快，故符合题意； 故答案为：D .例3. （2019·潍坊改编）如图，在矩形ABCD 中，AB =2,AD =3，动点P 沿着折线BCD 从点B 开始运动到点D ，设运动的路程为x ，△ADP 的面积为y ，则y 与x 之间的函数关系式是【答案】3031533522x y x x ≤≤⎧⎪=⎨-<≤⎪⎩.【解析】解：①当点P 在线段BC 上时，即0≤x ≤3时，132y AD AB =⨯⨯=;②当点P 在线段CD 上时，即3<x ≤5时，()11153352222y AD DP x x =⨯⨯=⨯⨯-=-; 综上所述，3031533522x y x x ≤≤⎧⎪=⎨-<≤⎪⎩.例4. （2019·深圳模拟）如图①，在菱形ABCD 中，动点P 从点B 出发，沿折线B →C →D →B 运动. 设点P 经过的路程为x ，△ABP 的面积为y . 把y 看成x 的函数，函数的图象如图②所示，则图②中的b 等于【答案】【解析】解：由图②可知，当x =4时△ABP 的面积最大，此时P 点运动至点C ，即菱形ABCD 的边长为4，又x =14时停止，即BD =6，DP连接AC交BD于O，AC⊥BD，∴BD=3，在Rt△BOC中，由勾股定理得：OC，∴AC=即b=12AC BC ⨯⨯=故答案为：例5. 如图1，在扇形OAB中，∠O=60°，动点P从点O出发，沿O→A→B以1cm/s的速度匀速运动至点B，图2是点P运动过程中，△OBP的面积y（cm2）随时间x（s）变化的图象，则a，b的值分别为【答案】4，443π+.【解析】解：由题意知：当点P运动至点A时，△OBP的面积为∵∠O=60°，∴△OAB为等边三角形，∴OA=4，即a=4，b=（OA+l AB）÷1=443π+.故答案为：4，443π+.例6. （2019·河南模拟）如图1，在矩形ABCD中，AB＜BC，点E为对角线AC上的一个动点，连接BE，DE，过E作EF⊥BC于F．设AE＝x，图1中某条线段的长为y，若表示y与x的函数关系的图象大致如图2所示，则这条线段可能是图1中的（）A．线段BE B．线段EF C．线段CE D．线段DE【答案】D.【解析】解：A、若线段BE是y，则y随x的增大先减小再增大，在点A的距离是BA，在点C时的距离是BC，因为BA＜BC，故A错误；B、若线段EF是y，则y随x的增大越来越小，故B错误；C、若线段CE是y，则y随x的增大越来越小，故C错误；D、若线段DE是y，则y随x的增大先减小再增大，在点A的距离是DA，在点C时的距离是DC，DA＞DC，故选项D正确；故答案为：D．例7. （2019·博罗县一模）如图，已知A，B是反比例函数y＝（k＞0，x＞0）图象上的两点，BC∥x轴，交y轴于点C，动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过P作PM⊥x轴，垂足为M．设三角形OMP的面积为S，P点运动时间为t，则S关于t的函数图象大致为（）A．B．C．D．【答案】A .【解析】解：设∠AOM ＝β，点P 运动的速度为x ， 当点P 从点O 运动到点A 的过程中， S ＝()()22111cos sin cos sin 222OM PM xt xt x t ββββ⨯⨯=⨯= 由于β及x 均为常量，即21cos sin 2x ββ为定值，可知本段图象应为抛物线，且S 随着t 的增大而增大；故选项B 、C 错误；当点P 从A 运动到B 时，由反比例函数性质可知△OPM 的面积为12k ，保持不变，故本段图象应为与横轴平行的线段；故选项C 错误； 故选：A ．例8. （2017·濮阳县一模）如图，等边△ABC 边长为2，四边形DEFG 是平行四边形，DG =2，DE =3，∠GDE =60°，BC 和DE 在同一条直线上，且点C 与点D 重合，现将△ABC 沿D →E 的方向以每秒1个单位的速度匀速运动，当点B 与点E 重合时停止，则在这个运动过程中，△ABC 与四边形DEFG 的重合部分的面积S 与运动时间t 之间的函数关系图象大致是（ ）A ．B ．C ．D ．【答案】B .【解析】解：分三种情况：①0≤t ≤2时，由重叠部分为边长为t 的等边三角形； 如图1，由题意知CD ＝t ，∠HDC ＝∠HCD ＝60°， ∴△CDH 是等边三角形，则S 2；即该段函数图象是开口朝上的抛物线的一部分，S 随t 的增大而增大； ②2＜t ≤3时，由重叠部分即为△ABC ； 如图2，S ＝4×22； 此段函数图象是一条平行于x 轴的线段； ③3＜t ≤5时由重叠部分是S △ABC ﹣S △HEC 如图3，根据题意可得CE ＝CD ﹣DE ＝t ﹣3，∠C ＝∠HEC ＝60°， ∴△CEH 为等边三角形，则S ＝S △ABC ﹣S △HEC ＝4×22﹣4（t ﹣3）2＝﹣4t 2+2t ﹣4； 此段函数图象为开口朝下的抛物线的一部分，且S 随t 的增大而减小综上所述，0≤t ≤2时函数图象是开口向上的抛物线的一部分，2＜t ≤3时函数图象是平行于x 轴的一部分，当3＜t ≤5时函数图象是开口向下的抛物线的一部分； 故答案为B .例9. （2019·衡阳）如图，在直角三角形ABC 中，∠C ＝90°，AC ＝BC ，E 是AB 的中点，过点E 作AC 和BC 的垂线，垂足分别为点D 和点F ，四边形CDEF 沿着CA 方向匀速运动，点C 与点A 重合时停止运动，设运动时间为t ，运动过程中四边形CDEF 与△ABC 的重叠部分面积为S ．则S 关于t 的函数图象大致为（）A．B．C．D．【答案】C.【解析】解：∵在直角三角形ABC中，∠C＝90°，AC＝BC，∴△ABC是等腰直角三角形，∵EF⊥BC，ED⊥AC，∴四边形EFCD是矩形，∵E是AB的中点，∴EF＝12AC，DE＝12BC，∴EF＝ED，∴四边形EFCD是正方形，设正方形的边长为a，如图1,当移动的距离小于a时，S＝正方形的面积﹣△EE′H的面积＝a2﹣12t2；当移动的距离大于a时，如图2，S＝S△AC′H＝12（2a﹣t）2＝12t2﹣2at+2a2，∴S关于t的函数图象大致为C选项，综上所述，移动距离小于正方形CDEF边长时，函数图象是开口朝下的抛物线一部分，且S随t的增大而减小；移动距离大于正方形CDEF边长时，函数图象是开口朝上的抛物线一部分，且S随t的增大而减小；故答案为：C．例10.a是不为1的有理数，我们把11a-成为a的差倒数，如2的差倒数是－1，－1的差倒数是0.5. 已知a1=5，a2是a1的差倒数，a3是a2的差倒数，a4是a3的差倒数……，以此类推，则a2019的值是.【答案】4 5 .【解析】解：由题意知：a1=5，a2=14-，a3=45，a4=5，……2019÷3=673，即a2019=4 5 .例11. （2019·潍坊）如图所示，在平面直角坐标系中，一组同心圆的圆心为坐标原点O，它们的半径分别为1,2,3，……，按照“加1”依次递增，一组平行线，l0，l1，l2，l3，……都与x轴垂直，相邻两直线的间距为1，其中l0与y轴重合. 若半径为2的圆与l1在第一象限交于点P1，半径为3的圆与l2在第一象限交于点P2，……，半径为n+1的圆与ln在第一象限交于点P n，则点P n的坐标为【答案】4.【解析】解：连接OP 1，设l 1与x 轴交于点A 1，由题意知：OP 1=2，OA 1=1， 在RtOP 1A 1中，由勾股定理得：P 1A 1即P 1(；同理得：P 2(，P 3(，P 4(…… 即P n(n .例12. （2019·连云港） 如图，将一等边三角形三条边各八等分按顺时针方向标注各等分点的序号0、1、2、3、4、5、6、7、8，如图所示，将和为8的点连接起来，得到了“三角形坐标系”.在建立的坐标系中，每一点的坐标用过这一点且平行（重合）于原三角形三条边的直线与三边交点的序号来表示（水平方向开始，按顺时针方向），如点A 的坐标为（1,2,5），点B 的坐标为（4,1,3），则点C 的坐标为【答案】（2,4,2）.【解析】由题意知，通过点C 的数字依次是2,4,2（顺时针），故答案为（2,4,2）.例13. （2019·衡阳）在平面直角坐标系中，抛物线y ＝x 2的图象如图所示．已知A 点坐标为（1，1），过点A 作AA 1∥x 轴交抛物线于点A 1，过点A 1作A 1A 2∥OA 交抛物线于点A 2，过点A 2作A 2A 3∥x 轴交抛物线于点A3，过点A3作A3A4∥OA交抛物线于点A4……，依次进行下去，则点A2019的坐标为．【答案】（﹣1010，10102）.【解析】解：∵A点坐标为（1，1），∴直线OA为y＝x，A1（﹣1，1），∵A1A2∥OA，∴直线A1A2为y＝x+2，联立y=x+2，y=x2得，A2（2，4），A3（﹣2，4），∵A3A4∥OA，∴直线A3A4为y＝x+6，同理得：A4（3，9），A5（﹣3，9）…，∴A2019（﹣1010，10102），故答案为（﹣1010，10102）．例14. （2019·怀化）探索与发现：下面是用分数（数字表示面积）砌成的“分数墙”，则整面“分数墙”的总面积是．【答案】n-1. 【解析】解：由题意“分数墙”的总面积＝2×12+3×13+…+n×1n＝n﹣1，故答案为n﹣1．。

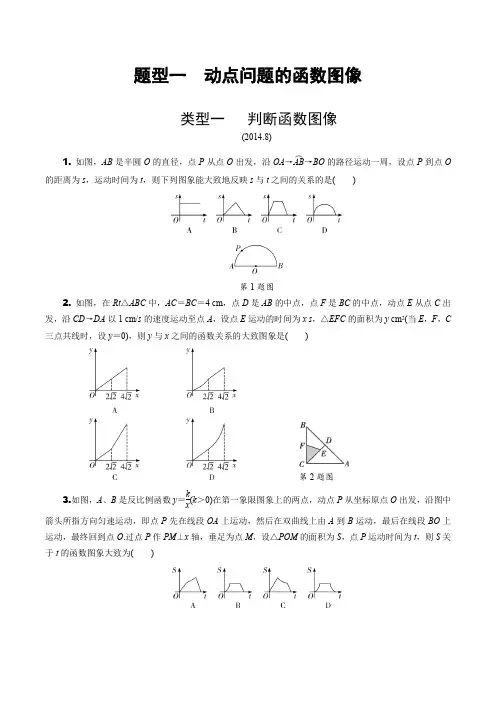
题型一 动点问题的函数图像类型一 判断函数图像(2014.8)1. 如图，AB 是半圆O 的直径，点P 从点O 出发，沿OA →AB ︵→BO 的路径运动一周，设点P 到点O的距离为s ，运动时间为t ，则下列图象能大致地反映s 与t 之间的关系的是( )第1题图2. 如图，在Rt △ABC 中，AC ＝BC ＝4 cm ，点D 是AB 的中点，点F 是BC 的中点，动点E 从点C 出发，沿CD →DA 以1 cm/s 的速度运动至点A ，设点E 运动的时间为x s ，△EFC 的面积为y cm 2(当E ，F ，C 三点共线时，设y ＝0)，则y 与x 之间的函数关系的大致图象是( )第2题图3.如图，A 、B 是反比例函数y ＝k x(k ＞0)在第一象限图象上的两点，动点P 从坐标原点O 出发，沿图中 箭头所指方向匀速运动，即点P 先在线段OA 上运动，然后在双曲线上由A 到B 运动，最后在线段BO 上运动，最终回到点O .过点P 作PM ⊥x 轴，垂足为点M ，设△POM 的面积为S ，点P 运动时间为t ，则S 关于t 的函数图象大致为( )第3题图4.如图，在菱形ABCD中，∠B＝60°，AB＝2，动点P从点B出发，以每秒1个单位长度的速度沿折线BA→AC运动到点C，同时动点Q从点A出发，以相同速度沿折线AC→CD运动到点D，当一个点停止运动时，另一个点也随之停止.设△APQ的面积为y，运动时间为x秒，则下列图象能大致反映y与x之间函数关系的是()第4题图5.如图，在矩形ABCD中，对角线AC与BD交于点O，点M为线段AC上一个动点，过点M作EF∥BD 交AD(或DC)于点E，交AB(或BC)于点F，已知AC＝5，设AM＝x，EF＝y，则y关于x的函数图象大致为()第5题图6. (2019衢州)如图，正方形ABCD的边长为4，点E是AB的中点，点P从点E出发，沿E→A→D→C 移动至终点C，设点P经过的路径长为x，△CPE的面积为y，则下列图象能大致反映y与x函数关系的是()第6题图类型二分析函数图像1.如图①，点P从矩形ABCD的顶点B出发，沿射线BC的方向以每秒1个单位长度的速度运动，过点P作PG⊥AP交射线DC于点G.如图②是点P运动时CG的长度y随时间t变化的图象，其中点Q是第一段曲线(抛物线的一部分)的最高点，则AB的长度是()第1题图A. 2B. 3C. 4D. 232.(2019郑州模拟)如图①，四边形ABCD中，AB∥CD，∠B＝90°，AC＝A D.动点P从点B出发，沿折线B－A－D－C方向以 1 cm/s的速度匀速运动，在整个运动过程中，△BCP的面积S(cm2)与运动时间t(s)的函数图象如图②所示，则AD等于()第2题图A. 5 cmB. 34 cmC. 8 cmD. 2 3 cm3.如图①，菱形ABCD中，∠B＝60°，动点P以每秒1个单位的速度自点A出发沿线段AB运动到点B，同时动点Q以每秒2个单位的速度自点B出发沿折线B－C－D运动到点D.图②是点P、Q运动时，△BPQ的面积S随时间t变化关系图象，则a的值是()第3题图A. 2B. 2.5C. 3D. 234.如图①，在正方形ABCD中，动点E从点A出发，沿A－B－C运动，当点E到达点C时停止运动，过点E作EF⊥AE，交CD于点F，设点E运动的路程为x，FC＝y(当点A，E重合时，点D，F重合；当点C，E重合时，不妨设y＝0)，y与x的函数关系的大致图象如图②，当点E在BC上运动时，FC的最大长度是1，则正方形ABCD的面积是()第4题图A. 8B. 12C. 16D. 4.85.如图①，在矩形ABCD中，动点P从点A出发，沿A→B→C运动，设P A＝x，点D到直线P A的距离为y，且y关于x的函数图象如图②所示，则当△PCD和△P AB的面积相等时，y的值为.第5题图6.如图①，已知点E，F，G，H是矩形ABCD各边的中点，动点M从点E出发，沿E→F→G匀速运动，设点M运动的路程为x，点M到矩形顶点B的距离为y，如果表示y关于x函数关系的图象如图②所示，那么四边形EFGH的面积是.第6题图参考答案类型一 判断函数图象1. C 【解析】点P 在OA 上从点O 向点A 运动的过程中，s 随着t 的增大而增大，点P 在AB ︵上运动时，s ＝OP ＝12AB (定值)，点P 在OB 上从点B 向点O 运动的过程中，s 随着t 的增大而减小． 2. A 【解析】∵在Rt △ABC 中，AC ＝BC ＝4，∴AB ＝42，AD ＝CD ＝22，CF ＝2，当点E 在CD 上时，CE ＝x ，点E 到BC 的距离h 1＝22x ，∴y ＝12×2×22x ＝22x (0≤x ≤22)；当点E 在AD 上时，BE ＝BD ＋DE ＝CD ＋DE ＝x ，∴点E 到FC 的距离h 2＝22BE ＝22x ，∴y ＝12×2×22x ＝22x (22≤x ≤42)． 3. D 【解析】设∠AOM ＝α，点P 运动的速度为a ，当点P 从点O 运动到点A 的过程中，S ＝12OM ·PM ＝12at ·cos α·at ·sin α＝12a 2·cos α·sin α·t 2，由于α及a 均为常量，从而可知图象本段应为抛物线，且S 随着t 的增大而增大；当点P 从A 运动到B 时，由反比例函数性质可知△OPM 的面积为12k ，保持不变，本段图象应为与x 轴平行的线段；同理可得，当点P 从B 运动到O 过程中，S 也是t 的二次函数，且S 随着t 的增大而减小．4. B 【解析】∵四边形ABCD 为菱形，且∠B ＝60°，AB ＝2，∴当0＜t ＜2时，△APQ 的面积y ＝12t ·(2－t )·sin60°＝－34t 2＋32t ，函数图象为开口向下的一段抛物线，且当t ＝1时，y 最大值为34；当2＜t ＜4时，△APQ 的面积y ＝12(t －2)·(t －2)·sin60°＝34(t －2)2，函数图象为开口向上的一段抛物线，且当t ＝4时，y 最大值为3，故选B .5. B 【解析】当0≤x ≤2.5时，如解图①，∵四边形ABCD 是矩形，∴OA ＝OB ＝OC ＝OD ，∴∠OAD ＝∠ODA ，∵EF ∥BD ，∴∠ODA ＝∠MEA ，∴∠OAD ＝∠MEA ，∴ME ＝MA ，同理可得AM ＝MF ，∴EM ＝AM ＝MF ，∴EF ＝2AM ，即y ＝2x ；当2.5<x ≤5时，如解图②，由题意知CM ＝AC －AM ＝5－x ，∵ME＝MC ＝MF ，∴EF ＝2MC ，即y ＝2(5－x )＝10－2x .综上所述，y ＝⎩⎪⎨⎪⎧2x （0≤x ≤2.5）10－2x （2.5<x ≤5）.图① 图②第5题解图6. C 【解析】∵AB ＝4，点E 是AB 的中点，∴AE ＝BE ＝2，当0≤x ≤2时，如解图①，y ＝S △CPE ＝12PE·BC＝2x，∴此段函数图象是正比例函数的一部分；当2<x≤6时，如解图②，y＝S△CPE＝S正方形ABCD－S△BCE －S△APE－S△PCD＝42－12×4×2－12×2×(x－2)－12×4×[4－(x－2)]＝x＋2，∴此段函数图象是一次函数的一部分；当6<x≤10时，如解图③，y＝S△CPE＝12PC·BC＝12(10－x)×4＝－2x＋20，∴此段函数图象是一次函数的一部分，综上所述，根据各段图象及x的取值范围，可得函数图象如选项C所示．图①图②图③第6题解图类型二 分析函数图象1. B 【解析】结合图形分析函数图象可得：当点P 运动到点C 的位置时，CG ＝0，∴BC ＝4.当点P运动到线段BC 的中点时，CG ＝43.∵∠B ＝90°，∴∠BAP ＋∠APB ＝90°，∵PG ⊥AP ，∴∠APG ＝90°，∴∠APB ＋∠CPG ＝90°，∴∠BAP ＝∠CPG ，又∵∠ABP ＝∠PCG ＝90°，∴△ABP ∽△PCG ，∴AB PC ＝BP CG，当点P 为BC 的中点时，BP ＝PC ＝2，∴AB 2＝243，解得AB ＝3. 2. B 【解析】结合图形分析函数图象可得，当t ＝3时，点P 到达A 处，即AB ＝3；如解图，过点A作AE ⊥CD 于点E ，则四边形ABCE 为矩形，∵AC ＝AD ，∴DE ＝CE ＝12CD .当S ＝15时，点P 到达点D 处，则S ＝12CD ·BC ＝12·2AB ·BC ＝3×BC ＝15，则BC ＝5，在Rt △ABC 中，由勾股定理得，AD ＝AC ＝AB 2＋BC 2＝34.第2题解图3. D 【解析】由题图②得，t ＝4时两点停止运动，∴点P 以每秒1个单位的速度从点A 运动到点B 用了4秒，∴AB ＝4，∵点Q 运动到点C 之前和之后，△BPQ 面积算法不同，即t ＝2时，S 的解析式发生变化，∴题图②中点M 对应的横坐标为2，此时P 为AB 中点，点C 与点Q 重合，如解图，连接AC ，∵菱形ABCD 中，AB ＝BC ＝4，∠B ＝60°，∴△ABC 是等边三角形，∴CP ⊥AB ，BP ＝12AB ＝2，∴CP ＝BC 2－BP 2＝42－22＝23，∴a ＝12BP ·CP ＝12×2×23＝2 3.第3题解图4. C 【解析】如解图，设AB ＝a ，当点E 在BC 上运动时(不与点B 、C 重合)，∵AE ⊥EF ，∴△EFC∽△AEB ，∴EC AB ＝FC EB ，即2a －x a ＝y x －a ，∴y ＝－1a x 2＋3x －2a ，－1a <0，当x ＝－32×（－1a ）＝32a 时，y 取得最大值，此时点E 为BC 的中点，y ＝1，把(32a ，1)代入y ＝－1ax 2＋3x －2a ，解得a ＝4，即AB ＝4，故正方形ABCD 的面积为4×4＝16.第4题解图5. 121313【解析】当P 点在AB 上运动时，D 点到AP 的距离不变，始终是AD 长，从图象可以看出AD ＝4，当P 点到达B 点时，从图象看出x ＝3，即AB ＝3.当△PCD 和△P AB 的面积相等时，P 点在BC 中点处，此时△ADP 面积为12×4×3＝6，在Rt △ABP 中，AP ＝AB 2＋BP 2＝13，则12AP ·y ＝6，解得y ＝121313. 6. 24 【解析】如解图，连接BD ，EG ，FH ，∵点E ，F ，G ，H 是矩形ABCD 各边的中点，∴EF ∥BD ∥GH ，EF ＝GH ＝12BD ，∴四边形EFGH 是平行四边形，又∵EF ＝EH ，∴平行四边形EFGH 是菱形，由题图②得BE ＝3，点M 运动到点G 时，运动路程为10，又∵EF ＝FG ，则可知菱形的边长为5，即EF ＝FG ＝GH ＝HE ＝5，∴AF ＝4，AD ＝8，∴S 菱形EFGH ＝12EG ·FH ＝24.第6题解图。

中考数学复习----《动点问题的函数图像》压轴真题练习（含答案解析）1．（2021•益阳）如图，已知▱ABCD的面积为4，点P在AB边上从左向右运动（不含端点），设△APD的面积为x，△BPC的面积为y，则y关于x的函数图象大致是（）A．B．C．D．【答案】B【解答】解：∵▱ABCD的面积为4，x+y是平行四边形面积的一半，∴x+y＝2，∴y＝2﹣x，∴y是x的一次函数，且当x＝0时，y＝2；x＝2时，y＝0；故只有选项B符合题意．2．（2021•河南）如图1，矩形ABCD中，点E为BC的中点，点P沿BC从点B运动到点C，设B，P两点间的距离为x，PA﹣PE＝y，图2是点P运动时y随x变化的关系图象，则BC的长为（）A．4B．5C．6D．7【答案】C【解答】解：由函数图象知：当x＝0，即P在B点时，BA﹣BE＝1．利用三角形两边之差小于第三边，得到PA﹣PE≤AE．∴y的最大值为AE，∴AE＝5．在Rt△ABE中，由勾股定理得：BA2+BE2＝AE2＝25，设BE的长度为t，则BA＝t+1，∴（t+1）2+t2＝25，即：t2+t﹣12＝0，∴（t+4）（t﹣3）＝0，由于t＞0，∴t+4＞0，∴t﹣3＝0，∴BC＝2BE＝2t＝2×3＝6．故选：C．3．（2022•鞍山）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，AB＝4cm，CD⊥AB，垂足为点D，动点M从点A出发沿AB方向以cm/s的速度匀速运动到点B，同时动点N从点C出发沿射线DC方向以1cm/s的速度匀速运动．当点M停止运动时，点N也随之停止，连接MN．设运动时间为ts，△MND的面积为Scm2，则下列图象能大致反映S与t之间函数关系的是（）A．B．C．D．【答案】B【解答】解：∵∠ACB＝90°，∠A＝30°，AB＝4，∴∠B＝60°，BC＝AB＝2，AC＝BC＝6，∵CD⊥AB，∴CD＝AC＝3，AD＝CD＝3，BD＝BC＝，∴当M在AD上时，0≤t≤3，MD＝AD﹣AM＝3﹣t，DN＝DC+CN＝3+t，∴S＝MD•DN＝（3﹣t）（3+t）＝﹣t2+，当M在BD上时，3＜t≤4，MD＝AM﹣AD＝t﹣3，∴S＝MD•DN＝（t﹣3）（3+t）＝t2﹣，故选：B．4．（2022•菏泽）如图，等腰Rt△ABC与矩形DEFG在同一水平线上，AB＝DE ＝2，DG＝3，现将等腰Rt△ABC沿箭头所指方向水平平移，平移距离x是自点C到达DE之时开始计算，至AB离开GF为止．等腰Rt△ABC与矩形DEFG的重合部分面积记为y，则能大致反映y与x的函数关系的图象为（）A．B．C．D．【答案】B【解答】解：如图，作CH⊥AB于点H，∵AB＝2，△ABC是等腰直角三角形，∴CH＝1，当0≤x≤1时，y＝×2x•x＝x2，当1＜x≤3时，y＝＝1，当3＜x≤4时，y＝1﹣＝﹣（x﹣3）2+1，故选：B．5．（2022•鄂尔多斯）如图①，在正方形ABCD中，点M是AB的中点，点N 是对角线BD上一动点，设DN＝x，AN+MN＝y，已知y与x之间的函数图象如图②所示，点E（a，2）是图象的最低点，那么a的值为（）A．B．2C．D．【答案】 A【解答】解：如图，连接AC交BD于点O，连接NC，连接MC交BD于点N′．∵四边形ABCD是正方形，∴O是BD的中点，∵点M是AB的中点，∴N′是△ABC的重心，∴N′O＝BO，∴N′D＝BD，∵A、C关于BD对称，∴NA＝NC，∴AN+MN＝NC+MN，∵当M、N、C共线时，y的值最小，∴y的值最小就是MC的长，∴MC＝2，设正方形的边长为m，则BM＝m，在Rt△BCM中，由勾股定理得：MC2＝BC2+MB2，∴20＝m2+（m）2，∴m＝4，∴BD＝4，∴a＝N′D＝BD＝×4＝，故选：A．6．（2021•鞍山）如图，△ABC是等边三角形，AB＝6cm，点M从点C出发沿CB方向以1cm/s的速度匀速运动到点B，同时点N从点C出发沿射线CA 方向以2cm/s的速度匀速运动，当点M停止运动时，点N也随之停止．过点M作MP∥CA交AB于点P，连接MN，NP，作△MNP关于直线MP对称的△MN′P，设运动时间为ts，△MN′P与△BMP重叠部分的面积为Scm2，则能表示S与t之间函数关系的大致图象为（）A．B．C．D．【答案】A【解答】解：如图1中，当点N′落在AB上时，取CN的中点T，连接MT．∵CM＝t（cm），CN＝2t（cm），CT＝TN，∴CT＝TN＝t（cm），∵△ABC是等边三角形，∴∠C＝∠A＝60°，∴△MCT是等边三角形，∴TM＝TC＝TN，∴∠CMN＝90°，∵MP∥AC，∴∠BPM＝∠A＝∠MPN＝60°，∠BMP＝∠C＝60°，∠C+∠CMP＝180°，∴∠CMP＝120°，△BMP是等边三角形，∴BM＝MP，∵∠CMP+∠MPN＝180°，∴CM∥PN，∵MP∥CN，∴四边形CMPN是平行四边形，∴PM＝CN＝BM＝2t，∴3t＝6，∴t＝2，如图2中，当0＜t≤2时，过点M作MK⊥AC于K，则MK＝CM•sin60°＝t，∴S＝•（6﹣t）•t＝﹣t2+t．如图3中，当2＜t≤6时，S＝•MQ•PQ＝×（6﹣t）×（6﹣t）＝×（6﹣t）2，观察图象可知，选项A符合题意，故选：A．7．（2021•威海）如图，在菱形ABCD中，AB＝2cm，∠D＝60°，点P，Q同时从点A出发，点P以1cm/s的速度沿A﹣C﹣D的方向运动，点Q以2cm/s 的速度沿A﹣B﹣C﹣D的方向运动，当其中一点到达D点时，两点停止运动．设运动时间为x（s），△APQ的面积为y（cm2），则下列图象中能大致反映y与x之间函数关系的是（）A．B．C．D．【答案】A【解答】解：∵四边形ABCD为菱形，∴AB＝BC＝CD＝DA＝2cm，∠B＝∠D＝60°．∴△ABC、△ACD都是等边三角形，∴∠CAB＝∠ACB＝∠ACD＝60°．如图1所示，当0≤x≤1时，AQ＝2xcm，AP＝xcm，作PE⊥AB于E，∴PE＝sin∠PAE×AP＝（cm），∴y＝AQ•PE＝×2x×＝，故D选项不正确；如图2，当1＜x≤2时，AP＝xcm，CQ＝（4﹣2x）cm，作QF⊥AC于点F，∴QF＝sin∠ACB•CQ＝（cm），∴y＝＝＝，故B选项不正确；如图3，当2＜x≤3时，CQ＝（2x﹣4）cm，CP＝（x﹣2）cm，∴PQ＝CQ﹣CP＝2x﹣4﹣x+2＝（x﹣2）cm，作AG⊥DC于点G，∴AG＝sin∠ACD•AC＝×2＝（cm），∴y＝＝＝．故C选项不正确，故选：A．8．（2021•日照）如图，平面图形ABD由直角边长为1的等腰直角△AOD和扇形BOD组成，点P在线段AB上，PQ⊥AB，且PQ交AD或交于点Q．设AP＝x（0＜x＜2），图中阴影部分表示的平面图形APQ（或APQD）的面积为y，则函数y关于x的大致图象是（）A．B．C．D．【答案】D【解答】解：当Q在AD上时，即点P在AO上时，有0＜x≤1，此时阴影部分为等腰直角三角形，∴y＝，该函数是二次函数，且开口向上，排除B，C选项；当点Q在弧BD上时，补全图形如图所示，阴影部分的面积等于等腰直角△AOD的面积加上扇形BOD的面积，再减去平面图形PBQ的面积即减去弓形QBF的面积，设∠QOB＝θ，则∠QOF＝2θ，∴，S弓形QBF＝﹣S△QOF，当θ＝45°时，AP＝x＝1+≈1.7，S弓形QBF＝﹣＝﹣，y＝+﹣（﹣）＝≈1.14，当θ＝30°时，AP＝x≈1.87，S弓形QBF＝﹣＝﹣，y＝+﹣（﹣）＝≈1.24，当θ＝60°时，AP＝x≈1.5，y≈0.98，在A，D选项中分别找到这两个特殊值，对比发现，选项D符合题意．故选：D．法二、当1＜x＜2时，即P在OB之间时，设∠QOD＝θ，则θ∈（0，），则PQ＝cosθ，OP＝sinθ，则弧QD的长为θπ，此时S阴影＝+θπ+sinθcosθ＝+θ+sin2θ，∴y随x的增大而增大，而且增加的速度越来越慢，分析四个选项中的图象，只有选项D符合．故选：D．9．（2021•辽宁）如图，在矩形ABCD中，AB＝6，AD＝4，E是CD的中点，射线AE与BC的延长线相交于点F，点M从A出发，沿A→B→F的路线匀速运动到点F停止．过点M作MN⊥AF于点N．设AN的长为x，△AMN 的面积为S，则能大致反映S与x之间函数关系的图象是（）A．B．C．D．【答案】B【解答】解：如图，∵E是CD的中点，∴CE＝DE，∵四边形ABCD是矩形，∴∠D＝∠DCF＝90°，AD＝BC＝4，在△ADE与△FCE中，，∴△ADE≌△FCE（SAS），∴CF＝AD＝4，∴BF＝CF+BC＝8，∴AF＝，当点M在AB上时，在Rt△AMN和Rt△AFB中，tan∠NAM＝，∴NM＝x＝x，∴△AMN的面积S＝×x×x＝x2，∴当点M在AB上时，函数图象是开口向上、经过原点的抛物线的一部分；当点M在BF上时，如图，AN＝x，NF＝10﹣x，在Rt△FMN和Rt△FBA中，tan∠F＝，∴＝﹣，∴△AMN的面积S＝＝﹣，∴当点M在BF上时，函数图象是开口向下的抛物线的一部分；故选：B．10．（2021•苏州）如图，线段AB＝10，点C、D在AB上，AC＝BD＝1．已知点P从点C出发，以每秒1个单位长度的速度沿着AB向点D移动，到达点D后停止移动．在点P移动过程中作如下操作：先以点P为圆心，PA、PB的长为半径分别作两个圆心角均为60°的扇形，再将两个扇形分别围成两个圆锥的侧面，设点P的移动时间为t（秒），两个圆锥的底面面积之和为S，则S关于t的函数图象大致是（）A．B．C．D．【答案】D【解答】解：∵AB＝10，AC＝BD＝1，∴CD＝10﹣1﹣1＝8，∵PC＝t，∴AP＝t+1，PB＝8﹣t+1＝9﹣t，设围成的两个圆锥底面圆半径分别为r和R则：2πr＝；．解得：r＝，R＝，∴两个圆锥的底面面积之和为S＝＝＝，根据函数关系式可以发现该函数图象是一个开口向上的二次函数．故选：D．11．（2021•甘肃）如图1，在△ABC中，AB＝BC，BD⊥AC于点D（AD＞BD）．动点M从A点出发，沿折线AB→BC方向运动，运动到点C停止．设点M的运动路程为x，△AMD的面积为y，y与x的函数图象如图2，则AC的长为（）A．3B．6C．8D．9【答案】B【解答】解：由图2知，AB+BC＝2，∵AB＝BC，∴AB＝，∵AB＝BC，BD⊥AC，∴AC＝2AD，∠ADB＝90°，在Rt△ABD中，AD²+BD²＝AB²＝13①，设点M到AC的距离为h，∴S△ADM＝AD•h，∵动点M从A点出发，沿折线AB→BC方向运动，∴当点M运动到点B时，△ADM的面积最大，即h＝BD，由图2知，△ADM的面积最大为3，∴AD•BD＝3，∴AD•BD＝6②，①+2×②得，AD²+BD²+2AD•BD＝13+2×6＝25，∴（AD+BD）²＝25，∴AD+BD＝5（负值舍去），∴BD＝5﹣AD③，将③代入②得，AD（5﹣AD）＝6，∴AD＝3或AD＝2，∵AD＞BD，∴AD＝3，∴AC＝2AD＝6，故选：B．12．（2021•百色）如图，矩形ABCD各边中点分别是E、F、G、H，AB＝2，BC＝2，M为AB上一动点，过点M作直线l⊥AB，若点M从点A开始沿着AB方向移动到点B即停（直线l随点M移动），直线l扫过矩形内部和四边形EFGH外部的面积之和记为S．设AM＝x，则S关于x的函数图象大致是（）A．B．C．D．【答案】D【解答】解：①当M点运动在AE段，此时S＝S△HAE+S△GHD﹣S△EOM﹣S△GPS，∵四边形ABCD是矩形，直线l⊥AB，H、E、F、G为AD、AB、BC、CD的中点，∴AH＝AD＝＝1，AE＝AB＝，S△HAE＝S△GHD，S△EOM＝S△GPS，∴S＝2S△HAE﹣2S△EOM，∴S△HAE＝AE•AH＝；∵直线l⊥AB，∴∠OME＝∠A＝90°，∠HEA＝∠OEM，∴△HAE∽△OME，∴，∴OM＝，又∵ME＝AE﹣AM＝﹣x，∴OM＝ME＝，∴S△EOM＝，∴S＝2S△HAE﹣2S△EOM＝，此时，对应抛物线开口向下；②当M点运动到在BE段，此时，S＝S△HAE+S△GHD+S△EO1M1+S△GP1S1，即S＝2S△HAE+2S△EO1M1，与①同理，O1M1＝，又∵M1E＝AM1﹣AE＝x﹣，∴O1M1＝M1E＝，∴S△EO1M1＝，∴S＝2S△HAE+2S△EO1M1＝，此时，对应抛物线开口向上，故选：D．13．（2021•鄂尔多斯）如图①，在矩形ABCD中，H为CD边上的一点，点M 从点A出发沿折线AH﹣HC﹣CB运动到点B停止，点N从点A出发沿AB 运动到点B停止，它们的运动速度都是1cm/s，若点M、N同时开始运动，设运动时间为t（s），△AMN的面积为S（cm2），已知S与t之间函数图象如图②所示，则下列结论正确的是（）①当0＜t≤6时，△AMN是等边三角形．②在运动过程中，使得△ADM为等腰三角形的点M一共有3个．③当0＜t≤6时，S＝．④当t＝9+时，△ADH∽△ABM．⑤当9＜t＜9+3时，S＝﹣3t+9+3．A．①③④B．①③⑤C．①②④D．③④⑤【答案】A【解答】解：由图②可知：点M、N两点经过6秒时，S最大，此时点M在点H处，点N在点B处并停止不动，如图，①∵点M、N两点的运动速度为1cm/s，∴AH＝AB＝6cm，∵四边形ABCD是矩形，∴CD＝AB＝6 cm．∵当t＝6s时，S＝9cm2，∴×AB×BC＝9．∴BC＝3cm．∵当6≤t≤9时，S＝且保持不变，∴点N在B处不动，点M在线段HC上运动，运动时间为（9﹣6）秒，∴HC＝3 cm，即点H为CD的中点．∴BH＝cm．∴AB＝AH＝BH＝6cm，∴△ABM为等边三角形．∴∠HAB＝60°．∵点M、N同时开始运动，速度均为1cm/s，∴AM＝AN，∴当0＜t≤6时，△AMN为等边三角形．故①正确；②如图，当点M在AD的垂直平分线上时，△ADM为等腰三角形：此时有两个符合条件的点；当AD＝AM时，△ADM为等腰三角形，如图：当DA＝DM时，△ADM为等腰三角形，如图：综上所述，在运动过程中，使得△ADM为等腰三角形的点M一共有4个．∴②不正确；③过点M作ME⊥AB于点E，如图，由题意：AM＝AN＝t，由①知：∠HAB＝60°．在Rt△AME中，∵sin∠MAE＝，∴ME＝AM•sin60°＝tcm，∴S＝AN×ME＝cm2．∴③正确；④当t＝9+时，CM＝cm，如图，由①知：BC＝3cm，∴MB＝BC﹣CM＝2cm．∵AB＝6cm，∴tan∠MAB＝，∴∠MAB＝30°．∵∠HAB＝60°，∴∠DAH＝90°﹣60°＝30°．∴∠DAH＝∠BAM．∵∠D＝∠B＝90°，∴△ADH∽△ABM．∴④正确；⑤当9＜t＜9+3时，此时点M在边BC上，如图，此时MB＝9+3﹣t，∴S＝×AB×MB＝×6×（9+3﹣t）＝27+9﹣3t．∴⑤不正确；综上，结论正确的有：①③④．故选：A．14．（2021•通辽）如图，在矩形ABCD中，AB＝4，BC＝3，动点P，Q同时从点A出发，点P沿A→B→C的路径运动，点Q沿A→D→C的路径运动，点P，Q的运动速度相同，当点P到达点C时，点Q也随之停止运动，连接PQ．设点P的运动路程为x，PQ2为y，则y关于x的函数图象大致是（）A．B．C．D．【答案】C【解答】解：当0≤x≤3时，在Rt△APQ中，∠QAP＝90°，AP＝AQ＝x，∴PQ2＝2x2．∴y＝PQ2＝2x2；当3≤x≤4时，DQ＝x﹣3，AP＝x，∴y＝PQ2＝32+32＝18；当4≤x≤7时，CP＝7﹣x，CQ＝7﹣x，∴y＝PQ2＝CP2+CQ2＝2x2﹣28x+98．故选：C．15．（2021•湖北）如图，AC为矩形ABCD的对角线，已知AD＝3，CD＝4，点P沿折线C﹣A﹣D以每秒1个单位长度的速度运动（运动到D点停止），过点P作PE⊥BC于点E，则△CPE的面积y与点P运动的路程x间的函数图象大致是（）A．B．C．D．【答案】D【解答】解：∵BC∥AD，∴∠ACB＝∠DAC，∵∠PEC＝∠D＝90°，∴△PCE∽△CAD，∴＝＝，∵AD＝3，CD＝4，∴AC＝＝5，∴当P在CA上时，即当0＜x≤5时，PE＝＝x，CE＝＝x，∴y＝PE•CE＝＝x2，当P在AD上运动时，即当5＜x≤8时，PE＝CD＝4，CE＝8﹣x，∴y＝PE•CE＝×4×（8﹣x）＝16﹣2x，综上，当0＜x≤5时，函数图象为二次函数图象，且y随x增大而增大，当5＜x≤8时，函数图象为一次函数图象，且y随x增大而减小，故选：D．16．（2021•衡阳）如图1，菱形ABCD的对角线AC与BD相交于点O，P、Q 两点同时从O点出发，以1厘米/秒的速度在菱形的对角线及边上运动．点P 的运动路线为O﹣A﹣D﹣O，点Q的运动路线为O﹣C﹣B﹣O．设运动的时间为x秒，P、Q间的距离为y厘米，y与x的函数关系的图象大致如图2所示，当点P在A﹣D段上运动且P、Q两点间的距离最短时，P、Q两点的运动路程之和为厘米．【答案】（2+3）【解答】解：由图分析易知：当点P从O→A运动时，点Q从O→C运动时，y不断增大，当点P运动到A点，点Q运动到C点时，由图象知此时y＝PQ＝2cm，∴AC＝2cm，∵四边形ABCD为菱形，∴AC⊥BD，OA＝OC＝＝cm，当点P运动到D点，Q运动到B点，结合图象，易知此时，y＝BD＝2cm，∴OD＝OB＝BD＝1cm，在Rt△ADO中，AD＝＝＝2（cm），∴AD＝AB＝BC＝DC＝2cm，如图，当点P在A﹣D段上运动，点P运动到点E处，点Q在C﹣B段上运动，点Q运动到点F处时，P、Q两点的距离最短，此时，OE＝OF＝＝，AE＝CF＝＝＝，∴当点P在A﹣D段上运动且P、Q两点间的距离最短时，P、Q两点的运动路程之和为：（cm），故答案为：（2+3）．17．（2021•武汉）如图（1），在△ABC中，AB＝AC，∠BAC＝90°，边AB上的点D从顶点A出发，向顶点B运动，同时，边BC上的点E从顶点B出发，向顶点C运动，D，E两点运动速度的大小相等，设x＝AD，y＝AE+CD，y 关于x的函数图象如图（2），图象过点（0，2），则图象最低点的横坐标是．【答案】﹣1【解答】解：∵图象过点（0，2），即当x＝AD＝BE＝0时，点D与A重合，点E与B重合，此时y＝AE+CD＝AB+AC＝2，∵△ABC为等腰直角三角形，∴AB＝AC＝1，过点A作AF⊥BC于点F，过点B作NB⊥BC，并使得BN＝AC，如图所示：∵AD＝BE，∠NBE＝∠CAD，∴△NBE≌△CAD（SAS），∴NE＝CD，又∵y＝AE+CD，∴y＝AE+CD＝AE+NE，当A、E、N三点共线时，y取得最小值，如图所示，此时：AD＝BE＝x，AC＝BN＝1，∴AF＝AC•sin45°＝，\又∵∠BEN＝∠FEA，∠＝∠AFE∴△NBE∽△AFE∴，即，解得：x＝，∴图象最低点的横坐标为：﹣1．故答案为：．18．（2022•营口）如图1，在四边形ABCD中，BC∥AD，∠D＝90°，∠A＝45°，动点P，Q同时从点A出发，点P以cm/s的速度沿AB向点B运动（运动到B点即停止），点Q以2cm/s的速度沿折线AD→DC向终点C运动，设点Q的运动时间为x（s），△APQ的面积为y（cm2），若y与x之间的函数关系的图象如图2所示，当x＝（s）时，则y＝cm2．【答案】【解答】解：过点D作DE⊥AB，垂足为E，在Rt△ADE中，∵∠AED＝90°，∠EAD＝45°，∴，∵点P的速度为cm/s，点Q的速度为2cm/s，∴AP＝x，AQ＝2x，∴，在△APQ和△AED中，＝，∠A＝45°，∴△AED∽△APQ，∴点Q在AD上运动时，△APQ为等腰直角三角形，∴AP＝PQ＝x，∴当点Q在AD上运动时，y＝AP•AQ＝×x×x＝x2，由图像可知，当y＝9此时面积最大，x＝3或﹣3（负值舍去），∴AD＝2x＝6cm，当3＜x≤4时，过点P作PF⊥AD于点F，如图：此时S△APQ＝S△APF+S四边形PQDF﹣S△ADQ，在Rt△APF中，AP＝x，∠PAF＝45°，∴AF＝PF＝x，FD＝6﹣x，QD＝2x﹣6，∴S△APQ＝x2+（x+2x﹣6）•（6﹣x）﹣×6×（2x﹣6），即y＝﹣x2+6x，当x＝时，y＝﹣（）2+6×＝，故答案为：．。

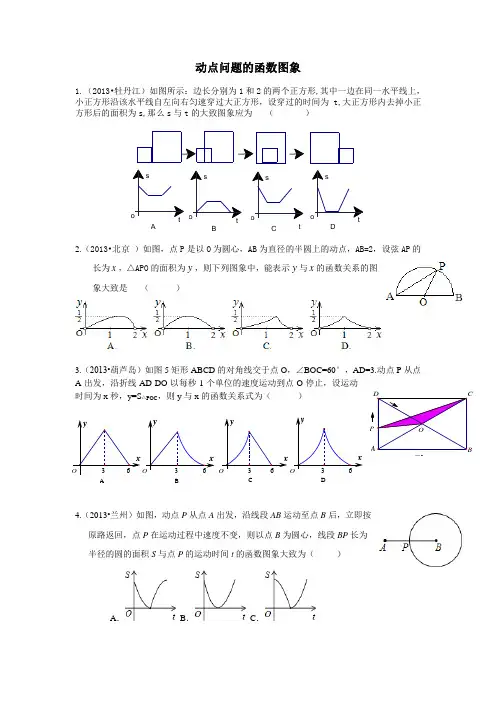
xxxxyy yyDCBA63636363OOOO图5OCD ABP 动点问题的函数图象1.（2013•牡丹江）如图所示：边长分别为1和2的两个正方形,其中一边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为t,大正方形内去掉小正方形后的面积为s,那么s 与t 的大致图象应为 （ ）2.（2013•北京 ）如图，点P 是以O 为圆心，AB 为直径的半圆上的动点，AB=2，设弦AP 的长为x ，△APO 的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是 （ ）3.（2013•葫芦岛）如图5矩形ABCD 的对角线交于点O ，∠BOC=60°，AD=3.动点P 从点A 出发，沿折线AD-DO 以每秒1个单位的速度运动到点O 停止，设运动时间为x 秒，y=S △POC ，则y 与x 的函数关系式为（ ）4.（2013•兰州）如图，动点P 从点A 出发，沿线段AB 运动至点B 后，立即按原路返回，点P在运动过程中速度不变，则以点B 为圆心，线段BP 长为半径的圆的面积S 与点P 的运动时间t 的函数图象大致为（ ）A ．B ． C．D C B A s t o s t o s t o o t sD ．5.（2013•铁岭）如图，点G 、E 、A 、B 在一条直线上，Rt △EFG 从如图所示是位置出发，沿直线AB 向右匀速运动，当点G 与B 重合时停止运动．设△EFG 与矩形ABCD 重合部分的面积为S ，运动时间为t ，则S 与t 的图象大致是（ ） A ．B ．C ．D ．6.（2012•铁岭）如图， ABCD 的边长为8，面积为32，四个全等的小平行四边形对称中心分别在ABCD 的顶点上，它们的各边与 ABCD 的各边分别平行，且与 ABCD 相似.若小平行四边形的一边长为 ，且0＜ ≤8，阴影部分的面积的和为 ，则与 之间的函数关系的大致图象是 （ ）A. B. C. D.7.（2011•安徽）如图，点P 是菱形ABCD 的对角线AC 上的一个动点，过点P 垂直于AC 的直线交菱形ABCD 的边于M 、N 两点．设AC ＝2，BD ＝1，AP ＝x ，△AMN 的面积为y ，则y 关于x 的函数图象大致形状是 （ ）8.（2011•葫芦岛）如图，在矩形中截取两个相同的圆作为圆柱的上下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱．设矩形的长与宽分别为y 和x ，则y 与x 函数的图象大致是( )．OOOOx x x x y y y y 1 2 1 2 1 2 1 2 A ．B ．C ．D ． x x y y x ABCDMN P9.（2012•营口）如图，菱形ABCD 的边长为2，∠B=30°．动点P 从点B 出发，沿B ﹣C ﹣D 的路线向点D 运动．设△ABP 的面积为y （B 、P 两点重合时，△ABP 的面积可以看做0），点P 运动的路程为x ，则y 与x 之间函数关系的图象大致为（ ）10.（2011•辽阳）如图，等边△ABC 的边长为4，M 为BC 上一动点(M 不与B 、C 重合)，若EB ＝1，∠EMF ＝60°，点E 在AB 边上，点F 在AC 边上．设BM ＝x ，CF ＝y ，则当点M 从点B 运动到点C 时，y 关于x 的函数图象是( )．11.（2011•营口）如图，半径为1的圆和边长为3的正方形在同一水平线上，圆沿水平线从左向右匀速穿过正方形，设穿过时间为t ，正方形除去圆部分的面积为S (阴影部分)，则S 与t 的大致图象为( )．12.（2013•营口）如图1，在矩形ABCD 中，动点E 从点B 出发，沿B A DA ．B ．C ．D ．A DEyC 方向运动至点C 处停止，设点E 运动的路程为x ，△BCE 的面积为y ，如果y 关于x 的函数图象如图2所示，则当7 x 时，点E 应运动到（ ）A ．点C 处B ．点D 处C ．点B 处D ．点A 处13.（2012•鞍山）如图，在直角梯形ABCD 中，AD ∥BC ，∠A=90°，AB=BC=4，DE ⊥BC 于点E ，且E 是BC 中点；动点P 从点E 出发沿路径ED→DA→AB 以每秒1个单位长度的速度向终点B 运动；设点P 的运动时间为t 秒，△PBC 的面积为S ，则下列能反映S 与t 的函数关系的图象是（ ） 14.15.（2013•自贡）如图，已知A 、B 是反比例函数上的两点，BC ∥x轴，交y 轴于C ，动点P 从坐标原点O 出发，沿O→A→B→C 匀速运动，终点为C ，过运动路线上任意一点P 作PM ⊥x 轴于M ，PN ⊥y 轴于N ，设四边形OMPN 的面积为S ，P 点运动的时间为t ，则S 关于t 的函数图象大致是（ ）A ．B ．C ．D ．A ．B ．C ．D ．16.（2012•烟台）如图，矩形ABCD 中，P 为CD 中点，点Q 为AB 上的动点（不与A ，B 重合）．过Q 作QM ⊥PA 于M ，QN ⊥PB 于N ．设AQ 的长度为x ，QM 与QN 的长度和为y ．则能表示y 与x 之间的函数关系的图象大致是（ ） A ． B ． C ． D ．17.（2012•岳阳）如图，两个边长相等的正方形ABCD 和EFGH ，正方形EFGH 的顶点E 固定在正方形ABCD 的对称中心位置，正方形EFGH 绕点E 顺时针方向旋转，设它们重叠部分的面积为S ，旋转的角度为θ，S 与θ的函数关系的大致图象是（ ） 18.（2012•攀枝花）如图，直角梯形AOCD 的边OC 在x 轴上，O为坐标原点，CD 垂直于x 轴，D （5，4），AD=2．若动点E 、F 同时从点O 出发，E 点沿折线OA→AD→DC 运动，到达C 点时停止；F 点沿OC 运动，到达C 点是停止，它们运动的速度都是每秒1个单位长度．设E 运动秒x 时，△EOF 的面积为y （平方单位），则y 关于x 的函数图象大致为（ ）A ．B ．C ．D ．19.（2012•桂林）如图，在边长为4的正方形ABCD 中，动点P 从A 点出发，以每秒1个单位A ．B ．C ．D ．长度的速度沿AB 向B 点运动，同时动点Q 从B 点出发，以每秒2个单位长度的速度沿BC →CD 方向运动，当P 运动到B 点时，P 、Q 两点同时停止运动．设P 点运动的时间为t ，△APQ 的面积为S ，则S 与t 的函数关系的图象是（ ）20.（2010•烟台）如图，AB 为半圆的直径，点P 为AB 上一动点，动点P 从点A 出发，沿AB 匀速运动到点B ，运动时间为t ，分别以AP 于PB 为直径做半圆，则图中阴影部分的面积S 与时间t 之间的函数图像大致为A B CD。

函数中的动点问题1. 点在线段上运动：根据线段长或图形面积求函数关系。

如：如图所示，点P在线段BC、CD、DA上运动，△ABP的面积变化情况的图象是什么样的？解析：看清横轴和纵轴表示的量。

答案：2. 双动点变化：两动点同时运动，分析图形面积变化图象。

如图1，在矩形ABCD中，点E是对角线AC 的三等分点（靠近点A），动点F从点C出发沿C→A→B运动，当点F与点B重合时停止运动。

设点F运动的路程为x，△BEF的面积为y，那么图2能表示y与x函数关系的大致图象吗？图1 图2解析：动点问题的函数图象，解决本题应首先看清横轴和纵轴表示的量，然后根据动点的行程判断y的变化情况。

答案：能。

3. 图形运动变化所形成的函数问题：图形整体运动时，形成的函数问题；如图，边长为1和2的两个正方形，其一边在同一水平线上，小正方形自左向右匀速穿过大正方形，设穿过的时间为t，阴影部分面积为S，那么S与t的函数图象大致是什么？解析：图形运动变化所形成的函数问题．关键是理解图形运动过程中的几个分界点。

答案：4. 实际问题中的运动变化图象如图，小亮在操场上玩，一段时间内沿M→A→B→M的路径匀速散步，能近似刻画小亮到出发点M的距离y与时间x之间关系的函数图象是（）解析：解决实际问题中的运动变化图象，要根据几何图形和图形上的数据分析得出所对应的函数的类型和所需要的条件，结合实际意义选出正确的图象。

答案：总结：研究在不同位置时点的运动变化所产生的线段、面积的变化关系是重点。

例题如图，M是边长为4的正方形AD边的中点，动点P自A点起，由A⇒B⇒C⇒D匀速运动，直线MP扫过正方形所形成面积为y，点P运动的路程为x，则表示y与x的函数关系的图象为（）A.B.C.D.解析：分别求出P 在AB 段、BC 段、CD 段的函数解析式或判断函数的类型，即可判断。

答案：解：点P 在AB 段时，函数解析式是：y ＝21AP•AM＝21×2x＝x ，是正比例函数y x =；点P 在BC 段时，函数解析式是：1()242y AM BP AB x =+⋅=-，是一次函数24y x =-；则2,1BC AB k k ==，BC AB k k ∴>。

关于动点问题的总结 “动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静关键:动中求静.数学思想：分类思想 函数思想 方程思想 数形结合思想 转化思想函数揭示了运动变化过程中量与量之间的变化规律,和动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,一、应用勾股定理建立函数解析式例1(2000年·上海)如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P,PH ⊥OA,垂足为H,△OPH 的重心为G.(1)当点P 在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH x =,GP y =,求y 关于x 的函数解析式，并写出函数的定义域(即自变量x 的取值范围).(3)如果△PGH 是等腰三角形,试求出线段PH的长.解:(1)当点P 在弧AB 上运动时,OP 保持不变,H MN G P O AB图1于是线段GO 、GP 、GH 中,有长度保持不变的线段，这条线段是GH=32NH=2132⋅OP=2. (2)在Rt △POH 中,22236x PH OP OH -=-=, ∴2362121x OH MH -==.在Rt △MPH 中,.∴y =GP=32MP=233631x + (0<x <6).(3)△PGH 是等腰三角形有三种可能情况:①GP=PH 时,x x =+233631,解得6=x . 经检验, 6=x 是原方程的根,且符合题意.②GP=GH 时, 2336312=+x ,解得0=x . 经检验, 0=x 是原方程的根,但不符合题意.③PH=GH 时,2=x .综上所述,如果△PGH 是等腰三角形,那么线段PH 的长为6或2.二、应用比例式建立函数解析式例2（2006年·山东）如图2,在△ABC 中,AB=AC=1,点D,E 在直线BC 上运动.设BD=,x CE=y .(1)如果∠BAC=30°,∠DAE=105°,试确定y 与x 之间的函数解析式；(2)如果∠BAC 的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.A EDC B图2解:(1)在△ABC 中,∵AB=AC,∠BAC=30°,∴∠ABC=∠ACB=75°, ∴∠ABD=∠ACE=105°.∵∠BAC=30°,∠DAE=105°, ∴∠DAB+∠CAE=75°, 又∠DAB+∠ADB=∠ABC=75°,∴∠CAE=∠ADB,∴△ADB ∽△EAC, ∴ACBD CE AB =, ∴11x y =, ∴xy 1=. (2)由于∠DAB+∠CAE=αβ-,又∠DAB+∠ADB=∠ABC=290α-︒,且函数关系式成立, ∴290α-︒=αβ-, 整理得=-2αβ︒90. 当=-2αβ︒90时,函数解析式x y 1=成立.例3(2005年·上海)如图3(1),在△ABC 中,∠ABC=90°,AB=4,BC=3. 点O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D,交线段OC 于点E.作EP ⊥ED,交射线AB 于点P,交射线CB 于点F.(1)求证: △ADE ∽△AEP.(2)设OA=x ,AP=y ,求y 关于x 的函数解析式,并写出它的定义域.(3)当BF=1时,求线段AP 的长.解:(1)连结OD.根据题意,得OD ⊥AB,∴∠ODA=90°,∠ODA=∠DEP.A 3(2)3(1)又由OD=OE,得∠ODE=∠OED.∴∠ADE=∠AEP, ∴△ADE ∽△AEP.(2)∵∠ABC=90°,AB=4,BC=3, ∴AC=5. ∵∠ABC=∠ADO=90°, ∴OD ∥BC, ∴53x OD =,54x AD =, ∴OD=x 53,AD=x 54. ∴AE=x x 53+=x 58. ∵△ADE ∽△AEP, ∴AE AD AP AE =, ∴x x y x 585458=. ∴x y 516= (8250≤<x ). (3)当BF=1时，①若EP 交线段CB 的延长线于点F,如图3(1)，则CF=4. ∵∠ADE=∠AEP, ∴∠PDE=∠PEC. ∵∠FBP=∠DEP=90°, ∠FPB=∠DPE,∴∠F=∠PDE, ∴∠F=∠FEC, ∴CF=CE.∴5-x 58=4,得85=x .可求得2=y ,即AP=2. ②若EP 交线段CB 于点F,如图3(2), 则CF=2.类似①,可得CF=CE.∴5-x 58=2,得815=x . 可求得6=y ,即AP=6.综上所述, 当BF=1时,线段AP 的长为2或6.三、应用求图形面积的方法建立函数关系式例4（2004年·上海）如图,在△ABC 中,∠BAC=90°,AB=AC=22,⊙A 的半径为1.若点O 在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .A B C O H(1)求y 关于x 的函数解析式,并写出函数的定义域.(2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A 相切时, △AOC 的面积.解:(1)过点A 作AH ⊥BC,垂足为H.∵∠BAC=90°,AB=AC=22, ∴BC=4,AH=21BC=2. ∴OC=4-x . ∵AH OC S AOC ⋅=∆21, ∴4+-=x y (40<<x ).(2)①当⊙O 与⊙A 外切时,在Rt △AOH 中,OA=1+x ,OH=x -2, ∴222)2(2)1(x x -+=+. 解得67=x . 此时,△AOC 的面积y =617674=-. ②当⊙O 与⊙A 内切时,在Rt △AOH 中,OA=1-x ,OH=2-x , ∴222)2(2)1(-+=-x x . 解得27=x . 此时,△AOC 的面积y =21274=-. 综上所述,当⊙O 与⊙A 相切时,△AOC 的面积为617或21.动态几何特点----问题背景是特殊图形，（特殊角、特殊图形的性质、图形的特殊位置。

【考点精讲】动点问题是中考的常考点，对于解决动点问题中，点动会牵扯到线动、面动，解决这类题目要“以静制动”，即把动态的问题转化为静态问题来解决，一般方法是抓住变化中的“不变量”，以不变应万变。

而对于动点问题的图象问题的解决，要抓住图形中的关键点，例如与x 轴、y 轴的交点，图象上的转折点、图象中与x 轴、y 轴平行的线等图象。

【典例精析】例题1 （贵州贵阳中考）如图，在直径为AB 的半圆O 上有一动点P 从A 点出发，按顺时针方向绕半圆匀速运动到B 点，然后再以相同的速度沿着直径回到A 点停止，线段OP 的长度d 与运动时间t 之间的函数关系用图象描述大致是（ ）（A ． Ｂ． C ． D ．思路导航：情境分三段，点P 在圆周上、在OB 上，在AO 上，因此图象分三段，根据在每一段上线段OP 的长度d 随运动时间t 的变化来确定。

答案：点P 在圆周上时，d 不随t 的变化而变化，故第一段图象平行x 轴，点P 在OB 上，d 随t 的增加而减小，直到0，故此段图象呈下降趋势，点P 在AO 上，d 随t 的增加而增大，直到增加到半径的长度，即与第一段图象齐平，故选A 。

点评：先根据运动过程理解函数与自变量的变化规律以及分段情况，然后对照所给图象找到满足问题情境变化的规律。

注意弄清函数图象中横轴和纵轴意义，以及每段图象的起始点。

例题2 矩形ABCD 中，AB ＝20cm ，BC ＝10cm ，有一点P 沿着矩形从A 向B 再向C 以2cm/s 的速度移动。

（1）求△APC 的面积S 与时间t 的函数解析式，并指出自变量的取值范围。

（2）当面积为20cm2时，求点P的位置。

思路导航：△APC的面积为12AP BC⋅或12AP AB⋅，只要利用含t的代数式表示AP和PC即可。

答案：解：（1）1210(010)21(302)20(1015) 2t tSt t⎧⨯⨯<≤⎪⎪=⎨⎪⨯-⨯<<⎪⎩，化简得：10(010)30020(1015)t tSt t<≤⎧=⎨-<<⎩。

动点问题的函数图象（北京习题集）（教师版）一．选择题（共3小题）1．（2019秋•西城区期末）如图，5AB =，O 是AB 的中点，P 是以点O 为圆心，AB 为直径的半圆上的一个动点（点P 与点A ，B 可以重合），连接PA ，过P 作PM AB ⊥于点M ．设AP x =，AP AM y -=，则下列图象中，能表示y 与x 的函数关系的图象大致是( )A ．B ．C ．D ．2．（2019秋•房山区期末）如图，在平面直角坐标系xOy 中，以(3,0)为圆心作P ，P 与x 轴交于A 、B ，与y 轴交于点(0,2)C ，Q 为P 上不同于A 、B 的任意一点，连接QA 、QB ，过P 点分别作PE QA ⊥于E ，PF QB ⊥于F ．设点Q 的横坐标为x ，22PE PF y +=．当Q 点在P 上顺时针从点A 运动到点B 的过程中，下列图象中能表示y 与x 的函数关系的部分图象是( )A ．B ．C．D．3．（2019•顺义区一模）如图，点A、C、E、F在直线l上，且2EF=，四边形ABCD，EFGH，EFNMAC=，1均为正方形，将正方形ABCD沿直线l向右平移，若起始位置为点C与点E重合，终止位置为点A与点F重合．设点C平移的距离为x，正方形ABCD的边位于矩形MNGH内部的长度为y，则y与x的函数图象大致为()A．B．C．D．二．填空题（共3小题）4．（2019秋•海淀区校级月考）如图1，点O为正六边形对角线的交点，机器人置于该正六边形的某顶点处，小宇操作机器人以每秒1个单位长度的速度在图1中给出的线段路径上运行，他将机器人运行的时间设为t秒，机器人到点A的距离设为y，得到的函数图象如图2．通过观察函数图象，可以得到下列推断：①机器人一定经过点D ； ②机器人一定经过点E ；③当3t =时，机器人一定位于点O ；④存在符合图2的运行路线，使机器人能够恰好经过六边形的全部6个顶点； 其中正确的是 （填序号）．5．（2016秋•西城区校级期中）小阳在如图1所示的扇形舞台上沿O M N --匀速行走，他从点O 出发，沿箭头所示的方向经过点M 再走到点N ，共用时70秒．有一台摄像机选择了一个固定的位置记录了小阳的走路过程，设小阳走路的时间为t （单位：秒），他与摄像机的距离为y （单位：米），表示y 与t 的函数关系的图象大致如图2，则这个固定位置可能是图1中的点 （在点P 、N 、Q 、M 、O 中选取）．6．（2016春•西城区期末）如图，在ABC ∆中，点P 从点A 出发向点C 运动，在运动过程中，设x 表示线段AP 的长，y 表示线段BP 的长，y 与x 之间的关系如图2所示，则线段AB 的长为 ，线段BC 的长为 ．三．解答题（共9小题）7．（2020春•海淀区校级月考）如图1，在ABC ∆中，点D 是线段BC 上的动点，将线段AD 绕点D 逆时针旋转90︒得到线段DE ，连接BE ．若已知8BC cm =，设B ，D 两点间的距离为xcm ，A ，D 两点间的距离为1y cm ，B ，E 两点距离为2y cm ．小明根据学习函数的经验，分别对函数1y ，2y 随x 的变化而变化的规律进行了探究，请补充完整．下面是小明的探究过程的几组对应值．（1）按照下表中自变量x 的值进行取点画图，测量分别得到了与x 的几组对应值如下表：（说明补全表格时相关数值保留一位小数） /x cm 0 1 2 3 4 5 6 7 8 1/y cm 7.036.20 5.44 4.76 4.21 3.85 3.73 3.87 4.26 2/y cma5.664.32b1.971.592.273.434.73（2）在同一平面直角坐标系xoy 中，描出补全后的表中各组数值所对应的点1(,)x y ，2(,)x y ，并画出函数1y ，2y 的图象；（3）结合函数图象（如图2)，解决问题： ①当E 在线段BC 上时，BD 的长约为 cm ； ②当BDE ∆为等腰三角形时，BD 的长x 约为 cm ．8．（2019秋•通州区期末）如图1，在钝角ABC ∆中，点P 为BC 上的一个动点，连接PA ，将射线PA 绕点P 逆时针旋转60︒，交线段AB 于点D ．已知30C ∠=︒，23CA cm =，7BC cm =，设B ，P 两点间的距离为xcm ，A ，D 两点间的距离ycm ．小牧根据学习函数的经验，对函数y 随自变量x 的变化而变化的规律进行了探究．下面是小牧探究的过程，请补充完整：（1）根据图形．可以判断此函数自变量x 的取值范围是 ；（2）通过取点、画图、测量，得到了x 与y 的几组值，如表： /x cm⋯ 0.51 1.02 1.91 3.47 34.16 4.47 ⋯ /y cm⋯3.973.222.421.66a2.022.50⋯通过测量．可以得到a 的值为 ；（3）在图2平面直角坐标系xOy 中．描出表中以各对对应值为坐标的点，画出该函数的图象； （4）结合画出的函数图象，解决问题：当 3.5AD cm =时，BP 的长度约为 cm ．9．（2019秋•朝阳区期末）如图，在矩形ABCD 中，E 是BA 延长线上的定点，M 为BC 边上的一个动点，连接ME ，将射线ME 绕点M 顺时针旋转76︒，交射线CD 于点F ，连接MD ．小东根据学习函数的经验，对线段BM ，DF ，DM 的长度之间的关系进行了探究． 下面是小东探究的过程，请补充完整：（1）对于点M 在BC 上的不同位置，画图、测量，得到了线段BM ，DF ，DM 的长度的几组值，如下表：位置1 位置2 位置3 位置4 位置5 位置6 位置7 位置8 位置9 /BM cm 0.00 0.53 1.00 1.69 2.17 2.96 3.46 3.79 4.00 /DF cm 0.00 1.00 1.74 2.49 2.69 2.21 1.14 0.00 1.00 /DM cm4.123.613.162.522.091.441.141.021.00在BM ，DF ，DM 的长度这三个量中，确定 的长度是自变量， 的长度和 的长度都是这个自变量的函数；（2）在同一平面直角坐标系xOy 中，画出（1）中所确定的函数的图象；（3）结合画出的函数图象，解决问题：当2DF cm =时，DM 的长度约为 cm ．10．（2020•西城区校级模拟）如图1，P 是矩形ABCD 内部的一定点，M 是AB 边上一动点，连接MP 并延长与矩形ABCD 的一边交于点N ，连接AN ．已知6AB cm =，设A ，M 两点间的距离为xcm ，M ，N 两点间的距离为1y cm ，A ，N 两点间的距离为2y cm ．小欣根据学习函数的经验，分别对函数1y ，2y 随自变量x 的变化而变化的规律进行了探究．下面是小欣的探究过程，请补充完整：（1）按照下表中自变量x 的值进行取点、画图、测量，分别得到了1y ，2y 与x 的几组对应值；/x cm 0 1 2 3 4 5 6 1/y cm 6.30 5.40 4.22 3.13 3.25 4.52 2/y cm6.306.346.436.695.754.813.98（2）在同一平面直角坐标系xOy 中，描出以补全后的表中各组对应值所对应的点1(,)x y ，并画出函数1y 的图象；（3）结合函数图象，解决问题：当AMN ∆为等腰三角形时，AM 的长度约为 cm ．11．（2019秋•房山区期末）如图，在正方形ABCD 中，5AB cm =，点E 在正方形边上沿B C D →→运动（含端点），连接AE ，以AE 为边，在线段右侧作正方形AEFG ，连接DF 、DG ．小颖根据学习函数的经验，在点E 运动过程中，对线段AE 、DF 、DG 的长度之间的关系进行了探究． 下面是小颖的探究过程，请补充完整：（1）对于点E 在BC 、CD 边上的不同位置，画图、测量，得到了线段AE 、DF 、DG 的长度的几组值，如下表：位置1 位置2 位置3 位置4 位置5 位置6 位置7 /AE cm 5.00 5.50 6.00 7.07 5.99 5.50 5.00 /DF cm5.00 3.55 3.72 5.00 3.71 3.55 5.00 /DG cm0.002.303.315.005.285.697.07在AE 、DF 和DG 的长度这三个量中，确定 的长度是自变量， 的长度和 的长度都是这个自变量的函数． （2）在同一平面直角坐标系xOy 中，画出（1）中所确定的函数的图象：（3）结合函数图象，解决问题：当GDF ∆为等腰三角形时，AE 的长约为 ．12．（2019春•西城区期末）如图1，在菱形ABCD 中，对角线AC ，BD 相交于点O ，4AC cm =，2BD cm =，E ，F 分别是AB ，BC 的中点，点P 是对角线AC 上的一个动点，设AP xcm =，1PE y cm =，2PF y cm =．小明根据学习函数的经验，分别对这两种函数随自变量的变化而变化的情况进行了探究，下面是小明探究过程，请补充完整：（1）画函数1y 的图象①按表中自变量的值进行取点、画图、测量，得到了1y 与x 的几组对应值：/x cm 0 0.5 1 1.5 2 2.5 3 3.5 4 1/y cm1.120.50.711.121.582.062.553.04②在图2所给坐标系中描出补全后的表中的各对应值为坐标的点，画出函数1y 的图象； （2）画函数2y 的图象，在同一坐标系中，画出函数2y 的图象； （3）根据画出的函数1y 的图象、函数2y 的图象，解决问题 ①函数1y 的最小值是 ；②函数1y 的图象与函数2y 的图象的交点表示的含义是 ； ③若PE PC =，AP 的长约为 cm13．（2019•怀柔区模拟）如图1，在直角梯形ABCD 中，动点P 从B 点出发，沿B C D A →→→匀速运动，设点P 运动的路程为x ，ABP ∆的面积为y ，图象如图2所示． （1）在这个变化中，自变量、因变量分别是 、 ； （2）当点P 运动的路程4x =时，ABP ∆的面积为y = ； （3）求AB 的长和梯形ABCD 的面积．14．（2019•朝阳区校级一模）如图，半圆O 的直径5AB cm =，点M 在AB 上且1AM cm =，点P 是半圆O 上的动点，过点B 作BQ PM ⊥交PM （或PM 的延长线）于点Q ．设PM xcm =，BQ ycm =．（当点P 与点A 或点B 重合时，y 的值为0)小石根据学习函数的经验，对函数y 随自变量x 的变化而变化的规律进行了探究． 下面是小石的探究过程，请补充完整：（1）通过取点、画图、测量，得到了x 与y 的几组值，如表： /x cm1 1.52 2.53 3.54 /y cm3.73.83.32.5（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：当PBM∆的面积为1时，PM的长度约为cm．15．（2019春•海淀区校级期末）如图，40∠的角平分线PD交AOB∠=︒，点C在OA上，点P为OB上一动点，CPB射线OA于D．设OCP∠的度数为y︒．∠的度数为x︒，CDP小明对x与y之间满足的等量关系进行了探究，下面是小明的探究过程，请补充完整；（1）x的取值范围是；（2）按照表中x的值进行取点、画图、计算，分别得到了y与x的几组对应值，补全表格；x︒5060708090y︒5（3）在平面直角坐标系xOy中，①描出表中各组数值所对应的点(,)x y；②描出当120x=︒时，y的值；（4）若AOBα∠=︒，题目中的其它条件不变，用含α、x的代数式表示y为．动点问题的函数图象（北京习题集）（教师版）参考答案与试题解析一．选择题（共3小题）1．（2019秋•西城区期末）如图，5AB =，O 是AB 的中点，P 是以点O 为圆心，AB 为直径的半圆上的一个动点（点P 与点A ，B 可以重合），连接PA ，过P 作PM AB ⊥于点M ．设AP x =，AP AM y -=，则下列图象中，能表示y 与x 的函数关系的图象大致是( )A ．B ．C ．D ．【分析】连接BP ，根据圆周角定理得到90APB ∠=︒，证明AMP APB ∆∆∽，根据相似三角形的性质得到215AM x =，得到215y x x =-，根据二次函数的图象判断．【解答】解：连接BP ，AB 为圆的直径，90APB ∴∠=︒，PM AB ⊥，90AMP ∴∠=︒，APB AMP ∴∠=∠，又A A ∠=∠， AMP APB ∴∆∆∽，∴AM AP AP AB =，即5AM xx =，解得，215AM x =，21(05)5y x x x ∴=-，故选：A ．【点评】本题考查了动点问题的函数图象：函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．解决本题的关键是利用圆周角定理得到90ACB ∠=︒．2．（2019秋•房山区期末）如图，在平面直角坐标系xOy 中，以(3,0)为圆心作P ，P 与x 轴交于A 、B ，与y 轴交于点(0,2)C ，Q 为P 上不同于A 、B 的任意一点，连接QA 、QB ，过P 点分别作PE QA ⊥于E ，PF QB ⊥于F ．设点Q 的横坐标为x ，22PE PF y +=．当Q 点在P 上顺时针从点A 运动到点B 的过程中，下列图象中能表示y 与x 的函数关系的部分图象是( )A ．B ．C ．D ．【分析】连接PC ．根据勾股定理求得213PC =，即圆的半径的平方13=；根据三个角是直角的四边形是矩形，得矩形PEQF ，则PE QF =，根据垂径定理，得QF BF =，则22222PE PF BF PF PC y +=+==，从而判断函数的图象． 【解答】解：连接PC ．C，P，(0,2)(3,0)213PC∴=．AC是直径，∴∠=︒．Q90又PE QA⊥于F，⊥于E，PF QB∴四边形PEQF是矩形．∴=．PE QF⊥于F，PF QB∴=．QF BF∴=．AE BF2222213∴=+=+==．y PE PF BF PF PC故选：A．【点评】此题综合运用矩形的判定和性质、垂径定理求得y的值，常数函数是平行于坐标轴的一条直线．3．（2019•顺义区一模）如图，点A、C、E、F在直线l上，且2EF=，四边形ABCD，EFGH，EFNMAC=，1均为正方形，将正方形ABCD沿直线l向右平移，若起始位置为点C与点E重合，终止位置为点A与点F重合．设点C平移的距离为x，正方形ABCD的边位于矩形MNGH内部的长度为y，则y与x的函数图象大致为()A．B．C ．D ．【分析】根据题意可以分析出各段的函数图象，从而可以解答本题． 【解答】解：由题意可得，点C 从点E 运动到点F 的过程中，y 随x 的增大而增大，函数解析式为222sin 45xy x =⨯=︒，函数图象是一条线段， 当点D 从点H 运动到点G 的过程中，y 随x 的增大不会发生变化，此过程函数图象是一条线段， 当点A 从点E 运动到点F 的过程中，y 随x 的增大而减小，函数图象是一条线段， 故选：A ．【点评】本题考查动点问题的函数图象，解答本题的关键是明确题意，利用数形结合的思想解答． 二．填空题（共3小题）4．（2019秋•海淀区校级月考）如图1，点O 为正六边形对角线的交点，机器人置于该正六边形的某顶点处，小宇操作机器人以每秒1个单位长度的速度在图1中给出的线段路径上运行，他将机器人运行的时间设为t 秒，机器人到点A 的距离设为y ，得到的函数图象如图2．通过观察函数图象，可以得到下列推断： ①机器人一定经过点D ； ②机器人一定经过点E ；③当3t =时，机器人一定位于点O ；④存在符合图2的运行路线，使机器人能够恰好经过六边形的全部6个顶点； 其中正确的是 ①③ （填序号）．【分析】①所有点中，只有点D 到A 距离为2个单位，即可求解；②因为机器人可能在F 点或B 点出发，当从B 出发时，不经过点E ，即可求解． ③当3t =时，机器人距离点A 距离为1个单位长度，机器人一定位于点O ，即可求解； ④由②知，机器人不经过点E ，即可求解．【解答】解：由图象可知，机器人距离点1A 个单位长度，可能在F 或B 点，则正六边形边长为1； ①所有点中，只有点D 到A 距离为2个单位，故①正确；②因为机器人可能在F点或B点出发，当从B出发时，不经过点E，故②错误．③观察图象t在34t=时，机器人距离点A距离为-之间时，图象具有对称性则可知，机器人在OB或OF上，则当31个单位长度，机器人一定位于点O，故③正确；④由②知，机器人不经过点E，故④错误；故答案为：①③．【点评】本题为动点问题的函数图象探究题，解答时要注意动点到达临界前后时图象的变化趋势．5．（2016秋•西城区校级期中）小阳在如图1所示的扇形舞台上沿O M N--匀速行走，他从点O出发，沿箭头所示的方向经过点M再走到点N，共用时70秒．有一台摄像机选择了一个固定的位置记录了小阳的走路过程，设小阳走路的时间为t（单位：秒），他与摄像机的距离为y（单位：米），表示y与t的函数关系的图象大致如图2，则这个固定位置可能是图1中的点P（在点P、N、Q、M、O中选取）．【分析】根据图1和图2，分别就点P、N、Q、M、O讨论，找哪一个点与图2符合即可作出判断．【解答】解：①如果固定位置在点O，开始应该是在原点，而图2开始是y轴的正半轴，所以不可能是O；②如果固定位置在点M或N，那么是运动过程中，一定有一处是0y=，而图2中没有这样的点，所以不可能是M 或N；③如果固定位置在点Q，则从O到M，是先y随t的增大而减小，再是y随t的增大而增大，而图2中，前面都是y随t的增大而减小，所以不可能是Q；④如果固定位置在点P，则从O到M是：y随t的增大而减小，且从M到N的圆弧的中点时，y随t的增大而减小，最后由中点到N是y随t的增大而增大，所以点P符合，则这个固定位置可能是图1中的点P；故答案为：P．【点评】本题主要考查了函数的图象，根据排查法和函数图象的基本特点解决此题．6．（2016春•西城区期末）如图，在ABC∆中，点P从点A出发向点C运动，在运动过程中，设x表示线段AP的长，y表示线段BP的长，y与x之间的关系如图2所示，则线段AB的长为2，线段BC的长为．【分析】如图1中，作BE AC ⊥于E ，由图2可知，2AB =，1AE =，4AC =，3EC =，在Rt ABE ∆，Rt BEC ∆中利用勾股定理即可解决问题．【解答】解：如图1中，作BE AC ⊥于E ．由图2可知，2AB =，1AE =，4AC =，3EC =， 在Rt ABE ∆中，90AEB ∠=︒，2222213BE AB AE ∴=-=-，在Rt BEC ∆中，2222(3)323BC EB EC ++=． 故答案分别为2，3【点评】本题考查动点问题的函数图象、勾股定理等知识，解题的关键是读懂图象信息，学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型． 三．解答题（共9小题）7．（2020春•海淀区校级月考）如图1，在ABC ∆中，点D 是线段BC 上的动点，将线段AD 绕点D 逆时针旋转90︒得到线段DE ，连接BE ．若已知8BC cm =，设B ，D 两点间的距离为xcm ，A ，D 两点间的距离为1y cm ，B ，E 两点距离为2y cm ．小明根据学习函数的经验，分别对函数1y ，2y 随x 的变化而变化的规律进行了探究，请补充完整．下面是小明的探究过程的几组对应值．（1）按照下表中自变量x 的值进行取点画图，测量分别得到了与x 的几组对应值如下表：（说明补全表格时相关数值保留一位小数） /x cm 0 1 2 3 4 5 6 7 8 1/y cm 7.036.20 5.44 4.76 4.21 3.85 3.73 3.87 4.26 2/y cma5.664.32b1.971.592.273.434.73（2）在同一平面直角坐标系xoy 中，描出补全后的表中各组数值所对应的点1(,)x y ，2(,)x y ，并画出函数1y ，2y 的图象；（3）结合函数图象（如图2)，解决问题： ①当E 在线段BC 上时，BD 的长约为 6 cm ； ②当BDE ∆为等腰三角形时，BD 的长x 约为 cm ． 【分析】（1）当0x =时，7.037.0a AD ==≈，即可求解； （2）描点即可；（3）①当E 在线段BC 上时，即：12x y y =+；②分BE DE =、BE BD =、DE BE =三种情况，分别求解即可． 【解答】解：（1）当0x =时，7.037.0a AD ==≈， 3.0b =； （2）描绘后表格如下图：（3）①当E 在线段BC 上时，即：12x y y =+， 从图象可以看出，当6x =时，126y y +=， 故答案为6；②当BE DE =时，即：12y y =，此时7.5x =或0， 故7.5x =；当BE BD =时，即：2y x =，在图上画出直线y x =，此时3x ≈；当DE BE =时，即：1y x =， 从上图可以看出 4.1x ≈； 故答案为：3或4.1或7.5．【点评】本题考查的是动点函数图象，此类题目通常在补全表格后，画出函数图象，依据图象求解相关问题，通常从图上上查阅的数值为近视值．8．（2019秋•通州区期末）如图1，在钝角ABC ∆中，点P 为BC 上的一个动点，连接PA ，将射线PA 绕点P 逆时针旋转60︒，交线段AB 于点D ．已知30C ∠=︒，23CA cm =，7BC cm =，设B ，P 两点间的距离为xcm ，A ，D 两点间的距离ycm ．小牧根据学习函数的经验，对函数y 随自变量x 的变化而变化的规律进行了探究．下面是小牧探究的过程，请补充完整：（1）根据图形．可以判断此函数自变量x 的取值范围是 05x ； （2）通过取点、画图、测量，得到了x 与y 的几组值，如表： /x cm⋯ 0.51 1.02 1.91 3.47 34.16 4.47 ⋯ /y cm⋯3.973.222.421.66a2.022.50⋯通过测量．可以得到a 的值为 ；（3）在图2平面直角坐标系xOy 中．描出表中以各对对应值为坐标的点，画出该函数的图象； （4）结合画出的函数图象，解决问题：当 3.5AD cm =时，BP 的长度约为 cm ．【分析】（1）可以作AH BC ⊥于点H ，由30C ∠=︒，23CA =，易得3AH =，3CH =，当射线PA 绕点P 逆时针旋转60︒，交线段AB 于点D ，点D 与点B 重合时，60AP B ∠'=︒，进而可得x 的取值范围； （2）通过测量即可得结果；（3）根据表格数据在平面直角坐标系中即可画出图象；（4）结合画出的函数图象，当 3.5AD cm =时，即可得BP 的长度． 【解答】解：（1）根据题意，如图，作AH BC ⊥于点H ，30C ∠=︒，23CA =， 3AH ∴=，3CH =，当射线PA 绕点P 逆时针旋转60︒，交线段AB 于点D ， 点D 与点B 重合时， 60AP B ∠'=︒，3tan30313P H AH ∴'=︒=⨯=， 2CP CH P H ∴'=-'=， 30C ∠=︒， 30CAP ∴∠'=︒， 2P C P A ∴'='=， 725P B ∴'=-=，05x ∴；故答案为：05x ； （2）通过测量可得： 1.74a =．故答案为1.74；（3）如图所示：即为所求作的函数图象；（4）观察图象可知：当 3.5AD cm =时，BP 的长度约为0.78或者4.81． 故答案为：0.78或者4.81．【点评】本题考查了动点问题的函数图象，解决本题的关键是根据表格数据准确画出图象．9．（2019秋•朝阳区期末）如图，在矩形ABCD 中，E 是BA 延长线上的定点，M 为BC 边上的一个动点，连接ME ，将射线ME 绕点M 顺时针旋转76︒，交射线CD 于点F ，连接MD ．小东根据学习函数的经验，对线段BM ，DF ，DM 的长度之间的关系进行了探究． 下面是小东探究的过程，请补充完整：（1）对于点M在BC上的不同位置，画图、测量，得到了线段BM，DF，DM的长度的几组值，如下表：位置1位置2位置3位置4位置5位置6位置7位置8位置9BM cm0.000.53 1.00 1.69 2.17 2.96 3.46 3.79 4.00/DF cm0.00 1.00 1.74 2.49 2.69 2.21 1.140.00 1.00/DM cm 4.12 3.61 3.16 2.52 2.09 1.44 1.14 1.02 1.00/在BM，DF，DM的长度这三个量中，确定BM的长度是自变量，的长度和的长度都是这个自变量的函数；（2）在同一平面直角坐标系xOy中，画出（1）中所确定的函数的图象；（3）结合画出的函数图象，解决问题：当2=时，DM的长度约为cm．DF cm【分析】（1）由函数的定义可得；（2）描点即可；（3）结合图象，即可求解．【解答】解：（1）由函数的定义可得：BM的长度是自变量，DF的长度和DM的长度都是这个自变量的函数，故答案为：BM，DF，DM；（2）如图所示．（3）由图象得到：当2=时，DM的长度约为2.98cm和1.35cm．DF cm【点评】本题考查的动点问题的函数图象，函数的作图，主要通过描点的方法作图，再根据题意测量出相应的长度．10．（2020•西城区校级模拟）如图1，P是矩形ABCD内部的一定点，M是AB边上一动点，连接MP并延长与矩形ABCD 的一边交于点N ，连接AN ．已知6AB cm =，设A ，M 两点间的距离为xcm ，M ，N 两点间的距离为1y cm ，A ，N 两点间的距离为2y cm ．小欣根据学习函数的经验，分别对函数1y ，2y 随自变量x 的变化而变化的规律进行了探究．下面是小欣的探究过程，请补充完整：（1）按照下表中自变量x 的值进行取点、画图、测量，分别得到了1y ，2y 与x 的几组对应值； /x cm 0 1 2 3 4 5 6 1/y cm 6.30 5.40 4.22 3.13 3.25 4.52 2/y cm6.306.346.436.695.754.813.98（2）在同一平面直角坐标系xOy 中，描出以补全后的表中各组对应值所对应的点1(,)x y ，并画出函数1y 的图象；（3）结合函数图象，解决问题：当AMN ∆为等腰三角形时，AM 的长度约为 3.3或4.8或5.7 cm ． 【分析】（1）利用图象法解决问题即可． （2）利用描点法画出函数图象即可解决问题．（3）通过图象求出直线y x =与两个函数图象的交点坐标以及函数1y 与2y 的交点坐标即可解决问题． 【解答】解：（1）观察图象可知(2,4.80)D ， 故答案为4.80．（2）两个函数图象如图所示：（3）两个函数与直线y x =的交点为A ，B ，函数1y 与2y 的交点为C ， 观察图象可知：(3.3,3.3)A ，(4.8,4.8)B ，(5.7,4)C ． AMN ∴∆为等腰三角形时，AM 的值约为3.3或4.8或5.7．故答案为3.3或4.8或5.7．【点评】本题考查动点问题的函数图象，函数图象等知识，解题的关键是学会利用图象法解决问题，属于中考常考题型．11．（2019秋•房山区期末）如图，在正方形ABCD 中，5AB cm =，点E 在正方形边上沿B C D →→运动（含端点），连接AE ，以AE 为边，在线段右侧作正方形AEFG ，连接DF 、DG ．小颖根据学习函数的经验，在点E 运动过程中，对线段AE 、DF 、DG 的长度之间的关系进行了探究． 下面是小颖的探究过程，请补充完整：（1）对于点E 在BC 、CD 边上的不同位置，画图、测量，得到了线段AE 、DF 、DG 的长度的几组值，如下表：位置1 位置2 位置3 位置4 位置5 位置6 位置7 /AE cm 5.00 5.50 6.00 7.07 5.99 5.50 5.00 /DF cm 5.00 3.55 3.72 5.00 3.71 3.55 5.00 /DG cm0.002.303.315.005.285.697.07在AE 、DF 和DG 的长度这三个量中，确定 DG 的长度是自变量， 的长度和 的长度都是这个自变量的函数．（2）在同一平面直角坐标系xOy 中，画出（1）中所确定的函数的图象：（3）结合函数图象，解决问题：当GDF∆为等腰三角形时，AE的长约为．【分析】（1）根据已知条件结合观察表格数据即可得结论；（2）根据表格数据即可画出函数图象；（3）两个函数图象的交点即为当GDF∆为等腰三角形时，AE的长．【解答】解：（1）根据已知条件，观察表格数据可知：确定DG的长度是自变量，AE的长度和DF的长度都是这个自变量的函数．故答案为：DG、AE、DF；（2）如图即为函数图象；（3）观察图象可知：两个函数图象的交点或5.65即为当GDF ∆为等腰三角形时，AE 的长． 故答案为7.07或5.00或5.65．【点评】本题考查了动点问题的函数图象，解决本题的关键是根据表格数据准确画出图象．12．（2019春•西城区期末）如图1，在菱形ABCD 中，对角线AC ，BD 相交于点O ，4AC cm =，2BD cm =，E ，F 分别是AB ，BC 的中点，点P 是对角线AC 上的一个动点，设AP xcm =，1PE y cm =，2PF y cm =．小明根据学习函数的经验，分别对这两种函数随自变量的变化而变化的情况进行了探究，下面是小明探究过程，请补充完整：（1）画函数1y 的图象①按表中自变量的值进行取点、画图、测量，得到了1y 与x 的几组对应值： /x cm 0 0.5 1 1.5 2 2.5 3 3.5 4 1/y cm1.120.50.711.121.582.062.553.04②在图2所给坐标系中描出补全后的表中的各对应值为坐标的点，画出函数1y 的图象； （2）画函数2y 的图象，在同一坐标系中，画出函数2y 的图象；（3）根据画出的函数1y 的图象、函数2y 的图象，解决问题 ①函数1y 的最小值是 0.5 ；②函数1y 的图象与函数2y 的图象的交点表示的含义是 ； ③若PE PC =，AP 的长约为 cm 【分析】（1）①由函数的对称性即可求解； ②补全表格后即可绘出函数图象；（2）1y 、2y 关于2x =对称，即可描点得到2y 的图象； （3）①从图象可以看出1y 的最小值；②函数1y 的图象与函数2y 的图象的交点点P 到达点O 处； ③画出4y x =-，与1y 的交点，即可求解．【解答】解：（1）①由函数的对称性知，当0.5x =时，10.71y =； ②补全表格后描绘得到以下图象：（2）1y 、2y 关于2x =对称，故描点得到2y 的图象，如下：（3）①从图象可以看出函数1y 的最小值为：0.5， 故答案为0.5；②函数1y 的图象与函数2y 的图象的交点点P 到达点O 处， 故答案为：点P 到达点O 处；③PE PC =，即：14y PC AC x x ==-=-， 在图上画出直线:4l y x =-，直线l 与1y 的交点坐标为： 2.5x =， 1.58y =， 故答案为2.5．【点评】本题考查的是动点函数图象，此类题目通常通过补齐表格点的数值，画出函数图象，从函数图象上查看相应数据，题目灵活性大，对应变力有很高的要求．13．（2019•怀柔区模拟）如图1，在直角梯形ABCD 中，动点P 从B 点出发，沿B C D A →→→匀速运动，设点P 运动的路程为x ，ABP ∆的面积为y ，图象如图2所示． （1）在这个变化中，自变量、因变量分别是 x 、 ； （2）当点P 运动的路程4x =时，ABP ∆的面积为y = ； （3）求AB 的长和梯形ABCD 的面积．【分析】（1）依据点P 运动的路程为x ，ABP ∆的面积为y ，即可得到自变量和因变量； （2）依据函数图象，即可得到点P 运动的路程4x =时，ABP ∆的面积；（3）根据图象得出BC 的长，以及此时三角形ABP 面积，利用三角形面积公式求出AB 的长即可；由函数图象得出DC 的长，利用梯形面积公式求出梯形ABCD 面积即可． 【解答】解：（1）点P 运动的路程为x ，ABP ∆的面积为y ，∴自变量为x ，因变量为y ，故答案为：x ，y ；（2）由图可得，当点P 运动的路程4x =时，ABP ∆的面积为16y =， 故答案为：16；（3）根据图象得：4BC =，此时ABP ∆为16，∴1162AB BC =，即14162AB ⨯⨯=， 解得：8AB =；由图象得：945DC =-=，则()()114582622ABCD S BC DC AB =⨯⨯+=⨯⨯+=梯形．【点评】此题考查了动点问题的函数图象，弄清函数图象上的信息是解本题的关键．14．（2019•朝阳区校级一模）如图，半圆O 的直径5AB cm =，点M 在AB 上且1AM cm =，点P 是半圆O 上的动点，过点B 作BQ PM ⊥交PM （或PM 的延长线）于点Q ．设PM xcm =，BQ ycm =．（当点P 与点A 或点B 重合时，y 的值为0)小石根据学习函数的经验，对函数y 随自变量x 的变化而变化的规律进行了探究． 下面是小石的探究过程，请补充完整：（1）通过取点、画图、测量，得到了x 与y 的几组值，如表： /x cm1 1.52 2.53 3.54 /y cm3.743.83.32.5（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；（3）结合画出的函数图象，解决问题：当PBM ∆的面积为1时，PM 的长度约为 cm ．【分析】（1）当2x =时，PM AB ⊥，此时Q 与M 重合，4BQ BM ==，当4x =时，点P 与B 重合，此时0BQ =； （2）利用描点法画出函数图象即可；（3）根据直角三角形30度角的性质，求出2y =，观察图象写出对应的x 的值即可． 【解答】解：（1）当2x =时，PM AB ⊥，此时Q 与M 重合，4BQ BM ==，。

专题02动点问题的函数图象【考点1】随时间变化的函数关系【例1】（2018•东城区二模）有一圆形苗圃如图1所示，中间有两条交叉过道AB，CD，它们为苗圃Oe 的直径，且AB CD⊥．入口K位于¶AD中点，园丁在苗圃圆周或两条交叉过道上匀速行进．设该园丁行进的时间为x，与入口K的距离为y，表示y与x的函数关系的图象大致如图2所示，则该园丁行进的路线可能是()A．A O D→→→→→D．O D B C→→→C．D O C→→B．C A O B【分析】采用排除法解题，注意由圆的对称性，D O A-路线呈现对称性，图象应用对称特征．--、B C【解析】解：按选项A中路线，图象应呈现对称性，故A错误；按选项C，距离K最近点应靠近D，故C错误；选项D中路线，B到C段图象应呈现对称性，故D排除．故选：B．【点拨】本题是动点函数图象问题，解答时注意动点到达临界点前后图象的变化趋势．【变式1-1】（2017•顺义区二模）如图，木杆AB斜靠在墙壁上，30∠=︒，4OABAB=米．当木杆的上端A 沿墙壁NO下滑时，木杆的底端B也随之沿着地面上的射线OM方向滑动．设木杆的顶端A匀速下滑到点O停止，则木杆的中点P到射线OM的距离y（米)与下滑的时间x（秒)之间的函数图象大致是( )A．B．C．D．【分析】作PQ OB⊥，根据三角函数求得OA的长，从而得出其中位线PQ的最大值，再由OA长度与下滑时间满足一次函数关系即可得出答案．【解析】解：如图，过点P作PQ OB⊥于点Q，//∴，PQ OAQ为AB中点，PPQ ∴为AOB ∆的中位线，即12PQ OA =， 30OAB ∠=︒Q ，4AB =，cos 4OA AB OAB ∴=∠==则OP =，当点A 匀速向下滑动时，OA 的长度随时间x 的变化满足一次函数关系， 由于12PQ OA =，PQ ∴的长度与下滑时间满足一次函数关系，且PQ B 选项，故选：B ．【点拨】本题主要考查动点问题的函数图象，解题的关键是根据点A 下滑是匀速得出一次函数关系及由中位线得出PQ 长度的最大值是解题的关键．【考点2】线段间的变量关系【例2】（2019•顺义区一模）如图，点A 、C 、E 、F 在直线l 上，且2AC =，1EF =，四边形ABCD ，EFGH ，EFNM 均为正方形，将正方形ABCD 沿直线l 向右平移，若起始位置为点C 与点E 重合，终止位置为点A 与点F 重合．设点C 平移的距离为x ，正方形ABCD 的边位于矩形MNGH 内部的长度为y ，则y 与x 的函数图象大致为( )A ．B ．C ．D ．【分析】根据题意可以分析出各段的函数图象，从而可以解答本题．【解析】解：由题意可得，点C 从点E 运动到点F 的过程中，y 随x 的增大而增大，函数解析式为2sin 45x y =⨯=︒，函数图象是一条线段，当点D 从点H 运动到点G 的过程中，y 随x 的增大不会发生变化，此过程函数图象是一条线段， 当点A 从点E 运动到点F 的过程中，y 随x 的增大而减小，函数图象是一条线段，故选：A ．【点拨】本题考查动点问题的函数图象，解答本题的关键是明确题意，利用数形结合的思想解答．【变式2-1】（2017•朝阳区一模）如图1，在ABC ∆中，AB BC =，AC m =，D ，E 分别是AB ，BC 边的中点，点P 为AC 边上的一个动点，连接PD ，PB ，PE ．设AP x =，图1中某条线段长为y ，若表示y 与x 的函数关系的图象大致如图2所示，则这条线段可能是( )A ．PDB ．PBC ．PED ．PC【分析】观察图2，确定x 为何值取得最小值即可一一判断．【解析】解：A 错误，观察图2可知PD 在4m x =取得最小值． B 、错误．观察图2可知PB 在2m x =取得最小值． C 、正确．观察图2可知PE 在34m x =取得最小值． D 、错误．观察图2可知PC 在x m =取得最小值为0．故选：C ．【点拨】本题主要考查了动点问题的函数图象，灵活应用所学知识是解题的关键，学会利用函数的最值解决问题，属于中考常考题型．【考点3】周长的变化【例3】（2017•东城区二模）如图，点E为菱形ABCD的BC边的中点，动点F在对角线AC上运动，连接BF、EF，设AF x=，BEF∆的周长为y，那么能表示y与x的函数关系的大致图象是()A．B．C．D．【分析】先根据正方形的对称性找到y的最小值，可知图象有最低点，再根据距离最低点x的值的大小>可判断正确的图形．AM MC()【解析】解：如图，连接DE与AC交于点M．则当点F运动到点M处时，三角形BEF∆的周长y最小，且AM MC>．通过分析动点F的运动轨迹可知，y是x的二次函数且有最低点，利用排除法可知图象大致为：故选：B．【点拨】本题考查了动点问题的函数图象．解决有关动点问题的函数图象类习题时，关键是要根据条件找到所给的两个变量之间的变化关系，尤其是在几何问题中，更要注意基本性质的掌握和灵活运用．【变式3-1】（2017•平谷区二模）如图，正方形ABCD中，动点P的运动路线为AB BC，动点Q的运动路线为对角线BD，点P，Q以同样的速度分别从A，B两点同时出发匀速前进，当一个点到达终点停止运动时，另一个点也随之停止．设点P的运动路程为x，PQ的长为y，则下列能大致表示y与x的函数关系的图象为()A．B．C．D．【分析】分两种情况：P点在AB上运动时，点P在BC上运动时；分别判定即可．【解析】解：P点在AB上运动时，y先变小再增大；点P在BC上运动时，y逐渐增大；故选：B．【变式3-2】（2017•石景山区二模）如图1，在矩形ABCD中，对角线AC与BD相交于点O，动点P从点B出发，在线段BC上匀速运动，到达点C时停止．设点P运动的路程为x，线段OP的长为y，如果y 与x的函数图象如图2所示，则矩形ABCD的面积是()A ．20B ．24C ．48D ．60【分析】根据点P 的移动规律，当OP BC ⊥时取最小值3，根据矩形的性质求得矩形的长与宽，易得该矩形的面积．【解析】解：如图2所示，当OP BC ⊥时，4BP CP ==，3OP =，所以26AB OP ==，28BC BP ==，所以矩形ABCD 的面积6848=⨯=．故选：C ．【点拨】本题考查了动点问题的函数图象，关键是根据所给函数图象和点的运动轨迹判断出4BP CP ==，3OP =．【考点4】面积的变化【例4】（2019•东城区二模）如图1，动点P 从菱形ABCD 的顶点A 出发，沿A C D →→以1/cm s 的速度运动到点D ．设点P 的运动时间为()s ，PAB ∆的面积为2()y cm ．表示y 与x 的函数关系的图象如图2所示，则a 的值为( )A B ．52 C ．2 D ．【分析】由图2知，菱形的边长为a ，对角线AC ，则对角线BD 为P在线段AC 上运动时，111222y AP BD =⨯=，即可求解．【解析】解：由图2知，菱形的边长为a ，对角线AC =，则对角线BD 为= 当点P 在线段AC 上运动时，111222y AP BD =⨯=，由图2知，当x =y a =，即12a = 解得：52a =， 故选：B ．【点拨】本题考查的是动点图象问题，涉及到二次函数、解直角三角形等知识，此类问题关键是：弄清楚不同时间段，图象和图形的对应关系，进而求解．【变式4-1】（2018•大兴区一模）如图，在矩形ABCD 中，2AB =，3BC =，点P 在矩形的边上沿B C D A →→→运动．设点P 运动的路程为x ，ABP ∆的面积为y ，则y 关于x 的函数图象大致是( )A ．B ．C ．D ．【分析】要能根据几何图形和图形上的数据分析得出所对应的函数的类型和所需要的条件，结合实际意义画出正确的图象．【解析】解：根据题意和图形可知：点P 按B C D A →→→的顺序在边长为1的正方形边上运动，APB ∆的面积分为3段；当点P 在BC 上移动时，底边不变高逐渐变大，故面积逐渐变大；当点P 在CD 上移动时，底边不变，高不变，故面积不变；当点P 在AD 上时，高不变，底边变小，故面积越来越小直到0为止．故选：B ．【点拨】考查点的运动变化后根据几何图形的面积确定函数的图象，图象需分段讨论．1．（2018•顺义区二模）已知正方形ABCD 的边长为4cm ，动点P 从A 出发，沿AD 边以1/cm s 的速度运动，动点Q 从B 出发，沿BC ，CD 边以2/cm s 的速度运动，点P ，Q 同时出发，运动到点D 均停止运动，设运动时间为x （秒)，BPQ 的面积为2()y cm ，则y 与x 之间的函数图象大致是( )A ．B ．C ．D ．【分析】根据题意，Q 点分别在BC 、CD 上运动时，形成不同的三角形，分别用x 表示即 可．【解析】解：（1）当02x 剟时，2BQ x =14242y x x =⨯⨯=当24x 剟时，如下图2111(44)4(4)(82)4(24)28222y x x x x x x =-+⨯-⨯---⨯⨯-=-++由上可知故选：B ．2．（2018•朝阳一模）如图，ABC ∆是等腰直角三角形，90A ∠=︒，6AB =，点P 是AB 边上一动点（点P 与点A 不重合），以AP 为边作正方形APDE ，设AP x =，正方形APDE 与ABC ∆重合部分（阴影部分）的面积为y ，则下列能大致反映y 与x 的函数关系的图象是( )A ．B ．C ．D ．【分析】如图1，当点D 落在BC 上，利用BPD ∆为等腰直角三角形得到3x =，所以当03x <…时，2y x =，当36x <…时，如图2，正方形APDE 与BC 相交于F 、G ，表示出26DF x =-，所以221(26)2DFG APDE y S S x x ∆=-=-⋅-正方形，然后利用所得的解析式对各选项进行判断．【解析】解：如图1，当点D 落在BC 上，ABC ∆Q 为等腰直角三角形，四边形APDE 为正方形， BPD ∴∆为等腰直角三角形，PB PD x ∴==， 26x ∴=，解得3x =，当03x <…时，2APDE y S x ==正方形，当36x <…时，如图2，正方形APDE 与BC 相交于F 、G ， 易得BPF ∆和DGF ∆都是等腰直角三角形，6PF PB x ∴==-，(6)26DF x x x ∴=--=-，22221(26)1218(6)182DFG APDE y S S x x x x x ∆∴=-=-⋅-=-+-=--+正方形，综上所述，22(03)(6)18(36)x x y x x ⎧<=⎨--+<⎩……． 故选：C ．3．（2018•东城一模）如图1是一座立交桥的示意图（道路宽度忽略不计），A 为入口，F ，G 为出口，其中直行道为AB ，CG ，EF ，且AB CG EF ==；弯道为以点O 为圆心的一段弧，且¶BC，¶CD ，¶DE 所对的圆心角均为90︒．甲、乙两车由A 口同时驶入立交桥，均以10/m s 的速度行驶，从不同出口驶出，其间两车到点O 的距离()y m 与时间()x s 的对应关系如图2所示．结合题目信息，下列说法错误的是( )A ．甲车在立交桥上共行驶8sB ．从F 口出比从G 口出多行驶40mC ．甲车从F 口出，乙车从G 口出D ．立交桥总长为150m【分析】根据题意、结合图象问题可得．【解析】解：由图象可知，两车通过¶BC，¶CD ，¶DE 弧时每段所用时间均为2s ，通过直行道AB ，CG ，EF 时，每段用时为3s ．因此，甲车所用时间为3238s ++=，故A 正确；根据两车运行路线，从F 口驶出比从G 口多走¶CD，¶DE 弧长之和，用时为4s ，则走40m ，故B 正确； 根据两车运行时间，可知甲先驶出，应从G 口驶出，故C 错误； 根据题意立交桥总长为(3233)10150m ⨯+⨯⨯=，过D 正确； 故选：C ．4．（2018•海淀一模）如图1，矩形的一条边长为x ，周长的一半为y ．定义(,)x y 为这个矩形的坐标．如图2，在平面直角坐标系中，直线1x =，3y =将第一象限划分成4个区域．已知矩形1的坐标的对应点A 落在如图所示的双曲线上，矩形2的坐标的对应点落在区域④中．则下面叙述中正确的是( )A ．点A 的横坐标有可能大于3B ．矩形1是正方形时，点A 位于区域②C ．当点A 沿双曲线向上移动时，矩形1的面积减小D ．当点A 位于区域①时，矩形1可能和矩形2全等【分析】A 、根据反比例函数k 一定，并根据图形得：当1x =时，3y <，得3k xy =<，因为y 是矩形周长的一半，即y x >，可判断点A 的横坐标不可能大于3；B 、根据正方形边长相等得：2y x =，得点A 是直线2y x =与双曲线的交点，画图，如图2，交点A 在区域③，可作判断；C 、先表示矩形面积22()S x y x xy x k x =-=-=-，当点A 沿双曲线向上移动时，x 的值会越来越小，矩形1的面积会越来越大，可作判断；D 、当点A 位于区域①，得1x <，另一边为：2y x ->，矩形2的坐标的对应点落在区域④中得：1x >，3y >，即另一边0y x ->，可作判断．【解析】解：设点(,)A x y ， A 、设反比例函数解析式为：(0)ky k x=≠， 由图形可知：当1x =时，3y <， 3k xy ∴=<， y x >Q ，3x ∴<，即点A 的横坐标不可能大于3，故选项A 不正确；B 、当矩形1为正方形时，边长为x ，2y x =，则点A 是直线2y x =与双曲线的交点，如图2，交点A 在区域③， 故选项B 不正确；C 、当一边为x ，则另一边为y x -，22()S x y x xy x k x =-=-=-， Q 当点A 沿双曲线向上移动时，x 的值会越来越小，∴矩形1的面积会越来越大，故选项C 不正确；D 、当点A 位于区域①时，Q 点(,)A x y ，1x ∴<，3y >，即另一边为：2y x ->，矩形2落在区域④中，1x >，3y >，即另一边0y x ->，∴当点A 位于区域①时，矩形1可能和矩形2全等；故选项④正确； 故选：D ．5．（2018•延庆县一模）某游泳池长25米，小林和小明两个人分别在游泳池的A ，B 两边，同时朝着另一边游泳，他们游泳的时间为（秒)，其中0180t 剟，到A 边距离为y （米)，图中的实线和虚线分别表示小林和小明在游泳过程中y 与t 的对应关系．下面有四个推断：①小明游泳的平均速度小于小林游泳的平均速度； ②小明游泳的距离大于小林游泳的距离； ③小明游75米时小林游了90米游泳； ④小明与小林共相遇5次； 其中正确的是( ) A ．①②B ．①③C ．③④D ．②④【分析】利用图象信息，一一判断即可；【解析】解：①错误．小明游泳的平均速度大于小林游泳的平均速度； ②正确．小明游泳的距离大于小林游泳的距离； ③错误，小明游75米时小林游了50米； ④正确．小明与小林共相遇5次； 故选：D ．6．（2018•通州一模）如图1，点O 为正六边形对角线的交点，机器人置于该正六边形的某顶点处，柱柱同学操控机器人以每秒1个单位长度的速度在图1中给出线段路径上运行，柱柱同学将机器人运行时间设为t 秒，机器人到点A 的距离设为y ，得到函数图象如图2，通过观察函数图象，可以得到下列推断：①该正六边形的边长为1；②当3t 时，机器人一定位于点O ；③机器人一定经过点D ；④机器人一定经过点E ；其中正确的有（ ）A ．①④B ．①③C ．①②③D ．②③④【分析】根据图象起始位置猜想点B 或F 为起点，则可以判断①正确，④错误．结合图象判断34t 剟图象的对称性可以判断②正确．结合图象易得③正确．【解答】解：由图象可知，机器人距离点1A 个单位长度，可能在F 或B 点，则正六边形边长为1．故①正确；观察图象t 在34-之间时，图象具有对称性则可知，机器人在OB 或OF 上，则当3t =时，机器人距离点A 距离为1个单位长度，机器人一定位于点O ，故②正确； 所有点中，只有点D 到A 距离为2个单位，故③正确；因为机器人可能在F 点或B 点出发，当从B 出发时，不经过点E ，故④错误． 故选：C ．7．（2017•东城一模）图1是某娱乐节目中一个游戏环节的录制现场，场地由等边ADE ∆和正方形ABCD 组成，正方形ABCD 两条对角线交于点O ，在AD 的中点P 处放置了一台主摄像机．游戏参与者行进的时间为x ，与主摄像机的距离为y ，若游戏参与者匀速行进，且表示y 与x 的函数关系式大致如图2所示，则游戏参与者的行进路线可能是（ ）A ．A O D →→B ．E AC →→C ．A ED →→D ．E A B →→【分析】根据各个选项中的路线进行分析，看哪条路线符号图2的函数图象即可解答本题．【解析】解：由题意可得，当经过的路线是A O D →→时，从A O →，y 随x 的增大先减小后增大且图象对称，从O D →，y 随x 的增大先减小后增大且函数图象对称，故选项A 符号要求；当经过的路线是E A C →→时，从E A →，y 随x 的增大先减小后增大，但后来增大的最大值小于刚开始的值，故选项B 不符号要求；当经过的路线是A E D →→时，从A E →，y 随x 的增大先减小后增大，但后来增大的最大值大于于刚开始的值，故选项C 不符号要求；当经过的路线是E A B →→时，从E A →，y 随x 的增大先减小后增大，但后来增大的最大值小于刚开始的值，故选项D 不符号要求； 故选：A ．8．（2017•房山区一模）如图1，已知点E ，F ，G ，H 是矩形ABCD 各边的中点，6AB =，8BC =，动点M 从点E 出发，沿E F G H E →→→→匀速运动，设点M 运动的路程x ，点M 到矩形的某一个顶点的距离为y ，如果表示y 关于x 函数关系的图象如图2所示，那么这个顶点是矩形的( )A ．点AB ．点BC ．点CD ．点D【分析】由图2得出始点E 到顶点的距离为3，只有顶点A ，B 满足，又由开始时先增大，得出只有顶点B 满足．【解析】解：由图2得出始点E 到顶点的距离为3， 6AB =Q ，∴只有顶点A ，B 满足，又Q 沿E F G H E →→→→匀速运动开始时先增大，∴只有顶点B 满足，故选：B ．9．（2018秋•朝阳期末）如图，在ABC∆中，AB AC=，MN是边BC上一条运动的线段（点M不与点B重合，点N不与点C重合），且12MN BC=，MD BC⊥交AB于点D，NE BC⊥交AC于点E，在MN从左至右的运动过程中，设BM x=，BMD∆的面积减去CNE∆的面积为y，则下列图象中，能表示y与x 的函数关系的图象大致是()A．B．C．D．【分析】设：12a BC=，B Cα∠=∠=，求出MN、CN、DM、AH、EN的长度，利用BMD CNES S S∆∆=-，即可求解．【解析】解：过点A作AH BC⊥，交BC于点H，则12BH HC BC==，设12a BC=，B Cα∠=∠=，则MN a=，2CN BC MN x a a x a x=--=--=-，tan tan DM BM B x α==g ，tan tan AH BH B a α==g ，tan ()tan EN CN C a x α==-g ，21tan tan ()(2)tan 222BMD CNEa a S S S BM DM CN EN x a a x ααα∆∆=-=-=-=-g g g g ， 其中，tan a αg 、2tan 2a α均为常数，故上述函数为一次函数， 故选：A ．10．（2017秋•海淀区期末）两个少年在绿茵场上游戏．小红从点A 出发沿线段AB 运动到点 B ，小兰从点C 出发，以相同的速度沿O e 逆时针运动一周回到点C ，两人的运动路线如图1所示，其中AC DB =．两人同时开始运动，直到都停止运动时游戏结束，其间他们与 点C 的距离y 与时间x （单位：秒）的对应关系如图2所示．则下列说法正确的是（ ）A ．小红的运动路程比小兰的长B ．两人分别在1.09秒和7.49秒的时刻相遇C ．当小红运动到点D 的时候，小兰已经经过了点DD ．在4.84秒时，两人的距离正好等于O e 的半径 【分析】利用图象信息一一判断即可解决问题．【解析】解：A 、小红的运动路程比小兰的短，故本选项不符合题意；B 、两人分别在1.09秒和7.49秒的时刻与点C 距离相等，故本选项不符合题意；C 、当小红运动到点D 的时候，小兰还没有经过了点D ，故本选项不符合题意； D 、当小红运动到点O 的时候，两人的距离正好等于O e 的半径，此时9.684.842t ==，故本选项正确；故选：D．。