2020年人教版八年级上册期末考试复习资料

2020年人教版八年级上册数学期末常考题型复习卷一．选择题1．下列长度的三条线段能组成三角形的是（）A．1，1，2B．4，4，9C．3，4，5D．6，16，82．下列图形中对称轴的条数小于3的是（）A．B．C．D．3．目前世界上刻度最小的标尺是钻石标尺，它的最小刻度为0.2nm（其中1nm＝10﹣9m），用科学记数法表示这个最小刻度（单位：m），结果是（）A．2×10﹣8m B．2×10﹣9m C．2×10﹣10m D．2×10﹣11m4．下列计算错误的是（）A．a2•a＝a3B．（ab）2＝a2b2C．（a2）3＝a6D．﹣a+2a＝﹣2a25．已知△ABC≌△A1B1C1，若∠C＝60°，则∠C1的度数为（）A．50°B．60°C．70°D．120°6．一副三角板如图方式摆放，BM平分∠ABD，DM平分∠BDC，则∠BMD的度数为（）A ．102°B．107.5°C．112.5°D．115°7．如图，在△ABC中，AB的垂直平分线DE交AB于点D，交AC于点E，且AC＝15cm，△BCE的周长等于25cm，则BC的长度等于（）A．5cm B．10cm C．15cm D．20cm8．如图，△ABC的三边AB、BC、CA长分别是10、15、20．其三条角平分线交于点O，将△ABC分为三个三角形，S△ABO：S△BCO：S△CAO等于（）A．1：1：1B．1：2：3C．2：3：4D．3：4：59．要使（6x﹣m）（3x+1）的结果不含x的一次项，则m的值等于（）A．2B．3C．0D．1知识点归纳总结 210．若x+y＝1且xy＝﹣2，则代数式（1﹣x）（1﹣y）的值等于（）A．﹣2B．0C．1D．211．为了疫情防控需要，某防护用品厂计划生产130000个口罩，但是在实际生产时，……，求实际每天生产口罩的个数，在这个题目中，若设实际每天生产口罩x个，可得方程，则题目中用“……”表示的条件应是（）A．每天比原计划多生产500个，结果延期10天完成B．每天比原计划少生产500个，结果提前10天完成C．每天比原计划少生产500个，结果延期10天完成D．每天比原计划多生产500个，结果提前10天完成12．如图，在△ABC中，∠ACB＝90°，Rt△ABC≌Rt△AB'C'，且∠ABC＝∠CAB'，连接BC'，并取BC'的中点D，则下列四种说法：①AC'∥BC；②△ACC'是等腰直角三角形；③AD平分∠CAB'；④AD⊥CB'．其中正确的个数为（）知识点归纳总结 3A．1个B．2个C．3个D．4个二．填空题13．如图，为了安全，建筑工地上的塔吊上部设计成三角形结构，这是利用了三角形的性．14．因式分解：7a2﹣7b2＝．15．当x时，分式有意义．16．如图，点D，E分别在线段AB，AC上，CD与BE相交于点P，已知AD＝AE．若△ABE≌△ACD，则可添加的条件为．知识点归纳总结 417．在平面直角坐标系中，点A（﹣3，﹣2）关于y轴的对称点为．18．已知25x2+kxy+4y2是一个完全平方式，那么k的值是．19．如图，在△ABC中，BD，CE是角平分线，它们交于点O，∠BOC＝140°，则∠A＝．20．如图，△ABC中，AB＝AC，BC＝4，△ABC的面积为20，腰AC的垂直平分线EF分别交边AC，AB于点E，F，若D为BC边的中点，M为线段EF上一动点，则△CDM的周长的最小值为．三．解答题21．计算：（1）3x3y•（2xy2﹣3xy）（2）（a﹣2b）（a2+2ab+4b2）．22．因式分解：（1）a2﹣1+b2﹣2ab （2）（p4+q4）2﹣（2p2q2）2．知识点归纳总结 523．解分式方程：（1）（2）．24．先化简，再求值：，其中x＝2020．25．如图，∠B＝30°，∠C＝50°，AD平分∠BAC，求∠DAC与∠ADB的度数．知识点归纳总结 626．如图：已知AD＝BE，BC＝EF，且BC∥EF，请说明线段AC和DF的关系．27．如图，点A，B，C都在网格的格点上，每小方格是边长为1个单位长度的正方形．利用格点和直尺画图并填空：（1）画出格点△ABC关于直线MN轴对称的△A'B'C′；（2）画出△ABC中BC边上的高线AD．知识点归纳总结728．在今年新冠肺炎防疫工作中，某公司购买了A、B两种不同型号的口罩，已知A型口罩的单价比B型口罩的单价多1.5元，且用8000元购买A型口罩的数量与用5000元购买B型口罩的数量相同．（1）A、B两种型号口罩的单价各是多少元？（2）根据疫情发展情况，该公司还需要增加购买一些口罩，增加购买B型口罩数量是A型口罩数量的2倍，若总费用不超过3800元，则增加购买A 型口罩的数量最多是多少个？29．在活动课上我们曾经探究过三角形内角和等于180°，四边形内角和等于360°，五边形内角和等于540°，…，请同学们仔细读题，看图，解决下面的问题：（1）如图①，△OAB、△OCD的顶点O重合，且∠A+∠B+∠C+∠D＝180°，则∠AOB+∠COD＝（直接写出结果）．（2）连接AD、BC，若AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线．知识点归纳总结8①如图②，如果∠AOB＝110°，那么∠COD的度数为（直接写出结果）．②如图③，若∠AOD＝∠BOC，AB与CD平行吗？请写出理由．30．若x满足（5﹣x）（x﹣2）＝2，求（x﹣5）2+（2﹣x）2的值．解：设5﹣x＝a，x﹣2＝b，则（5﹣x）（x﹣2）＝ab＝2，a+b＝（5﹣x）+（x﹣2）＝3，所以（x﹣5）2+（2﹣x）2＝（5﹣x）2+（x﹣2）2＝a2+b2＝（a+b）2﹣2ab＝32﹣2×2＝5．请运用上面的方法求解下面的问题：（1）若x满足（8﹣x）（x﹣2）＝5，求（8﹣x）2+（x﹣2）2的值；（2）已知正方形ABCD的边长为x，E、F分别是AD、DC上的点，且AE＝1，CF＝3，长方形EMFD的面积是35，求长方形EMFD的周长．知识点归纳总结931．如图，已知△ABC中，AB＝AC＝9cm，∠B＝∠C，BC＝6cm，点D为AB的中点．（1）如果点P在边BC上以1.5cm/s的速度由点B向点C运动，同时，点Q在边CA上由点C向点A运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，经过t秒后，△BPD与△CQP全等，求此时点Q的运动速度与运动时间t．（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，则经过后，点P与点Q 第一次在△ABC的边上相遇？（在横线上直接写出答案，不必书写解题过程）参考答案一．选择题1．解：A、1+1＝2，不能组成三角形，不符合题意；B、4+4＜9，不能组成三角形，不符合题意；知识点归纳总结10C、3+4＞5，能组成三角形，符合题意；D、6+8＜16，不能组成三角形，不符合题意；故选：C．2．解：A、有4条对称轴，故本选项不符合题意；B、有6条对称轴，故本选项不符合题意；C、有4条对称轴，故本选项不符合题意；D、有2条对称轴，故本选项符合题意．故选：D．3．解：0.2nm＝0.2×10﹣9m＝2×10﹣10m．故选：C．4．解：A、a2•a＝a3，故本选项不合题意；B、（ab）2＝a2b2，故本选项不合题意；C、（a2）3＝a6，故本选项不合题意；D、﹣a+2a＝a，故本选项符合题意；故选：D．5．解：∵△ABC≌△A1B1C1，∴∠C1＝∠C＝60°，知识点归纳总结11故选：B．6．解：∵BM平分∠ABD，DM平分∠BDC，∴∠MBD＝，∠BDM＝，∴∠BMD＝180°﹣∠MBD﹣∠BDM＝180°﹣30°﹣37.5°＝112.5°，故选：C．7．解：∵DE是AB的垂直平分线，∴EA＝EB，∵△BCE的周长＝BC+BE+EC＝BC+AE+EC＝BC+AC，∴BC+AC＝25cm，∴BC＝25﹣AC＝25﹣15＝10（cm），故选：B．8．解：过点O作OD⊥AC于D，OE⊥AB于E，OF⊥BC于F，∵点O是内心，知识点归纳总结12∴OE＝OF＝OD，∴S△ABO：S△BCO：S△CAO＝•AB•OE：•BC•OF：•AC•OD＝AB：BC：AC＝2：3：4，故选：C．9．解：（6x﹣m）（3x+1）＝18x2+6x﹣3mx﹣m＝18x2+（6﹣3m）x﹣m∵不含x的一次项，∴6﹣3m＝0，∴m＝2．故选：A．10．解：∵x+y＝1，xy＝﹣2，∴（1﹣x）（1﹣y）＝1﹣y﹣x+xy＝1﹣（x+y）+xy＝1﹣1+（﹣2）＝﹣2，故选：A．知识点归纳总结1311．解：根据方程可得：为了疫情防控需要，某防护用品厂计划生产130000个口罩，但是在实际生产时，每天比原计划多生产500个，结果提前10天完成，求实际每天生产口罩的个数．故选：D．12．解：∵Rt△ABC≌Rt△AB'C'，∴AB＝AB'，AC＝AC'，∠ABC＝∠AB'C'，∠ACB＝∠AC'B'＝90°，∵∠ABC＝∠CAB'，∴∠CAB'＝∠AB'C'，∴AC∥B'C'，∴∠CAC'+∠AC'B'＝90°，∴∠CAC'＝90°＝∠ACB，∴AC'∥BC，故①正确；∵AC＝AC'，∠CAC'＝90°，∴△CAC'是等腰直角三角形，故②正确；若AB＝AC'时，∵点D是BC'中点，∴AD⊥C'B，∠BAD＝∠C'AD，∴∠CAD＝∠B'AD，即AD平分∠CAB'，∵AB≠AC'，知识点归纳总结14∴③，④错误；故选：B．二．填空题13．解：为了安全，建筑工地上的塔吊上部设计成三角形结构，这是利用了三角形的稳定性，故答案为：稳定．14．解：7a2﹣7b2＝7（a2﹣b2）＝7（a+b）（a﹣b）．故答案为：7（a+b）（a﹣b）．15．解：根据题意，得2x+1≠0．解得x．故答案是：．16．解：添加条件：AB＝AC，在△ABE和△ACD中，，∴△ABE≌△ACD（SAS）；知识点归纳总结15添加条件：∠B＝∠C，在△ABE和△ACD中，，∴△ABE≌△ACD（AAS）；添加条件：∠AEB＝∠ADC，在△ABE和△ACD中，，∴△ABE≌△ACD（ASA）；故答案为：AB＝AC或∠B＝∠C或∠AEB＝∠ADC（答案不唯一）．17．解：点A（﹣3，﹣2）关于y轴的对称点为（3，﹣2），故答案为：（3，﹣2）．18．解：∵25x2+kxy+4y2是一个完全平方式，∴kxy＝±2•5x•2y，解得：k＝±20，故答案为：±20．知识点归纳总结1619．解：在△BOC中，∠BOC＝140°，∴∠OBC+∠OCB＝180°﹣140°＝40°．∵BD平分∠ABC，CE平分∠ACB，∴∠ABC＝2∠OBC，∠ACB＝2∠OCB，∴∠ABC+∠ACB＝2（∠OBC+∠OCB）＝80°，∴∠A＝180°﹣（∠ABC+∠ACB）＝100°．故答案为：100°．20．解：连接AD，MA．∵△ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，∴S△ABC＝BC•AD＝×4×AD＝20，解得AD＝10，∵EF是线段AC的垂直平分线，∴点A关于直线EF的对称点为点C，MA＝MC，∴MC+DM＝MA+DM≥AD，知识点归纳总结17∴AD的长为CM+MD的最小值，∴△CDM的周长最短＝（CM+MD）+CD＝AD+BC＝10+×4＝12．故答案为：12．三．解答题21．解：（1）3x3y•（2xy2﹣3xy）＝6x4y3﹣9x4y2；（2）（a﹣2b）（a2+2ab+4b2）＝a3+2a2b+4ab2﹣2a2b﹣4ab2﹣8b3＝a3﹣8b3．22．解：（1）原式＝（a2﹣2ab+b2）﹣1＝（a﹣b）2﹣1＝（a﹣b+1）（a﹣b﹣1）；（2）原式＝（p4+q4+2p2q2）（p4+q4﹣2p2q2）＝（p2+q2）2（p2﹣q2）2＝（p2+q2）2（p+q）2（p﹣q）2．知识点归纳总结1823．解：（1）两边同时乘以最简公分母（x﹣2），可得2x＝x﹣2+1，解得x＝﹣1，检验：当x＝﹣1时，x﹣2≠0，所以x＝﹣1是原分式方程的解；（2）两边同时乘以最简公分母（x+1）（x﹣1），可得x2+x﹣3x+1＝x2﹣1，解得x＝1；检验：当x＝1时，（x+1）（x﹣1）＝0，所以x＝1是原方程的增根，原方程无解．24．解：＝•＝•知识点归纳总结19＝，当x＝2020时，原式＝＝＝．25．解：∵∠B＝30°，∠C＝50°，∴∠BAC＝180°﹣30°﹣50°＝100°，∵AD平分∠BAC，∴∠DAC＝∠BAC＝50°，∴∠ADB＝∠DAC+∠C ＝80°．26．解：AC与DF的关系是相等且平行，理由：∵AD＝BE，∴AD+DB＝BE+DB，∴AB＝DE，∵BC∥EF，∴∠ABC＝∠DEF，在△ABC和△DEF中，，知识点归纳总结20∴△ABC≌△DEF（SAS），∴AC＝DE，∠A＝∠EDF，∴AC∥DF，即AC与DF的关系是相等且平行．27．解：（1）如图所示，△A'B'C′即为所求．（2）如图所示，AD即为所求．28．解：（1）设A型口罩的单价为x元，则B型口罩的单价为（x﹣1.5）元，根据题意，得：＝．解方程，得：x＝4．经检验：x＝4是原方程的根，且符合题意．所以x﹣1.5＝2.5．答：A型口罩的单价为4元，则B型口罩的单价为2.5元；知识点归纳总结21（2）设增加购买A型口罩的数量是m个，根据题意，得：2.5×2m+4m≤3800．解不等式，得：m≤422．因为m为正整数，所以正整数m的最大值为422．答：增加购买A型口罩的数量最多是422个．29．解：（1）∵∠AOB+∠COD+∠A+∠B+∠C +∠D＝180°×2＝360°，∠A+∠B+∠C+∠D＝180°，∴∠AOB+∠COD＝360°﹣180°＝180°．故答案为180°；（2）①∵AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线，∴∠OAB＝DAB，CBA，∠OCD＝BCD，∠ODC＝ADC，∴∠OAB+∠OBA+∠OCD+∠ODC＝×360°＝180°，在△OAB中，∠OAB+∠OBA＝180°﹣∠AOB，在△OCD中，∠OCD+∠ODC＝180°﹣∠COD，∴180°﹣∠AOB+180°﹣∠COD＝180°，∴∠AOB+∠COD＝180°；∵∠AOB＝110°，知识点归纳总结22∴∠COD＝180°﹣110°＝70°．故答案为：70°；②AB∥CD，理由如下：∵AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线，∴，CBA，，，∴∠OAB+∠OBA+∠OCD+∠ODC＝×360°＝180°，在△OAB中，∠OAB+∠OBA＝180°﹣∠AOB，在△OCD中，∠OCD+∠ODC＝180°﹣∠COD，∴180°﹣∠AOB+180°﹣∠COD＝180°，∴∠AOB+∠COD＝180°；∴∠ADO+∠BOD＝360°﹣（∠AOB+∠COD）＝360°﹣180°＝180°，∵∠AOD＝∠BOC，∴∠AOD＝∠BOC＝90°．在∠AOD中，∠DAO＝∠ADO＝180°﹣∠AOD＝180°﹣90°＝90°，∵，∴＝90°，知识点归纳总结23∴∠DAB+∠ADC＝180°，∴AB∥CD．30．解：（1）设8﹣x＝a，x﹣2＝b，则ab＝5，a+b＝6，∴（8﹣x）2+（x﹣2）2＝a2+b2＝（a+b）2﹣2ab＝36﹣10＝26．（2）∵AE＝1，CF＝3∴DE＝x﹣1，DF＝x﹣3，∵长方形EMFD的面积是35，∴DE•DF＝（x﹣1）（x﹣3）＝35，设x﹣1＝a，x﹣3＝b，则ab＝35，a﹣b＝2，∴（a+b）2＝（a﹣b）2+4ab＝4+140＝144，又∵a+b＞0，∴a+b＝12，∴长方形EMFD的周长＝2DE+2DF＝2（a+b）＝24．31．解：（1）①全等，理由如下：∵t＝1秒，∴BP＝CQ＝1×1.5＝1.5（厘米），∵AB＝9cm，点D为AB的中点，知识点归纳总结24∴BD＝4.5cm．又∵PC＝BC﹣BP，BC＝6cm，∴PC＝6﹣1.5＝4.5（cm），∴PC＝BD．又∵AB＝AC，∴∠B＝∠C，在△BDP和△CPQ中，，∴△BPD≌△CQP（SAS）；②假设△BPD≌△CQP，∵v P≠v Q，∴BP≠CQ，又∵△BPD≌△CQP，∠B＝∠C，则BP＝CP＝3，BD＝CQ＝4.5，∴点P，点Q运动的时间t＝BP÷1.5＝3÷1.5＝2（秒），∴v Q＝CQ÷t＝4.5÷2＝2.25（cm/s）；（2）设经过x秒后点P与点Q第一次相遇，知识点归纳总结25由题意，得2.2.5x＝1.5x+2×9+6，解得x＝32，∴点P共运动了32×1.5＝48（cm）．∵32×2.25＝72，∴点P、点Q在AC边上相遇，∴经过32秒点P与点Q第一次在边AC上相遇．故答案为：32；AC．知识点归纳总结26。

2020—2022学年部编版八年级上学期语文期末复习专项练习：词语的运用部编人教版八年级上册2020——2022学年度人教部编版八上语文期末复习专项练习二：词语的运用1．阅读下面语段，回答问题。

历史是一艘行进的船，时间是一张网。

我们每个人都在船上张网捕鱼。

有那勤奋聪明的就捕得多些，有____的，就捕得少些。

大家都在一条船上，到时大家都得扔掉网上岸。

翻检个人的捕获，在20世纪的作业中，有爱因斯坦这样的好手，创造了一个物理的新纪元；有毛泽东这样的伟人，创造了一个共和国。

而空手上岸的人也不在少数。

21世纪，我们将有什么样的创造，将出现什么样的世纪人物呢？这对有幸站在门槛上的人，至少是一个很大的鼓励和诱惑。

（1）根据语境，文中横线上应填入的一个词语是。

（2）从文中找出一个与“在20世纪的作业中”的“作业”意思相同的词语。

2.根据语境选词填空，最恰当的一项是( )这个战场，没有硝烟；这个战场，尚未停止，________早在一百多年前，林则徐就以虎门销烟的壮举，发出了中国人禁烟护国的强音；________一百多年之后的今天，禁毒工作仍然________，面对毒品的危害，谁都不能袖手旁观。

为了自己，为了民族，为了整个人类，我们必须对罪孽深重的毒品大声说：“不！”这声音，气贯长虹；这决心，________！A．由于所以绵绵不绝众口一词B．尽管但是任重道远众志成城C．既然那么纷至沓来众望所归D．尚且何况数不胜数众所周知3.依次填入下面括号里的关联词语，恰当的一项是( )我们________爱好写作，________想在这方面成才，________不能不首先掌握好“语言”这个工具，________要像木匠爱斧锯、画家爱颜料、战士爱武器那样爱我们赖以进行工作的工具。

A．如果并且所以而且B．既然并且就因此C．既然又就而且D．如果又所以因此4.选出依次填入下面语段横线处的词语最恰当的一项（）经典从来不是旧纸堆里的过往云烟，_________宛如长者的谆谆叮哼，在每一个时代都有可以落脚的现实意义，让人常读常新，________。

第一单元第1课《消息二则》1.文学常识《新闻两则》（《人民解放军百万大军横渡长江》选自《人民日报》，《中原我军解放南阳》选自《东北日报》）。

作者毛泽东，伟大的革命家、军事家、思想家，文学家，书法家，新中国的缔造者。

代表作品：《沁园春雪》《长征》《论持久战》等。

2.文章思想内容《我三十万大军胜利南渡长江》作者用富有感情的笔调，简明扼要地报道了渡江战斗的过程，赞扬了人民解放军英勇善战的精神，也从侧面反映出国民党军队军心涣散、毫无斗志的状况。

《人民解放军百万大军横渡长江》新闻报道了人民解放军百万大军胜利横渡长江的战况，歌颂了我军英勇善战的精神，展现了人民解放军的英雄气概，给全国人民和全军将士以极大的鼓舞，对瓦解敌军斗志、鼓舞我军士气起了很大的作用。

3.重点字词芜湖（wú）击溃（kuì）督战（dū）绥靖（suí jìng）阻遏（è）荻港（d í）摧枯拉朽（xiǔ）歼灭（jiān）要塞（sài）杜聿明（yù）锐不可当（dāng）第2课《首届诺贝尔奖颁发》1.文学常识诺贝尔奖，是以瑞典著名的化学家、硝化甘油炸药的发明人阿尔弗雷德?贝恩哈德?诺贝尔的部分遗产作为基金在1900年创立的，于1901年首次颁发。

诺贝尔奖分设物理学、化学、生理学或医学、文学及和平五个奖项。

消息是用概括的叙述方式，比较简明扼要的文字，迅速及时地报道国内外新近发生的、有价值的事实的一种文体。

一般来说，消息由标题、导语、主体、背景和结语五部分构成。

2.文章思想内容本文是路透社的一篇新闻，它介绍了首届诺贝尔奖颁发的时间、地点、获得者和原因，并补充说明了诺贝尔奖的资金来源、资金管理和评议情况，是一篇典型的新闻报道。

3.重点字词颁发（bān）仲裁（zhòng cái）遗嘱（zhǔ）巨额（é）第3课《“飞天”凌空》1.文学常识新闻特写是指采用类似于特写的手法，以形象化的描写作为主要表现手段，截取新闻事件中最具有价值、最生动感人、最富有特征的片段和部分予以放大，从而鲜明地再现典型人物、事件、场景的一种新闻体裁。

2019-2020人教版八年级英语上册期末复习专题训练三、阅读理解解题技巧及训练（含答案）一、阅读理解题型分类：1、文章主旨大意或段落大意题。

常见提问方式：（1）What is the best title of the passage？（2）What does the passage want to tell us？（3）What’s this passage mainly about?2、划线部分猜测和生词词义猜测题。

常见提问方式：（1）What does the underline word " " in Paragraph 1 mean？（2）What does the underlined word “It” refer to?3、细节事实细节题。

常见提问方式：（1）On his way home, John forgot ______.（2）Why did Jamie say "It's no use!"?（3）Jay Chou’s mother worked in a _______.（4）What happened after Beethoven became deaf?4、作者意图推理和判断题。

常见提问方式：（1）Which of the statements（陈述）is right?（2）What is TRUE about all kinds of energy in the passage? （3）Which is NOT the writer’s advice?（4）Why did the writer write the passage?5、文章来源和逻辑顺序。

常见提问方式：（1）What is the RIGHT order (顺序）of the following according to the passage? （2）Where can we read this passage ?6、生活常识和文化背景题。

人教版八年级数学上学期期末复习：第13章《轴对称》填空题精选一．填空题（共30小题）1．（2020春•渝中区校级期末）如图，P为△ABC内一点，过点P的线段MN分别交AB、BC于点M、N，且M、N分别在P A、PC的中垂线上．若∠ABC＝80°，则∠APC的度数为．2．（2020春•沙坪坝区期末）如图，在Rt△ABC中，∠C＝90°，∠A＝30°，AB＝6，BD是△ABC的角平分线，点P，点N分别是BD，AC边上的动点，点M在BC上，且BM＝1，则PM+PN的最小值为．3．（2019秋•九龙坡区校级期末）已知△ABC为等腰三角形，AB＝AC＝10，BC＝8，BD为∠ABC的平分线，点P 为线段BD上的一动点，过点P作线段AB的垂线，垂足为点M，连接AP，则PM+P A的最小值为．4．（2020春•沙坪坝区校级期末）如图所示，在等腰△ABC中，AB＝AC，∠B＝50°，D为BC的中点，点E在AB 上，∠AED＝73°，若点P是等腰△ABC的腰上的一点，则当△EDP为以DE为腰的等腰三角形时，∠EDP的度数是．5．（2019秋•渝中区校级期末）如图所示，在△ABC中，∠C＝90°，DE垂直平分AB，交BC于点E，垂足为点D，BE＝6cm，∠B＝15°，则AC等于．6．（2019秋•渝中区校级期末）在平面直角坐标系中，若点A（a，b）与点B（1，﹣2）关于y轴对称，则a+b＝．7．（2019秋•巴南区期末）如图，△ABC中，∠ABC的平分线与∠ACB的外角平分线相交于点D，点E，F分别在线段BD、CD上，点G在EF的延长线上，△EFD与△EFH关于直线EF对称，若∠A＝60°，∠BEH＝84°，∠HFG＝n°，则n＝．8．（2019秋•开州区期末）如图，△ABC中边AB的垂直平分线分别交BC、AB于点D、E，AE＝4cm，△ADC的周长为10cm，则△ABC的周长是cm．9．（2019秋•两江新区期末）如图，在△ABC中，DB和DC分别平分∠ABC和∠ACB，过D作EF∥BC，分别交AB、AC于点E、F，若EF＝5，BE＝3，则线段CF的长为．10．（2019秋•江津区期末）如图，在等腰△ABC的两腰AB、BC上分别取点D和E，使DB＝DE，此时恰有∠ADE= 12∠ACB，则∠A的度数是．11．（2019秋•九龙坡区期末）在平面直角坐标系中，点P（1，﹣5）关于x轴对称点的点的坐标是．12．（2019秋•梁平区期末）如图，△ABC是等边三角形，D，E分别是BC，AB的中点，且AD＝4cm．F是AD上一动点，则BF+EF的最小值为cm．13．（2019秋•江北区期末）如图，在△ABC中，AB＝AC，点D，E都在边BC上，∠BAD＝∠CAE，若BD＝7，则CE的长为．14．（2019秋•万州区期末）如图，已知：∠BAC的平分线与BC的垂直平分线相交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F，AB＝6，AC＝3，则BE＝．15．（2019秋•长寿区期末）在线段、直角、等腰三角形、直角三角形中，成轴对称图形的是．16．（2019秋•长寿区期末）等腰三角形一边长为4，另一边长为9，则它的周长是．17．（2019春•南岸区期末）如图，在△ABC中，过A作DE∥BC交∠ABC的平分线BD于点D、交∠ACB的平分线CE于点E．若BC＝7，DE＝9，则△ABC的周长为．18．（2018秋•南岸区期末）如图，在平面直角坐标系中，将△ABC三个顶点的横坐标分别乘以﹣1，而纵坐标保持不变，得到△A′B′C′，则△A′B′C′和△ABC关于对称（横线上填“x轴”、“y轴”或“原点”）．19．（2019春•渝中区校级期末）如图，△ABC中，AC＝BC，CE为△ABC的中线，BD为AC边上的高，BF平分∠CBD交CE于点G，连接AG交BD于点M，若∠AFG＝63°，则∠AMB的度数为°．20．（2018秋•渝中区期末）如图，已知∠BAC＝65°，D为∠BAC内部一点，过D作DB⊥AB于B，DC⊥AC于C，设点E、点F分别为AB、AC上的动点，当△DEF的周长最小时，∠EDF的度数为．21．（2018秋•合川区期末）如图，在△ABC中，∠ACB＝90°，CD是AB边上的高，∠BCD＝60°，若BD＝3cm，则AD＝cm．22．（2018秋•渝北区期末）如图，∠ABC＝20°，点D，E分别在射线BC，BA上，且BD＝3，BE＝3，点M，N 分别是射线BA，BC上的动点，求DM+MN+NE的最小值为．23．（2018秋•巴南区期末）如图，BE、CD分别是等边△ABC的高和角平分线，点O是它们的交点，若∠BOC＝m°，则m＝．24．（2018秋•江北区期末）在等腰△ABC中，一腰上的高与另一腰的夹角为26°，则底角的度数为．25．（2019春•沙坪坝区校级期末）如图，已知△ABC是等边三角形，点B、C、D、F在同一直线上，CD＝CE，DF＝DG，则∠F＝度．26．（2019春•南岸区校级期末）如图，在等腰△ABC中，AB＝BC，∠B＝120°，线段AB的垂直平分线分别交AB、AC于点D、E，若AC＝12，则DE＝．27．（2019春•沙坪坝区校级期末）如图，在直角三角形ABC中，∠A＝90°，AB＝8，AC＝15，BC＝17．D，P分别是线段AC，BC上的动点，则BD+DP的最小值是．28．（2019春•渝中区校级期末）在△ABC中，AB＝AC，AC的垂直平分线与AB所在直线相交所得的锐角为40°，∠C＝．29．（2019春•渝中区校级期末）如图，△ABC中，AC＝BC＝5，AB＝6，CD＝4，CD为△ABC的中线，点E、点F分别为线段CD、CA上的动点，连接AE、EF，则AE+EF的最小值为．30．（2018秋•九龙坡区校级期末）在平面直角坐标系中，点P（﹣2，﹣3）关于x轴对称点的坐标为．参考答案一．填空题（共30小题）1．【解答】解：∵∠ABC ＝80°，∴∠BMN +∠BNM ＝100°，∵M 、N 分别在P A 、PC 的中垂线上，∴MA ＝MP ，NP ＝NC ，∴∠MP A ＝∠MAP =12∠BMN ，∠NPC ＝∠NCP =12∠BNM ，∴∠MP A +∠NPC =12×100°＝50°，∴∠APC ＝180°﹣50°＝130°， 故答案为：130°．2．【解答】解：如图所示，作点M 关于BD 的对称点M '，连接PM '，则PM '＝PM ，BM ＝BM '＝1， ∴PN +PM ＝PN +PM '，当N ，P ，M '在同一直线上，且M 'N ⊥AC 时，PN +PM '的最小值等于垂线段M 'N 的长，此时，∵Rt △AM 'N 中，∠A ＝30°，∴M 'N =12AM '=12（6﹣1）=52，∴PM +PN 的最小值为52， 故答案为：52．3．【解答】解：如图，过点P 作PK ⊥BC 于K ，过点A 作AH ⊥BC 于H ．∵AB ＝AC ＝10，AH ⊥BC ，∴BH ＝CH ＝4，∴∠AHB ＝90°，∴AH =√AA 2−AA 2=√102−42=2√21，∵BD 平分∠ABC ，PM ⊥AB ，PK ⊥BC ，∴PM ＝PK ，∴P A +PM ＝P A +PK ≥AH ，∴P A +PM ≥2√21，∴P A +PM 的最小值为2√21．4．【解答】解：∵AB ＝AC ，∠B ＝50°，∠AED ＝73°，∴∠EDB ＝23°，∵当△DEP 是以DE 为腰的等腰三角形，①当点P 在AB 上，∵DE ＝DP 1，∴∠DP 1E ＝∠AED ＝73°，∴∠EDP 1＝180°﹣73°﹣73°＝34°，②当点P 在AC 上，∵AB ＝AC ，D 为BC 的中点，∴∠BAD ＝∠CAD ，过D 作DG ⊥AB 于G ，DH ⊥AC 于H ，∴DG ＝DH ，在Rt △DEG 与Rt △DP 2H 中，{AA =AA 2AA =AA， ∴Rt △DEG ≌Rt △DP 2H （HL ），∴∠AP 2D ＝∠AED ＝73°，∵∠BAC ＝180°﹣50°﹣50°＝80°，∴∠EDP 2＝134°，③当点P 在AC 上，同理证得Rt △DEG ≌Rt △DPH （HL ），∴∠EDG ＝∠P 3DH ，∴∠EDP 3＝∠GDH ＝180°﹣80°＝100°，④当点P 在AB 上，EP ＝ED 时，∠EDP =12（180°﹣73°）＝53.5°．故答案为：34°或53.5°或100°或134°．5．【解答】解：∵在△ABC 中，∠ACB ＝90°，∠B ＝15°，∴∠BAC＝90°﹣15°＝75°，∵DE垂直平分AB，BE＝6cm，∴BE＝AE＝6cm，∴∠EAB＝∠B＝15°，∴∠EAC＝75°﹣15°＝60°，∵∠C＝90°，∴∠AEC＝30°，∴AC=12AE=12×6cm＝3cm，故答案为：3cm．6．【解答】解：∵点A（a，b）与点B（1，﹣2）关于y轴对称，∴a＝﹣1，b＝﹣2，∴a+b＝﹣3，故答案为：﹣3．7．【解答】解：∵∠ABC的平分线与∠ACB的外角平分线相交于点D，∴∠ABD＝∠DBC，∠ACD＝∠DCM，设∠ABD＝∠DBC＝x，∠ACD＝∠DCM＝y，∵∠A+∠ABC＝∠ACM，∴12∠A+12∠ABC=12∠ACM，即30°+x＝y，∵∠D+∠DBC＝∠DCM，∴∠D+x＝y，∴∠D＝30°，∵EFD与△EFH关于直线EF对称，∠BEH＝84°，∴∠DEG＝∠HEG=180°−84°2=48°，∴∠HFG＝n°＝∠DFG＝48°+30°＝78°则n＝78．故答案为：78．8．【解答】解：∵DE是△ABC中边AB的垂直平分线，∴AD＝BD，AB＝2AE＝2×4＝8（cm），∵△ADC的周长为10cm，即AD+AC+CD＝BD+CD+AC＝BC+AC＝10cm，∴△ABC的周长为：AB+AC+BC＝8+10＝18（cm）．故答案为：18．9．【解答】解：∵BD平分∠ABC，∴∠ABD＝∠CBD，∵EF∥BC，∴∠EDB＝∠DBC，∴∠ABD＝∠EDB，∴BE＝ED，同理DF＝CF，∴EF＝3+CF＝5，∴CF＝2，故答案为：2．10．【解答】解：设∠B＝x．∵DB＝DE，∴∠DEB＝∠B＝x，∴∠ADE＝∠DEB+∠B＝2x，∴∠ACB＝2∠ADE＝4x．∵AB＝BC，∴∠ACB＝∠A＝4x．在△ABC中，∵∠A+∠B+∠C＝180°，∴4x+x+4x＝180°，∴x＝20°．即∠B＝20°∴∠A＝4x＝80°故答案为：80°11．【解答】解：点P（1，﹣5）关于x轴对称点的点的坐标是：（1，5）．故答案为：（1，5）．12．【解答】解：过C作CE⊥AB于E，交AD于F，连接BF，则BF+EF最小（根据两点之间线段最短；点到直线垂直距离最短），由于C和B关于AD对称，则BF+EF＝CE，∵等边△ABC中，BD＝CD，∴AD⊥BC，∴AD是BC的垂直平分线（三线合一），∴C和B关于直线AD对称，∴CF＝BF，即BF+EF＝CF+EF＝CE，∵AD⊥BC，CE⊥AB，∴∠ADB ＝∠CEB ＝90°，在△ADB 和△CEB 中，{∠AAA =∠AAAAAAA =AAAA AA =AA，∴△ADB ≌△CEB （AAS）， ∴CE ＝AD ＝4cm ，即BF +EF ＝4cm ．故答案为：4．13．【解答】解：∵AB ＝AC ，∴∠B ＝∠C ，在△BAD 和△CAE 中，{∠AAA =∠AAA AA =AAAA =AA ，∴△BAD ≌△CAE （ASA ），∴BD ＝CE ＝7，故答案为：7．14．【解答】解：连接CD ，BD ，∵AD 是∠BAC 的平分线，DE ⊥AB ，DF ⊥AC ，∴DF ＝DE ，∠F ＝∠DEB ＝90°，∠ADF ＝∠ADE ， ∴AE ＝AF ，∵DG 是BC 的垂直平分线，∴CD ＝BD ，在Rt △CDF 和Rt △BDE 中，{AA =AA AA =AA， ∴Rt △CDF ≌Rt △BDE （HL ），∴BE ＝CF ，∴AB ＝AE +BE ＝AF +BE ＝AC +CF +BE ＝AC +2BE ， ∵AB ＝6，AC ＝3，∴BE ＝1.5．故答案为：1.5．15．【解答】解：线段的垂直平分线所在的直线是对称轴，是轴对称图形，符合题意；直角的角平分线所在的直线就是对称轴，是轴对称图形，符合题意；等腰三角形底边中线所在的直线是对称轴，是轴对称图形，符合题意；直角三角形不一定是轴对称图形，不符合题意．故成轴对称图形的是：线段、直角、等腰三角形．故答案为：线段、直角、等腰三角形．16．【解答】解：当等腰三角形的三边为：4、4、9时，不符合三角形三边关系，因此这种情况不成立；当等腰三角形的三边为：4、9、9时，符合三角形三边关系，则三角形的周长为：4+9+9＝22．因此等腰三角形的周长为22．故填22．17．【解答】解：∵DE∥BC，∴∠E＝∠ECB，∠D＝∠DBC，∵CE平分∠ACB，BD平分∠ABC，∴∠ECB＝∠ACE，∠DBC＝∠ABD，∴∠E＝∠ACE，∠D＝∠ABD，∴AE＝AC，AB＝AD，∵AB+AC＝AD+AE＝DE＝9，BC＝7，∴△ABC的周长为AB+AC+BC＝DE+BC＝9+7＝16．故答案为16．18．【解答】解：∵横坐标乘以﹣1，∴横坐标相反，又纵坐标不变，∴关于y轴对称．故答案为：y轴．19．【解答】解：∵BD为AC边上的高，∴BD⊥AC，∴∠BDF＝90°，∵∠AFG＝63°，∴∠DBF＝90°﹣63°＝27°，∵BF平分∠CBD交CE于点G，∴∠CBD＝2∠DBF＝54°，∴∠ACB＝90°﹣∠CBD＝36°，∵AC＝BC，∴∠CAB＝∠CBA=12（180°﹣36°）＝72°，∴∠ABD＝72°﹣54°＝18°，∴∠ABG＝27°+18°＝45°，∵CE为△ABC的中线，∴CE⊥AB，∴CE垂直平分AB，∴AG＝BG，∴∠GAB＝∠GBA＝45°，∴∠AMB＝180°﹣45°﹣18°＝117°，故答案为：117．20．【解答】解：如图所示：延长DB和DC至M和N，使MB＝DB，NC＝DC，连接MN交AB、AC于点E、F，连接DE、DF，此时△DEF的周长最小．∵DB⊥AB，DC⊥AC，∴∠ABD＝∠ACD＝90°，∠BAC＝65°，∴∠BDC＝360°﹣90°﹣90°﹣65°＝115°，∴∠M+∠N＝180°﹣115°＝65°根据对称性质可知：DE＝ME，DF＝NF，∴∠EDM＝∠M，∠FDN＝∠N，∴∠EDM+∠FDN＝65°，∴∠EDF＝∠BDC﹣（∠EDM+∠FDN）＝115°﹣65°＝50°．故答案为50°．21．【解答】解：∵在△ABC中，∠ACB＝90°，CD是AB边上的高，∠BCD＝60°，BD＝3cm，∴BC＝2CD，可得：BC2﹣CD2＝4CD2﹣CD2＝9，解得：CD=√3cm，∴BC＝2√3cm，∴AC=AA√3=2cm，∴AB＝4cm，∴AD＝4﹣3＝1cm．故答案为：122．【解答】解：如图所示：作点D关于AB的对称点G，作点E关于BC的对称点H，连接GH交AB于点M、交BC于点N，连接DM、EN，此时DM+MN+NE的值最小．根据对称的性质可知：DB＝BG＝3，∠GBE＝∠DBE＝20°，BH＝BE＝3，∠HBD＝∠EBD＝20°，∴∠GBH＝60°，∴△BGH是等边三角形，∴GH＝GB＝HB＝3，∴DM+MN+NE的最小值为3．故答案为3．23．【解答】解：∵BE、CD分别是等边△ABC的高和角平分线，∴∠ODB＝90°，∠ABE＝30°，∴∠BOC＝∠ODB+∠DBE＝90°+30°＝120°，故答案为：12024．【解答】解：①∵AB＝AC，∠ABD＝26°，BD⊥AC，∴∠A＝64°，∴∠ABC＝∠C＝（180°﹣64°）÷2＝58°．②∵AB＝AC，∠ABD＝26°，BD⊥AC，∴∠BAC＝26°+90°＝116°∴∠ABC＝∠C＝（180°﹣116°）÷2＝32°．故答案为：58°或32°．25．【解答】解：∵△ABC是等边三角形，∴∠ACB＝60°，∠ACD＝120°，∵CE＝CD，∴∠CDE＝30°，∠FDG＝150°，∵DF＝DG，∴∠F＝15°．故答案为：15．26．【解答】解：连接BE，∵AB＝BC，∠B＝120°，∴∠A＝∠C＝30°，∵DE是线段AB的垂直平分线，∴EA＝EB，∴∠EBA＝∠A＝30°，∴∠CBE＝90°，又∠C＝30°，∴BE=12EC，∴AE=12EC，∴AE=13AC＝4，在Rt△ADE中，∠A＝30°，∴DE=12AE＝2，故答案为：2．27．【解答】解：作B关于AC的对称点E，过E作EP⊥BC于P，交AD于D，则AE＝AB＝8，此时，BD+DP的值最小，BD+DP的最小值＝EP，∵∠BAC＝∠BPE＝90°，∠C＝∠E，∴△ABC∽△PBE，∴AAAA=AAAA，∴1617=AA 15，∴PE =24017， 故答案为：24017．28．【解答】解：当△ABC 为锐角三角形时，如图1，设AC 的垂直平分线交线段AB 于点D ，交AC 于点E ，∵∠ADE ＝40°，DE ⊥AC ，∴∠A ＝90°﹣40°＝50°，∵AB ＝AC ，∴∠C =12（180°﹣∠A ）＝65°；当△ABC 为钝角三角形时，如图2，设AC 的垂直平分线交AC 于点E ，交AB 于点D ，∵∠ADE ＝40°，DE ⊥AC ，∴∠DAC ＝50°，∵AB ＝AC ，∴∠B ＝∠C ，∵∠B +∠C ＝∠DAB ，∴∠C ＝25°；综上可知∠C 的度数为65°或25°，故答案为：65°或25°．29．【解答】解：过B 作BF ⊥AC 于F ，交CD 于E ， 则BF 的长即为AE +EF 的最小值，∵AC ＝BC ＝5，CD 为△ABC 的中线，∴AD =12AB ＝3，∵S △ABC =12AB •CD =12AC •BF ，∴BF =6×45=245， ∴AE +EF 的最小值为245， 故答案为：245．30．【解答】解：点P （﹣2，﹣3）关于x 轴对称点的坐标为：（﹣2，3）． 故答案为：（﹣2，3）．。

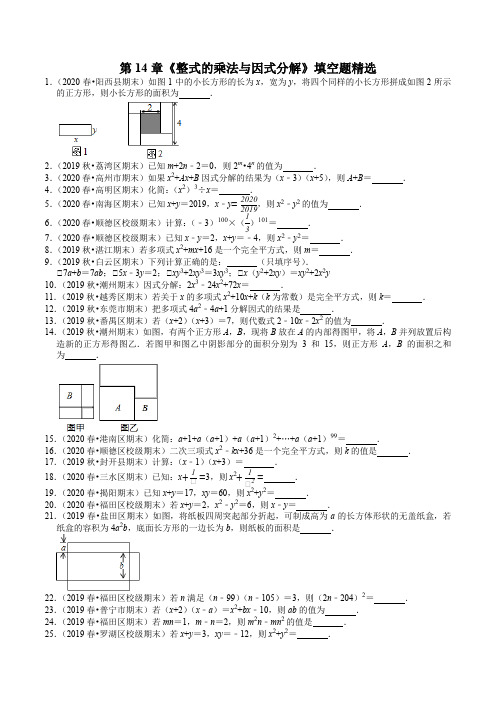
第14章《整式的乘法与因式分解》填空题精选1．（2020春•阳西县期末）如图1中的小长方形的长为x ，宽为y ，将四个同样的小长方形拼成如图2所示的正方形，则小长方形的面积为 ．2．（2019秋•荔湾区期末）已知m +2n ﹣2＝0，则2m •4n 的值为 ．3．（2020春•高州市期末）如果x 2+Ax +B 因式分解的结果为（x ﹣3）（x +5），则A +B ＝ ．4．（2020春•高明区期末）化简：（x 2）3÷x ＝ ．5．（2020春•南海区期末）已知x +y ＝2019，x ﹣y =20202019，则x 2﹣y 2的值为 ．6．（2020春•顺德区校级期末）计算：（﹣3）100×（13）101＝ ．7．（2020春•顺德区校级期末）已知x ﹣y ＝2，x +y ＝﹣4，则x 2﹣y 2＝ ．8．（2019秋•湛江期末）若多项式x 2+mx +16是一个完全平方式，则m ＝ ．9．（2019秋•白云区期末）下列计算正确的是： （只填序号）．①7a +b ＝7ab ；①5x ﹣3y ＝2；①xy 3+2xy 3＝3xy 3；①x （y 2+2xy ）＝xy 2+2x 2y10．（2019秋•潮州期末）因式分解：2x 3﹣24x 2+72x ＝ ．11．（2019秋•越秀区期末）若关于x 的多项式x 2+10x +k （k 为常数）是完全平方式，则k ＝ ．12．（2019秋•东莞市期末）把多项式4a 2﹣4a +1分解因式的结果是 ．13．（2019秋•番禺区期末）若（x +2）（x +3）＝7，则代数式2﹣10x ﹣2x 2的值为 ．14．（2019秋•潮州期末）如图，有两个正方形A ，B ，现将B 放在A 的内部得图甲，将A ，B 并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为3和15，则正方形A ，B 的面积之和为 ． 15．（2020春•港南区期末）化简：a +1+a （a +1）+a （a +1）2+…+a （a +1）99＝ ．16．（2020春•顺德区校级期末）二次三项式x 2﹣kx +36是一个完全平方式，则k 的值是 ．17．（2019秋•封开县期末）计算：（x ﹣1）（x +3）＝ ．18．（2020春•三水区期末）已知：x +1x =3，则x 2+1x 2= ． 19．（2020春•揭阳期末）已知x +y ＝17，xy ＝60，则x 2+y 2＝ ．20．（2020春•福田区校级期末）若x +y ＝2，x 2﹣y 2＝6，则x ﹣y ＝ ．21．（2019春•盐田区期末）如图，将纸板四周突起部分折起，可制成高为a 的长方体形状的无盖纸盒，若纸盒的容积为4a 2b ，底面长方形的一边长为b ，则纸板的面积是 ． 22．（2019春•福田区校级期末）若n 满足（n ﹣99）（n ﹣105）＝3，则（2n ﹣204）2＝ ．23．（2019春•普宁市期末）若（x +2）（x ﹣a ）＝x 2+bx ﹣10，则ab 的值为 ．24．（2019春•福田区期末）若mn ＝1，m ﹣n ＝2，则m 2n ﹣mn 2的值是 ．25．（2019春•罗湖区校级期末）若x +y ＝3，xy ＝﹣12，则x 2+y 2＝ ．26．（2019春•南海区期末）若2x＝5，2y＝3，则2x+y＝．27．（2018秋•中山市期末）已知m+2n+2＝0，则2m•4n的值为．28．（2018秋•天河区期末）若（x+p）与（x+5）的乘积中不含x的一次项，则p＝．29．（2018秋•白云区期末）一个正方形的边长增加了2cm，它的面积就增加44cm2，这个正方形的边长是：．30．（2019春•大埔县期末）若5x﹣3y＝2，则105x÷103y＝．31．（2019春•南海区期末）若（x+y）2＝49，xy＝12，则x2+y2＝．32．（2019春•天桥区期末）已知x2+mx+25是完全平方式，则m＝．33．（2018秋•番禺区期末）计算：（x+1）（x+2）＝．34．（2019春•罗湖区期末）n为正整数，若a9÷a n＝a5，则n＝．35．（2019春•顺德区期末）若x2+mx+1是完全平方式，则m＝．36．（2019秋•端州区期末）分解因式：4x3﹣9x＝．37．（2019秋•越秀区期末）点（﹣3，4）与点（a2，b2）关于y轴对称，则（a+b）（a﹣b）＝．38．（2019秋•潮州期末）计算：（2xy）2（﹣5x2y）＝．39．（2020春•顺德区校级期末）若a+b＝10，ab＝11，则代数式a2﹣ab+b2＝．40．（2020春•顺德区校级期末）计算：（a+2b）2＝．41．（2020春•顺德区校级期末）化简：（2x﹣y）（x+3y）＝．第14章《整式的乘法与因式分解》填空题精选参考答案与试题解析一．填空题（共41小题）1．【解答】解：由图2可知， {x +x =4x −x =2， 解得：{x =3x =1， 则小长方形的面积为xy ＝3．故答案为：3．2．【解答】解：由m +2n ﹣2＝0得m +2n ＝2，∴2m •4n ＝2m •22n ＝2m +2n ＝22＝4．故答案为：4．3．【解答】解：x 2+Ax +B ＝（x ﹣3）（x +5）＝x 2+2x ﹣15，得A ＝2，B ＝﹣15，∴A +B ＝2﹣15＝﹣13．故答案为：﹣13．4．【解答】解：（x 2）3÷x ＝x 6÷x ＝x 5，故答案为：x 5．5．【解答】解：x 2﹣y 2＝（x +y ）（x ﹣y ）＝2019×20202019=2020， 故答案为：2020．6．【解答】解：（﹣3）100×（13）101 ＝3100×（13）100×13 =(3×13)100×13=1100×13=1×13 =13． 故答案为：13． 7．【解答】解：∵x ﹣y ＝2，x +y ＝﹣4，∴x 2﹣y 2＝（x ﹣y ）（x +y ）＝2×（﹣4）＝﹣8．故答案为：﹣8．8．【解答】解：∵x 2+mx +16＝x 2+mx +42，∴mx ＝±2×4×x ，解得m ＝±8．故答案为：±8．9．【解答】解：∵7a 与b 、5x 与3y 都不是同类项，不能加减，故①①不正确； ∵xy 3与2xy 3是同类项，xy 3+2xy 3＝3xy 3，故①正确；∵x （y 2+2xy ）＝xy 2+2x 2y ，故①正确．故答案为：①①10．【解答】解：原式＝2x （x 2﹣12x +36）＝2x （x ﹣6）2，故答案为：2x （x ﹣6）211．【解答】解：∵关于x 的多项式x 2+10x +k 是完全平方式，∴x 2+10x +k ＝x 2+2•x •5+52，∴k ＝52＝25，故答案为：25．12．【解答】解：原式＝（2a ﹣1）2，故答案为：（2a ﹣1）2．13．【解答】解：∵（x +2）（x +3）＝7，∴x 2+5x ＝1，∴2﹣10x ﹣2x 2＝﹣2（x 2+5x ）+2＝﹣2×1+2＝0，故答案为：0．14．【解答】解：如图所示：设正方形A 、B 的边长分别为x ，y ，依题意得：{x 2−x 2−2(x −x )x =3(x +x )2−x 2−x 2=15， 化简得：{x 2−2xx +x 2=3x 2xx =15x 由①+①得：x 2+y 2＝18，∴x x +x x =x 2+x 2=18，故答案为18．15．【解答】解：原式＝（a +1）[1+a +a （a +1）+a （a +1）2+…+a （a +1）98] ＝（a +1）2[1+a +a （a +1）+a （a +1）2+…+a （a +1）97]＝（a +1）3[1+a +a （a +1）+a （a +1）2+…+a （a +1）96]＝…＝（a +1）100．故答案为：（a +1）100．16．【解答】解：∵二次三项式x 2﹣kx +36是一个完全平方式，∴k ＝±12，故答案为：±1217．【解答】解：（x ﹣1）（x +3）＝x 2+3x ﹣x ﹣3＝x 2+2x ﹣3．故答案为：x 2+2x ﹣3．18．【解答】解：∵x +1x =3，∴（x +1x ）2＝x 2+2+1x 2=9， ∴x 2+1x 2=7， 故答案为：7．19．【解答】解：∵x +y ＝17，xy ＝60，∴x 2+y 2＝（x +y ）2﹣2xy ＝172﹣2×60＝169．故本题答案为：169．20．【解答】解：∵x +y ＝2，x 2﹣y 2＝（x +y ）（x ﹣y ）＝6，∴x ﹣y ＝3，故答案为：3．21．【解答】解：根据题意得：4a 2b ÷ab ＝4a ，则纸板的面积为4a •b +4a •a •2+a •b •2＝4ab +8a 2+2ab ＝6ab +8a 2． 故答案为：6ab +8a 2．22．【解答】解：设t ＝n ﹣99，则n ＝t +99，∵（n ﹣99）（n ﹣105）＝3，∴t （t ﹣6）＝3，即t 2﹣6t ＝3，∴t 2﹣6t +9＝12，∴（t ﹣3）2＝12，∴原式＝4（n ﹣102）2＝4（t ﹣3）2＝4×12＝48．故答案为48．23．【解答】解：已知等式整理得：x 2+（2﹣a ）x ﹣2a ＝x 2+bx ﹣10， 可得2﹣a ＝b ，﹣2a ＝﹣10，解得：a ＝5，b ＝﹣3，则ab ＝﹣15，故答案为：﹣1524．【解答】解：∵mn ＝1，m ﹣n ＝2，∴m 2n ﹣mn 2＝mn （m ﹣n ）＝1×2＝2故答案为：2．25．【解答】解：∵x +y ＝3，xy ＝﹣12，∴x 2+y 2＝（x +y ）2﹣2xy ＝32﹣2×（﹣12）＝33．26．【解答】解：∵2x ＝5，2y ＝3，∴2x +y ＝2x ×2y ＝15．故答案为：15．27．【解答】解：∵m +2n +2＝0，∴m +2n ＝﹣2，∴2m •4n ＝2m •22n ＝2m +2n ＝2﹣2=14． 故答案为：14．28．【解答】解：（x +p ）（x +5）＝x 2+5x +px +5p ＝x 2+（5+p ）x +5p ， ∵乘积中不含x 的一次项，∴5+p ＝0，解得p ＝﹣5，故答案为：﹣5．29．【解答】解：设正方形的边长是xcm ，根据题意得：（x +2）2﹣x 2＝44，解得：x ＝10．故答案为：10cm ．30．【解答】解：∵5x ﹣3y ＝2，∴105x ÷103y ＝105x ﹣3y ＝102＝100．故答案为：100．31．【解答】解：∵（x +y ）2＝49，xy ＝12，∴x 2+y 2＝（x +y ）2﹣2xy ＝49﹣24＝25，故答案为：2532．【解答】解：∵x 2+mx +25＝x 2+mx +52是完全平方式，∴m＝±2×5＝±10．故答案为：±10．33．【解答】解：原式＝x2+2x+x+2＝x2+3x+2，故答案为：x2+3x+234．【解答】解：∵a9÷a n＝a5，∴9﹣n＝5，n＝4．故答案为：4．35．【解答】解：由于（x±1）2，＝x2±2x+1，＝x2+mx+1，∴m＝±2．故答案为：±2．36．【解答】解：原式＝x（4x2﹣9）＝x（2x+3）（2x﹣3），故答案为：x（2x+3）（2x﹣3）37．【解答】解：∵点（﹣3，4）与点（a2，b2）关于y轴对称，∴a2＝3，b2＝4．∴（a+b）（a﹣b）＝a2﹣b2＝3﹣4＝﹣1．故答案为：﹣1．38．【解答】解：原式＝4x2y2•（﹣5x2y）＝﹣20x4y3．故答案为：﹣20x4y3．39．【解答】解：当a+b＝10，ab＝11时，原式＝（a+b）2﹣3ab＝100﹣33＝67．故答案为：67．40．【解答】解：原式＝a2+4ab+4b2＝a2+4ab+4b2，故答案为：a2+4ab+4b2．41．【解答】解：原式＝2x2+6xy﹣xy﹣3y2＝2x2+5xy﹣3y2．故答案为：2x2+5xy﹣3y2．。

2020年人教版八年级上册数学期末常考题型复习卷
一．选择题
1．下列长度的三条线段能组成三角形的是（）
A．1，1，2B．4，4，9C．3，4，5D．6，16，8
2．下列图形中对称轴的条数小于3的是（）
A．B．C．D．
3．目前世界上刻度最小的标尺是钻石标尺，它的最小刻度为0.2nm（其中1nm＝10﹣9m），用科学记数法表示这个最小刻度（单位：m），结果是（）
A．2×10﹣8m B．2×10﹣9m C．2×10﹣10m D．2×10﹣11m
4．下列计算错误的是（）
A．a2•a＝a3B．（ab）2＝a2b2C．（a2）3＝a6D．﹣a+2a＝﹣2a2 5．已知△ABC≌△A1B1C1，若∠C＝60°，则∠C1的度数为（）
A．50°B．60°C．70°D．120°
6．一副三角板如图方式摆放，BM平分∠ABD，DM平分∠BDC，则∠BMD的度数为（）
A．102°B．107.5°C．112.5°D．115°
7．如图，在△ABC中，AB的垂直平分线DE交AB于点D，交AC于点E，且AC＝15cm，△BCE的周长等于25cm，则BC的长度等于（）
A．5cm B．10cm C．15cm D．20cm
8．如图，△ABC的三边AB、BC、CA长分别是10、15、20．其三条角平分线交于点O，将△ABC分为三个三角形，S△ABO：S△BCO：S△CAO等于（）。

人教版八年级上册期末考试知识点复习汇总人教版第一章从世界看中国1.中国的的地理位置从东西半球看，中国位于东半球；从南北半球看，中国位于北半球，从大洲和大洋的位置看，中国位于亚洲东部，太平洋的西岸。

2.中国优越的地理位置从纬度位置看，我国领土南北跨纬度很广，大部分位于中纬度地区，属北温带，南部少数地区位于北回归线以南的热带，没有寒带；从海陆位置看，我国位于亚欧大陆大的东部，与许多国家接壤，东临太平洋，有众多的岛屿的港湾，是一个海陆兼备的国家。

3.中国的国土面积约960万平方千米，仅次于俄罗斯，加拿大，居世界第三。

4.中国四至最北端：黑龙江漠河以北的黑龙江主航道的中心线上（53°N）。

最东端：黑龙江与乌苏里江主航道中心线的相交处（135°）。

最西端：新疆的帕米尔高原（73°E）。

最南端：南海的南沙群岛中的曾母暗沙（3°N）。

我国位于亚欧大陆东部，东临太平洋，陆上邻国14个，隔海相望的国家有6个。

14个陆上邻国分别是：朝鲜、俄罗斯、蒙古、哈萨克斯坦、吉尔吉斯斯坦、塔吉克斯坦、阿富汗、巴基斯坦、印度、尼泊尔、不丹、缅甸、老挝、越南；6个隔海相望的国家分别是：韩国、日本、菲律宾、马来西亚、印度尼西亚、文莱。

渤海附近有我国最大的盐场一一长芦盐场，东海有我国最大的渔场——舟山渔场。

5.我国濒临的海洋，自北向南依次是：渤海，黄海，东海，南海；台湾海峡属东海。

6.我国共有34省级行政单位，23个省，5个自治区，4个直辖市，2个特别行宁夏回族自治区、内蒙古自治区、西藏自治区、新疆维吾尔自治区。

2个特别行政区：香港特别行政区、澳门特别行政区。

中国最大的省级行政单位：新疆维吾尔自治区。

中国最小的省级行政单位：澳[门特别行政区。

中国人口最多的省级行政单位：广东省。

中国人口最少的省级行政单位：澳门特别行政区。

中国人口密度最大的省级行政单位：澳门特别行政区。

中国人口密度最小的省级行政单位：酉藏自治区。

2020年-2021年部编人教版八年级道德与法治上册全册期末知识点归纳第一单元走进社会生活第一课丰富的社会生活（一）我与社会1.感受社会生活（1）我们的社会生活绚丽多彩。

（2）人们在社会交往中形成了各种社会关系。

社会生活空间不断延展，我们会与越来越多的人打交道，对社会生活的感受越来越丰富，认识越来越深刻。

2.个人与社会的关系（1）个人是社会的有机组成部分。

（2）人的身份是在社会关系中确定的。

在不同的社会关系中，我们具有不同的身份。

3.几种主要的社会关系：血缘关系（家庭、家族成员之间的关系）、地缘关系（同乡、邻居）、业缘关系（同学、同事）。

（二）在社会中成长1.在社会课堂中成长（我们是怎样在社会课堂中成长的？）（1）在社会课堂中成长人的成长是不断社会化的过程。

我们会逐渐成长为一名合格的社会成员。

（2）我们的衣食住行、学习和娱乐等都与社会的方方面面发生着千丝万缕的联系。

人的生存和发展离不开社会，每个人都能从社会中获得物质支持和精神滋养。

2.亲社会行为的表现关注社会，了解社会，服务社会。

3.亲社会行为的作用有利于我们养成良好的行为习惯，塑造健康的人格，形成正确的价值观念，获得他人和社会的接纳与认可。

4.怎样养成亲社会行为？（1）树立积极的生活态度，关注社会，了解社会，服务社会，养成亲社会行为。

（2）亲社会行为在人际交往和社会实践中养成。

我们要主动了解社会，关注社会发展变化，积极投身于社会实践。

在社会生活中，我们要遵守社会规则和习俗，热心帮助他人，想他人之所想，急他人之所急。

（3）参与社会的过程，既是体验社会生活的过程，也是在实践中发展和成就自己的过程。

主动关心社会，积极融入社会，奉献社会，实现自己的人生价值。

第二课网络生活新空间（一）网络改变世界1.网络是怎样改变世界的？（1）网络丰富日常生活（2）网络推动社会进步2.网络怎样丰富日常生活？（1）网络让我们日常生活中的信息传递和交流变得方便迅捷；（2）互联网打破了传统人际交往的时空限制，促进了人际交往；（3）网络让我们的生活变得更加便利和丰富多彩。

2020人教版八年级英语期末复习专题训练二、完形填空解题技巧及训练（含答案）一、完形填空解题方法。

1、先看首句，快速进入语篇意境；通常情况下，出题人为了让考生能迅速进入语篇环境，第一句话通常是不会设置空格的，所以同学们一定要重视首句，要读懂并理解其中文意思。

2、注意划分句子，逐句阅读；完形填空是把一个完整的短文抽取部分单词后，加入一些干扰选项组合而成。

但无论怎样干扰，其文章的中心思想是不会变化。

而短文的中心思想必然要通过句子呈现，因此，同学们必须逐句划分，阅读分析。

3、对比选项并理解单词和短语的含义；初中阶段的完形填空通常会考察同学们对单词、短语的含义理解，因此，平时可要学会归纳和积累一些单词、词组。

4、注意辨析短语、单词和固定搭配；短语和单词的辨析，几乎是每篇完形填空的必考题，因此同学们要善于区分和总结同义词、近义词以及短语。

5、通篇阅读后，再确定选项，切记不要边读边选。

完形填空看似比较散，但通篇阅读后同学们会发现，完形填空有一个特点就是如果一个地方选错，那么下文一定会受到影响。

因此一定要避免边做边选，除非你十分确定的某个选项。

我们要练习上下文，根据句子的暗示和关键词，加以分析和推敲，才能最终确定答案。

二、解题技巧分布剖析。

例题1、阅读下面短文，根据短文内容，从 A、B、C 三个选项中选出可以填入空白处的正确答案。

Have you seen Peter Pan? It’s 1 really excellent film, and it’s been a very popular story with people 2 many years. It’s the story of a boy 3 Peter Pan. He believed in magic, and in never 4 up. He lives on an island. One day he meets some children, Wendy and her brothers, in London, and they decide 5 there with him.They have 6 of adventures there —and there’s danger, too. A bad man, a pirate, called Captain Hook, wants to kill Peter. In a famous 7 between Peter Pan and Captain Hook near the end of the film, Peter Pan and Captain Hook are sailing on the sea.Peter 8 Captain Hook over the side of the ship and a crocodile eats him. Thechildren clap their hands and cheer loudly 9 they are so excited. But in the end, Wendy misses her home, and is worried about 10 back, so she and her brothers leave Peter Pan and go back home.第一步、适当观察选项，理解选项考察的范围。