eviews 时间序列模型

Eviews残差单位根检验步骤1. 概述Eviews是一种广泛用于计量经济学研究的数据分析软件，它提供了一系列的统计分析工具，其中包括残差单位根检验。

残差单位根检验是判断时间序列数据是否平稳的重要方法之一，本文将介绍在Eviews 软件中进行残差单位根检验的具体步骤。

2. 数据准备在进行残差单位根检验之前，首先需要利用Eviews进行时间序列模型的拟合，得到模型的残差序列。

在Eviews中，可以使用最小二乘法、一般最小二乘法等方法估计时间序列模型，得到残差序列。

以ARMA(p,q)模型为例，其残差序列可以通过以下步骤获取：(1) 打开Eviews软件，导入所需数据；(2) 选择“Quick/Estimate Equation”或“Proc/Estimate Equation”，在弹出的窗口中输入ARMA(p,q)模型的方程形式，点击“OK”进行模型估计；(3) 在估计结果页面，找到残差序列并将其保存。

3. 单位根检验Eviews提供了多种单位根检验的方法，如ADF检验、Phillips-Perron检验等。

下面将以ADF检验为例，介绍在Eviews中进行残差单位根检验的步骤。

(1) 打开Eviews软件，打开保存的残差序列数据；(2) 选择“View/Residual Diagnostics/Unit Root Test”；(3) 在弹出的窗口中选择ADF单位根检验，设置滞后阶数和趋势项，并点击“OK”进行检验；(4) 在ADF单位根检验结果页面，查看检验统计量的数值及其显著性水平，进行单位根检验的判断。

4. 检验结果解读进行残差单位根检验后，需要对检验结果进行解读。

在Eviews中，一般使用的显著性水平为0.05，若检验统计量的值小于相应的临界值，就可以拒绝原假设，即残差序列是平稳的。

相反，若检验统计量的值大于临界值，则不能拒绝原假设，残差序列是非平稳的。

在解读检验结果时，需要注意控制滞后阶数和趋势项的选择，以及检验结果的稳健性和有效性。

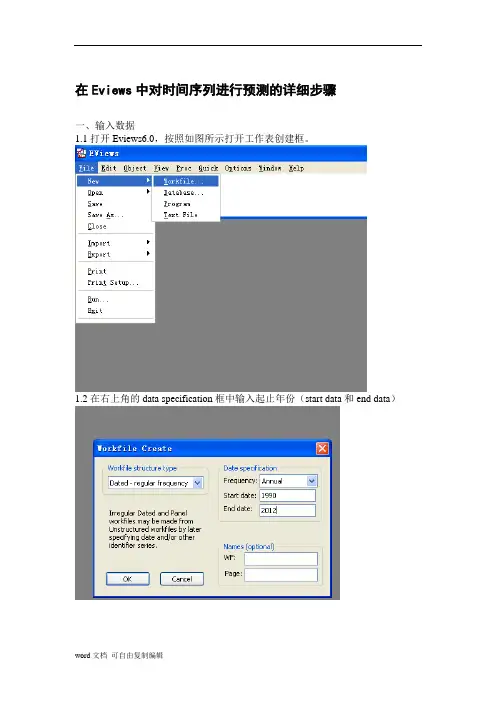
在Eviews中对时间序列进行预测的详细步骤一、输入数据1.1打开Eviews6.0，按照如图所示打开工作表创建框。

1.2在右上角的data specification框中输入起止年份（start data和end data）1.3输入数据：在输入框中输入data gdp（本文采用的数据为1990—2012年的GDP值）。

当然，data后面可以输入任何你想要定义的“英文名字”输入data gdp后注意按回车键，弹出表格窗口后在其中输入数据（也可复制进去数据：ctrl+v键）二、平稳性检验2.1在打开的数据窗口中点击View→Correlogram（1）在弹出的窗口中直接点OK即可↓2.2自相关图和偏相关图进行分析：最简单粗暴的方法就是看最右边的Prob值（即P值），当这列数据有多数都大于0.05（置信水平）时为白噪声序列=序列是平稳的。

本文中GDP数据P值均小于0.05，则为非白噪声。

需对序列进行差分。

三、取一阶差分3.1在输入框中输入第二列代码，这代表将数据gdp进行一阶差分，一阶差分后的值命名为dgdp.按回车键3.2在dgdp数据的窗口中重复2.1的操作，对序列的平稳性进行检验得到结果如下：惨！还是非白噪声，只能进行二阶差分了！四、取二阶差分4.1如第三列代码所示（记得不能重复命名）4.2对新的序列dgdp2进行平稳性检验，步骤同上，结果如下：MY GOD! 看见了木有，这回是白噪声了，P值多数都大于0.05！五、用最小二乘法对模型进行估计：输入ls dgdp2 c ar（2）（探索性建模）5.1AR（2）模型结果（准确的说这个模型应该是ARIMA的疏系数模型，本文重点不在这！如有需要请私信我！）5.2MA(2)模型结果5.3优化模型：根据AIC和SBC准则选择模型，值越小的拟合效果越好，本文的选择MA(2)模型。

5.4对模型进行检验：View→Residual Tests→Correlogram Q statistics检验结果如下：P值大于0.05，为白噪声序列，则平稳。

Eviews 面板数据之固定效应模型在面板数据线性回归模型中，如果对于不同的截面或不同的时间序列，只是模型的截距项是不同的，而模型的斜率系数是一样的，则称此模型为固定效应模型。

固定效应模型分为三类：1.个体固定效应模型个体固定效应模型是对于不同的纵剖面时间序列〔个体〕只有截距项不同的模型：2Kit i k kit it k y x u λβ==++∑(1)从时间和个体上看，面板数据回归模型的解释变量对被解释变量的边际影响均是一样的，而且除模型的解释变量之外，影响被解释变量的其他所有〔未包括在回归模型或不可观测的〕确定性变量的效应只是随个体变化而不随时间变化时。

检验：采用无约束模型和有约束模型的回归残差平方和之比构造F 统计量，以检验设定个体固定效应模型的合理性。

F 模型的零假设：RRSS 是有约束模型〔即混合数据回归模型〕的残差平方和，URSS 是无约束模型ANCOVA 估计的残差平方和或者LSDV 估计的残差平方和。

实践：一、数据：1996—2002年中国东北、华北、华东15个省级地区的居民家庭人均消费〔cp ，不变价格〕和人均收入〔ip ，不变价格〕居民，利用数据〔1〕建立面板数据〔panel data 〕工作文件；〔2〕定义序列名并输入数据；〔3〕估计选择面板模型；〔4〕面板单位根检验。

年人均消费〔consume 〕和人均收入〔ine 〕数据以及消费者价格指数〔p 〕分别见表1，2和3。

表3 1996—2002年中国东北、华北、华东15个省级地区的消费者物价指数步骤：〔1〕File——New——Workfile步骤：〔2〕Start date——End date——OK步骤：〔3〕Object——New Object步骤：〔4〕Type of object——Pool步骤：〔5〕输入所有序列名称步骤：〔6〕定义各变量点击sheet—输入consume？ine？p"步骤：〔7〕将表1、2、3中的数据复制到Eviews 中 2.估计操作：步骤：〔1〕点击poolmodel ——Estimate对话框说明Dependent variable:被解释变量；mon ：系数一样局部 Cross-section specific:截面系数不同局部步骤：〔2〕将截距项选择区选Fi*ed effects 〔固定效应〕 Cross-section ：Fi*ed 得到如下输出结果：接下来用F 统计量检验是应该建立混合回归模型，还是个体固定效应回归模型。

eviews实验指导ARIMA模型建模与预测在数据分析和时间序列预测的领域中，ARIMA 模型是一种非常强大且实用的工具。

通过eviews 软件来实现ARIMA 模型的建模与预测，可以帮助我们更高效地处理和分析数据，做出更准确的预测。

接下来，让我们逐步深入了解如何使用eviews 进行ARIMA 模型的建模与预测。

首先，我们要明白什么是 ARIMA 模型。

ARIMA 全称为自回归移动平均整合模型（Autoregressive Integrated Moving Average Model），它由三个部分组成：自回归（AR）部分、差分（I）部分和移动平均（MA）部分。

自回归（AR）部分是指当前值与过去若干个值之间存在线性关系。

例如，如果说一个时间序列在 AR(2)模型下，那么当前值就与前两个值有关。

移动平均（MA）部分则表示当前值受到过去若干个随机误差项的线性影响。

差分（I）部分用于将非平稳的时间序列转化为平稳序列。

平稳序列在统计特性上，如均值、方差等，不随时间变化而变化。

在 eviews 中进行 ARIMA 模型建模与预测，第一步是数据的导入和预处理。

打开 eviews 软件后，选择“File”菜单中的“Open”选项，找到我们要分析的数据文件。

数据的格式通常可以是 Excel、CSV 等常见格式。

导入数据后，需要对数据进行初步的观察和分析，了解其基本特征，比如均值、方差、趋势等。

接下来，判断数据的平稳性。

这是非常关键的一步，因为 ARIMA 模型要求数据是平稳的。

我们可以通过绘制时间序列图、计算自相关函数（ACF）和偏自相关函数（PACF）来直观地判断数据的平稳性。

如果时间序列图呈现明显的趋势或周期性，或者自相关函数和偏自相关函数衰减缓慢，那么很可能数据是非平稳的。

对于非平稳的数据，我们需要进行差分处理。

在 eviews 中，可以通过“Quick”菜单中的“Generate Series”选项来实现差分操作。

1.打开eviews软件，点击file-new-workfile，见对话框又三块空白处，选择时间序列dated-regular frequency。

在date specification中选择monthly，start（起始时间）输入2005M11，end（终止时间）输入2008M6（eviews的时间序列没有间隔序列输入就将时间进行调整）。

右下角为工作间取名字tmd。

点击ok。

在所创建的workfile中点击object-new object，选择series，以及填写名字tmd，点击OK。

将数据填写入内就生成了以tmd为名的数据集2. 点击view-United root test，test type选择ADF检验，滞后阶数中lag length 选择SIC检验，点击ok得结果如下：一阶差分：点击GENR命令按钮，在输入框中输入bod1=D(bod)，得到一阶差分后的结果：再对一阶差分后的数据同样进行平稳性检验（单根值检验）ADF序列零均值化①在命令窗口输入如下命令（如下图所示）：Scalar m=@mean(tmd)其中：Scalar命令在Eviews中表示生成标量数据（均值只是一个数，而不是序列）。

在tmd窗口下选择菜单操作方式：单击Genr在对话框中输入BOD1=BOD-m得到零均值后的新序列tmd1与之前的数据完全不同。

3. 在工作区双击序列图标tmd1，再选用菜单操作方式：View—>Correlogram，在出现的对话框点击OK。

4.估计模型中的未知参数识别透明度这组时间序列适合的模型后，需要进一步的估计模型中的具体参数，下面就用eviews软件进行估计。

由前面的图形看出：自相关系数和偏相关系数具有相似的衰减特点：衰减快，偏相关图中，2阶以后函数值趋于0，呈截尾性选AR(2)；而在自相关图中，在4阶以后函数值趋于0，呈拖尾性，因此可将q取3故可选MA(3)模型。

利用菜单操作建立ARMA模型。

经典线性回归模型经典回归模型在涉及到时间序列时，通常存在以下三个问题：1）非平稳性→ ADF单位根检验→ n阶单整→取原数据序列的n阶差分（化为平稳序列）2）序列相关性→D.W.检验/相关图/Q检验/LM检验→n阶自相关→自回归ar(p)模型修正3）多重共线性→相关系数矩阵→逐步回归修正注：以上三个问题中，前两个比较重要。

整体回归模型的思路：1）确定解释变量和被解释变量，找到相关数据。

数据选择的时候样本量最好多一点，做出来的模型结果也精确一些。

2）把EXCEL里的数据组导入到Eviews里。

3）对每个数据序列做ADF单位根检验。

4）对回归的数据组做序列相关性检验。

5）对所有解释变量做多重共线性检验。

6）根据上述结果，修正原先的回归模型。

7）进行模型回归，得到结论。

Eviews具体步骤和操作如下。

一、数据导入1）在EXCEL中输入数据，如下：除去第一行，一共2394个样本。

2）Eviews中创建数据库：File\new\workfile, 接下来就是这个界面（2394就是根据EXCEL里的样本数据来），OK3）建立子数据序列程序：Data x1再enter键就出来一个序列，空的，把EXCEL里对应的序列复制过来，一个子集就建立好了。

X1是回归方程中的一个解释变量，也可以取原来的名字，比如lnFDI，把方程中所有的解释变量、被解释变量都建立起子序列。

二、ADF单位根检验1）趋势。

打开一个子数据序列，先判断趋势：view\graph，出现一个界面，OK。

得到类似的图，下图就是有趋势的时间序列。

X1.4.2.0-.2-.4-.6-.8100020003000400050002）ADF检验。

直接在图形的界面上进行操作，view\unit root test，出现如下界面。

在第二个方框内根据时序的趋势选择，Intercept指截距，Trend为趋势，有趋势的时序选择第二个，OK，得到结果。

上述结果中，ADF值为-3.657113，t统计值小于5%，即拒绝原假设，故不存在单位根。

eviews阿尔蒙多项式法，也称为Almon polynomial method，是一种在计量经济学中常
用的时间序列分析方法之一。

该方法用于处理具有滞后效应的自变量对因变量的影响。

具体而言，Almon polynomial method将自变量的滞后效应建模为一个多项式函数。

这
个多项式函数可以用来拟合不同滞后期的影响，并且可以根据数据的特征进行调整。

在EViews软件中，可以使用Almon多项式法进行时间序列回归分析。

通过指定滞后
期数和多项式度数，可以估计出各个滞后期对应的权重系数，进而得到回归方程。

需要注意的是，Almon多项式法适用于具有滞后效应的数据分析，但并不适用于所有
情况。

在使用该方法时，需要考虑数据的特点和目标研究问题的要求，以便选择适当
的模型和方法进行分析。

eviewsEViews简介EViews（经济学视图）是一款专业的经济学和金融学软件，广泛应用于经济学研究、时间序列分析、计量经济学、计量金融学等领域。

EViews提供了丰富的数据处理和统计分析功能，能够帮助用户进行数据管理、模型估计、预测模拟、计量建模等工作。

EViews的功能特点数据管理功能：EViews可以对各种类型的数据进行导入、整理和处理，支持多种格式的数据读取（如Excel、CSV等），提供了对数据进行排序、筛选、合并等功能，方便用户对数据进行管理和分析。

统计分析功能：EViews提供了多种统计分析方法，包括描述性统计、相关分析、回归分析、时间序列分析等，用户可以通过简单的操作完成复杂的统计分析任务。

时间序列分析功能：EViews是一款专业的时间序列分析软件，提供了多种时间序列模型的估计和检验方法，包括ARIMA模型、ARCH/GARCH模型、VAR模型等，用户可以通过EViews进行时间序列的建模和预测。

计量经济学建模功能：EViews支持用户进行计量经济学的建模和分析工作，包括传统的OLS回归模型、面板数据模型、离散选择模型等，用户可以通过EViews进行模型估计、假设检验和参数解释等。

预测模拟功能：EViews提供了模型预测和模拟功能，可以根据已有的模型参数对未来的数据进行预测，同时可以进行模拟分析，模拟不同的数据情景，评估模型的鲁棒性和稳定性。

EViews的应用领域EViews广泛应用于经济学研究、金融学分析和政策制定等领域，包括宏观经济学、微观经济学、国际贸易、金融工程、风险管理等。

在学术界和政府机构中，EViews被广泛用于经济学研究和政策分析，为研究人员和决策者提供了强大的数据分析和建模工具。

总结EViews是一款功能强大的经济学和金融学软件，可以帮助用户进行数据处理、统计分析、时间序列建模等工作。

EViews在学术界和政府机构中得到广泛应用，成为经济学研究和政策分析的重要工具。

Eviews序列相关稳健标准误法序言Eviews是一种广泛使用的统计分析工具，具有强大的序列分析功能。

在进行序列分析时，我们经常要考虑序列的相关性及其稳健性。

本文将重点介绍Eviews中序列相关稳健标准误法的原理和应用。

一、序列相关性的概念及检验方法1.1 序列相关性的概念在时间序列分析中，序列相关性是指序列中各个观测值之间的相关关系。

如果序列中的观测值之间存在一定的相关性，那么我们就需要考虑相关性对模型估计和预测的影响。

1.2 序列相关性的检验方法在Eviews中，我们可以通过计算序列的自相关系数和偏自相关系数来检验序列相关性。

自相关系数是指序列与其自身滞后期的相关系数，而偏自相关系数则是通过排除中间滞后项的影响来计算序列间的相关系数。

二、序列相关稳健标准误法的原理2.1 序列相关稳健标准误法的概念在实际应用中，我们经常遇到序列中存在的异方差性和相关性问题。

传统的OLS估计方法在存在序列相关性和异方差性时会导致估计量的无偏性和有效性受到影响。

为了解决这一问题，引入了序列相关稳健标准误法。

2.2 序列相关稳健标准误法的原理序列相关稳健标准误法通过调整OLS估计量的标准误来适应序列相关性和异方差性的存在。

在Eviews中，我们可以通过设置相关稳健标准误来进行估计，以提高估计量的有效性和精确度。

三、Eviews中序列相关稳健标准误法的应用3.1 Eviews中设置序列相关稳健标准误的步骤在Eviews中，设置序列相关稳健标准误非常简单。

用户只需在进行估计时选择相关稳健标准误选项即可，Eviews会自动对估计量进行调整。

3.2 序列相关稳健标准误法的优势相比于传统的OLS估计方法，序列相关稳健标准误法能够更好地适应序列相关性和异方差性的存在，提高了估计量的精确度和有效性。

在实际应用中，我们更倾向于使用序列相关稳健标准误法来进行序列分析。

结论通过本文的介绍，我们了解了序列相关稳健标准误法在Eviews中的应用。

eviews的garch模型预测步骤Eviews中的GARCH模型预测步骤引言：GARCH模型是一种用于预测金融市场波动性的模型，它结合了ARCH模型和时间序列模型的优点，能够更准确地预测金融资产的风险。

在Eviews软件中，通过一系列简单的步骤，我们可以利用GARCH模型进行预测。

本文将介绍Eviews中使用GARCH模型进行预测的具体步骤。

步骤一：导入数据我们需要在Eviews中导入需要进行预测的数据。

可以通过多种方式导入数据，例如从Excel文件中导入或直接在Eviews中输入。

在导入数据时，确保数据的时间顺序正确，以便后续分析和预测。

步骤二：建立GARCH模型在Eviews中，建立GARCH模型非常简单。

首先，选择要建立GARCH模型的变量，在菜单栏中选择“Quick/Estimate Equation”或直接点击工具栏中的“Estimate Equation”按钮。

然后，在弹出的对话框中选择“ARCH/GARCH”模型，并设置相关参数，如模型阶数、残差类型等。

点击“OK”按钮后，Eviews会根据选择的参数自动建立GARCH模型。

步骤三：模型估计在建立GARCH模型后，需要对模型进行估计，以获得模型的参数估计值和其他统计信息。

在Eviews中，点击工具栏中的“Estimate”按钮或选择菜单栏中的“View/Estimation Output”选项，即可进行模型估计。

Eviews会自动计算模型的参数估计值、标准误差、t值等统计信息。

步骤四：模型诊断模型估计完成后，需要对模型进行诊断，以评估模型的拟合效果和可靠性。

在Eviews中，可以通过查看估计结果的统计信息和图形来进行模型诊断。

例如，可以检查模型的残差是否服从正态分布，是否存在异方差性等。

如果发现模型存在问题，可以对模型进行调整或选择其他模型。

步骤五：模型预测在进行模型诊断后，可以利用已估计的GARCH模型进行预测。

在Eviews中，选择菜单栏中的“Forecast/Forecast”选项，即可进行模型预测。

Eviews统计分析软件的基本使用方法一、介绍Eviews是一款专为经济学家和金融学家设计的统计分析软件，它提供了丰富的数据分析和计量经济模型建立功能。

本文将介绍Eviews的基本使用方法，包括数据导入、数据处理、计量经济模型建立和结果分析等方面。

二、数据导入使用Eviews进行统计分析的第一步是将数据导入软件中。

Eviews支持多种数据格式，包括Excel、CSV和SPSS等。

用户可以选择“File”菜单下的“New”选项来创建新的数据文件，然后选择“Import”选项将数据文件导入。

在导入数据时，用户需要指定数据的类型、路径和文件名等信息。

三、数据处理导入数据后，用户可以对数据进行处理和清洗，以准备后续的分析工作。

Eviews提供了多种数据处理功能，包括数据排序、变量选择、缺失值处理和数据转换等。

用户可以通过简单的拖放操作或者使用命令来完成这些处理任务。

四、计量经济模型建立Eviews的核心功能之一是计量经济模型的建立和估计。

用户可以通过Eviews提供的拖放界面来构建模型，也可以使用Eviews的命令语言进行模型编写。

Eviews支持多种计量经济模型，包括线性回归模型、时间序列模型和面板数据模型等。

用户可以根据自己的需求选择适合的模型进行建立。

五、模型估计建立模型后，用户需要对模型进行估计和检验。

Eviews提供了多种估计方法，包括最小二乘法、广义最小二乘法和面板数据估计等。

用户可以选择合适的估计方法，并根据需要进行参数估计和假设检验。

Eviews会根据用户的选择自动进行结果计算，并提供相应的输出。

六、结果分析完成模型估计后，用户需要对结果进行分析和解释。

Eviews提供了丰富的结果分析工具，包括参数估计的显著性检验、残差分析、模型拟合度检验和模型比较等。

用户可以通过简单的图表和统计量来展示和解释模型的结果。

七、时间序列分析除了建立和估计计量经济模型，Eviews还提供了强大的时间序列分析功能。