回溯法的应用—n后问题 后问题
例1(8-皇问题)
皇问题) 例1(8-皇问题) ( 皇问题
在8×8的棋盘上放置8个皇后,使得这8个皇 后不在同一行,同一列及同一斜角线上.如下 1 2 3 4 5 6 7 8 图6.1: Q
1 2 3 4 5 6 7 8
Q Q Q Q Q Q Q
5.1 回溯法的基本思想
(1)解空间 设问题的解向量为X=(x1,x2,…,xn) ,xi的取值范 围为有穷集Si .把xi的所有可能取值组合,称 为问题的解空间.每一个组合是问题的一个可 能解.
5.1 回溯法的基本思想
(1)解空间 例:0/1背包问题,S={0,1},当n=3时,0/1背 包问题的解空间是: {(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1, 1,0),(1,1,1)} 当输入规模为n时,有2n种可能的解.
A 2 C 3 F 4 L 4 2 G H 3 4 M N 1 B 3 D
4 4 I 2 O E 2 J 3 P 3 K 2 Q
----排列树 解空间大小: n!
5.1 回溯法的基本思想
(3)状态空间树的动态搜索
可行解和最优解: 可行解:满足约束条件的解,解空间中的一个子集 最优解:使目标函数取极值(极大或极小)的可行解,一 个或少数几个 例:货郎担问题,有nn种可能解. n!种可行解,只有一个或 几个解是最优解. 例:背包问题,有2n种可能解,有些是可行解,只有一个或 几个是最优解. 有些问题,只要可行解,不需要最优解,例如八后问题.
5.1 回溯法的基本思想
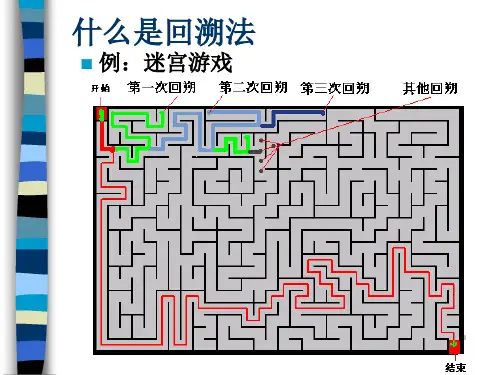
回溯法(backtracking)是一种系统地搜索问 题解的方法.为实现回溯,首先需要定义一个 解空间(solution space),然后以易于搜索 的方式组织解空间,最后用深度优先的方法搜 索解空间,获得问题的解.