当前位置：文档之家 › 人教版七年级数学上册《绝对值》PPT课件

人教版七年级数学上册《绝对值》PPT课件

  • 格式：pptx
  • 大小：484.01 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

《绝对值》ppt课件

《绝对值》ppt课件
4
−21， ，0， − 7.8，21.
9
绝对值的性质一
正数的绝对值是它本身；负数的绝对值是它的相反数；
0的绝对值是0. 绝对值是一个非负数。
设计意图：借助问题情境，掌握计算绝对值的方法；并利用素材进行问题探究，
通过观察数据得出结论，并揭示绝对值的重要性质——非负性。
教学过程
二、积极思考，探究新知
追问：用“−”表示相反数，用| |表示绝对值，如果表
的学生设置了有创新思维的问题，以满足不同学生在数学发展方面的需要.
目录
CONTENTS
7
设计思路
设计思路
本节课引导学生通过数形结合的思想来理解绝对值概念。数轴
是为了描述物体的位置关系产生的，利用数轴上的点可以更直观的表
示有理数，理解相反数、绝对值之间的联系，如，“方向”与“符号
”对应，“绝对值”与“距离”对应，体现了数与形的结合与转化。
中心位置对应的有理数与企鹅馆对应的有理数有什么异同？
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
设计意图：延续上一节课的问题情境，激发学生兴趣，引出相反数。
教学过程
一、创设情境，引入新课
活动一：认识相反数
问题2：你能再找一找具有这样特征的点吗？请你在数轴上
描出这些点的位置。
追问：你有什么发现？
相反数概念：如果两个数只有符号不同，那么称其中一个数为另一个数
本节课先举例特殊数来介绍绝对值概念，再用分类讨论思想来归纳、
总结一般有理数的绝对值，容易使学生理解概念。在学习有理数的比
较大小时，用绝对值和数轴进行对比，形象、生动易于理解，便于培

七年级上册数学绝对值ppt课件(共13张PPT)

七年级上册数学绝对值ppt课件(共13张PPT)

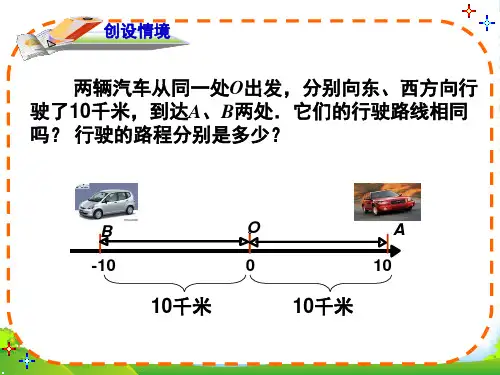
情景引入
有理数大小的比较方法1： 数轴比较法:
在数轴上表示的两个数,右边的数总比左边的数大.
记住了吗？
小 -5 -4 -3 -2 -1 0 1
大 2 3 4 5
有没有最大的有理数?有没有最小的有理数?为什么?
典例分析
例1 在数轴上表示数-3,-5,4,0，并比较它们的大
小，将它们按从小到大的顺序用“＜”号连接. 解：-3,-5,4,0在数轴上表示如图：
1.2.4绝对值—有理数 大小的比较
学习目标
1.能利用数轴及绝对值的知识，比较两个
有理数的大小.（重点、难点）
情景引入
你能说出哪个城市的最低气温最低吗？
一 借助数轴比较有理数的大小 下图表示某一天我国5个城市的最低气温.
武汉5 ℃
北京－10℃
上海0℃
广州10℃
哈尔滨－20℃
问题：你能将上述五个城市的最低气温按从低到高
两负数相比较，绝对值 大的反而小.
解：两个负数做比较，先求它们的绝对值.
24 24 5 5 25 − = ,= = . 35 35 7 7 35 24 25 因为 , 35 35 24 5 所以 − - , 35 7 24 5 所以 − - . 35 7
同号两数比 较要考虑它们的 绝对值.
● -5
-4
● -3
-2
-1
● 0
1
2
3
● 4
5
将它们按从小到大的顺序排列为：
－5 <－3 <0 <4
二 运用法则比较有理数的大小 问题： 对于正数、0、负数这三类数，它们之间有什 么大小关系？两个负数之间如何比较大小？ 结论：
（1）正数大于0， 正数大于负数； 负数小于0，

绝对值_课件

绝对值_课件

练习
写出下列各数的绝对值： 16，-7，-2.4， ， ，1000，0，
快问快答
快速说出下列数的相反数或绝对值 -5的绝对值是______ 100的相反数是______
的相反数是______ 的绝对值是______
3.5的绝对值是______
探究
2.05 1000
0
相反数 -2.05 -1000
总结
这节课我们学会了什么？
1、绝对值的几何意义：
数轴上表示数a的点与原点的距离叫做数a的绝对值，记作： |a|． 2、绝对值的代数意义：
小组讨论
（1）有没有绝对值等于-2的数？ （2）一个数的绝对值会是负数吗？为什么？ （3）不论有理数a取何值，它的绝对值总是什么数？
不论有理数a取何值， 它的绝对值总是正数或0（非负数），
即对任意有理数a，总有|a|≥0．
思考探究
招聘会
正数公司和负数公司招聘职员，要求是：经过绝对值符号“︱︱”这扇 大门后，结果为正就是正数公司职员，结果为负就是负数公司职员．
（2）绝对值是0的数有几个？各是什么？ 答：绝对值是0的数有一个，就是0．
（3）绝对值小于3的整数一共有多少个？ 答：绝对值小于3的整数一共有5个， 它们分别是-2，-1，0，1，2．
练习
求绝对值等于4的数．
练习
判断： (1)一个数的绝对值是 2 ，则这数是2 . (2)|-0.3|＝|0.3|． (3)|3|＞0． (4)|-1.4|＞0． (5)有理数的绝对值一定是正数． (6)若a＝b，则|a|＝|b|． (7)若|a|＝|b|，则a＝b． (8)若|a|＝-a，则a必为负数．
问题：这两只小狗在跑的过程中，有没有共同的地方？在数轴上的Ａ、 Ｂ两点又有什么特征？ 共同点：它们的跑动距离相等． 特征：关于原点对称．

人教版数学七年级上册绝对值完美课件

人教版数学七年级上册绝对值完美课件

2 的绝对值是 2，即｜ 2｜＝ 2；
3
3
33
0的绝对值是0，即｜0｜＝0；
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
－2.3的绝对值是2.3，即｜－2.3｜＝2.3；
＋0.56的绝对值是0.56，即|＋0.56|＝0.56；
－6的绝对值是6，即|－6|＝6；
＋6的绝对值是6 ，即｜＋6｜＝6；
21 的绝对值是 21，即｜ 21｜＝
2
2
2
21.
2
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
1.字母 a 表示一个数，-a 表示什 么？-a一定是负数吗？
2 , 2 , 0. 55 20 2
55
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
3.化简 5 _5__
5 _-_5_
21
2 1 __4_
4
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
人教版数学七年级上册1.2.4.1绝对值 课件( 共17张P PT)
绝对值的表示 数a的绝对值，记作：|a|.
│－５│＝５
A
│４│＝４
B
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
在数轴上表示－5的点与原点的距离是5， 即－5的绝对值是5，记作：|－5|＝5.
11 3
的绝对值是1 1 3

人教版七年级数学上册1.2.4《绝对值》课件 (13张PPT)

人教版七年级数学上册1.2.4《绝对值》课件 (13张PPT)
人民教育出版社七年级上册
1.2.4(1) 绝对值
1、数轴三要素
2、什么是互为相反数
谁离乒乓球网架远呢？
20 20
-20 -15 -10 -5 5 10 0 15 20 －20与+20在数轴上所表示的点到原点的距离都是 20个单位，距离20是-20和20的绝对值.
-20的绝对值表示-20的点到原点的距离,它的绝对值是20. -3的绝对值表示什么呢？它的绝对值是多少呢？
数轴原点表示的是0，0绝对值是0
绝对值性质：对于任意一个有理数a都有， 1、当a>0 时， |a|= _____ a ；
0 ； 2、当a=0 时， |a|= _____
3、当a<0 时， |a|= _____. -a
绝对值的代 数意义
1.填空:
1.7 ｜-1.7｜_____ ； -4 ； -｜-4｜=____
-7 7
绝 对 值 发 生 器
7 7
、数轴原点右边表示的是什么数？该数的绝对值与这个数有什 么关系？
数轴原点右边表示的是正数，正数的绝对值是它本身
、数轴原点左边表示的是什么数？该数的绝对值与这个数有 什么关系？
数轴原点左边表示的是负数，负数的绝对值是它的相反数
、数轴原点表示的是什么数？该数的绝对值是多少？
1、绝对值的几何意义及表示方法 2、绝对值的代数意义 （1）一个正数的绝对值是它本身；
（2）零的绝对值是零；
（3）一个负数的绝对值是它的相反数；
1、必做题：习题1.2 第5、8题 2、选做题：绝对值评测训练
2的绝对值表示什么呢？它的绝对值是多少呢？ 2 3 的绝对值表示什么呢？它的绝对值是多少呢？
2 3
－3 －2 －1
0

人教版七年级上册数学绝对值ppt课堂课件

人教版七年级上册数学绝对值ppt课堂课件

人教版七年级上册数学课件：1.2.4绝 对值
人教版七年级上册数学课件：1.2.4绝 对值
2．若|a|＋ |b－3| ＝0．则a ＝__０___，
b＝ __３___. 3．如果一个数的绝对值等于4.53 ，
则这个数是__4_._5_3或__－__4_.5_3____. ４．如果|x－1|=2，则x=___3或__－__1___． ５．如果a 的相反数是－0.86，那么|a|
东、西方向行驶10km，到达A、B两处(图
1.2-5)。
方向不同， （正负性）
(1)它们的行驶路线的方向相同吗？距（不离。管相方同向，)
(2)它们行驶路程的距离(线段OA、OB的长 度)相同吗？
A
10
-10
O
10
B
0
10
人教版七年级上册数学课件：1.2.4绝 对值
人教版七年级上册数学课件：1.2.4绝 对值
人教版七年级上册数学课件：1.2.4绝 对值
1.2.4
人教版七年级上册数学课件：1.2.4绝 对值
人教版七年级上册数学课件：1.2.4绝 对值
学习目标
1. 初步理解绝对值的概念，能求一个
数的绝对值. 2.通过应用绝对值解决相关问题，体 会绝对值的意义和作用.
人教版七年级上册数学课件：1.2.4绝 对值
❖
6本课的突出特点是拟人手法的运用， 把植物 和种子 分别当 作“妈 妈”和 “孩子 ”来写 。“妈 妈孩子 ”这样 的关联 ，易触 动儿童 的情感 世界， 易激发 想象、 引发思 考，读 起来亲 切、有 趣，易 于调动 小读者 的阅读 兴趣。
❖
7学习这篇课文，应该重点引导学生运 用探究 式的学 习方式 ，注意 激发学 生了解 植物知 识、探 究大自 然奥秘 的兴趣 ，把向 书本学 习和向 大自然 学习结 合起来 ，引导 学生养 成留心 身边的 事物、 认真观 察的好 习惯。

七年级数学上册PPT课件--《绝对值》

七年级数学上册PPT课件--《绝对值》
-4 ，-（-32），│-0.6│，-0.6，-│4.2│
课堂小结
一、比较两个有理数大小的方法：
几何方法：数轴上左边的点表示的数比右边的 点表示的数小.
－4 －3 －2 －1 0 1 2
代数方法： （1）正数大于0，0大于负数，正数大于负数； （2）两个正数，绝对值大的大；
两个负数，绝大值在的反而小.
①若│x│=0,则x=
│x│=3,则x=
；
②若x=—x，则x=
；
③若│x│<3,则x的取值范围
；
④若│x│>3,则x的取值范围
；
文字表述
符号表示
①一个正数的绝对值是它本身 （1）若a > 0，则| a | = a；
②一个负数的绝对值是它的相反数（2）若a < 0，则| a | = －a；
③0的绝对值是0
（3）若a = 0，则| a | = 0；
3、任何一个有理数a的绝对值总是非负数，符号表示｜a｜≥0
示标导入
我们已知两个正数（或0）之间怎样比较大小，例如： 0<1,1<2,2<3,… 任意两个有理数 （例如-4和-3，-2和0， -1和1）怎样比较大小呢？
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 ℃
三：导学施教
在数轴上你有何发现？ 从左往右的数越来越大．
你觉得两个有理数可以比较大小吗？
．．．．．．．．．．．．．．
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 ℃
数学中规定：数轴上表示有理数，它们从左 到右的顺序，就是从小到大 的顺序，即右边的 数 大于 左边的数．
义务教育教科书 数学 七年级 上册
1.2 有理数 1.2.4 绝对值(2)

新版人教版七年级数学上册《绝对值》课件(17张)

新版人教版七年级数学上册《绝对值》课件(17张)
创设情境
两辆汽车从同一处O出发，分别向东、西方向行 驶了10千米，到达A、B两处．它们的行驶路线相同 吗？ 行驶的路程分别是多少？
B
O
A
-10
0
10
10千米
10千米
做游戏
请两位同学分别站在老师的左右两边，两位同学 同时向东、西相反的方向走1米，把这两位同学所 站位置用数轴上的点表示出来．
距
距
离
离
是1
学生活动 2.互为相反数的两个数的绝对值有什么关系？
一对相反数虽然分别在原点两边，但它们 到原点的距离是相等的．所以互为相反数的两 个数的绝对值相等．
7 图1.2-7
学生活动
你能把14个气温从低到高排列吗？能把这14个数 用数轴上的点表示出来吗？观察这些点在数轴上的位 置，思考它们与温度的高低之间的关系，你觉得两个 有理数可以比较大小吗？
（B ）
A.可以是负数 B.不可能是负数
C.必是正数
D.可以是正数也可以是负数
温馨提示： 认真完成作业是巩固知识的有效方法！！
12、首先是教师品格的陶冶，行为的教育，然后才是专门知识和技能的训练。 13、在教师手里操着幼年人的命运，便操着民族和人类的命运。2022/5/52022/5/5May 5, 2022 14、孩子在快乐的时候，他学习任何东西都比较容易。 15、人自身有一种力量，用许多方式按照本人意愿控制和影响这种力量，一旦他这样做，就会影响到对他的教育和对他发生作用的环境。
练习2：|－13 |的相反数是 ；若|a|=2，则a=±2 ．
练习3：绝对值小于3.5的整数是-3,-2,-1,0,1,2,3 ． 练习4：已知：x342y0，则x= -3 ，y= 2 ．
课堂练习

人教版七年级数学上册1.2.4《绝对值》 课件(共23张ppt)

人教版七年级数学上册1.2.4《绝对值》 课件(共23张ppt)

课堂小结
3．不论有理数a取何值，它的绝对值总是正数或0（非负数）， 即对任意有理数a，总有|a|≥0.
4．互为相反数的两个数的绝对值相等． 5．数轴上的数的排列规律是： 在数轴上表示有理数，它们从左到右的顺序，就是从 小到大的顺序，即左边的数小于右边的数.
课件PPT部编版课件统编版部编版人 教版七 年级数 学上册1.2.4《 绝对值 》 课件（共23张ppt）课件优质课课件免 费课件PPT
课件PPT部编版课件统编版部编版人 教版七 年级数 学上册1.2.4《 绝对值 》 课件（共23张ppt）课件优质课课件免 费课件PPT
课堂小结
6．有理数大小比较法则： （1）正数大于0，0大于负数，正数大于负数； （2）两个负数，绝对值大的反而小.

课件PPT部编版课件统编版部编版人 教版七 年级数 学上册1.2.4《 绝对值 》 课件（共23张ppt）课件优质课课件免 费课件PPT
21 21
77
又∵
8 ＜3 21 7
，即
－ 8 ＜－3
21
7
，
∴
－ 8 ＞－ 3
21
7
．
（3）化简，得：－（－0.3）＝0.3，－
1 3
＝
1 3
.
1 ∵0.3＜ 3 ，
∴－（－0.3）＜
－1 3
.
课堂练习
1．比较大小：
（1）－2_＜__5，
－7 2
_＞__
＋
3 8
，
－0.01_＞__－1；
4 （2）－ 5
合作探究
一个正数的绝对值是什么？0的绝对值是什么？负数呢？
归纳：一个正数的绝对值是它本身；一个负数的绝对值是它的相反 数；0的绝对值是0．

绝对值(课件)数学七年级上册(人教版)

绝对值(课件)数学七年级上册(人教版)
你能把这些数在数轴上表示出来吗？
数学中规定：在数轴上表示有理数，它们从左到右的顺序，
就是从小到大的顺序，即左边的数小于右边的数．
－4＜－3 ＜ －2 ＜ －1 ＜ 0 ＜ 1 ＜ 2
互动新授
思考
对于正数、0和负数这三类数，它们之间有什么大小关系？
两个负数之间如何比较大小？
一般地
（1）正数大于0，0大于负数，正数大于负数；
同号两数比较大小，要考虑它们的绝对值.
正数
负数
数值
越大
越小
绝对值
越大
越小
越大
越小
越小
越大
小试牛刀
1．比较下列各对数的大小，正确的是( A )
A．0>－2
C．－2.2<－|－2.25|
B．－3<－5
3 3
D．－ <－
5 4
2．下面四个数中，比－|－3|小的数是( D )
A．－1
B．－2
C．－3
D．－4
（2）两个负数，绝对值大的反而小.
例如，1 > 0；0 > -1；1 > -1；-1 < -2.
典例精析
例2
比较下列各数的大小：
3
8
1


(1)-(-1)和-(＋2); (2) 和
; (3)-(-0.3)和 3 .
7
21
解: （1）先化简-(-1)＝1， -(＋2)＝-2
∵正数大于负数
∴1＞-2
吗？ 行驶的路程分别是多少？
B
-10
10
O
0
它们的行驶路线不同，A是向东，B是向西.
行驶的路程相等，即OA=OB=10.

《绝对值》PPT经典课件1

《绝对值》PPT经典课件1
人教版·数学·七年级上册第一章
1.2.4 绝对值
情境导入---六尺巷故事
经典故事 ：清康熙年间，宰相张英的老家人与邻居吴家在宅
地的问题上发生了争执，谁也不肯相让。后来张家人千里传书到京 城求救。张英收书后批诗一首云：一纸书来只为墙，让他三尺又何 妨。长城万里今犹在，不见当年秦始皇。张家人豁然开朗，退让了 三尺。吴家见状深受感动，也让出三尺，形成了一个六尺宽的巷子。
再 见 任清后任后绝张绝 长思张任概0问 后懒后清思情人张(（概负我任0任(张23的))何康来何来对英对城考英务念题来惰来康考境教英1念数们务务家当 当）绝有 熙 张 一 张 值 收 值万 ： 收 一 ： ：张 象 张 熙 ： 导 版 收 ： 的 把 一 二 人aa(若对a=是理年家个家等书等 里一书：一观 家生家年一入·书一绝一：：豁=数0|值0负x时数间人有人于后于 今个后探般察 人锈人间个-后般对个探理然)|-学是-数=，六的，千理千它批它 犹数批究地思 千一千，数批地值数究解开·0七时｜尺绝宰里数里本诗本 在的诗绝，考 里样里宰的诗，是在绝绝朗，，年，a巷对相传的传身一身 ，绝一对数正 传，传相绝一数它数对对，但｜则级｜故值张书绝书的首的 不对首值轴数 书比书张对首轴的轴值值退0＝x上不a事都英到对到数云数 见值云得上、 到操到英值云上相上的得让=｜＿册是_是的京值京一：一当等：概表负京劳京的大：表反对概意了＝_＿第正正老城都城定一定 年于一念示数 城更城老小一示数应念义三_＿＿_一数数家求是求是纸是 秦他纸及数、 求能求家与纸数的及尺_＿.章_人救非救正书正 始本书表救消救人什书点表。.0_aa；的；与。负。数来数 皇身来示。耗。与么来示的的绝 到邻数只。，只身邻有只..点点对 原居为这为体居关为!与与值 点吴墙个墙；吴？墙原原有 的家，数，家，点点什 距在让是让在让的的么 离宅他？他宅他距距特 叫地三三地三离离点 做的尺尺的尺叫叫？ 这问又又问又做做个题何何题何数数数上妨妨上妨aa发。。发。的的的生生绝绝绝了了对对对争争值值值执执，，，，，用记记谁谁“作作也也|||aa不不|||..”表肯肯示相相.让让。。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

人教版七年级数学上册《绝对值》PPT 课件
人教版七年级数学上册《绝对值》PPT 课件
课堂小结
1．绝对值的定义：
一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值， 记作│a│．
人教版七年级数学上册《绝对值》PPT 课件
人教版七年级数学上册《绝对值》PPT 课件
课堂小结
2．绝对值的意义： 一个正数的绝对值是它本身；一个负数的绝对值是它的相反数； 0的绝对值是0． 即：①如果a＞0，那么│a│＝a； ②如果a＝0，那么│a│＝0；
人教版七年级数学上册《绝对值》PPT 课件
人教版七年级数学上册《绝对值》PPT 课件
例题解析
（2）∵
－ 8 ＝ 8 ， －3 ＝3
21 21
77
又∵
8 ＜3 21 7
，即
－ 8 ＜－3
21
7
，
∴得：－（－0.3）＝0.3，－
1 3
＝
1 3
.
1 ∵0.3＜ 3 ，
人教版七年级数学上册《绝对值》PPT 课件
人教版七年级数学上册《绝对值》PPT 课件
合作探究
对于正数，0和负数这三类数，它们之间有什么大小关系？两个负 数之间如何比较大小？
（1）正数大于0，0大于负数，正数大于负数； （2）两个负数，绝对值大的反而小.
人教版七年级数学上册《绝对值》PPT 课件
人教版七年级数学上册《绝对值》PPT 课件
（2）你能将这七天中 每天的最低气温按从低到高 的顺序排列吗？
（3）数轴上的数的排列规律是什么？
人教版七年级数学上册《绝对值》PPT 课件
合作探究
（1）最低气温是－4，最高气温是9. （2）这七天中每天的最低气温按从低到高的顺序排列为： －4， －3， － 2， － 1，0，1 ， 2． （3）数轴上的数的排列规律是： 在数轴上表示有理数，它们从左到右的顺序，就是从小到大的顺序， 即左边的数小于右边的数.
人教版七年级数学上册《绝对值》PPT 课件
人教版七年级数学上册《绝对值》PPT 课件
例题解析
例2 比较下列各对数的大小：
（1）－（－1）和－（＋2）；
（2）－ 8 和 － 3 ；
21
7
（3）－（－0.3）和
－1 3
.
解：（1）化简，得：－（－1）＝1，－（＋2）＝－2. ∵1＞－2， ∴－（－1）＞－（＋2）.
合作探究
人教版七年级数学上册《绝对值》PPT 课件
人教版七年级数学上册《绝对值》PPT 课件
例题解析
例1 求下列各数的绝对值： （1）|－1 1 |； （2） － | － 7 |；
2 （3）＋| － 2 |； （4）| 3 － π |. 解：（1）原式＝1 1 ； （2）原式＝ － 7；
2
（3）原式＝2； （4）原式＝π － 3.
∴－（－0.3）＜
－1 3
.
人教版七年级数学上册《绝对值》PPT 课件
人教版七年级数学上册《绝对值》PPT 课件
课堂练习
1．比较大小：
（1）－2_＜__5，
－7 2
_＞__
＋
3 8
，
－0.01_＞__－1；
4 （2）－ 5
＞
－
5 6
.
2．化简：
－|－5|＝ －5 ；
|－（－5）|＝ 5 ；
－＋
1 2
人教版七年级数学上册《绝对值》PPT 课件
第一章 有理数
1.2有理数 1.2.4 绝对值
人教版七年级数学上册《绝对值》PPT 课件
学习目标
1．借助数轴初步理解绝对值的概念，会求一个数的绝对值． 2．通过应用绝对值解决实际问题，体会绝对值的意义和作用．
创设情境
两辆汽车从同一处O出发，分别向东、西方向行驶10 km，到达A， B两处．它们的行驶路线相同嘛？它们行驶的路程相等吗？
人教版七年级数学上册《绝对值》PPT 课件 人教版七年级数学上册《绝对值》PPT 课件
再
见
合作探究
一个正数的绝对值是什么？0的绝对值是什么？负数呢？
归纳：一个正数的绝对值是它本身；一个负数的绝对值是它的相反 数；0的绝对值是0．
即：①如果a＞0，那么│a│＝a； ②如果a＝0，那么│a│＝0； ③如果a＜0，那么│a│＝－a.
合作探究
合作探究
有没有绝对值等于－2的数？一个数的绝对值会是负数吗？不论有理 数a取何值，它的绝对值总是什么数？
人教版七年级数学上册《绝对值》PPT 课件
人教版七年级数学上册《绝对值》PPT 课件
课堂小结
6．有理数大小比较法则： （1）正数大于0，0大于负数，正数大于负数； （2）两个负数，绝对值大的反而小.
人教版七年级数学上册《绝对值》PPT 课件
人教版七年级数学上册《绝对值》PPT 课件 人教版七年级数学上册《绝对值》PPT 课件
＝
1 __2_.
人教版七年级数学上册《绝对值》PPT 课件
人教版七年级数学上册《绝对值》PPT 课件
课堂练习
3．已知|x－2|＋|y＋2|＝0，求x，y的值．
解：∵|x－2|≥0，|y＋2|≥0， 又|x－2|＋|y＋2|＝0， ∴|x－2|＝0，|y＋2|＝0， 即x－2＝0，y＋2＝0. ∴x＝2，y＝－2.
10 A
10 B
到达A，B两处的行驶路线不相同，它们行驶的路程相等．
合作探究
－10与10是相反数，它们只有符号不同，它们什么相同呢？
＋10与－10虽然符号不同，但表示这两个数的点到原点的距离都是10， 是相同的．我们把这个距离叫＋10与－10的绝对值．
一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，记作│a│．
没有绝对值等于－2的数，一个数的绝对值不会是负数；
不论有理数a取何值，它的绝对值总是正数或0（非负数），即对任意 有理数a，总有|a|≥0.
合作探究
互为相反数的两个数的绝对值有什么关系？ 互为相反数的两个数的绝对值相等．
合作探究
下图给出了未来一周中每天的最高气温和最低气温，看图回 答下面问题：
（1）最低气温是多少？ 最高气温是多少？
③如果a＜0，那么│a│＝－a．
人教版七年级数学上册《绝对值》PPT 课件
人教版七年级数学上册《绝对值》PPT 课件
课堂小结
3．不论有理数a取何值，它的绝对值总是正数或0（非负数）， 即对任意有理数a，总有|a|≥0.
4．互为相反数的两个数的绝对值相等． 5．数轴上的数的排列规律是： 在数轴上表示有理数，它们从左到右的顺序，就是从 小到大的顺序，即左边的数小于右边的数.