金电磁场理论第4章00阅读版

第四章 金属自由电子理论1.金属自由电子论作了哪些假设？得到了哪些结果？解：金属自由论假设金属中的价电子在一个平均势场中彼此独立，如同理想气体中的粒子一样是“自由”的，每个电子的运动由薛定谔方程来描述；电子满足泡利不相容原理，因此，电子不服从经典统计而服从量子的费米－狄拉克统计。

根据这个理论，不仅导出了魏德曼－佛兰兹定律，而且而得出电子气对晶体比热容的贡献是很小的。

2.金属自由电子论在k 空间的等能面和费米面是何形状？费米能量与哪些因素有关？解：金属自由电子论在k 空间的等能面和费米面都是球形。

费米能量与电子密度和温度有关。

3.在低温度下电子比热容比经典理论给出的结果小得多，为什么？解：因为在低温时，大多数电子的能量远低于费米能，由于受泡利原理的限制基本上不能参与热激发，而只有在费米面附近的电子才能被激发从而对比热容有贡献。

4.驰豫时间的物理意义是什么？它与哪些因素有关？解：驰豫时间的物理意义是指电子在两次碰撞之间的平均自由时间，它的引入是用来描写晶格对电子漂移运动的阻碍能力的。

驰豫时间的大小与温度、电子质量、电子浓度、电子所带电量及金属的电导率有关。

5.当2块金属接触时，为什么会产生接触电势差？解：由于2块金属中的电子气系统的费米能级高低不同而使热电子发射的逸出功不同，所以这2块金属接触时，会产生接触电势差。

6.已知一维金属晶体共含有N 个电子，晶体的长度为L ，设0=T K 。

试求： （1）电子的状态密度； （2）电子的费米能级； （3）晶体电子的平均能量。

解：(1)该一维金属晶体的电子状态密度为：dEdkdk dZ dE dZ E ⋅==)(ρ …………………………（1） 考虑在k 空间中，在半径为k 和dk k +的两线段之间所含的状态数为：dk Ldk dZ π=∆=k 2 …………………………（2） 又由于 mk E 222η=所以 mkdk dE 2η= …………………………（3） 将（2）和（3）式代入（1）式，并考虑到每个状态可容纳2个自旋相反的电子，得该一维金属晶体中自由电子的状态密度为：EmL E 22)(ηπρ= (4)（2）由于电子是费米子，服从费米—狄拉克统计，即在平衡时，能量为E 的能级被电子占据的几率为：11)(+=-TK E E B F eE f (5)于是，系统中的电子总数可表示为：⎰∞=)()(dE E E f N ρ (6)由于0=T K ，所以当0F E E >，有0)(=E f ，而当0F E E ≤，有1)(=E f ，故（6）式可简化为：⎰=)(FE dE E N ρ＝⎰0022FE dE E m L ηπ＝240FmE L ηπ由此可得： 222208mL N E Fηπ= (7)（3）在0=T K 时，晶体电子的平均能量为： ⎰∞=0)()(1dEE E Ef N E ρ＝dE EmL E N FE 2210⎰⋅ηπ＝230)(232F E m N L ηπ＝022223124F E mL N =ηπ 7.限制在边长为L 的正方形中的N 个自由电子，电子的能量为)(2),(222y x y x k k mk k E +=η。

2007-2008《电磁场理论》4-A 定D1.2. ( )两磁介质边界Γ两侧的磁位分别为()1|m rφΓ和()2|m r φΓ，磁导率分别为1μ和2μ，磁位的边界条件为 。

A ．()()1122||m m rr μφμφΓΓ= B ．1221||m m n n φφμμΓΓ∂∂=∂∂C ．()()2112||m m rrμφμφΓΓ=D ．1212||m m n n φφμμΓΓ∂∂=∂∂3. ( )磁矢位与磁感应强度的方向的关系互相 。

A ．方向相反B ．互相平行C ．互相垂直D ．方向相同4. ( ) 下面式子中， __________表明恒定磁场是非保守场。

A ． 0=⋅⎰l d H cB ． 0=⋅⎰s d B sC ． S d J l d H sc⋅=⋅⎰⎰ D ． ⎰⎰⎰⋅∂∂+⋅=⋅SSCS d tD l d BS J d 5. ( )非磁性良导体的复介电常数c jσεεω=-，满足1σωε>>，其中σ、ε、ω分别为电导率、介电常数和角频率，该良导体的电阻SR 为_______。

A.2ωμσB.)012j ωμσ+ C. )012j ωμσ- D. 02ωμσ6. ( )坡印亭定理的复数表示形式为__________。

A. ()()****E H j H B E D E J ω-∇⋅⨯=⋅-⋅+⋅B. ()()****E H j H B E D E J ω-∇⋅⨯=⋅-⋅+⋅ C. ()()****E H j H B E D E J ω-∇⋅⨯=⋅-⋅+⋅D. ()()****E H j H B E D E J ω-∇⋅⨯=⋅-⋅+⋅7. ( )电介质极化后，其内部存在 。

A ．自由正电荷B ．自由负电荷C ．自由正负电荷D ．电偶极子8. ( )在理想电介质中_____, (传导电流密度：c J ；自由电荷体密度：ρ)c c c c A. =0, =0 B. 0, =0C. 0, 0 D. =0, 0J J J J ρρρρ≠≠≠≠9. ( )导电媒质中电磁波的传播速度_______光速。

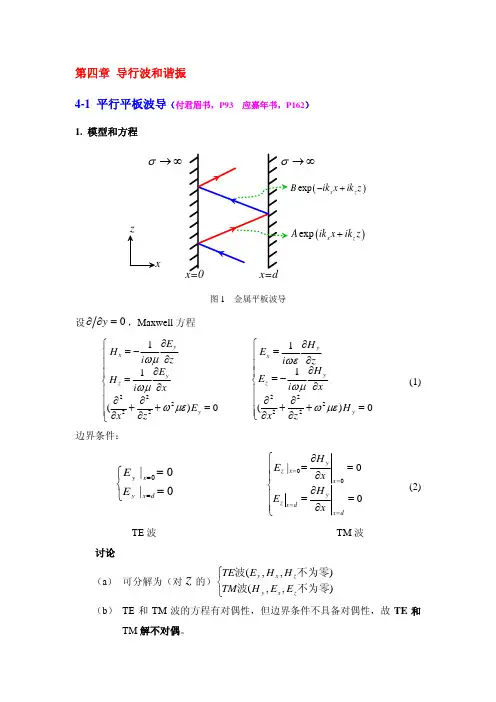
第4章 时变电磁场4.1基本内容概述这一章主要讨论时变电磁场的普遍规律，内容包括：电磁场的波动方程，动态矢量位和标量位，坡印廷定理与坡印廷矢量，时谐电磁场。

4.1.1波动方程在无源的线性、各向同性且无损耗的均匀媒质中，由麦克斯韦方程组可推导出电场E 和磁场H 满足波动方程0t με∂∇-=∂222EE （4.1）2220tμε∂∇-=∂H H （4.2）4.1.2 动态矢量位和标量位在时变电磁场中，动态矢量位A 和动态标量位ϕ的定义为=∇⨯B A （4.3）tϕ∂=--∇∂AE （4.4） 应用洛仑兹条件0tϕμε∂∇+=∂A （4.5） 可得到A 和ϕ的微分方程为222t μεμ∂∇-=-∂AA J （4.6）2221t ϕϕμερε∂∇-=-∂ （4.7）4.1.3 坡印廷定理和坡印廷矢量1．坡印廷定理坡印廷定理表征了电磁场能量守恒关系，其微分形式为11()()22t ∂-∇⨯=++∂E H H B E D E J （4.8） 积分形式为()d S-⨯⎰E H S d 11()d d d 22V V V V t =++⎰⎰H B E D E J （4.9） 坡印廷定理的物理意义：单位时间内通过曲面S 进入体积V 的电磁能量等于单位时间内体积V 中所增加的电磁场能量与损耗的能量之和。

2．坡印廷矢量S坡印廷矢量是描述电磁能量传输的一个重要物理量，其定义为=⨯S E H （2W m ） （4.10） 它表示单位时间内通过垂直于能量传输方向的单位面积的电磁能量，其方向就是电磁能量传输的方向。

4.1.4 时谐电磁场1．时谐电磁场的复数表示法以一定角频率作时谐变化的电磁场称为时谐电磁场或正弦电磁场。

时谐电磁场可用复数形式来表示(,)Re[()]j t t e ω=E r E r （4.10）其中()()()()()()()y x z j j j x xm y ym z zm E e E eE e φφφ=++r r r E r e r e r e r （4.11）称为电场强度E 的复数形式或复矢量。

第4章习题解答4.1 电导率为σ的均匀、线性、各向同性的导体球，半径为R ，其表面的电位分布为0cos Φθ。

试确定表面上各点的电流密度。

解：由于导体球的外部是空气，所有在导体球的表面只有切向分量，即0t t t 11sin sin J E e e e R R R θϕθσΦΦΦσσΦσθθθϕ⎛⎫∂∂==-∇=-+= ⎪∂∂⎝⎭4.2 如题4.2图所示平板电容器。

板间填充两种不同的导电媒质，其厚度分别为1d 和2d ，两平板的面积均为S 。

若在两极板上加上恒定的电压0U 。

试求板间的电位Φ、电场强度E 、电流密度J 以及各分界面上的自由电荷和电容器的漏电导。

解：理想电容器021==σσ，满足的定解问题为210 Φ∇= 和 220 Φ∇=以及12111112120121200x x d d x d x dx d x d V xxΦΦΦΦΦΦεε==+====∂∂====∂∂由直接积分法可以得到电位的通解为1 Ax B Φ=+ 和 2Cx D Φ=+由100x Φ==和1220x d d V Φ=+=可以确定出0=B 及)(210d d C V D +-=，则上式电位的表达式为1 Ax Φ= 和 2012()Cx V C d d Φ=+-+利用电位在介质分界面的边界条件，则确定出211201211202d d V C d d V A εεεεεε+=+=因此电位分布为2012112V x d d εΦεε=+ 和 102110221122112()V d Vx d d d d εεεΦεεεε-=+++而对应的电场强度和电位移矢量为2101221xE e V d d εεε=-+ 和 1201221xE e V d d εεε=-+以及12101221xD e V d d εεεε=-+ 和 12201221x D e V d d εεεε=-+根据静电比拟法()E ED J εσΦΦ⇔⇔⇔⇔得到对平板电容器内恒定电场的电位为2012112V x d d σΦσσ=+ 和 102110221122112()V d V x d d d d σσσΦσσσσ-=+++ 电场强度为2101221xE e V d d σσσ=-+ 和 1201221x E e V d d σσσ=-+电流密度矢量为12101221xJ e V d d σσσσ=-+ 和 12201221xJ e V d d σσσσ=-+ 此时的电流称为电容器的漏电流，对应的电导称为电容器的漏电导G ，有121221d d d d SSCCJ S E SSIG Vd d E lE lσσσσσ⋅⋅====+⋅⋅⎰⎰⎰⎰S ——极板的面积4.3 如题4.3图所示矩形导体片的电导率为σ，试求导电片上的电位分布以及导电片中各处的电流密度。

第1~2章 矢量分析 宏观电磁现象的基本规律1. 设：直角坐标系中，标量场zx yz xy u ++=的梯度为A，则M （1，1，1）处A= ，=⨯∇A 0 。

2. 已知矢量场xz e xy e z y e A z y x ˆ4ˆ)(ˆ2+++= ，则在M （1，1，1）处=⋅∇A 9 。

3. 亥姆霍兹定理指出，若唯一地确定一个矢量场（场量为A），则必须同时给定该场矢量的 旋度 及 散度 。

4. 任一矢量场在无限大空间不可能既是 无源场 又是 无旋场 ，但在局部空间 可以有 以及 。

5. 写出线性和各项同性介质中场量D 、E 、B 、H、J 所满足的方程（结构方程）： 。

6. 电流连续性方程的微分和积分形式分别为 和 。

7. 设理想导体的表面A 的电场强度为E 、磁场强度为B，则（a ）E 、B皆与A 垂直。

（b ）E 与A 垂直，B与A 平行。

（c ）E 与A 平行，B与A 垂直。

（d ）E 、B 皆与A 平行。

答案：B8. 两种不同的理想介质的交界面上，（A ）1212 , E E H H ==（B ）1212 , n n n n E E H H == (C) 1212 , t t t t E E H H == (D) 1212 , t t n n E E H H ==答案：C9. 设自由真空区域电场强度(V/m) )sin(ˆ0βz ωt E eE y -=，其中0E 、ω、β为常数。

则空间位移电流密度d J（A/m 2）为：ˆˆˆ222x y z e e e ++A⋅∇A ⨯∇E J H B E Dσ=μ=ε= , ,t q S d J S ∂∂-=⋅⎰ t J ∂ρ∂-=⋅∇ 0A ∇⋅=0A ∇⨯=（a ） )cos(ˆ0βz ωt E ey - （b ） )cos(ˆ0βz ωt ωE e y -（c ） )cos(ˆ00βz ωt E ωey -ε （d ） )cos(ˆ0βz ωt βE e y -- 答案：C 10. 已知无限大空间的相对介电常数为4=εr ，电场强度(V/m) 2cos ˆ0dxeE x πρ= ，其中0ρ、d 为常数。

高等电磁场理论金建铭pdf1 前言高等电磁场理论金建铭是研究波导结构中电磁场的理论，它可以计算这类系统的特性和参数。

高等电磁场理论金建铭的不同类型的结构可以实现复杂的电磁特性，如波导抽头，细长组织，抛物线组织等。

2 电磁场理论金建铭高等电磁场理论金建铭（EMTK）是根据力学控制理论建立的一种结构技术，由金建铭博士发明。

EMTK的核心是电磁场的研究，通过研究电磁场的运动轨迹，以及它们尤其是在不同材料中的效应，以实现不同的电磁特性。

EMTK可以用来模拟计算不同的材料的特性，既可以用于细微的电磁特性的计算，也可用于跨媒介材料系统的复杂电磁特性的仿真。

3 计算过程EMTK是基于一组建模条件来计算电磁场，这些条件包括电流，电容，磁通等物理参数，EMTK可以将这些参数用于模拟电磁场的行为。

EMTK也可以用来计算不同材料的特性及其效应，以及各种不同波导结构的电磁特性。

具体的计算过程可以分为：选择输入模型，对模型进行求解，得到结果，得出结论。

4 应用EMTK可以应用于光纤技术和微波技术方面，其在光纤技术领域中最大的应用在于可以用来设计新的光纤元件，如细长组织，特殊形状的波导抽头，可以在光纤通信系统中实现高效转换。

在微波通信技术领域，EMTK可以计算和仿真复杂结构间的各种电磁关系，允许实现高效并且有效的微波通信系统，这是传统技术很难实现的。

5 结论高等电磁场理论金建铭不仅有利于提高电磁场的计算效率，而且它的实用性更加趋向于普遍兼容。

从应用的角度来看，它可用于实现各种复杂的电磁特性，这是传统技术无法实现的，它可以用来设计出超高效，低功耗的光纤和微波通信系统。

因此，高等电磁场理论金建铭有着巨大的应用前景，可望成为提升电磁场技术水平和实现新型结构的一流工具。