习题6-2 定积分在几何学上的应用(二)
- 格式:pdf
- 大小:108.92 KB
- 文档页数:5


定积分在几何学上的应用笔记一、引言定积分是微积分中的重要内容之一,它在几何学中有广泛的应用。
本文将介绍定积分在几何学中的几个典型应用,并讨论其应用意义。
二、计算曲线长度在平面几何中,计算曲线的长度是一个经常出现的问题。
假设有一条平面曲线f(x)在区间[a, b]上,想要求出曲线的长度L。
利用定积分的概念,可以通过以下步骤进行计算:1. 将曲线分为无穷小的线段;2. 计算每个无穷小线段的长度;3. 对所有无穷小线段的长度求和,得到曲线的长度。
要计算曲线y = x^2在区间[0, 1]上的长度,可以将曲线分为无穷小线段y = x^2 + dx,其中dx为无穷小的自变量增量。
根据勾股定理,每个无穷小线段的长度为√(dx^2 + dy^2) = √(1 + (dy/dx)²)dx。
通过对所有无穷小线段的长度进行积分,即可求出曲线的长度L。
三、计算曲率曲率描述了曲线弯曲的程度,在计算曲线的曲率时,定积分也有应用。
假设有一条平面曲线f(x)在区间[a, b]上,想要求出曲线在某点x处的曲率K。
可以通过以下步骤进行计算:1. 根据曲线方程,求出曲线的切线斜率dy/dx;2. 计算切线斜率的导数d²y/dx²;3. 利用曲率公式K = |d²y/dx²| / (1 + (dy/dx)²)^(3/2),求出曲线的曲率。
通过将切线斜率的导数进行积分,可以得到曲线在区间[a, b]上的曲率函数,进而帮助我们分析曲线的特征。
四、计算曲面面积在空间几何中,计算曲面的面积也是一个常见的问题。
假设有一个曲面z = f(x, y),想要求出曲面的面积S。
可以使用定积分的方法进行计算:1. 将曲面分为无穷小的面元;2. 计算每个无穷小面元的面积;3. 对所有无穷小面元的面积求和,得到曲面的面积。
要计算平面上的一条曲线y = g(x)在[a, b]上旋转后生成的曲面的面积,可以先计算曲线上每个点x的切线斜率dy/dx,然后利用曲线的长度L求出无穷小面元的面积dS = 2πg(x)√(1 + (dy/dx)²)dx,最后通过求积分得到曲面的面积S。
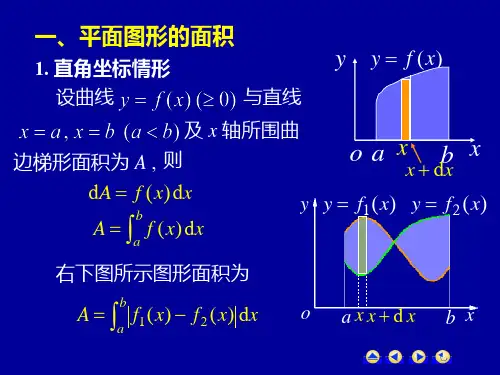

定积分在几何上的应用
定积分就是求函数f(X)在区间[a,b]中图线下包围的面积。
即由y=0,x=a,x=b,y=f(X)所围成图形的面积。
这个图形称为曲边梯形,特例是曲边三角形。
绕x轴旋转体体积公式是V=π∫[a,b]f(x)^2dx。
绕y轴旋转体积公式同理,将x,y互换即可,
V=π∫[a,b]φ(y)^2dy。
或者是V=2π∫[a,b]y*f(y)dy,也是绕x轴旋转体积。
绕x轴旋转体的侧面积为A=2π∫[a,b]y*(1+y'^2)^0.5dx,其中y'^2是y对x的导数的平方。
若定积分存在,则它是一个具体的数值,而不定积分是一个函数表达式,它们仅仅在数学上有一个计算关系(牛顿-莱布尼茨公式)。
一个函数,可以存在不定积分,而不存在定积分;也可以存在定积分,而不存在不定积分。
一个连续函数,一定存在定积分和不定积分;若只有有限个间断点,则定积分存在;若有跳跃间断点,则原函数一定不存在,即不定积分一定不存在。
几何,就是研究空间结构及性质的一门学科。
它是数学中最基本的研究内容之一,与分析、代数等等具有同样重要的地位,并且关系极为密切。
几何学发展历史悠长,内容丰富。
它和代数、分析、数论等等关系极其密切。


定积分在几何计算中的应用定积分是高等数学中的一个重要概念,它在几何计算中有着广泛的应用。
在几何学中,定积分可以用来计算曲线的长度、曲面的面积、体积等等。
下面我们就来看看定积分在几何计算中的应用。
定积分可以用来计算曲线的长度。
对于一条曲线,我们可以将其分成无数个小段,然后对每个小段的长度进行求和,最终得到整条曲线的长度。
这个过程可以用定积分来表示,即:L = ∫a^b √(1+(dy/dx)^2) dx其中,a和b分别表示曲线的起点和终点,dy/dx表示曲线在每个点的斜率。
这个式子的意义是,将曲线分成无数个小段,每个小段的长度为√(1+(dy/dx)^2) dx,然后对所有小段的长度进行求和,最终得到整条曲线的长度。
定积分可以用来计算曲面的面积。
对于一个曲面,我们可以将其分成无数个小面元,然后对每个小面元的面积进行求和,最终得到整个曲面的面积。
这个过程可以用定积分来表示,即:S = ∫∫D √(1+(∂z/∂x)^2+(∂z/∂y)^2) dxdy其中,D表示曲面的投影区域,z表示曲面在每个点的高度,∂z/∂x和∂z/∂y分别表示曲面在每个点在x和y方向上的斜率。
这个式子的意义是,将曲面分成无数个小面元,每个小面元的面积为√(1+(∂z/∂x)^2+(∂z/∂y)^2) dxdy,然后对所有小面元的面积进行求和,最终得到整个曲面的面积。
定积分可以用来计算体积。
对于一个立体图形,我们可以将其分成无数个小体元,然后对每个小体元的体积进行求和,最终得到整个立体图形的体积。
这个过程可以用定积分来表示,即:V = ∫∫∫E dxdydz其中,E表示立体图形的空间区域。
这个式子的意义是,将立体图形分成无数个小体元,每个小体元的体积为dxdydz,然后对所有小体元的体积进行求和,最终得到整个立体图形的体积。
定积分在几何计算中有着广泛的应用,可以用来计算曲线的长度、曲面的面积、体积等等。
这些应用不仅在数学中有着重要的意义,也在实际生活中有着广泛的应用,例如在建筑设计、工程计算等领域中都有着重要的作用。

定积分在几何,物理学中的简单应用
定积分是一种常见的数学工具,用来解决许多几何和物理问题。
它可以在几何学、物理学中解决积分、面积和容积计算题中应用。
首先,定积分在几何学中的简单应用。
比如,如果我们要计算一个几何图形的面积,则可以通过定积分来计算。
它可以计算任意形状的几何图形的面积,比如三角形、椭圆、圆形等。
它的应用范围非常广泛,比如可以用它来计算面积、周长、体积等。
其次,定积分也可以用在物理学中。
比如,如果我们要计算一个物体在多次不同力作用之下移动的路程,可以用定积分来计算。
它可以帮助我们精确地计算物体受力作用前后的距离,也可以帮助我们精确计算弹性作用力等。
最后,定积分也可以应用于物理学的温度问题中。
比如,我们可以通过定积分求出一个物体在单位温差下的热量传递,也可以求出一个物体的总热量。
还可以用它求解温度场、热传导率、热导率等问题。
以上是定积分在几何、物理学中的简单应用。
定积分是一种通用而有效的数学工具,在几何、物理学中都有着广泛的应用,不仅可以用来解决相关的面积、容积计算题,而且还可以用来解决物理热力学、温度等问题。
只要我们掌握它的基本使用方法以及它的一些特性和用途,就可以在几何、物理学中更好地应用它来解决其它问题。
- 1 -。


同济大学数学系《高等数学》第7版上册课后习题第六章定积分的应用习题6-1定积分的元素法本部分无课后习题.习题6-2定积分在几何学上的应用1.求图6-1中各阴影部分的面积:图6-1解:(1)解方程组,得到交点坐标为(0,0)和(1,1).如果取x为积分变量,则x的变化范围为[0,1],相应于[0,1]上的任一小区间[x,x+dx]的窄条面积近似于高为、底为dx的窄矩形的面积,因此有如果取y为积分变量,则y的变化范围为[0,1],相应于[0,1]上的任一小区间[y,y +dy]的窄条面积近似于高为dy、底为y-y2的窄矩形的面积,因此有(2)取x为积分变量,则易知x的变化范围为[0,1],相应于[0,1]上的任一小区间[x,x+dx]的窄条面积近似于高为e-e x、底为dx的窄矩形的面积,因此有如果取y为积分变量,则易知y的变化范围为[1,e],相应于[1,e]上的任一小区间[y,y+dy]的窄条面积近似于高为dy、底为lny的窄矩形的面积,因此有(3)解方程组,得到交点坐标为(-3,-6)和(1,2).如果取x为积分变量,则x的变化范围为[-3,1],相应于[-3,1]上的任一小区间[x,x+dx]的窄条面积近似于高为、底为dx的窄矩形的面积,因此有如果用y为积分变量,则y的变化范围为[-6,3],但是在[-6,2]上的任一小区间[y,y+dy]的窄条面积近似于高为dy、底为的窄矩形的面积,在[2,3]上的任一小区间[y,y+dy]的窄条面积近似于高为dy、宽为的窄矩形的面积,因此有由此可知以x为积分变量较易,因为图形边界曲线若分为上下两段,分别为y=2x和y=3-x2;若分为左右两段,分别为和,其中右段曲线的表示相对比较复杂,也就会导致计算形式复杂.(4)解方程组,得到交点坐标为(-1,1)和(3,9),同上,以x为积分变量计算较易.取x为积分变量,则x的变化范围为[-1,3],相应于[-1,3]上的任一小区间[x,x+dx]的窄条面积近似于高为2x+3-x2、底为dx的窄矩形的面积,则有2.求由下列各曲线所围成的图形的面积:(1)与(两部分都要计算);(2)与直线y=x及x=2;(3)与直线x=1;(4)y=lnx,y轴与直线y=lna,y=lnb(b>a>0).解:(1)图6-2中,可先计算图形D1(阴影部分)的面积,易求得与x2+y2=8的交点为(-2,2)和(2,2).取x为积分变量,则x的变化范围为[-2,2],相应于[-2,2]上的任一小区间[x,x+dx]的窄条面积近似于高为、底为dx的窄矩形的面积,因此有图形D2的面积为图6-2(2)图6-3中,取x为积分变量,则x的变化范围为[1,2],相应于[1,2]上的任一小区间[x,x+dx]的窄条面积近似于高为、底为dx的窄矩形的面积,因此有图6-3(3)图6-4中,取x为积分变量,则x的变化范围为[0,1],相应于[0,1]上的任一小区间[x,x+dx]的窄条面积近似于高为、底为dx的窄矩形的面积,因此有图6-4(4)图6-5中,取y为积分变量,则y的变化范围为[lna,lnb],相应于[lna,lnb]上的任一小区间[y,y+dy]的窄条面积近似于高为dy、底为e y的窄矩形的面积,因此有图6-53.求抛物线y=-x2+4x-3及其在点(0,-3)和(3,0)处的切线所围成的图形的面积.解:首先求得导数,因此抛物线在点(0,-3),(3,0)处的切线分别为y=4x-3,y=-2x+6,容易求得这两条切线交点为(见图6-6).因此所求面积为图6-64.求抛物线y2=2px及其在点处的法线所围成的图形的面积.解:利用隐函数求导方法,抛物线方程y2=2px两端分别对x求导,2yy′=2p.即得,因此法线斜率为k=-1,从而得到法线方程为(如图6-7),因此所求面积为图6-75.求由下列各曲线所围成的图形的面积:(1)ρ=2acosθ;(2)x=acos3t,y=asin3t;(3)ρ=2a(2+cosθ).解:(1)(2)由对称性可知,所求面积为第一象限部分面积的4倍,记曲线上的点为(x,y),因此(3)。

定积分在几何学上的应用习题
定积分可以被定义为把曲线投影到x轴上的最大面积,定积分在几何学上有着重要的应用,本文将介绍定积分在几何学上的应用习题。
首先,我们需要了解定积分的概念。
定积分可以表示为一种函数,称为定积分函数,它由两个变量组成:自变量 x定义域。
定义域是
向 x投影的曲线。
定积分用于求解积分问题,即求解一个曲线到 x
的最大面积。
其次,定积分的应用习题可以归结为两种:一种是求解面积和体积,另一种是计算两个函数之间的差值。
它们可以用定积分来求解。
首先,我们以求解面积和体积为例。
对于求解面积的问题,我们需要知道曲线的函数表达式和定义域,使用定积分就可以求解曲线到
x的最大面积。
体积则是沿着 y积分,求解曲线平面区域的体积。
另一方面,如果我们需要计算两个函数之间的差值,也可以用定积分来求解。
计算的方法是,将两个函数视为 y上的两条曲线,使
用定积分计算它们在 x上的最大面积差值,即面积之差,也就是两
个函数之间的差值。
最后,定积分在几何学上有着重要的应用,它可以用于解决求解面积和体积以及计算函数之间差值的问题。
定积分是一种有效的计算方法,可以帮助我们解决几何学中许多有趣的问题。
- 1 -。

13⎤12xy =2y x =xy 22=4−=x y .18βθ=roxy =θρ2cos 22a =1Aθd数学分析第五章 定积分§2 定积分在几何学上的应用二、特殊立体的体积1、旋转体的体积旋转体就是由一个平面图形绕这平面内 一条直线旋转一周而成的立体.这直线叫做 旋转轴.圆柱圆锥圆台数学分析第五章 定积分§2 定积分在几何学上的应用一般地,如果旋转体是由连续曲线 y = f ( x ) 、 直线 x = a 、 x = b 及 x 轴所围成的曲边梯形绕 x 轴旋转一周而成的立体,体积为多少?x ∈ [a , b ] 在[a , b]上任取小区 间[ x , x + dx ],取积分变量为 x ,yy = f ( x)ox x + dxx取以dx 为底的窄边梯形绕 x 轴旋转而成的薄 片的体积为体积元素, dV = π[ f ( x )]2 dx旋转体的体积为 V = ∫ π[ f ( x )]2 dxab数学分析第五章 定积分2 3 2 3 2 3§2 定积分在几何学上的应用例 1 求星形线 x + y = a ( a > 0) 绕 x 轴旋转 构成旋转体的体积.y解 ∵y =a −x ,2 32 32 3⎛ ∴y =⎜ ⎜a − x ⎝2 2 3a 2 32 3⎞ ⎟ ⎟ ⎠3x ∈ [− a , a ]3−aoa x旋转体的体积⎛ V = ∫ π⎜ a −x ⎜ −a ⎝2 3⎞ ⎟ dx = 32 πa 3 . ⎟ 105 ⎠数学分析第五章 定积分§2 定积分在几何学上的应用类似地,如果旋转体是由连续曲线x = ϕ ( y ) 、直线 y = c 、 y = d 及 y 轴所围成的曲边梯形绕 y 轴旋转一周而成的立体, y 体积为dV = ∫ π [ϕ ( y )] dy2 cdx = ϕ ( y)co x数学分析第五章 定积分§2 定积分在几何学上的应用补充 如果旋转体是由连续曲线 y = f ( x )、 直线 x = a 、 x = b 及 x 轴所围成的曲边梯形绕 y 轴旋转一周而成的立体,体积为V y = 2π ∫ x | f ( x ) | dxab数学分析第五章 定积分§2 定积分在几何学上的应用2、平行截面面积为已知的立体的体积如果一个立体不是旋转体,但却知道该立 体上垂直于一定轴的各个截面面积,那么,这 个立体的体积也可用定积分来计算.A( x ) 表 示 过点 ox 且垂直于 x 轴dV = A( x )dx ,axx + dxbx的截面面积, A( x ) 为 x 的已知连续函数立体体积 V =∫baA ( x ) dx .数学分析第五章 定积分§2 定积分在几何学上的应用例2求以半径为 R 的圆为底、平行且等于底圆半径的线段为顶、高为 h 的正劈锥体的体积.解取坐标系如图 底圆方程为yx 2 + y 2 = R2 ,o2xRx垂直于 x 轴的截面为等腰三角形截面面积 A( x ) = h ⋅ y = h R − x 立体体积 V = h∫− RR2 221 2 R − x dx = πR h. 2数学分析第五章 定积分§2 定积分在几何学上的应用三、平面曲线的弧长设 A 、 B 是曲线弧上的两 y 个端点,在弧上插入分点M2 M1 M n −1B = MnA = M 0 , M1 ,Mi ,A = M0, M n −1 , M n = Box并依次连接相邻分点得一内接折线,当分点的数目 无限增加且每个小弧段都缩向一点时,此折线的长∑ | M i −1 M i |的极限存在,则称此极限为 曲线弧 AB 的弧长.i =1 n数学分析第五章 定积分§2 定积分在几何学上的应用1、直角坐标系情形y设曲线 y = f ( x ) ( a ≤ x ≤ b ) , 其中 f ( x ) 在[a , b]上有一阶连续导数} dy用积分元素法: 取积分变量为 x , o 在[a, b]上取小区间[ x, x + dx],以小切线段的长代替小弧段Δ s 的长2 2a x x + dx bx2 ′ = 1 + y dx 小切线段的长 ( dx ) + (dy ) 2 ′ 弧长元素 ds = 1 + y dx曲线段的弧长s = ∫ 1 + y′ dx .2 ab数学分析第五章 定积分§2 定积分在几何学上的应用2 32 例 1 计算曲线 y = x 上相应于 x 从 a 到 b 的 3一段弧的长度.解 ∵ y′ = x ,1 2∴ ds = 1 + ( x )2 dx = 1 + xdx ,a b1 2所求弧长为s = ∫ab2 1 + xdx = [(1 + b ) − (1 + a ) ]. 33 2 3 2。