2019年中考数学_微测试系列_圆的基本性质和圆的有关位置关系(含解析)北师大版

圆与圆的位置关系(解析版)圆与圆的位置关系（解析版）圆与圆的位置关系是几何学中常见的问题。

在解析几何中，我们可以通过方程和图形的分析来确定两个圆之间的位置关系。

本文将详细介绍圆与圆的位置关系及其解析方法。

I. 两个圆的位置关系当给定两个圆的方程时，我们可以通过以下几种情况来判断它们的位置关系：1. 相离(disjoint)如果两个圆不相交，它们互相分离，也就是说没有公共点。

我们可以通过计算它们的半径之和和两个圆心之间的距离来判断。

如果半径之和小于圆心之间的距离，即 r1 + r2 < d，那么两个圆相离。

2. 外切（tangent exterior）如果两个圆的外部只有一个公共点，我们称它们相切于外部。

这意味着两个圆心之间的距离等于它们的半径之和，并且没有其他公共点。

我们可以通过计算两个圆心之间的距离和两个圆的半径之和来判断。

如果半径之和等于圆心之间的距离，即 r1 + r2 = d，那么两个圆相切于外部。

3. 内切（tangent interior）如果两个圆的内部只有一个公共点，我们称它们相切于内部。

这意味着两个圆的半径之差等于它们的圆心之间的距离，并且没有其他公共点。

我们可以通过计算两个圆的半径之差和两个圆心之间的距离来判断。

如果圆心之间的距离等于半径之差，即 d = |r1 - r2|，那么两个圆相切于内部。

4. 相交（intersect）如果两个圆有两个公共点，我们称它们相交。

这意味着两个圆心之间的距离小于半径之和，并且有两个公共点。

我们可以通过计算两个圆心之间的距离和两个圆的半径之和来判断。

如果半径之和大于圆心之间的距离，即 r1 + r2 > d，那么两个圆相交。

II. 解析方法在解析几何中，我们可以利用两个圆的方程来求解它们的位置关系。

假设第一个圆的方程为(x - h1)^2 + (y - k1)^2 = r1^2，第二个圆的方程为(x - h2)^2 + (y - k2)^2 = r2^2，其中(h1, k1)和(h2, k2)分别代表两个圆的圆心坐标，r1和r2分别代表两个圆的半径。

中考数学考点一遍过考点18 圆的性质及与圆有关的位置关系圆的性质及与圆有关的位置关系是中考数学中的一个重要考点。

在这个考点中，我们需要掌握圆的定义、圆弧、圆心角、弧长和扇形面积的计算方法，以及圆与直线的位置关系。

首先，我们来看一下圆的定义。

圆是由平面上距离圆心相等的点构成的集合。

圆是一种特殊的椭圆，其所有点到圆心的距离都相等。

在圆的性质中，圆弧是一个重要的概念。

圆弧是圆上两个点之间的一段弧线。

我们可以使用圆心角来描述圆弧的大小。

圆心角是以圆心为顶点的角，其对应的弧所对的圆心角大小等于弧所对的圆弧长度的一半。

通过圆心角的大小，我们可以判断圆弧的长度。

根据圆的性质，我们可以计算圆的弧长和扇形面积。

弧长是圆弧的长度，可以通过圆心角的大小和半径的关系来计算。

弧长等于圆心角的弧度数乘以半径。

扇形面积是由圆心角和半径所围成的扇形的面积，可以通过圆心角的大小和半径的关系来计算。

扇形面积等于圆心角的弧度数乘以半径的平方再除以2。

除了圆弧、圆心角、弧长和扇形面积的计算方法，我们还需要了解圆与直线的位置关系。

当直线与圆相交时，可以根据相交的情况判断它们的关系。

如果直线与圆相交于两个不同的点，我们可以得到两条相交弧。

如果直线与圆相切于一个点，那么这条直线被称为切线。

同时，切线与半径垂直。

综上所述，圆的性质及与圆有关的位置关系是中考数学中的一个重要考点。

我们需要掌握圆的定义、圆弧、圆心角、弧长和扇形面积的计算方法，以及圆与直线的位置关系。

通过熟练掌握这些知识，我们可以在中考数学考试中轻松应对相关题目。

希望同学们能够通过不断练习和巩固知识，顺利掌握这个考点，取得好成绩。

九年级数学圆知识点总结北师大版一、圆的定义1、以点O与直线距离r为半径所画的圆称为以点O为圆心，以r为半径的圆2、圆上任意两点间的部分称为弧3、连接圆上任意两点的线段称为弦4、经过圆心且两个端点都在圆周上的线段称为直径二、圆的性质1、圆的对称性1)圆是中心对称图形，对称中心是圆心2)圆是轴对称图形，过圆心的每条直线都是圆的对称轴2、圆的旋转不变性圆任意半径所对的圆周角等于二分之一的半径所对的圆心角3、圆的直径所对的性质圆的直径所对的圆周角是直角；在同圆或等圆中，相等的圆周角所对的弦相等，所对的弧相等，所对的弦的弦心距相等。

4、圆的标准方程和一般方程圆的标准方程：(x - a)2 + (y - b)2 = r2；圆的一般方程：x2 + y2 + Dx + Ey + F = 0(D2 + E2 - 4F > 0)5、直线与圆的位置关系设直线L与圆O有交点A，B；若点A，B重合，则称直线与圆相切；若点A，B不重合，则称直线与圆相割；经过两点A，B画一直线L，则称直线L为圆O的割线；经过圆心O画一直线L‘，则称直线L’为圆O的切线。

三、点与圆的位置关系设P(x，y)，O为坐标原点，则：设d为点P到O的距离；r为半径；d与r的关系可总结为：当d < r时，点P在圆内；当d = r时，点P在圆上；当d > r时，点P在圆外。

四、垂径定理及其推论1、垂径定理：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧。

推论1：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧(在“平分弦(不是直径)的直径垂直于弦”的前提下“垂直于弦的直径平分弦”也成立)推论2：弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

推论3：平分弧的直径垂直平分弧所对的弦。

九年级数学圆知识点总结一、圆的基本性质1、圆的定义：线段OA绕着它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆。

2、圆心：固定端点O称为圆心3、半径：线段OA称为圆的半径4、圆心角：从定点O引出的射线在圆内部分称为圆心角5、圆周角：顶点在圆心上的角叫做圆心角，在圆心同侧，且顶点在圆上的角叫做圆周角6、圆的周长：圆上任意一点到圆心的距离(半径)和过该店画弧的两条线段的弧度之和叫做圆的周长7、圆的面积：圆所占平面的大小叫做圆的面积二、与圆有关的位置关系1、点与圆的位置关系：以点P与圆O的为例(设P是一点，则PO是点到圆心的距离)，P在⊙O外，PO>r；P在⊙O上，PO＝r；P在⊙O 内，PO<r。

2019年新人教版中考数学微测试系列专题18 圆的基本性质和圆的有关位置关系学校：___________姓名：___________班级：___________1.【辽宁阜新2015年中考数学试卷】如图，点A，B，C是⊙O上的三点，已知∠AOB=100°，那么∠ACB的度数是（）A．30° B．40° C．50° D．60°【答案】C．【解析】考点：圆周角定理．2．【湖北襄阳2015年中考数学试卷】点O是△ABC的外心，若∠BOC=80°，则∠BAC的度数为（）A．40° B．100° C．40°或140° D．40°或100°【答案】C．【解析】试题分析：如图所示：∵O是△ABC的外心，∠BOC=80°，∴∠A=40°，∠A′=140°，故∠BAC的度数为：40°或140°．故选C．考点：1．三角形的外接圆与外心；2．圆周角定理；3．分类讨论．3.【2015届浙江省杭州市5月中考模拟】如图，A、D是⊙O上的两个点，BC是直径，若∠D=35°，则∠OAC的度数是（）A．35° B．55° C．65° D．70°【答案】B.【解析】考点：圆周角定理．4.【2015届湖南省邵阳市邵阳县中考二模】如图，⊙O是△ABC的外接圆，AD是⊙O的直径，EA是⊙O的切线．若∠EAC=120°，则∠ABC的度数是（）A．80° B．70° C．60° D．50°【答案】C.【解析】试题解析：∵EA是⊙O的切线，AD是⊙O的直径，∴∠EAD=90°，∵∠EAC=120°，∴∠DAC=∠EAC-∠EAD=30°，∵AD是⊙O的直径，∴∠ACD=90°，∴∠ADC=180°-∠A CD-∠DAC=60°，∴∠ABC=∠ADC=60°（圆周角定理），故选：C．考点：切线的性质．5.【辽宁沈阳2015年中考数学试题】如图，在△ABC中，AB=AC，∠B=30°，以点A为圆心，以3cm为半径作⊙A，当AB= cm时，BC与⊙A相切．【答案】6．【解析】考点：切线的判定．6.【黑龙江牡丹江2015年中考数学试题】如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=8，CD=6，则BE= ．【答案】.【解析】试题分析： 连接OC ，如图：∵AB=8，CD=6，∴根据垂径定理（垂直于弦的直径平分弦并且平分弦所对的弧）得出CE=ED=12CD=3，∴OC=OB=12AB=4，在Rt △OEC 中，由勾股定理求出OE=2234考点：1.垂径定理；2.勾股定理．7.【2015届湖北省黄冈市启黄中学中考模拟】如图所示，经过B （2，0）、C （6，0）两点的⊙H 与y 轴的负半轴相切于点A ，双曲线y=xk 经过圆心H ，则k= ．【答案】﹣83．【解析】考点：1．切线的性质；2．反比例函数图象上点的坐标特征．8.【2015届山东省枣庄市滕州市中考二模】如图，在Rt△AOB中，OA=OB=4，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则线段PQ长度的最小值为．【解析】考点：切线的性质．9．【辽宁盘锦2015年中考数学试题】如图1，AB为⊙O的直径，点P是直径AB上任意一点，过点P作弦CD⊥AB，垂足为P，过点B的直线与线段AD的延长线交于点F，且∠F=∠ABC．（1）若CD=BP=4，求⊙O的半径；（2）求证：直线BF是⊙O的切线；（3）当点P与点O重合时，过点A作⊙O的切线交线段BC的延长线于点E，在其它条件不变的情况下，判断四边形AEBF是什么特殊的四边形？请在图2中补全图象并证明你的结论．【答案】（1）198；（2）证明见解析；（3）四边形AEBF是平行四边形，证明见解析.【解析】（2）∵∠A=∠C，∠F=∠ABC，∴△PBC∽△BFA，∴∠ABF=∠CPB，∵CD⊥AB，∴∠ABF=∠CPB=90°，∴直线BF是⊙O的切线；（3）四边形AEBF是平行四边形；理由：如图2所示：∵CD⊥AB，垂足为P，∴当点P与点O重合时，CD=AB，∴OC=OD，∵AE是⊙O 的切线，∴BA⊥AE，∵CD⊥AB，∴DC∥AE，∵AO=OB，∴OC是△ABE的中位线，∴AE=2OC，∵∠D=∠ABC，∠F=∠ABC，∴∠D=∠F，∴CD∥BF，∵AE∥BF，∵OA=OB，∴OD是△ABF的中位线，∴BF=2OD，∴AE=BF，∴四边形AEBF是平行四边形．考点：1．圆的综合题；2．三角形中位线定理；3．平行四边形的判定；4．综合题．10.【2015届浙江省宁波市江北区中考模拟】已知：如图，△ABC 中，∠BAC=90°，点D 在BC 边上，且BD=BA ，过点B 画AD 的垂线交AC 于点O ，以O 为圆心，AO 为半径画圆．（1）求证：BC 是⊙O 的切线；（2）若⊙O 的半径为8，tan ∠C=34，求线段AB 的长，sin ∠ADB 的值． 【答案】（1）证明见解析；（2）10103． 【解析】试题解析：（1）连接OD ，如图：∵BA=BD，BO⊥AD（已知），∴∠ABO=∠DBO（等腰三角形顶角三线合一），在△ABO和△DBO 中，根据边角边判定△ABO≌△DBO，∴OD=OA．，∵OA为半径，∴OD也为半径，∴∠ODB=∠OAB=90°，∴BD⊥OD，∴BC是⊙O的切线；考点：1．切线的判定；2．三角形全等的判定和性质；3．锐角三角函数．。

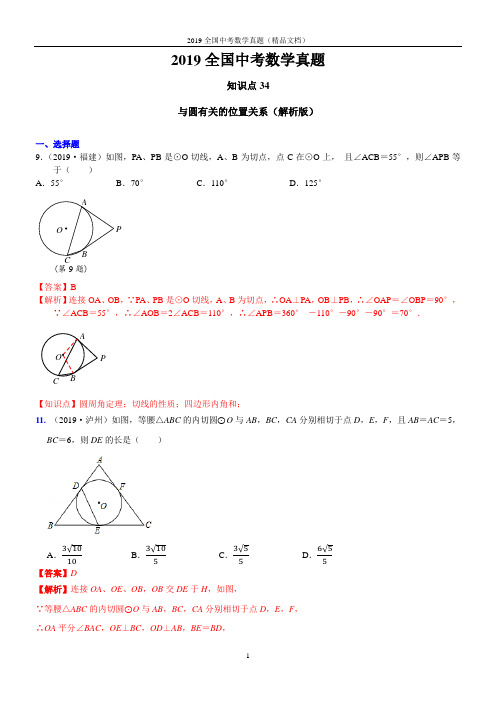
2019全国中考数学真题知识点34与圆有关的位置关系（解析版）一、选择题9．（2019·福建）如图，PA 、PB 是⊙O 切线，A 、B 为切点，点C 在⊙O 上， 且∠ACB ＝55°，则∠APB 等于（ ）A ．55°B ．70°C ．110°D ．125°【答案】B【解析】连接OA 、OB ，∵PA 、PB 是⊙O 切线，A 、B 为切点，∴OA ⊥PA ，OB ⊥PB ，∴∠OAP ＝∠OBP ＝90°，∵∠ACB ＝55°，∴∠AOB ＝2∠ACB ＝110°，∴∠APB ＝360° －110°－90°－90°＝70°．【知识点】圆周角定理；切线的性质；四边形内角和；11. （2019·泸州）如图，等腰△ABC 的内切圆⊙O 与AB ，BC ，CA 分别相切于点D ，E ，F ，且AB ＝AC ＝5，BC ＝6，则DE 的长是（ ）A ．3√1010B ．3√105C ．3√55D ．6√55【答案】D【解析】连接OA 、OE 、OB ，OB 交DE 于H ，如图，∵等腰△ABC 的内切圆⊙O 与AB ，BC ，CA 分别相切于点D ，E ，F ，∴OA 平分∠BAC ，OE ⊥BC ，OD ⊥AB ，BE ＝BD ，PP (第9题)∵AB ＝AC ，∴AO ⊥BC ，∴点A 、O 、E 共线，即AE ⊥BC ，∴BE ＝CE ＝3，在Rt △ABE 中，AE =√52−32=4，∵BD ＝BE ＝3，∴AD ＝2，设⊙O 的半径为r ，则OD ＝OE ＝r ，AO ＝4﹣r ，在Rt △AOD 中，r 2+22＝（4﹣r ）2，解得r =32，在Rt △BOE 中，OB =√32+(32)2=3√52，∵BE ＝BD ，OE ＝OD ，∴OB 垂直平分DE ，∴DH ＝EH ，OB ⊥DE ，∵12HE •OB =12OE •BE ，∴HE =OE⋅BE OB =3×32362=3√55，∴DE ＝2EH =6√55．故选：D ．5．（2019·苏州）如图，AB 为⊙O 的切线．切点为A ，连接AO ，BO ，BO 与⊙O 交于点C ，延长BO 与⊙O 交于点D ，连接AD 若∠ABO =36°，则∠ADC 的度数为（ ）A ．54 °B ．36°C ．32 °D ．27°（第5题）【答案】D 【解析】本题考查了切线的性质、直角三角形的性质、等腰三角形的性质以及三角形的外角性质．∵AB 为⊙O 的切线，∴∠OAB =90°，∵∠ABO =36°，∴∠AOB =90°-∠ABO =54°，∵OA =OD ，∴∠ADC =∠OAD ，∵∠AOB =∠ADC +∠OAD ，∴∠ADC=∠AOB =27°，故选D ．1. （2019·无锡）如图，P A 是⊙O 的切线，切点为A ，PO 的延长线交⊙O于点B ，若∠P =40°，则∠B 的度数为 （ ）A.20°B.25°C.40°D.50°OA B【答案】B【解析】∵P A 是⊙O 的切线，切点为A ，∴OA ⊥AP ，∴∠OAP =90°，∵∠APB =40°，∴∠AOP =50°，∵OA =OB ，∴∠B =∠OAB =∠AOP =25°．故选B ．2.（2019·自贡）如图，已知A 、B 两点的坐标分别为（8，0）、（0，8），点C 、F 分别是直线x=-5和x 轴上的动点，CF=10，点D 是线段CF 的中点，连接AD 交y 轴于点E ，当△ABE 的面积取得最小值时，tan ∠BAD 的值是（ ）A .817 B. 717 C.49 D.59【答案】B.【解析】∵A （8，0），B （0，8），∠AOB =900，∴△AOB 是等腰直角三角形，∴AB =8√2，∠OBA =450，取D （-5，0），当C 、F 分别在直线x =-5和x 轴上运动时，∵线段DH 是Rt △CFD 斜边上中线，∴DH =12CF =10，故D 在以H 为圆心,半径为5的圆上运动，当AD 与圆H 相切时，△ABE 的面积最小.在Rt △ADH 中，AH =OH +OA =13,∴AD =√AH 2−AD 2=12.∵∠AOE =∠ADH =900，∠EAO =∠HAD ，∴△AOE ∽△ADH ，∴OEAO =DHAD ，即OE8=512，∴OE =103，∴BE =OB -OE =143.∵S △ABE =12BE ·OA =12AB ·EG ，∴EG=BE·OAAB =143×88√2=7√23.在Rt△BGE中，∠EBG=450，∴BG=EG=7√23，∴AG=AB-BG=17√23.在Rt△AEG中，tan∠BAD=EGAG =717.故选B.3. (2019·台州)如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则 O的半径为( )A. B.3 C.4 D.4-【答案】A【解析】∵ O与AB,AC相切,∴OD⊥AB,OE⊥AC,又∵OD＝OE,∴∠DAO＝∠EAO,又∵AB＝AC,∴BO＝CO,∴∠DAO＝30°,BO＝4,∴OD＝OAtan∠DAO又∵在Rt△AOB中,AO=,∴OD＝故选A.4.（2019·重庆B卷）如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，若∠C＝40°则∠B 的度数为（ ）A.60°B.50°C.40°D.30°【答案】Ｂ【解析】圆的切线垂直于经过切点的半径，因为AC 是⊙O 的切线，A 为切点，所以∠BAC ＝90°，根据三角形内角和定理，若∠C ＝40°则∠B 的度数为50°. 故选Ｂ．5. （2019·重庆A 卷）如图，AB 是⊙O 的直径，AC 是⊙O 的切线，A 为切点，BC 与⊙O 交于点D ，连结OD ．若∠C ＝50°，则∠AOD 的度数为 （ ）A ．40°B ．50°C ．80°D ．100°【答案】C【解析】∵AC 是⊙O 的切线，∴AC ⊥AB ．∵∠C ＝50°，∴∠B ＝90°－∠C ＝40°．∵OB ＝OD ，∴∠B ＝∠ODB ＝40°．∴∠AOD ＝∠B ＋∠ODB ＝80°．故选C ．二、填空题1.（2019·岳阳）如图，AB 为⊙O 的直径，点P 为AB 延长线上的一点，过点P 作⊙O 的切线PE ，切点为M ，过A 、B 两点分别作PE 的垂线AC 、BD ，垂足分别为C 、D ，连接AM ，则下列结论正确的是_____．（写出所有正确结论的序号）①AM 平分∠CAB ；②AM 2=AC ·AB ；③若AB =4，∠APE =30°，则BM 的长为3； ④若AC =3，BD =1，则有CM =DM．A【答案】①②④【解析】连接OM，BM∵PE是⊙O的切线，∴OM⊥PE．∵AC⊥PE，∴AC∥OM．∴∠CAM＝∠AMO．∵OA＝OM，∴∠AMO＝∠MAO．∴∠CAM=∠MAO．∴AM平分∠CAB．选项①正确；∵AB为直径，∴∠AMB=90º=∠ACM．∵∠CAM=∠MAO，∴△AMC∽△ABM．∴AC AM AM AB=．∴AM2=AC·AB．选项②正确；∵∠P=30°，∴∠MOP=60°．∵AB=4，∴半径r=2．∴60221803BMlππ⨯==．选项③错误；∵BD∥OM∥AC，OA=OB，∴CM=MD．∵∠CAM ＋∠AMC =90°，∠AMC ＋∠BMD =90°，∴∠CAM ＝∠BMD ．∵∠ACM =∠BDM =90°，∴△ACM ∽△MDB ． ∴AC CM DM BD=． ∴CM ·DM =3×1=3．∴CM =DM．选项④正确；综上所述，结论正确的有①②④．2. （2019·无锡）如图，在△ABC 中，AC ∶BC ∶AB =5∶12∶13，O 在△ABC 内自由移动，若O 的半径为1，且圆心O 在△ABC 内所能到达的区域的面积为103，则△ABC 的周长为__________.【答案】25【解析】如图，圆心O 在△ABC 内所能到达的区域是△O 1O 2O 3，∵△O 1O 2O 3三边向外扩大1得到△ACB ，∴它的三边之比也是5∶12∶13， ∵△O 1O 2O 3的面积=103，∴O 1O 2=53，O 2O 3=4，O 1O 3=133，连接AO 1 与CO 2，并延长相交于I ，过I 作ID ⊥AC 于D ，交O 1O 2于E ，过I 作IG ⊥BC 于G 交O 3O 2于F ，则I 是Rt △ABC与Rt △O 1O 2O 3的公共内心，四边形IEO 2F 四边形IDCG 都是正方形，∴IE =IF = 1223122313O O O O O O O O O O ⨯++ =23，ED =1，∴ID =IE +ED =53，设△ACB 的三边分别为5m 、12m 、13m ，则有ID =AC BC AC BC AB ⨯++=2m =53，解得m =56，△ABC 的周长=30m =25.4. （2019·眉山）如图，在Rt △AOB 中，OA =OB=O 的半径为2，点P 是AB边上的动点，过点P 作⊙O 的一条切线PQ （点Q 为切点），则线段PQ 长的最小值为．【答案】【解析】连接OQ ，如图所示，∵PQ 是⊙O 的切线，∴OQ ⊥PQ ，根据勾股定理知：PQ 2=OP 2-OQ 2，∴当PO ⊥AB 时，线段PQ 最短，∵在Rt △AOB 中，OA=OB=，∴S △AOB =12OA•OB=12AB •OP ，即OP=OA OB AB•=4，∴PQ= ．故答案为：5. (2019·宁波)如图,Rt △ABC 中,∠C ＝90°,AC ＝12 ,点D 在边BC 上,CD ＝5,BD ＝13.点P 是线段AD 上一动点,当半径为6的P 与△ABC 的一边相切时,AP 的长为________.【答案】132或【解析】半径为6的P 与△ABC 的一边相切,可能与AC,BC,AB 相切,故分类讨论: ①当P 与AC 相切时,点P 到AC 的距离为6,但点P 在线段AD 上运动,距离最大在点D 处取到,为5,故这种情况不存在; ②当P 与AC 相切时,点P 到BC 的距离为6,如图PE ＝6,PE ⊥AC,∴PE 为△ACD 的中位线,点P 为AD 中点,∴AP ＝113=22AD ;③当P 与AB 相切时,点P 到AB 的距离为6,即PF ＝6,PF ⊥AB,过点D 作DG ⊥AB 于点G,∴△APF ∽△ADG ∽△ABC,∴PF AC AP AB=,其中,PF ＝6,AC ＝12,AB ,∴AP ＝综上所述,AP 的长为132或6.7.8.9.10.三、解答题23．（2019·衡阳）如图，点A 、B 、C 在半径为8的⊙O 上，过点B 作BD ∥AC ，交OA 延长线于点D ，连接BC ，且∠BCA ＝∠OAC ＝30°．（1）求证：BD 是⊙O 的切线；（2）求图中阴影部分的面积．解：（1）证明：连接OB 交AC 于E ，由∠BCA ＝30°，∴∠AOB ＝60°．在∆AOE 中，∵∠OAC ＝30°，∴∠OEA ＝90°，所以OB ⊥AC ．∵BD ∥AC ，∴OB ⊥BD ．又B 在圆上，∴BD 为⊙O 的切线；（2）由半径为8，所以OA =OB =8．在∆AOC 中，∠OAC ＝∠OCA ＝30°，∠COA ＝120°，∴AC ＝．由∠BCA ＝∠OAC ＝30°，∴OA ∥BC ，而BD ∥AC ，∴四边形ABCD 是平行四边形.∴BD ＝∴∆OBD 的面积为12×8×，扇形OAB 的面积为16×π×82＝323π，∴阴影部分的面积为323π． 24．（2019·淮安）如图，AB 是⊙O 的直径，AC 与⊙O 交于点F ，弦AD 平分∠BAC ，DE ⊥AC ，垂足为E.(1)试判断直线DE 与⊙O 的位置关系，并说明理由；(2)若⊙O 的半径为2，∠BAC=60°，求线段EF 的长.第24题图【解题过程】（1）直线DE 与⊙O 相切.理由如下：第24题答图1如图所示，连接OD ，则OA=OD ，∴∠ODA=∠BAD.∵弦AD 平分∠BAC ，∴∠FAD=∠BAD.∴∠FAD=∠ODA ，∴OD ∥AF.又∵DE ⊥AC ，∴DE ⊥OD ，∴直线DE 与⊙O 相切.（2）连接BD ，∵AB 是⊙O 的直径，∴∠ADB=90°.第24题答图1∵AD 平分∠BAC，∠BAC=60°， ∴∠FAD=∠BAD=30°，∠B=60°， ∴∠DFE=∠B=60°. ∵⊙O 的半径为2， ∴AB=4，∴3223430cos =⨯=︒⋅=AB AD ， ∴3213230sin =⨯=︒⋅=AB DE ， ∴13360tan ==︒=DE EF .22．（2019·常德，22题，7分）如图6，⊙O 与△ABC 的AC 边相切于点C ，与AB 、BC 边分别交于点D 、E ，DE ∥OA ，CE 是⊙O 的直径． （1）求证：AB 是⊙O 的切线；（2）若BD ＝4，CE ＝6，求AC 的长．【解题过程】证明：（1）连接OD ，∵DE ∥OA ，∴∠AOC ＝∠OED ，∠AOD ＝∠ODE ，∵OD ＝OE ，∴∠OED ＝∠ODE ，∴∠AOC ＝∠AOD ，又∵OA ＝OA ，OD ＝OC ，∴△AOC ≌△AOD （SAS ），∴∠ADO ＝∠ACO ．∵CE 是⊙O 的直径，AC 为⊙O 的切线，∴OC ⊥AC ，∴∠ OCA ＝90°，∴∠ADO ＝＝90°，∴OD ⊥AB ， ∵OD 为⊙O 的半径，∴AB 是⊙O 的切线．图6CB（2）∵CE ＝6，∴OD ＝OC ＝3，∵∠BDO ＝90°，∴222BO BD OD =+，∵BD ＝4，∴OB＝5， ∴BC ＝8，∵∠BDO ＝∠ OCA ＝90°，∠B ＝∠B ，∴△BDO ∽△BCA ，∴BD OD BC AC =，∴438AC=，∴AC ＝6． 21．（2019·武汉）已知AB 是⊙O 的直径，AM 和BN 是⊙O 的两条切线，DC 与⊙O 相切于点E ，分别交AM 、BN于D 、C 两点（1） 如图1，求证：AB 2＝4AD ·BC（2） 如图2，连接OE 并延长交AM 于点F ，连接CF ．若∠ADE ＝2∠OFC ，AD ＝1，求图中阴影部分的面积图1 图2【解题过程】 证明：（1）如图1，连接OD ，OC ，OE ． ∵AD ，BC ，CD 是⊙O 的切线，∴OA ⊥AD ，OB ⊥BC ，OE ⊥CD ，AD ＝ED ，BC ＝EC ，∠ODE ＝12∠ADC ，∠OCE ＝12∠BCD ∴AD //BC ，∴∠ODE ＋∠OCE ＝12（∠ADC ＋∠BCD ）＝90°， ∵∠ODE ＋∠DOE ＝90°，∴∠DOE ＝∠OCE ． 又∵∠OED ＝∠CEO ＝90°， ∴△ODE ∽△COE ．∴OE ECED OE =，OE 2＝ED ·EC ∴4OE 2＝4AD ·BC ，∴AB 2＝4AD ·BC （2）解：如图2，由（1）知∠ADE ＝∠BOE ，∵∠ADE ＝2∠OFC ，∠BOE ＝∠2COF ， ∴∠COF ＝∠OFC ，∴△COF 等腰三角形。

中考总复习：圆的有关概念、性质与圆有关的位置关系—知识讲解（基础）【考纲要求】1. 圆的基本性质和位置关系是中考考查的重点，但圆中复杂证明及两圆位置关系中证明会有下降趋势，不会有太复杂的大题出现；2.中考试题中将更侧重于具体问题中考查圆的定义及点与圆的位置关系，对应用、创新、开放探究型题目，会根据当前的政治形势、新闻背景和实际生活去命题，进一步体现数学来源于生活，又应用于生活．【知识网络】【考点梳理】考点一、圆的有关概念及性质1．圆的有关概念圆、圆心、半径、等圆；弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧；三角形的外接圆、三角形的内切圆、三角形的外心、三角形的内心、圆心角、圆周角． 要点诠释：等弧：在同圆或等圆中，能够互相重合的弧叫做等弧．2．圆的对称性圆是轴对称图形，任何一条直径所在直线都是它的对称轴，圆有无数条对称轴；圆是以圆心为对称中心的中心对称图形；圆具有旋转不变性．3．圆的确定不在同一直线上的三个点确定一个圆．要点诠释：圆心确定圆的位置，半径确定圆的大小．4．垂直于弦的直径垂径定理 垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．推论 平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧．要点诠释：在图中(1)直径CD ，(2)CD ⊥AB ，(3)AM ＝MB ，(4)C C A B =，(5)AD BD =．若上述5个条件有2个成立，则另外3个也成立．因此，垂径定理也称“五二三定理”．即知二推三． 注意：(1)(3)作条件时，应限制AB 不能为直径．5．圆心角、弧、弦之间的关系定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量也相等．6．圆周角圆周角定理在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论1 在同圆或等圆中，相等的圆周角所对的弧也相等．推论2 半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径．要点诠释：圆周角性质的前提是在同圆或等圆中．考点二、与圆有关的位置关系1．点和圆的位置关系设⊙O的半径为r，点P到圆心的距离OP＝d，则有：点P在圆外⇔d＞r；点P在圆上⇔d＝r；点P在圆内⇔d＜r．要点诠释：圆的确定：①过一点的圆有无数个，如图所示．②过两点A、B的圆有无数个，如图所示．③经过在同一直线上的三点不能作圆．④不在同一直线上的三点确定一个圆．如图所示．2．直线和圆的位置关系（1）切线的判定切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线．(会过圆上一点画圆的切线)（2）切线的性质切线的性质定理圆的切线垂直于过切点的半径．（3）切线长和切线长定理切线长经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长．切线长定理从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角．要点诠释：直线l是⊙O的切线，必须符合两个条件：①直线l经过⊙O上的一点A；②OA⊥l．3．圆和圆的位置关系(1)基本概念两圆相离、相切、外离、外切、相交、内切、内含的定义．(2)请看下表：要点诠释：①相切包括内切和外切，相离包括外离和内含．其中相切和相交是重点．②同心圆是内含的特殊情况．③圆与圆的位置关系可以从两个圆的相对运动来理解．④“R-r”时，要特别注意，R＞r．【典型例题】类型一、圆的性质及垂径定理的应用1．已知：如图所示，在⊙O 中，弦AB 的中点为C ，过点C 的半径为OD ．(1)若AB ＝OC ＝1，求CD 的长；(2)若半径OD ＝R ，∠AOB ＝120°，求CD 的长.【思路点拨】如图所示，一般的，若∠AOB ＝2n °，OD ⊥AB 于C ，OA ＝R ，OC ＝h ，则AB ＝2R ·sin n °＝2n ·tan n °＝CD ＝R －h ；AD 的长180n R π=． 【答案与解析】解：∵半径OD 经过弦AB 的中点C ，∴半径OD ⊥AB ．(1)∵AB ＝AC ＝BC∵OC ＝1，由勾股定理得OA ＝2．∴CD ＝OD －OC ＝OA －OC ＝1，即CD ＝1.(2)∵OD ⊥AB ，OA ＝OB ，∴∠AOD ＝∠BOD ．∴∠AOB ＝120°，∴∠AOC ＝60°．∵OC ＝OA ·cos ∠AOC ＝OA ·cos60°＝12R ， ∴1122CD OD OC R R R =-=-=． 【总结升华】圆的半径、弦长的一半、弦心距三条线段组成一个直角三角形，其中一个锐角为弦所对圆心角的一半，可充分利用它们的关系解决有关垂径定理的计算问题．举一反三：【变式】在足球比赛场上，甲、乙两名队员互相配合向对方球门进攻，当甲带球冲到A 点时，乙已跟随冲到B 点(如图所示)，此时甲是自己直接射门好还是迅速将球回传给乙，让乙射门好呢?(不考虑其他因素)【答案】解：过M 、N 、B 三点作圆，显然A 点在圆外，设MA 交圆于C ，则∠MAN ＜∠MCN ．而∠MCN＝∠MBN，∴∠MAN＜∠MBN．因此在B点射门较好．即甲应迅速将球回传给乙，让乙射门．2．（2015•大庆模拟）已知AB是⊙O的直径，C是圆周上的动点，P是弧AC的中点．（1）如图1，求证：OP∥BC；（2）如图2，PC交AB于D，当△ODC是等腰三角形时，求∠A的度数．【思路点拨】（1）连结AC，延长PO交AC于H，如图1，由P是弧AC的中点，根据垂径定理得PH⊥AC，再根据圆周角定理，由AB是⊙O的直径得∠ACB=90°，然后根据OP∥BC；（2）如图2，根据圆心角、弧、弦的关系，以及三角形内角和等推论证来求得∠A的度数.【答案与解析】（1）证明：连结AC，延长PO交AC于H，如图1，∵P是弧AB的中点，∴PH⊥AC，∵AB是⊙O的直径，∴∠ACB=90°，∴BC⊥AC，∴OP∥BC；（2）解：如图2，∵P是弧AC的中点，∴PA=PC，∴∠PAC=∠PCA，∵OA=OC，∴∠OAC=∠OCA，∴∠PAO=∠PCO，当DO=DC，设∠DCO=x，则∠DOC=x，∠PAO=x，∴∠OPC=∠OCP=x，∠PDO=2x，∵∠OPA=∠PAO=x，∴∠POD=2x，在△POD中，x+2x+2x=180°，解得x=36°，即∠PAO=36°，当CO=CD，设∠DCO=x，则∠OPC=x，∠PAO=x，∴∠POD=2x，∴∠ODC=∠POD+∠OPC=3x，∵CD=CO，∴∠DOC=∠ODC=3x，在△POC中，x+x+5x=180°，解得x=（）°，即∠PAO=（）°．综上所述，∠A的度数为36°或（）°．【总结升华】本题考查了圆周角定理及其推论同时考查了等腰三角形的性质、垂径定理和三角形内角和定理．举一反三：【变式】（2015•温州模拟）如图，在Rt△ABC中，∠ACB=90°，AC=5，CB=12，AD是△ABC的角平分线，过A、C、D三点的圆与斜边AB交于点E，连接DE．（1）求BE的长；（2）求△ACD外接圆的半径．【答案】解：（1）∵∠ACB=90°，且∠ACB为圆O的圆周角（已知），∴AD为圆O的直径（90°的圆周角所对的弦为圆的直径），∴∠AED=90°（直径所对的圆周角为直角），又AD是△ABC的角平分线（已知），∴∠CAD=∠EAD（角平分线定义），∴CD=DE（在同圆或等圆中，相等的圆周角所对的弦相等），在Rt△ACD和Rt△AED中，，∴Rt△ACD≌Rt△AED（HL），∴AC=AE（全等三角形的对应边相等）；∵△ABC为直角三角形，且AC=5，CB=12，∴根据勾股定理得：AB==13，∴BE=13﹣AC=13﹣5=8；（2）由（1）得到∠AED=90°，则有∠BED=90°，设CD=DE=x，则DB=BC﹣CD=12﹣x，EB=AB﹣AE=AB﹣AC=13﹣5=8，在Rt△BED中，根据勾股定理得：BD2=BE2+ED2，即（12﹣x）2=x2+82，解得：x=，∴CD=，又AC=5，△ACD为直角三角形，∴根据勾股定理得：AD==，根据AD是△ACD外接圆直径，∴△ACD外接圆的半径为：×=．类型二、圆的切线判定与性质的应用3．如图所示，AB＝AC，O是BC的中点，⊙O与AB相切于点D，求证：AC与⊙O相切．【思路点拨】AC与⊙O有无公共点在已知条件中没有说明，因此只能过点O向AC作垂线段OE，长等于⊙O的半径，则垂足E必在⊙O上，从而AC与⊙O相切．【答案与解析】证明：连接OD，作OE⊥AC，垂足为E，连结OA．∵AB与⊙O相切于点D，∴OD⊥AB．∵AB＝AC，OB＝OC，∴∠1＝∠2，∴OE＝OD．∵OD为⊙O半径，∴AC与⊙O相切．【总结升华】如果已知直线经过圆上一点，那么连半径，证垂直；如果已知直线与圆是否有公共点在条件中并没有给出，那么作垂直，证半径．举一反三：【变式】如图所示，在Rt△ABC中，∠C＝90°，BC＝a，AC＝b，AB＝c．求△ABC的内切圆的半径．【答案】解：设△ABC的内切圆与三边的切点分别为D、E、F，根据切线长定理可得：AE＝AF，BF＝BD，CD＝CE，而AE+CE＝b，CD+BD＝a，AF+BF＝c，可求2a b c CE +-=． 连接OE 、OD ，易证OE ＝CE ． 即直角三角形的内切圆半径2a b c r +-=．4．如图所示，已知：△ABC 内接于⊙O ，点D 在OC 的延长线上，1sin 2B =，∠D ＝30°． (1)求证：AD 是⊙O 的切线；(2)若AC ＝6，求AD 的长．【思路点拨】（1）连接OA ，根据圆周角定理求出∠O 的度数，根据三角形的内角和定理求出∠OAD ，根据切线的判定推出即可；（2）得出等边三角形AOC ，求出OA ，根据勾股定理求出AD 的长即可．【答案与解析】(1)证明：连接OA ，∵1sin 2B =，∴∠B ＝30°． ∵∠AOC ＝2∠B ，∴∠AOC ＝60°．∵∠D ＝30°，∴∠OAD ＝180°－∠D －∠AOD ＝90°．∴AD 是⊙O 的切线．(2)解：∵OA ＝OC ，∠AOC ＝60°，∴△AOC 是等边三角形，∴OA ＝AC ＝6．∵∠OAD ＝90°，∠D ＝30°，∴AD AO ＝【总结升华】证明直线是圆的切线的方法：①有半径，证垂直；②有垂直，证半径．举一反三：【变式】如图所示，半径OA⊥OB，P是OB延长线上一点，PA交⊙O于D，过D作⊙O的切线交PO于C 点，求证：PC＝CD．【答案】证明：连接OD．∵CE切⊙O于D，∴OD⊥CE．∴∠2+∠3＝90°．∵OA⊥OB，∴∠P+∠A＝90°．∵OD＝OA，∴∠3＝∠A．．∴∠P＝∠2．又∵∠1＝∠2，∴∠P＝∠1．∴PC＝CD．类型三、切线的性质与等腰三角形、勾股定理综合运用5．已知AB是⊙O的直径，点P是AB延长线上的一个动点，过P作⊙O的切线，切点为C，∠APC 的平分线交AC于点D，求∠CDP的度数.【思路点拨】连接OC，根据题意，可知OC⊥PC，∠CPD+∠DPA+∠A+∠ACO=90°，可推出∠DPA+∠A=45°，即∠CDP=45°．【答案与解析】解：连接OC，∵OC=OA，，PD平分∠APC，∴∠CPD=∠DPA，∠A=∠ACO，∵PC为⊙O的切线，∴OC⊥PC，∵∠CPD+∠DPA+∠A+∠ACO=90°，∴∠DPA+∠A=45°，即∠CDP=45°．本题主要考查切线的性质、等边三角形的性质、角平分线的性质、外角的性质，解题的关键在于做好辅助线构建直角三角形，求证∠CPD+∠DPA+∠A+∠ACO=90°，即可求出∠CDP=45°．6．如图所示，AB是⊙O的直径，AF是⊙O的弦，AE平分∠BAF，交⊙O于点E，过点E作直线ED⊥AF于点D，交AB的延长线于点C．(1)求证：CD是⊙O的切线；(2)若DE＝4，sinC＝35，求AE的长．【思路点拨】构造半径、半弦、弦心距的直角三角形．【答案与解析】解：(1)证明：连接OE，BF，交于点G，则BF⊥AF，BF∥CD．∵OA＝OE，∴∠OAE＝∠OEA．∵∠OAE＝∠FAE，∴∠OEA＝∠FAE．∴OE∥AF，∵AF⊥DE，∴OE⊥CD．∴CD为⊙O的切线．(2)解：∵ BF∥DE，OE∥AF，∠D＝90°，∴四边形DEGF为矩形．∴BF＝2GF＝2DE＝8．∵BF∥CD，∴∠C＝∠ABF．可求得OA＝OB＝5，OG＝3．∴DF＝EG＝2，AF＝AB·sinC＝6．∴AD＝8，AE=．【总结升华】(1)通过挖掘图形的性质，将分散的条件sinC＝35，DE＝4，集中到一个直角三角形中，使问题最终得到解决；(2)本题第(2)问还可以适当改变后进行变式训练，如改为：若DF＝2，sinC＝35，求AE的长；(3)第(2)问还可以过O作OM⊥AF于M后得OM＝DE＝4，sin∠AOM＝sinC＝35加以解决.。

考点20.与圆有关的位置关系及计算（精讲）【命题趋势】与圆相关的位置关系也是各地中考数学中的必考考点之一，主要内容包括点、直线与圆的位置关系、切线的性质和判定、三角形的内切圆和外接圆三块，在解答题中想必还会考查切线的性质和判定，和直角三角形结合的求线段长的问题和三角函数结合的求角度的问题等知识点综合，考查形式多样，多以动点、动图的形式给出，难度较大。

关键是掌握基础知识、基本方法，力争拿到全分。

【知识清单】1：点、直线与圆的位置关系类（☆☆）1）点和圆的位置关系：已知⊙O的半径为r，点P到圆心O的距离为d，则：图1图2(1)d<r⇔点在⊙O内，如图1；(2)d=r⇔点在⊙O上，如图2；(3)d>r⇔点在⊙O外，如图3．解题技巧：掌握已知点的位置，可以确定该点到圆心的距离与半径的关系，反过来已知点到圆心的距离与半径的关系，可以确定该点与圆的位置关系。

2）直线和圆的位置关系：设⊙O的半径为r，圆心到直线l的距离为d，则直线和圆的位置关系如下：图1图2图3(1)d>r⇔相离，如图1；(2)d=r⇔相切，如图2；(3)d<r⇔相交，如图3。

2：切线的性质与判定（☆☆☆）1）切线的性质：（1）切线与圆只有一个公共点；（2）切线到圆心的距离等于圆的半径；（3）切线垂直于经过切点的半径。

解题技巧：利用切线的性质解决问题时，通常连过切点的半径，利用直角三角形的性质来解决问题。

2）切线的判定（1）与圆只有一个公共点的直线是圆的切线（定义法）；（2）到圆心的距离等于半径的直线是圆的切线（数量关系法）；（3）经过半径外端点并且垂直于这条半径的直线是圆的切线（判定定理法）。

切线判定常用的证明方法：①知道直线和圆有公共点时，连半径，证垂直；②不知道直线与圆有没有公共点时，作垂直，证垂线段等于半径。

3）切线长定理定义：在经过圆外一点的圆的切线上，这点和切点之间的线段的长，叫做这点到圆的切线长。

定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

百度文库：精选试题专题18 圆的基本性质和圆的有关位置关系学校：___________姓名：___________班级：___________一、选择题：（共4个小题）OACOBBOCOAB的度数为（中、弦=50°、则∥半径∠、∠】1．【2015巴中如图、在⊙）A．25° B．50° C．60° D．30°【答案】A．【解析】【考点定位】1．圆周角定理；2．平行线的性质．OABCDABBCDD点的切中、=120°、过2．【2015内江】如图、在⊙是直径、∠的内接四边形PDABPADP的度数为（线）与直线交于点、则∠A．40° B．35° C．30° D．45°【答案】C．【解析】BDDABCABADBABD=90是直径、∴∠试题分析：连接、∵∠=90°、∴∠=180°﹣∠=60°、∵DABPDADPABD=30°、故选C．是切线、∴∠=∠°﹣∠=30°、∵备战中考模拟试卷．百度文库：精选试题【考点定位】切线的性质．CANDAMMNOABMN为3．【2015雅安】如图所示、、连接是⊙的直径、作、点⊥、、垂足为点AM?ANAC BDFADCMABEAN=、交、现给出以下结论：①于点、连接于点上一点、且、交1BM?AM MFAEMANACMANMMOB +∠=；②∠；④∠=90°；③=∠．；⑤2）其中正确结论的个数是（A．2 B．3 C．4 D．5【答案】D．【解析】【考点定位】1．圆周角定理；2．垂径定理；3．压轴题．ECDOAADBCOBOAB于点、切⊙分别切⊙的在直径、于两点、、4．【2015达州】如图、为半圆OCOD、连接、下列结论：、22AO?S:SAD:ECBCDOCADCDDEOCOD、⑤、③=、④：：①∠=90°、②+=BOCΔAODΔ2CDDE?OD?）、正确的有（备战中考模拟试卷．百度文库：精选试题A．2个 B．3个 C．4个 D．5个．【答案】C 【解析】DEOD?ODCDEOEDOODCEDODOC、即=90°、又∠、∴∴∠=∠=∠∽△、∴△ODCD2CDDEOD??、选项⑤正确；BOCBAODAODADOACOBAOD+∠=90°、∴△=90°、∠、=∠∵∠+∠∽△=∠2SADADAD22AODΔ?)?(?()∴、选项③正确；2AOOBAOS BOCΔDEOD?COEODE、选项④错误；、∴同理△∽△OEOC C．故选．切线的性质；2．切线长定理；3．相似三角形的判定与性质；4．综合题【考点定位】1．个小题）（共4、二填空题：ABPCABOAOC是线段】是⊙的直径、点如图、线段°、点在圆上、∠=80崇左【5．2015APCPC．的度数是____度（写出一个即可）延长线上的一动点、连结、则∠备战中考模拟试卷．百度文库：精选试题度都可以．30°．只要小于40【答案】【解析】1APCAPCAOCOBCOBC°．只3040、故∠试题分析：∵∠=°．故答案为：∠＜=40°、∠＞∠240度都可以．要小于【考点定位】1．圆周角定理；2．三角形的外角性质．AO在格点上、则∠6．【2015天水】如图、边长为1的小正方形构成的网格中、半径为1的⊙ED．的正切值为1【答案】．2【解析】【考点定位】1．圆周角定理；2．锐角三角函数的定义；3．网格型．sinBOOOABCAD=7．【2015包头】如图、⊙的直径、若⊙是△的外接圆、的半径是4、是⊙1AC．、则线段的长为4备战中考模拟试卷．百度文库：精选试题【答案】2．【解析】【考点定位】1．圆周角定理；2．解直角三角形．AD CEOCABDO的中点、弦上一点、点是直径、点中、是8．【2015广元】如图、在⊙是⊙ABEDECGADCFBCPQAC．⊥、分别交于点、、过点、的切线交、连接的延长线于点、连接于点给出下列结论：BADABCGPGDPACQ的外心． =是△；①∠=∠③点；②其中正确结论是________ （只需填写序号）．【答案】②③．【解析】BADABC不一定相等、选项①错误；与∠试题分析：∠GDOGDPABDABOADBCFABAE、∴∠=∠=90°、∵、又的直径、∴∠∵为圆为圆⊥的切线、∴∠PADBAEPPAEBADAPEABDABDAPEAPE=∠∽△∠、∴∠=90°、∴∠=∠、又∠、又∠==∠、∴△GPDGDPGPDGPGD、选项②正确；、∴∠=∠=、∴ABACQPAQP 也就是这个直角三角的中点、=90°、如果能说明由是斜边是直径、则∠那么RtBQDBQDRtBCE中、∠8=90°-∠56∠、、而∠△形外接圆的圆心了．△7=中、∠=90°-BQDCPQPAPCP； =所以、则∠∠所以、∠所以∠、∠∠、∠6=5 8=7 =；由②知：∠3=5=4备战中考模拟试卷．百度文库：精选试题APCPQPPACQ的外心、选项③正确．= =是△、则点则正确的选项序号有②③．故答案为：②③．【考点定位】1．切线的性质；2．圆周角定理；3．三角形的外接圆与外心；4．相似三角形的判定与性质．三、解答题：（共2个小题）ABCOABACBDOABCDAO的、∥为⊙作⊙2015泸州9．【】如图、△的弦、且内接于⊙、过点、=AEDCEADBCF．与与的延长线交于点、交于点切线ABCE是平行四边形；（1）求证：四边形AECDOF 的长．（2）若=5=6、、求417．【答案】（1）证明见试题解析；（2）21【解析】AOBCHOFABCDNMEC=4、双向延长分别交、、（2）连接、根据切割线定理求得、交于点于点ABDCOFH 是等腰梯形、根据对称性、圆周角定理和垂径定理的综合应用证明△、证明四边形DMFBFN、并由勾股定理列式求解即可．∽△∽△AOBCHOFABCDNMAEO的切线、、∵是⊙（2）如图、连接、交于点、双向延长分别交、与点、备战中考模拟试卷．百度文库：精选试题22CECECDAEECDEAECE=46、（已舍去、∵==6、+5）、解得：（=5由切割线定理得、、∴=?ABDCABACBDCE=4、又根据对称性和==负数）、由圆的对称性、知四边形=是等腰梯形、且AOBCMNABDCOFxOHYFHzABBCC、、、∵垂径定理、得=垂直平分=6、、垂直平分=4、=、设=、11BCFHzOFHDMFBFNDBFDFBCFHzCF、∴=5、∴、易得△=+=﹣∽△=3﹣=3+、=∽△2252?zBNDMBFDF3?z22????、即、①、、yxOHOHOFOFxy313?z569y?xz???、∵、∴、解得：、①÷②得：②得：②、①+34z43?x2y13174417222222))(x??(x z?yx?xOF==．、∴、∴、∴432121【考点定位】1．切线的性质；2．平行四边形的判定．RtABCABCACACBCAB及=90°、中、∠【10．2015成都】如图、在、△的垂直平分线分别与DEFBFBCOBEFEBFEFG、的平分线交．⊙于点是△的延长线相交于点的外接圆、、、∠、且=HBDFH．交于点、、连接ABCEBF；≌△（1）求证：△BDO的位置关系、并说明理由；）试判断与⊙（2ABHGHB的值．、求 ?）若（3=1备战中考模拟试卷．百度文库：精选试题?2 2）相切、理由见试题解析；（．）【答案】（1）证明见试题解析；（【解析】BEABCEABCEBFEAEHDFACAE、=由≌△为线段=1的垂直平分线、得到、=得到（3）连接、、由△、22224EF?2AB??2BF?BC?1?AECE =、故、、即可得出结论进而得到=22HF2EF?EHFBH、得到为角平分线、易证△又因为为等腰直角三角形、故122222EF?HF??HFHB?HG?FHBGHF∽△．、得到、再由△2EBFCDEABFABCCBFFDAC、=90°、∴∠=90°、∴∠=90°、∵∠⊥=试题解析：（1）∵∠、∴∠ASAABCEBFEFBBCBFDCEDECBEF、∵）=（∵∠、∴△=∠、∴∠；=∠≌△CDBDADDFACDCBDOOB、∴∠是、∴（2）的垂直平分线、∴与⊙=相切．理由：连接=、∵OBEOBFEFBDBEOBFDBEOBOFOBFOFBDCEDCE=90°、∠+∠、、∵∠∵∠=∠∠=∠、、∵∴∠=、∴∠==OBDOBBDDBEOBE⊥与⊙∴∠、∴+∠相切；=90°、∴BEEBFABACAECEABCDFEAEH、的垂直平分线、∴、∴==1、∵△（3）连接=、≌△、∵为线段2?2AB2?BC?1BF?AECE∴=、、∴∴=??22222224??BEBF???1?1?EF EFHBHEBH5°、为角平分线、∴∠=4=、又∵∠22HF2EF?EHFHFGHEFHBFEBG、为等腰直角三角形、∴=∠∴∠=∠=45°、∠=45°、∴△12222EF??HF?FHBGHFGHFGHFFBGHFG、∴、∴△∽△∠、∵∠=∠=45°、∠∴=2备战中考模拟试卷．百度文库：精选试题HFHG22HG?HB?HF?2?2?HF?HG?HB．、∴、∴HFHB．圆周角定理；3定与性质；【考点定位】1．全等三角形的判2．相似三角形的判定与性质；4．探究型．备战中考模拟试卷．。