ANSYS结构分析指 复合材料

基于ANSYS有限元的复合材料传动轴失效分析基于ANSYS有限元的复合材料传动轴失效分析1. 引言复合材料在传动轴应用中越来越广泛，其具有较高的强度和刚度，以及较低的密度和惯性矩。

然而，由于其复杂的结构和复杂的加载条件，传动轴在运行过程中可能会发生失效。

因此，基于有限元分析的复合材料传动轴失效分析显得尤为重要。

2. 传动轴结构和材料传动轴主要有轴状结构，通常由多个复合材料组件组成，如纤维增强聚合物复合材料（FRP）和碳纤维增强复合材料（CFRP）。

这些材料的组合可以提供较高的轴向和环向强度，从而提供更好的传递力矩和转速。

3. 复合材料传动轴的失效模式复合材料传动轴的失效模式包括弯曲破坏、蠕变破坏、疲劳破坏和环剪切破坏等。

这些失效模式通常是由不同的应力和应变引起的，并在不同的加载条件下发生。

4. 有限元模型的建立基于ANSYS有限元软件，可以建立复合材料传动轴的三维有限元模型。

模型的几何形状和材料属性可以根据实际情况进行设定。

5. 材料参数的输入复合材料的性能参数需要根据实际测试数据进行输入。

这些参数包括纤维体积分数、纤维方向的弹性模量和剪切模量，基体材料的弹性模量和剪切模量等。

这些参数的准确性对于分析结果的准确性至关重要。

6. 边界条件和加载条件的设定在进行有限元分析之前，需要确定边界条件和加载条件。

边界条件通常包括固定支撑和固定约束等，以保证模型的稳定性。

加载条件通常包括径向和环向的力矩和转速等。

7. 模型分析和结果评价通过对复合材料传动轴模型进行有限元分析，可以得到应力和应变的分布图，以及轴的变形情况。

利用这些结果可以评估轴的失效模式和强度。

8. 参数敏感性分析和优化设计在分析过程中，可以对模型的几何形状和材料参数进行敏感性分析。

通过调整这些参数，可以优化设计，提高传动轴的性能和可靠性。

9. 模型验证和实验验证为了验证有限元模型的准确性，可以进行实验验证。

将有限元分析结果与实验结果进行对比和验证，以确定模型的准确性和可靠性。

Ａ一１３玻璃钢学会第十六届玻璃钢／复合材料学术年会论文集２００６年Ａｍｙｓ在复合材料结构优化设计中的应用覃海艺，邓京兰（武汉理工大学材料科学与工程学院，武汉４３００７０）摘要：优化设计方法在复合材料结构设计中起着十分重要的作用。

本文详细介绍了Ａｎｓｙｓ两种优化设计方法．目标函数最优设计和拓扑优化设计的过程，并运用目标函数最优设计方法对复合材料夹层结构进行了最优结构层合设计和运用拓扑优化设计方＇法对玻璃钢圆凳进行了最佳形状设计。

结果证明Ａｎｓｙｓ优化设计方法在复合材料结构设计中的有效性。

关键词：Ａｎｓｙｓ；优化设计方法；目标函数最优设计；拓扑优化设计；复合材料ｌ前言复合材料是由两种或多种性质不同的材料组成，具有比强度、比刚度高、耐疲劳性能好及材料与性能可设计强等特点，广泛应用于汽车、建筑、航空、卫生等领域。

复合材料通过各相组分性能的互补和关联获得优异的性能，因此复合材料各组分之间及材料整体结构的合理布置，充分发挥复合材料的性能已成为设计的关键所在…。

Ａｎｓｙｓ软件是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件。

优化设计是一种寻找确定最优设计方案的技术，Ａｎｓｙｓ强大的优化设计功能已广泛地应用于复合材料制品的结构设计心Ｊ。

２Ａｎｓｙｓ中的优化设计方法【３娟ｊ２．１目标函数最优设计“最优设计”是指满足所有的设计要求，而且所需（如重量、面积、体积、应力、费用等）的方案最小，即目标函数值最小。

也就是说，最优设计方案是一个最有效率的方案。

在Ａｎｓｙｓ中设计方案的任何方面都是可以优化的，如尺寸（如厚度）、形状（如过渡圆角的大小）、支撑位置、制造费用、自然频率、材料特性等。

实际上，所有可以参数化的Ａｎｓｙｓ选项都可以作优化设计。

目标函数最优设计是通过改变设计变量（自变量）的数值，使状态变量（设计变量的函数，因变量）在满足一定条件时，目标函数（因设计变量的改变而有所改变）的值最小。

目标函数最优设计的一般步骤为①生成循环所用的分析文件，该文件须包括整个分析的过程，并满足以下条件：参数化建立模型（ＰＲＥＩｙ７），对模型进行初次求解（ＳＯＬＵＴＩＯＮ），对初次求解的结果提取并指定状态变量和目标函数（ＰＯＳＴｌ／ＰＯＳＴ２６）；②在Ａｎｓｙｓ数据库里建立与分析文件中变量相对应的参数，这一步是标准的做法，但不是必须的（ＢＥＧＩＮ或ＯＰＴ）；③进入ＯＰＴ优化处理器，指定要进行优化设计循环的分析文件（ｏＰＴ）；④声明优化变量：指定哪些参数是设计变量，哪些参数是状态变量，哪个参数是目标函数；⑤选择优化工具或优化算法：优化算法是使单个函数（目标函数）在控制条件下达到最小值的传统算法，包括零阶算法和一阶算法；⑥指定优化循环控制方式，每种优化方法和工具都有相应的循环控制参数，比如最大迭代次数等；⑦进行优化分析；⑧查看设计序列结果（ＯＰＴ）和后处理（ＰＯＳＴｌ／ＰＯＳＴ２６）。

ANSYS复合材料仿真分析在ANSYS 中可以定义多种材料属性：主菜单-> preprocesser -> Material Prop -> Material Models -> 打开Define Material Model Behavior 对话框-> 顶部菜单中：Material -> New Model ... -> 弹出Define Material ID 对话框-> 定义更多的材料ANSYS复合材料仿真分析2009-05-23 23:31复合材料，是由两种或两种以上性质不同的材料组成。

主要组分是增强材料和基体材料。

复合材料不仅保持了增强材料和基体材料本身的优点，而且通过各相组分性能的互补和关联，获得优异的性能。

复合材料具有比强度大、比刚度高、抗疲劳性能好、各向异性、以及材料性能可设计的特点，应用于航空领域中，可以获得显著的减重效益，并改善结构性能。

目前，复合材料技术已成为影响飞机发展的关键技术之一，逐渐应用于飞机等结构的主承力构件中，西方先进战斗机上复合材料使用量已达结构总重量的25%以上。

飞机结构中，复合材料最常见的结构形式有板壳、实体、夹层、杆梁等结构。

板壳结构如机翼蒙皮，实体结构如结构连接件，夹层结构如某些薄翼型和楔型结构，杆梁结构如梁、肋、壁板。

此外，采用缠绕工艺制造的筒身结构也可视为层合结构的一种形式。

一.复合材料设计分析与有限元方法复合材料层合结构的设计，就是对铺层层数、铺层厚度及铺层角的设计。

采用传统的等代设计（等刚度、等强度）、准网络设计等设计方法，复合材料的优异性能难以充分发挥。

在复合材料结构分析中，已经广泛采用有限元数值仿真分析，其基本原理在本质上与各向同性材料相同，只是离散方法和本构矩阵不同。

复合材料有限元法中的离散化是双重的，包括了对结构的离散和每一铺层的离散。

这样的离散可以使铺层的力学性能、铺层方向、铺层形式直接体现在刚度矩阵中。

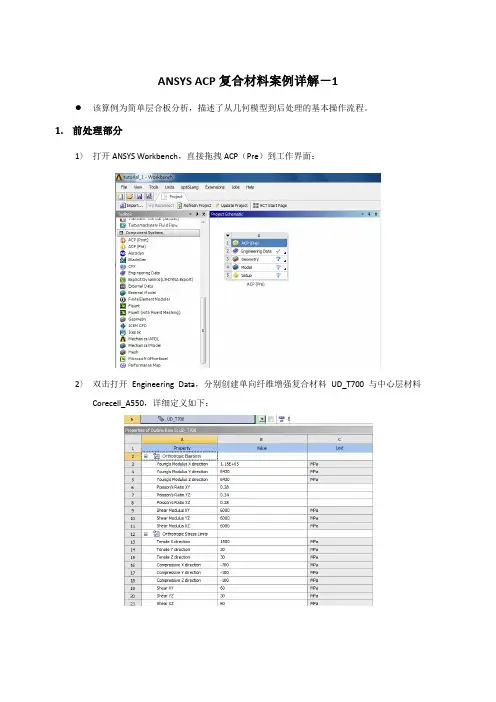
ANSYS ACP复合材料案例详解－1该算例为简单层合板分析，描述了从几何模型到后处理的基本操作流程。

1.前处理部分1〉打开ANSYS Workbench，直接拖拽ACP（Pre）到工作界面：2〉双击打开Engineering Data，分别创建单向纤维增强复合材料UD_T700与中心层材料Corecell_A550，详细定义如下：3〉返回Project，打开DesignModeler界面，设置单位制：4〉创建草图：5〉生成surface：6〉双击Model，打开Mechanical界面，设置厚度（此处厚度设置与铺层厚度无关）：7〉网格设置，生成网格：8〉更新流程：9〉双击或者右键-Edit打开ACP，可以看到，Engineering Data中的材料已经自动导入ACP：10〉注意单位设置，另外，ACP操作的每一步都需点击update图标才能更新：11〉创建层板与厚度（Fabrics）：12〉创建Stackups：13〉创建子层合板Sub Laminate：14〉创建铺层参考方向Rosetts：15〉定义Oriented Selection Sets，Point选择几何上的任一点即可，带[]部分，点击[]，再点击左侧相关项，即可自动导入；其中三Resetts代表的是铺层材料的0°方向，16〉查看参考方向，铺层零度方向，以及法向等可点击工具栏图标，如下：17〉右键点击Modeling Groups，创建三个层组，命名如下：18〉在sandwich_bottom下进行第一个层设置，命名为bottom_1，如下：19〉在sandwich_core下进行第二个层设置，命名为core_2，如下：20〉在sandwich_top下进行第三个层设置，命名为top_3，如下：21〉更新，层定义应该如下图所示：22〉返回workbench主界面，更新ACP流程：拖拽Static Structural流程到界面，将ACP的A5连接到Static Structural的B4，选择传递壳数据，连接好的流程见下图：23〉更新结构分析流程，双击打开Mechanical界面，四条边固定支撑，面上施加0.1Mpa压力，边界条件设置如图：2.求解，点击Solve直接求解3.后处理1〉拖拽ACP(Post)流程到ACP(Pre)上，连接效果如下：2〉将Static Structural的结果Solution与ACP后处理的Results部分连接，求解结果文件将被读入到后处理模块，如图：3〉更新流程，保证静态分析与ACP前处理流程上都是绿色对勾标志，刷新ACP后处理的Results部分:4〉双击打开ACP(Post)，在Solution分支下查看变形结果，设置如下：5〉变形结果云图：6〉接下来，配置组合失效准则，创建复合材料结构的失效结果图，两种材料的强度极限最初在Engineer Data中已经定义好。

基于Matlab和Ansys的复合材料板的分析本文通过使用MATLAB和ansys这两款软件对假设的复合材料层积板进行结构分析，对该材料同一点施加相同的力之后，观察比对其余相同节点的位移及和扭转角。

假定的复合材料分析的模型问题阐述：假设一个对称的、尺寸为的方形积层板，使用SI单位的碳纤维（Gr70%-Epoxy30%）为复材，铺层角为，共有4层，每层厚度为1mm。

在底端约束固定，于顶端中央的节点上施加一个Z 方向（垂直于复合材料板平面的方向为Z方向）的集中力，是对其进行静力分析。

基于MATLAB的复合材料层合板的分析复合材料板的刚度矩阵称为层积板。

常见的层积板是以正交材料堆叠而成。

层积板中各层的正交材料有，又是以高强度线状材料与基底材料压制而成。

在复合材料力学中，我们可以列出弹性剪切模量G、泊松比、杨氏模量E的关系方程式。

二维正交材料，各应变的关系式为：（1）（2）（3）若定义：（4）（5）则上式可写成：（6）其中（7）现在假设刚度矩阵为挠度矩阵的逆矩阵，也就是：（8）第（8）式可改写成：（9）其中刚度矩阵（10）又由于和的关系式，因此，也就是，刚度矩阵为对称矩阵。

通常我们将当做依参数，利用来定义。

、、和则当做独立参数，由材料性质直接决定。

二维的正交材料的坐标转换二维的正交材料的坐标变换如图1-1所示。

YX╮╮╮旋转图1-1 二维材料坐标变换在上图中1、2代表单层材料的坐标系统，而X、Y则代表积层板的空间坐标系统。

当各层的材料方向，与积层板的坐标方向不同时，需要将刚度矩阵作坐标变换，也就是以X、Y坐标表示。

其应力转换关系式为：（11）其中是转换矩阵。

假设两坐标系统之间的夹角为，矩阵可表示为：（12）上式化简为：（13）然后，将主轴应力，以空间的坐标轴表示。

（14）其中为转换矩阵的逆矩阵，其内容如下：（15）由于习惯上剪应变都是以角表示，而角的值为剪应变的两倍，因此：（16）上式可表示为，其中称为转换矩阵，其内容如下：（17）因此可将应变坐标写成：（18）上式可表示为，其中的内容如下;（19）将列出如下：或者（20）对于空间坐标系统，也可写成如上的关系式：（21）依照式（11）和式（12）应力的关系，将主轴应力旋转至空间坐标系统，可对应变做同样的转换：（22）将（20）与（21）两式代入（22）式，可得：（23）重新整理式（23），将等式两侧同乘可得：（24）由前述（10）式知，将等式左侧的主轴应力，依照（14）和（15）的关系，旋转至空间坐标系统，并将（24）式代入，可得：（25）上式可简化如下：（26）其中：=(27)层积板中各层的刚度可以用下式表示。

Ansys复合材料结构分析总结说明：整理自Simwe论坛，复合材料版块，原创fea_stud，大家要感他呀目录1#复合材料结构分析总结（一）-一概述篇5#复合材料结构分析总结（二）-一建模篇10#复合材料结构分析总结（三）分析篇13#复合材料结构分析总结（四）-优化篇做了一年多的复合材料压力容器的分析工作，也积累了一些分析经验，到了总结的时候了，回想起来，总最初采用I-deas，到MSC.Patran、Nastran，到最后选定Ansys为自己的分析工具，确实有一些东西值得和大家分享，与从事复合材料结构分析的朋友门共同探讨。

（一）概述篇复合材料是由一种以上具有不同性质的材料构成，其主要优点是具有优异的材料性能，在工程应用中典型的一种复合材料为纤维增强复合材料，这种材料的特性表现为正交各向异性，对于这种材料的模拟，很多的程序都提供了一些处理方法，在I-Deas、Nastran、Ansys中都有相应的处理方法。

笔者最初是用I-Deas下建立各项异性材料结合三维实体结构单元来模拟（由于研究对象是厚壁容器，不宜采用壳单元），分析结果还是非常好的，而且l-Deas强大的建模功能，但由于课题要求要进行压力容器的优化分析，而且必须要自己写优化程序，I-Deas的二次开发功能开放性不是很强，所以改为MSC.Patran, Patran提供了一种非常好的二次开发编程语言PCL（以后在MSC的版中专门给大家贴出这部分容），采用Patran结合Nastran的分析环境，建立了基于正交各项异性和各项异性两种分析模型，但最终发现，在得到的最后结果中，复合材料层之间的应力结果始终不合理，而模型是没有问题的（因为在I-Deas中，相同的模型结果是合理的），于是最后转向Ansys，刚开始接触Ansys,真有相见恨晚的感觉，丰富的单元库，开放的二次开发环境（APDL语言），下面就重点写Ansys的容。

在ANSY醉序中，可以通过各项异性单元（Solid 64 ）来模拟，另外还专门提供了一类层合单元（Layer Elements ）来模拟层合结构（Shell 99, Shell 91, Shell 181, Solid 46和Solid 191 ）的复合材料。

基于Matlab 和Ansys 的复合材料板的分析本文通过使用MATLAB 和ansys 这两款软件对假设的复合材料层积板进行结构分析，对该材料同一点施加相同的力之后，观察比对其余相同节点的位移及和扭转角。

假定的复合材料分析的模型问题阐述：假设一个对称的、尺寸为4.04.0⨯的方形积层板，使用SI 单位的碳纤维（Gr70%-Epoxy30%）为复材，铺层角为︒45，共有4层，每层厚度为1mm 。

在底端约束固定，于顶端中央的节点上施加一个Z 方向（垂直于复合材料板平面的方向为Z 方向）的集中力N F z 100=，是对其进行静力分析。

基于MATLAB 的复合材料层合板的分析 复合材料板的刚度矩阵称为层积板。

常见的层积板是以正交材料堆叠而成。

层积板中各层的正交材料有，又是以高强度线状材料与基底材料压制而成。

在复合材料力学中，我们可以列出弹性剪切模量G 、泊松比ν、杨氏模量E 的关系方程式。

二维正交材料，各应变的关系式为：）（2121111σνσε-E = （1））（2121221σσνε+-E = （2）1212121τγG =（3） 若定义： {}}{T 1221γεεε= （4）{}}{T 1221τσσσ= （5）则上式可写成：{}[]{}σεS = （6）其中[]⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡--=12222111211000101G E E E E S νν （7） 现在假设刚度矩阵[]Q 为挠度矩阵[]S 的逆矩阵，也就是：[][]1-=S Q （8）第（8）式可改写成：{}[]{}εσQ = （9）其中刚度矩阵[]⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡----=1221122211221121121222112100011011G E E E E Q νννννννννν （10） 又由于21ν和12ν的关系式121221E E νν=，因此2112Q Q =，也就是2112211211212211νννννν-=-E E ，刚度矩阵[]Q 为对称矩阵[][]TQ Q =。