《圆锥的认识和体积》习题

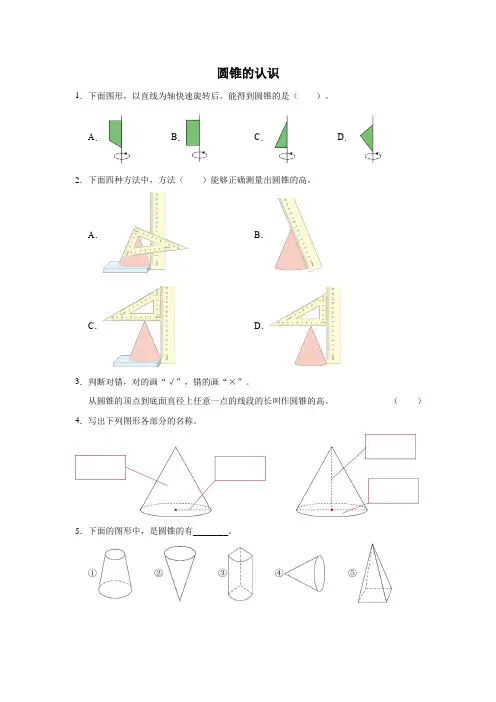
圆锥的认识1．下面图形，以直线为轴快速旋转后，能得到圆锥的是（）。

A．B．C．D．2．下面四种方法中，方法（）能够正确测量出圆锥的高。

A．B．C．D．3．判断对错，对的画“√”，错的画“×”。

从圆锥的顶点到底面直径上任意一点的线段的长叫作圆锥的高。

（）4．写出下列图形各部分的名称。

5．下面的图形中，是圆锥的有________。

①②③④⑤参考答案1．【答案】C【解析】选项A，直角梯形以下底所在的直线为轴旋转一周，得到的是圆柱和圆锥的组合体，不是圆锥，不符合题意；选项B，长方形以长所在的直线为轴旋转一周，得到的是圆柱，不是圆锥，不符合题意；选项C，直角三角形以一条直角边所在的直线为轴旋转一周，得到的是圆锥，符合题意；选项Ｄ，直角三角形，以斜边所在的直线为轴旋转一周，得到的是两个圆锥的组合体，不是圆锥，不符合题意。

2．【答案】C【解析】圆锥的高不能直接测量，我们可以根据“一组平行线之间的距离处处相等”来测量。

具体步骤如下：先把圆锥的底面放在水平放置的平板上；再用另一块平板（或一把尺子）水平地放在圆锥的顶点上面；最后用刻度尺竖直地量出平板（或尺子）和底面之间的距离。

通过观察，选项A，B，D均不符合要求，只有C正确。

3．【答案】×【解析】从圆锥的顶点到底面圆心的距离是圆锥的高。

题干说法错误。

4．【答案】【解析】圆锥是由1个底面和1个侧面组成的，它的底面是一个圆，侧面是一个曲面。

圆锥的顶点到底面圆心的距离叫作圆锥的高。

5．【答案】②④【解析】圆锥的特征：圆锥有1个底面和1个侧面，底面是一个圆，侧面是一个曲面，根据圆锥的这些特征判断即可。

图形①和图形③都有2个底面，不符合圆锥的特征，不是圆锥；图形⑤的底面不是圆，不符合圆锥的特征，不是圆锥；图形②和图形④都有1个底面和1个侧面，底面是一个圆，侧面是一个曲面，符合圆锥的特征，是圆锥。

圆锥的体积练习题圆锥是一种常见的几何图形，它由一个圆和一条连接圆心与圆上一点的曲线组成。

计算圆锥的体积是数学中的基本知识之一。

在本文中，我们将通过一些练习题来熟悉如何计算圆锥的体积，并掌握相关的计算方法。

练习题1：已知一个圆锥的半径为5cm，高度为12cm，求该圆锥的体积。

解答：根据圆锥的体积公式：V = 1/3 * π * r^2 * h，其中V表示体积，π表示圆周率，r表示半径，h表示高度。

将给定的数值代入公式中，得到 V = 1/3 * π * (5cm)^2 * 12cm = 1/3 * π * 25cm^2 * 12cm = 1/3 * π * 300cm^3 = 100πcm^3，约等于314.16cm^3。

练习题2：已知一个圆锥的底面半径为8cm，体积为150.72cm^3，求该圆锥的高度。

解答：将已知的数值代入圆锥的体积公式，得到 150.72cm^3 = 1/3 * π * (8cm)^2 * h，化简得 150.72cm^3 = 1/3 * π * 64cm^2 * h。

两边同时除以 1/3 * π * 64cm^2，得到 h = 150.72cm^3 / (1/3 * π * 64cm^2) = 3.14cm。

练习题3：一个圆锥体的底面半径是10cm，高度是15cm，如果将该圆锥切割成一个高度为3cm的小圆锥和一个高度为12cm的大圆锥，求这两个圆锥的体积之比。

解答：首先求出小圆锥的体积，根据体积公式，小圆锥的体积 V1 =1/3 * π * (10cm)^2 * 3cm = 1/3 * π * 100cm^2 * 3cm = 100πcm^3。

然后求出大圆锥的体积，大圆锥的高度是15cm，减去小圆锥的高度3cm，得到大圆锥的高度是12cm。

根据体积公式，大圆锥的体积 V2 = 1/3 * π * (10cm)^2 * 12cm = 1/3 * π * 100cm^2 * 12cm = 400πcm^3。

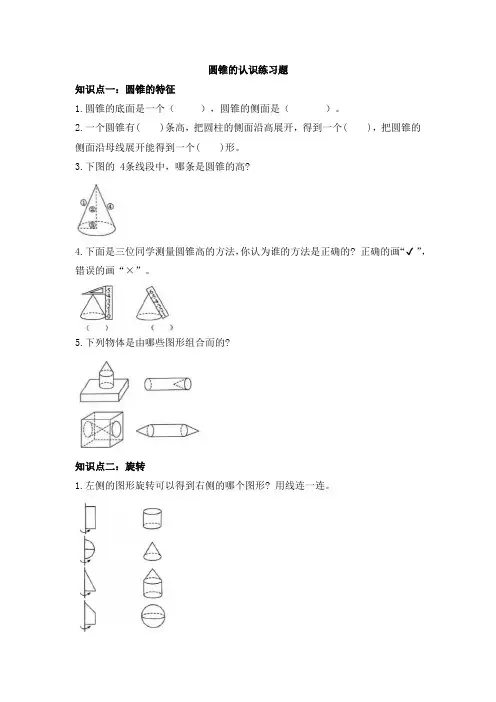
圆锥的认识练习题
知识点一：圆锥的特征
1.圆锥的底面是一个（），圆锥的侧面是（）。

2.一个圆锥有( )条高，把圆柱的侧面沿高展开，得到一个( )，把圆锥的侧面沿母线展开能得到一个( )形。

3.下图的 4条线段中，哪条是圆锥的高?
4.下面是三位同学测量圆锥高的方法，你认为谁的方法是正确的? 正确的画“✔”，错误的画“×”。

5.下列物体是由哪些图形组合而的?
知识点二：旋转
1.左侧的图形旋转可以得到右侧的哪个图形? 用线连一连。

3.以小棒所在直线为轴将三角形纸片旋转一周后能得到圆锥吗? 如果能，说出圆锥的高和底面半径。

2.将下面的三角形以 2cm的直角边所在直线为轴旋转一周，可以得到一个( )，
这个图形的高是( ) cm,底面周长是( ) cm。

知识点三：切圆锥
1、把一个圆锥形木块从顶点向底面垂直剖开，剖面是一个( )三角形。

圆锥体积专项练习60题(有答案过程)ok1.以AC为轴旋转一圈所形成的立体图形是一个圆锥体，其底面半径为AC的长度，高为BC的长度。

因此，圆锥体积为1/3π(AC^2)(BC)立方厘米。

2.以BC为轴旋转一周所得到的旋转体是一个圆锥体，其底面半径为BC的长度，高为AB的长度。

因此，圆锥体积为1/3π(BC^2)(AB)立方厘米。

3.将一个体积为150立方厘米的圆柱削成最大的圆锥，削去的体积为原圆锥体积减去最大圆锥体积。

最大圆锥的底面半径为圆柱的底面半径，高为圆柱的高。

因此，最大圆锥体积为1/3π(3^2)(6)立方厘米，削去的体积为原圆柱体积减去最大圆锥体积，即150-56.52=93.48立方厘米。

4.将圆柱削成等底等高的圆锥后，其底面半径和高均为原圆柱的底面半径和高。

设圆柱的底面半径和高分别为r和h，则原圆柱体积为π(r^2)(h)，后来的圆锥体积为1/3π(r^2)(h)。

根据题意，有π(r^2)(h)-1/3π(r^2)(h)=6.28，解得r=2，h=6.因此，原圆柱体积为π(2^2)(6)=24π立方分米，后来的圆锥体积为1/3π(2^2)(6)=8π立方分米。

5.将长方体削成最大的圆锥体，其底面半径为长方体的长和宽的一半的平均值，即(4/2+2/2)/2=1.5分米，高为长方体的高。

因此，最大圆锥体积为1/3π(1.5^2)(3)=3.375π立方分米。

6.将长方体削成最大的圆锥体，其底面半径为长方体的长和宽的一半的平均值，即(5/2+4/2)/2=2.25分米，高为长方体的高。

因此，最大圆锥体积为1/3π(2.25^2)(6)=22.5π/3立方分米。

7.将长1米的圆柱体平均切成3个同样大小的圆柱体后，每个圆柱体的高为原圆柱体的高，底面半径为原圆柱体底面半径的1/3.设原圆柱体的底面半径和高分别为r和h，则原圆柱体积为π(r^2)(h)，每个切割后的圆柱体积为1/3π((r/3)^2)(h)，总表面积增加60平方厘米，因此有2πrh+60=3π(r/3)^2+3π(r/3)h，解得r=3，h=10.因此，原圆柱体积为π(3^2)(10)=90π立方厘米，将其削成最大的圆锥体，其底面半径为3/2分米，高为10厘米。

圆锥体的体积经典练习题汇编1. 圆锥体的定义圆锥体是一种由圆锥面和一个尖点（顶点）组成的立体图形。

其中，顶点位于圆锥面之上。

2. 圆锥体的体积计算公式圆锥体的体积计算公式为：V = 1/3 * π * r^2 * h其中，V表示体积，π表示圆周率，r表示圆锥底面半径，h表示圆锥的高。

3. 练题练题1已知圆锥体的底面半径为5 cm，高为8 cm，求其体积。

解答根据圆锥体的体积计算公式，代入已知值可得：V = 1/3 * π * (5 cm)^2 * 8 cmV = 1/3 * π * 25 cm^2 * 8 cmV = 1/3 * π * 200 cm^3练题2已知圆锥体的体积为100 cm^3，底面半径为 3 cm，求其高度。

解答根据圆锥体的体积计算公式，代入已知值可得：100 cm^3 = 1/3 * π * (3 cm)^2 * h300 cm^3 = π * 9 cm^2 * hh = 300 cm^3 / (π * 9 cm^2)练题3已知圆锥体的体积为150 cm^3，高度为12 cm，求其底面半径。

解答根据圆锥体的体积计算公式，代入已知值可得：150 cm^3 = 1/3 * π * r^2 * 12 cm450 cm^3 = π * r^2 * 12 cmr^2 = 450 cm^3 / (π * 12 cm)r = √(450 cm^3 / (π * 12 cm))4. 总结本篇文档介绍了圆锥体的定义、体积计算公式以及三个经典练题。

通过练题的解答，读者可以了解如何利用圆锥体的体积计算公式来求解相关问题。

在求解过程中，注意单位的转化和计算的准确性。

计算结果均为近似值，取不同位数的近似结果时应注意精度问题。

希望本文档能对读者在学习和应用圆锥体的体积计算方面提供帮助。

如果有任何疑问或需要进一步的解答，请随时向作者提问。

圆锥体积专项练习60题(有答案)ok1.求以直角边AC为轴旋转一圈所得立体图形的体积。

2.以BC为轴旋转直角三角形ABC一周，求旋转体的体积。

3.将体积为150立方厘米的圆柱削成最大的圆锥，求削去的体积。

4.将一个圆柱削成等底等高的圆锥后，体积减少了6.28立方分米。

求原圆柱和圆锥的体积。

5.将长4分米，宽2分米，高3分米的长方体木料削成最大的圆锥体，求圆锥体的体积。

6.将长5分米，宽4分米，高6分米的长方体削成最大的圆锥，求圆锥的体积。

7.将长1米的圆柱体均匀切成3个同样大小的圆柱体后，表面积增加60平方厘米。

如果将原圆柱削成最大的圆锥体，求圆锥体的体积。

8.将底面直径为5厘米的圆锥完全浸没在底面半径为5厘米的圆柱形水箱中，水面上升了3厘米。

求圆锥的高。

9.将一个铅圆锥浸入底面周长为12.56米，高为6米的圆柱形水池，水面上升了3分米。

求铅圆锥的体积。

10.在底面直径为8厘米的圆柱形量杯内装有水，放入底面直径为2厘米的小圆锥形铁件后，水面上升了1厘米。

求小圆锥形铁件的高。

11.在一底面半径为10厘米的圆柱形杯子中盛有水，水里放着一个底面直径为10厘米的圆锥。

当圆锥取出时，水面下降了5厘米。

求圆锥的高。

12.一个底面积为8平方米，高为1.5米的圆锥形沙堆，用这些沙子在5米宽的路上铺2厘米厚的路面，能铺多少米？13.将长30厘米，宽10厘米，高8厘米的长方体铁块熔铸成底面积为100平方厘米的圆锥体铁块，求圆锥铁块的高。

14.一个长方体货车箱长4米，宽1.5米，高4米，装满沙子后卸下，沙子堆成一个底面积为多少平方米，高为2米的圆锥形。

15.将正方体的棱长之和为48厘米的铸件铸造成底面积为32平方厘米的圆锥体，求圆锥体的高。

16.在打谷场上有一堆底面周长为18.84米，高为1.5米的圆锥形稻谷堆，将稻谷装入内直径为6米的圆柱形粮囤内，求稻谷堆的高度。

17.一个高为12厘米的圆锥形中装满了水，将其倒入等底等高的圆柱形中，求水面的高度。

1.3 圆锥的认识与体积一、填空。

1．用同样多的材料，分别制作等底等高的圆柱体和圆锥体零件，那么做出的圆锥体零件的个数是圆柱体零件的个数的( )倍。

2．把一个圆柱削成一个最大的圆锥，如果圆锥体积是15立方分米，就要削去( )立方分米。

3．一个圆柱和一个圆锥的体积相等，圆柱的底面积是圆锥底面积的3倍，圆柱的高是圆锥的高的( )。

4．若一个圆柱与一个圆锥的体积和底面积都分别相等，那么，这个圆柱的高是圆锥高的( )。

二、判断(对的画“√"，错的画"X")。

1．圆锥的体积相当于圆柱体积的。

( ) 2．圆柱的体积比与它等底等高的圆锥的体积大。

( ) 3．3个同样的圆柱体铁块，可以熔铸成9个等底等高的圆锥体铁块。

( )三、计算下面图形的体积。

(单位:厘米)1.圆锥底面半径是6厘米，高是10厘米。

2.圆锥底面直径是10厘米，高是3厘米。

四、解决问题。

1．一个圆锥体零件，底面直径是0.4米，高是底面半径的3倍。

这个零件的体积是多少立方分米？2．有一个近似于圆锥形的小麦堆，测得底面周长是12.56米，高是0.75米，如果每立方米小麦重吨，这堆小麦大约有多少吨？(得数保留一位小数)3．一个圆锥体的体积是120立方厘米，底面积是15平方厘米，它的高是多少厘米？五、想一想、做一做1、把下面的图形旋转一周，可以得到哪个立体图形？用线连一连。

2．如图，用两个完全一样的圆柱体钢材外别制造圆锥体零件这两个零件哪个体积大？怎样证明？3．把一个底面直径为10厘米的圆锥体铅块完全放入底面半径为10厘米、装有水的圆柱体容器中，这时水面上升1厘米，这块圆锥体铅块的高是多少厘米？练习二一、1.3 2.30 3.194.13二、1.错 2.对 3.错三、1.V=376.8立方厘米2.V=75.8立方厘米四、1.V=25.12立方分米2.d=4米V=3.14立方米2.355吨3.h=24厘米五、1. 略2.一样大证明略3.12厘米。

西师大版数学六年级下册2.2 圆锥认识及体积练习卷姓名:________ 班级:________ 成绩:________小朋友，带上你一段时间的学习成果，一起来做个自我检测吧，相信你一定是最棒的！一、选择题1 . 在②号位置看到的图形是（）A．B．C．2 . 一个长方体的底面周长与高分别与一个圆柱体的底面周长和高相等，那么体积（）A．圆柱体B．圆柱体大C．相等D．无法确定3 . 等底等高的圆柱的体积是圆锥体积的（）A．4倍B．3倍C．D．4 . 一个圆柱和一个圆锥底面一样大，要使它们都体积相等，圆柱的高应该是圆锥高的（）A．3倍B．C．5 . 两块同样的长方形纸板，卷成形状不同的圆柱（接头处不重叠），并装上两个底面，那么制成的两个圆柱体的（）相等。

A．底面积B．侧面积C．表面积二、填空题6 . 一个直角三角形的两条直角边分别是3厘米和6厘米，以3厘米的直角边为轴旋转一周，可以得到一个，它的体积是立方厘米．7 . 把一个圆柱体木料削成一个最大的圆锥，要削掉36立方分米的木料，这个圆锥的体积是（______）立方分米，削去部分是圆柱体积的（______）。

8 . 把一个棱长为3厘米的方体铁块熔铸成一个底面积是9平方厘米的圆锥形铁块，原来正方体铁块的体积是（_____）立方厘米，这个圆锥形铁块的高是（____）厘米。

9 . 一个圆锥的底面半径是9厘米，高是1分米，它的体积是：3.14×9×9××1=84.78（立方厘米）．．（判断对错）10 . 一个圆锥，它的底面半径和高与一个正方体的棱长相等，如果正方体的体积是a立方厘米，那么圆锥的体积是立方厘米．11 . 如图，先把一张长10cm，宽6cm的长方形纸板沿对角线分成两个完全相同的直角三角形．再以其中一个直角三角形较长的直角边所在直线为轴，将纸板快速转动，可以形成一个体，它的体积是cm3．12 . 如图，转动长方形ABCD，当以长边（_____）为轴旋转时，底面半径是（_____）cm，当以短边（_____）为轴旋转时，底面半径是（_____）cm。

2.2《圆锥认识及体积》练习一、填空1.在是圆锥的图形下面打“√”。

2.（1）一个圆柱和一个圆锥等底等高，圆锥的体积比圆柱的体积少0.8立方分米，那么，圆锥的体积是（）立方分米，圆柱的体积是（）立方分米。

（2）一个圆柱和一个圆锥等底等高，它们的体积一共是60立方厘米，那么，圆柱的体积是（）立方厘米，圆锥的体积是（）立方厘米。

（3）将一根长5米的圆柱形木料锯成4段，表面积增加60平方分米，这根木料的体积是（）立方米。

（4）将棱长为6分米的正方体木块削成一个最大的圆锥，这个圆锥的体积是（）立方分米，一共削去（）立方分米的木料。

（5）一个圆锥的底面周长是12.56分米，高是6分米，它的体积是（）立方分米。

（6）圆锥的底面半径是1厘米，体积是6.28立方厘米，这个圆锥的高是（）厘米。

3.选一选。

（1）圆柱的体积比与它等底等高的圆锥的体积大（）。

①2倍②1倍③13④23（2）一个圆锥的体积是a立方厘米，和它等底等高的圆柱的体积是（）立方厘米。

a ②a ③3a ④2a①13（3）一个高是2分米，底面半径为6厘米的圆锥的体积是（）立方厘米。

①75.36 ②753.6 ③2260.8 ④226.08（4）把一个圆柱削成一个最大的圆锥，如果圆锥体积是72立方厘米，就要削去其他部分（）立方厘米。

①72 ②144 ③216 ④24（5）从不同方向看一个立体图形的形状如下，这个图形是（）。

①圆锥②圆柱③正方体④长方体4.计算下面图形的体积。

（单位：厘米）升级跷跷板5.有一个粮囤，上面是圆锥形，下面是圆柱形，底面直径是2米，圆柱高1.8米，圆锥高是0.6米，如果每立方米粮食重700千克，这个粮囤能装粮多少千克？6.汶川大地震后，急需一批帐篷，山东某帐篷厂想生产一批帐篷（如下图）支援灾区。

请你帮忙算一下：（1）这种帐篷的占地面积是多少平方米？（2）这种帐篷里面的空间有多大？智慧摩天轮7.等底等高的圆柱和圆锥的体积相差16立方米，圆锥的体积是多少立方米？8.把一个体积是282.6立方厘米的铁块熔铸成一个高是9厘米的圆锥形机器零件，这个圆锥形机器零件的底面积是多少平方厘米？9.一个近似圆锥形的麦堆，底面周长为12.56米，高为1.5米，每立方米小麦重900千克，这堆小麦一共重多少千克？10.在一个底面直径是2021的圆柱形容器里，放入一块底面半径为3厘米的圆锥形铁块，全部浸没在水中，这时水面上升了0.3厘米。

人教版六年级数学下册《3.2圆锥的认识》课时练习题（含答案）一、填空题1．下面一排图形各自绕轴旋转一周后会得到哪些图形？( )( )( )2．圆锥的底面是一个( )，从圆锥的( )到( )的距离是圆锥的高。

3．标出下面圆锥的底面、侧面和高。

4．一个底面直径10厘米、高15厘米的圆锥形木料，过圆锥形木料的顶点把圆锥垂直于底面切割成形状、大小完全相同的两块，表面积增加了( )平方厘米。

5．圆锥的侧面展开图是一个( )，将圆锥沿高展开，所得到的横截面是一个( )。

二、判断题6．圆锥有无数条高．( )7．图旋转一周可以得到。

( )8．从圆锥的顶点沿着高将它切成两半，所得到的截面是等腰三角形。

( )9．圆锥的高和圆柱的高都有无数条。

( )10．一个圆锥的底面半径和高相等，过顶点和直径把这个圆锥切开，切面一定是等腰直角三角形。

( )三、选择题11．从圆锥的顶点向底面做垂直切割，所得到的截面是一个（）。

A．长方形B．圆C．三角形D．等腰三角形12．将一个圆锥沿高切成两部分，切面是（）。

A．扇形B．等边三角形C．等腰三角形D．长方形13．如图所示，把一张三条边长分别是5cm、12cm和13cm的直角三角形硬纸贴在木棒上，快速转动木棒，转出的圆锥高是（）cm，底面半径是（）cm。

A．5，12 B．12，5 C．13，5 D．12，1314．小华从正面看一个几何体，所看到的的形状是正方形，这个几何体不可能是（）。

A．长方体B．正方体C．圆柱D．圆锥15．把一个圆锥沿底面直径到顶点切开，切面是一个（）。

A．圆形B．三角形C．扇形D．无法确定四、连线题16．下面图形转动后会形成什么图形？五、解决问题17．把一个圆锥体浸没在底面周长为18.84厘米，高为10厘米的圆柱形容器里，这时水面高度升高了3厘米，这个圆锥体的体积是多少立方厘米？18．将一个底面直径18厘米，高是8厘米的圆锥形木块分成形状、大小完全相同的两个木块后，表面积比原来增加了多少平方厘米？19．一个圆锥的底面周长是18.84厘米，高是4厘米．从圆锥的顶点沿着高将它切成两半后，表面积比原来的圆锥增加了多少平方厘米？参考答案1．圆锥##圆锥体圆柱##圆柱体球##球体2．圆顶点底面圆心3．4．1505．扇形等腰三角形6．×7．×8．√9．×10．√11．D12．C13．B14．D15．B16．17．18.84÷3.14÷2＝6÷2＝3（厘米）3.14×32×3＝3.14×9×3＝3.14×27＝84.78（立方厘米）答：这个圆锥体的体积是84.78立方厘米。

人教版六年级数学下册
第3单元《圆锥的体积》课后练习题（附答案）
3.6 圆锥的体积
1.填一填。

（1）一个圆柱的体积是28.26立方米，与它等底等高的圆锥的体积是（）立方米。

（2）一个圆锥的体积是47.1立方厘米，与它等底等高的圆柱的体积是（）立方厘米。

2.计算出下图圆锥的体积。

3.把一个底面半径1厘米，高9厘米的圆柱表木块加工成一个最大的圆锥。

圆锥的体积是多少？要削去多少立方厘米的木料？
4.一个底面半径是6厘米的圆柱形玻璃器皿里装有一部分水，水中浸没着一个高9厘米的圆锥体铅锤。

当铅锤从水中取出后，水面下降了0.5厘米。

这个圆锥体的底面积是多少平方厘米？（π取3.14）
答案:
1．（1）9.42 （2）141.9 2．×3.14×22×3=12.56dm3 3．×3.14×12×9=9.42 cm3
×3.14×12×9=18.84cm3 4．3.14×62×0.5÷÷9=18.84cm2。

小学几何：圆锥的认识知识点及例题一、圆锥的认识1、圆锥的组成2、测量圆锥高的方法第一步：把圆锥的底面放平；第二步：用一块平板水平放在圆锥的顶点上面；第三步：竖直地量出平板和圆锥底面之间的距离。

二、圆锥体积的计算圆锥的体积等于与它等底等高的圆柱体积的圆锥的体积=×底面积×高V=Sh三、方法应用题分析：1）题意分析：本题主要考查同学们对于圆锥体积计算公式的应用。

2）解题思路：本题可以先根据圆锥体的底面周长求出底面半径，进而求出其底面积，然后求出这个小麦堆一共有多少立方米（体积)，最后与750相乘，即可求出小麦的重量。

解答：r===4（m)V=πr²·h=×3.14×42×3=50.24（m3）这堆小麦的重量为：750×50.24=37680（kg）答：这堆小麦重37680千克。

思考：求圆锥的体积，要根据具体条件而定。

如果已知圆锥的底面积和高可以直接应用公式：V=S·h，求出体积；如果给出的是底面半径、直径或周长和高，就要先求出底面积，再应用公式来求体积。

分析：1）题意分析：本题主要考查同学们对于圆锥体积公式的运用情况。

2）解题思路：本题要求圆锥的底面积，可以列方程求解，也可直接利用公式来求出底面积。

解答：解法1：设圆锥的底面积为平方厘米。

×6=542=54=27解法2：S=3V÷h=3×54÷6=27（平方厘米）答：圆锥的底面积是27平方厘米。

思考：如果已知圆锥的体积和底面积，求高可以用以下公式：h=V÷÷S或h=3V÷S；同理，如果已知圆锥的体积和高，求底面积，可以根据公式S=3V÷h求出。

分析：1）题意分析：本题主要考查同学们运用圆柱与圆锥之间的关系解决生活中的问题的能力。

2）解题思路：要使削成的圆锥的体积最大，则圆锥与圆柱需等底等高，削成的圆锥的体积等于圆柱体积的，削去的部分是圆柱体积的。

圆锥体的认识练习题
1. 请简要解释什么是圆锥体。

圆锥体是一个由一个圆和与这个圆共面并以圆心为一端点的线段连接起来的几何图形。

2. 圆锥体的所有顶点都在一个平面上吗？为什么？
是的，圆锥体的所有顶点都在一个平面上。

这是因为圆锥体的顶点是由圆和与圆共面的线段连接而成的，所以它们都在同一个平面上。

3. 如何计算圆锥体的体积？
圆锥体的体积可以通过以下公式计算：V = (1/3) * π * r^2 * h，其中V表示圆锥体的体积，π是一个数值（约等于3.），r表示圆锥体底面的半径，h表示圆锥体的高度。

4. 如何计算圆锥体的侧面积？
圆锥体的侧面积可以通过以下公式计算：A = π * r * l，其中A
表示圆锥体的侧面积，r表示圆锥体底面半径，l表示圆锥体的斜高。

5. 圆锥体与其他几何体有哪些相似之处？
圆锥体与其他几何体有一些相似之处。

例如，像圆柱体和球体
一样，圆锥体也有半径和高度这两个重要的特征。

此外，圆锥体也
可以通过旋转一个形状（如一个三角形）来得到，就像圆柱体可以
通过旋转一个矩形而得到。

这些练习题旨在帮助您更好地理解圆锥体的概念和相关计算。

希望您能够通过解答这些问题来加深对圆锥体的认识和掌握。

圆锥体积练习题及答案圆锥体积练习题及答案圆锥体积是数学中的一个重要概念，它常常在几何题中出现。

掌握圆锥体积的计算方法对于解题非常有帮助。

下面将给出一些圆锥体积的练习题及答案，希望能够帮助大家更好地理解和应用这一知识点。

练习题一：一个圆锥的底面半径为3cm，高度为5cm，求其体积。

解答一：圆锥的体积公式为V = 1/3 * π * r^2 * h，其中V表示体积，π表示圆周率，r 表示底面半径，h表示高度。

代入题目给出的数值，得到V = 1/3 * π * 3^2 * 5 = 15π cm^3。

所以该圆锥的体积为15π cm^3。

练习题二：一个圆锥的体积为36π cm^3，底面半径为4cm，求其高度。

解答二：根据圆锥的体积公式V = 1/3 * π * r^2 * h，可以得到h = 3V / (π * r^2)。

代入题目给出的数值，得到h = 3 * 36π / (π * 4^2) = 27 / 2 cm。

所以该圆锥的高度为27 / 2 cm。

练习题三：一个圆锥的底面半径为6cm，体积为72π cm^3，求其高度。

解答三：根据圆锥的体积公式V = 1/3 * π * r^2 * h，可以得到h = 3V / (π * r^2)。

代入题目给出的数值，得到h = 3 * 72π / (π * 6^2) = 6 cm。

所以该圆锥的高度为6 cm。

练习题四：一个圆锥的底面半径为8cm，高度为10cm，求其体积。

解答四：根据圆锥的体积公式V = 1/3 * π * r^2 * h，可以代入题目给出的数值，得到V= 1/3 * π * 8^2 * 10 = 213.333π cm^3。

所以该圆锥的体积为213.333π cm^3。

练习题五：一个圆锥的体积为100π cm^3，高度为12cm，求其底面半径。

解答五：根据圆锥的体积公式V = 1/3 * π * r^2 * h，可以得到r = √(3V / (π * h))。

六年级数学圆锥的认识和体积试题1.有一个圆锥体沙堆，底面积是3.6平方米，高2米。

将这些沙铺在一个长4米，宽2米的长方体沙坑里，能铺多厚？【答案】0.3米【解析】本题是考察圆锥体积的转化问题。

S=3.6平方米，h=2米V锥= V=sh÷3=3.6×2÷3=2.4（立方米）h=2.4÷4÷2=0.3（米）答：能铺0.3米厚。

2.一块长方体的铅块，长2m，宽1.5m，高0.8m，现把它熔铸成底面积为9dm2，高为2m的圆锥体．能熔铸成多少个这样的圆锥体？【答案】9平方分米=0.09平方米，2×1.5×0.8÷（×0.09×2），=2.4÷0.06，=40（个）；答：能熔铸成40个这样的圆锥体。

【解析】先依据长方体的体积公式求出铅块的体积，再据圆锥的体积公式求出圆锥体的体积，用长方体的体积除以圆锥体的体积，即可得解。

3.（5分）（2013•甘州区校级模拟）一个圆锥形小麦堆，高1米，底面周长18.84米，如果每立方米小麦重0.75吨，这堆小麦大约有多少吨？【答案】答：这堆小麦大约有7.065吨【解析】根据圆锥的底面周长求出底面半径，再代入圆锥的体积公式求出体积，进而求得重量即可．解：r=C÷2π，=18.84÷（2×3.14），=3（米）；=πr2h，V锥=×3.14×32×1，=×3.14×9×1，=9.42（立方米）；9.42×0.75=7.065（吨）；答：这堆小麦大约有7.065吨．点评：此题考查了圆锥的体积公式的实际应用．4.（2014•重庆模拟）如果一个圆锥体的底面半径扩大2倍，高缩小为原来的一半，它的体积是原来体积的（）A.2倍B.一半C.不变【答案】A【解析】根据圆锥的体积公式，v=sh÷3，圆锥体的底面半径扩大2倍，它的底面积就扩大4倍，因为圆的半径扩大2倍圆的面积就扩大4倍，高缩小为原来的一半，由此得解．解：圆锥体的底面半径扩大2倍，它的底面积就扩大4倍，又知高缩小为原来的一半，由此得此它的体积就扩大2倍．故选A．点评：此题的解答主要根据因数与积的变化规律来解答，5.（3分）一个近似的圆锥形沙堆，底面积是12.56平方米，高3米．如果每立方米沙重2吨，这堆沙大约重多少吨？（得数保留一位小数）【答案】答：这堆沙大约重25吨．【解析】根据圆锥的体积公式V=sh，求出圆锥形沙堆的体积，进而求出沙堆的重量．解：×12.56×3×2=12.56×1×2=25.12≈25（吨）答：这堆沙大约重25吨．点评：此题主要考查了圆锥的体积公式的实际应用，注意计算时不要忘了乘，另外还要注意用四舍五入法求近似值．6.（1分）（2014•永宁县）一个盛满水的圆锥形容器，水深18厘米，将水全部倒入和它等底等高的圆柱形容器里，水深是厘米．【答案】6【解析】圆锥的体积=×底面积×高，圆柱的体积=底面积×高，再据这些水的体积不变，即可求出倒入圆柱中的水的高度．解：设圆锥的底面积为S，圆柱的高为h，则圆锥的体积为S×18=6S（立方厘米），因为圆柱与圆锥等底等高，所以圆柱中水的高为：6S÷S=6（厘米），答：水深为6厘米．故答案为：6．点评：此题考查了圆锥与圆柱体积的计算方法，关键是明白：水的体积不变．7.下面（）图形旋转就会形成圆锥。

（完整版）《圆锥的认识及其体积》练习题《圆锥的认识及其体积》练习题教学目标：1、认识圆锥，圆锥的高和侧面，掌握圆锥的特征，会看圆锥的平面图，会正确测量圆锥的高。

2、探索出圆锥体积和圆柱体积之间的关系，初步掌握圆锥体积的计算公式，并能运用公式正确地计算圆锥的体积，解决实际生活中有关圆锥体积计算的简单问题。

3、培养学生的自主探索意识，激发学生强烈的求知欲望。

教学重、难点：1、正确理解圆锥的组成。

2、正确探索出圆锥体积和圆柱体积之间的关系。

教学内容：圆锥的认识及其体积的应用【知识点讲解】1.圆锥的特征：（1）圆锥有一个顶点，它的底面是一个圆。

（2）圆锥有一个曲面，这个曲面叫做侧面。

（3）从圆锥的顶点到底面圆心的距离叫做高。

沿着曲面上的线都不是圆锥的高。

（4）由于圆锥只有一个顶点，所以圆锥只有一条高。

（5）圆锥的侧面展开后是一个扇形.2.圆锥的体积：圆锥的体积＝31×圆柱的体积＝31×底面积×高，字母公式：V ＝31Sh【巩固练习】一.填空1.一个圆柱和一个圆锥的底面积和高分别相等，圆锥的体积是圆柱体积的（），圆柱的体积是圆锥体积的（）．2.一个圆锥体底面直径和高都是6厘米，它的体积是( )立方厘米。

3.一个圆锥体的底面周长是12.56分米,高是6分米,它的体积是( )立方分米。

4.等底等高的圆柱和圆锥的体积相差16立方米，这个圆柱的体积是（）立方米，圆锥的体积是（）立方米。

5.一个圆锥的体积是7.2立方米，与它等底等高的圆柱的体积是（）立方米。

6.将棱长为6分米的正方体木块，削成一个最大的圆锥体，这个圆锥的体积是（）立方分米，一共削去（）立方分米的木料7..一个圆柱和圆锥等底等高，它们的体积一共60立方厘米，那么，圆柱的体积是（）立方厘米，圆锥的体积是（）立方厘米。

8.一个圆柱的底面半径是3厘米，高是2厘米，这个圆柱的底面周长是（）厘米，底面积是（）平方厘米，侧面积是（）平方厘米，表面积是（）平方厘米，体积是（）立方厘米，和它等底等高的圆锥的体积是（）立方厘米。